Monolithically Integrated Michelson Interferometer Using an InGaAs/InAlAs Quantum Cascade Laser at λ = 4 µm
Abstract
:1. Introduction
2. Materials and Methods
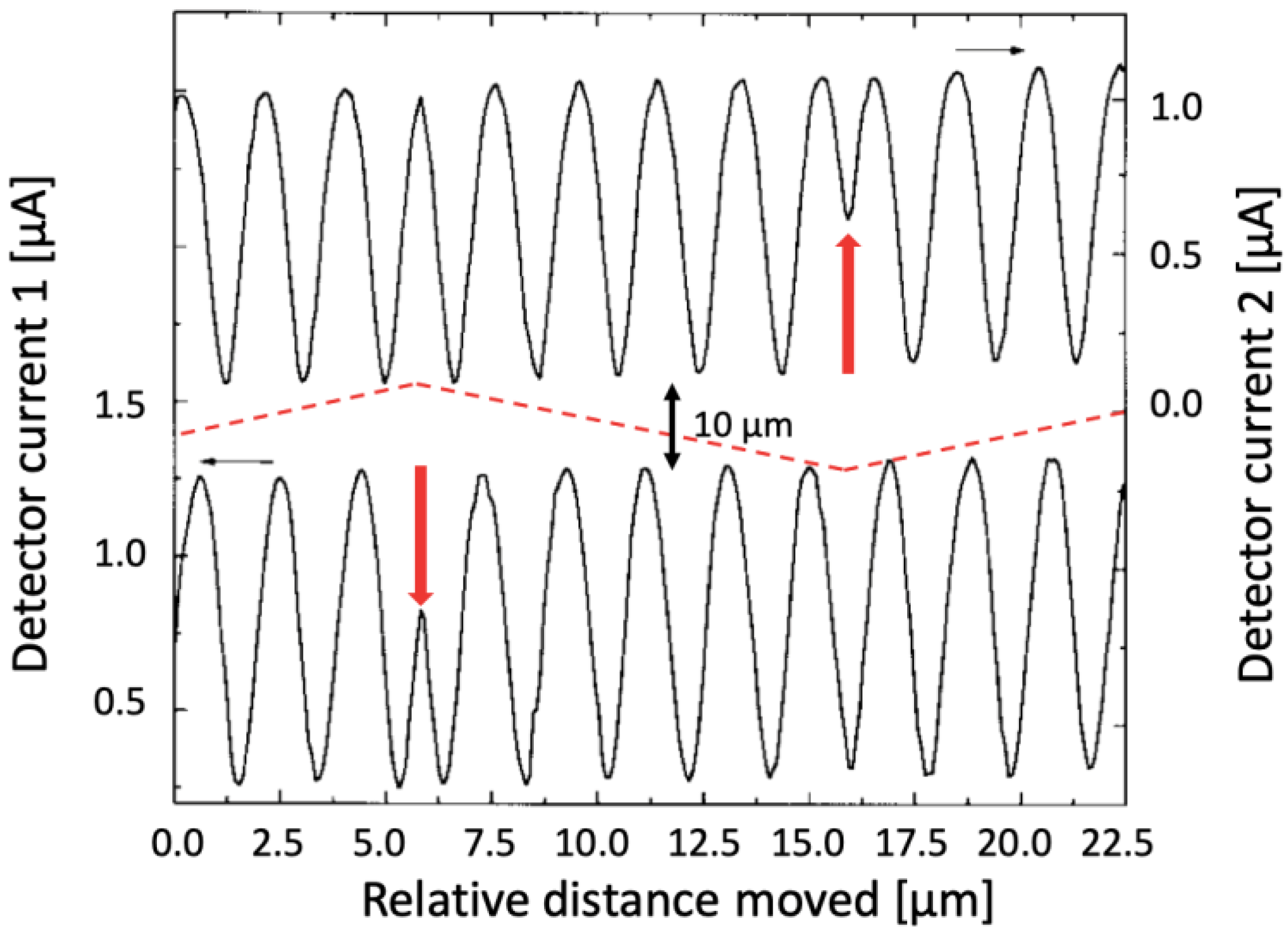
3. Results
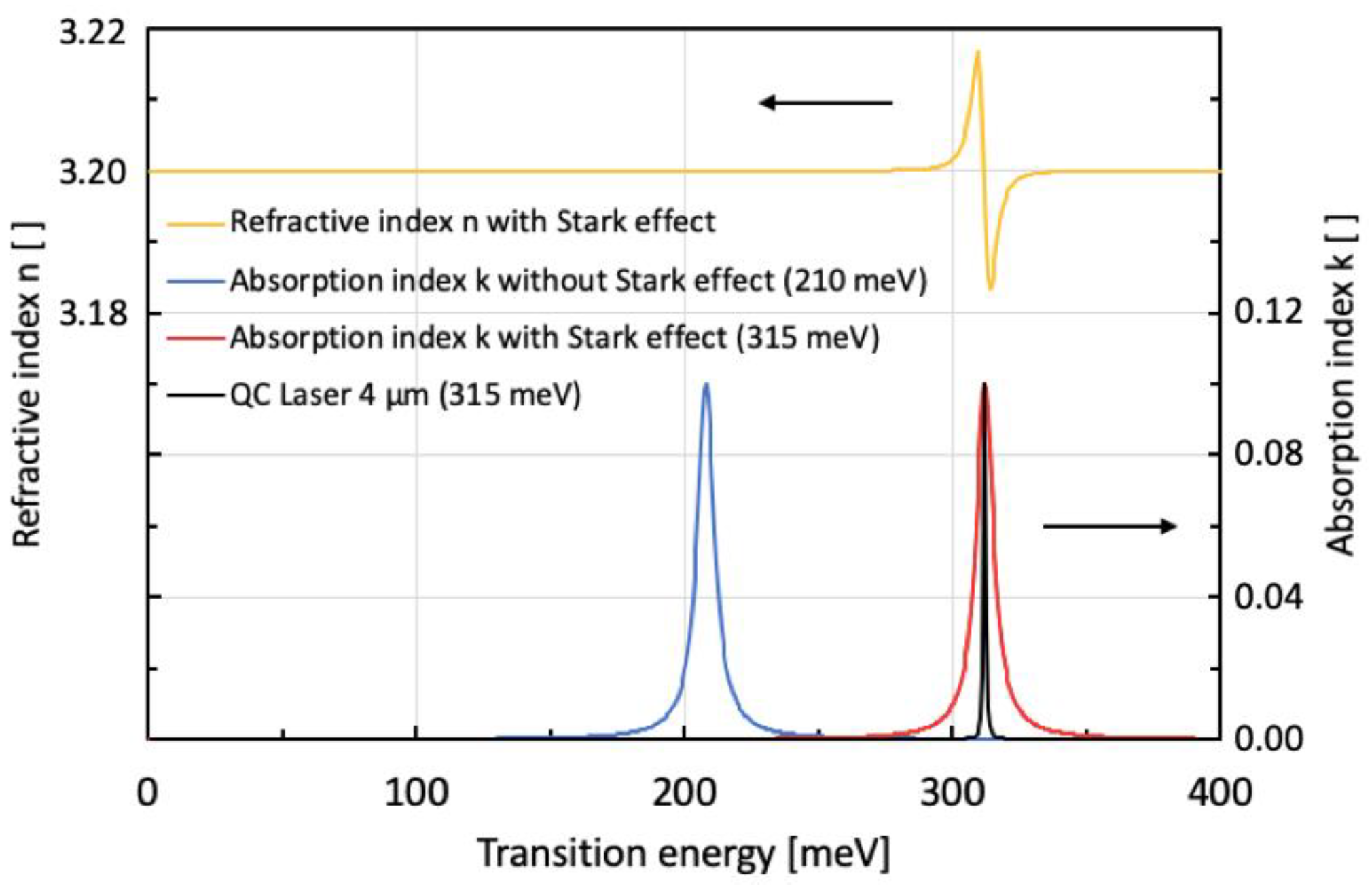
4. Discussion and Most Suitable Applications
5. Specific Use in Modern CNC Machine Tools
6. Use for Absolute Distance Measurements
7. Conclusions
8. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Michelson, A.A. The relative motion of the earth and the luminiferous ether. Am. J. Sci. 1881, 22, 120–129. [Google Scholar] [CrossRef]
- Michelson, A.A.; Morley, E.W. On the relative motion of the earth and the luminiferous ether. Am. J. Sci. 1887, 34, 333–345. [Google Scholar] [CrossRef]
- Einstein, A. Zur Elektrodynamik bewegter Körper (in German). Ann. Der Phys. 1905, 322, 891–921. [Google Scholar] [CrossRef]
- Nolte, D.D. After the Gold Rush: The Trials of Albert Michelson. In Interference: The History of Optical Interferometry and the Scientists Who Tamed Light; Oxford University Press: Oxford, UK, 2023. [Google Scholar] [CrossRef]
- Cui, J.; He, Z.; Jiu, Y.; Tan, J.; Sun, T. Homodyne laser interferometer involving minimal quadrature phase error to obtain subnanometer nonlinearity. Appl. Opt. 2016, 55, 7086–7092. [Google Scholar] [CrossRef]
- Wang, J.; Cai, Z.; Yu, J.; Luo, H.; Ma, C. Nanometer-scale displacement measurement based on an orthogonal dual Michelson interferometer. Chin. Opt. Lett. 2023, 21, 101201. [Google Scholar] [CrossRef]
- Jestel, D.; Baus, A.; Voges, E. Integrated-optic interferometric microdisplacement sensor in glass with thermo-optic phase modulation. Electron. Lett. 1990, 26, 1144–1145. [Google Scholar] [CrossRef]
- Ulbers, G. A sensor for dimensional metrology with an interferometer using integrated optics technology. Measurement 1991, 9, 13–16. [Google Scholar] [CrossRef]
- Yuan, L.; Yang, J.; Liu, Z.; Sun, J. In-fiber integrated Michelson interferometer. Opt. Lett. 2006, 31, 2692–2694. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Zhang, Q.; Lou, R.; He, S.; Yang, X. Fibre-optic Michelson interferometer for detecting coolant level and refractive index. Z. Für Naturforschung A 2022, 77, 621–627. [Google Scholar] [CrossRef]
- Suhara, T.; Taniguchi, T.; Uemukai, M.; Nishihara, H.; Hirata, T.; Iio, S.; Suehiro, M. Monolithic integrated-optic position/displacement sensor using wavguide gratings and QW-DFB laser. IEEE Photonics Technol. Lett. 1995, 7, 1195–1197. [Google Scholar] [CrossRef]
- Hofstetter, D.; Zappe, H.P.; Dändliker, R. Monolithically integrated optical displacement sensor in GaAs/AlGaAs. Electron. Lett. 1995, 31, 2121–2122. [Google Scholar] [CrossRef]
- Hofstetter, D.; Zappe, H.P.; Dändliker, R. Optical displacement measurement with GaAs/AlGaAs-based monolithically integrated Michelson interferometers. IEEE J. Light. Technol. 1997, 4, 663–670. [Google Scholar] [CrossRef]
- Englert, C.R.; Harlander, J.M.; Marr, K.D.; Harding, B.J.; Makela, J.J.; Fae, T.; Brown, C.M.; Ratnam, M.V.; Bhaskara Rao, S.V.; Immer, T.J. Michelson interferometer for global high-resolution thermospherical imaging (MIGHI) on-orbit wind observations: Data analysis and instrument performance. Space Sci. Rev. 2023, 219, 27. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Song, Q.; Peng, H.; Xiao, Q.; Zhao, D.; Jia, B. Dual-wavelength Michelson interferometer employing time delay estimation for distributed disturbance location. Opt. Fiber Technol. 2020, 56, 102181. [Google Scholar] [CrossRef]
- Volkov, P.; Lukyanov, A.; Goryunov, A.; Semikov, D.; Vyazankin, O. Low-coherence homodyne interferometer for sub-megahertz fiber optic sensor readout. Sensors 2024, 24, 552. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.-G.; Zhao, Y.; Peng, Y.; Tong, R.-J.; Zheng, H.-K.; Zhao, J.; Hu, S. In-fiber optofluidic Michelson interferometer for detecting small volume and low concentration chemicals with a fiber ring cavity laser. Sens. Actuators B Chem. 2022, 370, 132467. [Google Scholar] [CrossRef]
- Hei, K.; Anandarajah, K.; Martin, E.P.; Shi, G.; Anandarajah, P.M.; Bhattacharya, N. Absolute distance measurement with a gain-switched dual optical frequency comb. Opt. Express 2021, 29, 8108–8116. [Google Scholar] [CrossRef] [PubMed]
- Van den Berg, S.A.; van Eldik, S.; Bhattacharya, N. Mode-resolved frequency comb interferometry for high-accuracy long distance mesaurement. Sci. Rep. 2015, 5, 14661. [Google Scholar] [CrossRef] [PubMed]
- Volkov, P.; Lukyanov, A.; Goryunov, A.; Semikov, D.; Vopilkin, E.; Kraev, S. Fiber optic impact location system based on a tracking tandem low-coherence interferometer. Sensors 2023, 23, 772. [Google Scholar] [CrossRef] [PubMed]
- Faist, J.; Capasso, F.; Sivco, D.; Sirtori, C.; Hutchinson, A.L.; Cho, A.L. Quantum Cascade Laser. Science 1994, 264, 553–556. [Google Scholar] [CrossRef]
- Beck, M.; Hofstetter, D.; Aellen, T.; Faist, J.; Oesterle, U.; Ilegems, M.; Gini, E.; Melchior, H. Continuous-wave operation of a mid-infrared semiconductor laser at room temperature. Science 2002, 295, 301–305. [Google Scholar] [CrossRef] [PubMed]
- Jozwik, J.; Kuric, I.; Semotiuk, L. Laser interferometer diagnostics of CNC machine tools. Commun.-Sci. Lett. Univ. Žilina 2014, 16, 169–175. [Google Scholar] [CrossRef]
- Technical Description of an Existing Laser Interferometer for CNC-Machines in Mechanical Workshops. Lasertex Interferometer: Lasertex HPI-3D. 2024. Available online: https://lasertex.eu/products/dmi-hpi-3d/ (accessed on 20 May 2024).
- Yu, J.S.; Evans, A.; Slivken, S.; Darvish, S.M.; Razeghi, M. Short wavelength (λ ~ 4.3 µm) high-performance continuous-wave quantum-cascade lasers. IEEE Photonics Technol. Lett. 2005, 17, 1154–1156. [Google Scholar] [CrossRef]
- Hofstetter, D.; Beck, M.; Aellen, T.; Faist, J.; Oesterle, U.; Ilegems, M.; Gini, E.; Melchior, H. Distributed-feedback quantum cascade lasers emitting in the 9-µm band with InP top cladding layers. IEEE Photonics Technol. Lett. 2002, 14, 18–20. [Google Scholar] [CrossRef]
- Hofstetter, D.; Faist, J.; Beck, M.; Mueller, A.; Oesterle, U. Demonstration of high-performance 10.16 µm quantum cascade distributed feedback lasers fabricated without epitxial regrowth. Appl. Phys. Lett. 1999, 75, 665–667. [Google Scholar] [CrossRef]
- Ishutkin, S.; Arykov, V.; Yunusov, I.; Stepanenko, M.; Smirnov, V.; Troyan, O.; Zhidik, Y. The method of low-temperature ICP etching of InP/InGaAs heterostructures in Cl2-based plasma for integrated optics applications. Micromachines 2021, 12, 1535. [Google Scholar] [CrossRef]
- Hofstetter, D.; Beck, M.; Aellen, T.; Faist, J. High-temperature operation of distributed feedback quantum-cascade lasers at 5.3 µm. Appl. Phys. Lett. 2001, 78, 396–398. [Google Scholar] [CrossRef]
- Hofstetter, D.; Zappe, H.P.; Epler, J.E.; Söchtig, J. Single-growth-step GaAs/AlGaAs distributed Bragg reflector laser with holographically-defined recessed gratings. Electron. Lett. 1994, 30, 1858–1859. [Google Scholar] [CrossRef]
- Alpes Lasers SA, Avenue des Pâquiers 1, NE 2072 St. Blaise, Switzerland. Complete List of Available Room Temperature DFB Lasers. 2024. Available online: https://alpeslasers.ch/lasers-on-stock/sbcw10186.pdf (accessed on 17 April 2024).
- Lyakh, A.; Maulini, R.; Tsekoun, A.; Go, R.; Von der Porten, S.; Pflügl, C.; Diehl, L.; Capasso, F.; Patel, C.K.N. High-performance continuous-wave room temperature 4.0-µm quantum cascade lasers with single-facet optical emission exceeding 2 W. Proc. Natl. Acad. Sci. USA 2010, 107, 18799–18802. [Google Scholar] [CrossRef]
- DRS Daylight Solutions, 16465 Via Esprillo, San Diego, CA 92127, USA. 2023. Available online: https://daylightsolutions.com/products/CW-MHF/ (accessed on 21 June 2024).
- Kasztelanic, R.; Filipkowski, A.; Pysz, D.; Nguyen, H.T.; Stepien, R.; Liang, S.; Troles, J.; Karioja, P.; Buczynski, R. Development of gradient index microlenses for the broadband infrared range. Opt. Express 2022, 30, 2338–2352. [Google Scholar] [CrossRef]
- Zhang, C.; Gui, Y.; Xia, K.; Jia, G.; Liu, C.; Zhang, J.; Li, J.; Yang, Z. Preparation of infrared axial gradient refractive index lens based on powder stacking and the sintering thermal diffusion method. Opt. Mater. Express 2022, 12, 584–592. [Google Scholar] [CrossRef]
- Hofstetter, D.; Beck, M.; Faist, J. Quantum-cascade-laser structures as photodetectors. Appl. Phys. Lett. 2002, 81, 2683–2685. [Google Scholar] [CrossRef]
- Chen, X.F.; Liu, W.; An, J.M.; Liu, Y.; Xu, K.; Wang, X.; Liu, J.G.; Ji, Y.F.; Zhu, N.H. Photonic integrated technology for multi-wavelength laser emission. Chin. Sci. Bull. 2010, 56, 3064–3071. [Google Scholar] [CrossRef]
- Miller, D.A.B.; Chemla, D.S.; Damen, T.C.; Gossard, A.C.; Wiegmann, W.; Wood, T.H.; Burrus, C.A. Bandedge electroabsorption in quantum well structures: The quantum-confined Stark effect. Phys. Rev. Lett. 1984, 53, 2173–2177. [Google Scholar] [CrossRef]
- Harwit, A.; Harris, J.S., Jr. Obersvation of Stark shifts in quantum well intersubband transitions. Appl. Phys. Lett. 1987, 50, 685–687. [Google Scholar] [CrossRef]
- Bar-Joseph, I.; Klingshirn, C.; Miller, D.A.B.; Chemla, D.S.; Koren, U.; Miller, B.I. Quantum-confined Stark effect in InGaAs/InP quantum wells grown by organometallic vapor phase epitaxy. Appl. Phys. Lett. 1987, 50, 1010–1012. [Google Scholar] [CrossRef]
- Weiner, J.S.; Miller, D.A.B.; Chemla, D.S. Quadratic electro-optic effect due to the quantum-confined Stark effect in quantum wells. Appl. Phys. Lett. 1987, 50, 842–844. [Google Scholar] [CrossRef]
- Rocha, W.G.M.; Pilling, S. Determination of optical constants n and k of thin films from absorbance data using Kramers-Kronig relationship. Spectrochim. Acta Part A Mol. Biomol. Spectrocopy 2013, 123, 436–446. [Google Scholar] [CrossRef] [PubMed]
- Gross, E.; Nevet, A.; Pesach, A.; Monroy, E.; Schacham, S.; Orenstein, M.; Segev, M.; Bahir, G. Measuring the refractive index around intersubband transition in GaN/AlN multi quantum wells. Opt. Express 2013, 21, 3800–3808. [Google Scholar] [CrossRef] [PubMed]
- Almogy, G.; Shakouri, A.; Yariv, A. Observation of birefringence induced by intersubband transitions in quantum wells. Appl. Phys. Lett. 1993, 63, 2720–2722. [Google Scholar] [CrossRef]
- Huang, Y.-Z. Comparison of modal and material gain for strong guiding slab waveguides. IEE Proc. Optoelectron. 2001, 148, 131–133. [Google Scholar] [CrossRef]
- Wolf, J.M.; Riedi, S.; Süess, M.J.; Beck, M.; Faist, J. 3.36 µm single-mode quantum cascade laser with a dissipation below 250 mW. Opt. Express 2016, 24, 662–671. [Google Scholar] [CrossRef] [PubMed]
- Collins, D. Where Are Glass Scale Linear Encoders Used? Heidenhain Webpage 2022. Linear Motion Tips. Available online: https://www.heidenhain.com/products/linear-encoders/sealed/lc-100 (accessed on 3 May 2024).
- PICOSCALE Sensor Heads of ‘SmarAct’ Motion and Metrology Systems. 2024. Available online: https://www.smaract.com/en/picoscale-advantages (accessed on 20 May 2024).
- Na, Q.; Xie, Q.; Zhang, N.; Zhang, L.; Li, Y.; Chen, B.; Peng, T.; Zuo, G.; Zhuang, D.; Song, J. Optical frequency shifted FMCW Lidar system for unambiguous measurement of distance and velocity. Opt. Lasers Eng. 2023, 164, 107523. [Google Scholar] [CrossRef]



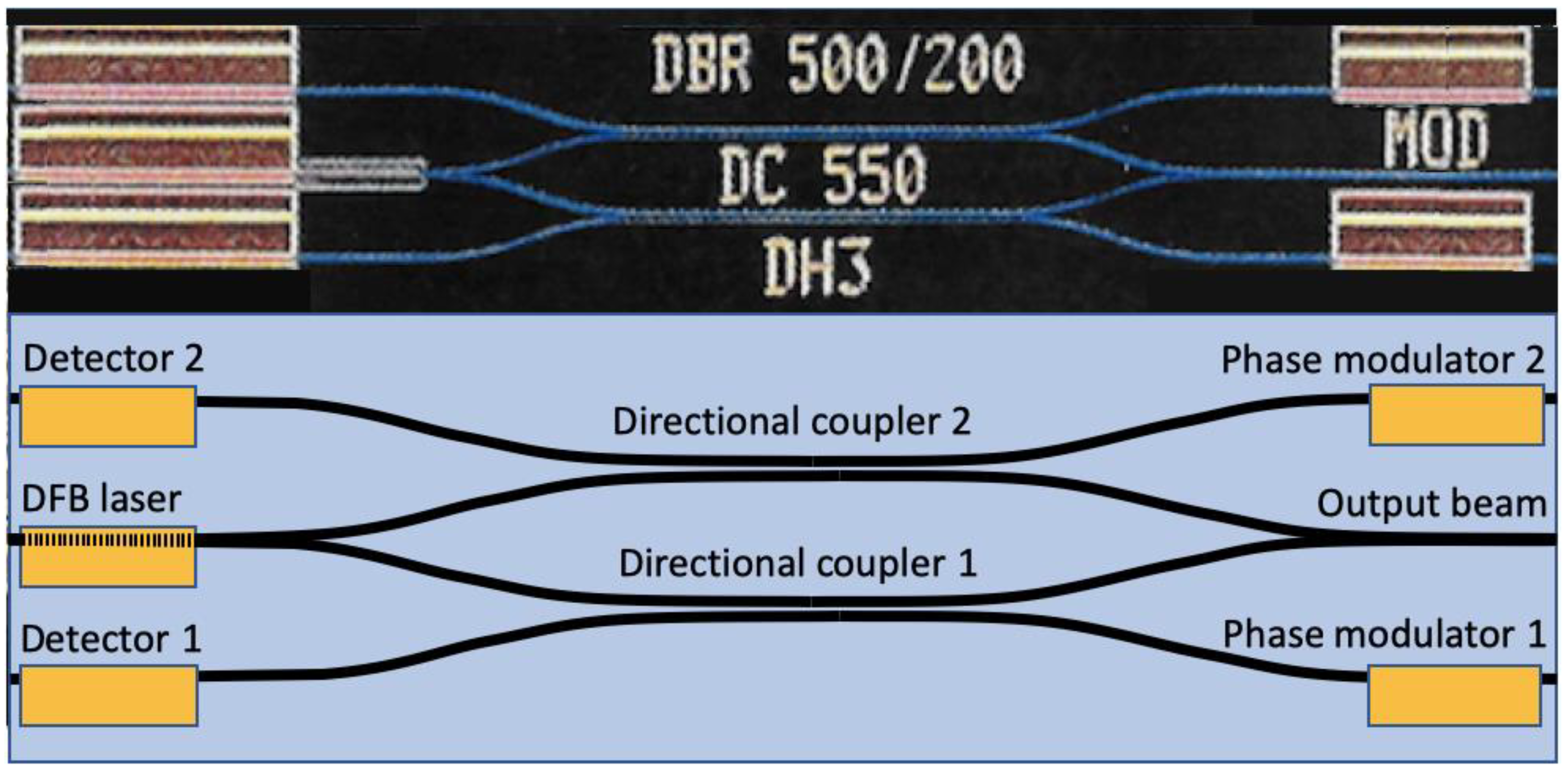



| Layer Descriptions | Materials | Thicknesses | Doping Levels |
|---|---|---|---|
| Cap layer | InP | 0.5 µm | Si, 2 × 1019 cm−3 |
| Upper clad | InP | 1.8 µm | Si, 2 × 1017 cm−3 |
| Grating | In0.53Ga0.47As | 0.2 µm | Si, 5 × 1017 cm−3 |
| Upper waveguide | In0.53Ga0.47As | 0.3 µm | Si, 8 × 1016 cm−3 |
| Active region | In0.68Ga0.32As/In0.39Al0.61As | 1.4 µm | Si, 1 × 1017 cm−3 |
| Lower waveguide | In0.53Ga0.47As | 0.3 µm | Si, 8 × 1016 cm−3 |
| Substrate | InP | − | Si, 6 × 1016 cm−3 |
| Layer Descriptions | Materials | Thicknesses | Doping Levels |
|---|---|---|---|
| Barrier 1/QW 1 | In0.39Al0.61As/In0.68Ga0.32As | 41 Å/10 Å | − |
| Barrier 2/QW 2 | In0.39Al0.61As/In0.68Ga0.32As | 15 Å/39 Å | − |
| Barrier 3/QW 3 | In0.39Al0.61As/In0.68Ga0.32As | 15 Å/34 Å | − |
| Barrier 4/QW 4 | In0.39Al0.61As/In0.68Ga0.32As | 16 Å/31 Å | − |
| Barrier 5/QW 5 | In0.39Al0.61As/In0.68Ga0.32As | 23 Å/23 Å | − |
| Barrier 6/QW 6 | In0.39Al0.61As/In0.68Ga0.32As | 18 Å/20 Å | − |
| Barrier 7/QW 7 | In0.39Al0.61As/In0.68Ga0.32As | 19 Å/18 Å | Si, 1 × 1017 cm−3 |
| Barrier 8/QW 8 | In0.39Al0.61As/In0.68Ga0.32As | 20 Å/17 Å | Si, 1 × 1017 cm−3 |
| Barrier 9/QW 9 | In0.39Al0.61As/In0.68Ga0.32As | 22 Å/16 Å | − |
| Barrier 10/QW 10 | In0.39Al0.61As/In0.68Ga0.32As | 22 Å/15 Å | − |
| Barrier 11/QW 11 | In0.39Al0.61As/In0.68Ga0.32As | 29 Å/15 Å | − |
| Component | Width | Length | Loss | Separation | Splitting | Sensitivity | Responsivity |
|---|---|---|---|---|---|---|---|
| Waveguide | 8 µm | 5 mm | 1 cm−1 | − | − | − | − |
| DFB-Laser | 8 µm | 500 µm | 10 cm−1 | − | − | − | 100 mW/A |
| Directional Coupler | 8 µm | 450 µm | 1 cm−1 | 4 µm | 50%/50% | − | − |
| Phase Modulator | 8 µm | 800 µm | 1 cm−1 | − | − | − | − |
| Photodetector | 8 µm | 500 µm | 10 cm−1 | − | − | 10 mA/W | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofstetter, D.; Beck, H.; Bour, D.P. Monolithically Integrated Michelson Interferometer Using an InGaAs/InAlAs Quantum Cascade Laser at λ = 4 µm. Photonics 2024, 11, 593. https://doi.org/10.3390/photonics11070593
Hofstetter D, Beck H, Bour DP. Monolithically Integrated Michelson Interferometer Using an InGaAs/InAlAs Quantum Cascade Laser at λ = 4 µm. Photonics. 2024; 11(7):593. https://doi.org/10.3390/photonics11070593
Chicago/Turabian StyleHofstetter, Daniel, Hans Beck, and David P. Bour. 2024. "Monolithically Integrated Michelson Interferometer Using an InGaAs/InAlAs Quantum Cascade Laser at λ = 4 µm" Photonics 11, no. 7: 593. https://doi.org/10.3390/photonics11070593
APA StyleHofstetter, D., Beck, H., & Bour, D. P. (2024). Monolithically Integrated Michelson Interferometer Using an InGaAs/InAlAs Quantum Cascade Laser at λ = 4 µm. Photonics, 11(7), 593. https://doi.org/10.3390/photonics11070593






