Fast 2D Subpixel Displacement Estimation
Abstract
1. Introduction
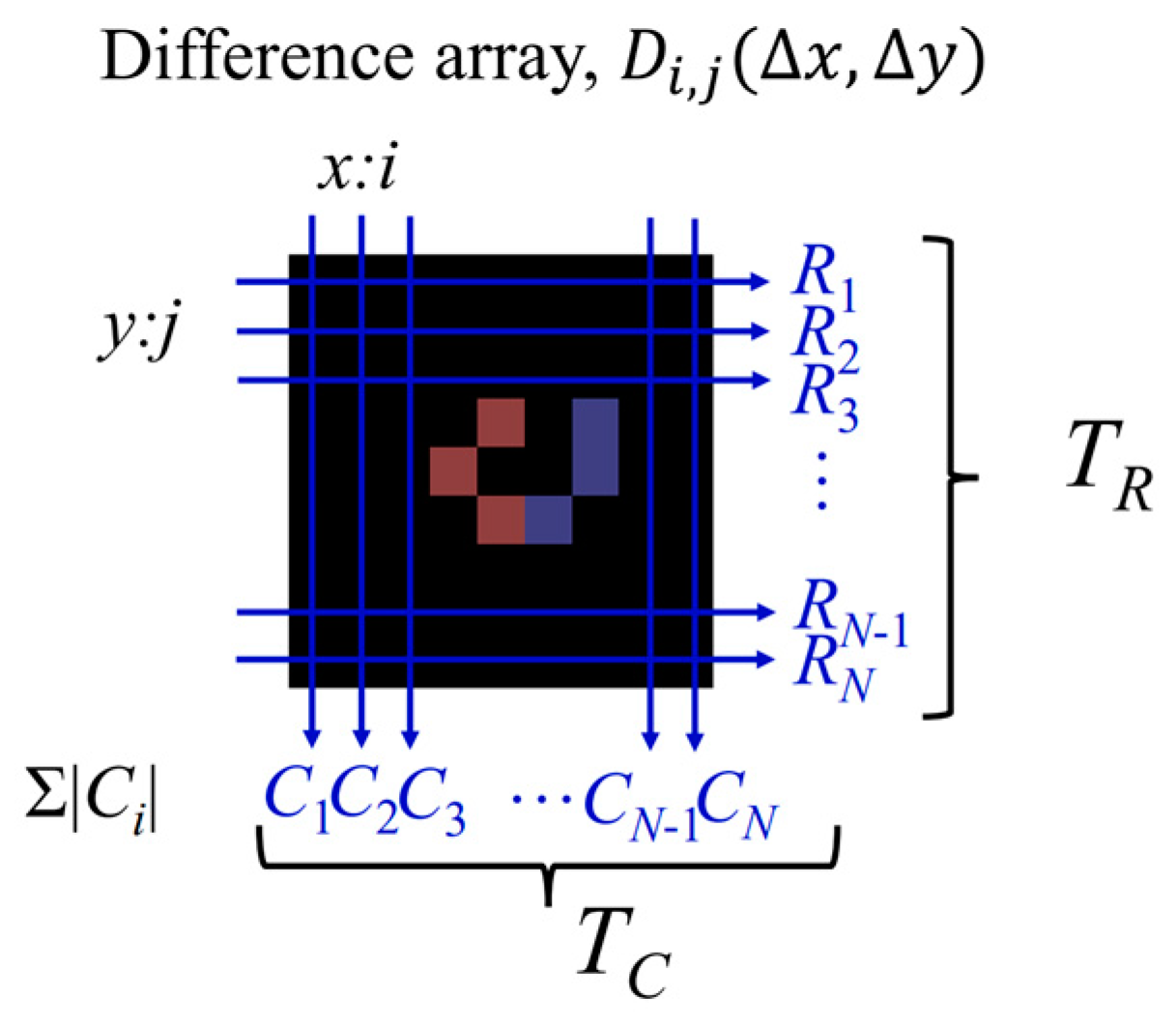
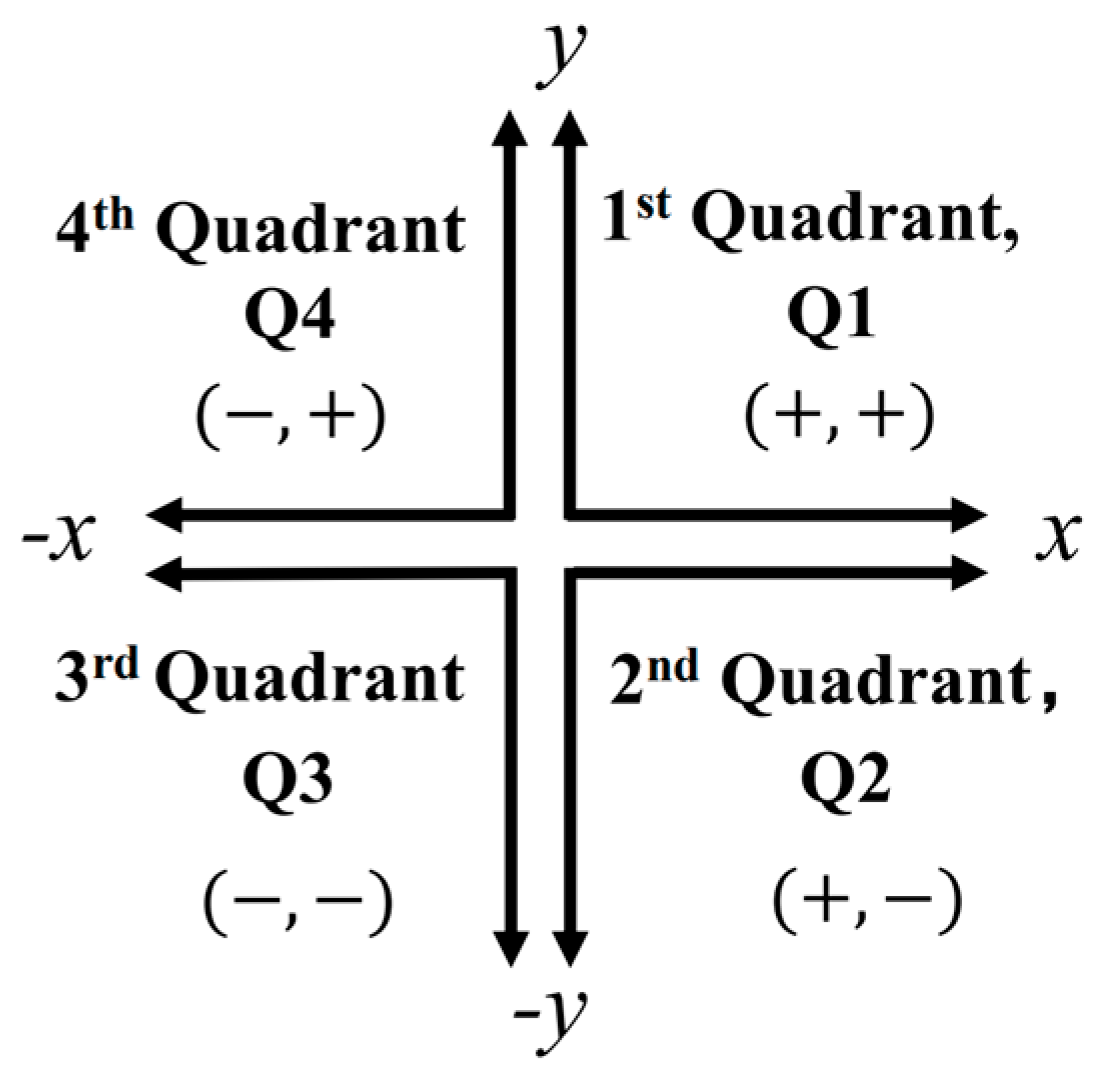
2. Two-Dimensional Theory
2.1. Continuous Model 2D Motion
2.2. Discrete Model 2D Motion
3. Two-Dimensional Simulation Results
3.1. Subtraction Method: Object without Noise
3.2. Subtraction Method: Simulated Object with Noise
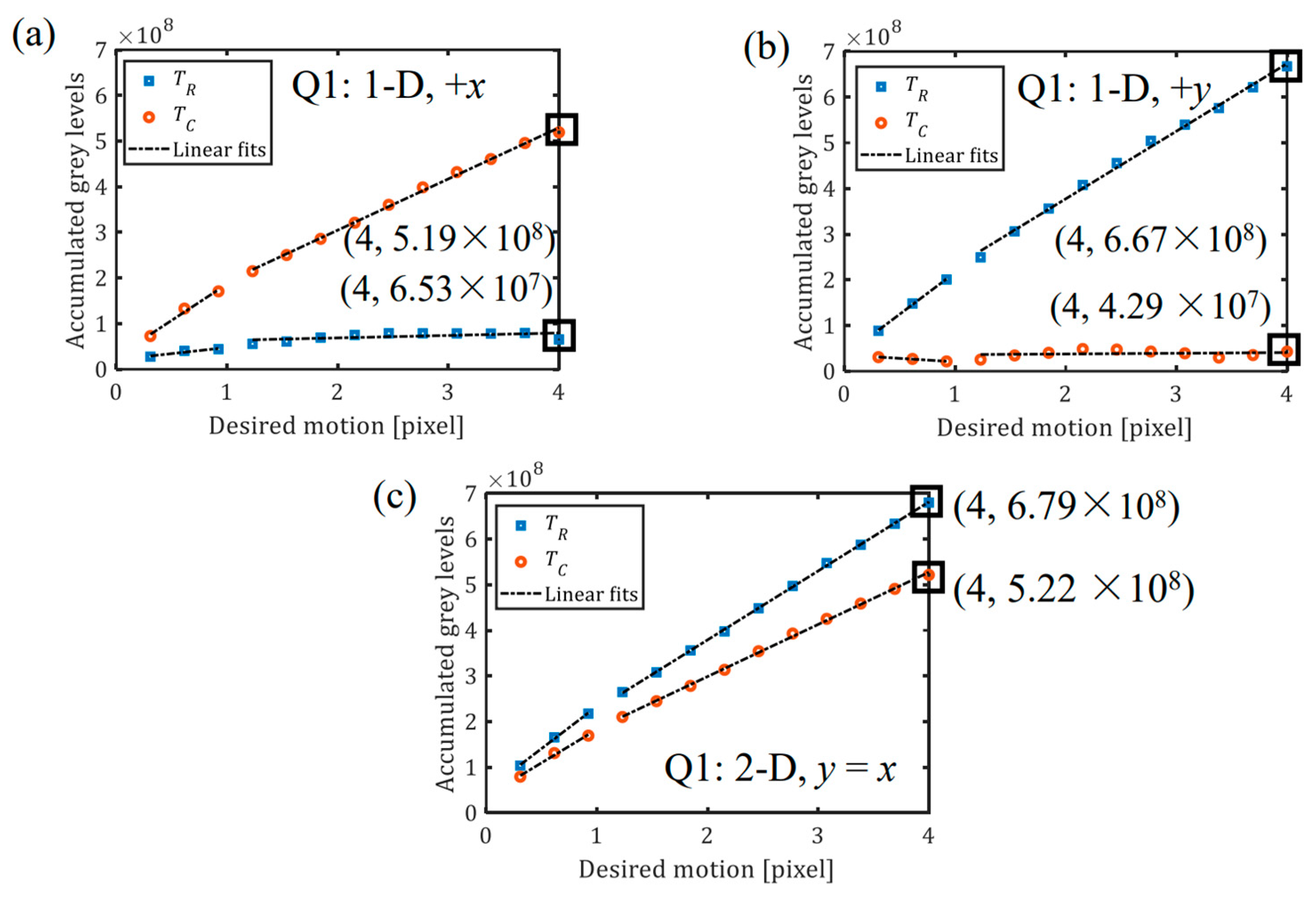
4. Two-Dimensional Experiment Results
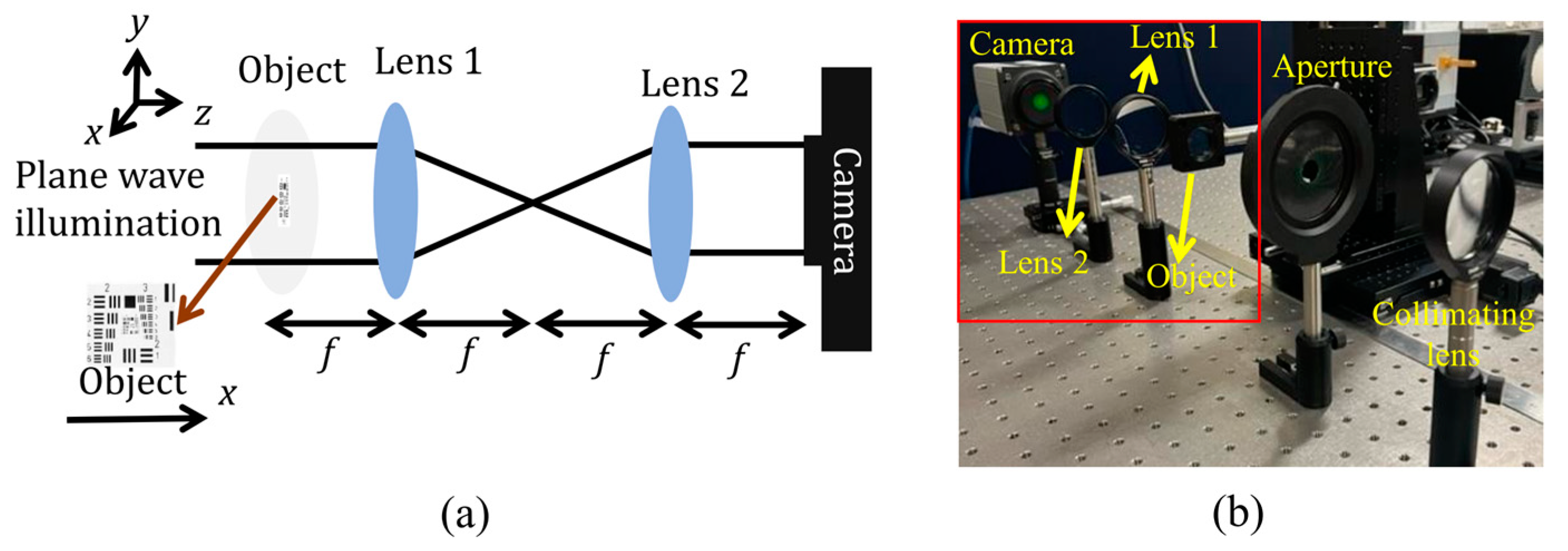
4.1. Image Capturing
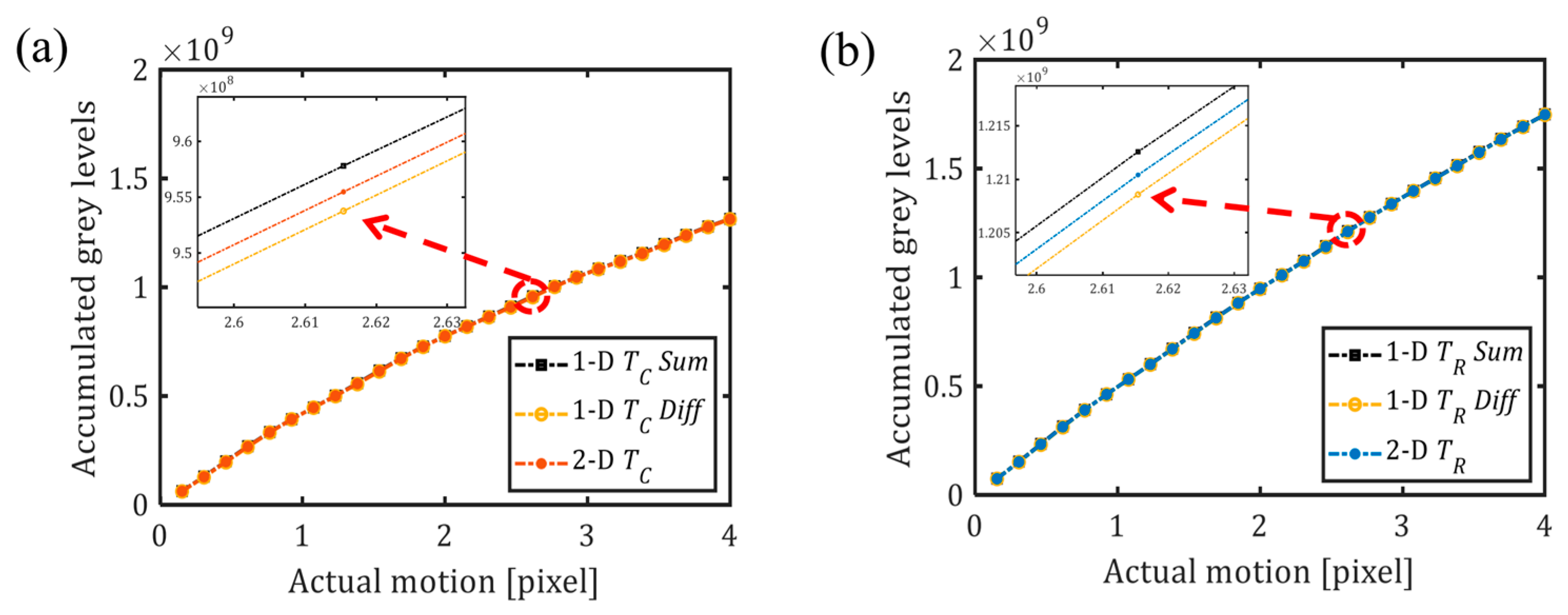
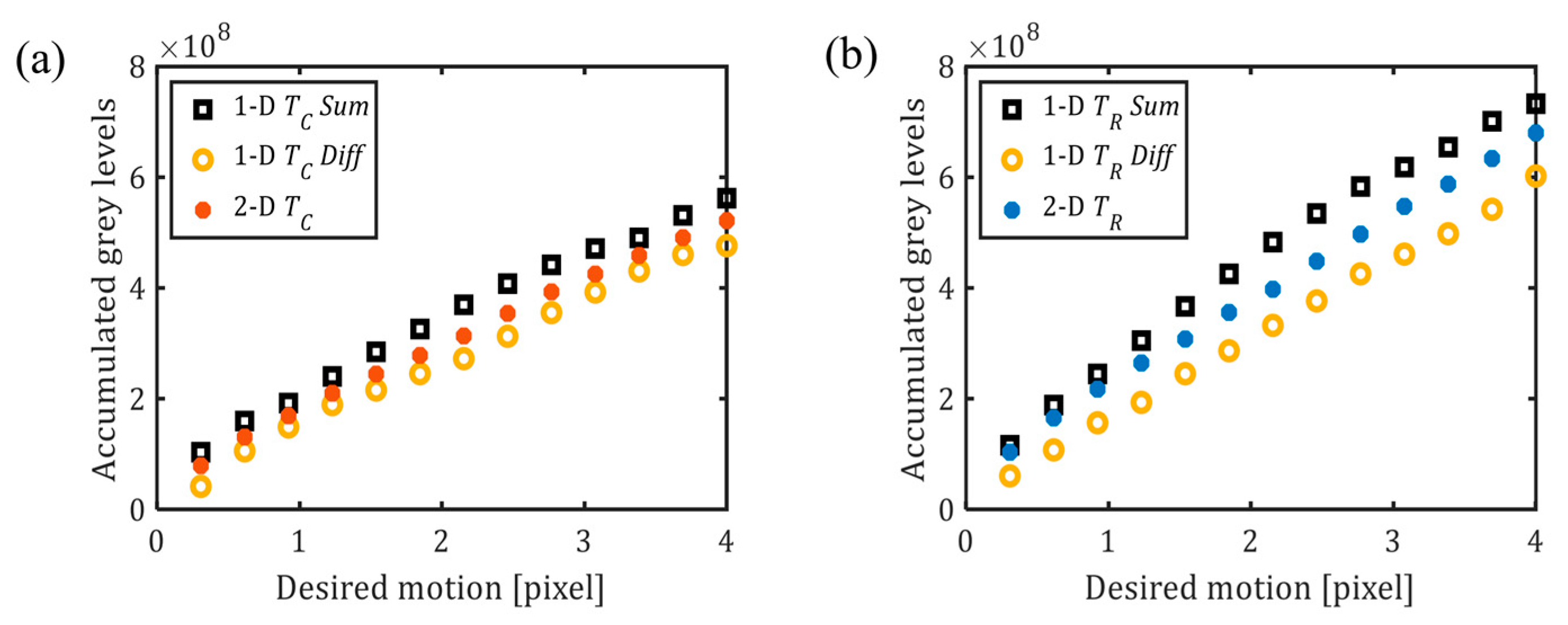
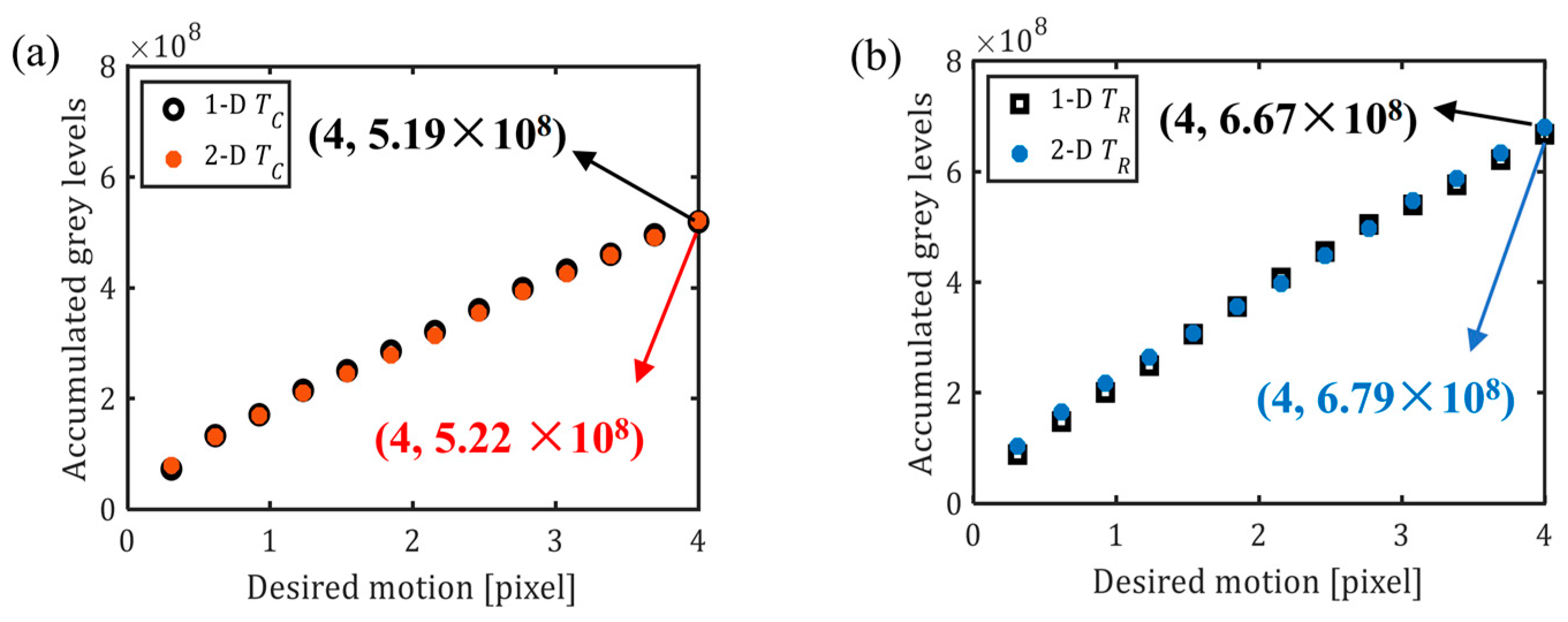
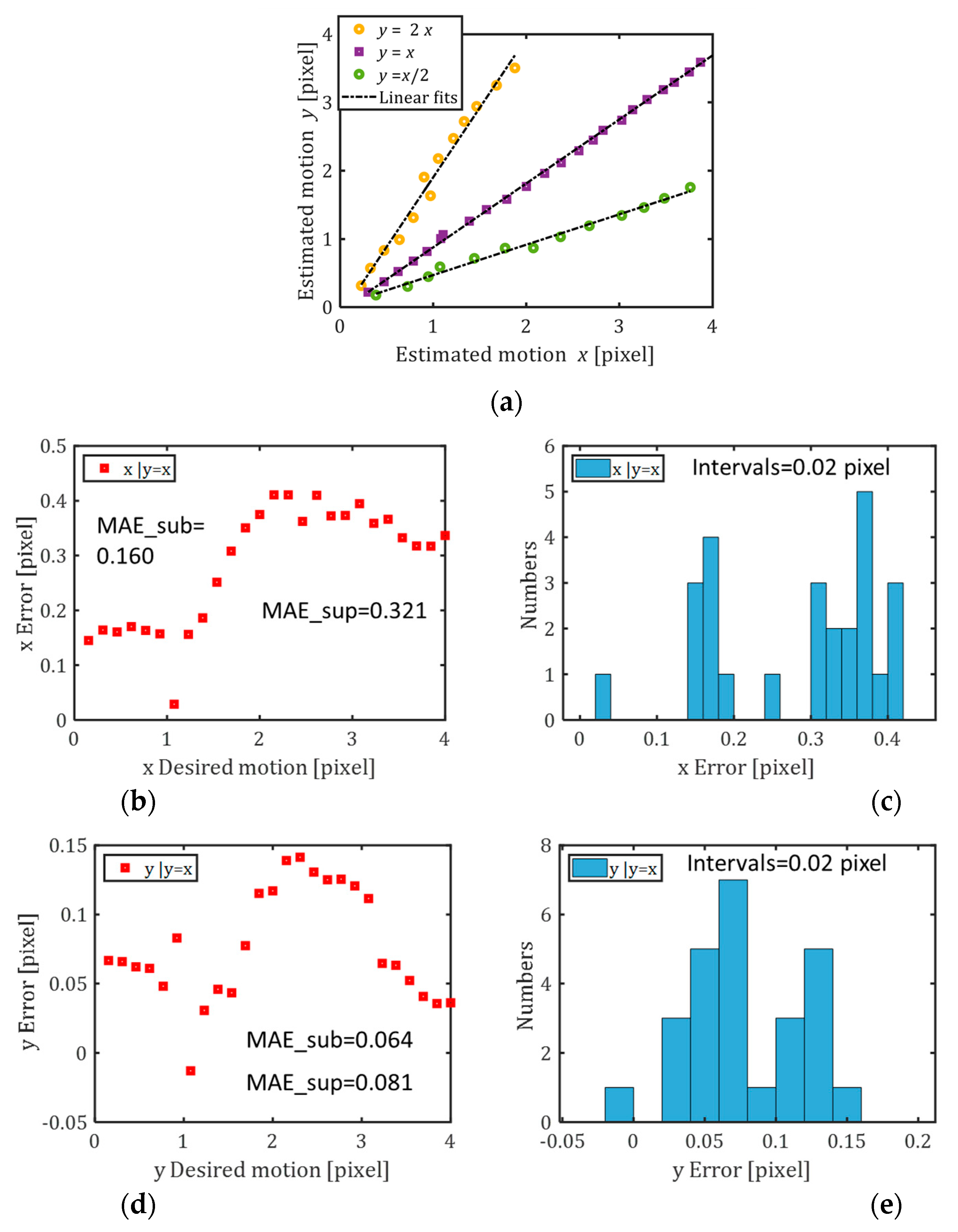
4.2. Examination of 2D Experimental Results
4.3. Calibration: 1D and 2D
4.4. Object with Diffuser
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, Z.; Geng, D.; Owens, A. Self-Supervised Motion Magnification by Backpropagating Through Optical Flow. Adv. Neural Inf. Process. Syst. 2024, 36, 1–21. [Google Scholar]
- Konstantinidis, D.; Stathaki, T.; Argyriou, V. Phase amplified correlation for improved sub-pixel motion estimation. IEEE Trans. Image Process. 2019, 28, 3089–3101. [Google Scholar] [CrossRef] [PubMed]
- Chi, Y.M.; Tran, T.D.; Etienne-Cummings, R. Optical flow approximation of sub-pixel accurate block matching for video coding. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing-ICASSP’07, Honolulu, HI, USA, 15–20 April 2007; Volume 1, p. I-1017. [Google Scholar]
- Tico, M.; Alenius, S.; Vehvilainen, M. Method of motion estimation for image stabilization. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 14–19 May 2006; Volume 2, p. II-277-280. [Google Scholar]
- Ruan, H.; Tan, Z.; Chen, L.; Wan, W.; Cao, J. Efficient sub-pixel convolutional neural network for terahertz image super-resolution. Opt. Lett. 2022, 47, 3115–3118. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Yang, T.; Niu, Y. Subpixel computer vision detection based on wavelet transform. IEEE Access 2020, 8, 88273–88281. [Google Scholar] [CrossRef]
- Yoneyama, S. Basic principle of digital image correlation for in-plane displacement and strain measurement. Adv. Compos. Mater. 2016, 25, 105–123. [Google Scholar] [CrossRef]
- Wan, M.; Healy, J.J.; Sheridan, J.J. Fast subpixel displacement measurement: Part I: 1-D Analysis, simulation, and experiment. Opt. Eng. 2022, 61, 043105. [Google Scholar] [CrossRef]
- Guizar-Sicairos, M.; Thurman, S.T.; Fienup, J.R. Efficient subpixel image registration algorithms. Opt. Lett. 2008, 33, 156–158. [Google Scholar] [CrossRef] [PubMed]
- Karybali, I.; Psarakis, E.; Berberidis, K.; Evangelidis, G. An efficient spatial domain technique for subpixel image registration, Sig. Process. Image Commun. 2008, 23, 711–724. [Google Scholar] [CrossRef]
- Michaelis, D.; Neal, D.R.; Wieneke, B. Peak-locking reduction for particle image velocimetry, Meas. Sci. Technol. 2016, 27, 104005. [Google Scholar]
- Tong, W. Subpixel image registration with reduced bias. Opt. Lett. 2011, 36, 763–765. [Google Scholar] [CrossRef] [PubMed]
- Mas, D.; Ferrer, B.; Sheridan, J.T.; Espinosa, J. Resolution limits to object tracking with subpixel accuracy. Opt. Lett. 2012, 37, 4877–4879. [Google Scholar] [CrossRef] [PubMed]
- Mas, D.; Perez, J.; Ferrer, B.; Espinosa, J. Realistic limits for subpixel movement detection. Appl. Opt. 2016, 55, 4974–4979. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Li, M.; Zhang, W.; Gu, J. Subpixel matching using double-precision gradient-based method for digital image correlation. Sensors 2021, 21, 3140. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Zhang, Y.; Li, Z. Motion estimation of the common carotid artery wall in ultrasound images using an improved sub-pixel block matching method. Optik 2022, 270, 169929. [Google Scholar] [CrossRef]
- Marinel, C.; Mathon, B.; Losson, O.; Macaire, L. Comparison of Phase-based Sub-Pixel Motion Estimation Methods. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Bordeaux, France, 16–19 October 2022; pp. 561–565. [Google Scholar]
- Tu, B.; Ren, Q.; Li, Q.; He, W.; He, W. Hyperspectral image classification using a superpixel-pixel-subpixel multilevel network. IEEE Trans. Instrum. Meas. 2023, 72, 5013616. [Google Scholar] [CrossRef]
- Wan, M.; Healy, J.J.; Sheridan, J.T. Fast, sub-pixel accurate, displacement measurement method: Optical and terahertz systems. Opt. Lett. 2020, 45, 6611–6614. [Google Scholar] [CrossRef] [PubMed]
- Healy, J.J.; Wan, M.; Sheridan, J.T. Direction-sensitive fast measurement of sub-sampling-period delays. In Proceedings of the 8th International Conference on Signal Processing and Integrated Networks, SPIN-2021, Noida, India, 26–27 August 2021; pp. 228–232. [Google Scholar]
- Ferrer, B.; Tomás, M.B.; Wan, M.; Sheridan, J.T.; Mas, D. Comparative Analysis of Discrete Subtraction and Cross-Correlation for Subpixel Object Tracking. Appl. Sci. 2023, 13, 8271. [Google Scholar] [CrossRef]
- Wan, M. Optical Imaging Techniques in the THz Regime. PhD Thesis, University College Dublin, Dublin, Ireland, 2021. [Google Scholar]





Q1 | +x (m: PC,1 or PR,1) | +y (m: MC,1 or MR,1) | y = x 2D | ||||
|---|---|---|---|---|---|---|---|
| Range (Pixels) | (i) 0.15~1 | (ii) 1~4 | (i) 0.15~1 | (ii) 1~4 | (i) 0.15~1 | (ii) 1~4 | |
| TC | m c R2 | 4.328 × 108 −2.67 × 106 0.9994 | 2.934 × 108 1.697 × 108 0.9946 | 3.359 × 105 2575 0.9996 | 2.639 × 105 8.961 × 104 0.9963 | 4.328 × 108 −2.671 × 106 0.9994 | 2.934 × 108 1.697 × 108 0.9946 |
| TR | m c R2 | 2.85 × 105 −632.8 0.9997 | 2.122 × 105 9.971 × 105 0.9947 | 5.053 × 108 −6.998 × 105 0.9996 | 4.168 × 108 1.059 × 108 0.9989 | 5.053 × 108 −7.044 × 105 0.9996 | 4.167 × 108 1.059 × 108 0.9989 |
| Data (TC & TR) | y = 2x | y = x | y = x/2 | ||
|---|---|---|---|---|---|
| 1D Calibration | x: 0~2 y: 0~4 | x: 0~4 y: 0~4 | x: 0~4 y: 0~4 | x: 0~4 y: 0~2 | x: 0~4 y: 0~4 |
| m | 1.998 | 2.004 | 0.9991 | 0.5036 | 0.4978 |
| c | 0.0018 | 0.0205 | 0.0017 | −0.0118 | −0.0019 |
| R2 | 0.9988 | 0.9931 | 0.9996 | 0.998 | 0.9965 |
| RMSE | 0.0405 | 0.0955 | 0.0237 | 0.0256 | 0.0338 |
Q1 | +x (m: PC,1 or PR,1) | +y (m: MC,1 or MR,1) | y = x 2D | ||||
|---|---|---|---|---|---|---|---|
| Range (Pixel) | (i) 0.3~1 | (ii) 1~4 | (i) 0.3~1 | (ii) 1~4 | (i) 0.3~1 | (ii) 1~4 | |
TC | m c R2 | 1.592 × 108 2.758 × 107 0.9828 | 1.123 × 108 8.017 × 107 0.9976 | −1.51 × 107 3.573 × 107 0.9914 | 1.533 × 106 3.469 × 107 0.0367 | 1.462 × 108 3.654 × 107 0.9924 | 1.143 × 108 7.018 × 107 0.9989 |
TR | m c R2 | 2.673 × 107 2.094 × 107 0.9061 | 5.356 × 106 5.805 × 107 0.3275 | 1.825 × 108 3.361 × 107 0.9987 | 1.48 × 108 8.124 × 107 0.9961 | 1.851 × 108 4.833 × 107 0.9975 | 1.511 × 108 7.677 × 107 0.9996 |
| Data (TC & TR) | y = 2x | y = x | y = x/2 |
|---|---|---|---|
| 1D Calibration | +x: 0~4 pixels +y: 0~4 pixels | ||
| m | 2.037 | 0.9375 | 0.4453 |
| c | −0.1316 | −0.05981 | 0.02585 |
| R2 | 0.9811 | 0.9992 | 0.9903 |
| RMSE | 0.1386 | 0.0332 | 0.0475 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, M.; Healy, J.J.; Sheridan, J.T. Fast 2D Subpixel Displacement Estimation. Photonics 2024, 11, 625. https://doi.org/10.3390/photonics11070625
Wan M, Healy JJ, Sheridan JT. Fast 2D Subpixel Displacement Estimation. Photonics. 2024; 11(7):625. https://doi.org/10.3390/photonics11070625
Chicago/Turabian StyleWan, Min, John J. Healy, and John T. Sheridan. 2024. "Fast 2D Subpixel Displacement Estimation" Photonics 11, no. 7: 625. https://doi.org/10.3390/photonics11070625
APA StyleWan, M., Healy, J. J., & Sheridan, J. T. (2024). Fast 2D Subpixel Displacement Estimation. Photonics, 11(7), 625. https://doi.org/10.3390/photonics11070625






