The Suppression Effect of an Imaging System on the Geometric Tilt-to-Length Coupling in a Test Mass Interferometer
Abstract
:1. Introduction
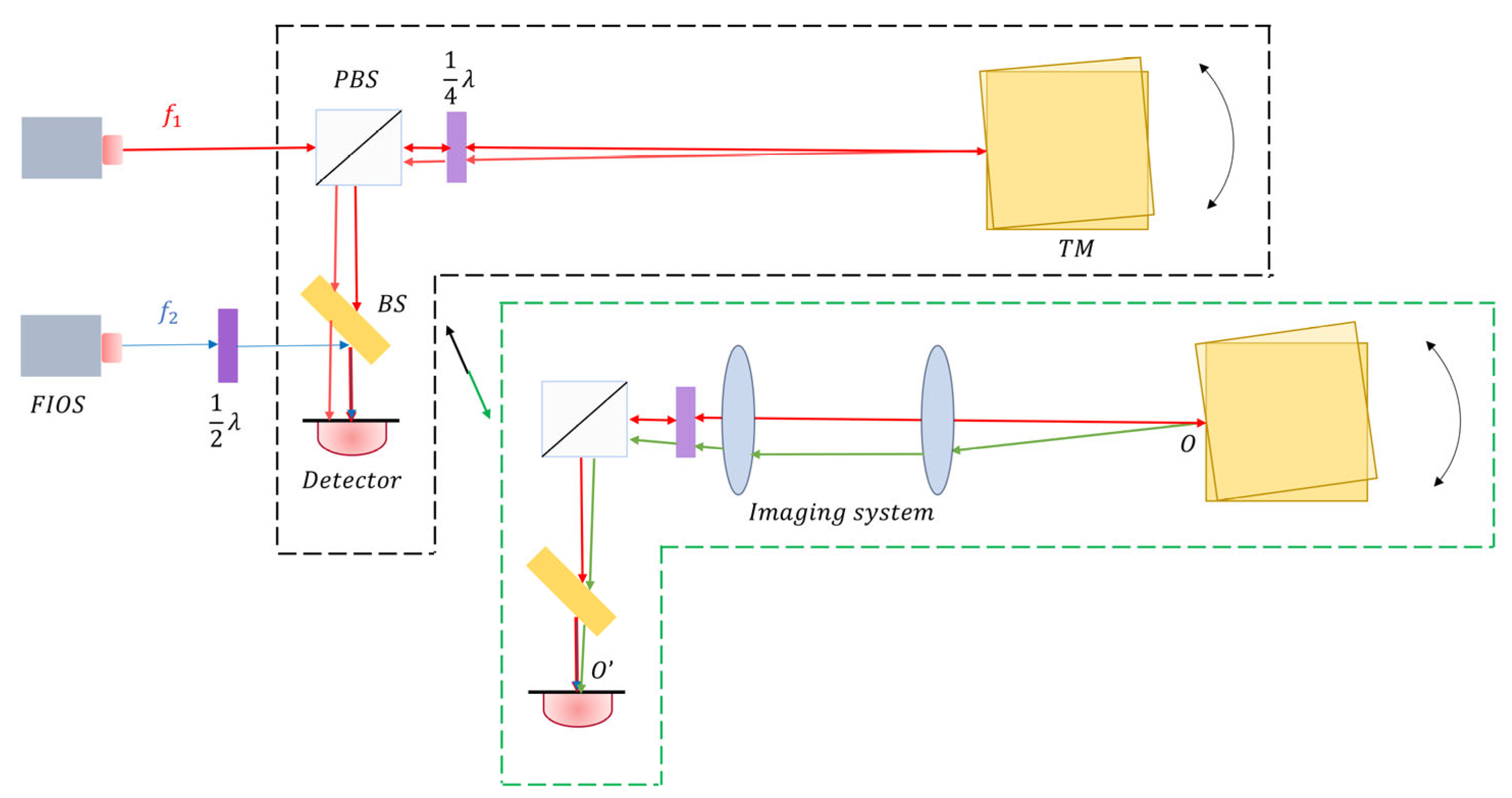
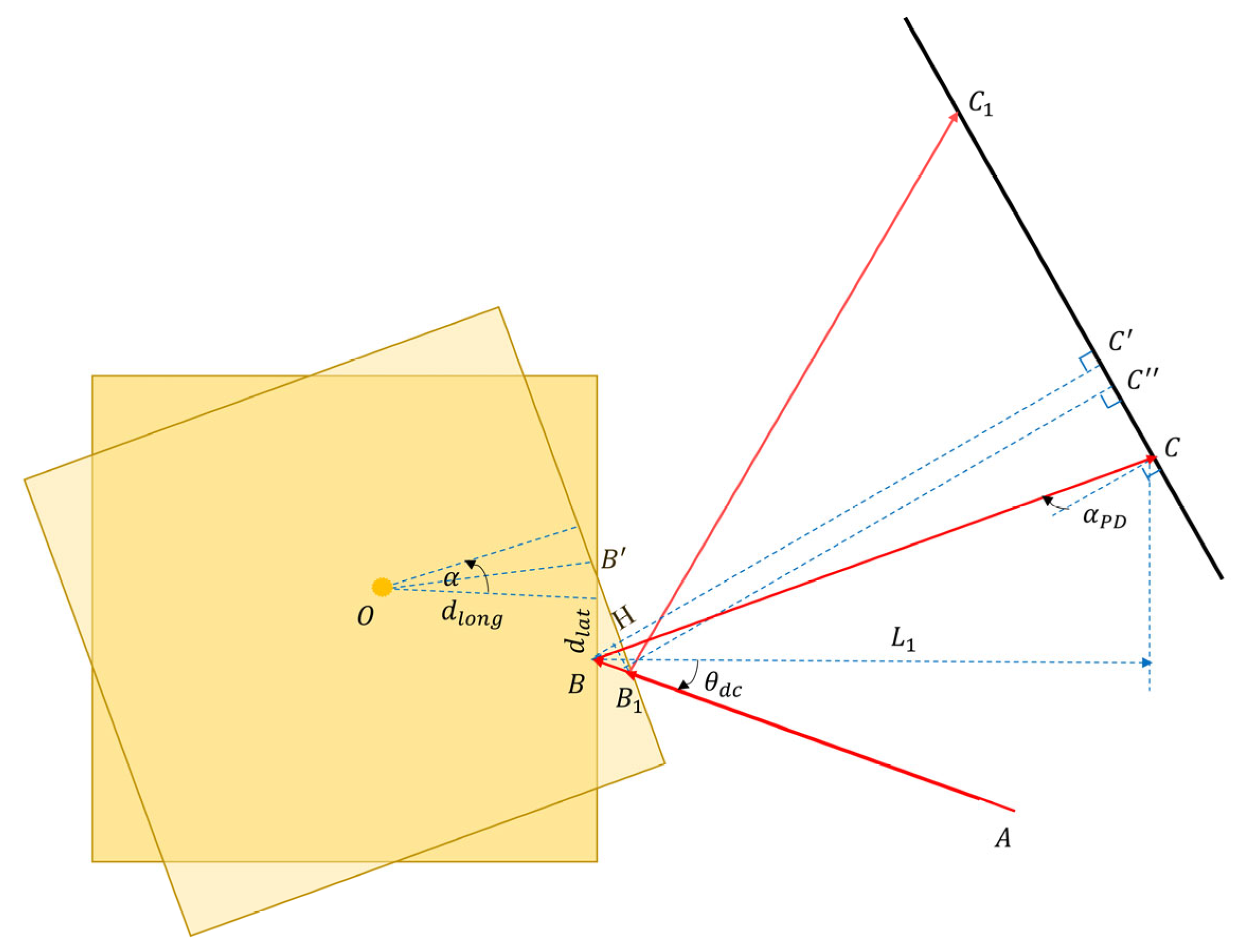
2. Geometric TTL Coupling Effect in the TM Interferometer
2.1. Theoretical Model
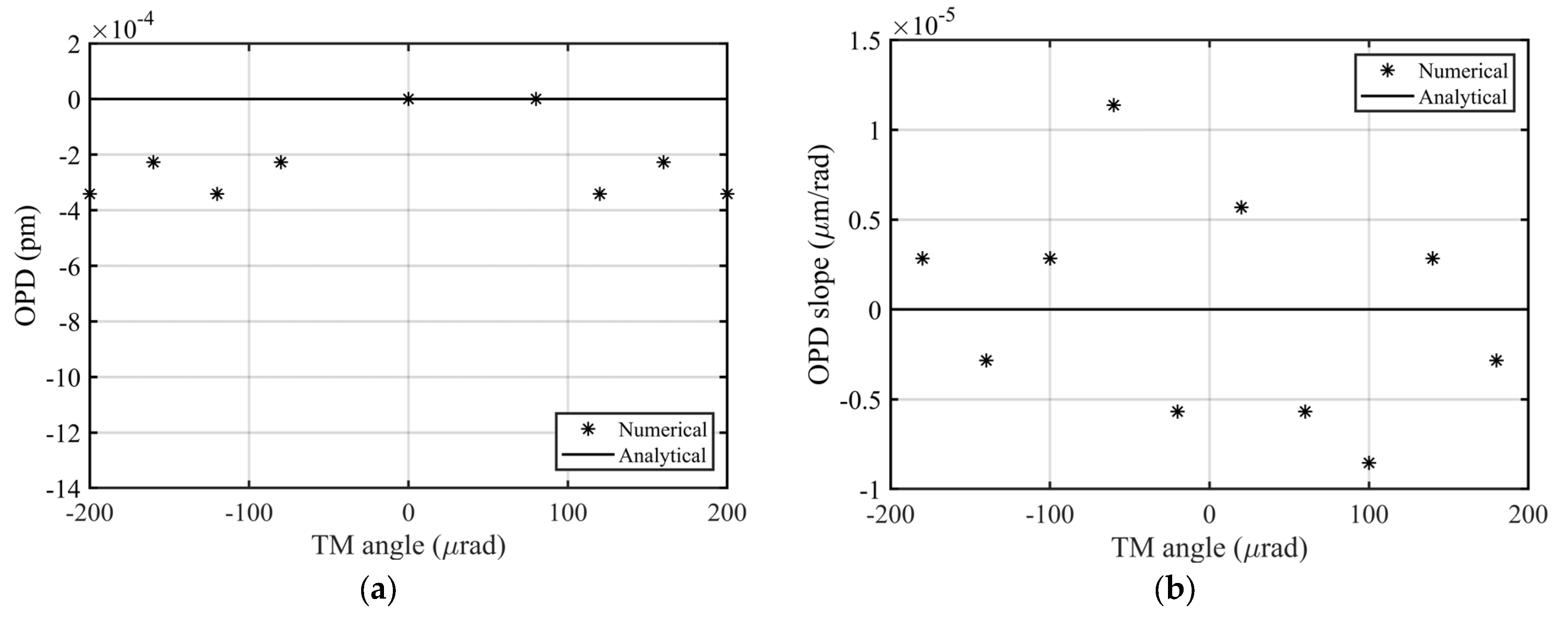
2.2. Numerical Simulation Verification
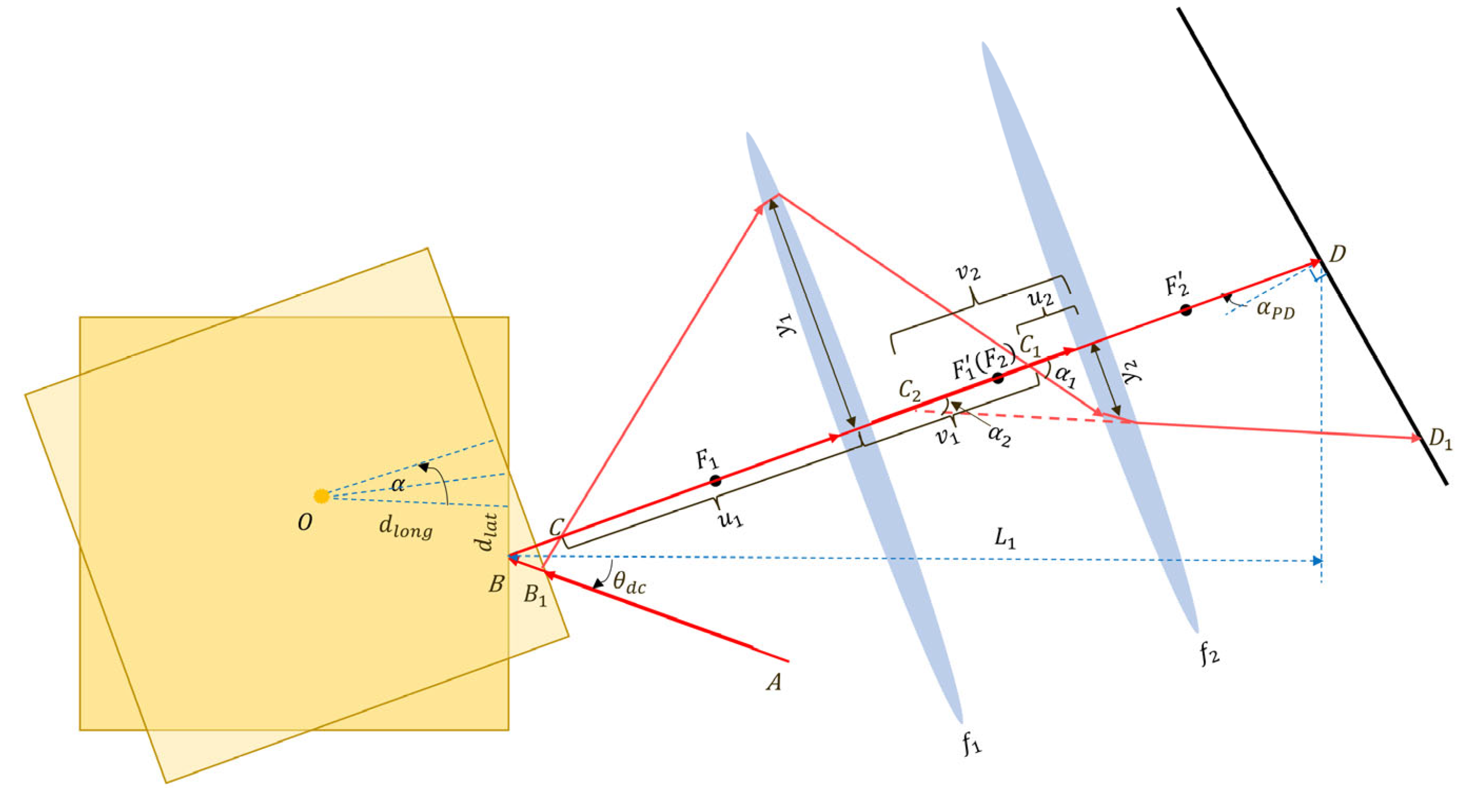
3. Geometric TTL Coupling Effect with Imaging System in the TM Interferometer
3.1. Theoretical Model
3.2. Discussion on TTL Coupling Based on the Two Typical Conjugate Relationships in an Actual TM Interferometer Design
3.2.1. Conjugation between the Reflection Point and the Detector
3.2.2. Conjugation between the Center of Rotation and the Detector
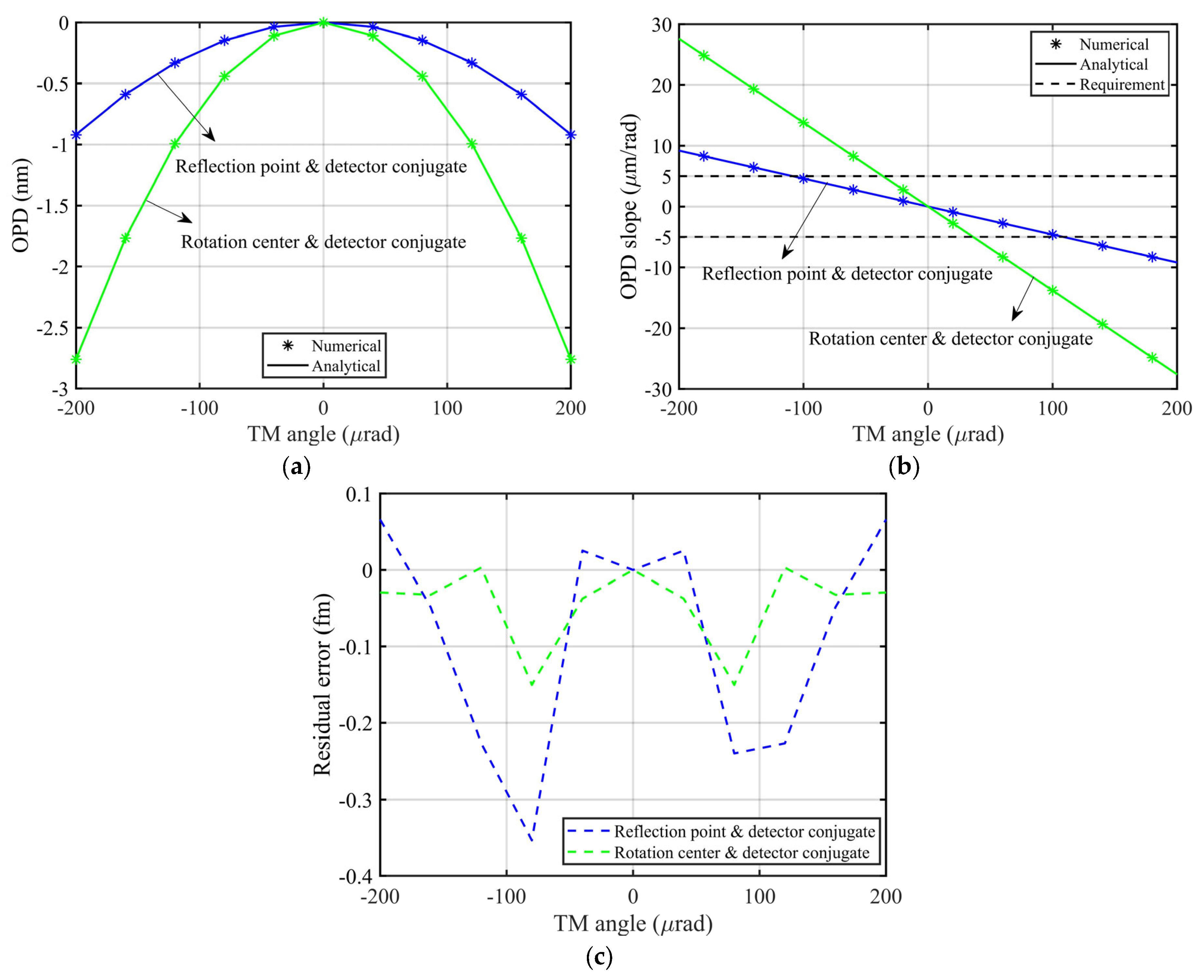
3.3. Optimal Conjugate Relationship and Its Corresponding Position
4. Numerical Simulation Verification of the TTL Coupling with the Imaging System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Danzmann, K.; Rüdiger, A. LISA technology: Concept, status, prospects. Class. Quantum Grav. 2003, 20, S1–S9. [Google Scholar] [CrossRef]
- Jennrich, O. LISA technology and instrumentation. Class. Quantum Grav. 2009, 26, 153001. [Google Scholar] [CrossRef]
- Hu, W.-R.; Wu, Y.-L. The Taiji Program in Space for gravitational wave physics and the nature of gravity. Natl. Sci. Rev. 2017, 4, 685–686. [Google Scholar] [CrossRef]
- Luo, Z.; Guo, Z.; Jin, G.; Wu, Y.; Hu, W. A brief analysis to Taiji: Science and technology. Results Phys. 2020, 16, 102918. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, Y.; Wu, Y.; Hu, W.; Jin, G. The Taiji program: A concise overview. Prog. Theor. Exp. Phys. 2021, 2021, 05A108. [Google Scholar] [CrossRef]
- Tao, W.; Deng, X.; Diao, Y.; Gao, R.; Qi, K.; Wang, S.; Luo, Z.; Sha, W.; Liu, H. Design and Construction of the Optical Bench Interferometer for the Taiji Program. Sensors 2023, 23, 9141. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Meng, L.; Xu, X.; Niu, Y.; Qi, K.; Bian, W.; Yang, Q.; Liu, H.; Jia, J.; Wang, J. Research on Semi-Physical Simulation Testing of Inter-Satellite Laser Interference in the China Taiji Space Gravitational Wave Detection Program. Appl. Sci. 2021, 11, 7872. [Google Scholar] [CrossRef]
- Gong, Y.; Luo, J.; Wang, B. Concepts and status of Chinese space gravitational wave detection projects. Nat. Astron. 2021, 5, 881–889. [Google Scholar] [CrossRef]
- Luo, J.; Chen, L.-S.; Duan, H.-Z.; Gong, Y.-G.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M.; et al. TianQin: A space-borne gravitational wave detector. Class. Quantum Grav. 2016, 33, 035010. [Google Scholar] [CrossRef]
- Armano, M.; Audley, H.; Auger, G.; Baird, J.T.; Bassan, M.; Binetruy, P.; Born, M.; Bortoluzzi, D.; Brandt, N.; Caleno, M.; et al. Sub-Femto-gFree Fall for Space-Based Gravitational Wave Observatories: LISA Pathfinder Results. Phys. Rev. Lett. 2016, 116, 231101. [Google Scholar] [CrossRef]
- Sasso, C.P.; Mana, G.; Mottini, S. Telescope jitters and phase noise in the LISA interferometer. Opt. Express 2019, 27, 16855–16870. [Google Scholar] [CrossRef] [PubMed]
- Tröbs, M.; Schuster, S.; Lieser, M.; Zwetz, M.; Chwalla, M.; Danzmann, K.; Barránco, G.F.; Fitzsimons, E.D.; Gerberding, O.; Heinzel, G.; et al. Reducing tilt-to-length coupling for the LISA test mass interferometer. Class. Quantum Grav. 2018, 35, 105001. [Google Scholar] [CrossRef]
- Wegener, H.; Müller, V.; Heinzel, G.; Misfeldt, M. Tilt-to-Length Coupling in the GRACE Follow-On Laser Ranging Interferometer. J. Spacecr. Rocket. 2020, 57, 1362–1372. [Google Scholar] [CrossRef]
- Chwalla, M.; Danzmann, K.; Fernández Barranco, G.; Fitzsimons, E.; Gerberding, O.; Heinzel, G.; Killow, C.J.; Lieser, M.; Perreur-Lloyd, M.; Robertson, D.; et al. Design and construction of an optical test bed for LISA imaging systems and tilt-to-length coupling. Class. Quantum Grav. 2016, 33, 245015. [Google Scholar] [CrossRef]
- Schuster, S. Tilt-to-Length Coupling and Diffraction Aspects in Satellite Interferometry. Ph.D. Thesis, Leibniz Universität, Hannover, Germany, 2017. [Google Scholar]
- Wanner, G. Complex Optical Systems in Space: Numerical Modelling of the Heterodyne Interferometry of LISA Pathfinder and LISA. Ph.D. Thesis, Leibniz Universität, Hannover, Germany, 2010. [Google Scholar]
- Lee, Y. Development of an Advanced Tilt Actuator for Tilt-to-Length Coupling Investigations. Ph.D. Thesis, Leibniz Universität, Hannover, Germany, 2021. [Google Scholar]
- Schuster, S.; Wanner, G.; Tröbs MHeinzel, G. Vanishing tilt-to-length coupling for a singular case in two-beam laser interferometers with Gaussian beams. Appl. Opt. 2015, 54, 1010–1014. [Google Scholar] [CrossRef]
- Schuster, S.; Tröbs, M.; Wanner GHeinzel, G. Experimental demonstration of reduced tilt-to-length coupling by a two-lens imaging system. Opt. Express 2016, 24, 10466–10475. [Google Scholar] [CrossRef] [PubMed]
- Chwalla, M.; Danzmann, K.; Alvarez, M.D.; Delgado, J.J.E.; Barranco, G.F.; Fitzsimons, E.; Gerberding, O.; Heinzel, G.; Killow, C.J.; Lieser, M.; et al. Optical Suppression of Tilt-to-Length Coupling in the LISA Long-Arm Interferometer. Phys. Rev. Appl. 2020, 14, 014030. [Google Scholar] [CrossRef]
- Paczkowski, S.; Giusteri, R.; Hewitson, M.; Karnesis, N.; Fitzsimons, E.D.; Wanner GHeinzel, G. Postprocessing subtraction of tilt-to-length noise in LISA. Phys. Rev. D 2022, 106, 042005. [Google Scholar] [CrossRef]
- Wanner, G.; Karnesis, N. Preliminary results on the suppression of sensing cross-talk in LISA Pathfinder. J. Phys. Conf. Ser. 2017, 840, 012043. [Google Scholar] [CrossRef]
- Hartig, M.-S. Tilt-To-Length Coupling in LISA Pathfinder: Model, Data Analysis and Take-Away Messages for LISA. Ph.D. Thesis, Leibniz Universität, Hannover, Germany, 2022. [Google Scholar]
- Hartig, M.-S.; Schuster, S.; Heinzel, G.; Wanner, G. Non-geometric tilt-to-length coupling in precision interferometry: Mechanisms and analytical descriptions. J. Opt. 2023, 25, 055601. [Google Scholar] [CrossRef]
- Hartig, M.-S.; Schuster, S.; Wanner, G. Geometric tilt-to-length coupling in precision interferometry: Mechanisms and analytical descriptions. J. Opt. 2022, 24, 065601. [Google Scholar] [CrossRef]
- Hartig, M.-S.; Wanner, G. Tilt-to-length coupling in LISA Pathfinder: Analytical modeling. Phys. Rev. D 2023, 108, 022008. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Z.; Li, Y.; Fang, C.; Liu, H.; Gao, H. Method to Remove Tilt-to-Length Coupling Caused by Interference of Flat-Top Beam and Gaussian Beam. Appl. Sci. 2019, 9, 4112. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999; pp. 160–175. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Wang, S.; Qi, K.; Zhao, M.; Liu, H.; Yang, R.; Li, P.; Tao, W.; Luo, Z.; Gao, R. The Suppression Effect of an Imaging System on the Geometric Tilt-to-Length Coupling in a Test Mass Interferometer. Photonics 2024, 11, 638. https://doi.org/10.3390/photonics11070638
Shen J, Wang S, Qi K, Zhao M, Liu H, Yang R, Li P, Tao W, Luo Z, Gao R. The Suppression Effect of an Imaging System on the Geometric Tilt-to-Length Coupling in a Test Mass Interferometer. Photonics. 2024; 11(7):638. https://doi.org/10.3390/photonics11070638
Chicago/Turabian StyleShen, Jia, Shaoxin Wang, Keqi Qi, Mengyang Zhao, Heshan Liu, Ran Yang, Pan Li, Wei Tao, Ziren Luo, and Ruihong Gao. 2024. "The Suppression Effect of an Imaging System on the Geometric Tilt-to-Length Coupling in a Test Mass Interferometer" Photonics 11, no. 7: 638. https://doi.org/10.3390/photonics11070638
APA StyleShen, J., Wang, S., Qi, K., Zhao, M., Liu, H., Yang, R., Li, P., Tao, W., Luo, Z., & Gao, R. (2024). The Suppression Effect of an Imaging System on the Geometric Tilt-to-Length Coupling in a Test Mass Interferometer. Photonics, 11(7), 638. https://doi.org/10.3390/photonics11070638




