Tunable Radiation Patterns on Temperature-Dependent Materials
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Tuning the Scattering and Far Field for Temperature-Dependent Materials
3.2. Tuning the Scattering and Far Field of Hybrid Structures for Opposite Illumination
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
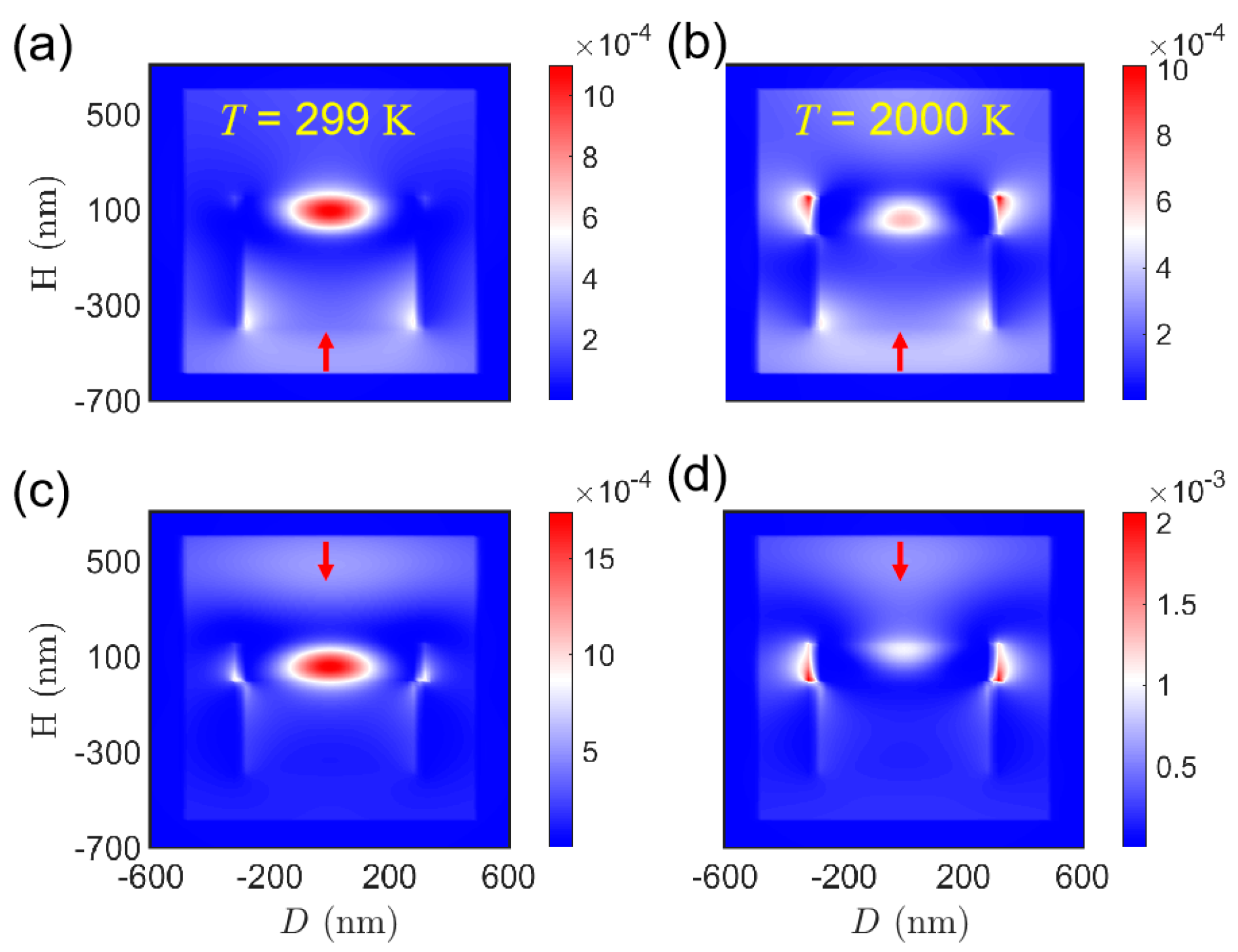
Appendix A.1. Far Fields and Radiation Patterns
Appendix A.2. Antennas Based on ENZ Materials
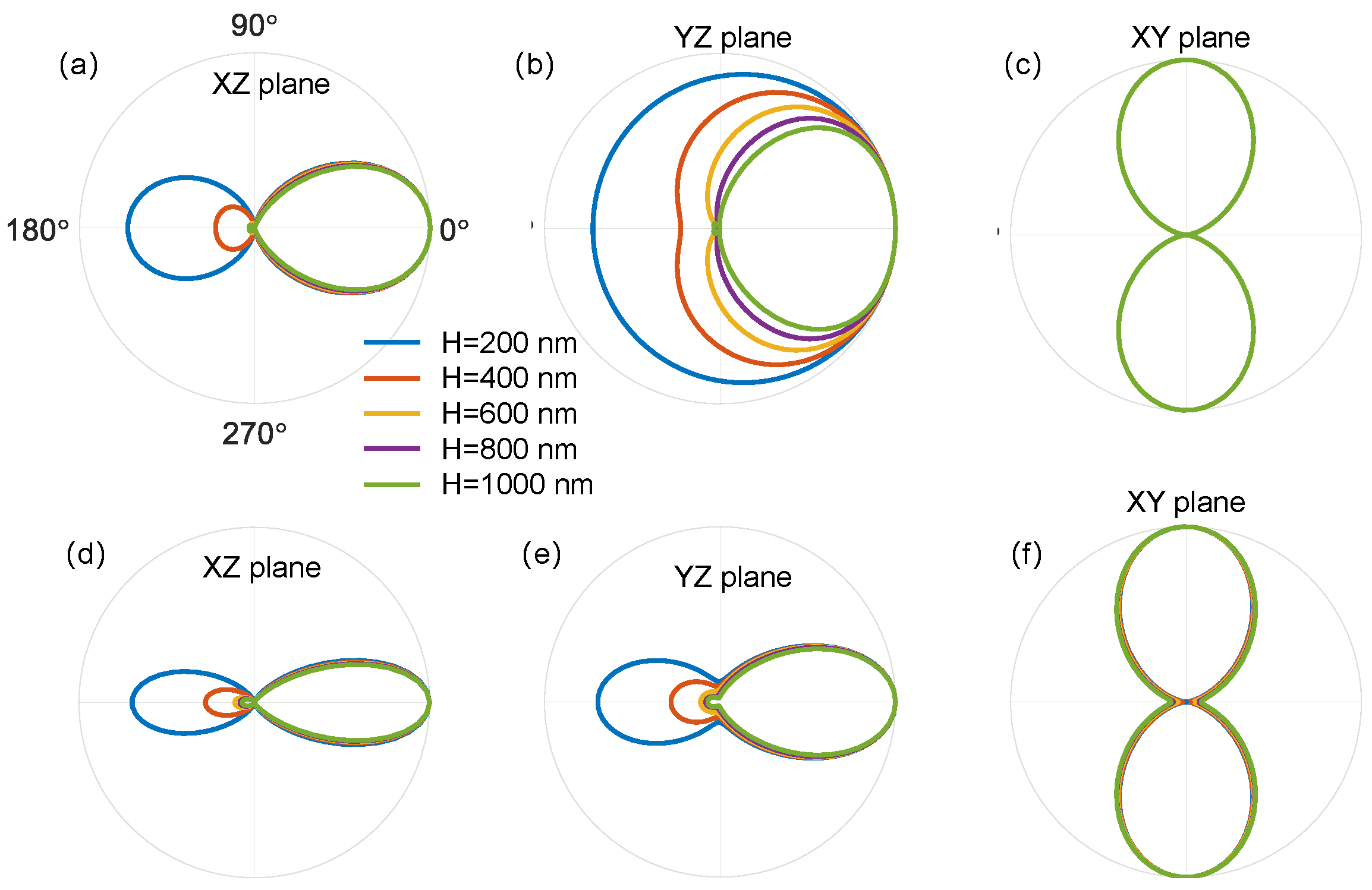
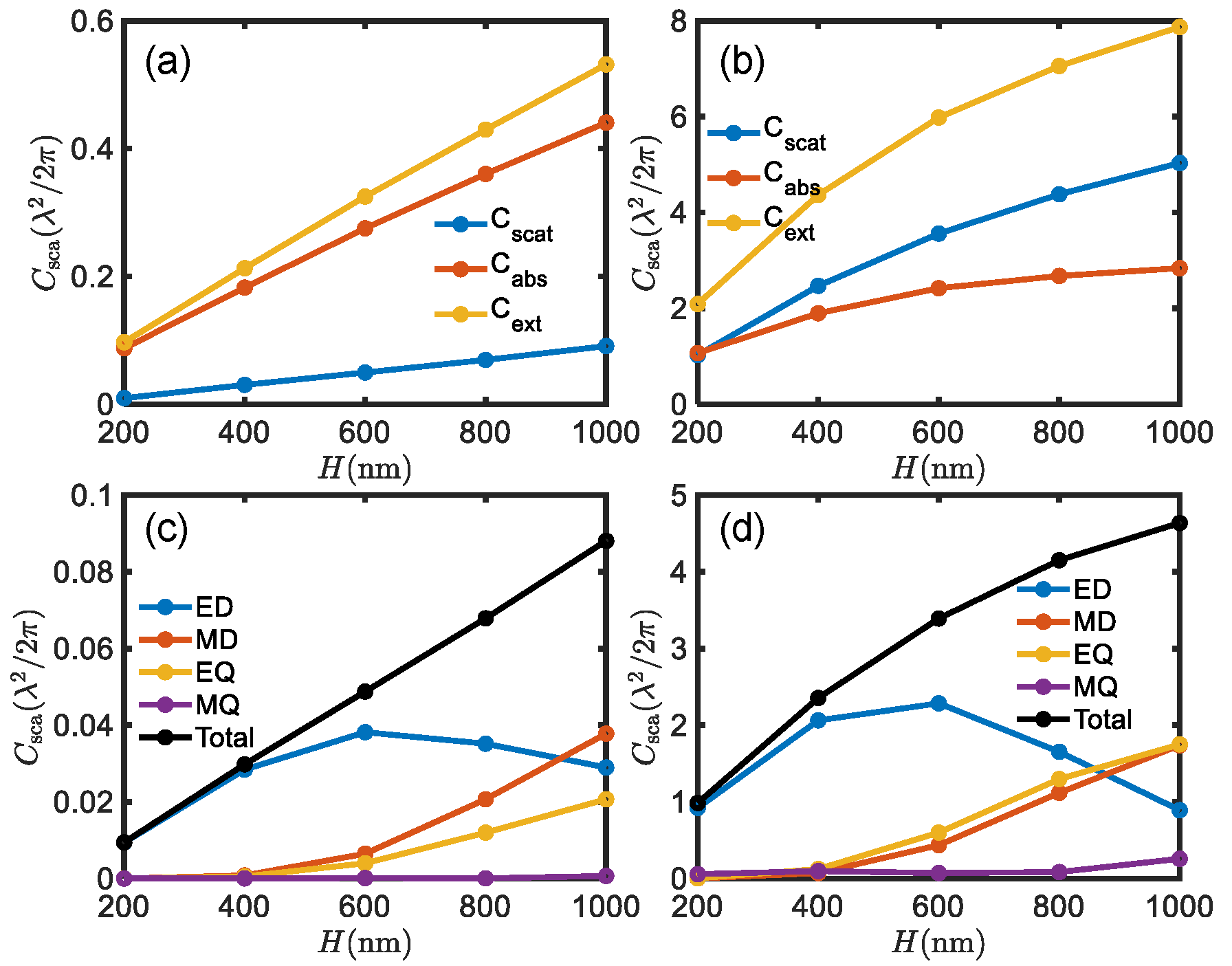
Appendix A.3. Antennas Based on Al0.18Ga0.82As
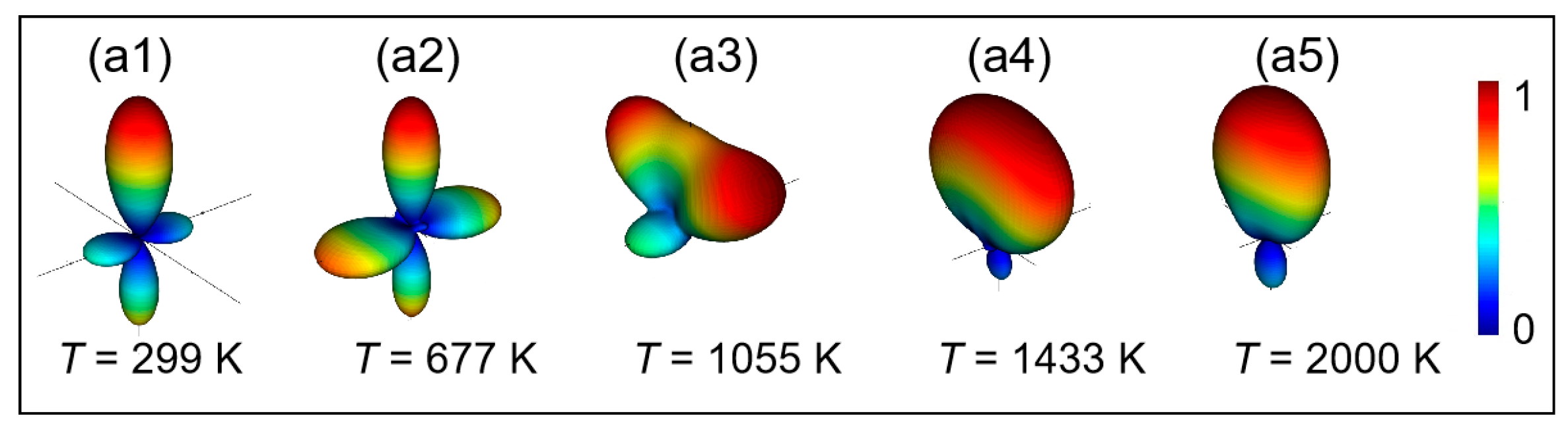
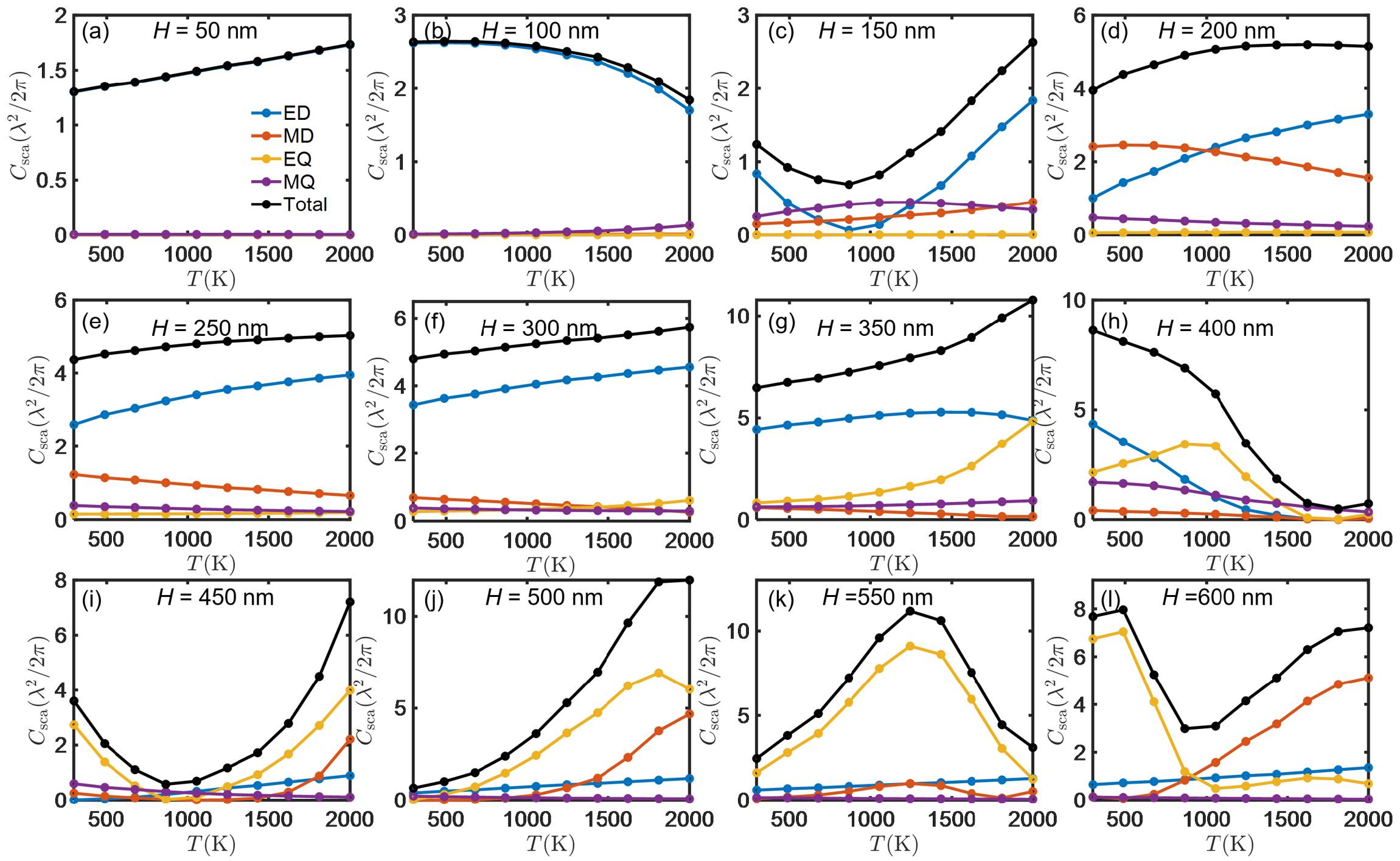
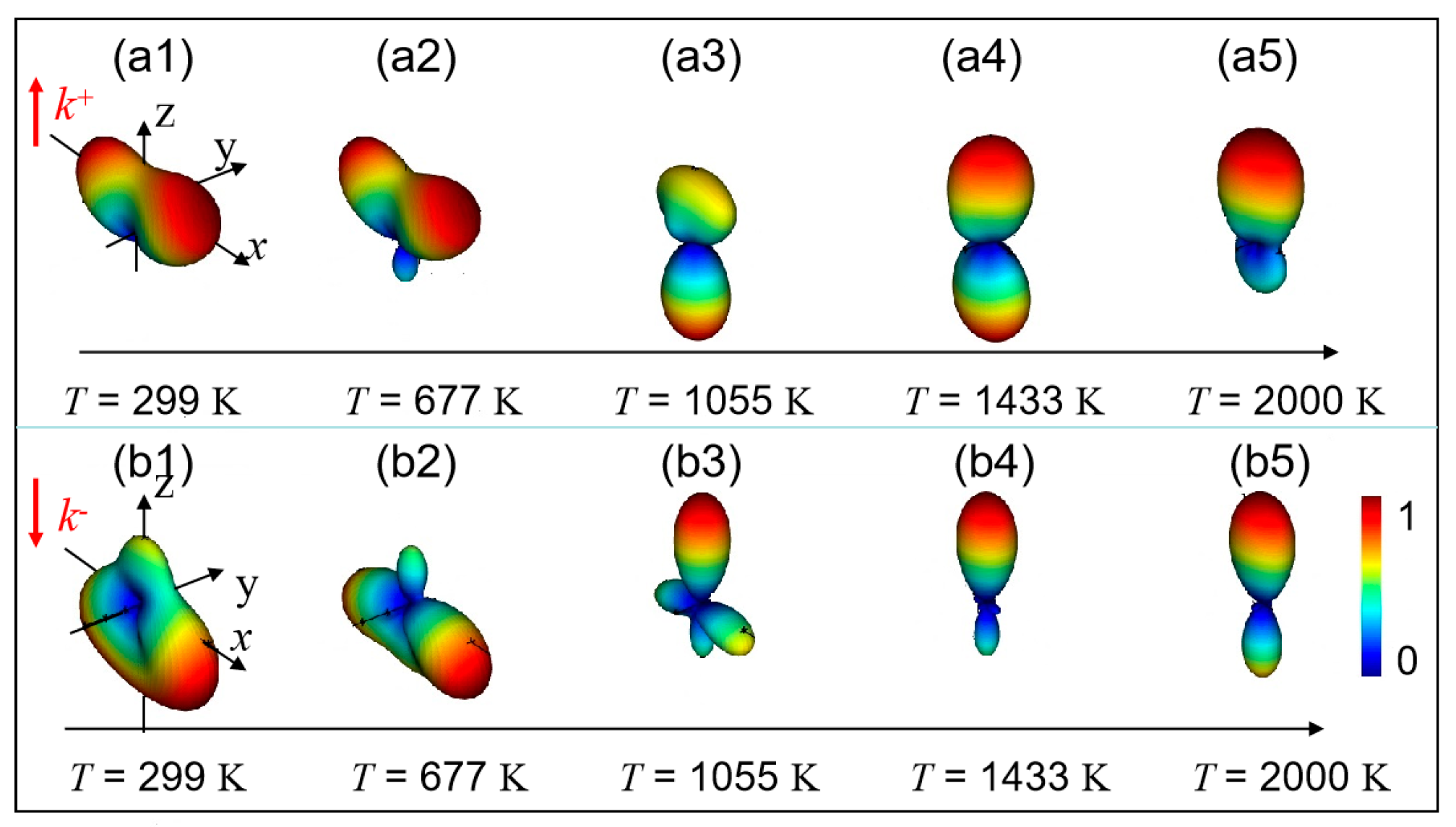
Appendix A.4. Field Distribution of the Hybrid Nonreciprocal Nonlinear Antennas
References
- Kinsey, N.; Devault, C.; Kim, J.; Boltasseva, A. Epsilon-Near-Zero Al-doped ZnO for ultrafast switching at telecom wavelengths. Optica 2015, 2, 616. [Google Scholar] [CrossRef]
- Alam, M.Z.; Leon, I.D.; Boyd, R.W. Large optical nonlinearity of indium tin oxide in its epsilon-near-zero region. Science 2016, 352, 795. [Google Scholar] [CrossRef] [PubMed]
- Argyropoulos, C.; Chen, P.-Y.; D’Aguanno, G.; Engheta, N.; Alu, A. Boosting optical nonlinearities in ϵ-near-zero plasmonic channels. Phys. Rev. Condens. Matter Mater. Phys. 2012, 85, 045129. [Google Scholar] [CrossRef]
- Mobini, E.; Alaee, R.; Boyd, R.W.; Dolgaleva, K. Giant asymmetric second-harmonic generation in bianisotropic metasurfaces based on bound states in the continuum. ACS Photonics 2021, 8, 3234–3240. [Google Scholar] [CrossRef]
- Ng, J.; Chen, C.; Chan, C.T. Metamaterial frequency-selective superabsorber. Opt. Lett. 2009, 34, 644–646. [Google Scholar] [CrossRef] [PubMed]
- Miroshnichenko, A.E.; Tribelsky, M.I. Ultimate absorption in light scattering by a finite obstacle. Phys. Rev. Lett. 2018, 120, 033902. [Google Scholar] [CrossRef] [PubMed]
- Clement, S.; Campbell, J.M.; Deng, W.; Guller, A.; Nisar, S.; Liu, G.; Wilson, B.C.; Goldys, E.M. Mechanisms for tuning engineered nanomaterials to enhance radiation therapy of cancer. Adv. Sci. 2020, 7, 2003584. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.P.; Sarangan, A.M. Temperature-dependent Sellmeier equation for the refractive index of Al(x)Ga(1-x)As. Opt. Lett. 2007, 32, 536–538. [Google Scholar] [CrossRef] [PubMed]
- Paul, J.; Miscuglio, M.; Gui, Y.; Sorger, V.J.; Wahlstrand, J.K. Two beam coupling by a hot electron nonlinearity. Opt. Lett. 2021, 46, 428–431. [Google Scholar] [CrossRef] [PubMed]
- Lui, C.H.; Mak, R.F.; Shan, R.; Heinz, R.F. Dynamics of Photoexcited GaAs band-edge absorption with subpicosecond Resolution. Phys. Rev. Lett. 2010, 105, 127404. [Google Scholar] [CrossRef] [PubMed]
- Agranat, M.B.; Ashitkov, S.I.; Ovchinnikov, A.V.; Sitnikov, D.S.; Yurkevich, A.A.; Chefonov, O.V.; Perel’man, L.T.; Anisimov, S.I.; Fortov, V.E.E. Thermal emission of hot electrons in a metal. JETP Lett. 2015, 101, 598–602. [Google Scholar] [CrossRef]
- Gehrsitz, S.; Reinhart, F.K. The relative index of AlxGa1−xAs below the band gap. J. Appl. Phys. 2000, 87, 7825–7837. [Google Scholar] [CrossRef]
- Russell, K.J.; Liu, T.L.; Cui, S.; Hu, E.L. Ultrafast photoluminescence from graphene. Nat. Photonics 2012, 6, 459–462. [Google Scholar] [CrossRef]
- Orad, R.; Enno, G.; Zahirul, A.M.; Israel, D.L.; Jeremy, U.; Boyd, R.W. Beyond the perturbative description of the nonliner optical response of low-index materials. Opt. Lett. 2017, 42, 3225. [Google Scholar]
- Heng, W.; Kang, D.; Chuhao, J.; Zhiqiang, Y.; Ting, M. Extended drude model for intraband-transition-induced optical nonlinearity. Phys. Rev. Appl. 2019, 11, 064062. [Google Scholar]
- Alaee, R.; Rockstuhl, C.; Fernandez-Corbaton, I. Exact multipolar decompositions with applications in nanophotonics. Adv. Opt. Mater. 2019, 7, 1800783.1–1800783.14. [Google Scholar] [CrossRef]
- Alaee, R.; Rockstuhl, C.; Fernandez-Corbaton, I. An electromagnetic multipole expansion beyond the long-wavelength approximation. Opt. Commun. 2018, 407, 17–21. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Alaee, R.; Filter, R.; Lehr, D.; Lederer, F.; Rockstuhl, C. A generalized Kerker condition for highly directive nanoantennas. Opt. Lett. 2015, 40, 2645–2648. [Google Scholar] [PubMed]
- Liu, W.; Kivshar, Y.S. Generalized Kerker effects in nanophotonics and meta-optics. Opt. Express 2018, 26, 13085–13105. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, L.; Wu, F.; Huang, K. Tunable Radiation Patterns on Temperature-Dependent Materials. Photonics 2024, 11, 646. https://doi.org/10.3390/photonics11070646
Cheng L, Wu F, Huang K. Tunable Radiation Patterns on Temperature-Dependent Materials. Photonics. 2024; 11(7):646. https://doi.org/10.3390/photonics11070646
Chicago/Turabian StyleCheng, Lin, Fan Wu, and Kun Huang. 2024. "Tunable Radiation Patterns on Temperature-Dependent Materials" Photonics 11, no. 7: 646. https://doi.org/10.3390/photonics11070646
APA StyleCheng, L., Wu, F., & Huang, K. (2024). Tunable Radiation Patterns on Temperature-Dependent Materials. Photonics, 11(7), 646. https://doi.org/10.3390/photonics11070646





