Design and Fabrication of Metasurfaces-Based Polarizing Beam Splitter with Tailored Deflection Angles for 940-nm Wavelength
Abstract
:1. Introduction
2. Methods
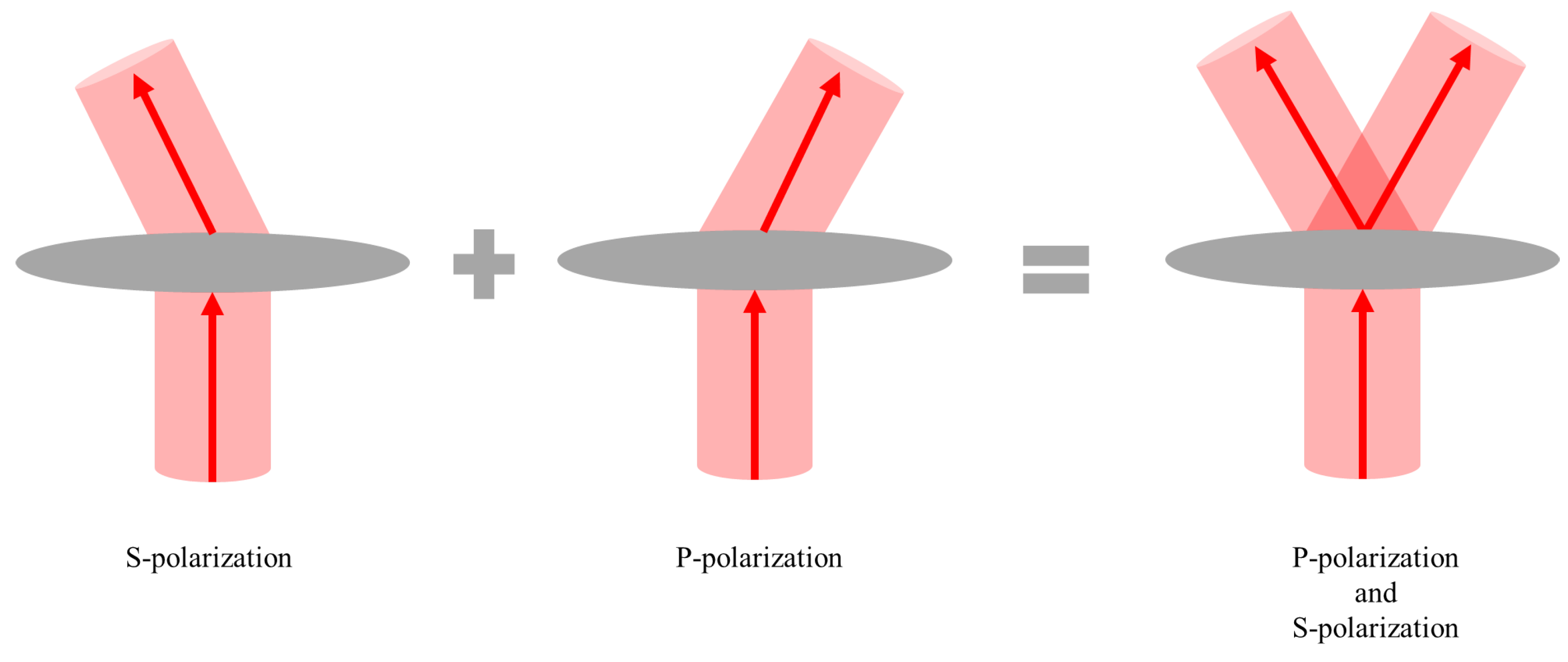
2.1. Ideal Phase Profile of the Metasurface
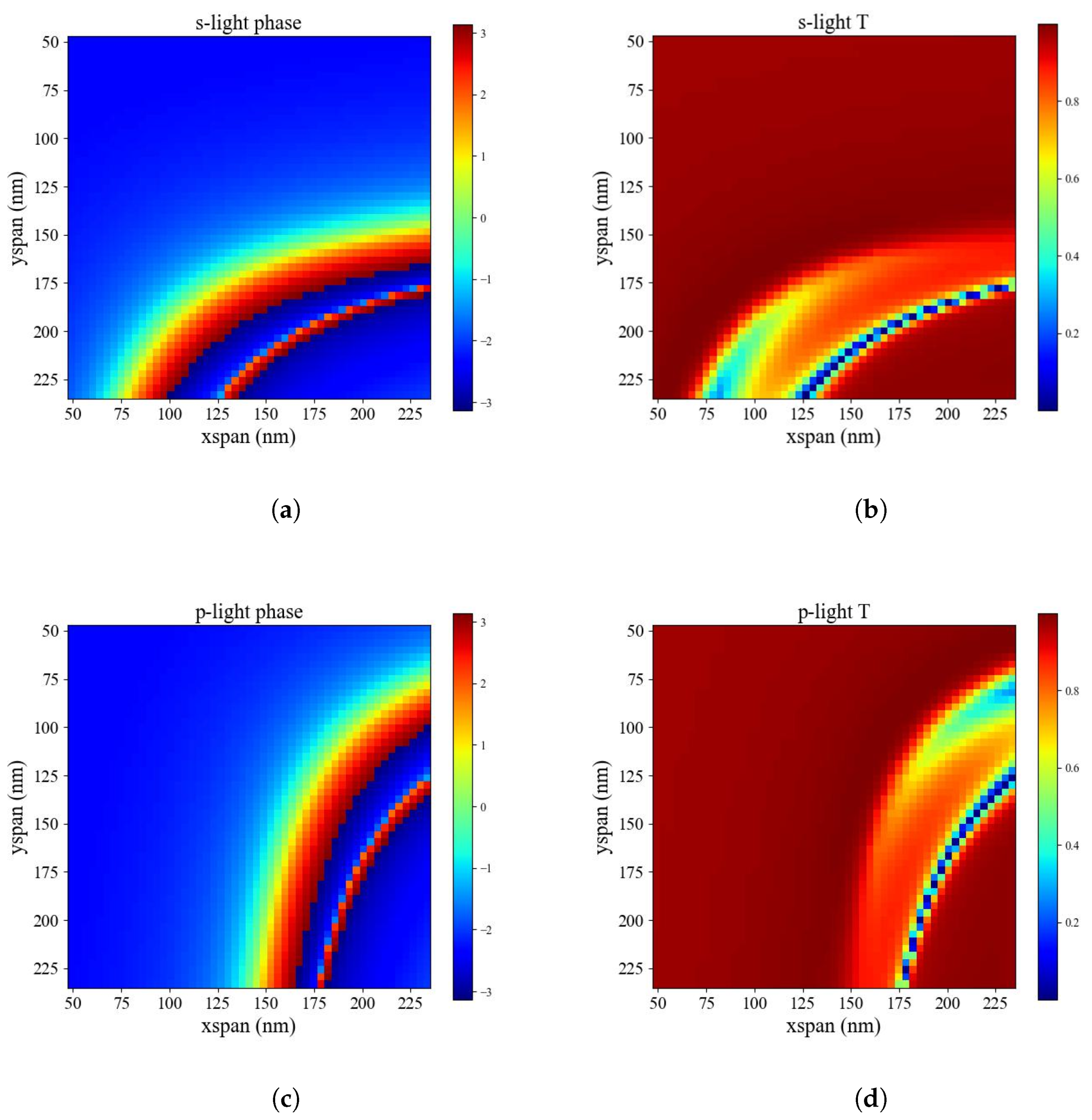
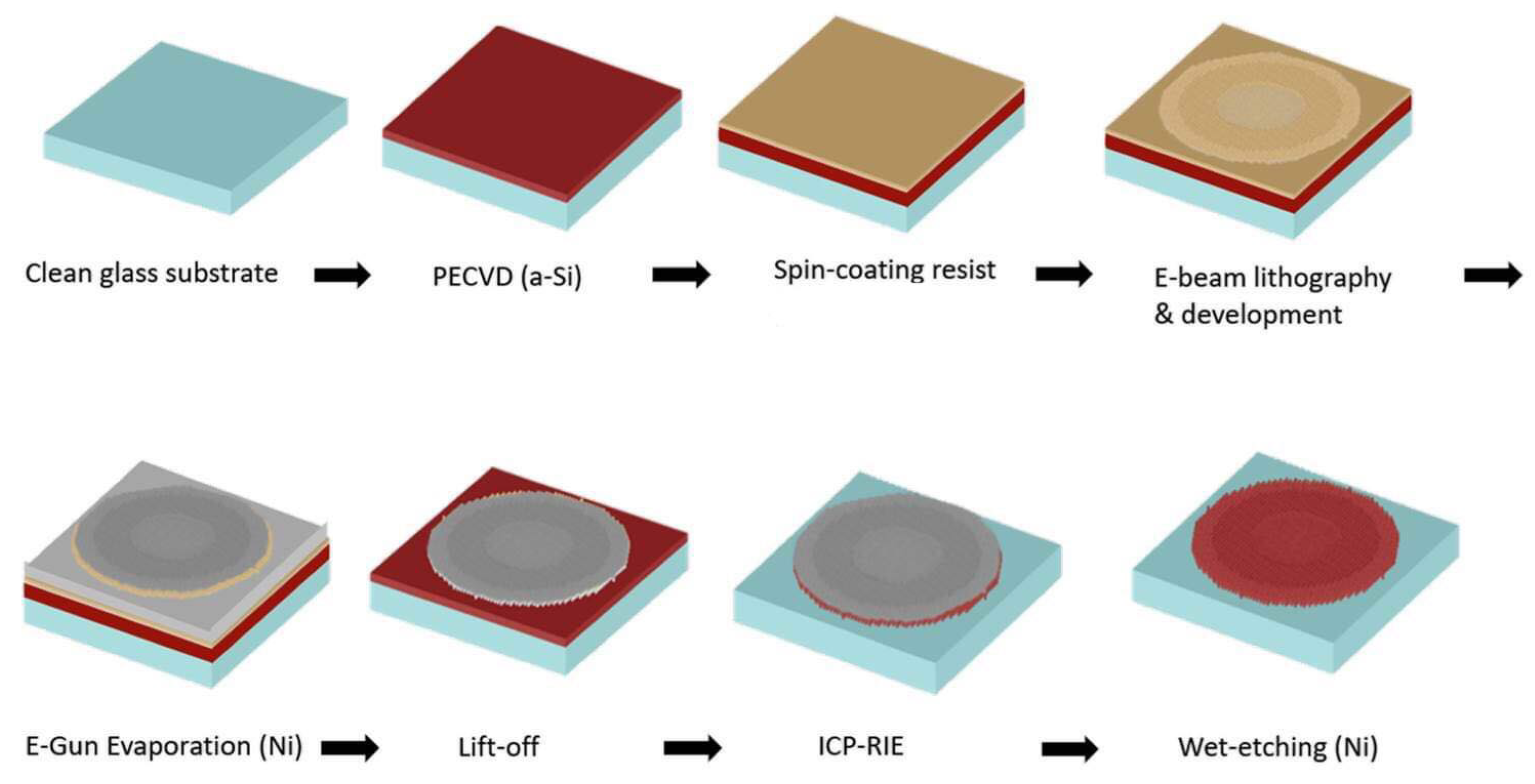
2.2. Design of Metasurface
3. Results
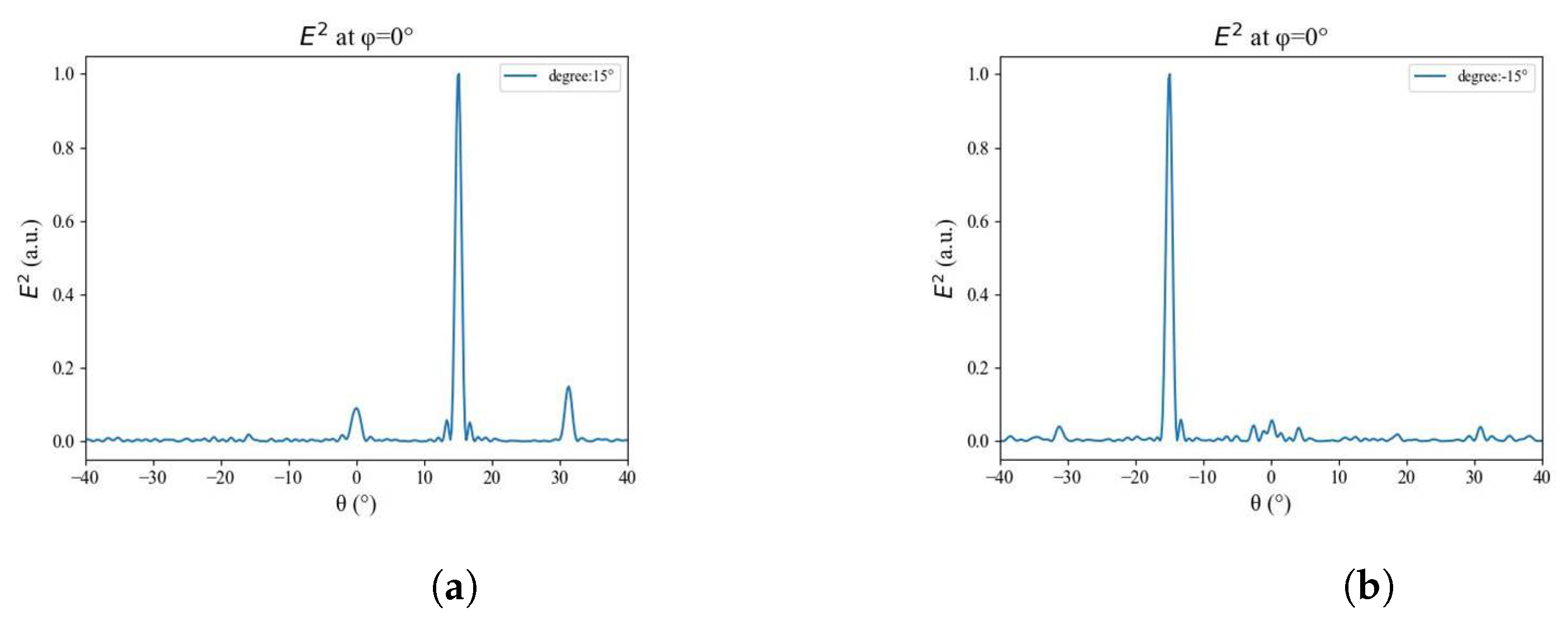
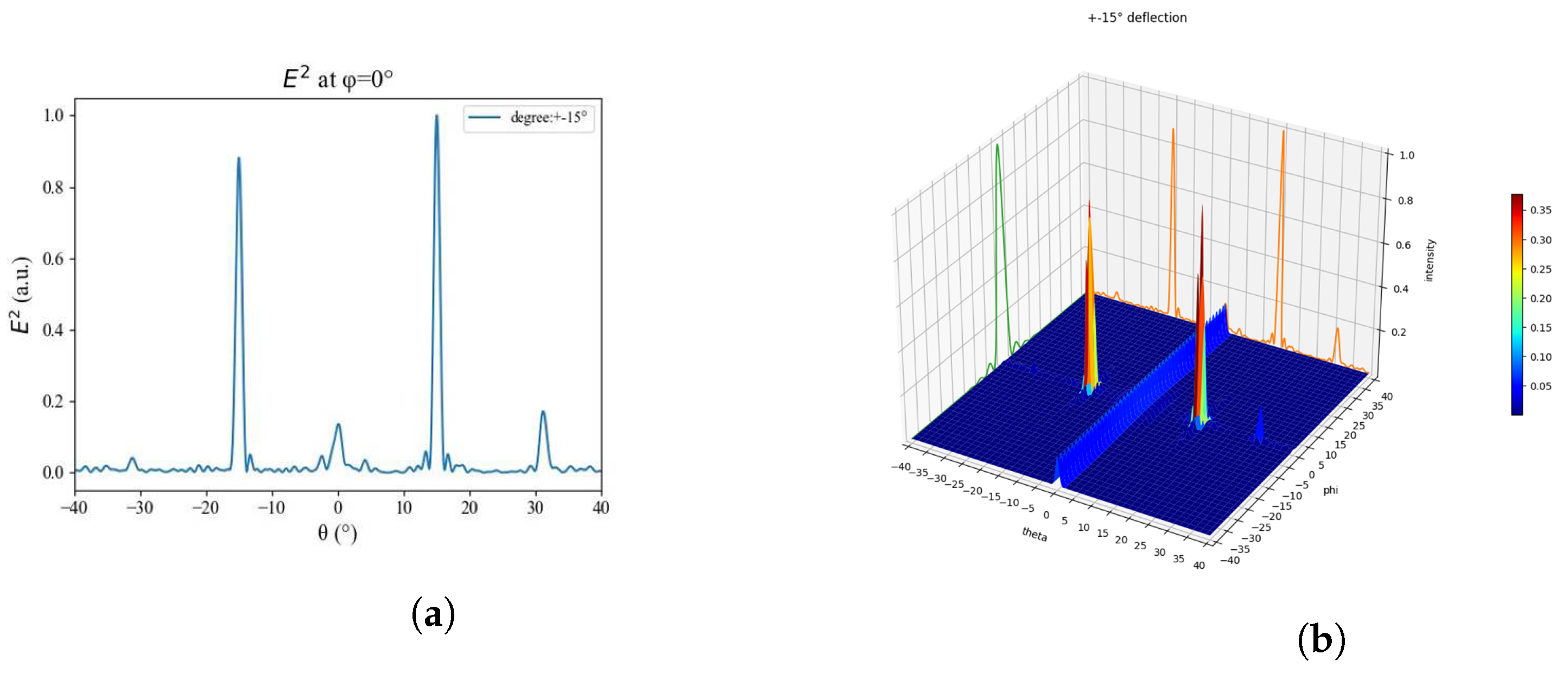
3.1. Simulation Results
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schnabel, R.; Bunkowski, A.; Burmeister, O.; Danzmann, K. Three-port beam splitters-combiners for interferometer applications. Opt. Lett. 2006, 31, 658–660. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Powers, P.E.; Sarangan, A.M.; Zhan, Q. Optical characterization of wiregrid micropolarizers designed for infrared imaging polarimetry. Opt. Lett. 2008, 33, 1653–1655. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Liu, W. Broadband polarizing beam splitter with an embedded metal-wire nanograting. Opt. Lett. 2005, 30, 1434–1436. [Google Scholar] [CrossRef] [PubMed]
- Okuno, M.; Sugita, A.; Jinguji, K.; Kawachi, M. Birefringence control of silica waveguides on Si and its application to a polarization-beam splitter/switch. J. Light. Technol. 1994, 12, 625–633. [Google Scholar] [CrossRef]
- Reyes-Vera, E.; Usuga-Restrepo, J.; Jimenez-Durango, C.; Montoya-Cardona, J.; Gomez-Cardona, N. Design of low-loss and highly birefringent porous-core photonic crystal fiber and its application to terahertz polarization beam splitter. IEEE Photonics J. 2018, 10, 1–13. [Google Scholar] [CrossRef]
- Pu, C.; Zhu, Z.; Lo, Y.H. Surface micro-machined polarization beam splitting system. In Proceedings of the 1998 IEEE/LEOS Summer Topical Meeting. Digest. Broadband Optical Networks and Technologies: An Emerging Reality. Optical MEMS. Smart Pixels. Organic Optics and Optoelectronics (Cat. No. 98TH8369), Monterey, CA, USA, 20–24 July 1998; pp. II25–II26. [Google Scholar]
- Liu, T.; Zakharian, A.R.; Fallahi, M.; Moloney, J.V.; Mansuripur, M. Design of a compact photonic-crystal-based polarizing beam splitter. IEEE Photonics Technol. Lett. 2005, 17, 1435–1437. [Google Scholar]
- Tseng, M.L.; Hsiao, H.H.; Chu, C.H.; Chen, M.K.; Sun, G.; Liu, A.Q.; Tsai, D.P. Metalenses: Advances and applications. Adv. Opt. Mater. 2018, 6, 1800554. [Google Scholar] [CrossRef]
- Kamali, S.M.; Arbabi, E.; Arbabi, A.; Faraon, A. A review of dielectric optical metasurfaces for wavefront control. Nanophotonics 2018, 7, 1041–1068. [Google Scholar] [CrossRef]
- Chen, H.T.; Taylor, A.J.; Yu, N. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar] [CrossRef]
- Hu, J.; Bandyopadhyay, S.; Liu, Y.h.; Shao, L.Y. A review on metasurface: From principle to smart metadevices. Front. Phys. 2021, 8, 586087. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, S.; Zentgraf, T. Metasurface holography: From fundamentals to applications. Nanophotonics 2018, 7, 1169–1190. [Google Scholar] [CrossRef]
- Shen, Z.; Huang, D. A review on metasurface beam splitters. Nanomanufacturing 2022, 2, 194–228. [Google Scholar] [CrossRef]
- Chen, X.; Zou, H.; Su, M.; Tang, L.; Wang, C.; Chen, S.; Su, C.; Li, Y. All-dielectric metasurface-based beam splitter with arbitrary splitting ratio. Nanomaterials 2021, 11, 1137. [Google Scholar] [CrossRef]
- Zhang, D.; Ren, M.; Wu, W.; Gao, N.; Yu, X.; Cai, W.; Zhang, X.; Xu, J. Nanoscale beam splitters based on gradient metasurfaces. Opt. Lett. 2018, 43, 267–270. [Google Scholar] [CrossRef] [PubMed]
- Jia, S.L.; Wan, X.; Bao, D.; Zhao, Y.J.; Cui, T.J. Independent controls of orthogonally polarized transmitted waves using a Huygens metasurface. Laser Photonics Rev. 2015, 9, 545–553. [Google Scholar] [CrossRef]
- Emani, N.K.; Khaidarov, E.; Paniagua-Domínguez, R.; Fu, Y.H.; Valuckas, V.; Lu, S.; Zhang, X.; Tan, S.T.; Demir, H.V.; Kuznetsov, A.I. High-efficiency and low-loss gallium nitride dielectric metasurfaces for nanophotonics at visible wavelengths. Appl. Phys. Lett. 2017, 111, 221101. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Wu, T.; Liu, Y.; Wang, Y.; Yu, Z.; Ye, H.; Yu, L. Efficient polarization beam splitter based on all-dielectric metasurface in visible region. Nanoscale Res. Lett. 2019, 14, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Xia, C.; Ren, Y.; Lin, P.; Wang, Y.; Xu, T. Silicon metasurface-based infrared polarizing beam splitter with on-demand deflection angles. Opt. Lett. 2023, 48, 1722–1725. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.Y.; Lin, C.P.; Su, G.D.J. Ultrawide-angle and high-efficiency metalens in hexagonal arrangement. Sci. Rep. 2020, 10, 15677. [Google Scholar] [CrossRef]
- Saleh, B.E.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, R.; Ma, Y. Characteristic Analysis of Compact Spectrometer Based on Off-Axis Meta-Lens. Appl. Sci. 2018, 8, 321. [Google Scholar] [CrossRef]
- Fu, R.; Li, Z.; Zheng, G.; Chen, M.; Yang, Y.; Tao, J.; Wu, L.; Deng, Q. Reconfigurable step-zoom metalens without optical and mechanical compensations. Opt. Express 2019, 27, 12221–12230. [Google Scholar] [CrossRef] [PubMed]
- Zuo, H.; Choi, D.Y.; Gai, X.; Ma, P.; Xu, L.; Neshev, D.N.; Zhang, B.; Luther-Davies, B. High-efficiency all-dielectric metalenses for mid-infrared imaging. Adv. Opt. Mater. 2017, 5, 1700585. [Google Scholar] [CrossRef]





| [16] | [17] | [18] | [19] | Our Method | |
|---|---|---|---|---|---|
| material | Metal | GaN | Si | Si | a-Si |
| working band | 33.3 mm | 430∼470 nm | 583 nm | 940 nm | 940 nm |
| deflection angle | /−42∘ | ||||
| thickness | 2 mm | 460 nm | 260 nm | 7.5 μm | 570 nm |
| s-/p- deflection efficiency | 49%/49% | 37%/26.4% | 63.7%/66.4% | 20%/27% | 41.54%/36.92% |
| research type | sim & exp | sim & exp | sim | sim & exp | sim & exp |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, K.-C.; Pan, J.-L.; Weng, J.-L.; Lee, Y.-H.; Chiang, J.-A.; Su, G.-D. Design and Fabrication of Metasurfaces-Based Polarizing Beam Splitter with Tailored Deflection Angles for 940-nm Wavelength. Photonics 2024, 11, 655. https://doi.org/10.3390/photonics11070655
Peng K-C, Pan J-L, Weng J-L, Lee Y-H, Chiang J-A, Su G-D. Design and Fabrication of Metasurfaces-Based Polarizing Beam Splitter with Tailored Deflection Angles for 940-nm Wavelength. Photonics. 2024; 11(7):655. https://doi.org/10.3390/photonics11070655
Chicago/Turabian StylePeng, Kuan-Cheng, Ju-Lin Pan, Jin-Li Weng, Yun-Han Lee, Jui-An Chiang, and Guo-Dung Su. 2024. "Design and Fabrication of Metasurfaces-Based Polarizing Beam Splitter with Tailored Deflection Angles for 940-nm Wavelength" Photonics 11, no. 7: 655. https://doi.org/10.3390/photonics11070655
APA StylePeng, K.-C., Pan, J.-L., Weng, J.-L., Lee, Y.-H., Chiang, J.-A., & Su, G.-D. (2024). Design and Fabrication of Metasurfaces-Based Polarizing Beam Splitter with Tailored Deflection Angles for 940-nm Wavelength. Photonics, 11(7), 655. https://doi.org/10.3390/photonics11070655






