Analogue of High-Q Transparency Band and Sensitivity in All-Dielectric Metasurfaces Supporting Bound States in the Continuum
Abstract
1. Introduction
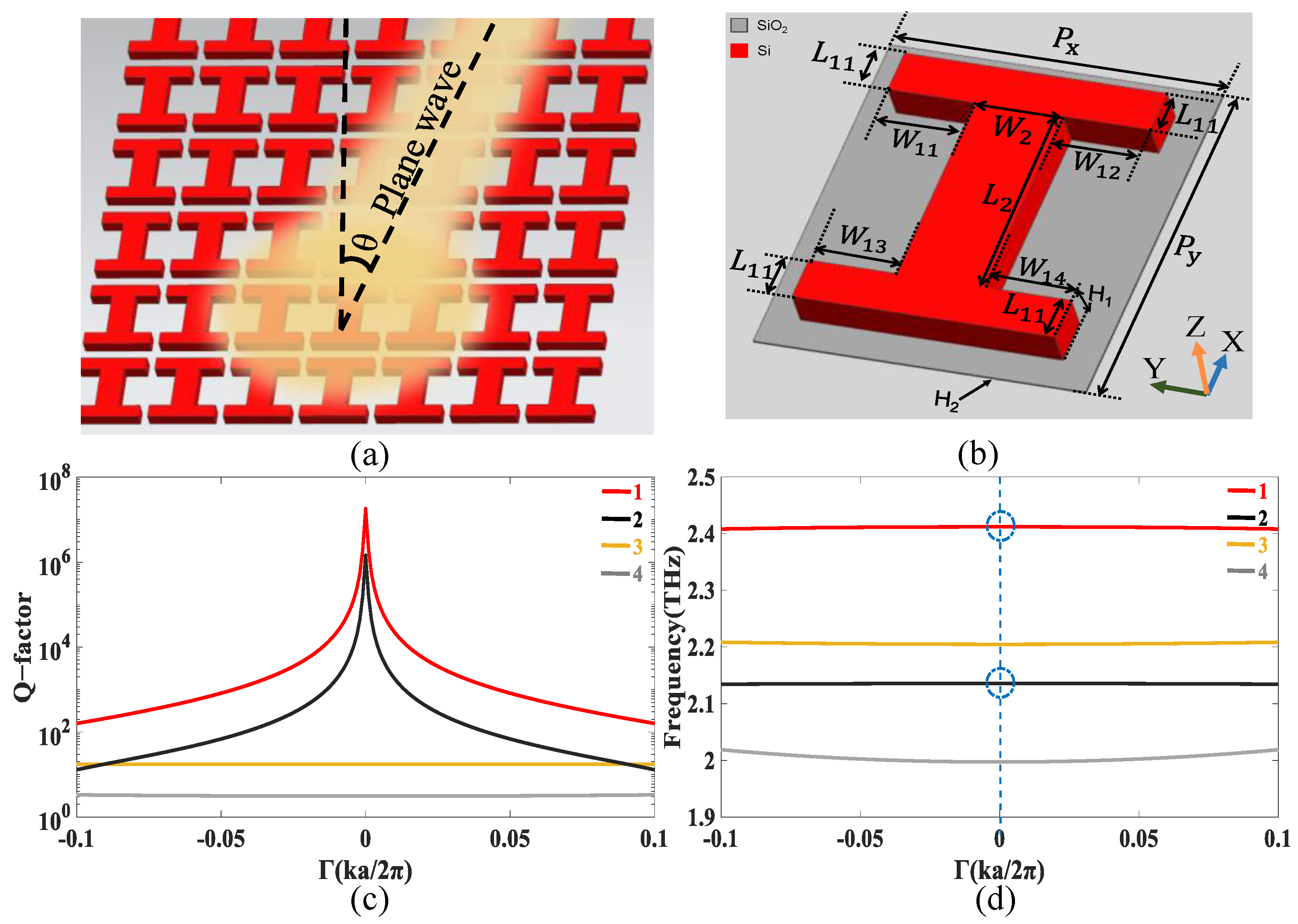
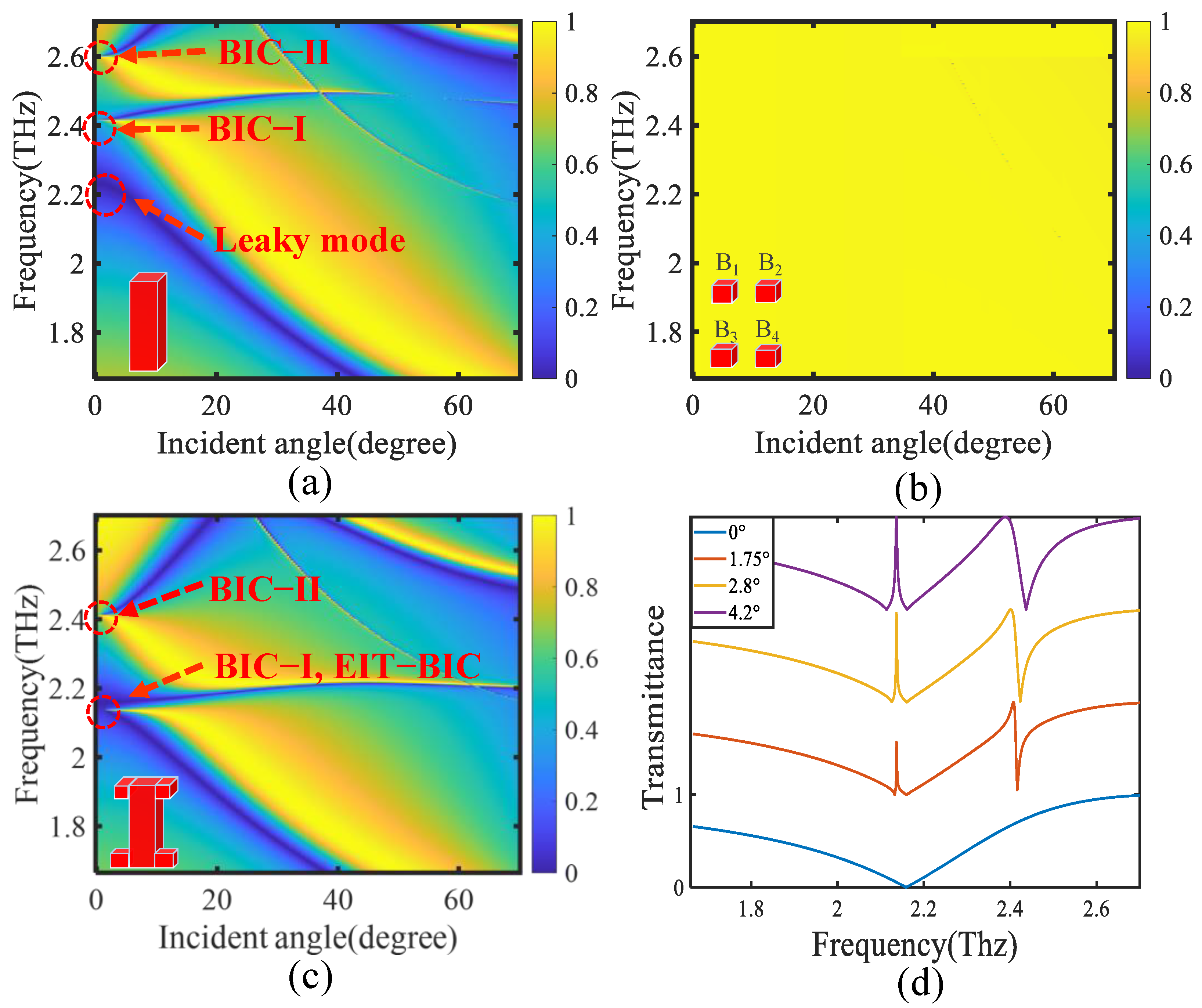
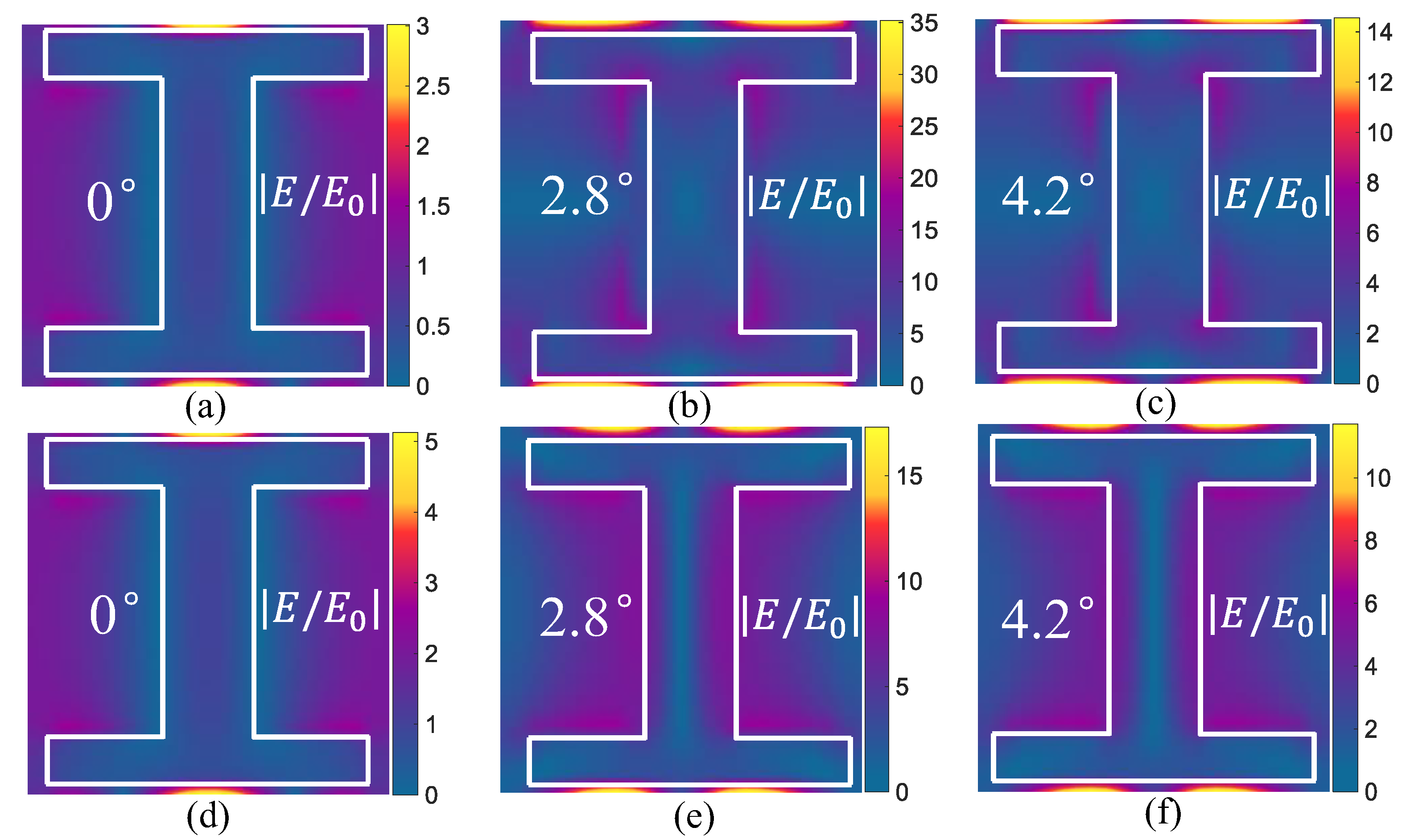
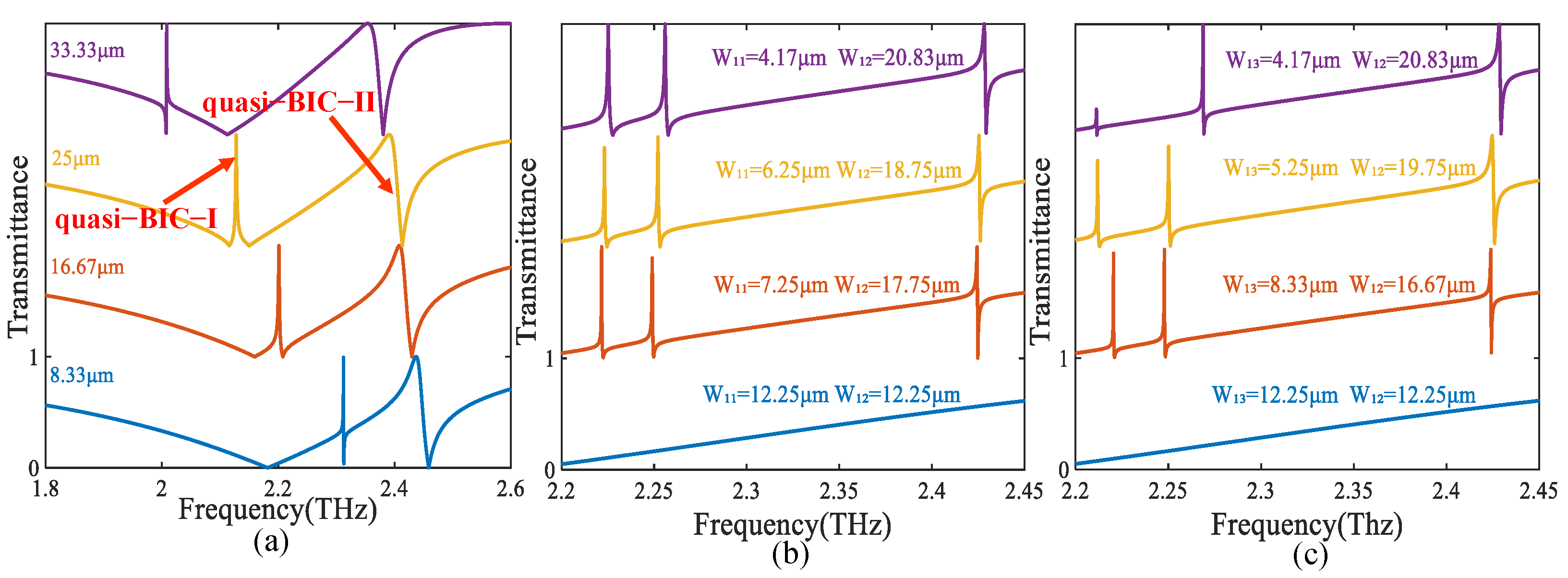
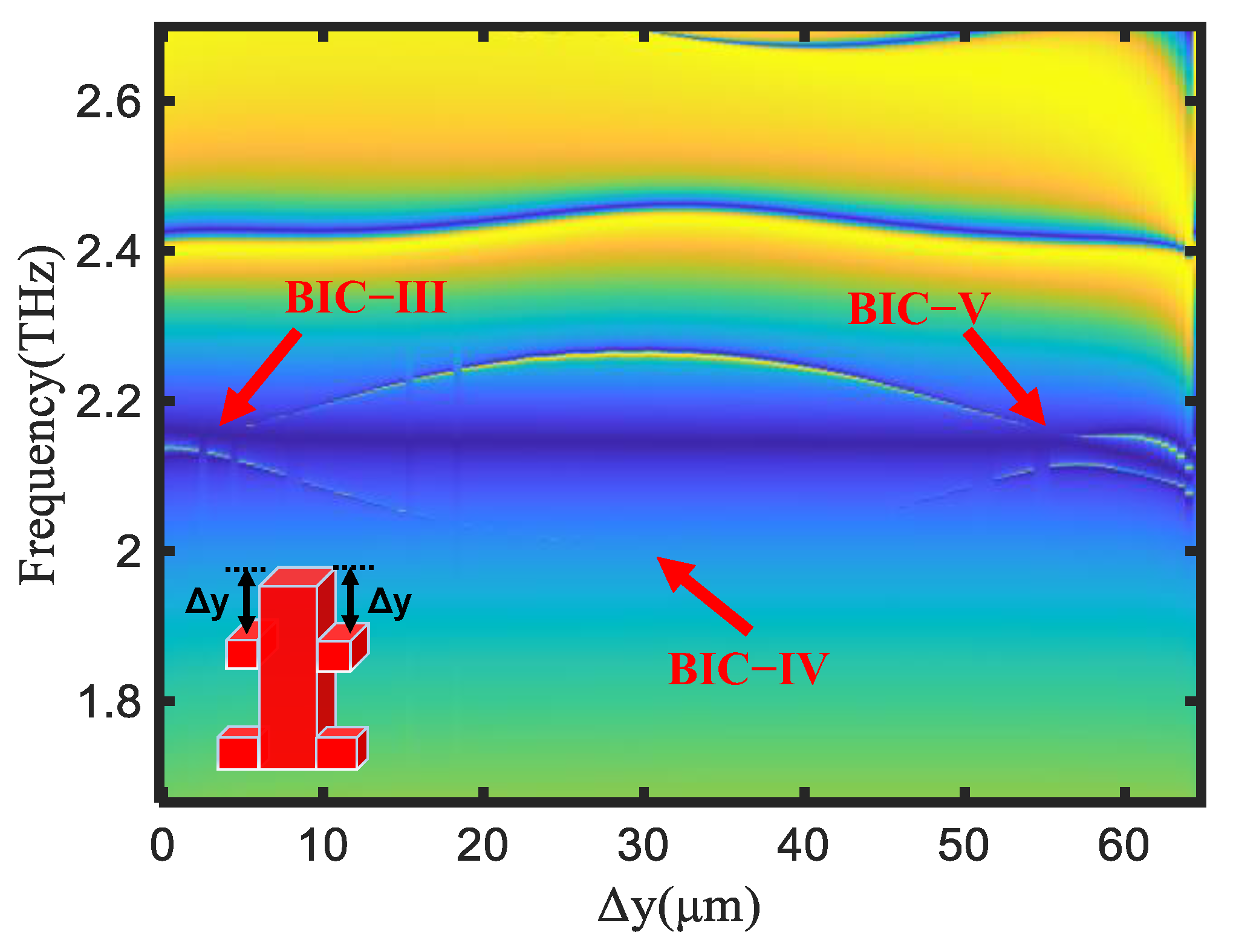
2. Analysis and Discussion
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljacic, M. Bound States in the Continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar]
- Marinica, D.C.; Borisov, A.G.; Shabanov, S.V. Bound States in the Continuum in Photonics. Phys. Rev. Lett. 2008, 100, 183902. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Xu, L.; Powell, D.A.; Padilla, W.J.; Miroshnichenko, A.E. Resonant Leaky Modes in All-Dielectric Metasystems: Fundamentals and Applications. Phys. Rep.-Rev. Sect. Phys. Lett. 2023, 1008, 1–66. [Google Scholar] [CrossRef]
- Friedrich, H.; Wintgen, D. Interfering Resonances and Bound States in the Continuum. Phys. Rev. A Gen. Phys. 1985, 32, 3231–3242. [Google Scholar] [PubMed]
- Wang, B.; Liu, W.; Zhao, M.; Wang, J.; Zhang, Y.; Chen, A.; Guan, F.; Liu, X.; Shi, L.; Zi, J. Generating Optical Vortex Beams by Momentum-Space Polarization Vortices Centred at Bound States in the Continuum. Nat. Photonics 2020, 14, 623–628. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.; Du, T.; Ma, H.; Jiang, X. Tailoring Bound States in the Continuum in Symmetric Photonic Crystal Slabs by Coupling Strengths. Opt. Express 2022, 30, 8049–8062. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Tong, M.; Hu, S.; He, W.; Cheng, X.; Jiang, T. Spatiotemporal Lineshape Tailoring in Bic-Mediated Reconfigurable Metamaterials. Adv. Funct. Mater. 2022, 32, 2203680. [Google Scholar] [CrossRef]
- Feng, S.; Liu, T.; Chen, W.; Wu, F.; Xiao, S. Enhanced Sum-Frequency Generation from Etchless Lithium Niobate Empowered by Dual Quasi-Bound States in the Continuum. Sci. China Phys. Mech. Astron. 2023, 66, 124214. [Google Scholar] [CrossRef]
- Hu, Y.; Xie, S.; Bai, C.; Shen, W.; Yang, J. Quasi-Bound States in the Continuum Enabled Strong Terahertz Chiroptical Response in Bilayer Metallic Metasurfaces. Crystals 2022, 12, 1052. [Google Scholar] [CrossRef]
- Overvig, A.; Yu, N.; Alù, A. Chiral Quasi-Bound States in the Continuum. Phys. Rev. Lett. 2021, 126, 073001. [Google Scholar] [CrossRef]
- Shi, T.; Deng, Z.-L.; Geng, G.; Zeng, X.; Zeng, Y.; Hu, G.; Overvig, A.; Li, J.; Qiu, C.-W.; Alù, A.; et al. Planar Chiral Metasurfaces with Maximal and Tunable Chiroptical Response Driven by Bound States in the Continuum. Nat. Commun. 2022, 13, 4111. [Google Scholar] [CrossRef] [PubMed]
- Hwang, M.-S.; Lee, H.-C.; Kim, K.-H.; Jeong, K.-Y.; Kwon, S.-H.; Koshelev, K.; Kivshar, Y.; Park, H.-G. Ultralow-Threshold Laser Using Super-Bound States in the Continuum. Nat. Commun. 2021, 12, 4135. [Google Scholar] [CrossRef]
- Yu, Y.; Sakanas, A.; Zali, A.R.; Semenova, E.; Yvind, K.; Mørk, J. Ultra-Coherent Fano Laser Based on a Bound State in the Continuum. Nat. Photonics 2021, 15, 758–764. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, M.; Liu, W.; Guan, F.; Liu, X.; Shi, L.; Chan, C.T.; Zi, J. Shifting Beams at Normal Incidence Via Controlling Momentum-Space Geometric Phases. Nat. Commun. 2021, 12, 6046. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhu, Y.; Duan, J.; Qin, M.; Wu, F.; Xiao, S. Enhancing Goos-Hanchen Shift Based on Magnetic Dipole Quasi-Bound States in the Continuum in All-Dielectric Metasurfaces. Opt. Express 2021, 29, 29541–29549. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Qin, M.; Wu, F.; Xiao, S. High-Efficiency Optical Frequency Mixing in an All-Dielectric Metasurface Enabled by Multiple Bound States in the Continuum. Phys. Rev. B 2023, 107, 075441. [Google Scholar] [CrossRef]
- Wang, X.; Duan, J.; Chen, W.; Zhou, C.; Liu, T.; Xiao, S. Controlling Light Absorption of Graphene at Critical Coupling through Magnetic Dipole Quasi-Bound States in the Continuum Resonance. Phys. Rev. B 2020, 102, 155432. [Google Scholar] [CrossRef]
- Vertchenko, L.; DeVault, C.; Malureanu, R.; Mazur, E.; Lavrinenko, A. Near-Zero Index Photonic Crystals with Directive Bound States in the Continuum. Laser Photonics Rev. 2021, 15, 2000559. [Google Scholar] [CrossRef]
- Carletti, L.; Koshelev, K.; De Angelis, C.; Kivshar, Y. Giant Nonlinear Response at the Nanoscale Driven by Bound States in the Continuum. Phys. Rev. Lett. 2018, 121, 033903. [Google Scholar] [CrossRef]
- Fang, C.; Yang, Q.; Yuan, Q.; Gu, L.; Gan, X.; Shao, Y.; Liu, Y.; Han, G.; Hao, Y. Efficient Second-Harmonic Generation from Silicon Slotted Nanocubes with Bound States in the Continuum. Laser Photonics Rev. 2022, 16, 2100498. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Y.; Lin, Y.; Xiang, J.; Feng, T.; Cao, Q.; Li, J.; Lan, S.; Liu, J. High-Q Quasibound States in the Continuum for Nonlinear Metasurfaces. Phys. Rev. Lett. 2019, 123, 253901. [Google Scholar] [PubMed]
- Al-Ani, I.A.M.; As’Ham, K.; Huang, L.; Miroshnichenko, A.E.; Hattori, H.T. Enhanced Strong Coupling of Tmdc Monolayers by Bound State in the Continuum. Laser Photonics Rev. 2021, 15, 2100240. [Google Scholar] [CrossRef]
- Huang, L.; Krasnok, A.; Alú, A.; Yu, Y.; Neshev, D.; Miroshnichenko, A.E. Enhanced Light-Matter Interaction in Two-Dimensional Transition Metal Dichalcogenides. Rep. Prog. Phys. 2022, 85, 046401. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Z.; Du, Y.; Qin, J. Ultrasensitive Terahertz Sensing with High-Q Toroidal Dipole Resonance Governed by Bound States in the Continuum in All-Dielectric Metasurface. Nanophotonics 2021, 10, 1295–1307. [Google Scholar]
- Lee, J.; Zhen, B.; Chua, S.L.; Qiu, W.J.; Joannopoulos, J.D.; Soljacic, M.; Shapira, O. Observation and Differentiation of Unique High-Q Optical Resonances near Zero Wave Vector in Macroscopic Photonic Crystal Slabs. Phys. Rev. Lett. 2012, 109, 067401. [Google Scholar]
- Hsu, C.W.; Zhen, B.; Chua, S.-L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Bloch Surface Eigenstates within the Radiation Continuum. Light. Sci. Appl. 2013, 2, e84. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, C.; Liang, Y.; Li, Z.; Noda, S. Analytical Perspective for Bound States in the Continuum in Photonic Crystal Slabs. Phys. Rev. Lett. 2014, 113, 037401. [Google Scholar] [CrossRef]
- Niu, J.; Zhai, Y.; Han, Q.; Liu, J.; Yang, B. Resonance-Trapped Bound States in He Continuum in Metallic Thz Metasurfaces. Opt. Lett. 2021, 46, 162–165. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Chen, C.; Kaj, K.; Hammock, I.; Huang, Y.; Averitt, R.D.; Zhang, X. Terahertz Investigation of Bound States in the Continuum of Metallic Metasurfaces. Optica 2020, 7, 1548–1554. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, Q.; Wang, Y.; Xie, S. Bound States in the Continuum in the Double-Period Rectangular Hole Arrays Perforated in One Layer of Photonic Crystal Slab in the Visible Wavelength Region. Opt. Commun. 2019, 436, 151–160. [Google Scholar] [CrossRef]
- Liang, L.; Zheng, Q.; Nan, X.; Dong, Y. Asymmetric All-Dielectric Active Metasurface for Efficient Dual Reflection Modulation. Opt. Commun. 2022, 505, 127539. [Google Scholar] [CrossRef]
- Liu, M.; Choi, D.-Y. Extreme Huygens’ Metasurfaces Based on Quasibound States in the Continuum. Nano Lett. 2018, 18, 8062–8069. [Google Scholar] [CrossRef] [PubMed]
- Abujetas, D.R.; van Hoof, N.; Huurne, S.T.; Rivas, J.G.; Sánchez-Gil, J.A. Spectral and Temporal Evidence O Robust Photonic Bound States in the Continuum on Terahertz Metasurfaces. Optica 2019, 6, 996–1001. [Google Scholar]
- Liao, Z.; Ma, Q.; Wang, L.; Yang, Z.; Li, M.; Deng, F.; Hong, W. Guiding-Mode-Assisted Double-Bics in an All-Dielectric Metasurface. Opt. Express 2022, 30, 24676–24688. [Google Scholar] [CrossRef]
- Limonov, M.F.; Rybin, M.V.; Poddubny, A.N.; Kivshar, Y.S. Fano Resonances in Photonics. Nat. Photonics 2017, 11, 543–554. [Google Scholar] [CrossRef]
- Ma, K.; Zhang, Y.; Su, H.; Yi, G.; Yu, C.; Wu, Y. Tunable Fano and Eit-Like Resonances in a Nested Feedback Ring Resonator. J. Lightwave Technol. 2022, 40, 2040–2044. [Google Scholar] [CrossRef]
- Han, S.; Pitchappa, P.; Wang, W.; Srivastava, Y.K.; Rybin, M.V.; Singh, R. Extended Bound States in the Continuum with Symmetry-Broken Terahertz Dielectric Metasurfaces. Adv. Opt. Mater. 2021, 9, 2002001. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically Resonant Dielectric Nanostructures. Science 2016, 354, aag2472. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Lee, J.; Chua, S.-L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Observation of Trapped Light within the Radiation Continuum. Nature 2013, 499, 188–191. [Google Scholar] [CrossRef]
- Gao, X.; Hsu, C.W.; Zhen, B.; Lin, X.; Joannopoulos, J.D.; Soljačić, M.; Chen, H. Formation Mechanism of Guided Resonances and Bound States in the Continuum in Photonic Crystal Slabs. Sci. Rep. 2016, 6, 31908. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Ovcharenko, A.I.; Blanchard, C.; Hugonin, J.-P.; Sauvan, C. Bound States in the Continuum in Symmetric and Asymmetric Photonic Crystal Slabs. Phys. Rev. B 2020, 101, 155303. [Google Scholar] [CrossRef]
- Algorri, J.F.; Zografopoulos, D.C.; Ferraro, A.; García-Cámara, B.; Beccherelli, R.; Sánchez-Pena, J.M. Ultrahigh-Quality Factor Resonant Dielectric Metasurfaces Based on Hollow Nanocuboids. Opt. Express 2019, 27, 6320–6330. [Google Scholar] [CrossRef]
- Han, S.; Cong, L.; Srivastava, Y.K.; Qiang, B.; Rybin, M.V.; Kumar, A.; Jain, R.; Lim, W.X.; Achanta, V.G.; Prabhu, S.S.; et al. All-Dielectric Active Terahertz Photonics Driven by Bound States in the Continuum. Adv. Mater. 2019, 31, e1901921. [Google Scholar] [CrossRef]
- Kyaw, C.; Yahiaoui, R.; Burrow, J.A.; Tran, V.; Keelen, K.; Sims, W.; Red, E.C.; Rockward, W.S.; Thomas, M.A.; Sarangan, A.; et al. Polarization-Selective Modulation of Supercavity Resonances Originating from Bound States in the Continuum. Commun. Phys. 2020, 3, 212. [Google Scholar] [CrossRef]
- Romano, S.; Zito, G.; Yépez, S.N.L.; Cabrini, S.; Penzo, E.; Coppola, G.; Rendina, I.; Mocellaark, V. Tuning the Exponential Sensitivity of a Bound-State-in-Continuum Optical Sensor. Opt. Express 2019, 27, 18776–18786. [Google Scholar] [CrossRef]
- Srivastava, Y.K.; Ako, R.T.; Gupta, M.; Bhaskaran, M.; Sriram, S.; Singh, R. Terahertz Sensing of 7 Nm Dielectric Film with Bound States in the Continuum Metasurfaces. Appl. Phys. Lett. 2019, 115, 151105. [Google Scholar] [CrossRef]
- Xiao, S.; Qin, M.; Duan, J.; Wu, F.; Liu, T. Polarization-Controlled Dynamically Switchable High-Harmonic Generation from All-Dielectric Metasurfaces Governed by Dual Bound States in the Continuum. Phys. Rev. B 2022, 105, 195440. [Google Scholar] [CrossRef]
- Papasimakis, N.; Fedotov, V.A.; Zheludev, N.I.; Prosvirnin, S.L. Metamaterial Analog of Electromagnetically Induced Transparency. Phys. Rev. Lett. 2008, 101, 253903. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Li, H.; Xu, H.; Zhao, M.; Xiong, C.; Zhang, B.; Wu, K. Slow Light Effect Based on Tunable Plasmon-Induced Transparency of Monolayer Black Phosphorus. J. Phys. D Appl. Phys. 2019, 52, 405203. [Google Scholar] [CrossRef]
- Lukin, M.D.; Imamoğlu, A. Controlling Photons Using Electromagnetically Induced Transparency. Nature 2001, 413, 273–276. [Google Scholar] [CrossRef]
- Dong, Z.-G.; Liu, H.; Cao, J.-X.; Li, T.; Wang, S.-M.; Zhu, S.-N.; Zhang, X. Enhanced Sensing Performance by the Plasmonic Analog of Electromagnetically Induced Transparency in Active Metamaterials. Appl. Phys. Lett. 2010, 97, 114101. [Google Scholar] [CrossRef]
- Gu, J.; Singh, R.; Liu, X.; Zhang, X.; Ma, Y.; Zhang, S.; Maier, S.A.; Tian, Z.; Azad, A.K.; Chen, H.-T.; et al. Active Control of Electromagnetically Induced Transparency Analogue in Terahertz Metamaterials. Nat. Commun. 2012, 3, 1151. [Google Scholar] [CrossRef]
- Algorri, J.F.; Dell’olio, F.; Roldán-Varona, P.; Rodríguez-Cobo, L.; Lopez-Higuera, J.-M.; Sánchez-Pena, J.M.; Dmitriev, V.; Zografopoulos, D. Analogue of Electromagnetically Induced Transparency in Square Slotted Silicon Metasurfaces Supporting Bound States in the Continuum. Opt. Express 2022, 30, 4615–4630. [Google Scholar] [CrossRef]
- Cong, L.; Singh, R. Symmetry-Protected Dual Bound States in the Continuum in Metamaterials. Adv. Opt. Mater. 2019, 7, 1900383. [Google Scholar] [CrossRef]
- Shi, W.; Gu, J.; Zhang, X.; Xu, Q.; Han, J.; Yang, Q.; Cong, L.; Zhang, W. Terahertz Bound States in the Continuum with Incident Angle Robustness Induced by a Dual Period Metagrating. Photonics Res. 2022, 10, 810–819. [Google Scholar] [CrossRef]
- Yang, Y.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. All-Dielectric Metasurface Analogue of Electromagnetically Induced Transparency. Nat. Commun. 2014, 5, 5753. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, W.; Boulesbaa, A.; Kravchenko, I.I.; Briggs, D.P.; Puretzky, A.; Geohegan, D.; Valentine, J. Nonlinear Fano-Resonant Dielectric Metasurfaces. Nano Lett. 2015, 15, 7388–7393. [Google Scholar] [CrossRef]
- Huang, L.J.; Xu, L.; Woolley, M.; Miroshnichenko, A.E. Trends in Quantum Nanophotonics. Adv. Quantum Technol. 2020, 3, 1900126. [Google Scholar]
- Wang, X.; Wang, J.; Zhao, X.; Shi, L.; Zi, J. Realizing Tunable Evolution of Bound States in the Continuum and Circularly Polarized Points by Symmetry Breaking. ACS Photonics 2022, 10, 2316–2322. [Google Scholar] [CrossRef]
- Luo, Z.; Ren, X.; Wang, Q.; Cheng, Q.; Cui, T. Anisotropic and Nonlinear Metasurface for Multiple Functions. Sci. China-Inf. Sci. 2021, 64, 192301. [Google Scholar] [CrossRef]
- Wu, C.; Li, Q.; Zhao, S.; Zhang, Z.; Liu, X.; Wei, S.; Li, H. Broadband Efficient Polarization-Pure Airy Beam Generation Based on Three-Layer Metasurface. Phys. Status Solidi B-Basic Solid State Phys. 2021, 258, 2000621. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shuai, L.; Xie, S.; Nan, H.; Guan, X. Analogue of High-Q Transparency Band and Sensitivity in All-Dielectric Metasurfaces Supporting Bound States in the Continuum. Photonics 2024, 11, 775. https://doi.org/10.3390/photonics11080775
Shuai L, Xie S, Nan H, Guan X. Analogue of High-Q Transparency Band and Sensitivity in All-Dielectric Metasurfaces Supporting Bound States in the Continuum. Photonics. 2024; 11(8):775. https://doi.org/10.3390/photonics11080775
Chicago/Turabian StyleShuai, Ling, Suxia Xie, Haoxuan Nan, and Xin Guan. 2024. "Analogue of High-Q Transparency Band and Sensitivity in All-Dielectric Metasurfaces Supporting Bound States in the Continuum" Photonics 11, no. 8: 775. https://doi.org/10.3390/photonics11080775
APA StyleShuai, L., Xie, S., Nan, H., & Guan, X. (2024). Analogue of High-Q Transparency Band and Sensitivity in All-Dielectric Metasurfaces Supporting Bound States in the Continuum. Photonics, 11(8), 775. https://doi.org/10.3390/photonics11080775



