Controlling the Shape of a Double DNA-like Helix as an Element of Metamaterials
Abstract
:1. Introduction
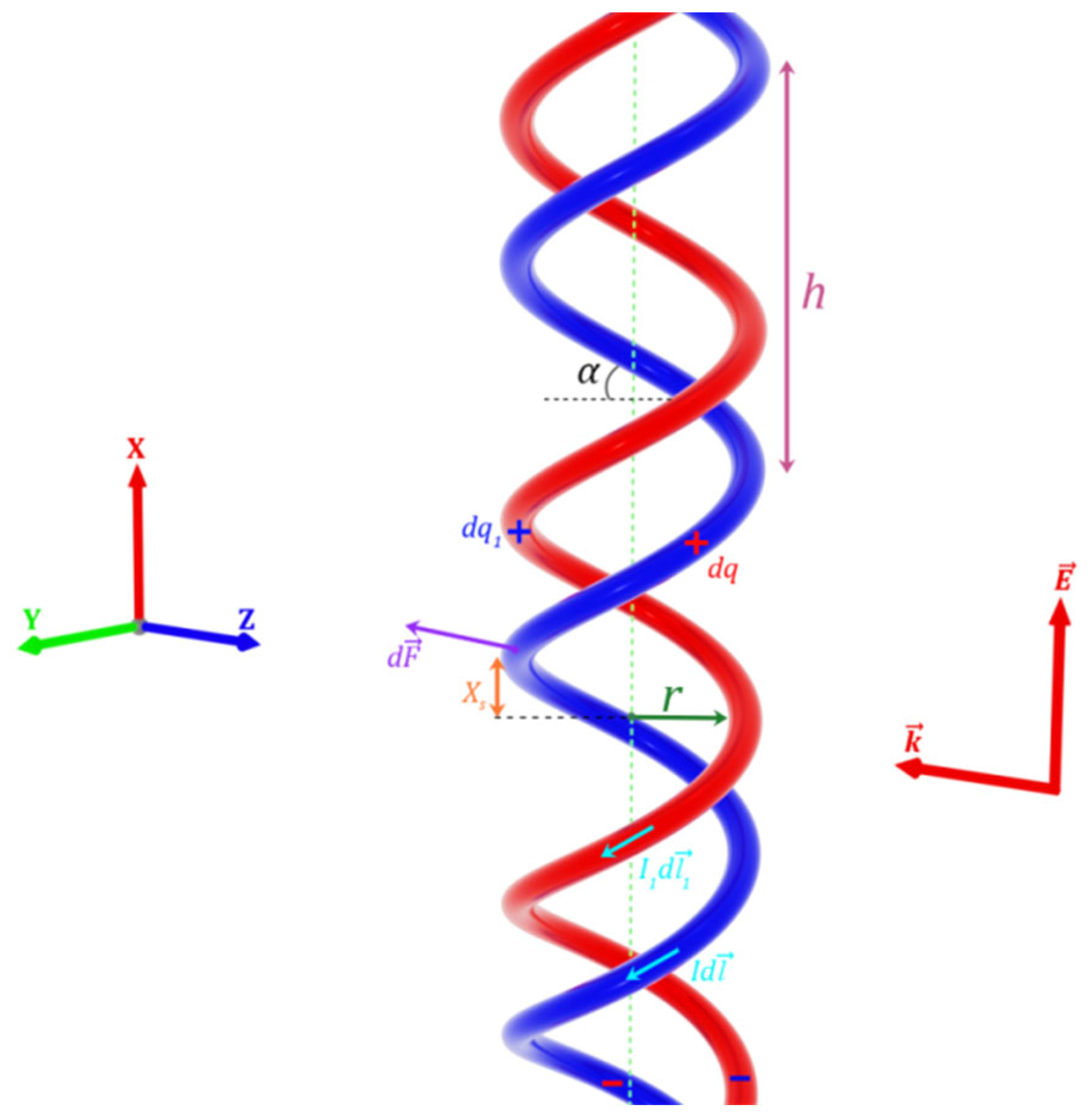
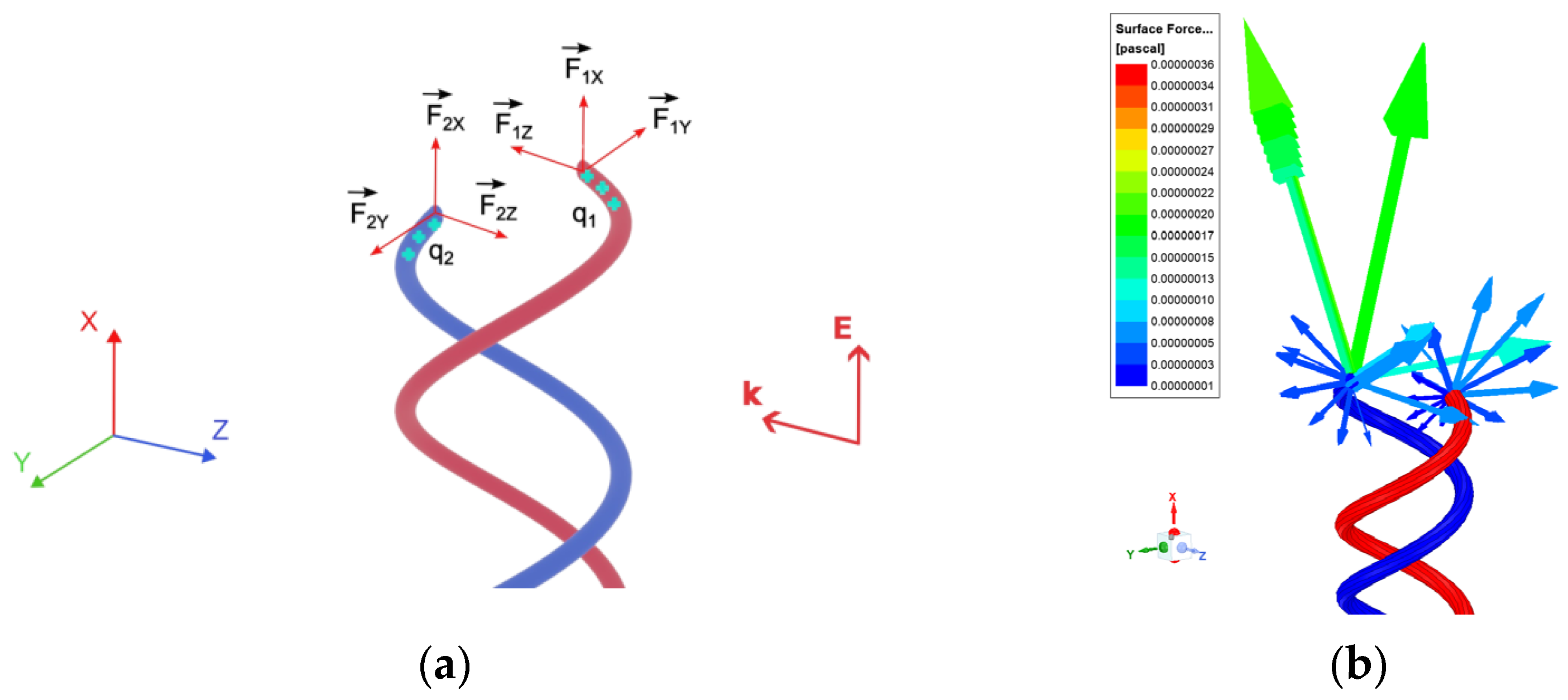
2. The Theoretical Calculation of Forces in a Double DNA-like Helix in the Field of an Electromagnetic Wave in a Long Wavelength Approximation
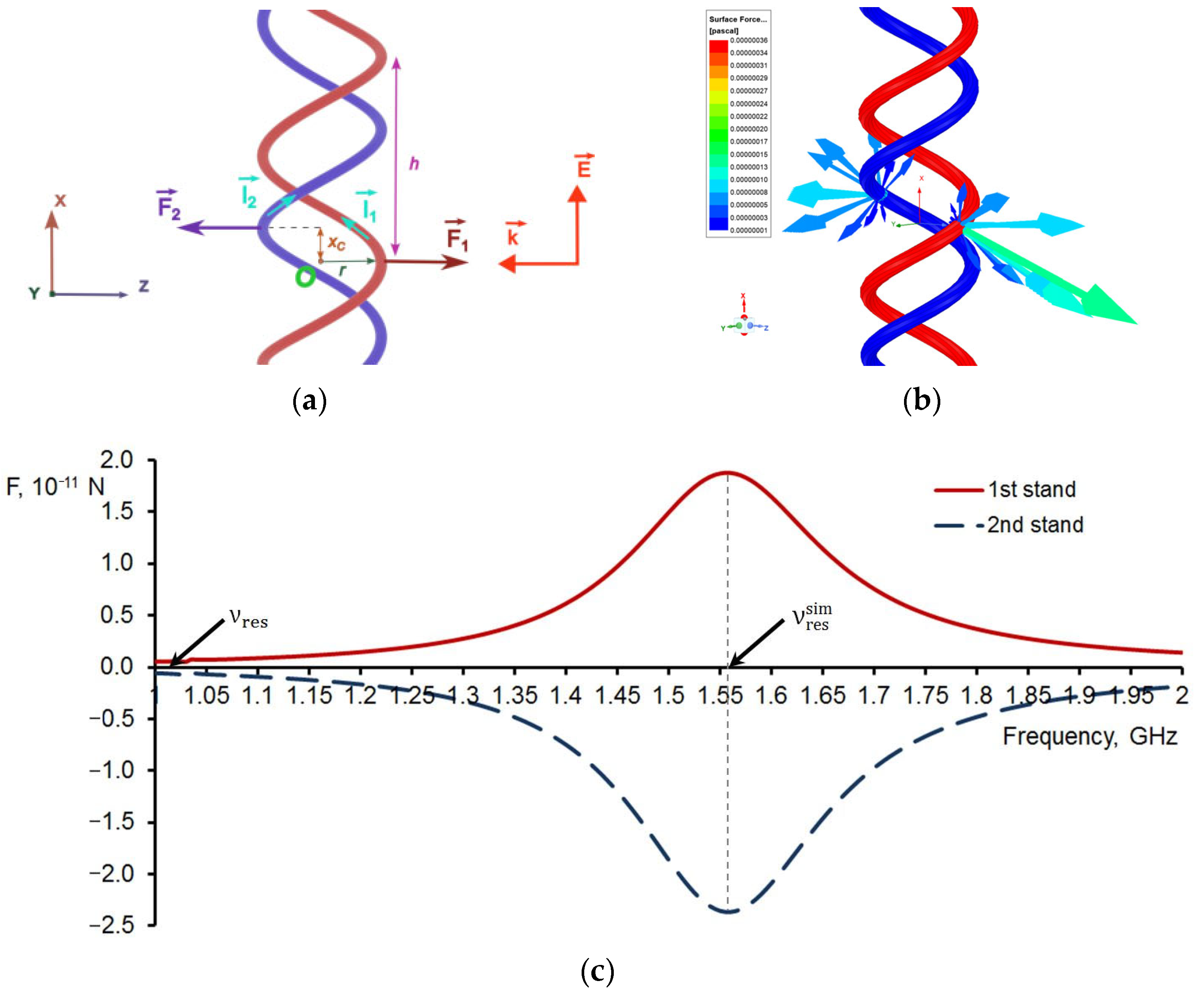
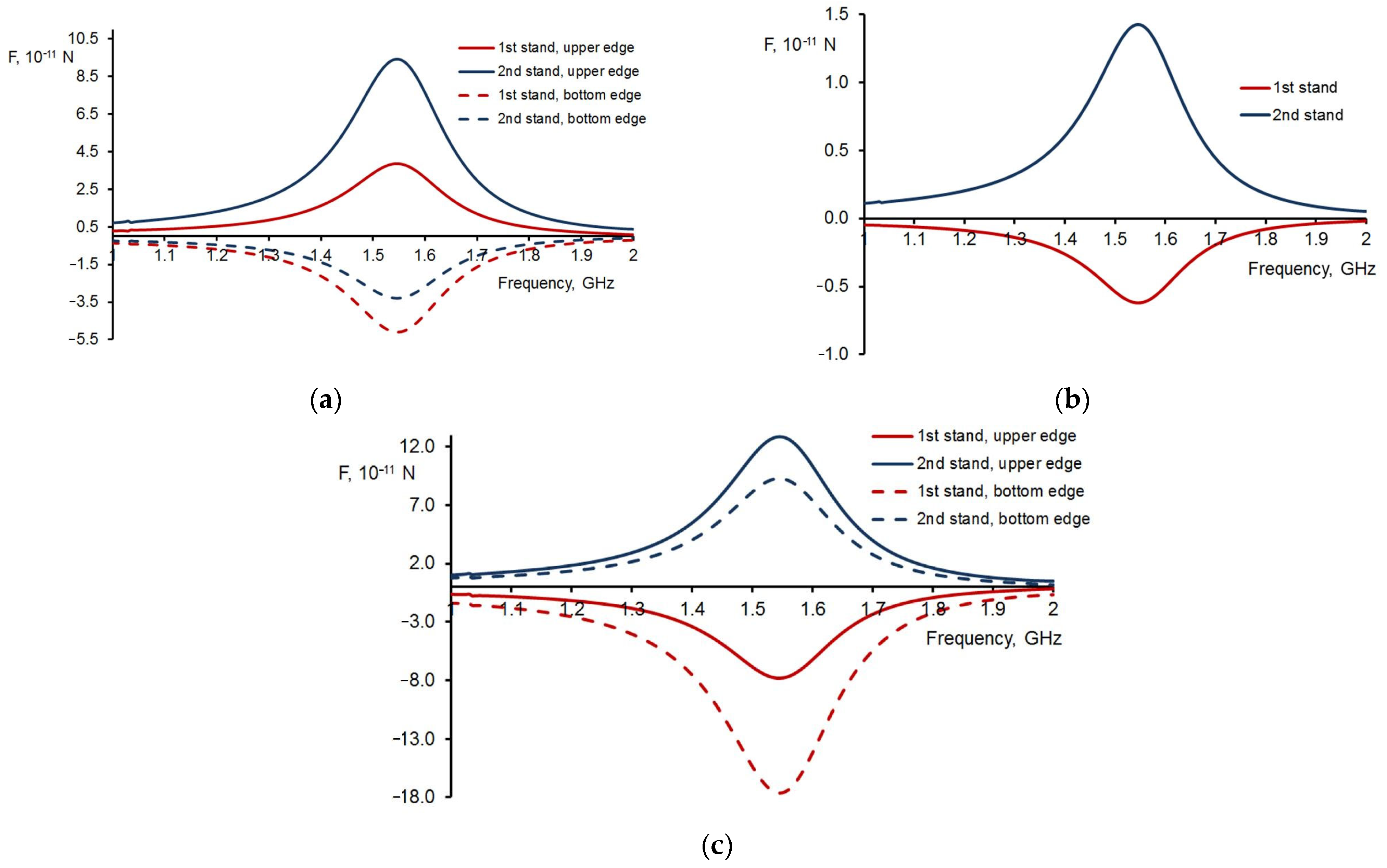
3. The Simulation of Forces at the Edges and in the Center of a Double DNA-like Helix in the Field of a Microwave Electromagnetic Wave
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Semchenko, I.V.; Mikhalka, I.S.; Khakhomov, S.A.; Samofalov, A.L.; Balmakou, A.P. DNA-like Helices as Nanosized Polarizers of Electromagnetic Waves. Front. Nanotechnol. 2022, 4, 794213. [Google Scholar] [CrossRef]
- Semchenko, I.V.; Khakhomov, S.A. Application of DNA molecules in nature-inspired technologies: A mini review. Front. Nanotechnol. 2023, 5, 1185429. [Google Scholar] [CrossRef]
- Ploeser, J.M.; Loring, H.S. The ultraviolet absorption spectra of the pyrimidine ribonucleosides and ribonucleotides. J. Biol. Chem. 1949, 178, 431–437. [Google Scholar] [CrossRef] [PubMed]
- Voet, D.; Gratzer, W.B.; Cox, R.A.; Doty, P. Absorption spectra of nucleotides, polynucleotides, and nucleic acids in the far ultraviolet. Biopolym. Orig. Res. Biomol. 1963, 1, 193–208. [Google Scholar] [CrossRef]
- Konev, S.; Volotovsky, I. Photobiology; BSU: Minsk, Belarus, 1979; 385p. (In Russian) [Google Scholar]
- Watson, J.D.; Crick, F.H.C. A Structure for Deoxyribose Nucleic Acid. Nature 1953, 171, 737–738. [Google Scholar] [CrossRef]
- Watson, J.D.; Baker, T.A.; Bell, S.P.; Gann, A.; Levine, M.; Losick, R. Molecular Biology of the Gene, 7th ed.; Pearson: London, UK, 2013; 912p. [Google Scholar]
- Wohlgamuth, C.H.; McWilliams, M.A.; Slinker, J.D. DNA as a molecular wire: Distance and sequence dependence. Anal. Chem. 2013, 85, 8634–8640. [Google Scholar] [CrossRef] [PubMed]
- Eley, D.D.; Spivey, D.I. Semiconductivity of organic substances. Part 7—The polyamides. Trans. Faraday Soc. 1961, 57, 2280–2287. [Google Scholar] [CrossRef]
- Snart, R.S. The electrical properties and stability of DNA to UV radiation and aromatic hydrocarbons. Biopolym. Orig. Res. Biomol. 1973, 12, 1493–1503. [Google Scholar] [CrossRef]
- Tran, P.; Alavi, B.; Gruner, G. Charge transport along the λ-DNA double helix. Phys. Rev. Lett. 2000, 85, 1564. [Google Scholar] [CrossRef]
- Warman, J.M.; de Haas, M.P.; Rupprecht, A. DNA: A molecular wire? Chem. Phys. Lett. 1996, 249, 319–322. [Google Scholar] [CrossRef]
- Dewarrat, F. Electric Characterization of DNA; Basel University: Basel, Switzerland, 2002; 96p. [Google Scholar]
- Fink, H.W.; Schönenberger, C. Electrical conduction through DNA molecules. Nature 1999, 398, 407–410. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Tabata, H.; Kawai, T. Self-assembled DNA networks and their electrical conductivity. Appl. Phys. Lett. 2000, 77, 3105–3106. [Google Scholar] [CrossRef]
- Yoo, K.H.; Ha, D.H.; Lee, J.O.; Park, J.W.; Kim, J.; Kim, J.J.; Choi, H.Y. Electrical conduction through poly (dA)-poly (dT) and poly (dG)-poly (dC) DNA molecules. Phys. Rev. Lett. 2001, 87, 198102. [Google Scholar] [CrossRef]
- Porath, D.; Bezryadin, A.; De Vries, S.; Dekker, C. Direct measurement of electrical transport through DNA molecules. Nature 2000, 403, 635–638. [Google Scholar] [CrossRef] [PubMed]
- Kasumov, A.Y.; Kociak, M.; Gueron, S.; Reulet, B.; Volkov, V.T.; Klinov, D.V.; Bouchiat, H. Proximity-induced superconductivity in DNA. Science 2001, 291, 280–282. [Google Scholar] [CrossRef] [PubMed]
- Legrand, O.; Côte, D.; Bockelmann, U. Single molecule study of DNA conductivity in aqueous environment. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2006, 73, 031925. [Google Scholar] [CrossRef]
- Zhang, Y.; Austin, R.H.; Kraeft, J.; Cox, E.C.; Ong, N.P. Insulating behavior of λ-DNA on the micron scale. Phys. Rev. Lett. 2002, 89, 198102. [Google Scholar] [CrossRef]
- Guo, X.; Gorodetsky, A.A.; Hone, J.; Barton, J.K.; Nuckolls, C. Conductivity of a single DNA duplex bridging a carbon nanotube gap. Nat. Nanotechnol. 2008, 3, 163–167. [Google Scholar] [CrossRef]
- Gomez-Navarro, C.; Moreno-Herrero, F.; De Pablo, P.J.; Colchero, J.; Gomez-Herrero, J.; Baro, A.M. Contactless experiments on individual DNA molecules show no evidence for molecular wire behavior. Proc. Natl. Acad. Sci. USA 2002, 99, 8484–8487. [Google Scholar] [CrossRef]
- Hu, B.N.; Gao, C.; Dong, H.L. A brief analysis of the conductivity of DNA. Acta Polym. Sin. 2024, 55, 129–141. [Google Scholar]
- Fink, H.W. Electrical conduction through DNA molecules. Electronic Properties of Novel MATERIALS-MOLECULAR Nanostructures. In Proceedings of the XIV International Winterschool/EuroConference, Kirchberg, Austria, 4–11 March 2000; Volume 544, pp. 457–461. [Google Scholar]
- Mallajosyula, S.S.; Pati, S.K. Toward DNA conductivity: A theoretical perspective. J. Phys. Chem. Lett. 2010, 1, 1881–1894. [Google Scholar] [CrossRef]
- Hodzic, V.; Hodzic, V.; Newcomb, R.W. Modeling of the electrical conductivity of DNA. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 2360–2364. [Google Scholar] [CrossRef]
- Wang, J. Electrical conductivity of double stranded DNA measured with ac impedance spectroscopy. Phys. Rev. B—Condens. Matter Mater. Phys. 2008, 78, 245304. [Google Scholar] [CrossRef]
- Charra, F.; Agranovich, V.M.; Kajzar, F. Organic Nanophotonics; Springer Science Business Media: Berlin, Germany, 2003; pp. 193–206. [Google Scholar]
- Travers, A.; Muskhelishvili, G. DNA supercoiling—A global transcriptional regulator for enterobacterial growth? Nat. Rev. Microbiol. 2005, 3, 157–169. [Google Scholar] [CrossRef]
- Dharmadhikari, A.K.; Bharambe, H.; Dharmadhikari, J.A.; D’Souza, J.S.; Mathur, D. DNA damage by OH radicals produced using intense, ultrashort, long wavelength laser pulses. Phys. Rev. Lett. 2014, 112, 138105. [Google Scholar] [CrossRef] [PubMed]
- D’Souza, J.S.; Dharmadhikari, J.A.; Dharmadhikari, A.K.; Rao, B.J.; Mathur, D. Effect of intense, ultrashort laser pulses on DNA plasmids in their native state: Strand breakages induced by in situ electrons and radicals. Phys. Rev. Lett. 2011, 106, 118101. [Google Scholar] [CrossRef]
- Baccarelli, I.; Bald, I.; Gianturco, F.A.; Illenberger, E.; Kopyra, J. Electron-induced damage of DNA and its components: Experiments and theoretical models. Phys. Rep. 2011, 508, 1–44. [Google Scholar] [CrossRef]
- Ma, Q.; Gao, W.; Xiao, Q.; Ding, L.; Gao, T.; Zhou, Y.; Gao, X.; Yan, T.; Liu, C.; Gu, Z.; et al. Directly wireless communication of human minds via non-invasive brain-computer-metasurface platform. eLight 2022, 2, 11. [Google Scholar] [CrossRef]
- Chen, L.; Ma, Q.; Luo, S.S.; Ye, F.J.; Cui, H.Y.; Cui, T.J. Touch-Programmable Metasurface for Various Electromagnetic Manipulations and Encryptions. Small 2022, 18, 2203871. [Google Scholar] [CrossRef]
- Gao, X.; Ma, Q.; Gu, Z.; Cui, W.Y.; Liu, C.; Zhang, J.; Cui, T.J. Programmable surface plasmonic neural networks for microwave detection and processing. Nat. Electron. 2023, 6, 319–328. [Google Scholar] [CrossRef]
- Wang, P.; Krasavin, A.V.; Liu, L.; Jiang, Y.; Li, Z.; Guo, X.; Tong, L.; Zayats, A.V. Molecular plasmonics with metamaterials. Chem. Rev. 2022, 122, 15031–15081. [Google Scholar] [CrossRef]
- Torres-Huerta, A.L.; Antonio-Pérez, A.; García-Huante, Y.; Alcázar-Ramírez, N.J.; Rueda-Silva, J.C. Biomolecule-based optical metamaterials: Design and applications. Biosensors 2022, 12, 962. [Google Scholar] [CrossRef] [PubMed]
- Kowerdziej, R.; Ferraro, A.; Zografopoulos, D.C.; Caputo, R. Soft-Matter-Based Hybrid and Active Metamaterials. Adv. Opt. Mater. 2022, 10, 2200750. [Google Scholar] [CrossRef]
- Chen, Y.; Ai, B.; Wong, Z.J. Soft optical metamaterials. Nano Converg. 2020, 7, 18. [Google Scholar] [CrossRef]
- Kuzyk, A.; Schreiber, R.; Fan, Z.; Pardatscher, G.; Roller, E.M.; Högele, A.; Simmel, F.C.; Govorov, A.O.; Liedl, T. DNA-based self-assembly of chiral plasmonic nanostructures with tailored optical response. Nature 2012, 483, 311–314. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, R.; Luong, N.; Fan, Z.; Kuzyk, A.; Nickels, P.C.; Zhang, T.; Smith, D.M.; Yurke, B.; Kuang, W.; Govorov, A.O.; et al. Chiral plasmonic DNA nanostructures with switchable circular dichroism. Nat. Commun. 2013, 4, 2948. [Google Scholar] [CrossRef] [PubMed]
- Kuzyk, A.; Schreiber, R.; Zhang, H.; Govorov, A.O.; Liedl, T.; Liu, N. Reconfigurable 3D plasmonic metamolecules. Nat. Mater. 2014, 13, 862–866. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.E.; Ahn, H.Y.; Mun, J.; Lee, Y.Y.; Kim, M.; Cho, N.H.; Chang, K.; Kim, W.S.; Rho, J.; Nam, K.T. Amino-acid-and peptide-directed synthesis of chiral plasmonic gold nanoparticles. Nature 2018, 556, 360–365. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, X.; Wang, M.; Dong, J.; Zheng, Y. High-performance ultrathin active chiral metamaterials. ACS Nano 2018, 12, 5030–5041. [Google Scholar] [CrossRef]
- Ahn, H.Y.; Yoo, S.; Cho, N.H.; Kim, R.M.; Kim, H.; Huh, J.H.; Lee, S.; Nam, K.T. Bioinspired toolkit based on intermolecular encoder toward evolutionary 4D chiral plasmonic materials. Acc. Chem. Res. 2019, 52, 2768–2783. [Google Scholar] [CrossRef]
- Ji, R.; Wang, S.W.; Liu, X.; Guo, H.; Lu, W. Hybrid Helix Metamaterials for Giant and Ultrawide Circular Dichroism. ACS Photonics 2016, 3, 2368–2374. [Google Scholar] [CrossRef]
- He, Z.; Shi, K.; Li, J.; Chao, J. Self-assembly of DNA origami for nanofabrication, biosensing, drug delivery, and computational storage. Iscience 2023, 26, 106638. [Google Scholar] [CrossRef]
- Semchenko, I.V.; Mikhalka, I.S.; Faniayeu, I.A.; Khakhomov, S.A.; Balmakou, A.P.; Tretyakov, S.A. Optical forces acting on a double DNA-like helix, its unwinding and strands rupture. Photonics 2020, 7, 83. [Google Scholar] [CrossRef]
- Semchenko, I.; Khakhomov, S.; Balmakou, A.; Mikhalka, I. Interaction forces of electric currents and charges in a double DNA-like helix and its equilibrium. In Proceedings of the 2018 12th International Congress on Artificial Materials for Novel Wave Phenomena (Metamaterials), Espoo, Finland, 27 August–1 September 2018; pp. 281–283. [Google Scholar]
- Semchenko, I.V.; Mikhalka, I.S.; Khakhomov, S.A.; Balmakou, A.P. The interaction of strands in a double DNA-like helix at high-frequency resonance. In Proceedings of the 13th International Congress on Artificial Materials for Novel Wave Phenomena Metamaterials, Rome, Italy, 16–21 September 2019; pp. 16–21. [Google Scholar]
- Semchenko, I.V.; Khakhomov, S.A.; Mikhalka, I.S.; Samofalov, A.L.; Somov, P.V. Polarization Selectivity of a Double DNA-like Helix as an Element of Metamaterials and Metasurfaces. J. Appl. Spectrosc. 2023, 90, 419–426. [Google Scholar] [CrossRef]
- Lagarkov, A.N.; Semenenko, V.N.; Chistyaev, V.A.; Ryabov, D.E.; Tretyakov, S.A.; Simovski, C.R. Resonance properties of bi-helix media at microwaves. Electromagnetics 1997, 17, 213–237. [Google Scholar] [CrossRef]
- Semchenko, I.V.; Khakhomov, S.A.; Asadchy, V.S.; Naumova, E.V.; Prinz, V.Y.; Golod, S.V.; Sinitsyn, G.V. Investigation of the properties of weakly reflective metamaterials with compensated chirality. Crystallogr. Rep. 2014, 59, 480–485. [Google Scholar] [CrossRef]
- Semchenko, I.V.; Khakhomov, S.A.; Asadchy, V.S.; Golod, S.V.; Naumova, E.V.; Prinz, V.Y.; Malevich, V.L. Investigation of electromagnetic properties of a high absorptive, weakly reflective metamaterial—Substrate system with compensated chirality. J. Appl. Phys. 2017, 121, 015108. [Google Scholar] [CrossRef]
- Gansel, J.K.; Thiel, M.; Rill, M.S.; Decker, M.; Bade, K.; Saile, V.; Wegener, M. Gold helix photonic metamaterial as broadband circular polarizer. Science 2009, 325, 1513–1515. [Google Scholar] [CrossRef]
- Slobozhanyuk, A.P.; Lapine, M.; Powell, D.A.; Shadrivov, I.V.; Kivshar, Y.S.; McPhedran, R.C.; Belov, P.A. Flexible helices for nonlinear metamaterials. Adv. Mater. 2013, 25, 3409–3412. [Google Scholar] [CrossRef]
- Zhao, Z.; Gao, D.; Bao, C.; Zhou, X.; Lu, T.; Chen, L. High extinction ratio circular polarizer with conical double-helical metamaterials. J. Light. Technol. 2012, 30, 2442–2446. [Google Scholar] [CrossRef]
- Kaschke, J.; Wegener, M. Gold triple-helix mid-infrared metamaterial by STED-inspired laser lithography. Opt. Lett. 2015, 40, 3986–3989. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Tasco, V.; Todisco, F.; Cuscunà, M.; Benedetti, A.; Sanvitto, D.; Passaseo, A. Triple-helical nanowires by tomographic rotatory growth for chiral photonics. Nat. Commun. 2015, 6, 6484. [Google Scholar] [CrossRef] [PubMed]
- Schaferling, M.; Yin, X.; Engheta, N.; Giessen, H. Helical plasmonic nanostructures as prototypical chiral near-field sources. ACS Photonics 2014, 1, 530–537. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Semchenko, I.V.; Mikhalka, I.S.; Samofalov, A.L.; Khakhomov, S.A. Controlling the Shape of a Double DNA-like Helix as an Element of Metamaterials. Photonics 2024, 11, 788. https://doi.org/10.3390/photonics11090788
Semchenko IV, Mikhalka IS, Samofalov AL, Khakhomov SA. Controlling the Shape of a Double DNA-like Helix as an Element of Metamaterials. Photonics. 2024; 11(9):788. https://doi.org/10.3390/photonics11090788
Chicago/Turabian StyleSemchenko, Igor V., Ivan S. Mikhalka, Andrey L. Samofalov, and Sergei A. Khakhomov. 2024. "Controlling the Shape of a Double DNA-like Helix as an Element of Metamaterials" Photonics 11, no. 9: 788. https://doi.org/10.3390/photonics11090788
APA StyleSemchenko, I. V., Mikhalka, I. S., Samofalov, A. L., & Khakhomov, S. A. (2024). Controlling the Shape of a Double DNA-like Helix as an Element of Metamaterials. Photonics, 11(9), 788. https://doi.org/10.3390/photonics11090788





