Super-Oscillating Diffractive Optical Spot Generators
Abstract
:1. Introduction
2. PDFT-Based Design of Super-Oscillating DOEs
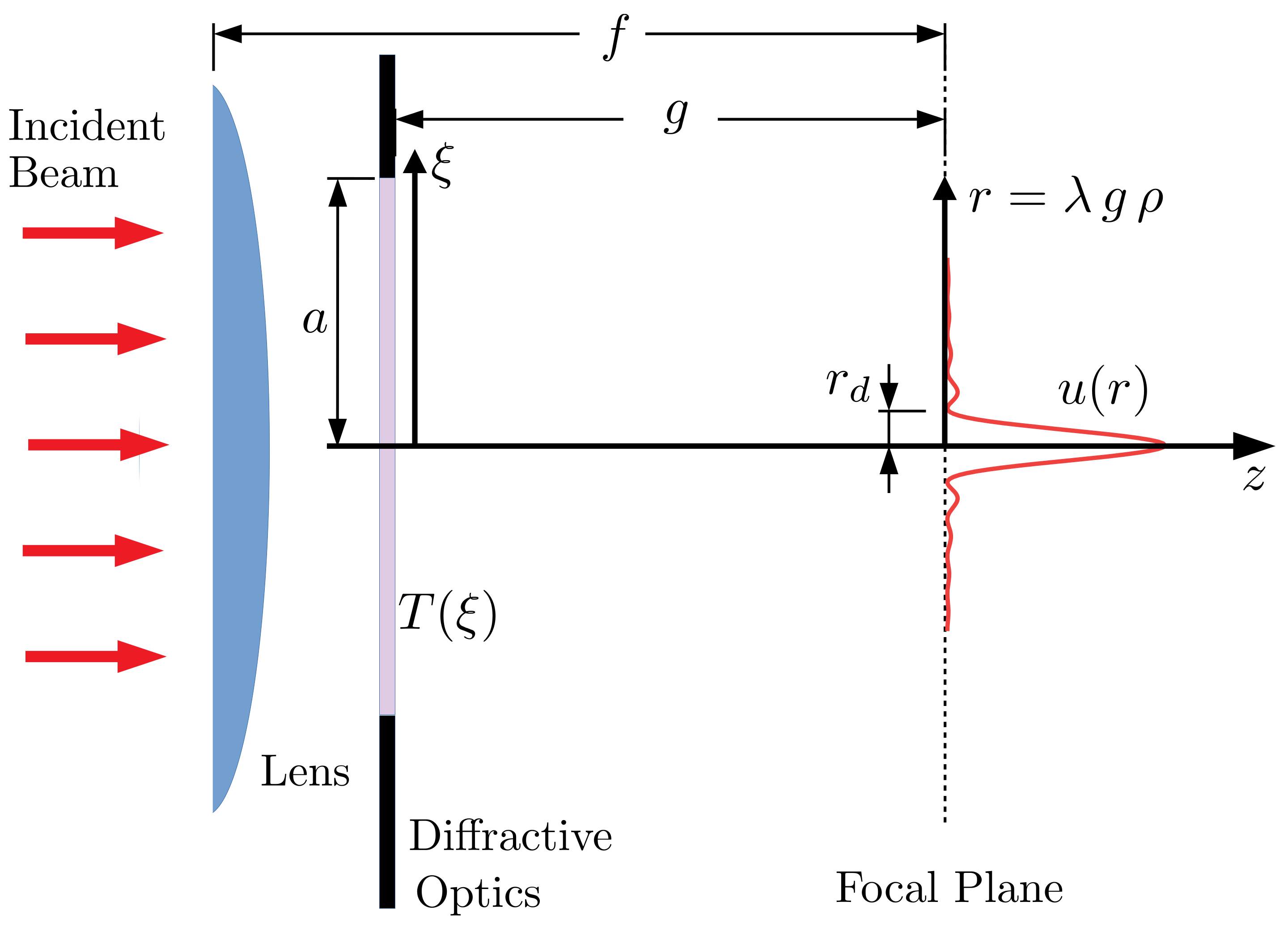
2.1. Optical System Model
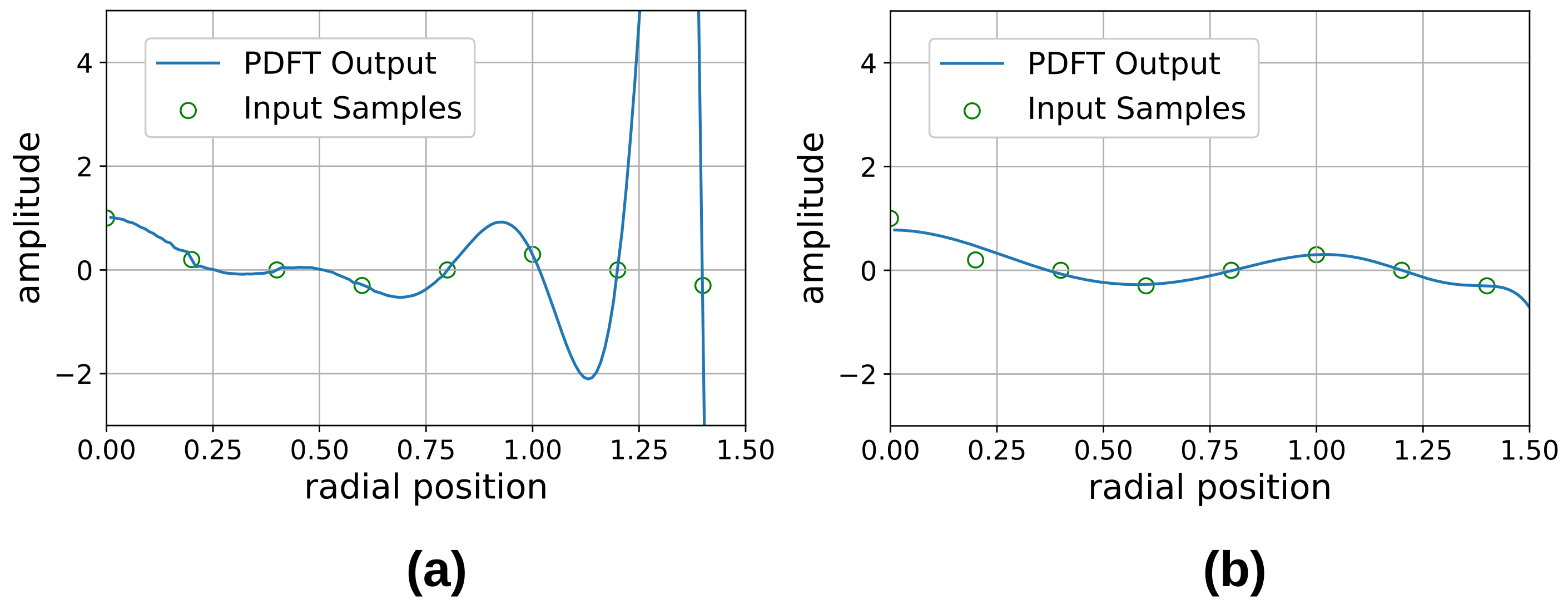
2.2. The PDFT Algorithm in Cylindrical Coordinates
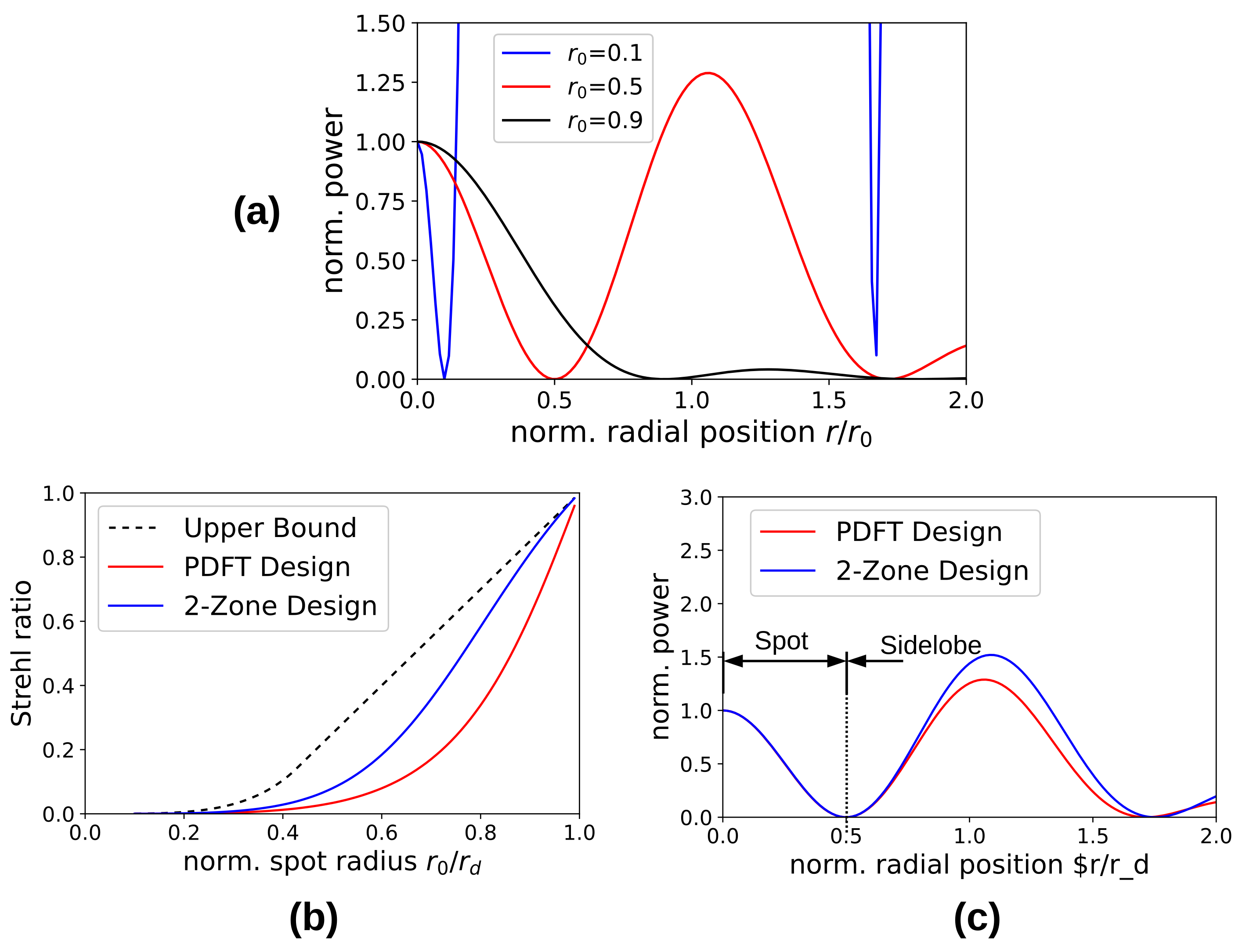
3. Examples of Super-Oscillating Filter Functions
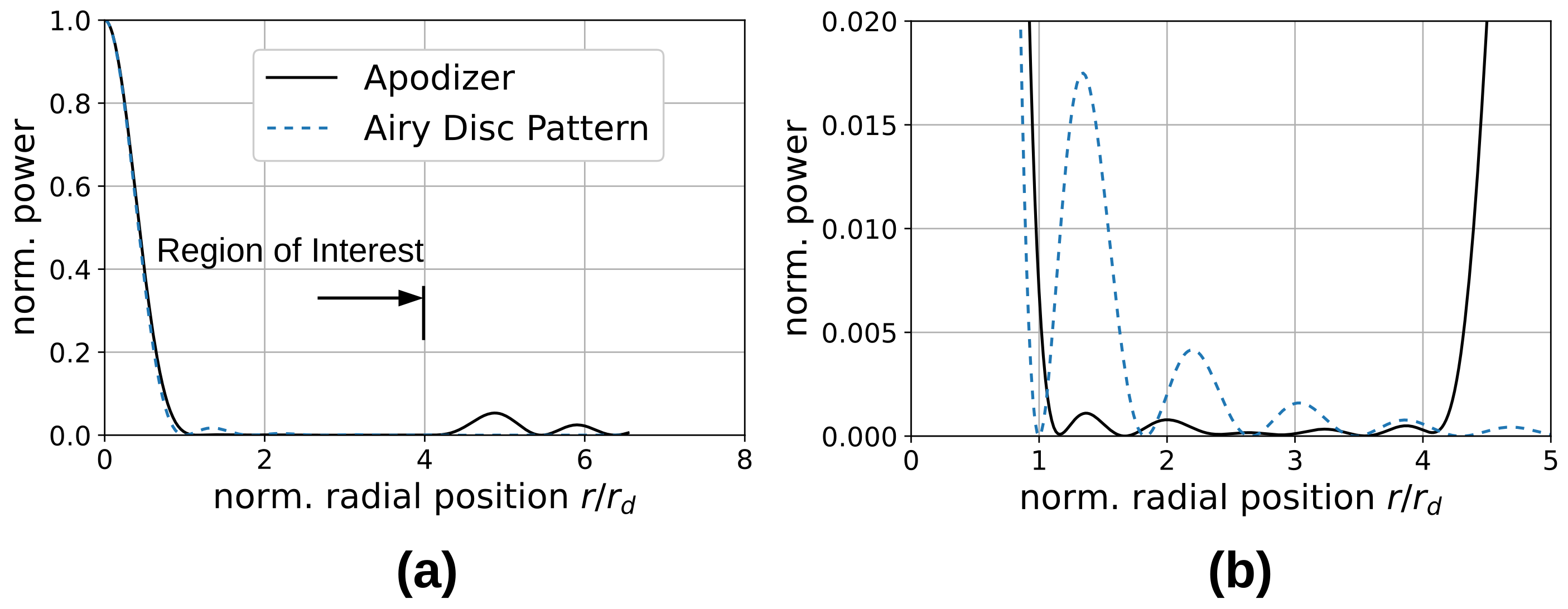
3.1. Regularized PDFT Design
3.2. Side-Lobe Suppression
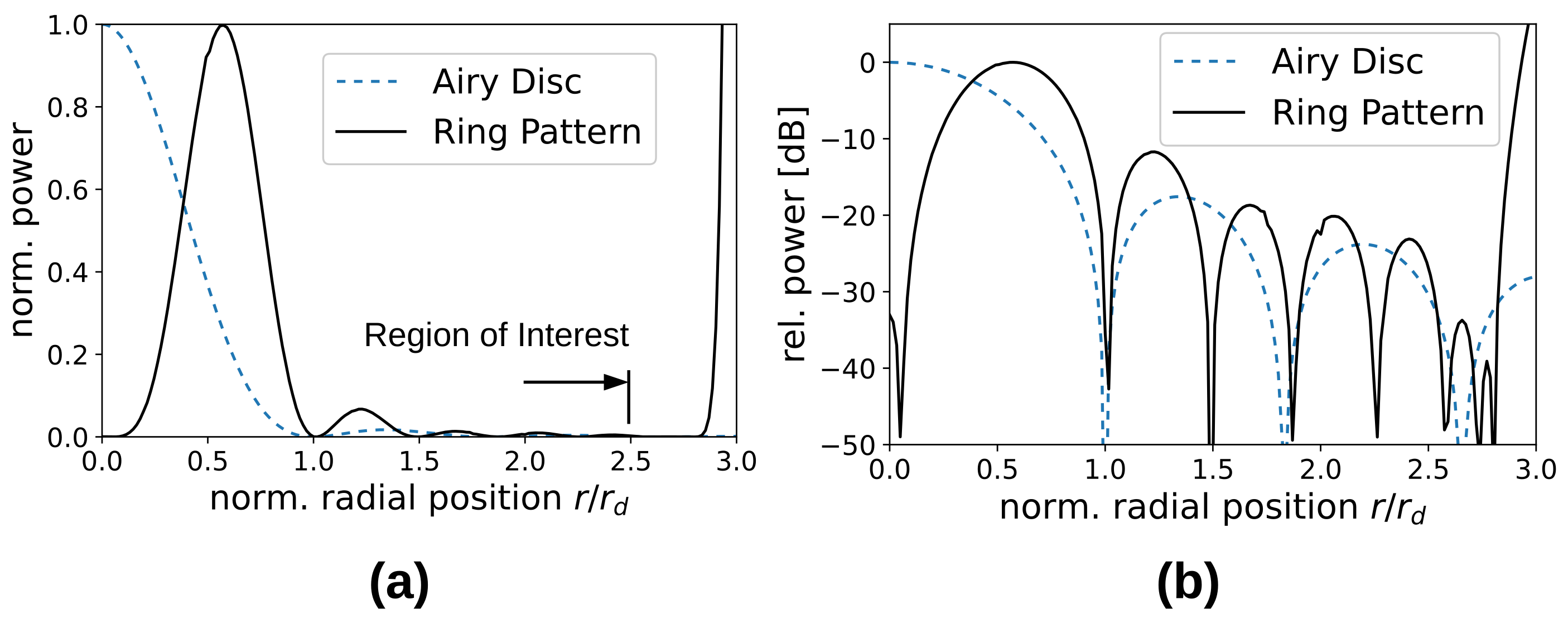
3.3. Superresolved Ring
4. Phase-Only Encoding of PDFT Designs
5. Super-Resolving Spot-Generators
5.1. Spot Generator DOE Design
5.1.1. PDFT Design
5.1.2. Non-Linear Design
5.2. Numerical Characterization of Spot Generator Designs
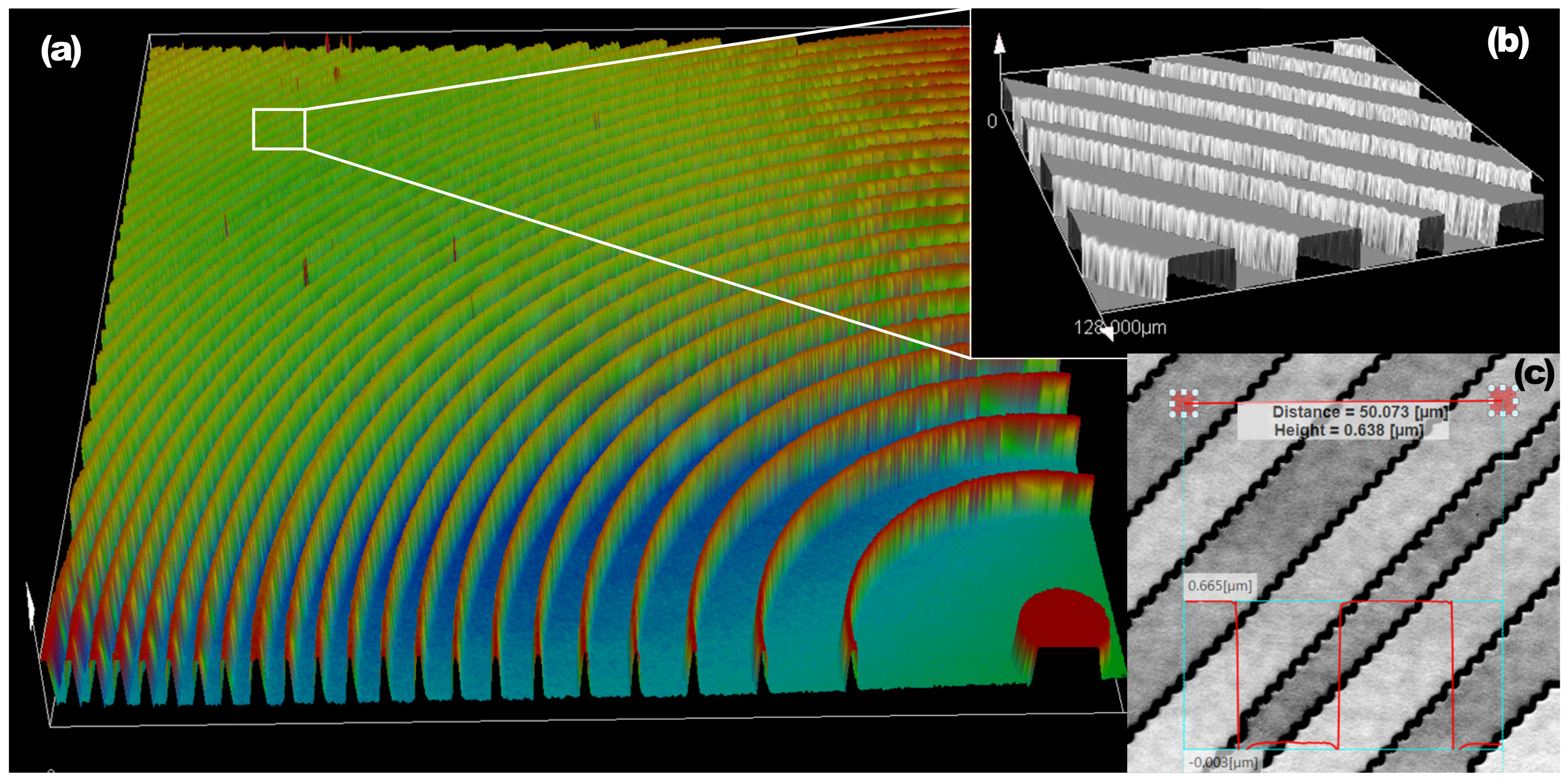
5.3. Fabrication of Diffractive Optical Spot Generators
6. Experimental Characterization of the DOE Response
7. Discussion and Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DOE | Diffractive optical element |
| PDFT | Prior discrete Fourier transform |
| PSF | Point spread function |
| FS | Fused silica |
| Al | Aluminum metal |
References
- di Francia, T. Super-gain antennas and optical resolving power. Nuovo Cimento Suppl. 1952, 9, 426–438. [Google Scholar] [CrossRef]
- Sales, T.R.M.; Morris, G.M. Diffractive superresolution elements. J. Opt. Soc. Am. A 1997, 14, 1637–1646. [Google Scholar] [CrossRef]
- Reza, N.; Hazra, L. Toraldo filters with concentric unequal annuli of fixed phase by evolutionary programming. J. Opt. Soc. Am. A 2013, 30, 189–195. [Google Scholar] [CrossRef] [PubMed]
- Katzav, E.; Schwartz, M. Yield-optimized superoscillations. IEEE Trans. Signal Process. 2013, 61, 3113–3118. [Google Scholar] [CrossRef]
- Wong, A.M.H.; Eleftheriades, G.V. An optical super-microscope for far-field, real-time imaging beyond the diffraction limit. Sci. Rep. 2013, 3, 1715. [Google Scholar] [CrossRef]
- Rogers, E.T.F.; Savo, S.; Lindberg, J.; Roy, T.; Dennis, M.R.; Zheludev, N.I. Super-oscillatory optical needle. Appl. Phys. Lett. 2013, 102, 031108. [Google Scholar] [CrossRef]
- Chen, G.; Wen, Z.Q.; Qiu, C.W. Superoscillation: From physics to optical applications. Light Sci. Appl. 2019, 8, 56. [Google Scholar] [CrossRef]
- Yang, H.; Lin, E.Y.H.; Kutulakos, K.N.; Eleftheriades, G.V. Computational nonscanning incoherent superoscillatory imaging. ACS Photonics 2022, 9, 290–295. [Google Scholar] [CrossRef]
- Zheludev, N.I.; Yuan, G. Optical superoscillation technologies beyond the diffraction limit. Nat. Rev. Phys. 2022, 4, 16–32. [Google Scholar] [CrossRef]
- Sales, T.R.M.; Morris, G.M. Fundamental limits of optical superresolution. Opt. Lett. 1997, 22, 582–584. [Google Scholar] [CrossRef]
- Kempf, A. Black holes, bandwidths and Beethoven. J. Math. Phys. 2000, 41, 2360–2374. [Google Scholar] [CrossRef]
- Ferreira, P.J.S.G.; Kempf, A. The energy expense of superoscillations. In Proceedings of the 2002 11th European Signal Processing Conference, Toulouse, France, 3–6 September 2002; pp. 1–4. [Google Scholar]
- Byrne, C.L.; Fitzgerald, R.M. Reconstruction from partial information with applications to tomography. Siam J. Appl. Math. 1982, 42, 933–940. [Google Scholar] [CrossRef]
- Byrne, C.L.; Fitzgerald, R.M.; Fiddy, M.A.; Hall, T.J.; Darling, A.M. Image restoration and resolution enhancement. J. Opt. Soc. Am. 1983, 73, 1481–1487. [Google Scholar] [CrossRef]
- Byrne, C.L.; Fiddy, M.A. Estimation of continuous object distributions from limited Fourier magnitude measurements. J. Opt. Soc. Am. A 1987, 4, 112–117. [Google Scholar] [CrossRef]
- Byrne, C.L.; Fiddy, M.A. Images as power spectra; reconstruction as a Wiener filter approximation. Inverse Probl. 1988, 4, 399–409. [Google Scholar] [CrossRef]
- Testorf, M.; Fiddy, M. Imaging from real scattered field data using a linear spectral estimation technique. Inverse Probl. 2001, 17, 1645–1658. [Google Scholar] [CrossRef]
- Byrne, C.L. Signal Processing—A Mathematical Approach; A K Peters: Wellesley, MA, USA, 2005; Chapter 23; pp. 129–134. [Google Scholar]
- Shieh, H.M.; Byrne, C.L.; Fiddy, M.A. Image reconstruction: A unifying model for resolution enhancement and data extrapolation. Tutorial. J. Opt. Soc. Am. A 2006, 23, 258–266. [Google Scholar] [CrossRef] [PubMed]
- Testorf, M.E. Performance limits and trade-offs of superresolution imaging systems. In Proceedings of the Unconventional and Indirect Imaging, Image Reconstruction, and Wavefront Sensing 2018, San Diego, CA, USA, 19–23 August 2018; Dolne, J.J., Bones, P.J., Eds.; International Society for Optics and Photonics. SPIE: Bellingham, WA, USA, 2018; Volume 10772, p. 107720G. [Google Scholar] [CrossRef]
- Dong, X.H.; Wong, A.M.H.; Kim, M.; Eleftheriades, G.V. Superresolution far-field imaging of complex objects using reduced superoscillating ripples. Optica 2017, 4, 1126–1133. [Google Scholar] [CrossRef]
- Feirreira, P.J.S.; Kempf, A. Superoscillations: Faster than the Nyquist rate. IEEE Trans. Signal Process. 2006, 54, 3732–3740. [Google Scholar] [CrossRef]
- Lee, D.G.; Ferreira, P.J.S.G. Direct construction of superoscillations. IEEE Trans. Signal Process. 2014, 62, 3125–3134. [Google Scholar] [CrossRef]
- Gadamsetti, P.; Testorf, M.; Gonzalez, D.A.; Batoni, P.; Poutous, M.K. Implementation of a superresolution far-field spot-generator with 1/5 the diffraction limit. Results Opt. 2021, 3, 100067. [Google Scholar] [CrossRef]
- Gadamsetti, P.; Testorf, M.E.; Batoni, P.; Poutous, M.K. Optical super-resolving phase filters with random anti-reflection subwavelength surface structures. In Proceedings of the Optical Components and Materials XVIII, Online, 6–12 March 2021; Jiang, S., Digonnet, M.J.F., Eds.; International Society for Optics and Photonics. SPIE: Bellingham, WA, USA, 2021; Volume 11682, p. 1168214. [Google Scholar] [CrossRef]
- Iizuka, K. Engineering Optics, 2nd ed.; Springer: New York, NY, USA, 1986; Chapter 2.8; pp. 46–54. [Google Scholar]
- Papoulis, A. Systems and Transforms with Applications to Optics; McGraw-Hill: New York, NY, USA, 1968; Chapter 5; pp. 140–175. [Google Scholar]
- Mendlovic, D.; Shabtay, G.; Levi, U.; Zalevsky, Z.; Marom, E. Encoding technique for design of zero-order (on-axis) Fraunhofer computer-generated holograms. Appl. Opt. 1997, 36, 8427–8434. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.X.; Lu, R.D.; Gong, L. Tailoring light with a digital micromirror device. Ann. Phys. 2015, 527, 447–470. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Testorf, M.E.; Gadamsetti, P.; Batoni, P.; Poutous, M.K. Super-Oscillating Diffractive Optical Spot Generators. Photonics 2024, 11, 790. https://doi.org/10.3390/photonics11090790
Testorf ME, Gadamsetti P, Batoni P, Poutous MK. Super-Oscillating Diffractive Optical Spot Generators. Photonics. 2024; 11(9):790. https://doi.org/10.3390/photonics11090790
Chicago/Turabian StyleTestorf, Markus E., Praneeth Gadamsetti, Paolo Batoni, and Menelaos K. Poutous. 2024. "Super-Oscillating Diffractive Optical Spot Generators" Photonics 11, no. 9: 790. https://doi.org/10.3390/photonics11090790




