Theoretical Investigation of the Influence of Correlated Electric Fields on Wavefront Shaping
Abstract
1. Introduction
2. Simulation Methodology
2.1. Simulations Based on Maxwell’s Equations
2.2. Speckle Statistics
2.3. Monte Carlo Simulation
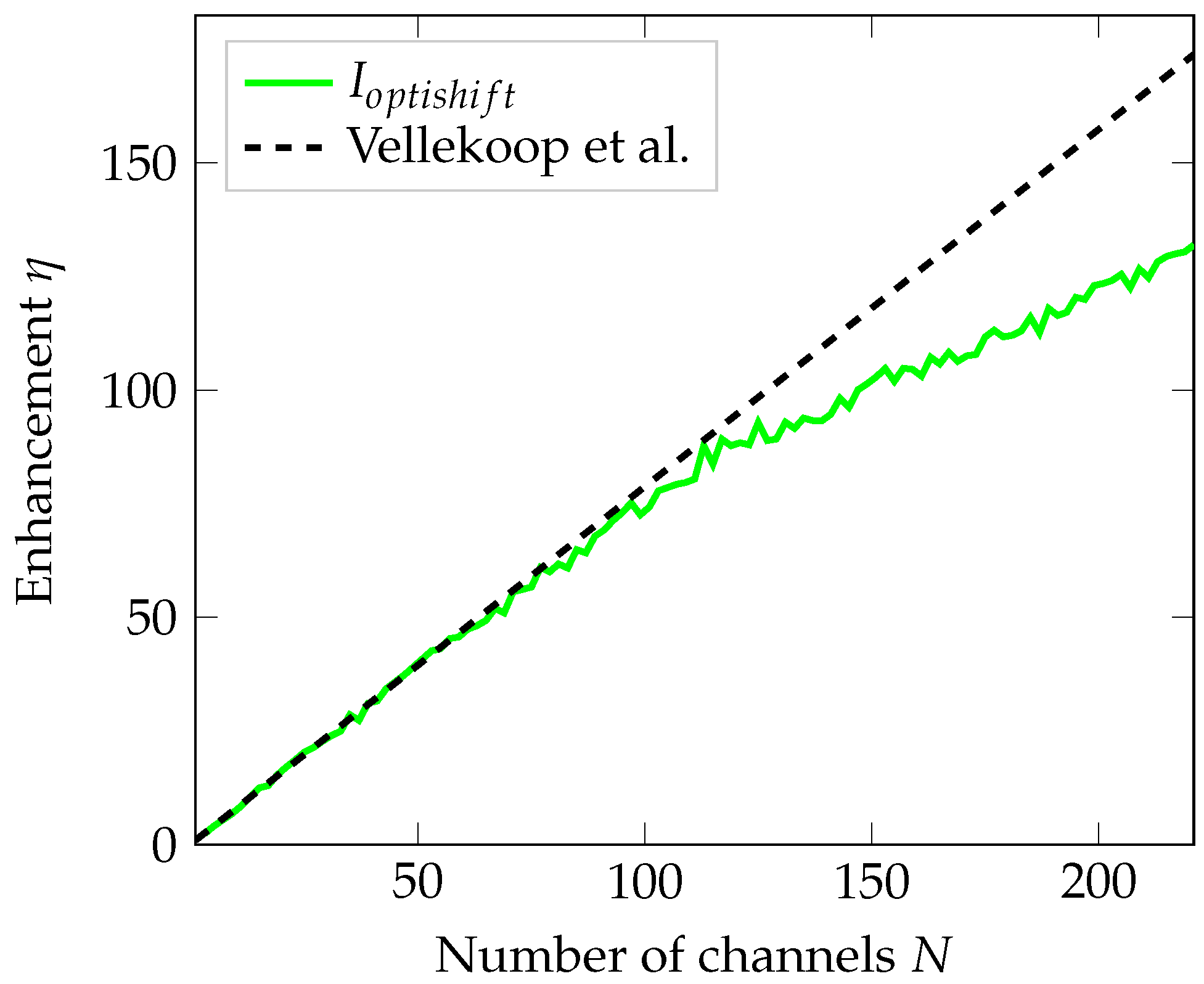
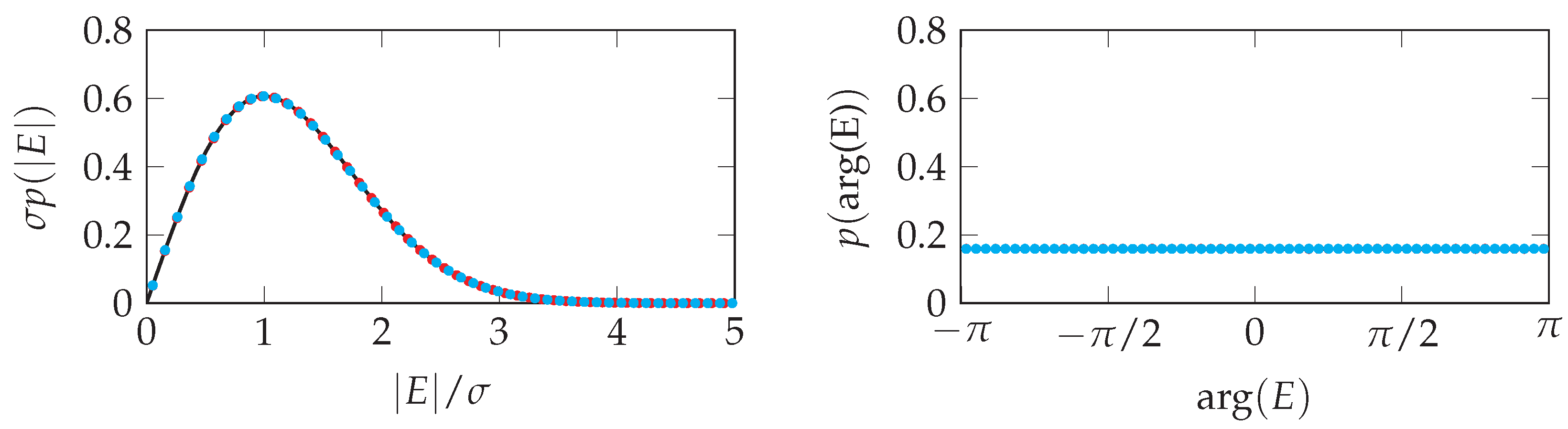
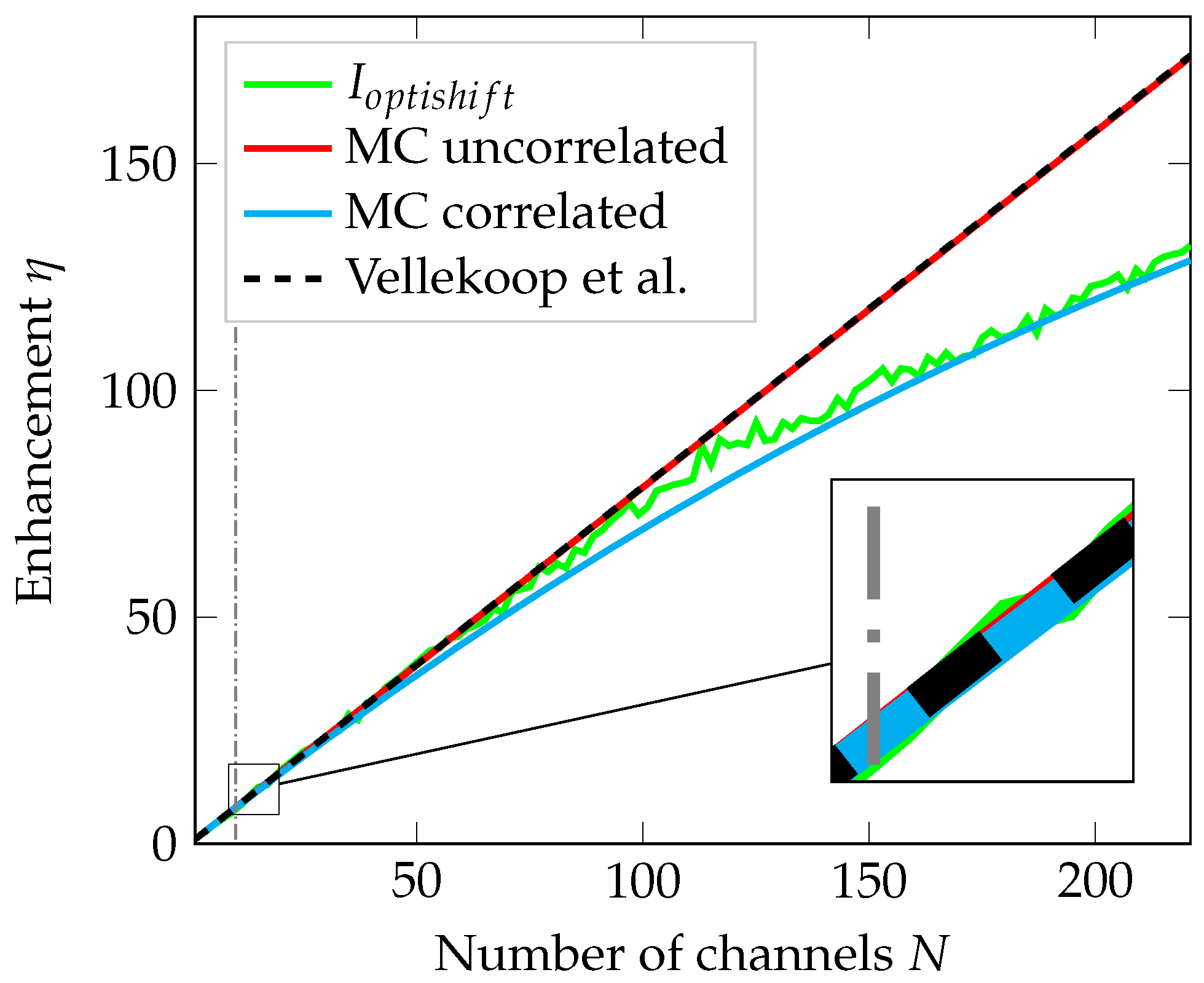
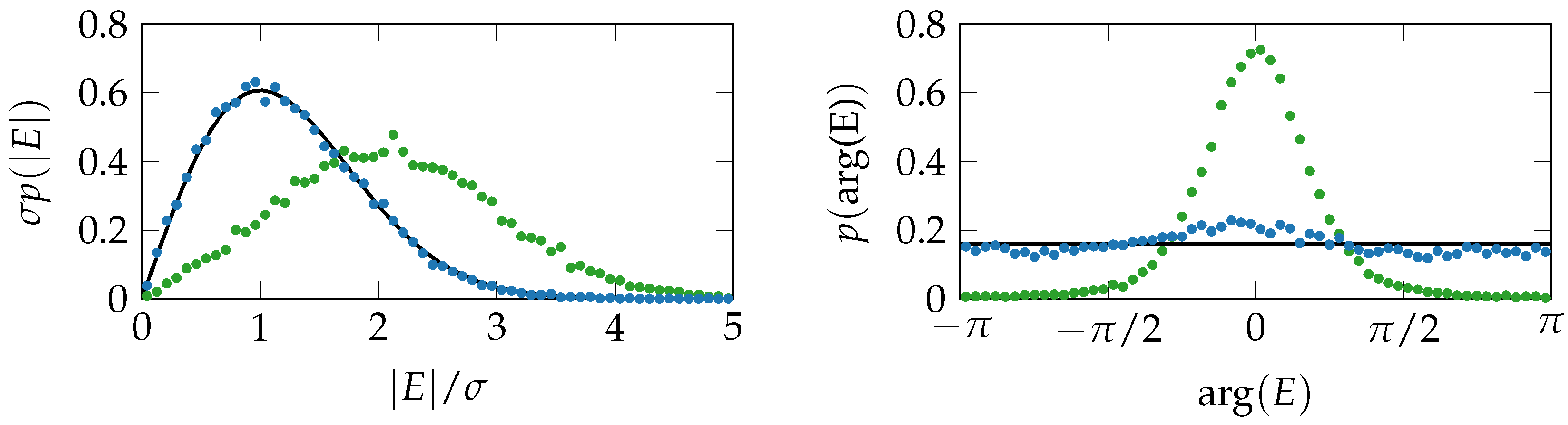
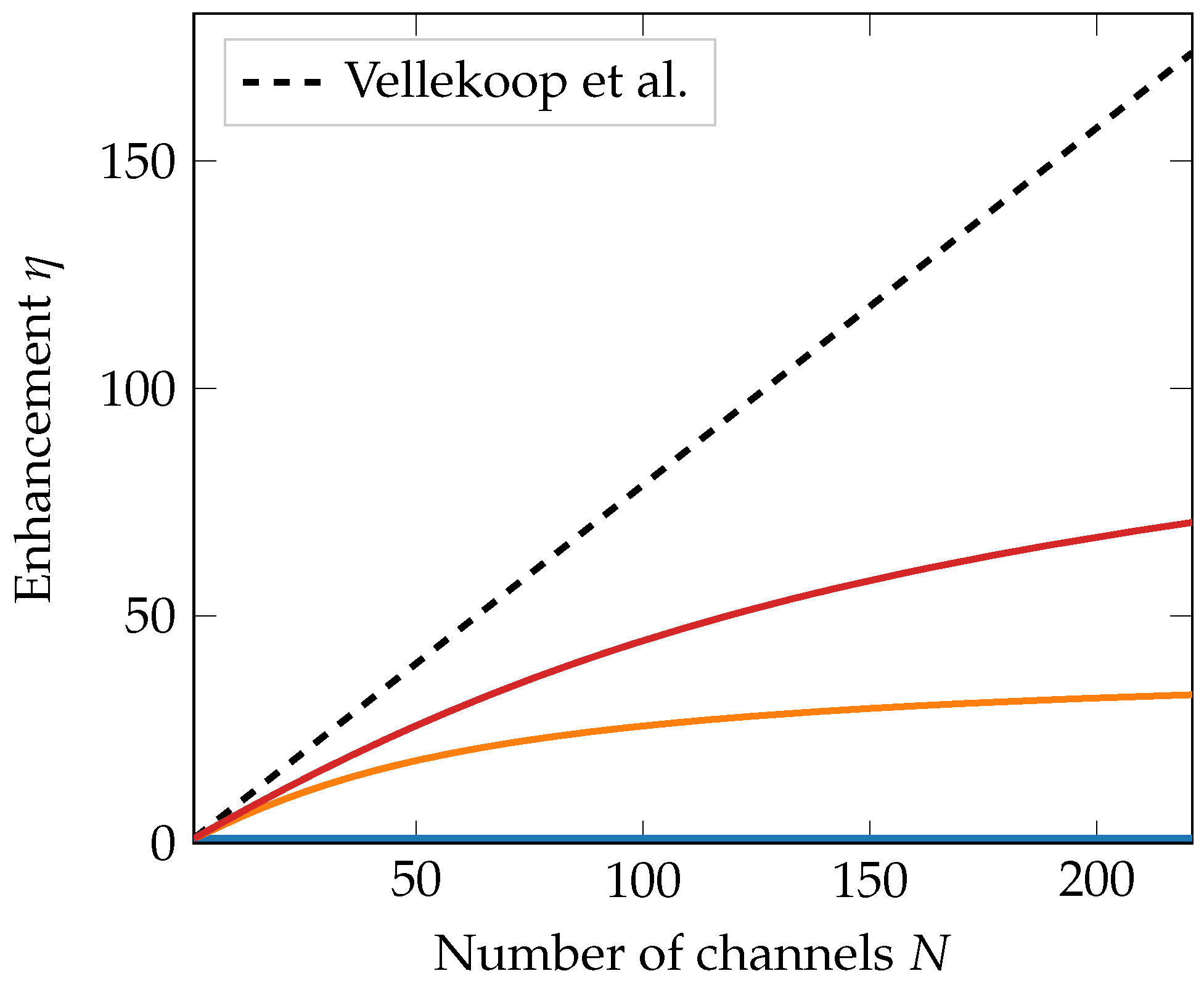
3. Results
3.1. Number of Transmission Channels in a Quasi-Two-Dimensional Sample
3.2. Deviations from the Circular Complex Gaussian Distribution
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vellekoop, I.M.; Mosk, A.P. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 2007, 32, 2309–2311. [Google Scholar] [CrossRef] [PubMed]
- Vellekoop, I.M.; Lagendijk, A.; Mosk, A. Exploiting disorder for perfect focusing. Nat. Photonics 2010, 4, 320–322. [Google Scholar] [CrossRef]
- Vellekoop, I.M. Feedback-based wavefront shaping. Opt. Express 2015, 23, 12189–12206. [Google Scholar] [CrossRef]
- Gigan, S.; Katz, O.; de Aguiar, H.B.; Andresen, E.R.; Aubry, A.; Bertolotti, J.; Bossy, E.; Bouchet, D.; Brake, J.; Brasselet, S.; et al. Roadmap on wavefront shaping and deep imaging in complex media. J. Phys. Photonics 2022, 4, 042501. [Google Scholar] [CrossRef]
- Devaud, L.; Rauer, B.; Mauras, S.; Rotter, S.; Gigan, S. Correlating light fields through disordered media across multiple degrees of freedom. arXiv 2023, arXiv:2312.08506. [Google Scholar]
- Song, L.; Zhou, Z.; Wang, X.; Zhao, X.; Elson, D.S. Simulation of speckle patterns with predefined correlation distributions. Biomed. Opt. Express 2016, 7, 798–809. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Choi, Y.; Yoon, C.; Choi, W.; Kim, J.; Park, Q. Maximal energy transport through disordered media with the implementation of transmission eigenchannels. Nat. Photonics 2012, 6, 581–585. [Google Scholar] [CrossRef]
- Verrier, N.; Depraeter, L.; Felbacq, D.; Gross, M. Measuring enhanced optical correlations induced by transmission open channels in a slab geometry. Phys. Rev. B 2016, 93, 161114. [Google Scholar] [CrossRef]
- Sarma, R.; Yamilov, A.G.; Petrenko, S.; Bromberg, Y.; Cao, H. Control of Energy Density inside a Disordered Medium by Coupling to Open or Closed Channels. Phys. Rev. Lett. 2016, 117, 086803. [Google Scholar] [CrossRef]
- Yilmaz, H.; Hsu, C.W.; Yamilov, A.; Cao, H. Transverse localization of transmission eigenchannels. Nat. Photonics 2019, 13, 352–358. [Google Scholar] [CrossRef]
- Bender, N.; Yamilov, A.; Yilmaz, H.; Cao, H. Fluctuations and Correlations of Transmission Eigenchannels in Diffusive Media. Phys. Rev. Lett. 2020, 125, 165901. [Google Scholar] [CrossRef] [PubMed]
- Venderbosch, P.; van der Meer, R.; de Goede, M.; Kassenberg, B.; Snijders, H.; Epping, J.; Taballione, C.; van den Vlekkert, H.; Renema, J.J.; Pinkse, P.W.H. Observation of Open Scattering Channels. In Proceedings of the Integrated Photonics Research, Silicon and Nanophotonics, Maastricht, The Netherlands, 24–28 July 2022; Optica Publishing Group: Washington, DC, USA, 2022. [Google Scholar]
- Cao, H.; Mosk, A.P.; Rotter, S. Shaping the propagation of light in complex media. Nat. Phys. 2022, 18, 994–1007. [Google Scholar] [CrossRef]
- Pai, P.; Bosch, J.; Kühmayer, M.; Rotter, S.; Mosk, A.P. Scattering invariant modes of light in complex media. Opt. Express 2015, 23, 12189–12206. [Google Scholar] [CrossRef]
- Katz, O.; Small, E.; Silberberg, Y. Looking around corners and through thin turbid layers in real time with scattered incoherent light. Nat. Photonics 2012, 6, 549–553. [Google Scholar] [CrossRef]
- Jauregui-Sánchez, Y.; Penketh, H.; Bertolotti, J. Tracking moving objects through scattering media via speckle correlations. Nat. Commun. 2022, 13, 5779. [Google Scholar] [CrossRef]
- Judkewitz, B.; Horstmeyer, R.; Vellekoop, I.M.; Papadopoulos, I.N.; Yang, C. Translation correlations in anisotropically scattering media. Nat. Phys. 2015, 11, 684–689. [Google Scholar] [CrossRef]
- Schott, S.; Bertolotti, J.; Léger, J.F.; Bourdieu, L.; Gigan, S. Characterization of the angular memory effect of scattered light in biological tissues. Opt. Express 2015, 23, 13505–13516. [Google Scholar] [CrossRef]
- Osnabrugge, G.; Horstmeyer, R.; Papadopoulos, I.N.; Judkewitz, B.; Vellekoop, I.M. Generalized optical memory effect. Optica 2017, 4, 886–892. [Google Scholar] [CrossRef]
- Yilmaz, H.; Hsu, C.W.; Goetschy, A.; Bittner, S.; Rotter, S.; Yamilov, A.; Cao, H. Angular Memory Effect of Transmission Eigenchannels. Phys. Rev. Lett. 2019, 123, 203901. [Google Scholar] [CrossRef] [PubMed]
- Imry, Y. Active Transmission Channels and Universal Conductance Fluctuations. Europhys. Lett. 1986, 1, 249. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical Optics, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2015. [Google Scholar]
- Goodman, J.W. Speckle Phenomena in Optics: Theory and Applications, 2nd ed.; SPIE: Bellingham, WA, USA, 2020. [Google Scholar]
- Ott, F.; Fritzsche, N.; Kienle, A. Numerical simulation of phase-optimized light beams in two-dimensional scattering media. J. Opt. Soc. Am. 2022, 39, 2410–2421. [Google Scholar] [CrossRef]
- Bar, C.; Alterman, M.; Gkioulekas, I.; Levin, A. Monte-Carlo simulation of the memory effect in random media beyond the diffusion limit. In Proceedings of the Optical Coherence Imaging Techniques and Imaging in Scattering Media III, Munich, Germany, 23–27 June 2019; Volume EB105 of SPIE Proceedings. Optica Publishing Group: Washington, DC, USA, 2019. [Google Scholar]
- Bewick, J.A.J.; Munro, P.R.T.; Arridge, S.R.; Guggenheim, J.A. Scalable full-wave simulation of coherent light propagation through biological tissue. In Proceedings of the 2021 IEEE Photonics Conference (IPC), Vancouver, BC, Canada, 18–21 October 2021; pp. 1–2. [Google Scholar]
- Neves, S.; Araujo, F. Fast and Small Nonlinear Pseudorandom Number Generators for Computer Simulation. In Parallel Processing and Applied Mathematics; Wyrzykowski, R., Dongarra, J., Karczewski, K., Waśniewski, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 92–101. [Google Scholar]
- Ciglarič, T.; Češnovar, R.; Štrumbelj, E. An OpenCL library for parallel random number generators. J. Supercomput. 2019, 75, 3866–3881. [Google Scholar] [CrossRef]
- Gilli, M.; Maringer, D.; Schumann, E. Numerical Methods and Optimization in Finance, 1st ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Dainty, J.C. The Statistics of Speckle Patterns; Elsevier: Amsterdam, The Netherlands, 1977; Volume 14, pp. 1–46. [Google Scholar]
- Griffiths, D.J. Introduction to Electrodynamics, 5th ed.; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Ojambati, O.S.; Hosmer-Quint, J.T.; Gorter, K.-J.; Mosk, A.P.; Vos, W.L. Controlling the intensity of light in large areas at the interfaces of a scattering medium. Phys. Rev. A 2016, 94, 043834. [Google Scholar] [CrossRef]
- Von Mises, R. Über die ’Ganzzahligkeit’ der Atomgewichte und verwandte Fragen. Phys. Z. 1918, 19, 490–500. [Google Scholar]
- Best, D.J.; Fisher, N.I. Efficient Simulation of the von Mises Distribution. J. Appl. Stat. 1979, 28, 152–157. [Google Scholar] [CrossRef]
- Fisher, N.I. Statistical Analysis of Circular Data; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Fritzsche, N.; Ott, F.; Pink, K.; Kienle, A. Focusing Coherent Light through Volume Scattering Phantoms via Wavefront Shaping. Sensors 2023, 23, 8397. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fritzsche, N.; Ott, F.; Hevisov, D.; Reitzle, D.; Kienle, A. Theoretical Investigation of the Influence of Correlated Electric Fields on Wavefront Shaping. Photonics 2024, 11, 797. https://doi.org/10.3390/photonics11090797
Fritzsche N, Ott F, Hevisov D, Reitzle D, Kienle A. Theoretical Investigation of the Influence of Correlated Electric Fields on Wavefront Shaping. Photonics. 2024; 11(9):797. https://doi.org/10.3390/photonics11090797
Chicago/Turabian StyleFritzsche, Niklas, Felix Ott, David Hevisov, Dominik Reitzle, and Alwin Kienle. 2024. "Theoretical Investigation of the Influence of Correlated Electric Fields on Wavefront Shaping" Photonics 11, no. 9: 797. https://doi.org/10.3390/photonics11090797
APA StyleFritzsche, N., Ott, F., Hevisov, D., Reitzle, D., & Kienle, A. (2024). Theoretical Investigation of the Influence of Correlated Electric Fields on Wavefront Shaping. Photonics, 11(9), 797. https://doi.org/10.3390/photonics11090797




