A Novel Electromagnetic Wavelength Measurement Method Based on Photoacoustic Effect and Photoacoustic Response Characteristics of Nanomaterials
Abstract
1. Introduction
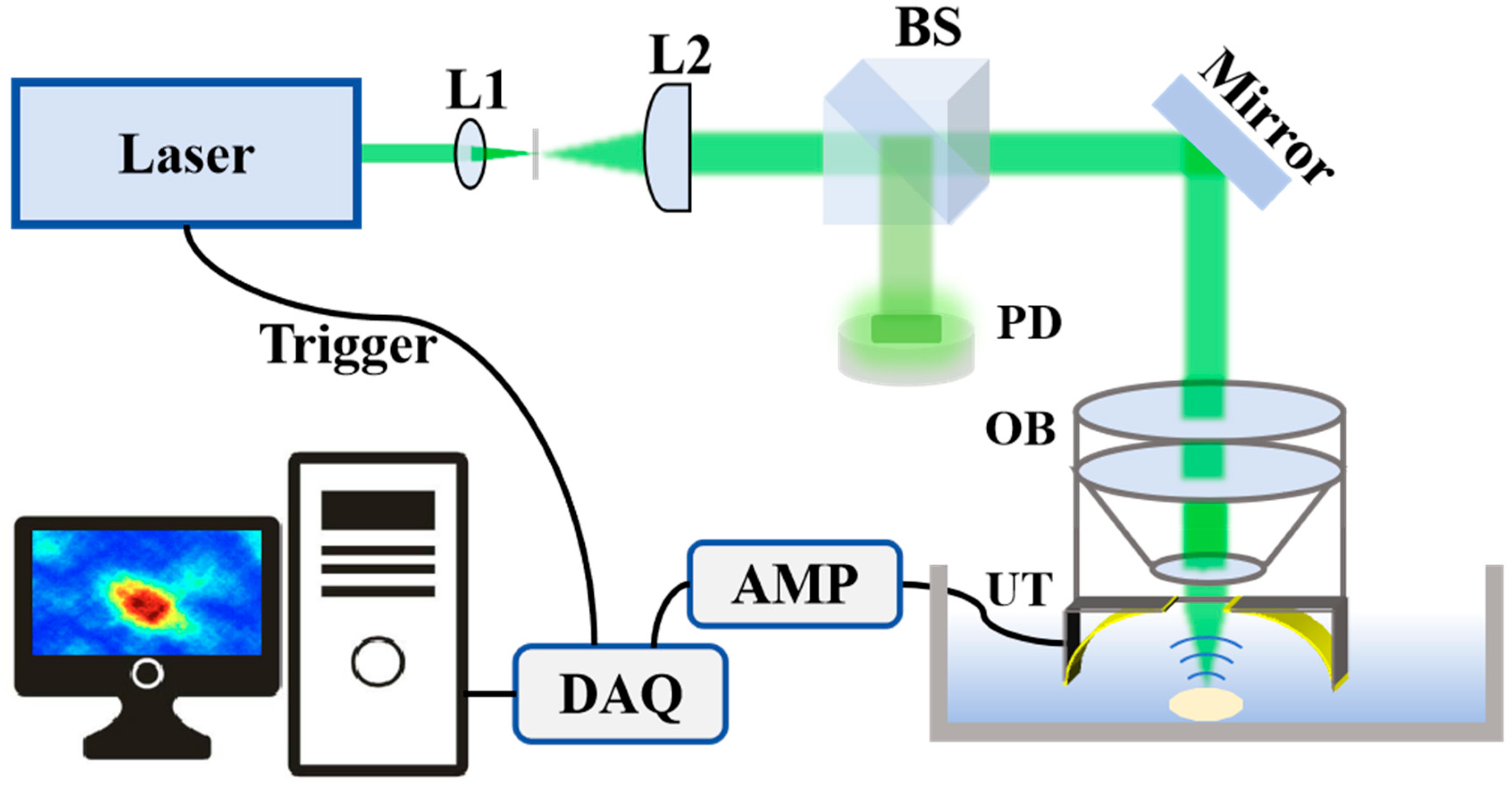
2. Methods and System
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abreu, M.; Candan, G.; Failache, H. Wavemeter. An instrument to determine coherent light beam wavelength. In Proceedings of the IEEE Instrumentation & Measurement Technology Conference, Waltham, MA, USA, 21–23 May 2002. [Google Scholar] [CrossRef]
- Solomakha, D.A.; Toropov, A.K. Laser wavelength measurements (review). Sov. J. Quantum Electron. 1977, 7, 1637–1660. [Google Scholar] [CrossRef]
- Coddington, I.; Swann, W.C.; Newbury, N.R. Erratum: Coherent Multiheterodyne Spectroscopy Using Stabilized Optical Frequency Combs. Phys. Rev. Lett. 2008, 100, 013902. [Google Scholar] [CrossRef]
- Cao, T.L.; Yao, J.Q.; Zheng, Y. Ways of wavelength mesasurement of terahertz wave based on Fabry-Perot interferometer. Opt. Instrum. 2008, 30, 13–16. [Google Scholar]
- Das, D.; Banerjee, A.; Barthwal, S.; Natarajana, V. A rubidium-stabilized ring-cavity resonator for optical frequency metrology: Precise measurement of the D1 line in 133Cs. Eur. Phys. J. Dat. Mol. Opt. Plasma Phys. 2006, 38, 545–552. [Google Scholar] [CrossRef]
- Qi, X.; Xiao, H.; Han, X.; Xia, D.; Chen, X. Frequency Measurement for Terahertz Waves Based on High Magnetic Field Technology. In Proceedings of the 44th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Paris, France, 1–6 September 2019. [Google Scholar] [CrossRef]
- Yee, D.S.; Jang, Y.D.; Kim, Y.C.; Seo, D.C. Terahertz spectrum analyzer based on frequency and power measurement. Opt. Lett. 2010, 35, 2532–2534. [Google Scholar] [CrossRef]
- Zou, X.; Yao, J. Microwave frequency measurement with improved measurement range and resolution. Electron. Lett. 2009, 45, 497–498. [Google Scholar] [CrossRef]
- Lau, K.Y.; Nabiev, R.F.; Chang-Hasnain, C.J.; Eng, L.E. Spectrodetector: Novel monolithic wavelength reader and photodetector. Electron. Lett. 2002, 31, 1373–1374. [Google Scholar] [CrossRef]
- Badran, H. A Low Cost Instantaneous Frequency Measurement System. Electromagn. Res. M 2017, 59, 171–180. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, Y.S.; Zhao, Y.S.; Li, P. Advances in Spectroscopic Characters of Space Objects. J. Clin. Otorhinolaryngol. 2017, 37, 672–678. [Google Scholar]
- Ivanov, A.A.; Morozov, O.G.; Andreev, V.A.; Morozov, G.A.; Faskhutdinov, L.M. Microwave photonic system for instantaneous frequency measurement based on principles of “frequency-amplitude” conversion in fiber Bragg grating and additional frequency separation. In Proceedings of the XIV International Scientific and Technical Conference on Optical Technologies in Telecommunications, Samara, Russia, 23–26 November 2016; International Society for Optics and Photonics: San Diego, CA, USA, 2017. [Google Scholar] [CrossRef]
- Dai, J.; Xu, K.; Duan, R.; Zhang, X.; Wang, D.; Wu, J.; Lin, J. Instantaneous frequency measurement based on complementary microwave photonic filters with a shared Mach–Zehnder interferometer. Opt. Commun. 2011, 284, 5738–5741. [Google Scholar] [CrossRef]
- Thattey, S.S.; Dongare, A.S.; Dasgupta, K.; More, S.R.; Nair, L.G. A wavemeter for measuring changes in wavelength of pulsed dye lasers. Rev. Sci. Instrum. 1994, 65, 2470–2474. [Google Scholar] [CrossRef]
- Saitoh, T.; Nakamura, K.; Takahashi, Y.; Miyagi, K. Optical spectrum analyzer utilizing MEMS scanning mirror. IEEE Photonics Technol. Lett. 2006, 18, 767–769. [Google Scholar] [CrossRef]
- Petley, B.W.; Morris, K. A simple CW laser digital wavemeter. Opt. Quantum Electron. 1978, 10, 277–278. [Google Scholar] [CrossRef]
- Karpowicz, N.; Dai, J.; Lu, X.; Chen, Y.; Yamaguchi, M.; Zhao, H. Coherent heterodyne time-domain spectrometry covering the entire “terahertz gap”. Appl. Phys. Lett. 2008, 92, 011131. [Google Scholar] [CrossRef]
- Ach, F.; Schmiedel, A.; Kaemling, A.; Fischer, C.; Viöl, W. High power infrared laser beam monitoring by optical measurement of mirror surface deformation. Laser Phys. Lett. 2010, 2, 267–271. [Google Scholar] [CrossRef]
- Zhang, B.; Peng, Z.; Xia, Y.; Sun, Z.; Zheng, K.; Zhu, Q.; Dong, J.; Lu, Z. High precise time division multiplex UV pulse waveform measurement system for high power laser facility. Fusion Eng. Des. 2021, 173, 112878. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.F.; Chen, D.D.; Wang, X.S.; Zhang, Z.; Yang, Y.C.; Jiang, L.H.; Qi, W.Z.; Ye, Z.Y.; He, S.Q.; et al. Fluorination Enhances NIR-II Fluorescence of Polymer Dots for Quantitative Brain Tumor Imaging. Angew. Chem. Int. Ed. 2020, 132, 21235–21243. [Google Scholar] [CrossRef]
- Wang, W.P.; Huang, L.; Zhou, H.J.; Gong, S.; Zeng, H.X.; Zhou, J.; Yang, Z.Q.; Zhang, Y.X. Low Frequency Terahertz Induced Thermoacoustic Signal Characteristics and Its Application in Solid-State Terahertz Transmitter Power Detection. IEEE Trans. Terahertz Sci. Technol. 2022, 12, 673–677. [Google Scholar] [CrossRef]
- Satapathy, A.; Sawant, K.K.; Mondal, S.; Raj, A.A.B.; Mahimkar, K.; Kandasubramanian, B. Recent Progress on MXenes as an Attenuator of Terahertz Radiation. J. Electron. Mater. 2023, 52, 1749–1768. [Google Scholar] [CrossRef]
- Titova, L.V.; Li, G.; Natu, V.; Huang, S.; Barsoum, M.W. 2D MXenes: Terahertz Properties and Applications. In Proceedings of the 45th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Buffalo, NY, USA, 8–13 November 2020. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Gong, P.; Ma, W.D.; Hao, R.; Fang, X.Y. Effects of substitution of group-V atoms for carbon or silicon atoms on optical properties of silicon carbide nanotubes. Chin. Phys. B 2021, 30, 67803. [Google Scholar] [CrossRef]
- Henaish, A.; Abouhaswa, A. Effect of WO3 nanoparticle doping on the physical properties of PVC polymer. Bull. Mater. Sci. 2020, 43, 149. [Google Scholar] [CrossRef]
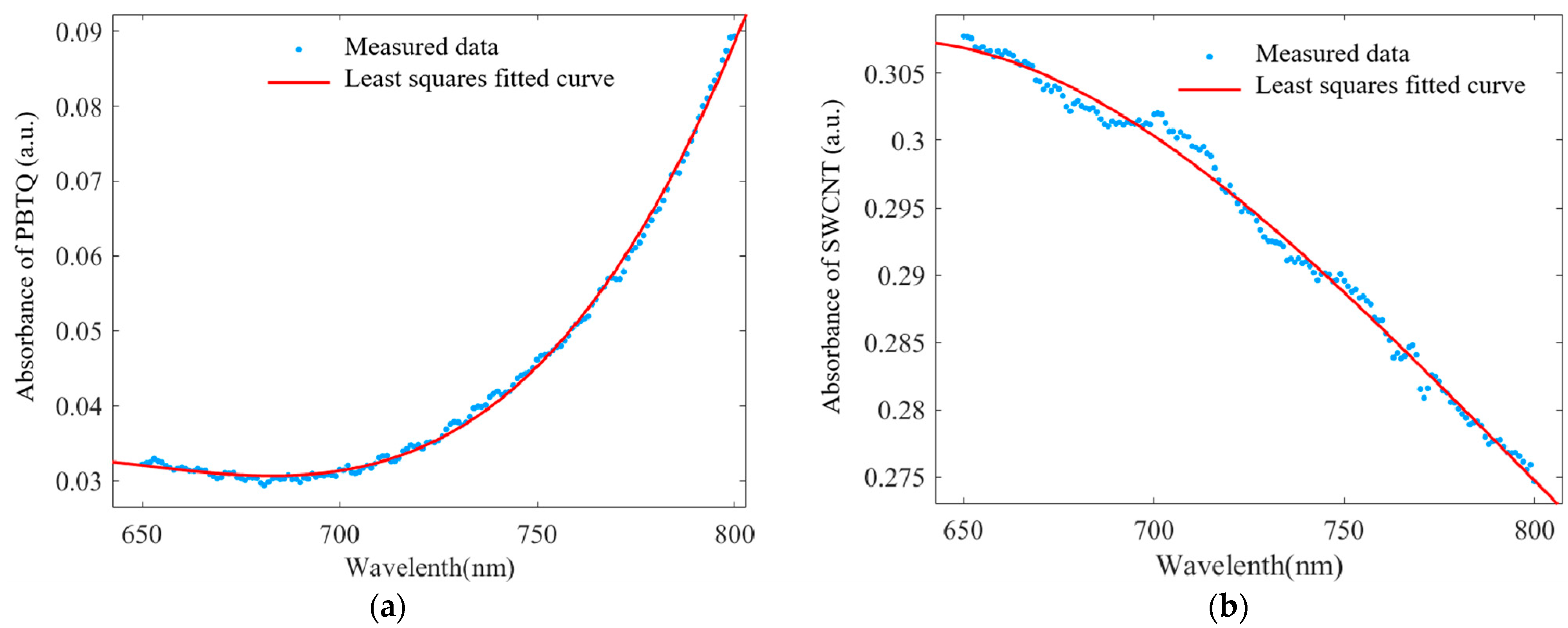
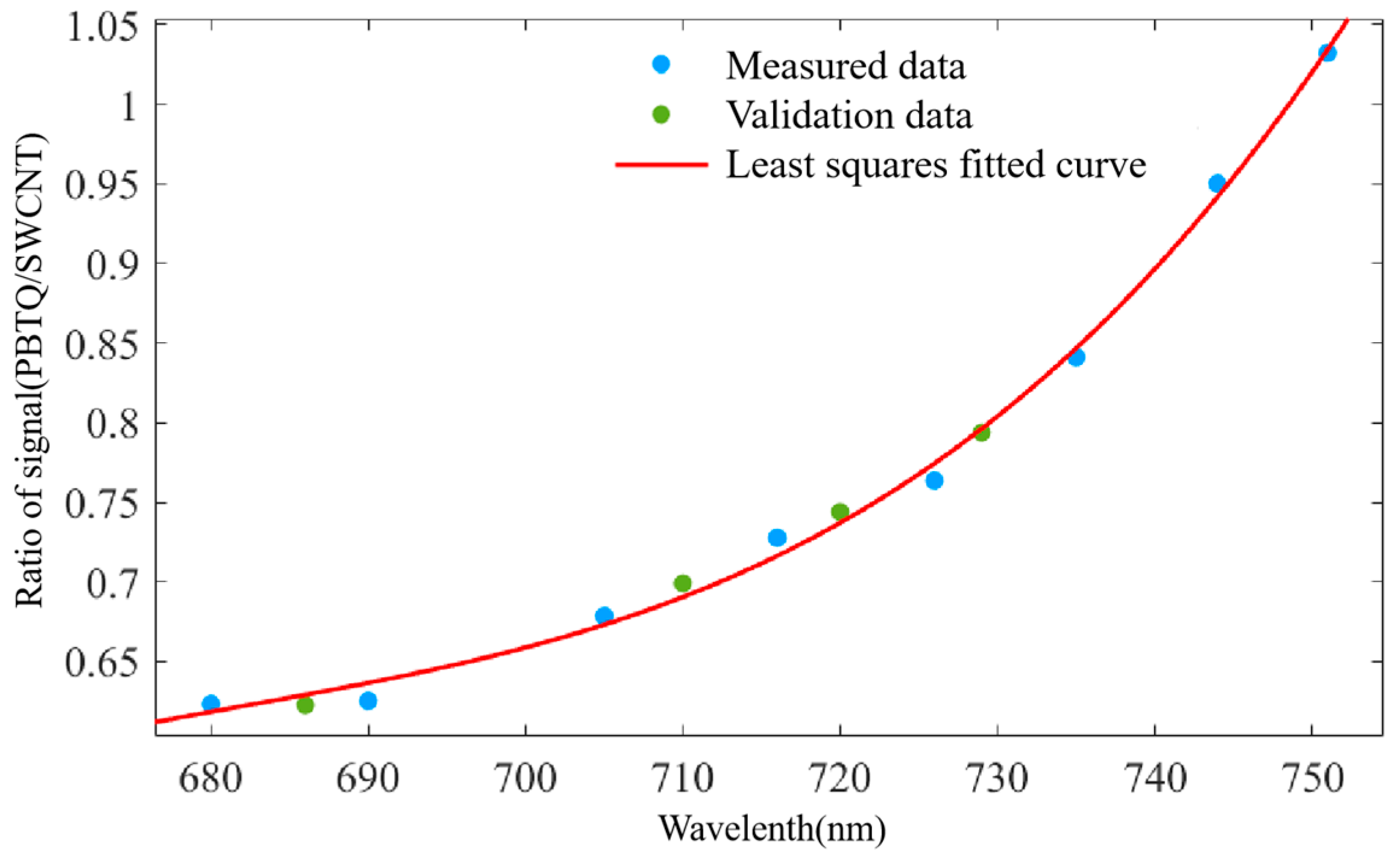
| MATERIAL | SSE | RMSE | |
|---|---|---|---|
| PBTQ | 0.998 | 8.016 × 10−5 | 7.385 × 10−4 |
| SWCNT | 0.9942 | 1.111 × 10−4 | 8.694 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Zhong, R.; Zhang, Z.; Huang, L. A Novel Electromagnetic Wavelength Measurement Method Based on Photoacoustic Effect and Photoacoustic Response Characteristics of Nanomaterials. Photonics 2024, 11, 831. https://doi.org/10.3390/photonics11090831
Huang Y, Zhong R, Zhang Z, Huang L. A Novel Electromagnetic Wavelength Measurement Method Based on Photoacoustic Effect and Photoacoustic Response Characteristics of Nanomaterials. Photonics. 2024; 11(9):831. https://doi.org/10.3390/photonics11090831
Chicago/Turabian StyleHuang, Yijie, Renbin Zhong, Zhenhui Zhang, and Lin Huang. 2024. "A Novel Electromagnetic Wavelength Measurement Method Based on Photoacoustic Effect and Photoacoustic Response Characteristics of Nanomaterials" Photonics 11, no. 9: 831. https://doi.org/10.3390/photonics11090831
APA StyleHuang, Y., Zhong, R., Zhang, Z., & Huang, L. (2024). A Novel Electromagnetic Wavelength Measurement Method Based on Photoacoustic Effect and Photoacoustic Response Characteristics of Nanomaterials. Photonics, 11(9), 831. https://doi.org/10.3390/photonics11090831






