High-Ratio Nonlinear Compression of Picosecond Lasers Based on Thin Plates
Abstract
1. Introduction
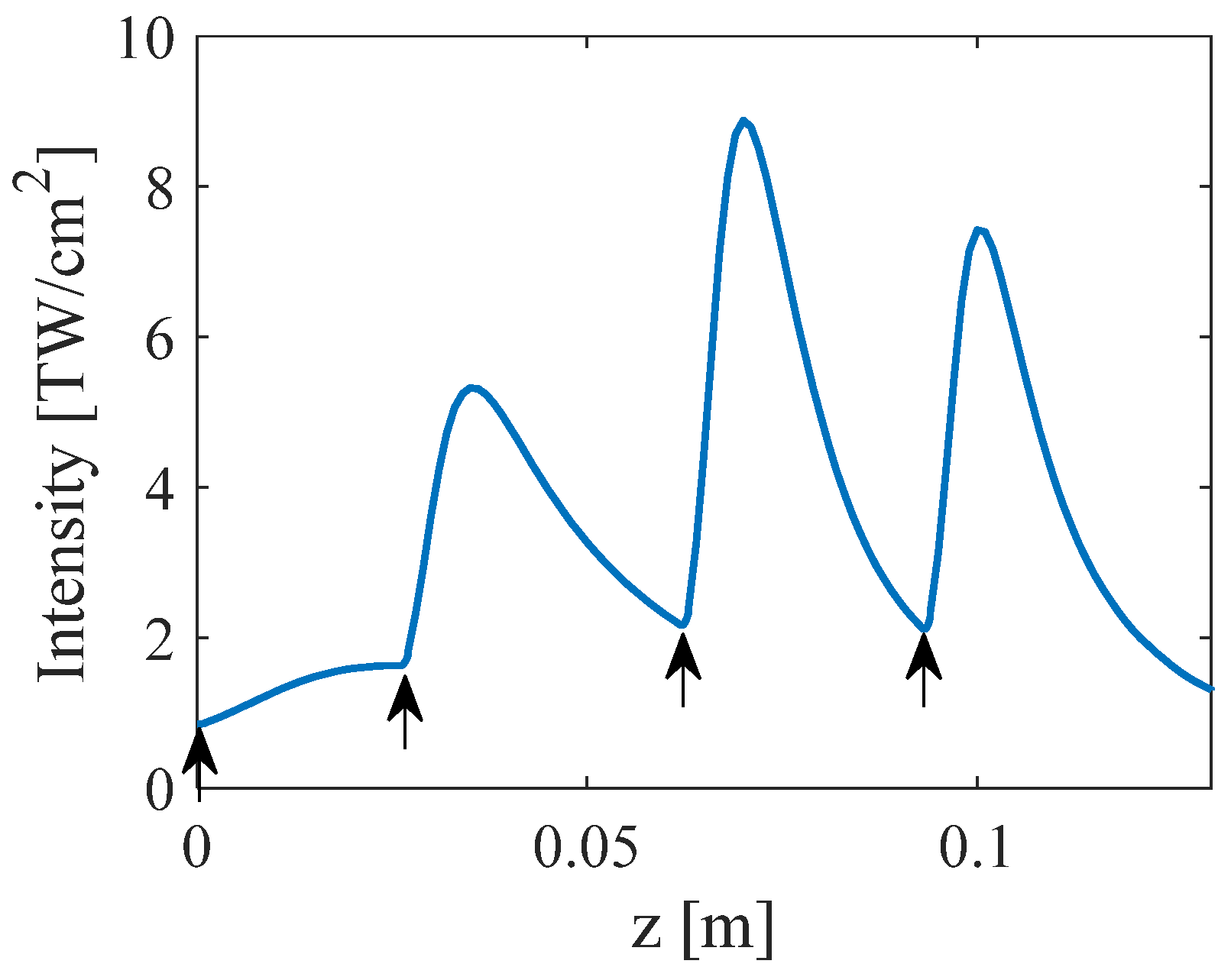
2. Two-Stage Thin-Plate-Based Nonlinear Compression: Design
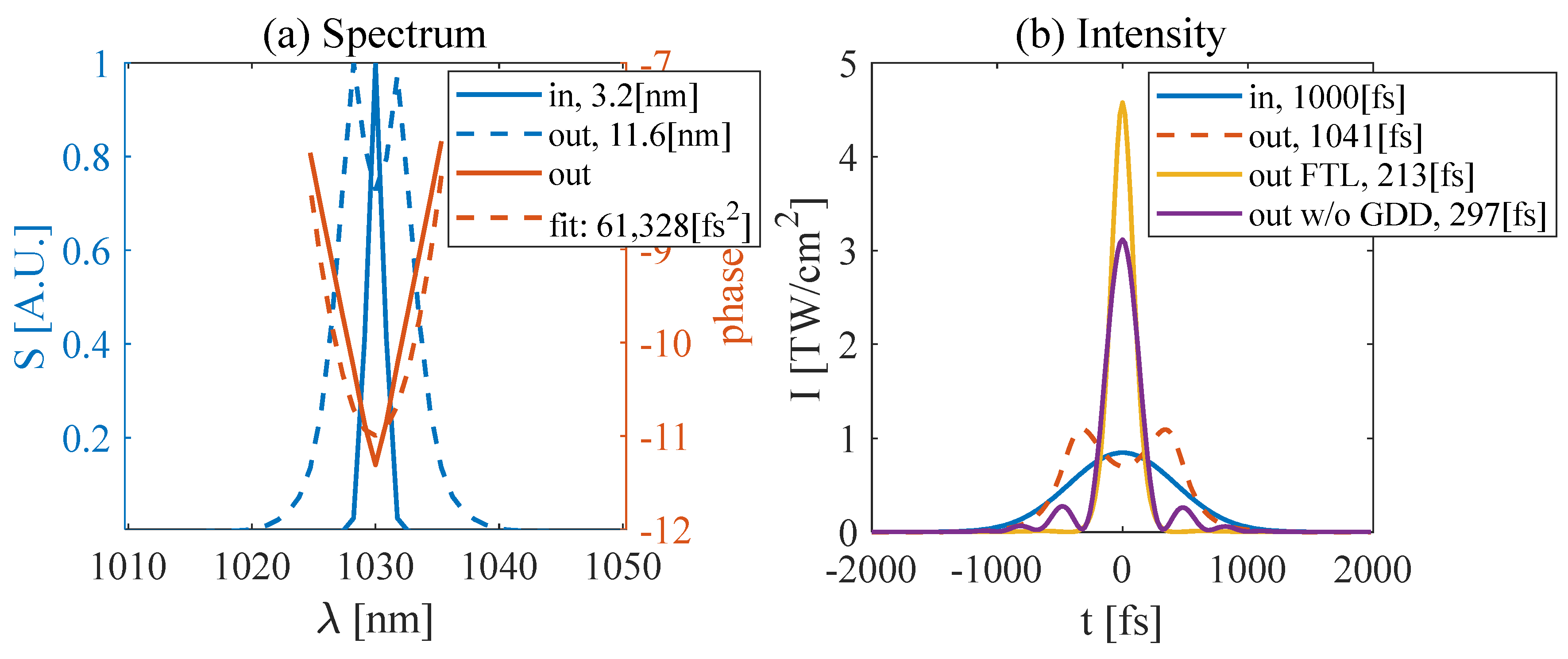
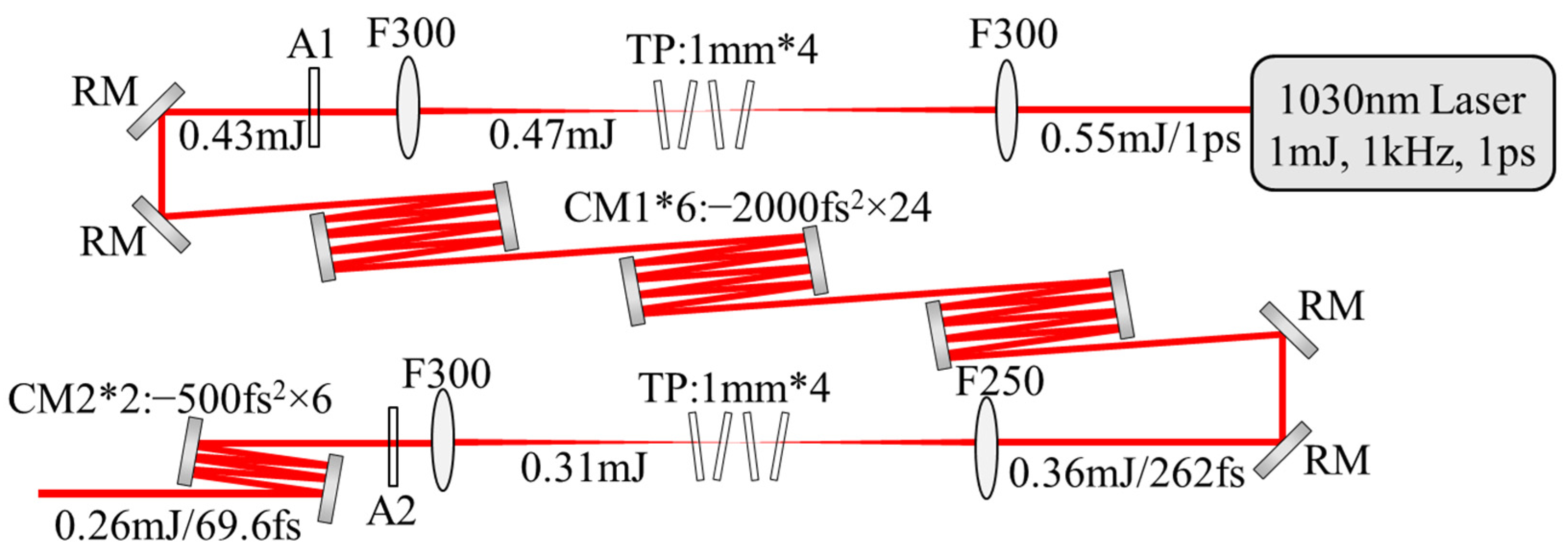
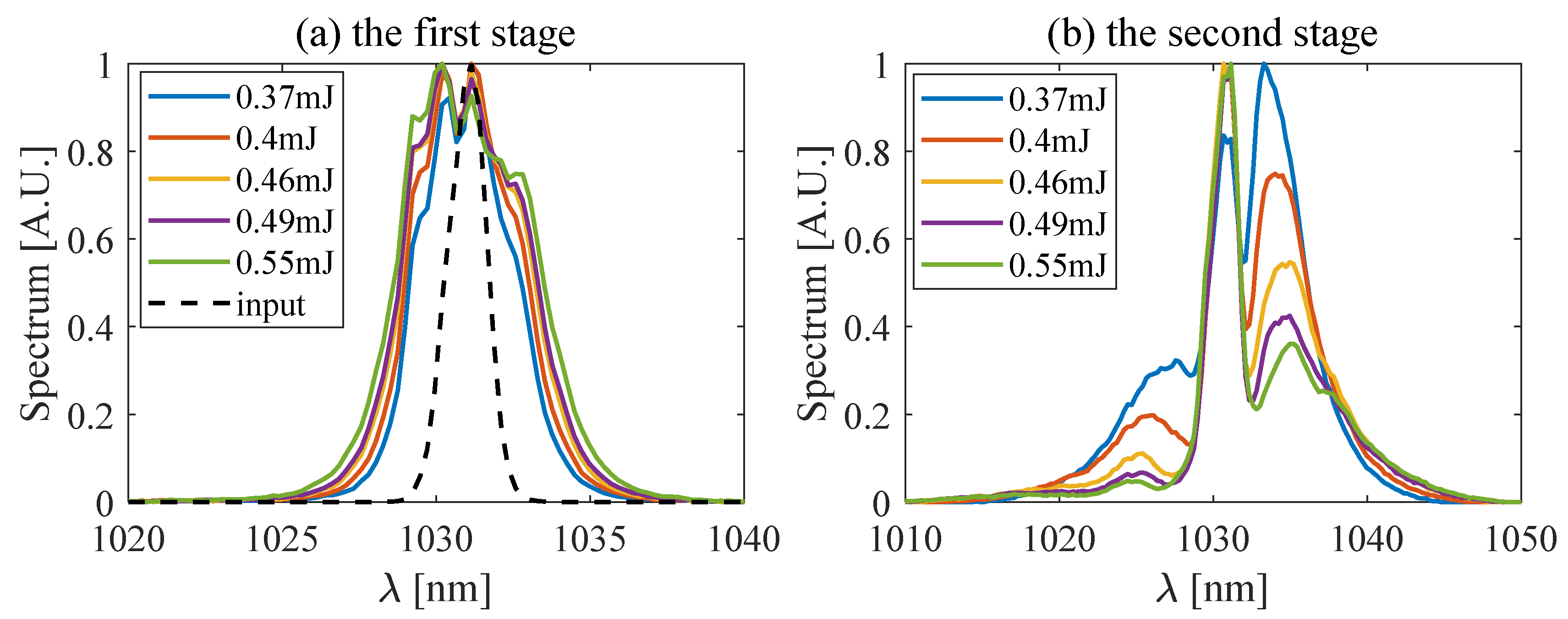
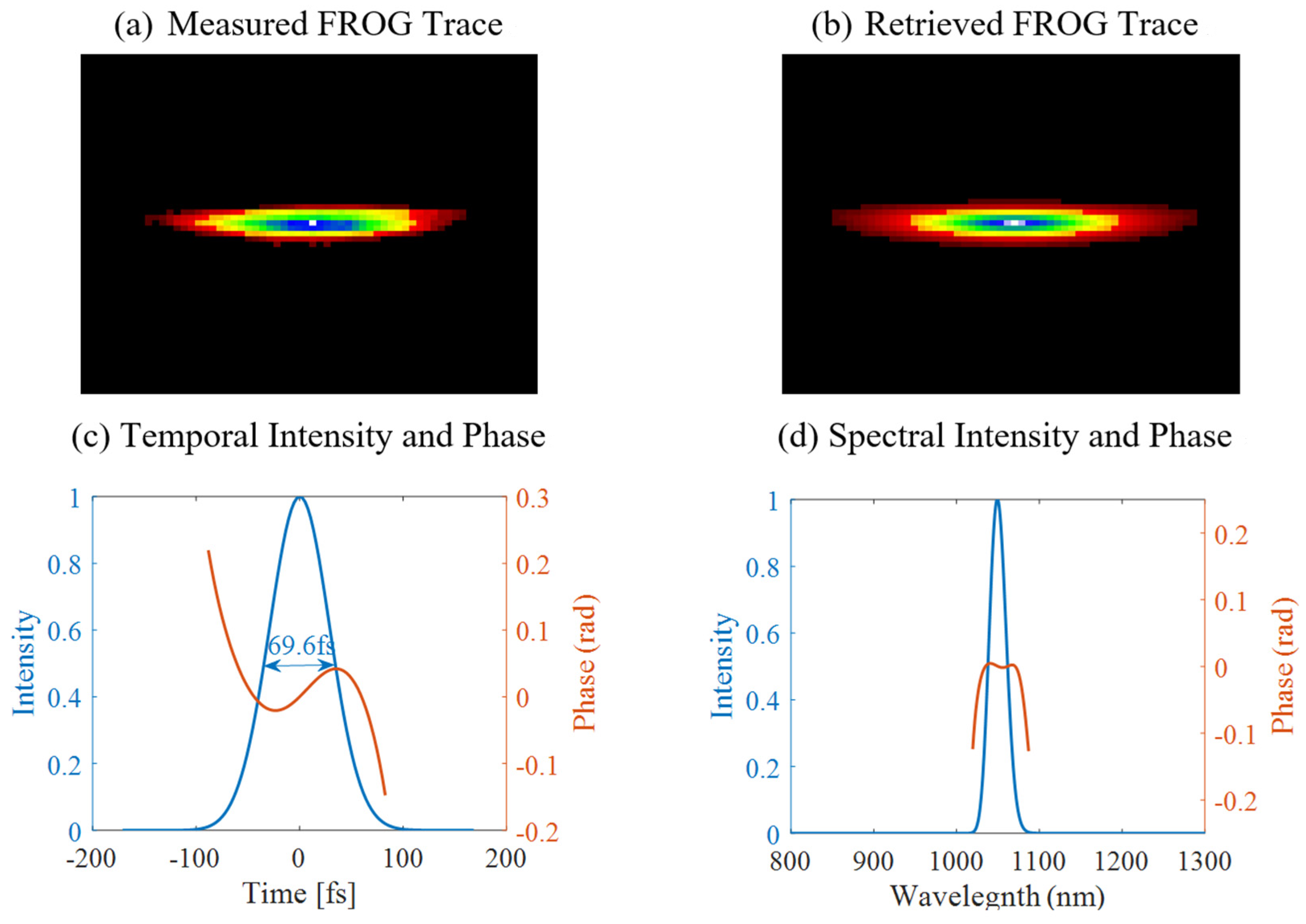
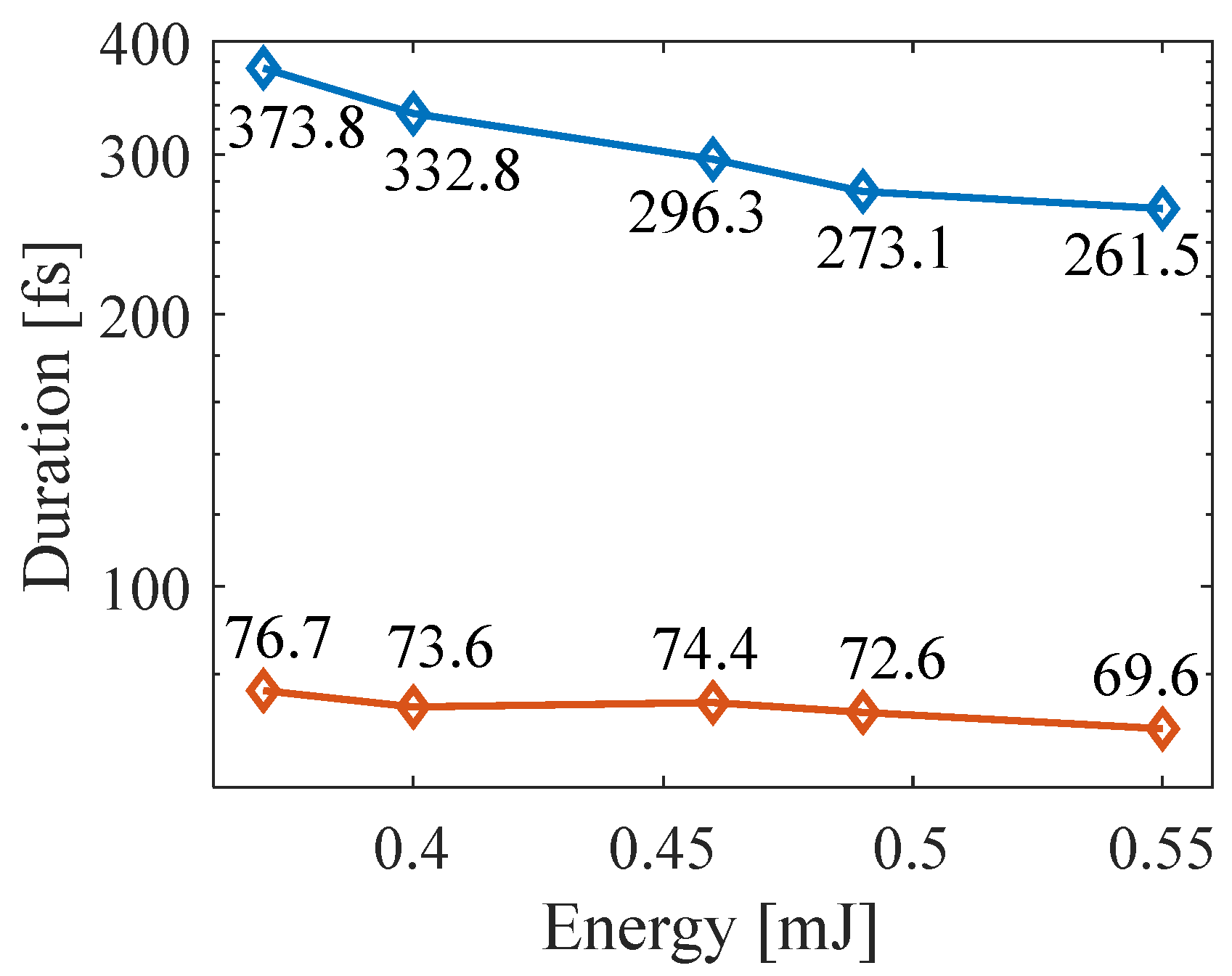
3. Two-Stage Thin-Plate-Based Nonlinear Compression: Experiment
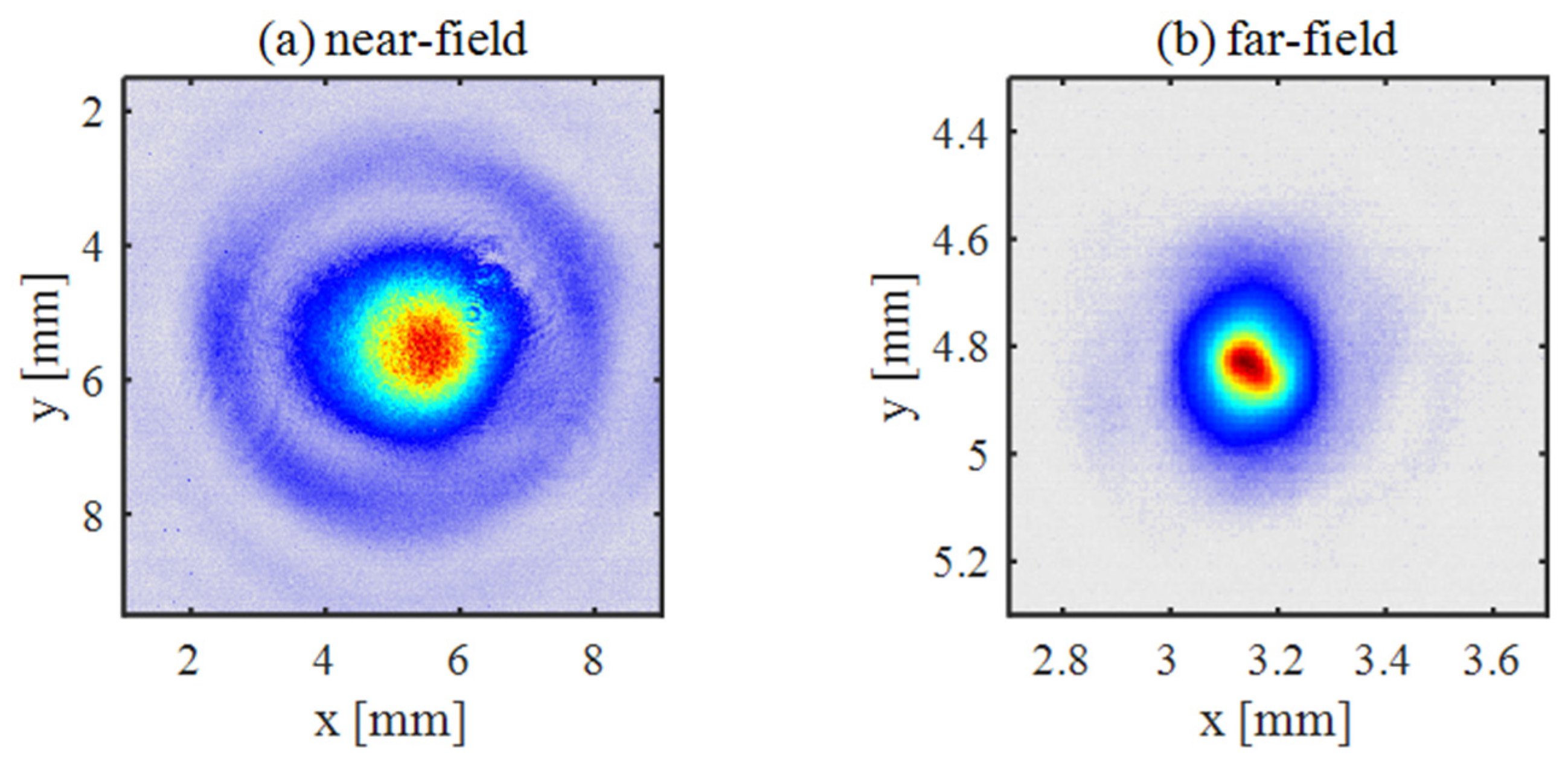
4. Spatial Profile of the Laser Pulse
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Joshi, C.; Corde, S.; Mori, W.B. Perspectives on the generation of electron beams from plasma-based accelerators and their near and long term applications. Phys. Plasmas 2020, 27, 070602. [Google Scholar] [CrossRef]
- Ziegler, T.; Göthel, I.; Assenbaum, S.; Bernert, C.; Brack, F.-E.; Cowan, T.E.; Dover, N.P.; Gaus, L.; Kluge, T.; Kraft, S.; et al. Laser-driven high-energy proton beams from cascaded acceleration regimes. Nat. Phys. 2024, 20, 1211–1216. [Google Scholar] [CrossRef]
- Götte, N.; Winkler, T.; Meinl, T.; Kusserow, T.; Zielinski, B.; Sarpe, C.; Senftleben, A.; Hillmer, H.; Baumert, T. Temporal airy pulses for controlled high aspect ratio nanomachining of dielectrics. Optica 2016, 3, 389. [Google Scholar] [CrossRef]
- Butkus, S. Micromachining of transparent, semiconducting and metallic substrates using femtosecond laser beams. J. Laser Micro/Nanoeng. 2016, 11, 81. [Google Scholar] [CrossRef]
- Hauri, C.; Kornelis, W.; Helbing, F.; Heinrich, A.; Couairon, A.; Mysyrowicz, A.; Biegert, J.; Keller, U. Generation of intense, carrier-envelope phase-locked few-cycle laser pulses through filamentation. Appl. Phys. B 2004, 79, 673. [Google Scholar] [CrossRef]
- Hauri, C.P.; Guandalini, A.; Eckle, P.; Kornelis, W.; Biegert, J.; Keller, U. Generation of intense few-cycle laser pulses through filamentation parameter dependence. Opt. Express 2005, 13, 7541. [Google Scholar] [CrossRef]
- Théberge, F.; Aközbek, N.; Liu, W.; Becker, A.; Chin, S.L. Tunable ultrashort laser pulses generated through filamentation in gases. Phys. Rev. Lett. 2006, 97, 023904. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, Y.; Chan, Y.; Deng, F.; Zhang, J. Coherent generation and control of tunable narrowband THz radiation from a laser-induced air-plasma filament. Opt. Lett. 2023, 48, 2881. [Google Scholar] [CrossRef]
- Pac Chong, M.L.; Garriga Francis, K.J.; Yiwen, E.; Zhang, X.C. Single-shot local measurement of terahertz correlated second harmonic generation in laser air plasma filaments. Opt. Lett. 2024, 49, 226. [Google Scholar] [CrossRef]
- Kasparian, J.; Rodriguez, M.; Méjean, G.; Yu, J.; Salmon, E.; Wille, H.; Bourayou, R.; Frey, S.; André, Y.-B.; Mysyrowicz, A.; et al. White-light filaments for atmospheric analysis. Science 2003, 301, 61. [Google Scholar]
- Chin, S.L.; Xu, H.L.; Luo, Q.; Théberge, F.; Liu, W.; Daigle, J.F.; Kamali, Y.; Simard, P.T.; Bernhardt, J.; Hosseini, S.A.; et al. Filamentation “remote” sensing of chemical and biological agents/pollutants using only one femtosecond laser source. Appl. Phys. B 2009, 95, 1. [Google Scholar] [CrossRef]
- Dicaire, I.; Jukna, V.; Praz, C.; Milián, C.; Summerer, L.; Couairon, A. Spaceborne laser filamentation for atmospheric remote sensing. Laser Photonics Rev. 2016, 10, 481. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, H.; Liu, J.; Liang, H.; Ju, J.; Wang, T.; Tian, Y.; Wang, C.; Liu, Y.; Chin, S.L.; et al. Laser-filamentation induced water condensation and snow formation in a cloud chamber filled with different ambient gases. Opt. Express 2016, 24, 7364. [Google Scholar] [CrossRef] [PubMed]
- Houard, A.; Walch, P.; Produit, T.; Moreno, V.; Mahieu, B.; Sunjerga, A.; Herkommer, C.; Mostajabi, A.; Andral, U.; André, Y.-B.; et al. Laser-guided lightning. Nat. Photonics 2023, 17, 231. [Google Scholar] [CrossRef]
- Wolf, J.P. Short-pulse lasers for weather control. Rep. Prog. Phys. 2018, 81, 026001. [Google Scholar] [CrossRef]
- Jhajj, N.; Rosenthal, E.; Birnbaum, R.; Wahlstrand, J.; Milchberg, H. Demonstration of long-lived high-power optical waveguides in air. Phys. Rev. X 2014, 4, 011027. [Google Scholar]
- Rosenthal, E.; Jhajj, N.; Wahlstrand, J.K.; Milchberg, H. Collection of remote optical signals by air waveguides. Optica 2014, 1, 5. [Google Scholar] [CrossRef]
- Russbueldt, P.; Mans, T.; Weitenberg, J.; Hoffmann, H.D.; Poprawe, A.R. Compact diode-pumped 1.1 kW YbYAG Innoslab femtosecond amplifier. Opt. Lett. 2010, 35, 4169. [Google Scholar] [CrossRef]
- Nubbemeyer, T.; Kaumanns, M.; Ueffing, M.; Gorjan, M.; Alismail, A.; Fattahi, H.; Brons, J.; Pronin, O.; Barros, H.G.; Major, Z.; et al. 1 kW, 200 mJ picosecond thin-disk laser system. Opt. Lett. 2017, 42, 1381. [Google Scholar] [CrossRef]
- Eidam, T.; Hanf, S.; Seise, E.; Andersen, T.V.; Gabler, T.; Wirth, C.; Schreiber, T.; Limpert, J.; Tünnermann, A. Femtosecond fiber CPA system emitting 830 W average output power. Opt. Lett. 2010, 35, 94. [Google Scholar] [CrossRef]
- Voronin, A.A.; Zheltikov, A.M.; Ditmire, T.; Rus, B.; Korn, G. Subexawatt few-cycle lightwave generation via multipetawatt pulse compression. Opt. Commun. 2013, 291, 299. [Google Scholar] [CrossRef]
- Lassonde, P.; Mironov, S.; Fourmaux, S.; Payeur, S.; Khazanov, E.; Sergeev, A.; Kieffer, J.-C.; Mourou, G. High energy femtosecond pulse compression. Laser Phys. Lett. 2016, 13, 075401. [Google Scholar] [CrossRef]
- Schulte, J.; Sartorius, T.; Weitenberg, J.; Vernaleken, A.; Russbueldt, P. Nonlinear pulse compression in a multi-pass cell. Opt. Lett. 2016, 41, 4511. [Google Scholar] [CrossRef] [PubMed]
- Ueffing, M.; Reiger, S.; Kaumanns, M.; Pervak, V.; Trubetskov, M.; Nubbemeyer, T.; Krausz, F. Nonlinear pulse compression in a gas-filled multipass cell. Opt. Lett. 2018, 43, 2070. [Google Scholar] [CrossRef] [PubMed]
- Lavenu, L.; Natile, M.; Guichard, F.; Zaouter, Y.; Delen, X.; Hanna, M.; Mottay, E.; Georges, P. Nonlinear pulse compression based on a gas-filled multipass cell. Opt. Lett. 2018, 43, 2252. [Google Scholar] [CrossRef]
- Kaumanns, M.; Pervak, V.; Kormin, D.; Leshchenko, V.; Kessel, A.; Ueffing, M.; Chen, Y.; Nubbemeyer, T. Multipass spectral broadening of 18 mJ pulses compressible from 1.3 ps to 41 fs. Opt. Lett. 2018, 43, 5877. [Google Scholar] [CrossRef]
- Balla, P.; Bin Wahid, A.; Sytcevich, I.; Guo, C.; Viotti, A.-L.; Silletti, L.; Cartella, A.; Alisauskas, S.; Tavakol, H.; Grosse-Wortmann, U.; et al. Postcompression of picosecond pulses into the few-cycle regime. Opt. Lett. 2020, 45, 2572. [Google Scholar] [CrossRef]
- Kaumanns, M.; Kormin, D.; Nubbemeyer, T.; Pervak, V.; Karsch, S. Spectral broadening of 112 mJ, 1.3 ps pulses at 5 kHz in a LG10 multipass cell with compressibility to 37 fs. Opt. Lett. 2021, 46, 929. [Google Scholar] [CrossRef]
- Pfaff, Y.; Forster, C.; Barbiero, G.; Rampp, M.; Klingebiel, S.; Brons, J.; Teisset, C.Y.; Wang, H.; Jung, R.; Jaksic, J.; et al. Nonlinear pulse compression of a thin-disk amplifier and contrast enhancement via nonlinear ellipse rotation. Opt. Express 2022, 30, 10981. [Google Scholar] [CrossRef]
- Weitenberg, J.; Vernaleken, A.; Schulte, J.; Ozawa, A.; Sartorius, T.; Pervak, V.; Hoffmann, H.-D.; Udem, T.; Russbüldt, P.; Hänsch, T.W. Multi-pass-cell-based nonlinear pulse compression to 115 fs at 7.5 uJ pulse energy and 300 W average power. Opt. Express 2017, 25, 20502–20510. [Google Scholar] [CrossRef]
- Fan, G.; Carpeggiani, P.A.; Tao, Z.; Coccia, G.; Safaei, R.; Kaksis, E.; Pugzlys, A.; Légaré, F.; Schmidt, B.E.; Baltuška, A. 70 mJ nonlinear compression and scaling route for an Yb amplifier using large-core hollow fibers. Opt. Lett. 2021, 46, 896–899. [Google Scholar] [CrossRef] [PubMed]
- Nagy, T.; Hädrich, S.; Simon, P.; Blumenstein, A.; Walther, N.; Klas, R.; Buldt, J.; Stark, H.; Breitkopf, S.; Jójárt, P.; et al. Generation of three-cycle multi-millijoule laser pulses at 318 W average power. Optica 2019, 6, 1423. [Google Scholar] [CrossRef]
- Mironov, S.Y.; Wheeler, J.; Gonin, R.; Cojocaru, G.; Ungureanu, R.; Banici, R.; Serbanescu, M.; Dabu, R.; Mourou, G.; A Khazanov, E. 100 J-level pulse compression for peak power enhancement. Quantum Electron. 2017, 47, 173. [Google Scholar] [CrossRef]
- Khazanov, E.A.; Mironov, S.Y.; Mourou, G. Nonlinear compression of high-power laser pulses: Compression after compressor approach. Phys. Uspekhi 2019, 62, 1096–1124. [Google Scholar] [CrossRef]
- Bleotu, P.G.; Wheeler, J.; Mironov, S.Y.; Ginzburg, V.; Masruri, M.; Naziru, A.; Secareanu, R.; Ursescu, D.; Perez, F.; De Sousa, J.; et al. Post-compression of high-energy, sub-picosecond laser pulses. High Power Laser Sci. Eng. 2023, 11, e30. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, K.; Li, Z.; Zuo, Y.; Wu, Z.; Zeng, X.; Wang, X.; Wang, X.; Mu, J.; Feng, G. High-Ratio Nonlinear Compression of Picosecond Lasers Based on Thin Plates. Photonics 2025, 12, 21. https://doi.org/10.3390/photonics12010021
Zhou K, Li Z, Zuo Y, Wu Z, Zeng X, Wang X, Wang X, Mu J, Feng G. High-Ratio Nonlinear Compression of Picosecond Lasers Based on Thin Plates. Photonics. 2025; 12(1):21. https://doi.org/10.3390/photonics12010021
Chicago/Turabian StyleZhou, Kainan, Zhaoli Li, Yanlei Zuo, Zhaohui Wu, Xiaoming Zeng, Xiao Wang, Xiaodong Wang, Jie Mu, and Guoying Feng. 2025. "High-Ratio Nonlinear Compression of Picosecond Lasers Based on Thin Plates" Photonics 12, no. 1: 21. https://doi.org/10.3390/photonics12010021
APA StyleZhou, K., Li, Z., Zuo, Y., Wu, Z., Zeng, X., Wang, X., Wang, X., Mu, J., & Feng, G. (2025). High-Ratio Nonlinear Compression of Picosecond Lasers Based on Thin Plates. Photonics, 12(1), 21. https://doi.org/10.3390/photonics12010021




