Simulated Microfluidic Device Constructed Using Terahertz Metamaterial for Sensing and Switching Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Device Design and Definition of Parameters
2.2. Simulation Method
2.3. Illustration of Possible Fabrication Method and Experimental Setup
3. Results and Discussions
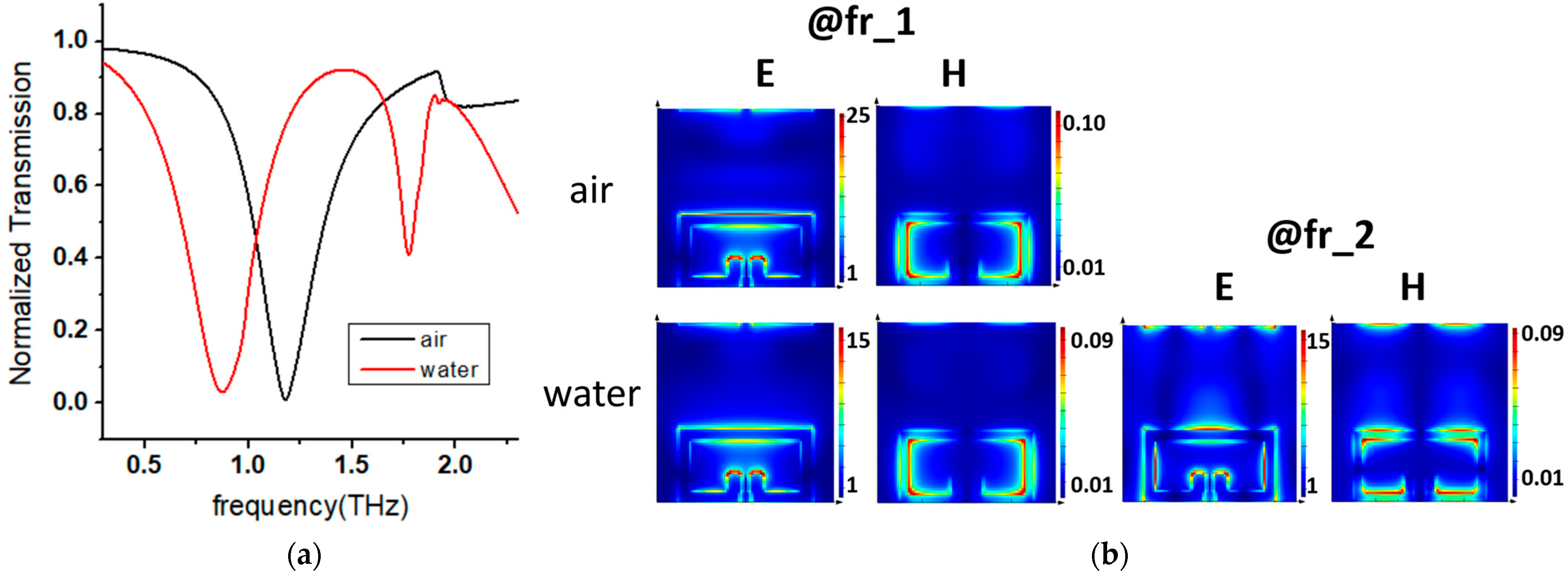
3.1. The Baseline Performance of a Typical Device
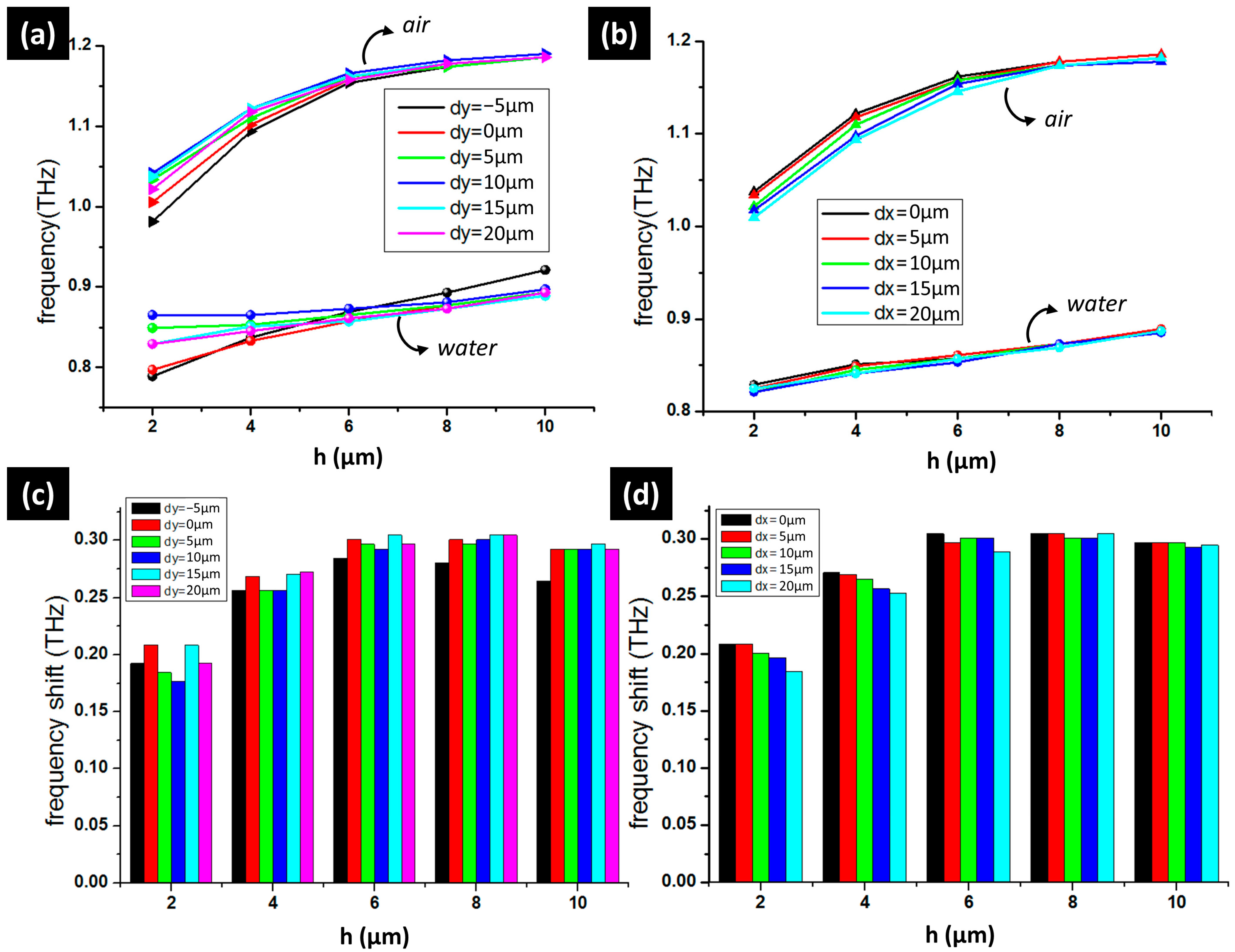
3.2. Impacts of h, Δx, and Δy on Sensing with the First Resonance
3.2.1. RI Sensing
3.2.2. Pressure Sensing
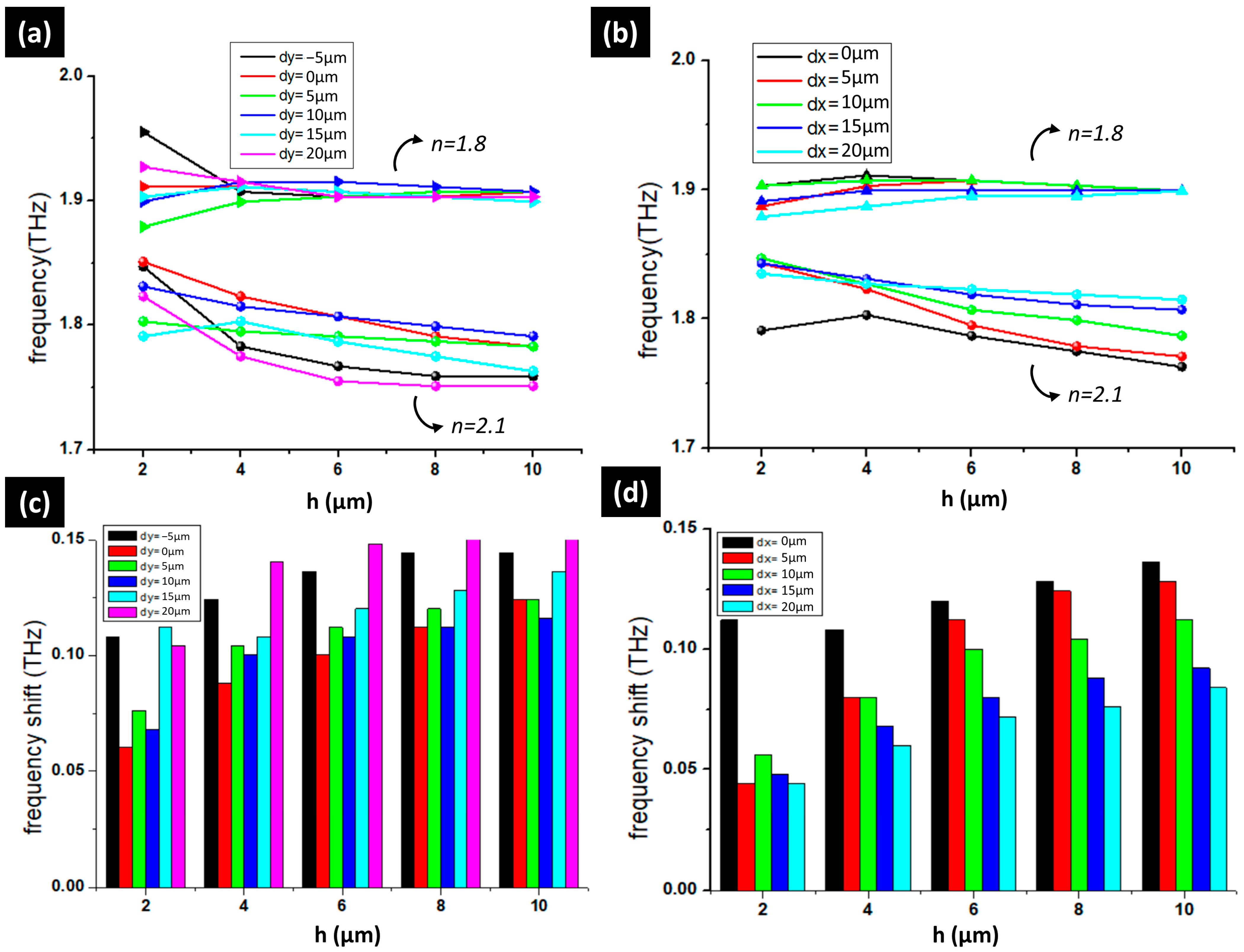
3.3. Impacts of h, Δx, and Δy on Sensing with the Second Resonance
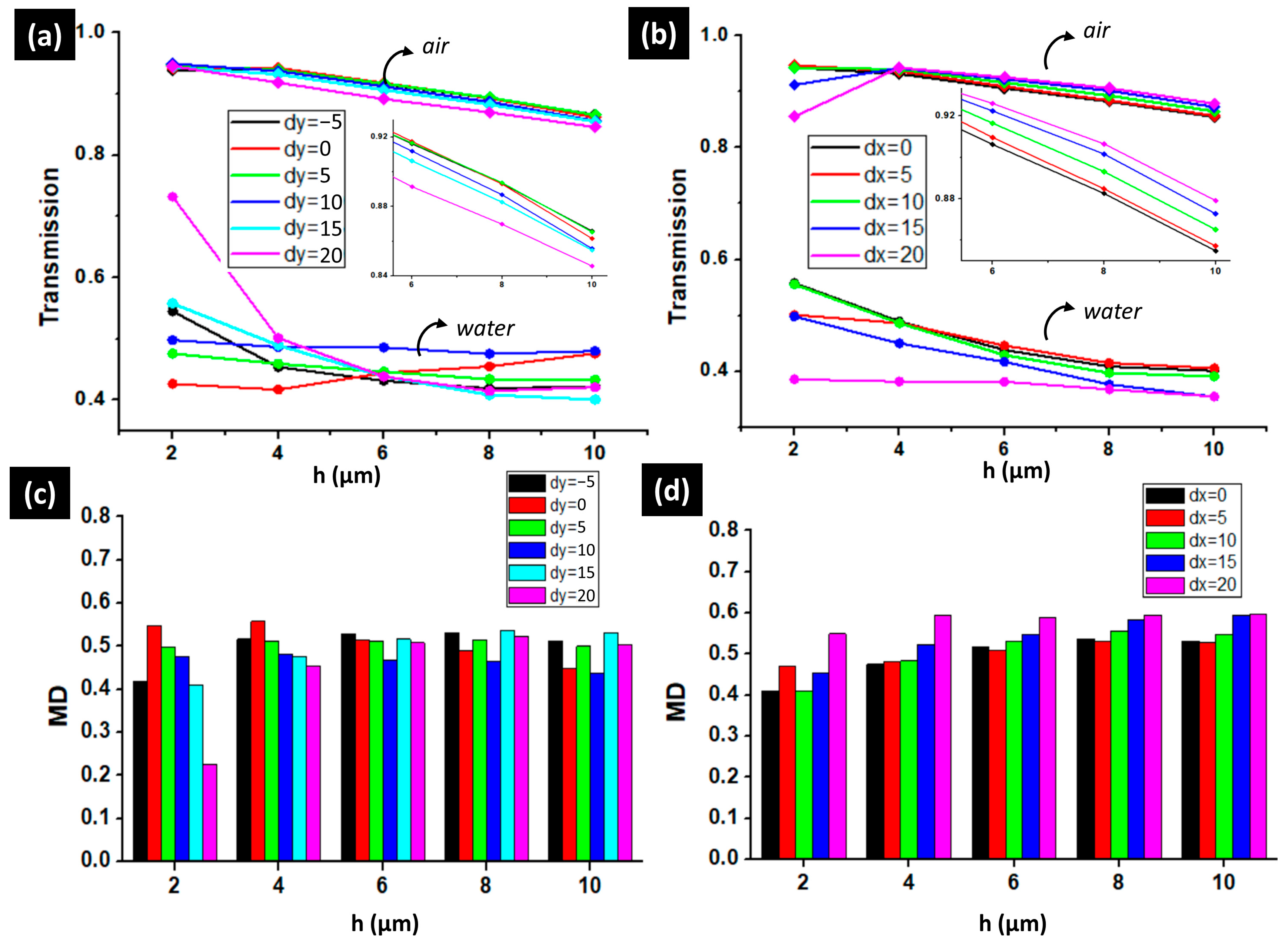
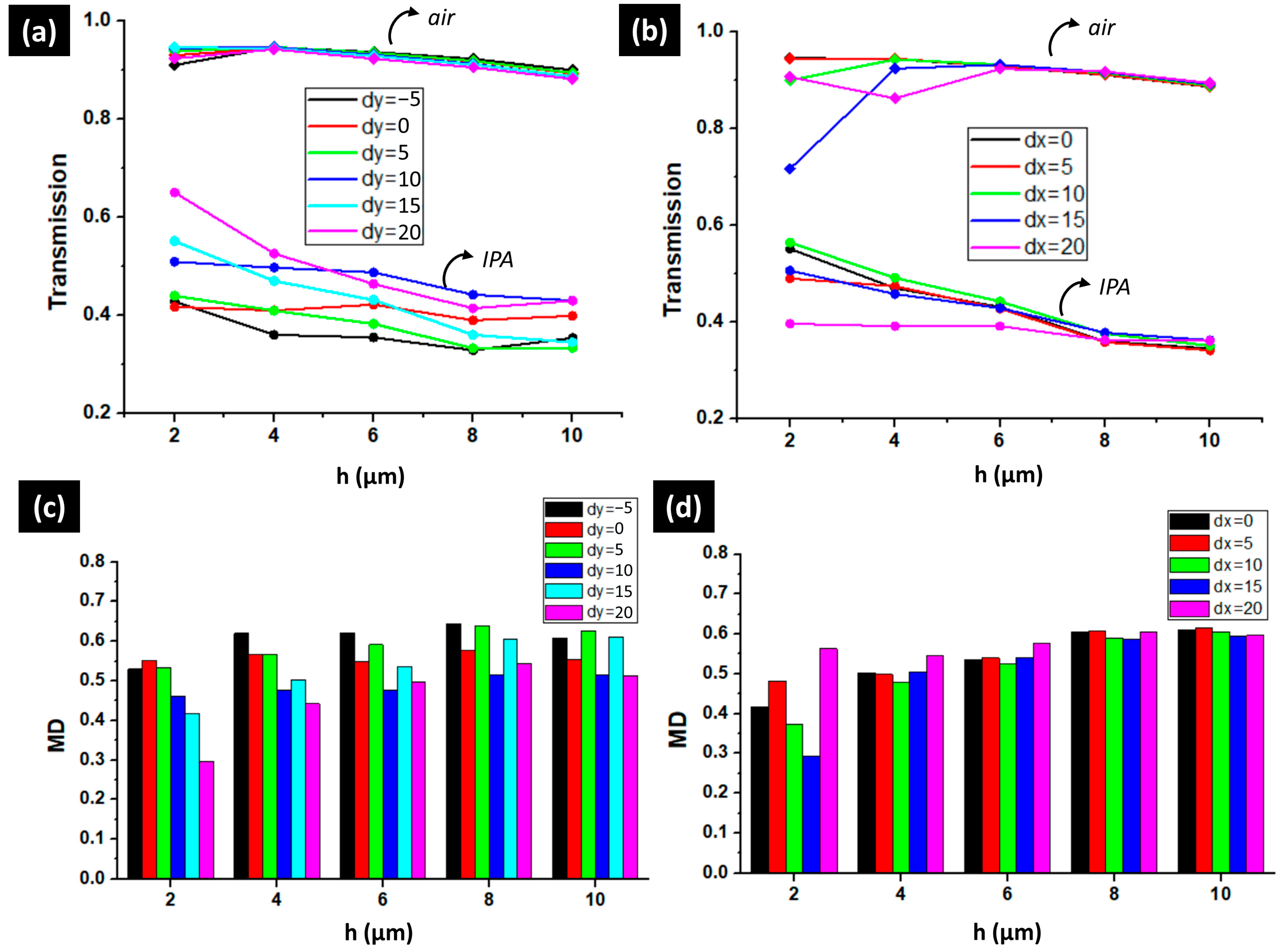
3.4. Impacts of h, Δx, and Δy on Amplitude Modulation of 2nd Resonance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| THz | terahertz |
| SRR | split-ring resonator |
| RI | refractive index |
| IPA | isopropyl alcohol |
| MD | modulation depth |
| FDTD | finite-difference time-domain |
| EM | electromagnetic |
| PML | perfectly matched layer |
| SD | standard deviation |
References
- Chen, H.T.; Padilla, W.J.; Zide, J.M.; Gossard, A.C.; Taylor, A.J.; Averitt, R.D. Active terahertz metamaterial devices. Nature 2006, 444, 597–600. [Google Scholar] [CrossRef] [PubMed]
- Choi, M.; Lee, S.H.; Kim, Y.; Kang, S.B.; Shin, J.; Kwak, M.H.; Kang, K.Y.; Lee, Y.H.; Park, N.; Min, B. A terahertz metamaterial with unnaturally high refractive index. Nature 2011, 470, 369–373. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.K.; Kang, J.H.; Kwon, J.; Lee, J.S.; Lee, S.; Woo, D.H.; Kim, J.H.; Song, C.S.; Park, Q.H.; Seo, M. Nano metamaterials for ultrasensitive Terahertz biosensing. Sci. Rep. 2017, 7, 8146. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Niu, J.; Jin, X.; Qian, X.; Xiao, C.; Wang, W. Molecularly Resonant Metamaterials for Broad-Band Electromagnetic Stealth. Adv. Sci. 2023, 10, 2301170. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Xu, Q.; Tian, C.; Wang, Q.; Xu, Y.; Li, Y.; Gu, J.; Tian, Z.; Ouyang, C.; et al. High-efficiency dielectric metasurfaces for polarization-dependent terahertz wavefront manipulation. Adv. Opt. Mater. 2018, 6, 1700773. [Google Scholar] [CrossRef]
- Saadeldin, A.S.; Hameed, M.F.O.; Elkaramany, E.M.; Obayya, S.S. Highly sensitive terahertz metamaterial sensor. IEEE Sens. J. 2019, 19, 7993–7999. [Google Scholar] [CrossRef]
- Yuan, G.; Rogers, K.S.; Rogers, E.T.; Zheludev, N.I. Far-field superoscillatory metamaterial superlens. Phys. Rev. Appl. 2019, 11, 064016. [Google Scholar] [CrossRef]
- Alrayes, N.; Hussein, M.I. Metamaterial-based sensor design using split ring resonator and Hilbert fractal for biomedical application. Sens. Bio-Sens. Res. 2021, 31, 100395. [Google Scholar] [CrossRef]
- Xiong, Z.; Shang, L.; Yang, J.; Chen, L.; Guo, J.; Liu, Q.; Danso, S.A.; Li, G. Terahertz sensor with resonance enhancement based on square split-ring resonators. IEEE Access 2021, 9, 59211–59221. [Google Scholar] [CrossRef]
- Han, J.; Lakhtakia, A. Semiconductor split-ring resonators for thermally tunable terahertz metamaterials. J. Mod. Opt. 2009, 56, 554–557. [Google Scholar] [CrossRef]
- Driscoll, T.; Andreev, G.O.; Basov, D.N.; Palit, S.; Cho, S.Y.; Jokerst, N.M.; Smith, D.R. Tuned permeability in terahertz split-ring resonators for devices and sensors. Appl. Phys. Lett. 2007, 91, 062511. [Google Scholar] [CrossRef]
- Zhu, M.; Lin, Y.S.; Lee, C. Coupling effect combined with incident polarization to modulate double split-ring-resonator in terahertz frequency range. J. Appl. Phys. 2014, 116, 173106. [Google Scholar] [CrossRef]
- Zhu, M.; Lee, C. A design of terahertz broadband filters and its effect in eliminating asymmetric characteristics in device structures. J. Light. Technol. 2015, 33, 3280–3285. [Google Scholar] [CrossRef]
- Zhu, M.; Lee, C. Facile metal transfer method for fabricating unconventional metamaterial devices. Opt. Mater. Express 2015, 5, 733–741. [Google Scholar] [CrossRef]
- Han, N.R.; Chen, Z.C.; Lim, C.S.; Ng, B.; Hong, M.H. Broadband multi-layer terahertz metamaterials fabrication and characterization on flexible substrates. Opt. Express 2011, 19, 6990–6998. [Google Scholar] [CrossRef]
- Linden, S.; Enkrich, C.; Wegener, M.; Zhou, J.; Koschny, T.; Soukoulis, C.M. Magnetic response of metamaterials at 100 terahertz. Science 2004, 306, 1351–1353. [Google Scholar] [CrossRef]
- Tao, H.; Chieffo, L.R.; Brenckle, M.A.; Siebert, S.M.; Liu, M.; Strikwerda, A.C.; Fan, K.; Kaplan, D.L.; Zhang, X.; Averitt, R.D.; et al. Metamaterials on paper as a sensing platform. Adv. Mater. 2011, 23, 3197. [Google Scholar] [CrossRef]
- Park, S.J.; Hong, J.T.; Choi, S.J.; Kim, H.S.; Park, W.K.; Han, S.T.; Park, J.Y.; Lee, S.; Kim, D.S.; Ahn, Y.H. Detection of microorganisms using terahertz metamaterials. Sci. Rep. 2014, 4, 4988. [Google Scholar] [CrossRef]
- Wang, W.; Yan, F.; Tan, S.; Zhou, H.; Hou, Y. Ultrasensitive terahertz metamaterial sensor based on vertical split ring resonators. Photonics Res. 2017, 5, 571–577. [Google Scholar] [CrossRef]
- Park, S.J.; Cha, S.H.; Shin, G.A.; Ahn, Y.H. Sensing viruses using terahertz nano-gap metamaterials. Biomed. Opt. Express 2017, 8, 3551–3558. [Google Scholar] [CrossRef]
- Meng, K.; Park, S.J.; Burnett, A.D.; Gill, T.; Wood, C.D.; Rosamond, M.; Li, L.H.; Chen, L.; Bacon, D.R.; Freeman, J.R.; et al. Increasing the sensitivity of terahertz split ring resonator metamaterials for dielectric sensing by localized substrate etching. Opt. Express 2019, 27, 23164–23172. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.; Chen, J.; Li, J. Selective trapping of micro-particles on terahertz metamaterial with macro gesture manipulation. J. Phys. D Appl. Phys. 2019, 52, 085104. [Google Scholar] [CrossRef]
- Rakhshani, M.R. Refractive index sensor based on dual side-coupled rectangular resonators and nanorods array for medical applications. Opt. Quantum Electron. 2021, 53, 232. [Google Scholar] [CrossRef]
- Rigamonti, G.; Bello, V.; Merlo, S. Spectral optical readout of rectangular–miniature hollow glass tubing for refractive index sensing. Sensors 2018, 18, 603. [Google Scholar] [CrossRef]
- Kuzin, A.; Panda, K.; Chernyshev, V.; Florya, I.; Kovalyuk, V.; An, P.; Golikov, A.; Chulkova, G.; Kolesov, D.; Gorin, D.; et al. Microfluidic–nanophotonic sensor for on-chip analysis of complex refractive index. Appl. Phys. Lett. 2024, 124, 063701. [Google Scholar] [CrossRef]
- Du, C.; Zhou, D.; Guo, H.H.; Pang, Y.Q.; Shi, H.Y.; Liu, W.F.; Su, J.Z.; Singh, C.; Trukhanov, S.; Trukhanov, A.; et al. An ultra-broadband terahertz metamaterial coherent absorber using multilayer electric ring resonator structures based on anti-reflection coating. Nanoscale 2020, 12, 9769–9775. [Google Scholar] [CrossRef]
- Wang, B.X.; Xu, C.; Duan, G.; Xu, W.; Pi, F. Review of broadband metamaterial absorbers: From principles, design strategies, and tunable properties to functional applications. Adv. Funct. Mater. 2023, 33, 2213818. [Google Scholar] [CrossRef]
- Pitchappa, P.; Manjappa, M.; Ho, C.P.; Qian, Y.; Singh, R.; Singh, N.; Lee, C. Active control of near-field coupling in conductively coupled microelectromechanical system metamaterial devices. Appl. Phys. Lett. 2016, 108, 111102. [Google Scholar] [CrossRef]
- Manjappa, M.; Pitchappa, P.; Singh, N.; Wang, N.; Zheludev, N.I.; Lee, C.; Singh, R. Reconfigurable MEMS Fano metasurfaces with multiple-input–output states for logic operations at terahertz frequencies. Nat. Commun. 2018, 9, 4056. [Google Scholar] [CrossRef]
- Tan, T.C.; Srivastava, Y.K.; Ako, R.T.; Wang, W.; Bhaskaran, M.; Sriram, S.; Al-Naib, I.; Plum, E.; Singh, R. Active control of nanodielectric-induced THz quasi-BIC in flexible metasurfaces: A platform for modulation and sensing. Adv. Mater. 2021, 33, 2100836. [Google Scholar] [CrossRef]
- Dong, Y.; Yu, D.; Li, G.; Lin, M.; Bian, L.A. Terahertz metamaterial modulator based on phase change material VO2. Symmetry 2021, 13, 2230. [Google Scholar] [CrossRef]
- Cong, L.; Srivastava, Y.K.; Zhang, H.; Zhang, X.; Han, J.; Singh, R. All-optical active THz metasurfaces for ultrafast polarization switching and dynamic beam splitting. Light Sci. Appl. 2018, 7, 28. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Fu, Q.; Fan, Y.; Wu, H.; Qiu, K.; Yang, R.; Cai, W.; Zhang, N.; Zhang, F. Thermally controllable Mie resonances in a water-based metamaterial. Sci. Rep. 2019, 9, 5417. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.S.; Sultana, J.; Biabanifard, M.; Vafapour, Z.; Nine, M.J.; Dinovitser, A.; Cordeiro, C.M.B.; Ng, B.H.; Abbott, D. Tunable localized surface plasmon graphene metasurface for multiband superabsorption and terahertz sensing. Carbon 2020, 158, 559–567. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Hu, F.; Li, D.; Teng, H.; Rong, Q.; Zhang, W.; Han, J.; Liang, H. Four resonators based high sensitive te-rahertz metamaterial biosensor used for measuring concentration of protein. J. Phys. D Appl. Phys. 2019, 52, 095105. [Google Scholar] [CrossRef]
- Aslinezhad, M. High sensitivity refractive index and temperature sensor based on semiconductor metamaterial perfect absorber in the terahertz band. Opt. Commun. 2020, 463, 125411. [Google Scholar] [CrossRef]
- Li, D.; Hu, F.; Zhang, H.; Chen, Z.; Huang, G.; Tang, F.; Lin, S.; Zou, Y.; Zhou, Y. Identification of early-stage cervical cancer tissue using metamaterial terahertz biosensor with two resonant absorption frequencies. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 1–7. [Google Scholar] [CrossRef]
- Wang, Z.; Geng, Z.; Fang, W. Exploring performance of THz metamaterial biosensor based on flexible thin-film. Opt. Express 2020, 28, 26370–26384. [Google Scholar] [CrossRef]
- Lin, S.; Xu, X.; Hu, F.; Chen, Z.; Wang, Y.; Zhang, L.; Peng, Z.; Li, D.; Zeng, L.; Chen, Y.; et al. Using antibody modified terahertz metamaterial biosensor to detect concentration of carcinoembryonic antigen. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 1–7. [Google Scholar] [CrossRef]
- Yao, H.; Mei, H.; Zhang, W.; Zhong, S.; Wang, X. Theoretical and experimental research on terahertz metamaterial sensor with flexible substrate. IEEE Photonics J. 2021, 14, 1–9. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, M.; Fu, Y.; Cai, H.; Zeng, X.; Chen, X.; Qiu, X.; Tian, Z.; Shi, S.; Yu, D.; et al. Design and Simulation of THz Metasurface Sensor Based on Transmission and Reflection Modes for Aqueous Solution Detection. Plasmonics 2024, 19, 1–11. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Z.; Zhang, Y.; Liu, S. Side-polished D-type fiber SPR sensor for RI sensing with temperature compensation. IEEE Sens. J. 2021, 21, 16621–16628. [Google Scholar] [CrossRef]
- Dong, X.; Zeng, L.; Chu, D.; Sun, X. Highly sensitive refractive index sensing based on a novel Mach-Zehnder interferometer with TCF-PCF composite structure. Infrared Phys. Techn. 2022, 123, 104134. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, P.; Lin, Y.S. Tunable split-disk metamaterial absorber for sensing application. Nanomaterials 2021, 11, 598. [Google Scholar] [CrossRef] [PubMed]
- Shih, K.; Pitchappa, P.; Manjappa, M.; Ho, C.P.; Singh, R.; Lee, C. Microfluidic metamaterial sensor: Selective trapping and remote sensing of microparticles. J. Appl. Phys. 2017, 121, 023102. [Google Scholar] [CrossRef]
- Sun, H.; Hu, Y.; Tang, Y.; You, J.; Zhou, J.; Liu, H.; Zheng, X. Ultrafast polarization-dependent all-optical switching of germanium-based metaphotonic devices. Photon. Res. 2020, 8, 263–270. [Google Scholar] [CrossRef]
- He, W.; Tong, M.; Xu, Z.; Hu, Y.; Cheng, X.A.; Jiang, T. Ultrafast all-optical terahertz modulation based on an inverse-designed metasurface. Photon. Res. 2021, 9, 1099–1108. [Google Scholar] [CrossRef]
- Chen, X.; Tian, Z.; Lu, Y.; Xu, Y.; Zhang, X.; Ouyang, C.; Gu, J.; Han, J.; Zhang, W. Electrically tunable perfect terahertz absorber based on a graphene salisbury screen hybrid metasurface. Adv. Opt. Mater. 2020, 8, 1900660. [Google Scholar] [CrossRef]
- Xu, R.; Xu, X.; Yang, B.R.; Gui, X.; Qin, Z.; Lin, Y.S. Actively logical modulation of MEMS-based terahertz metamaterial. Photon. Res. 2021, 9, 1409–1415. [Google Scholar] [CrossRef]
- Hou, X.F.; Li, Y.Y.; Wu, X.J.; He, G.Y.; Wang, M.W. A thermal tunable terahertz metamaterial absorber based on strontium titanate. Phys. Scr. 2022, 97, 085507. [Google Scholar] [CrossRef]
- Singh, R.; Al-Naib, I.A.; Koch, M.; Zhang, W. Sharp Fano resonances in THz metamaterials. Opt. Express 2011, 19, 6312–6319. [Google Scholar] [CrossRef]


| References | [21] | [34] | [35] | [36] | [37] | [38] | [39] | [40] | [41] | Our work (before optimization) |
| Sensitivity (GHz/RIU) | 71 | 66 | 85 | 68 | 74 | 243 | 76.5 | 100 | 66.7 | 282 (1st resonance) 433 (2nd resonance) |
| References | [23] | [24] | [25] | [42] | [43] | [44] | Our work (before optimization) | |||
| Sensitivity (nm/RIU) | 1090 | 483.4 | 138 | 2260 | 226.7 | 3567 | 6.1 × 104~1.1 × 105 (1st resonance) 3.6 × 104~4.1 × 104 (2nd resonance) | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, M.; Fu, X.; Yang, H.; Song, Q.; Wang, H.-L.; Ma, S. Simulated Microfluidic Device Constructed Using Terahertz Metamaterial for Sensing and Switching Applications. Photonics 2025, 12, 194. https://doi.org/10.3390/photonics12030194
Zhu M, Fu X, Yang H, Song Q, Wang H-L, Ma S. Simulated Microfluidic Device Constructed Using Terahertz Metamaterial for Sensing and Switching Applications. Photonics. 2025; 12(3):194. https://doi.org/10.3390/photonics12030194
Chicago/Turabian StyleZhu, Mei, Xiuxiu Fu, Hongfang Yang, Qianqian Song, Hai-Lung Wang, and Shengqian Ma. 2025. "Simulated Microfluidic Device Constructed Using Terahertz Metamaterial for Sensing and Switching Applications" Photonics 12, no. 3: 194. https://doi.org/10.3390/photonics12030194
APA StyleZhu, M., Fu, X., Yang, H., Song, Q., Wang, H.-L., & Ma, S. (2025). Simulated Microfluidic Device Constructed Using Terahertz Metamaterial for Sensing and Switching Applications. Photonics, 12(3), 194. https://doi.org/10.3390/photonics12030194





