Harnessing Ultra-Intense Long-Wave Infrared Lasers: New Frontiers in Fundamental and Applied Research
Abstract
:1. Introduction
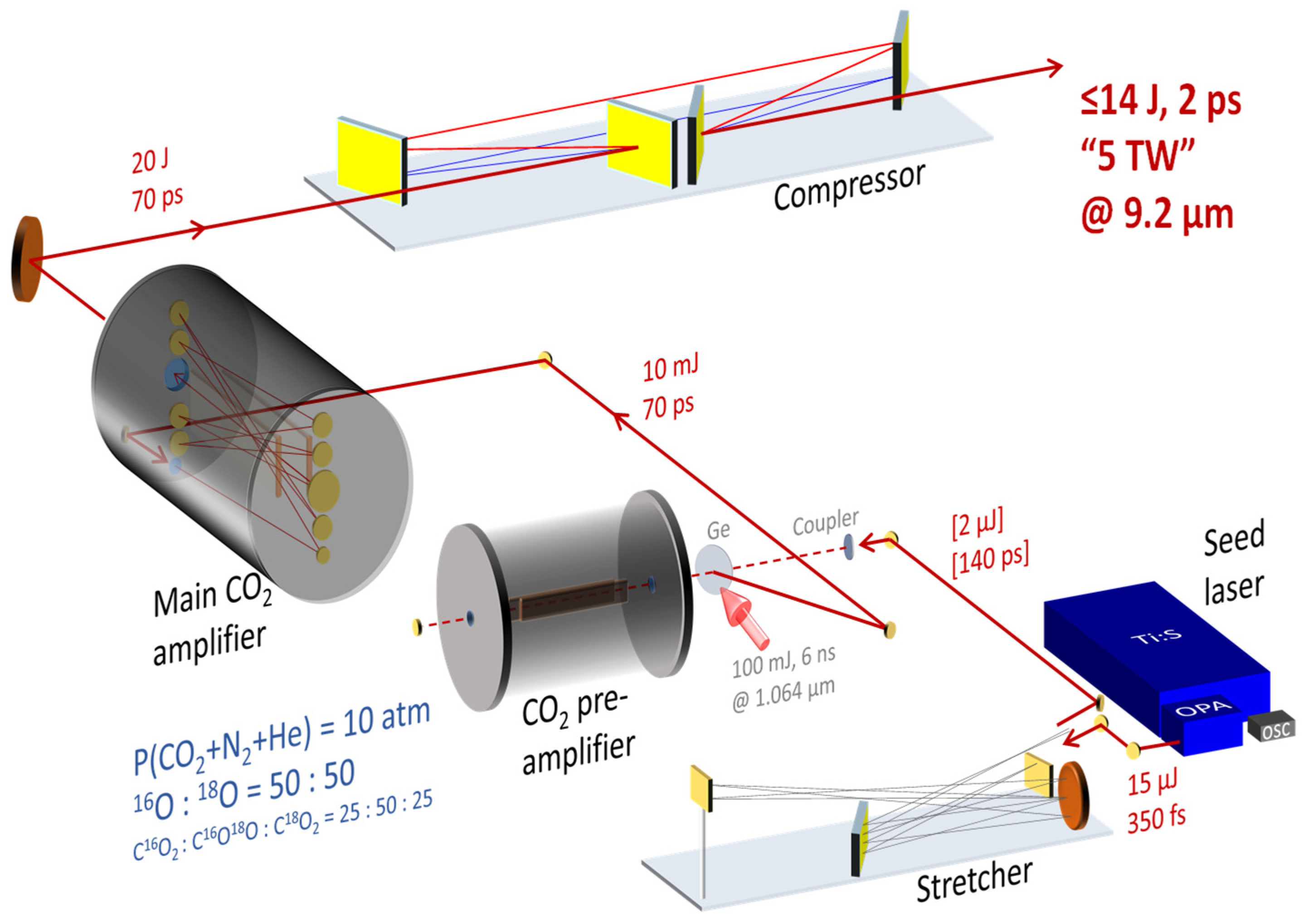
- Section 2.1 provides a brief history of high-peak-power LWIR lasers. The state-of-the-art is exemplified by the BNL system, which utilizes chirped pulse amplification (CPA) [4] and a multi-isotope, high-pressure CO2 gas laser medium operating at = 9.2 µm [2]. The combination of these innovations, unprecedented for CO2 lasers, marks a significant milestone in advancing LWIR laser technology, addressing the stringent demands of modern ultra-high-peak-power systems.
- Section 2.2 outlines ongoing research and development efforts aimed at advancing ultra-intense LWIR lasers into the sub-picosecond time domain—potentially down to a few optical cycles—and achieving ~100 TW peak intensity in a single beam.
- Section 2.3 addresses the potential for developing high-repetition-rate, terawatt-class LWIR lasers with kilowatt-level average power and briefly discusses the possibilities for compact, mobile, short-pulse, optically pumped CO2 lasers.
- Section 3.1 compiles topics on wavelength scaling in fundamental laser-matter interaction processes, including ionization, laser propagation in plasma up to critical plasma density and the relativistic self-focusing regime, ponderomotive electron motion, and generation of plasma waves.
- Section 3.2 delves into laser wakefield electron acceleration (LWFA), focusing on how long-wavelength lasers facilitate the formation of large-scale plasma bubbles in low-density plasmas. The unique capabilities of the ATF—integrating the LWIR laser with NIR lasers and an RF electron linear accelerator (linac)—support trailblazing research aimed at addressing key challenges in exploring and improving the performance of laser–plasma accelerators. These efforts have far-reaching implications, including the ambitious goal of developing a TeV-class electron–positron ( collider, a transformative breakthrough with the potential to redefine the frontiers of particle physics.
- Section 3.3 explores laser-driven ion acceleration, highlighting how the reduction in critical plasma density enables novel mono-energetic acceleration regimes. These include laser hole-boring through plasma and collisionless electrostatic shock wave acceleration.
- Section 4.1 highlights LWIR lasers’ capability in generating intense THz radiation and extending High Harmonic Generation (HHG) into the X-ray region.
- Section 4.2 starts with reviewing pioneering ATF experiments in inverse Compton scattering (ICS) focused on investigating nonlinear ICS processes and single-shot, phase-contrast tomography. The -proportional increase in the number of photons per joule of laser energy positions LWIR lasers as promising tools for these and future advanced applications where we examine the ability of LWIR beams to create intense X-ray and gamma sources via ICS. Such sources can complement synchrotron light sources or serve as particle-to-radiation converters in gamma colliders.
- Section 5.1 addresses the terawatt LWIR radiation channeling through air and its observation in ATF experiments.
- Section 5.2 describes secondary effects and applications that emerge from LWIR filaments, including remote detection of ionizing sources and RF waves generation.
2. Short-Pulse LWIR Lasers with CO2 Amplifiers
2.1. History and State-Of-The-Art
2.2. Paths to Femtoseconds
2.3. High Repetition Rate Prospects
3. Plasma Accelerators
3.1. Wavelength Scaling in Laser–Plasma Interactions
3.1.1. Ionization
3.1.2. Critical Plasma Density
3.1.3. Laser Self-Focusing and Channeling
3.1.4. Laser Energy Loss on Propagation
3.2. Electron Acceleration in Plasma Waves
3.2.1. Regimes of Laser-Driven Plasma Acceleration
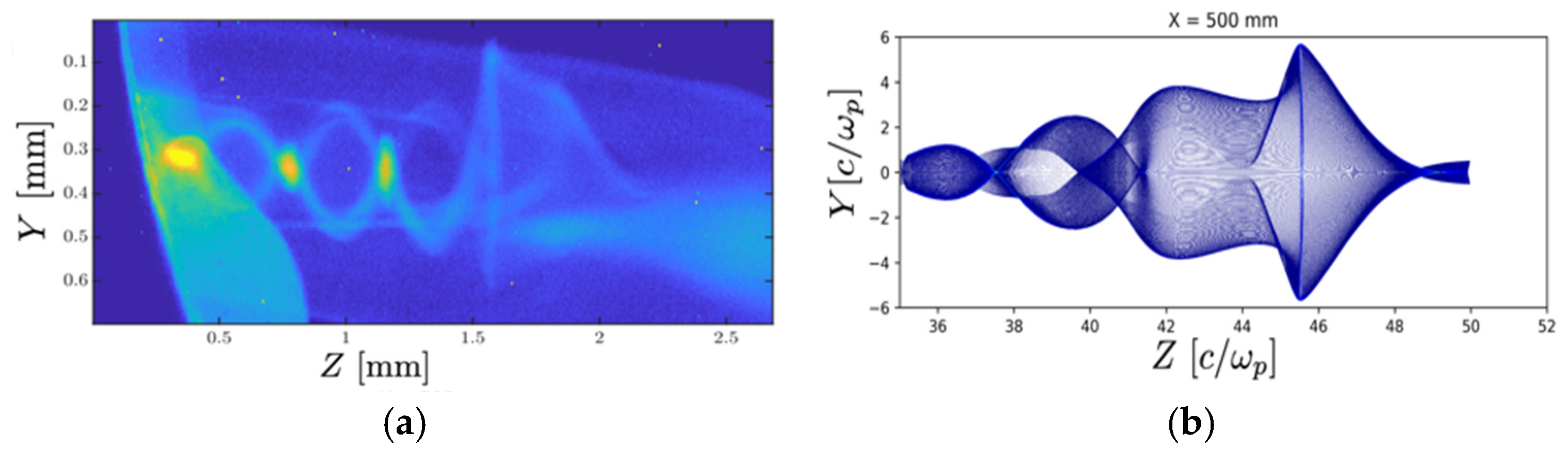
3.2.2. SM-LWFA Driven by LWIR Laser
3.2.3. Low-Density Bubble Regime
- Laser Power Requirements: The LWIR laser demonstrates significantly reduced power requirements compared to its NIR counterpart at equivalent plasma densities, highlighting the longer wavelength efficiency in driving plasma waves. Increasing plasma density leads to reduced power requirements for both lasers.
- Electron Energy Gain: Higher plasma density leads to a greater acceleration gradient. However, the net acceleration per stage decreases due to the inverse quadratic relationship between the laser depletion length and the plasma frequency. The reduced energy requirement for LWIR lasers leads to proportionally faster depletion, resulting in a smaller electron energy gain per stage, necessitating more stages for high-energy applications.
- Bunch charge: While the required laser peak power and energy seem more practically accessible at higher densities, the amount of accelerated charge is reduced.
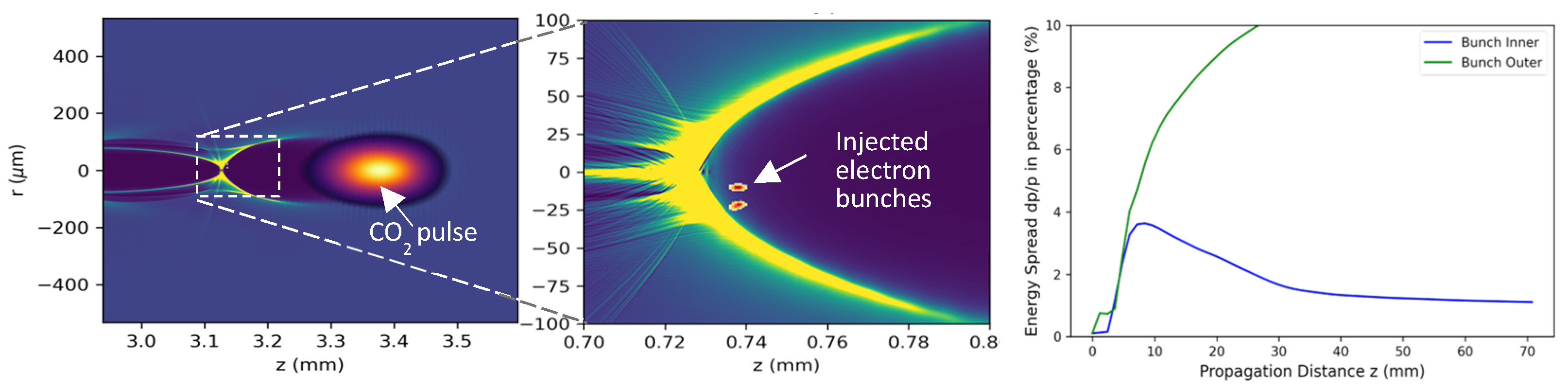
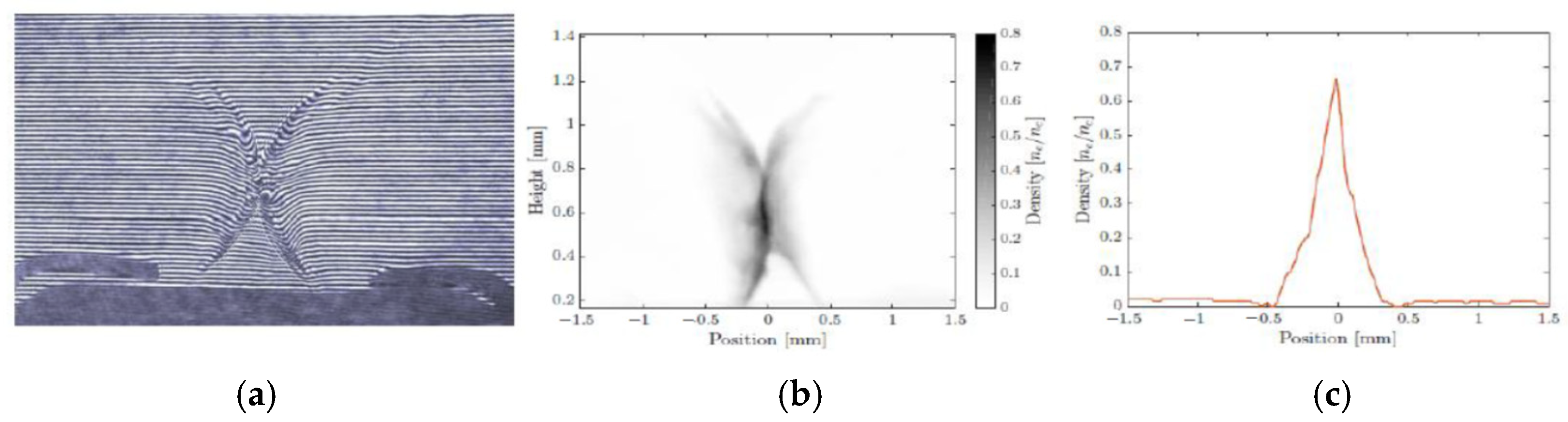
3.2.4. Ultra-Low Emittance LWFA
3.3. Ion Acceleration
3.3.1. Solid Targets
3.3.2. Gas Targets
3.3.3. Experimental Results and Prospects
4. Radiation Sources
4.1. From THz to EUV and Beyond
4.2. Inverse Compton Scattering
4.2.1. ATF Experiments
4.2.2. Possible Light Sources Based on LWIR Lasers
4.2.3. Electron–Positron and Gamma Colliders
5. Directed Energy
5.1. Mega-Filaments
5.2. Applications
6. Conclusions
- Inverse Cherenkov Electron Acceleration: Relativistic electron acceleration in gas using radially polarized LWIR laser beams [138], laying the groundwork for direct electron acceleration in a vacuum [139] and enabling the generation of strong longitudinal magnetic fields when converting to azimuthally polarized beams [140].
- First Staged Laser Accelerator: The STELLA experiment demonstrated the first two-stage, monoenergetic Inverse Free Electron Laser (IFEL) accelerator [141].
- High Gain Harmonic Generation (HGHG): The pioneering FEL method is now widely used in accelerator facilities globally [142].
- Multiple Innovations in IFEL Technique: Achievements include monoenergetic electron acceleration using helical undulators (RUBICON experiment) [143], high-duty-cycle IFEL operation with bursts of electron bunches interacting with laser pulses circulating through a laser amplifier [144] and boosting the ICS photon energy by integrating the ICS process at the output of the IFEL accelerator [145].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ATF | Accelerator Test Facility |
| BNL | Directory of open access journals |
| CW | Continuous wave |
| DC | Dispersive compression |
| CPA | Chirped pulse amplification |
| CTR | Coherent transition radiation |
| DOE | U.S. Department of Energy |
| ELI-NP | Extreme Light Infrastructure—Nuclear Physics |
| EM | Electromagnetic |
| EUV | Extreme ultraviolet |
| FEC | Field-enhancement cavity |
| FEL | Free electron laser |
| GVD | Group velocity dispersion |
| HHG | High-harmonic generation |
| ICS | Inverse Compton scattering |
| IFEL | Inverse free electron laser |
| IP | Interaction point |
| LHC | Large Hadron Collider |
| LWFA | Laser wakefield acceleration |
| LWIR | Long wave infrared |
| NIR | Near-infrared |
| OPO | Optical parametric oscillator |
| OPCPA | Optical parametric chirped pulse amplification |
| OR | Optical rectification |
| RF | Radiofrequency |
| RPA | Radiation pressure acceleration |
| RSF | Relativistic self-focusing |
| SLS | Synchrotron light source |
| SM | Self-modulated |
| SPM | Self-phase modulation |
| TNSA | Target normal sheath acceleration |
| UCLA | University of California in Los Angeles |
References
- Haberberger, D.; Tochitsky, S.; Joshi, C. Fifteen terawatt picosecond CO2 laser system. Opt. Express 2010, 18, 17865–17875. [Google Scholar] [CrossRef] [PubMed]
- Polyanskiy, M.N.; Pogorelsky, I.V.; Babzien, M.; Kupfer, R.; Vafaei-Najafabadi, N.; Palmer, M.A. High-peak-power long-wave infrared lasers with CO2 amplifiers. Photonics 2021, 8, 101. [Google Scholar] [CrossRef]
- BNL Accelerator Test Facility. Home Page. Available online: www.bnl.gov/atf/.
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219–221. [Google Scholar] [CrossRef]
- Yang, Y.; Lee, J.; Wang, J. Energetic picosecond 10.2-μm pulses generated in a BGGSe crystal for nonlinear seeding of terawatt-class CO2 amplifiers. Opt. Express 2024, 32, 11182–11192. [Google Scholar] [CrossRef]
- Yin, Y.; Chew, A.; Ren, X.; Li, J.; Wang, Y.; Wu, Y.; Chang, Z. Towards Terawatt sub-cycle long-wave infrared pulses via chirped optical parametric amplification and indirect pulse shaping. Sci. Rep. 2017, 7, 45794. [Google Scholar] [CrossRef]
- Chang, Z.; Fang, L.; Fedorov, V.; Geiger, C.; Ghimire, S.; Heide, C.; Ishii, N.; Itatani, J.; Joshi, C.; Kobayashi, Y.; et al. Intense infrared lasers for strong-field science. Adv. Opt. Photonics 2022, 14, 652–782. [Google Scholar] [CrossRef]
- Kast, S.J.; Schwarzschild, B.M. Performance comparison of pulsed discharge and E-beam controlled CO2 lasers. J. Appl. Phys. 1973, 44, 1631–1637. [Google Scholar] [CrossRef]
- Goldstone, P.D.; Allen, G.; Jansen, H.; Saxman, A.; Singer, S.; Thuot, M. The Antares Facility for Inertial Fusion Experiments—Status and Plans. In Laser Interaction and Related Plasma Phenomena; Hora, H., Miley, G.H., Eds.; Springer: Boston, MA, USA, 1984. [Google Scholar] [CrossRef]
- Jie Ma, J.; Qin, Z.; Xie, G.; Qian, L.; Tang, D. Review of mid-infrared mode-locked laser sources in the 2.0 μm–3.5 μm spectral region. Appl. Phys. Rev. 2019, 6, 021317. [Google Scholar] [CrossRef]
- Alcock, A.; Corkum, P. Ultra-fast switching of infrared radiation by laser-produced carriers in semiconductors. Can. J. Phys. 1979, 57, 1280–1290. [Google Scholar] [CrossRef]
- Alcock, A.J.; Leopold, K.; Richardson, M.C. Continuously tunable high-pressure CO2 laser with uv photopreionization. Appl. Phys. Lett. 1973, 23, 562–564. [Google Scholar] [CrossRef]
- Shimada, T.; Bigio, I.J.; Kurnit, N.A.; Harrison, R.F. Large-volume high-pressure CO2 laser for ultrashort pulse amplification. In Proceedings of the 1988 Conference on Lasers and Electro-Optics, OSA Technical Digest, Anaheim, CA, USA, 25–29 April 1988; Volume 7, p. FD2. [Google Scholar]
- Polyanskiy, M.N.; Pogorelsky, I.V.; Babzien, M.; Kupfer, R.; Palmer, M.A. Ultrashort-pulse, terawatt, long-wave infrared lasers based on high-pressure CO2 amplifiers. EPJ Web Conf. 2021, 255, 11010. [Google Scholar] [CrossRef]
- Polyanskiy, M.N.; Pogorelsky, I.V.; Yakimenko, V. Picosecond pulse amplification in isotopic CO2 active medium. Opt. Express 2011, 19, 7717–7725. [Google Scholar] [CrossRef]
- Polyanskiy, M.N.; Pogorelsky, I.V.; Babzien, M.; Palmer, M.A. Demonstration of a 2 ps, 5 TW peak power, long-wave infrared laser based on chirped-pulse amplification with mixed isotope CO2 amplifiers. OSA Contin. 2020, 3, 459–472. [Google Scholar] [CrossRef]
- Polyanskiy, M.N.; Pogorelsky, I.V.; Babzien, M.; Kupfer, R.; Li, W.; Palmer, M.A. 9.3 Microns: Toward a next-generation CO2 laser. In Proceedings of the 2022 IEEE Advanced Accelerator Concepts Workshop (AAC), Long Island, NY, USA, 6–11 November 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Polyanskiy, M.N.; Pogorelsky, I.V.; Babzien, M.; Li, W.H.; Kupfer, R.; Palmer, M.A. Multi-terawatt, sub-picosecond long-wave infrared laser for next-generation article accelerators. In Proceedings of the 14th International Particle Accelerator Conference, Venice, Italy, 7–12 May 2023. [Google Scholar] [CrossRef]
- Pogorelsky, I.V.; Polyanskiy, M.N.; Kimura, W.D. Mid-infrared lasers for energy frontier plasma accelerators. Phys. Rev. Acc. Beams 2016, 19, 091001. [Google Scholar] [CrossRef]
- Kupfer, R.; Wang, F.; Wishart, J.F.; Babzien, M.; Polyanskiy, M.N.; Pogorelsky, I.V.; Rao, T.; Cultrera, L.; Vafaei-Najafabadi, N.; Palmer, M.A. Raman wavelength conversion in ionic liquids. Phys. Rev. Appl. 2023, 19, 014052. [Google Scholar] [CrossRef]
- Qu, S.; Liang, H.; Liu, K.; Zou, X.; Li, W.; Wang, Q.J.; Zhang, Y. 9 μm few-cycle optical parametric chirped-pulse amplifier based on LiGaS2. Opt. Lett. 2019, 44, 2422–2425. [Google Scholar] [CrossRef] [PubMed]
- Corkum, P. Amplification of picosecond 10 μm pulses in multi-atmosphere CO2 lasers. IEEE J. Quan. Electron. 1985, 21, 216–232. [Google Scholar] [CrossRef]
- Gustafson, T.; Kelley, P.; Fisher, R. Subpicosecond pulse generation using the optical Kerr effect. IEEE J. Quan. Electron. 1969, 5, 325. [Google Scholar] [CrossRef]
- Voronin, A.A.; Zheltikov, A.M.; Ditmire, T.; Rus, B.; Korn, G. Subexawatt few-cycle lightwave generation via multipetawatt pulse compression. Opt. Commun. 2013, 291, 299–303. [Google Scholar] [CrossRef]
- Hädrich, S.; Kienel, M.; Müller, M.; Klenke, A.; Rothhardt, J.; Klas, R.; Gottschall, T.; Eidam, T.; Drozdy, A.; Jójárt, P.; et al. Energetic sub-2-cycle laser with 216W average power. Opt. Lett. 2016, 41, 4332–4335. [Google Scholar] [CrossRef]
- Hemmer, M.; Baudisch, M.; Thai, A.; Couairon, A.; Biegert, J. Self-compression to sub-3-cycle duration of mid-infrared optical pulses in dielectrics. Opt. Express 2013, 21, 28095–28102. [Google Scholar] [CrossRef]
- Shumakova, V.; Malevich, P.; Ališauskas, S.; Voronin, A.; Zheltikov, A.M.; Faccio, D.; Kartashov, D.; Baltuška, A.; Pugžlys, A. Multi-millijoule few-cycle mid-infrared pulses through nonlinear selfcompression in bulk. Nat. Commun. 2016, 13, 12877. [Google Scholar] [CrossRef]
- Bravy, B.G.; Gordienko, V.M.; Platonenko, V.T. Self-compression of terawatt level picosecond 10 μm laser pulses in NaCl. Laser Phys. Lett. 2014, 11, 065401. [Google Scholar] [CrossRef]
- Pigeon, J.; Tochitsky, S.; Joshi, C. Generation of high power, sub-picosecond, 10 μm pulses via self-phase modulation followed by compression. AIP Conf. Proc. 2016, 1777, 110005. [Google Scholar] [CrossRef]
- Bravy, B.G.; Gordienko, V.M.; Platonenko, V.T. Kerr-assisted self-compression of mid-IR femtosecond laser pulse in dielectrics: Nonlinear medium choice. J. Russ. Laser Res. 2016, 37, 465–472. [Google Scholar] [CrossRef]
- Pogorelsky, I.; Polyanskiy, M.; Babzien, M.; Palmer, M. Experiment on long-wave IR terawatt laser pulse compression to sub-picoseconds. In Proceedings of the OSA High-brightness Sources and Light-driven Interactions Congress, Washington, DC, USA, 16 November 2020. [Google Scholar] [CrossRef]
- Polyanskiy, M.N.; Pogorelsky, I.V.; Babzien, M.; Vodopyanov, K.L.; Palmer, M.A. Nonlinear refraction and absorption properties of optical materials for high-peak-power long-wave-infrared lasers. Opt. Mater. Express 2024, 14, 696–714. [Google Scholar] [CrossRef]
- Polyanskiy, M.N.; Pogorelsky, I.V.; Babzien, M.; Kupfer, R.; Vodopyanov, K.L.; Palmer, M.A. Post-compression of long-wave infrared 2 picosecond sub-terawatt pulses in bulk materials. Opt. Express 2021, 29, 31714–31725. [Google Scholar] [CrossRef] [PubMed]
- Pogorelsky, I.V.; Polyanskiy, M.N.; Babzien, M.; Simmonds, A.; Palmer, M.A. Terawatt-class femtosecond long-wave infrared laser. Front. Phys. 2024, 12, 1390225. [Google Scholar] [CrossRef]
- von Bergmann, H. High pressure CO2 amplifiers for picosecond pulse amplification. Proc. SPIE Int. Soc. Opt. Eng. 2019, 11042, 110420N. [Google Scholar] [CrossRef]
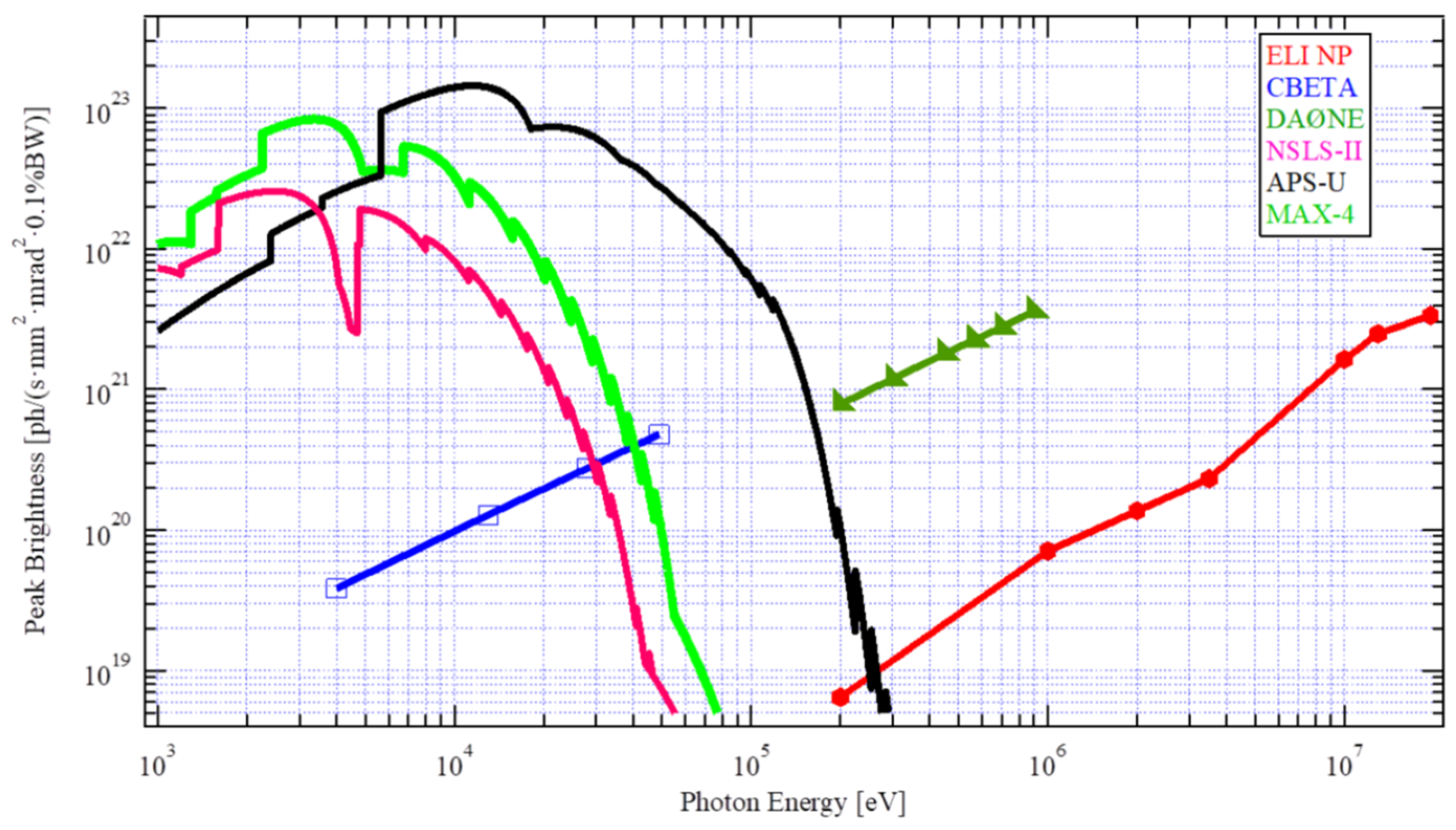
- Pogorelsky, I.V.; Polyanskiy, M.N.; Shaftan, T. Converting conventional electron accelerators to high peak brilliance Compton light sources. Phys. Rev. Accel. Beams 2020, 23, 120702. [Google Scholar] [CrossRef]
- Chang, T.Y.; Wood, O.R. Optically pumped 33-atm CO2 laser. Appl. Phys. Lett. 1973, 23, 370–373. [Google Scholar] [CrossRef]
- Stenersen, K.; Wang, G. Direct optical pumping of high-pressure CO2 and N2O lasers with a pulsed HF pump laser. IEEE J. Quant. Electron. 1986, 22, 2236–2241. [Google Scholar] [CrossRef]
- Martyshkin, D.; Karki, K.; Fedorov, V.; Mirov, S. Room temperature, nanosecond, 60 mJ/pulse Fe:ZnSe master oscillator power amplifier system operating at 3.8–5.0 µm. Opt. Express 2021, 29, 2387–2393. [Google Scholar] [CrossRef] [PubMed]
- Tochitsky, S.; Tovey, D.; Pigeon, J.J.; Pogorelsky, I.V.; Joshi, C.; Polyanskiy, M.; Mirov, S.B. Status and prospects of optically pumped high-pressure CO2 amplifiers. In Proceedings of the Advanced Accelerator Concepts Workshop, Long Island, NY, USA, 6 November 2022. [Google Scholar]
- Keldysh, L. Ionization in the field of strong electromagnetic wave. Sov. Phys. JETP 1964, 20, 1307–1314. [Google Scholar] [CrossRef]
- Woodbury, D.; Goffin, A.; Schwartz, R.M.; Isaacs, J.; Milchberg, H.M. Self-guiding of long-wave infrared laser pulses mediated by avalanche ionization. Phys. Rev. Lett. 2020, 125, 133201. [Google Scholar] [CrossRef] [PubMed]
- Sprangle, P.; Tang, C.M.; Esarey, E. Relativistic self-focusing of short-pulse radiation beams in plasmas. IEEE Trans. Plasma Sci. 1987, 15, 145–153. [Google Scholar] [CrossRef]
- Durfee, C.G., III; Milchberg, H.M. Light pipe for high intensity laser pulses. Phys. Rev. Lett. 1993, 71, 2409–2412. [Google Scholar] [CrossRef]
- Kaganovich, D.; Sasorov, P.; Cohen, C.; Zigler, A. Variable profile capillary discharge for improved phase matching in a laser wakefield accelerator. Appl. Phys. Lett. 1999, 75, 772–774. [Google Scholar] [CrossRef]
- Spence, D.J.; Hooker, S.M. Investigation of a hydrogen plasma waveguide. Phys. Rev. E 2000, 63, 015401. [Google Scholar] [CrossRef] [PubMed]
- Miao, B.; Rockafellow, E.; Shrock, J.E.; Hancock, S.W.; Gordon, D.; Milchberg, H.M. Benchmarking of hydrodynamic plasma channels for multi-GeV laser-driven electron acceleration. Phys. Rev. Accel. Beams 2024, 27, 081302. [Google Scholar] [CrossRef]
- Pogorelsky, I.V.; Pavlishin, I.V.; Ben-Zvi, I.; Kumita, T.; Kamiya, Y.; Hirose, T.; Greenberg, B.; Kaganovich, D.; Zigler, A.; Andreev, N.; et al. Transmission of high-power CO2 laser pulses through a plasma channel. Appl. Phys. Lett. 2003, 83, 3459–3461. [Google Scholar] [CrossRef]
- Dawson, J.M. Nonlinear electron oscillations in a cold plasma. Phys. Rev. 1959, 113, 383–387. [Google Scholar] [CrossRef]
- Esarey, E.; Shadwick, B.A.; Schroeder, C.B.; Leemans, W.P. Nonlinear Pump Depletion and Electron Dephasing in Laser Wakefield Accelerators. In Proceedings of the Advanced Accelerator Concepts Workshop, AIP, New York, NY, USA, 21–26 June 2004; Volume 737, pp. 578–584. [Google Scholar] [CrossRef]
- Frost, L.S.; Phelps, A.V. Rotational excitation and momentum transfer cross sections for electrons in H2 and N2 from transport coefficients. Phys. Rev. 1962, 127, 1621–1633. [Google Scholar] [CrossRef]
- Engelhardt, A.G.; Phelps, A.V. Elastic and inelastic collision cross sections in hydrogen and deuterium from transport coefficients. Phys. Rev. 1963, 131, 2115–2118. [Google Scholar] [CrossRef]
- Esarey, E.; Schroeder, C.B.; Leemans, W.P. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 2009, 81, 1229. [Google Scholar] [CrossRef]
- Esarey, E.; Sprangle, P.; Krall, J.; Ting, A. Overview of plasma-based accelerator concepts. IEEE Trans. Plasma Sci. 1996, 24, 252–288. [Google Scholar] [CrossRef]
- Tajima, T.; Dawson, J.M. Laser electron accelerator. Phys. Rev. Lett. 1979, 43, 267–270. [Google Scholar] [CrossRef]
- Akhiezer, A.I.; Polovin, R.V. Theory of wave motion of an electron plasma. Zhurnal Eksperimental Teor. Fiz. 1956, 30, 915–928, Sov. Phys. JETP 1956, 3, 696–705. [Google Scholar]
- Andreev, N.E.; Gorbunov, L.M.; Kirsanov, V.I.; Pogosova, A.A.; Ramazashvili, R.R. Resonant excitation of wakefields by a laser pulse in a plasma. JETP Lett. 1992, 55, 571–576. [Google Scholar]
- Krall, J.; Ting, A.; Esarey, E.; Sprangle, P. Enhanced acceleration in a self-modulated-laser wake-field accelerator. Phys. Rev. E 1993, 48, 2157–2161. [Google Scholar] [CrossRef] [PubMed]
- Pukhov, A.; Meyer-ter-Vehn, J. Laser wake field acceleration: The highly non-linear broken-wave regime. Appl. Phys. B 2002, 74, 355–361. [Google Scholar] [CrossRef]
- Horton, A.; Tajima, T. Pump depletion in the plasma-beat-wave accelerator. Phys. Rev. A 1986, 34, 4110. [Google Scholar] [CrossRef] [PubMed]
- King, P.M.; Miller, K.; Lemos, N.; Shaw, J.L.; Kraus, B.F.; Thibodeau, M.; Hegelich, B.M.; Hinojosa, J.; Michel, P.; Joshi, C.; et al. Predominant contribution of direct laser acceleration to high-energy electron spectra in a low-density self-modulated laser wakefield accelerator. Phys. Rev. Accel. Beams 2021, 24, 011302. [Google Scholar] [CrossRef]
- Andreev, N.E.; Kuznetsov, S.V.; Pogosova, A.A.; Steinhauer, L.C.; Kimura, W.D. Modeling of laser wakefield acceleration at CO2 laser wavelengths. Phys. Rev. ST Accel. Beams 2003, 6, 041301. [Google Scholar] [CrossRef]
- Kumar, P.; Yu, K.; Rafal, Z.; Amorim, L.D.; Downer, M.C.; Welch, J.; Litvinenko, V.N.; Vafaei-Najafabadi, N.; Samulyak, R. Simulation study of CO2 laser-plasma interactions and self-modulated wakefield acceleration. Phys. Plasmas 2019, 26, 083106. [Google Scholar] [CrossRef]
- Zgadzaj, R.; Welch, J.; Cao, Y.; Amorim, L.D.; Cheng, A.; Gaikwad, A.; Iapozzutto, P.; Kumar, P.; Litvinenko, V.N.; Petrushina, I.; et al. Plasma electron acceleration driven by a long-wave-infrared laser. Nat. Commun. 2024, 15, 4037. [Google Scholar] [CrossRef] [PubMed]
- Malka, V.; Fritzler, S.; Lefebvre, E.; Aleonard, M.-M.; Burgy, F.; Chambaret, J.-P.; Chemin, J.-F.; Krushelnick, K.; Malka, G.; Mangles, S.P.D.; et al. Electron acceleration by a wake field forced by an intense ultrashort laser pulse. Science 2002, 298, 1596–1600. [Google Scholar] [CrossRef]
- Woodbury, D.; Feder, L.; Shumakova, V.; Gollner, C.; Schwartz, R.; Miao, B.; Salehi, F.; Korolov, A.; Pugžlys, A.; Baltuška, A.; et al. Laser wake field acceleration with mid-IR laser pulses. Opt. Lett. 2018, 43, 1131–1134. [Google Scholar] [CrossRef] [PubMed]
- Gaikwad, A.S.; Petrushina, I.; Pogorelsky, I.V.; Kusche, K.; Li, W.; Miller, K.G.; Trommer, E.; Romasky, B.; Petrusky, M.E.; Petrusky, M.E.; et al. Field mapping of CO2-laser-driven LWFA at low density using electron beam probing. In Proceedings of the the 66th Annual Meeting of the APS Division of Plasma Physics, Atlanta, Georgia, 7–11 October 2024. [Google Scholar]
- Gonsalves, A.J.; Nakamura, K.; Daniels, J.; Benedetti, C.; Pieronek, C.; de Raadt, T.C.H.; Steinke, S.; Bin, J.H.; Bulanov, S.S.; van Tilborg, J.; et al. Petawatt laser guiding and electron beam acceleration to 8 GeV in a laser-heated capillary discharge waveguide. Phys. Rev. Lett. 2019, 122, 084801. [Google Scholar] [CrossRef] [PubMed]
- Aniculaesei, C.; Ha, T.; Yoffe, S.; Labun, L.; Milton, S.; McCary, E.; Spinks, M.M.; Quevedo, H.J.; Labun, O.Z.; Sain, R.; et al. The acceleration of a high-charge electron bunch to 10 GeV in a 10-cm nanoparticle-assisted wakefield accelerator. Matter Radiat. Extrem. 2024, 9, 014001. [Google Scholar] [CrossRef]
- 2023 P5 Report: Exploring the Quantum Universe|Pathways to Innovation and Discovery in Particle Physics; High Energy Physics Advisory Panel (HEPAP), US Department of Energy: Washington, DC, USA, 2023.
- Schroeder, C.B.; Esarey, E.; Geddes, C.G.R.; Benedetti, C.; Leemans, W.P. Physics considerations for laser plasma linear colliders. Phys. Rev. ST Accel. Beams 2010, 13, 101301. [Google Scholar] [CrossRef]
- Schroeder, C.B.; Albert, F.; Benedetti, C.; Bromage, J.; Bruhwiler, D.; Bulanov, S.; Campbell, E.; Cook, N.; Cros, B.; Downer, M.; et al. Linear colliders based on laser-plasma accelerators. JINST 2023, 18, T06001. [Google Scholar] [CrossRef]
- Schroeder, C.B.; Esarey, E.; Leemans, W.P. Beamstrahlung considerations in laser-plasma-accelerator-based linear colliders. Phys. Rev. ST Accel. Beams 2012, 15, 051301. [Google Scholar] [CrossRef]
- Downer, M.C. (The University of Texas, Austin, TX, USA). Personal communication, 2024.
- Xu, X.L.; Wu, Y.P.; Zhang, C.J.; Li, F.; Wan, Y.; Hua, J.F.; Pai, C.-H.; Lu, W. Low emittance electron beam generation from a laser wakefield accelerator using two laser pulses with different wavelengths. Phys. Rev. ST Accel. Beams 2014, 17, 061301. [Google Scholar] [CrossRef]
- Schroeder, C.B.; Vay, J.-L.; Esarey, E.; Bulanov, S.S.; Benedetti, C.; Yu, L.-L.; Chen, M.; Geddes, C.G.R.; Leemans, W.P. Thermal emittance from ionization-induced trapping in plasma accelerators. Phys. Rev. ST Accel. Beams 2014, 17, 101301. [Google Scholar] [CrossRef]
- Wang, W.; Feng, K.; Ke, L.; Yu, C.; Xu, Y.; Qi, R.; Chen, Y.; Qin, Z.; Zhang, Z.; Fang, M.; et al. Free-electron lasing at 27 nanometers based on a laser wakefield accelerator. Nature 2021, 595, 516–520. [Google Scholar] [CrossRef]
- Fuchs, J.; Antici, P.; d’Humieres, E.; Lefebvre, E.; Borghesi, M.; Brambrink, E.; Cecchetti, C.A.; Kaluza, M.; Malka, V.; Manclossi, M.; et al. Laser-driven proton scaling laws and new paths towards energy increase. Nat. Phys. 2006, 2, 48. [Google Scholar] [CrossRef]
- Wilks, S.C.; Langdon, A.B.; Cowan, T.E.; Roth, M.; Singh, M.; Hatchett, S.; Key, M.H.; Pennington, D.; MacKinnon, A.; Snavely, R.A. Energetic proton generation in ultra-intense laser solid interactions. Phys. Plasmas 2001, 8, 542. [Google Scholar] [CrossRef]
- Pogorelsky, I.V.; Yakimenko, V.; Polyanskiy, M.; Shkolnikov, P.; Ispiryan, M.; Neely, D.; McKenna, P.; Carroll, D.; Najmudin, Z.; Willingale, L. Ultrafast CO2 laser technology: Application in ion acceleration. Nucl. Instrum. Meth. Phys. Res. A 2010, 620, 67–70. [Google Scholar] [CrossRef]
- Park, J.; Bin, J.H.; Steinke, S.; Ji, Q.; Bulanov, S.S.; Thévenet, M.; Vay, J.-L.; Schenkel, T.; Geddes, C.G.R.; Schroeder, C.B.; et al. Target normal sheath acceleration with a large laser focal diameter. Phys. Plasmas 2020, 27, 123104. [Google Scholar] [CrossRef]
- Robinson, A.P.L.; Zepf, M.; Kar, S.; Evans, R.G.; Bellei, C. Radiation pressure acceleration of thin foils with circularly polarized laser pulses. New J. Phys. 2008, 10, 013021. [Google Scholar] [CrossRef]
- Macchi, A. Theory of light sail acceleration by intense lasers: An overview. High Power Laser Sci. Eng. 2014, 2, e10. [Google Scholar] [CrossRef]
- Robinson, A.P.L.; Gibbon, P.; Zepf, M.; Kar, S.; Evans, R.G.; Bellei, C. Relativistically correct hole-boring and ion acceleration by circularly polarized laser pulses. Plasma Phys. Contr. Fusion 2009, 51, 024004. [Google Scholar] [CrossRef]
- Schlegel, T.; Naumova, N.; Tikhonchuk, V.T.; Labaune, C.; Sokolov, I.V.; Mourou, G. Relativistic laser piston model: Ponderomotive ion acceleration in dense plasmas using ultraintense laser pulses. Phys. Plasmas 2009, 16, 083103. [Google Scholar] [CrossRef]
- Moiseev, S.S.; Sagdeev, R.Z. Collisionless shock waves in a plasma in a weak magnetic field. J. Nucl. Energy C 1963, 51, 43–47. [Google Scholar] [CrossRef]
- Fiuza, F.; Fonseca, R.; Tonge, J.; Mori, W.; Silva, L. Weibel-instability-mediated collisionless shocks in the laboratory with ultraintense lasers. Phys. Rev. Lett. 2012, 108, 235004. [Google Scholar] [CrossRef]
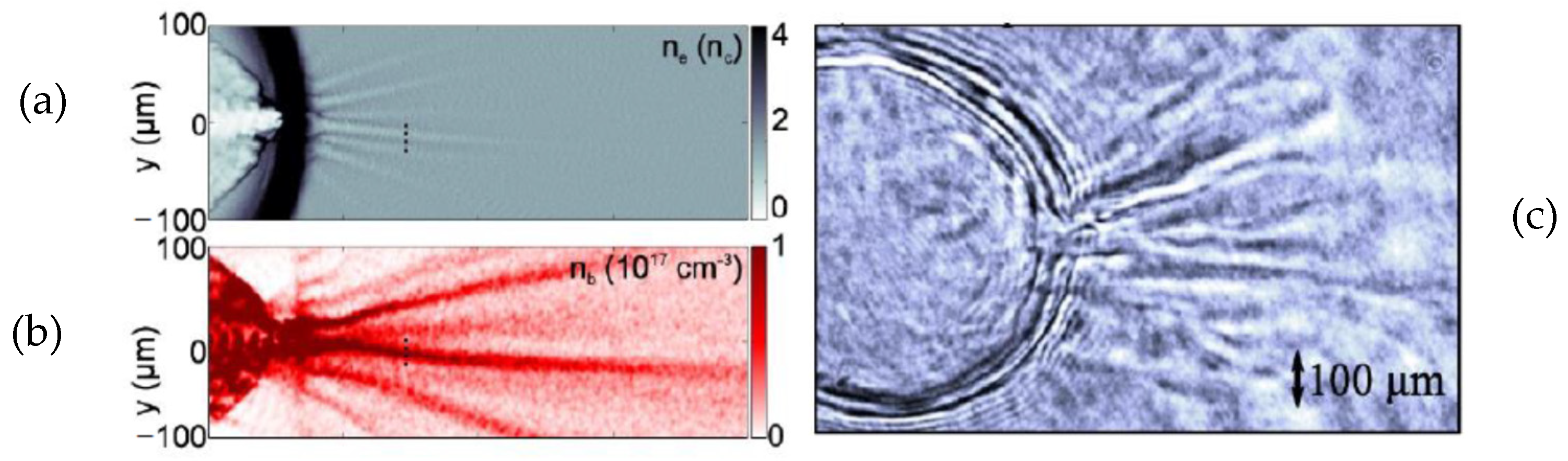
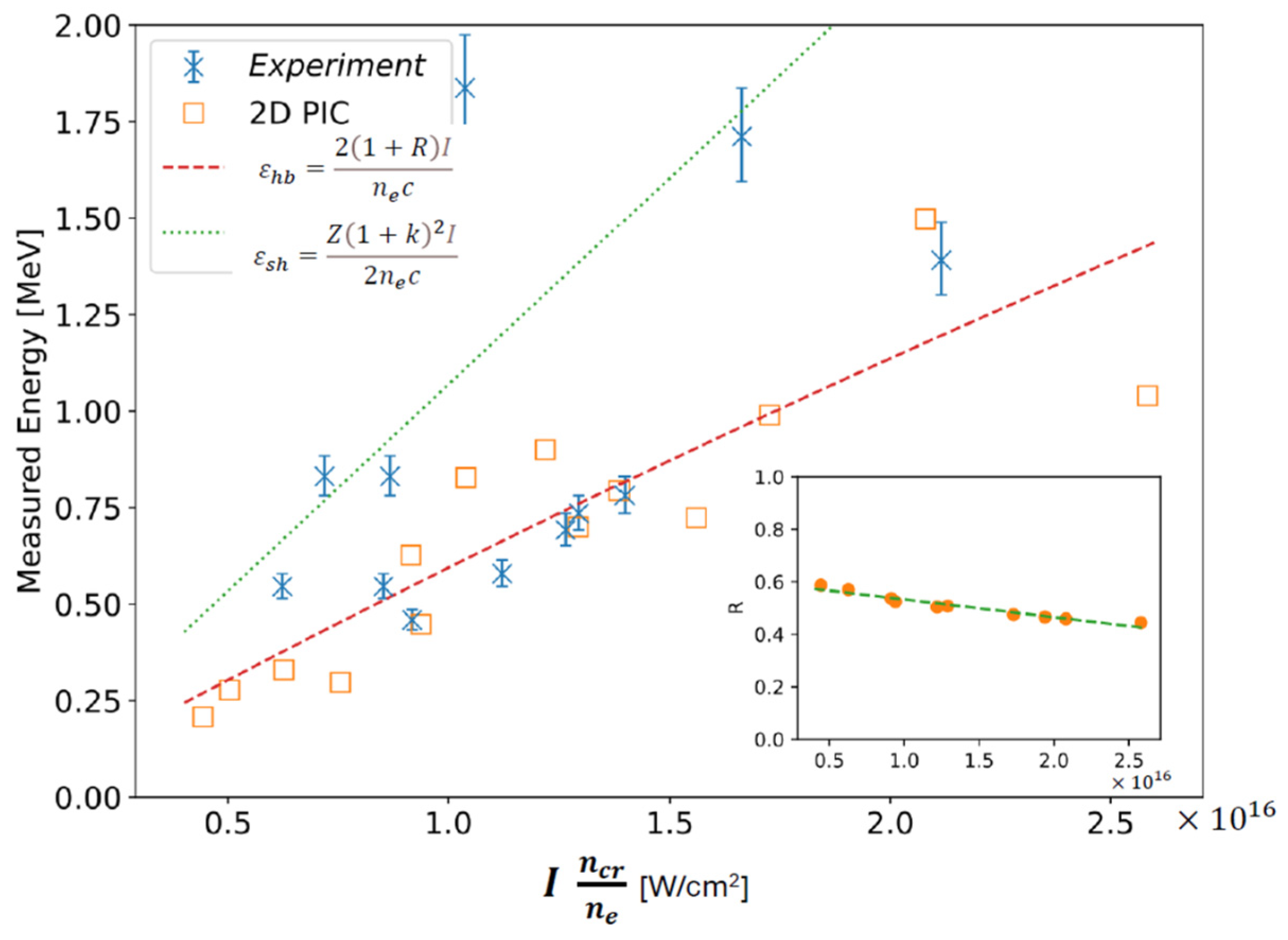
- Haberberger, D.; Tochitsky, S.; Fiuza, F.; Gong, C.; Fonseca, R.A.; Silva, L.O.; Mori, W.B.; Joshi, C. Collisionless shocks in laser produced plasma generate monoenergetic high-energy proton beams. Nat. Phys. 2011, 8, 95–99. [Google Scholar] [CrossRef]
- Palmer, C.A.J.; Dover, N.P.; Pogorelsky, I.; Babzien, M.; Dudnikova, G.I.; Ispiriyan, M.; Polyanskiy, M.N.; Schreiber, J.; Shkolnikov, P.; Yakimenko, V.; et al. Monoenergetic proton beams accelerated by a radiation pressure driven shock. Phys. Rev. Lett. 2011, 106, 014801. [Google Scholar] [CrossRef] [PubMed]
- Palmer, C.A.J.; Dover, N.P.; Pogorelsky, I.; Streeter, M.J.V.; Najmudin, Z. Manipulation of laser-generated energetic proton spectra in near critical density plasma. J. Plasma Phys. 2015, 81, 365810103. [Google Scholar] [CrossRef]
- Dover, N.P.; Cook, N.; Tresca, O.; Ettlinger, O.C.; Maharjan, C.; Polyanskiy, M.N.; Shkolnikov, P.; Pogorelsky, I.; Najmudin, Z. Optical shaping of gas targets for laser-plasma ion sources. J. Plasma Phys. 2016, 82, 415820101. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Ting, A.; Hafizi, B.; Helle, M.H.; Johnson, L.A.; Polyanskiy, M.N.; Pogorelsky, I.V.; Babzien, M.; Dover, N.P.; Ettlinger, O.C.; et al. Proton acceleration in an overdense hydrogen plasma by intense CO2 laser pulses with nonlinear propagation effects in the underdense pre-plasma. Phys. Plasmas 2023, 30, 053106. [Google Scholar] [CrossRef]
- Savert, A.; Mangles, S.P.D.; Schnell, M.; Siminos, E.; Cole, J.M.; Leier, M.; Reuter, M.; Schwab, M.B.; Möller, M.; Poder, K.; et al. Direct observation of the injection dynamics of a laser wakefield accelerator using few-femtosecond shadowgraphy. Phys. Rev. Lett. 2015, 115, 055002. [Google Scholar] [CrossRef]
- Ettlinger, O.C. Studies of Near-Critical Density Laser Plasma Interactions for Ion Acceleration. PhD Thesis, Imperial College London, London, UK, 12 January 2018. [Google Scholar]
- Dover, N.P.; Tresca, O.; Cook, N.; Ettlinger, O.C.; Kingham, R.J.; Maharjan, C.; Polyanskiy, M.N.; Shkolnikov, P.; Pogorelsky, I.; Najmudin, Z. Optical imaging of laser-driven fast electron Weibel-like filamentation in overcritical density plasma. Phys. Rev. Lett. 2025, 134, 025102. [Google Scholar] [CrossRef]
- Bakshi, V. (Ed.) EUV Lithography; SPIE: Bellingham, WA, USA, 2009. [Google Scholar]
- Ueno, Y.; Ariga, T.; Soumagne, G.; Higashiguchi, T.; Kubodera, S.; Pogorelsky, I.; Pavlishin, I.; Stolyarov, D.; Babzien, M.; Kusche, K.; et al. Efficient extreme ultraviolet plasma source generated by a CO2 laser and a liquid xenon microjet target. Appl. Phys. Lett. 2007, 90, 191503. [Google Scholar] [CrossRef]
- Microsoft Word—Laser Technology Workshop Report_20240117_Update. Available online: https://science.osti.gov/-/media/ardap/pdf/2024/Laser-Technology-Workshop-Report_20240105_final.pdf (accessed on 10 February 2024).
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef]
- Krause, J.L.; Schafer, K.J.; Kulander, K.C. High-order harmonic generation from atoms and ions in the high intensity regime. Phys. Rev. Lett. 1992, 68, 3535–3538. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Nishimura, K.; Shao, R.; Suda, A.; Midorikawa, K.; Lan, P.; Takahashi, E.J. High efficiency ultrafast water-window harmonic generation for single-shot soft X-ray spectroscopy. Commun. Phys. 2020, 3, 92. [Google Scholar] [CrossRef]
- Tate, J.; Auguste, T.; Muller, H.G.; Salieres, P.; Agostini, P.; DiMauro, L.F. Scaling of Wave-Packet Dynamics in an Intense Midinfrared Field. Phys. Rev. Lett. 2007, 98, 013901. [Google Scholar] [CrossRef] [PubMed]
- Popmintchev, T.; Chen, M.-C.; Popmintchev, D.; Arpin, P.; Brown, S.; Alisauskas, S.; Andriukaitis, G.; Balčiunas, T.; Mücke, O.D.; Pugzlys, A.; et al. Bright coherent ultrahigh harmonics in the keV x-ray regime from mid-infrared femtosecond lasers. Science 2012, 336, 1287–1291. [Google Scholar] [CrossRef]
- Li, X.; Qiu, T.; Zhang, J.; Baldini, E.; Lu, J.; Rappe, A.M.; Nelson, K.A. Terahertz field-induced ferroelectricity in quantum paraelectric SrTiO3. Science 2019, 364, 1079. [Google Scholar] [CrossRef]
- Nanni, E.A.; Huang, W.R.; Hong, K.-H.; Ravi, K.; Fallahi, A.; Moriena, G.; Dwayne Miller, R.J.; Kärtner, F.X. Terahertz driven linear electron acceleration. Nat. Commun. 2015, 6, 8486. [Google Scholar] [CrossRef]
- Pickwell, E.; Wallace, V.P. Biomedical applications of terahertz technology. J. Phys. D 2006, 39, R301. [Google Scholar] [CrossRef]
- Fitzgerald, A.J.; Berry, E.; Zinov’ev, N.N.; Homer-Vanniasinkam, S.; Miles, R.E.; Chamberlain, J.M.; Smith, M.A. Catalogue of human tissue optical properties at terahertz frequencies. J. Biol. Phys. 2003, 29, 123–128. [Google Scholar] [CrossRef]
- Casalbuoni, S.; Schmidt, B.; Schmüser, P.; Arsov, V.; Wesch, S. Ultrabroadband terahertz source and beamline based on coherent transition radiation. Phys. Rev. ST Accel. Beams 2009, 12, 030705. [Google Scholar] [CrossRef]
- Fülöp, J.A.; Polónyi Gy Monoszlai, B.; Andriukaitis, G.; Balciunas, T.; Pugzlys, A.; Arthur, G.; Baltuska, A.; Hebling, J. Highly efficient scalable monolithic semiconductor terahertz pulse source. Optica 2016, 3, 1075–1078. [Google Scholar] [CrossRef]
- Krasilnikov, M.; Aboulbanine, Z.; Adhikari, G.; Aftab, N.; Asoyan, A.; Boonpornprasert, P.; Davtyan, H.; Georgiev, G.; Good, J.; Grebinyk, A.; et al. First high peak and average power single-pass THz FEL based on high brightness photoinjector. arXiv 2024, arXiv:2405.19152. [Google Scholar]
- Tóth, G.; Illés, G.; Nazymbekov, G.; Mbithi, N.; Almási, G.; Hebling, J. Possibility of CO2 laser-pumped multi-millijoule-level ultrafast pulse terahertz sources. Sci. Rep. 2024, 14, 999. [Google Scholar] [CrossRef]
- Liao, G.-Q.; Liu, H.; Scott, G.G.; Zhang, Y.-H.; Zhu, B.-J.; Zhang, Z.; Li, Y.T.; Armstrong, C.; Zemaityte, E.; Bradford, P.; et al. Towards terawatt-scale spectrally tunable terahertz pulses via relativistic laser-foil interactions. Phys. Rev. X 2020, 10, 031062. [Google Scholar] [CrossRef]
- Petrillo, V.; Bacci, A.; Zinati, R.B.A.; Chaikovska, I.; Curatolo, C.; Ferrario, M.; Maroli, C.; Ronsivalle, C.; Rossi, A.; Serafini, L.; et al. Photon flux and spectrum of gamma-ray sources. Nucl. Instrum. Methods Phys. Res. A 2012, 693, 109–116. [Google Scholar] [CrossRef]
- Pogorelsky, I.V.; Ben-Zvi, I.; Hirose, T.; Kashiwagi, S.; Yakimenko, V.; Kusche, K.; Siddons, P.; Skaritka, J.; Kumita, T.; Tsunemi, A.; et al. Demonstration of 8×1018 photons/second peaked at 1.8 Å in a relativistic Thomson scattering experiment. Phys. Rev. ST Accel. Beams 2000, 3, 090702. [Google Scholar] [CrossRef]
- Endrizzi, M.; Gureyev, T.E.; Delogu, P.; Oliva, P.; Golosio, B.; Carpinelli, M.; Pogorelsky, I.; Yakimenko, V.; Bottigli, U. Quantitative phase retrieval with picosecond x-ray pulses from the ATF Inverse Compton Scattering source. Opt. Express 2011, 19, 2748–2753. [Google Scholar] [CrossRef] [PubMed]
- Oliva, P.; Carpinelli, M.; Golosio, B.; Delogu, P.; Endrizzi, M.; Park, J.; Pogorelsky, I.; Yakimenko, V.; Williams, O.; Rosenzweig, J. Quantitative evaluation of single-shot inline phase contrast imaging using an inverse Compton X-ray source. Appl. Phys. Lett. 2010, 97, 134104. [Google Scholar] [CrossRef]
- Babzien, B.; Ben-Zvi, I.; Kusche, K.; Pavlishin, I.V.; Pogorelsky, I.V.; Siddons, D.P.; Yakimenko, V.; Cline, D.; Zhou, F.; Hirose, T.; et al. Observation of the second harmonic in Thomson scattering from relativistic electrons. Phys. Rev. Lett. 2006, 96, 054802. [Google Scholar] [CrossRef] [PubMed]
- Sakai, Y.; Pogorelsky, I.; Williams, O.; O’Shea, F.; Barber, S.; Gadjev, I.; Duris, J.; Musumeci, P.; Fedurin, M.; Korostyshevsky, A.; et al. Observation of redshifting and harmonic radiation in inverse Compton scattering. Phys. Rev. STAB 2015, 18, 060702. [Google Scholar] [CrossRef]
- Krafft, G.; Priebe, G. Compton sources of electromagnetic radiation. Rev. Accel. Sci. Techol. 2010, 3, 147. [Google Scholar] [CrossRef]
- Feser, M. The Lyncean Compact Light Source: X-ray synchrotron radiation for analytical and imaging applications (Conference Presentation). In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 19 September 2017; Volume 10387, p. 1038703. [Google Scholar] [CrossRef]
- Akagi, T.; Kosuge, A.; Araki, S.; Hajima, R.; Honda, Y.; Miyajima, T.; Mori, M.; Nagai, R.; Nakamura, N.; Shimada, M.; et al. Narrow-band photon beam via laser Compton scattering in an energy recovery linac. Phys. Rev. Accel. Beams 2016, 19, 114701. [Google Scholar] [CrossRef]
- Zamfir, V.; Tanaka, K.; Ur, C. Extreme Light Infrastructure—Nuclear Physics (ELI-NP). Europhys. News 2019, 50, 23–25. [Google Scholar] [CrossRef]
- Deitrick, K.E.; Franck, C.; Hofstaetter, G.H.; Kostroun, V.O.; Smolenski, K.W.; Crone, J.; Owen, H.L.; Muratori, B.D. A hard x-ray compact Compton source at CBETA. In Proceedings of the IPAC2019, Melbourne, Australia, 19–24 May 2019. [Google Scholar] [CrossRef]
- Alesini, D.; Chaikovska, I.; Guiducci, S.; Milardi, C.; Variola, A.; Zobov, M.; Zomer, F. DAΦNE γ-rays factory. IEEE Trans. Nucl. Sci. 2016, 63, 913–920. [Google Scholar] [CrossRef]
- Hirose, T.; Dobashi, K.; Kurihara, Y.; Muto, T.; Omori, T.; Okugi, T.; Sakai, I.; Urakawa, J.; Washio, M. Polarized positron source for the linear collider, JLC. Nucl. Instrum. Methods Phys. Res. A 2000, 455, 15. [Google Scholar] [CrossRef]
- Yakimenko, V.; Pogorelsky, I.V. Polarized γ source based on Compton backscattering in a laser cavity. Phys. Rev. STAB 2006, 9, 091001. [Google Scholar] [CrossRef]
- Shen, Y.R. The Principles of Nonlinear Optics; John Wiley & Sons: Hoboken, NJ, USA, 1984; Chapter 17. [Google Scholar]
- Durand, M.; Houard, A.; Prade, B.; Mysyrowicz, A.; Durecu, A.; Moreau, B.; Fleury, D.; Vasseur, O.; Borchert, H.; Diener, K.; et al. Kilometer range filamentation. Opt. Express 2013, 21, 26836–26845. [Google Scholar] [CrossRef]
- Mechain, G.; Couairon, A.; André, Y.-B.; D’Amico, C.; Franco, M.; Prade, B.; Tzortzakis, S.; Mysyrowicz, A.; Sauerbrey, R. Long range self-channeling of infrared laser pulses in air: A new propagation regime without ionization. App. Phys. B 2004, 79, 379–382. [Google Scholar] [CrossRef]
- Tochitsky, S.Y.; Welch, E.C.; Matteo, D.A.; Panagiotopoulos, P.; Kolesik, M.; Moloney, J.V.; Joshi, C. Self-channeling of a multi-Joule 10 µm picosecond pulse train through long distances in air. Opt. Express 2024, 32, 2067–2080. [Google Scholar] [CrossRef] [PubMed]
- Tochitsky, S.; Welch, E.; Polyanskiy, M.; Pogorelsky, I.; Panagiotopoulos, P.; Kolesik, M.; Wright, E.M.; Koch, S.W.; Moloney, J.V.; Pigeon, J.; et al. Megafilament in air formed by self-guided terawatt long-wavelength infrared laser. Nat. Photon. 2019, 13, 41–46. [Google Scholar] [CrossRef]
- Tochitsky, S.; Welch, E.; Panagiotopoulos, P.; Polyanskiy, M.; Pogorelsky, I.; Kolesik, M.; Koch, S.W.; Moloney, J.V.; Joshi, C. Filamentation of long-wave infrared pulses in the atmosphere. JOSA B 2019, 36, G40–G51. [Google Scholar] [CrossRef]
- Isaacs, J.; Miao, C.; Sprangle, P. Remote monostatic detection of radioactive material by laser-induced breakdown. Phys. Plasmas 2016, 23, 033507. [Google Scholar] [CrossRef]
- Zingale, A.; Waczynski, S.; Pogorelsky, I.; Polyanskiy, M.; Sears, J.; Lakis, R.E.; Milchberg, H.M. Remote detection of radioactive material using a short pulse CO2 laser. arXiv 2024, arXiv:2408.13640. [Google Scholar] [CrossRef]
- Zingale, A.; Waczynski, S.; Sears, J.; Lakis, R.E.; Milchberg, H.M. Atmospheric effects on the laser-driven avalanche-based remote detection of radiation. Opt. Lett. 2023, 48, 2480. [Google Scholar] [CrossRef] [PubMed]
- Englesbe, A.; Elle, J.; Schwartz, R.; Garrett, T.; Woodbury, D.; Jang, D.; Kim, K.-Y.; Milchberg, H.; Reid, R.; Lucero, A.; et al. Ultrabroadband microwave radiation from near- and mid-infrared laser-produced plasmas in air. Phys. Rev. A 2021, 104, 013107. [Google Scholar] [CrossRef]
- Thornton, E.A. Optimizing Ultra-Broadband Microwave Radiation Through Plasma Dynamics of USPL Filaments. Ph.D. Thesis, University of North Texas, Denton, TX, USA, July 2024. [Google Scholar]
- Kimura, W.D.; Kim, G.H.; Romea, R.D.; Steinhauer, L.C.; Pogorelsky, I.V.; Kusche, K.P.; Fernow, R.C.; Wang, X.; Liu, Y. Laser acceleration of relativistic electrons using the inverse Cherenkov effect. Phys. Rev. Lett. 1995, 74, 546–549. [Google Scholar] [CrossRef]
- Li, W.H.; Pogorelsky, I.V.; Palmer, M.A. Direct Acceleration of an electron beam with a radially polarized long-wave infrared laser. Photonics 2024, 11, 1066. [Google Scholar] [CrossRef]
- Jana, K.; Mi, Y.; Møller, S.H.; Ko, D.H.; Gholam-Mirzaei, S.; Abdollahpour, D.; Sederberg, S.; Corkum, P.B. Quantum control of flying doughnut terahertz pulses. Sci. Adv. 2024, 10, eadl1803. [Google Scholar] [CrossRef] [PubMed]
- Kimura, W.D.; Campbell, L.P.; Dilley, C.E.; Gottschalk, S.C.; Quimby, D.C.; van Steenbergen, A.; Babzien, M.; Ben-Zvi, I.; Gallardo, J.C.; Kusche, K.P.; et al. Detailed experimental results for laser acceleration staging. Phys. Rev. ST Accel. Beams 2001, 4, 101301. [Google Scholar] [CrossRef]
- Yu, L.-H.; Babzien, M.; Ben-Zvi, I.; DiMauro, L.F.; Doyuran, A.; Graves, W.; Johnson, E.; Babzien, M.; Ben-Zvi, I.; Gallardo, J.C.; et al. High-gain harmonic-generation free-electron laser. Science 2000, 289, 932–934. [Google Scholar] [CrossRef] [PubMed]
- Duris, J.; Musumeci, P.; Babzien, M.; Fedurin, M.; Kusche, K.; Li, R.K.; Moody, J.; Pogorelsky, I.; Polyanskiy, M.; Rosenzweig, J.B.; et al. High-quality electron beams from a helical inverse free-electron laser accelerator. Nat. Commun. 2014, 5, 4928. [Google Scholar] [CrossRef] [PubMed]
- Ovodenko, A.; Agustsson, R.; Babzien, M.; Campese, T.; Fedurin, M.; Murokh, A.; Pogorelsky, I.; Polyanskiy, M.; Rosenzweig, J.; Sakai, Y.; et al. High duty cycle inverse Compton scattering x-ray source. Appl. Phys. Lett. 2016, 109, 253504. [Google Scholar] [CrossRef]
- Gadjev, I.; Sudar, N.; Babzien, M.; Duris, J.; Hoang, P.; Fedurin, M.; Kusche, K.; Malone, R.; Musumeci, P.; Palmer, M.; et al. An inverse free electron laser acceleration-driven Compton scattering X-ray source. Sci. Rep. 2019, 9, 532. [Google Scholar] [CrossRef] [PubMed]







| Parameter | Value | |||
|---|---|---|---|---|
| Laser wavelength (μm) | 0.8 | 9.2 | 0.8 | 9.2 |
| Plasma density (1016 cm−3) | 1.1 | 1.1 | 11 | 11 |
| Plasma wavelength (μm) | 313 | 313 | 99 | 99 |
| Laser pulse duration (fs) | 390 | 390 | 130 | 130 |
| Laser radius (μm) | 200 | 200 | 63 | 63 |
| Laser peak power (TW) | 3000 | 23 | 300 | 2.3 |
| Laser energy per stage (J) | 1200 | 9 | 40 | 0.3 |
| Electrons per bunch (109) | 12 | 12 | 4 | 4 |
| Accelerating field (GeV/m) | 4.3 | 4.3 | 12.6 | 12.6 |
| Stage length (m) | 25 | 0.19 | 0.79 | 0.06 |
| Energy gain per stage (GeV) | 100 | 0.75 | 10 | 0.075 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pogorelsky, I.V.; Polyanskiy, M.N. Harnessing Ultra-Intense Long-Wave Infrared Lasers: New Frontiers in Fundamental and Applied Research. Photonics 2025, 12, 221. https://doi.org/10.3390/photonics12030221
Pogorelsky IV, Polyanskiy MN. Harnessing Ultra-Intense Long-Wave Infrared Lasers: New Frontiers in Fundamental and Applied Research. Photonics. 2025; 12(3):221. https://doi.org/10.3390/photonics12030221
Chicago/Turabian StylePogorelsky, Igor V., and Mikhail N. Polyanskiy. 2025. "Harnessing Ultra-Intense Long-Wave Infrared Lasers: New Frontiers in Fundamental and Applied Research" Photonics 12, no. 3: 221. https://doi.org/10.3390/photonics12030221
APA StylePogorelsky, I. V., & Polyanskiy, M. N. (2025). Harnessing Ultra-Intense Long-Wave Infrared Lasers: New Frontiers in Fundamental and Applied Research. Photonics, 12(3), 221. https://doi.org/10.3390/photonics12030221




