Temperature Control Performance Improvement of High-Power Laser Diode with Assistance of Machine Learning
Abstract
:1. Introduction
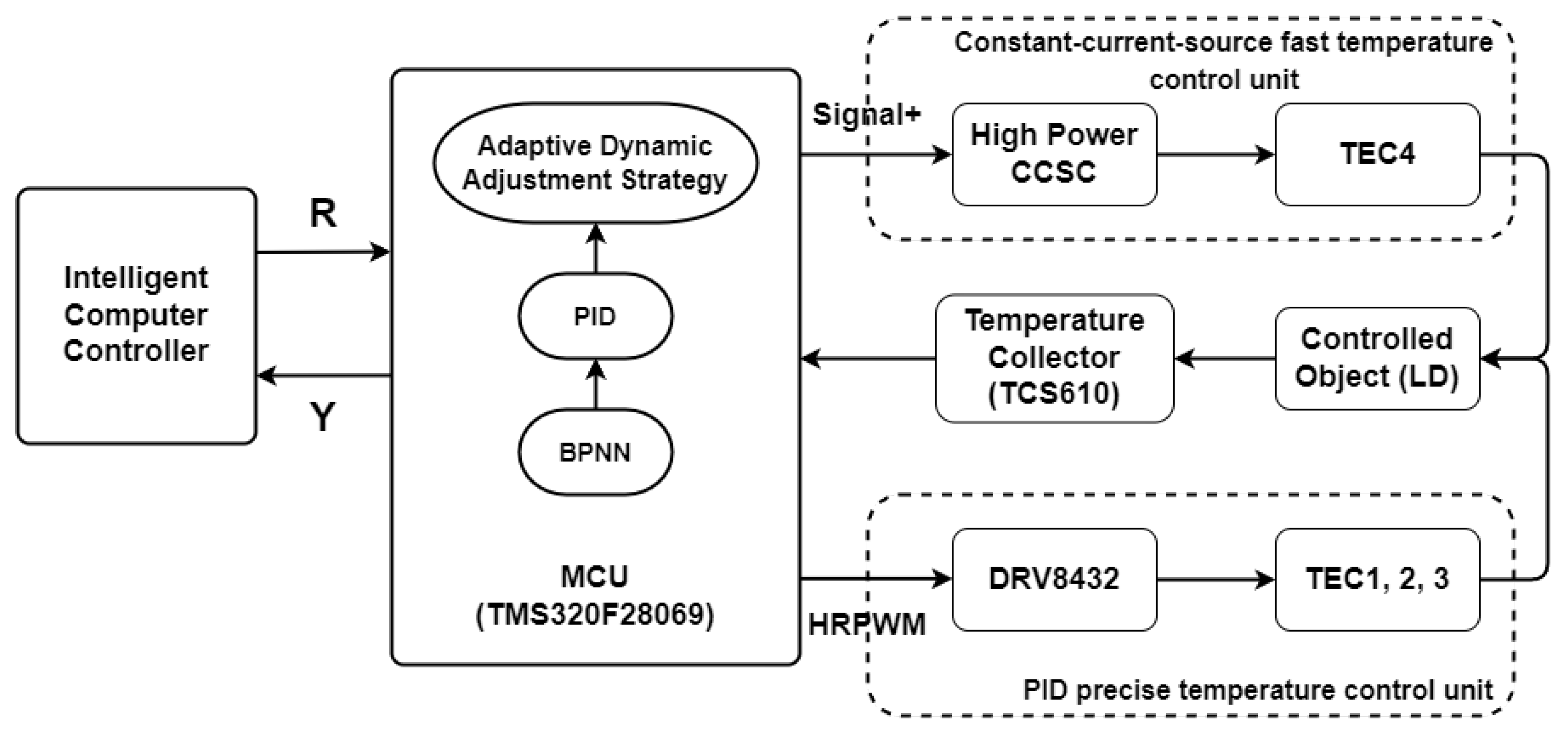
2. Experiment Design
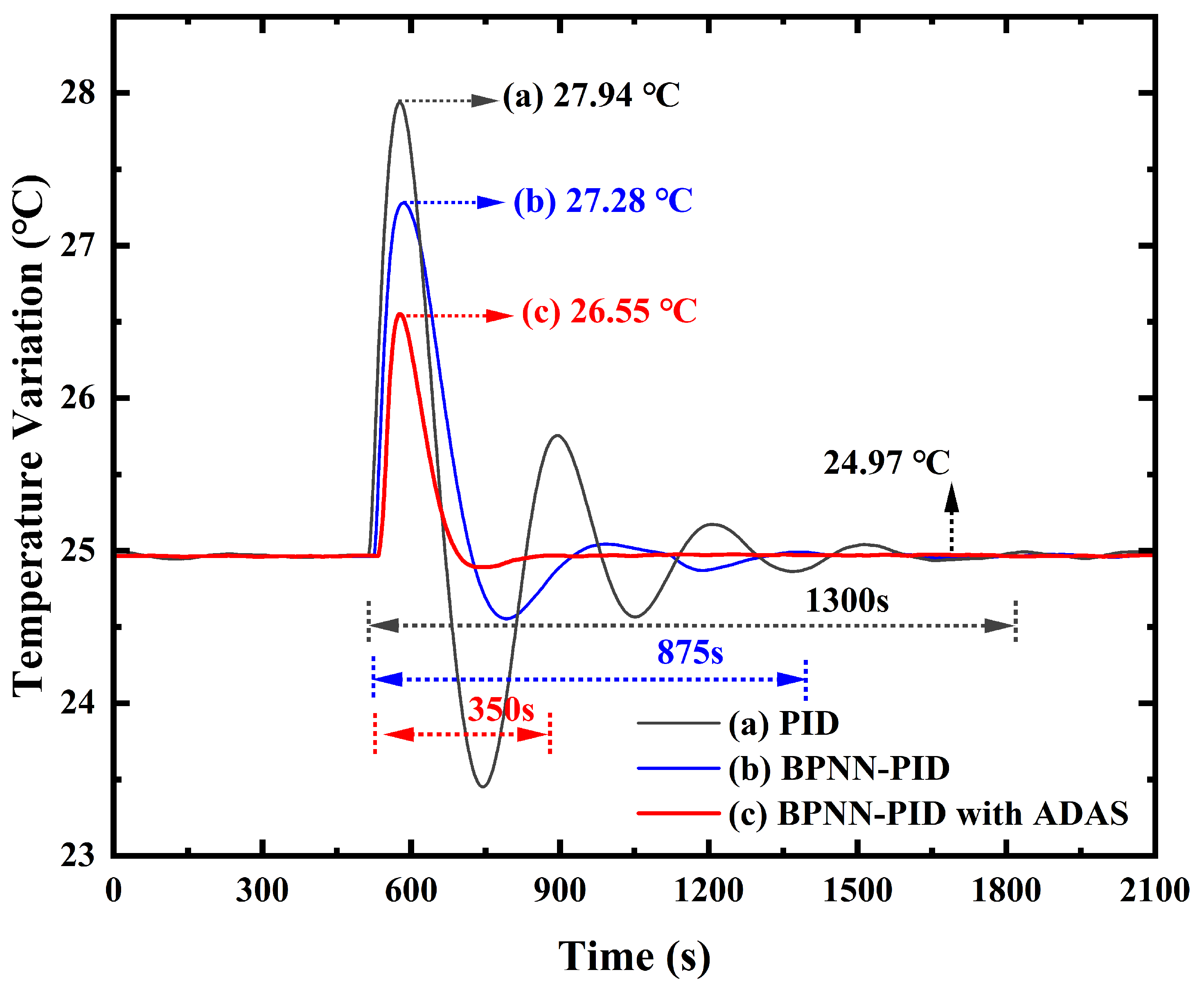
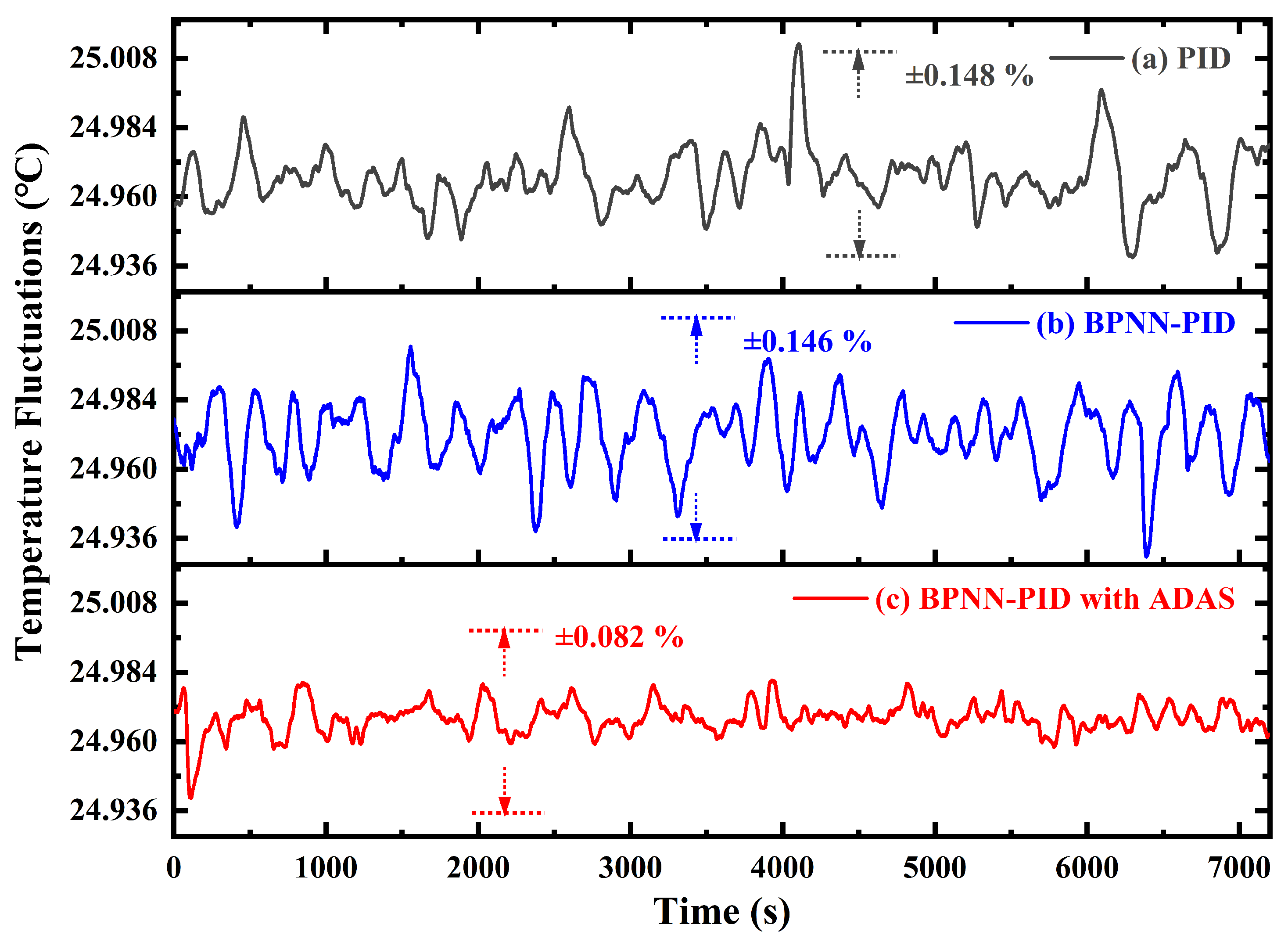
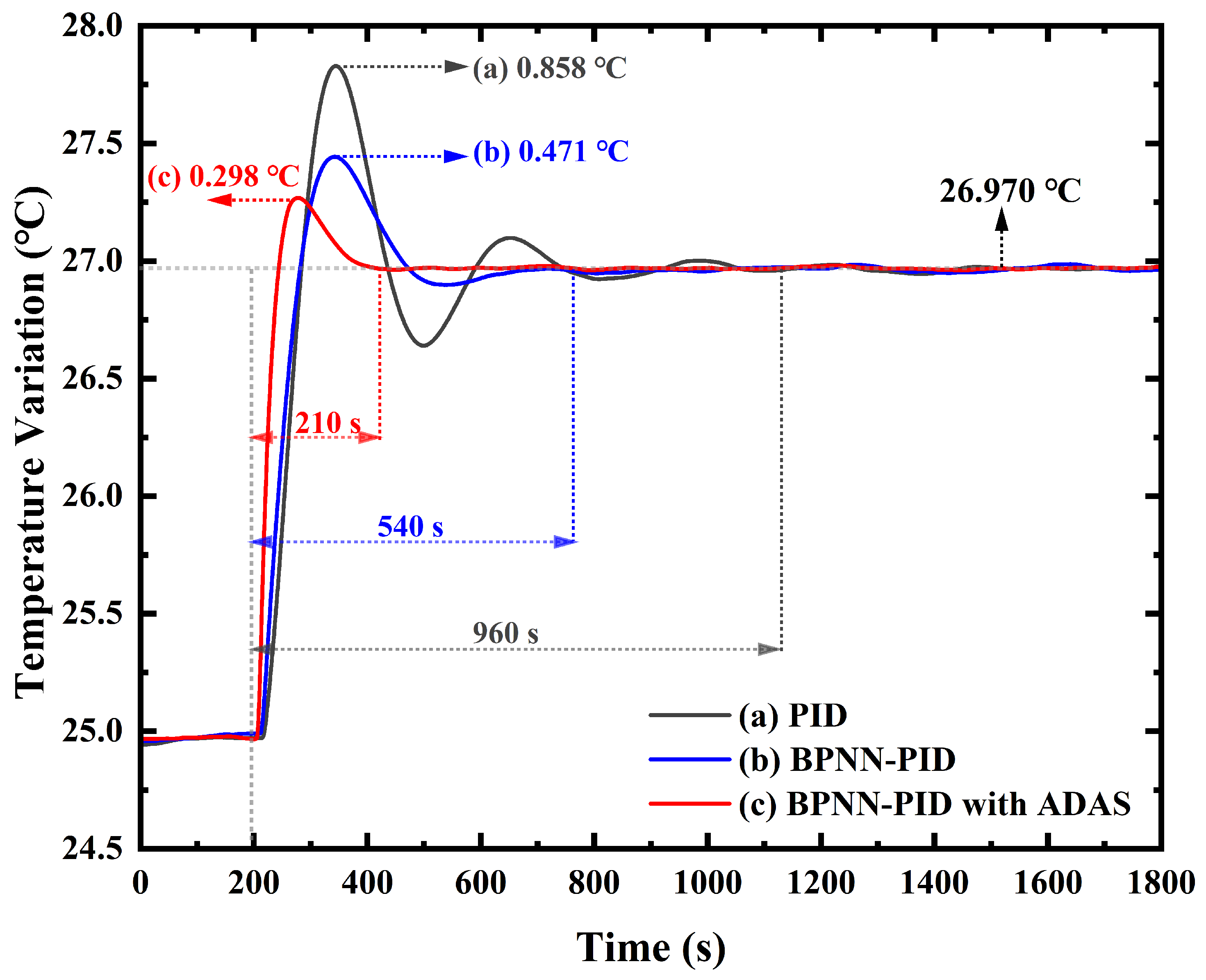
3. Experimental Results
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sokolowski, W.; Hangst, A.; Buehler, M.; Killi, A.; Ryba, T.; Benz, S.; Armbruster, B.; Olschowsky, P. Latest developments in high brightness diode lasers and their applications. In Proceedings of the Photonics West—Lasers and Applications in Science and Engineering, San Francisco, CA, USA, 2–7 February 2013. [Google Scholar] [CrossRef]
- Gao, S.; Gong, M.; Liu, H.; Wang, D. Influence of LD temperature fluctuation on the performance of corner-pumped TEM00 CW composite Nd:YAG laser. Laser Phys. 2010, 20, 790–792. [Google Scholar] [CrossRef]
- Álvarez, J.; Pimienta, J.; Mercado, E.; Sarmiento, R. An extended laser cavity centered at 780 nm for high-resolution laser spectroscopy applications. Laser Phys. 2023, 33, 055005. [Google Scholar] [CrossRef]
- Tritt, T.M. Thermoelectric Materials: Principles, Structure, Properties, and Applications. In Encyclopedia of Materials: Science and Technology, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar] [CrossRef]
- Zhao, D.; Tan, G. A review of thermoelectric cooling: Materials, modeling and applications. Appl. Therm. Eng. 2014, 66, 15–24. [Google Scholar] [CrossRef]
- Barker, J.; Khan, M.; Solomos, T. Mechanism of the Pasteur effect. Nature 1964, 201, 1126–1127. [Google Scholar] [CrossRef]
- Bärwolff, A.; Puchert, R.; Enders, P.; Menzel, U.; Ackermann, D. Analysis of thermal behaviour of high power semiconductor laser arrays by means of the finite element method (FEM). J. Therm. Anal. Calorim. 1995, 45, 417–436. [Google Scholar] [CrossRef]
- Puchert, R.; Menzel, U.; Bärwolff, A.; Voβ, M.; Lier, C. Influence of heat source distributions in GaAs/GaAlAs quantum-well high-power laser arrays on temperature profile and thermal resistance. J. Therm. Anal. Calorim. 1997, 48, 1273–1282. [Google Scholar] [CrossRef]
- Ebert, T.; Treusch, H.G.; Loosen, P.; Poprawe, R. Optimization of microchannel heatsinks for high-power diode lasers in copper technology. In Proceedings of the Fabrication, Testing, Reliability, and Applications of Semiconductor Lasers III; Linden, K.J., Fallahi, M., Linden, K.J., Wang, S.C., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 1998; Volume 3285, pp. 25–29. [Google Scholar] [CrossRef]
- Wang, Y. PID Temperature Control. In Conveyor Belt Furnace Thermal Processing; Springer International Publishing: Cham, Switzerland, 2018; pp. 63–76. [Google Scholar] [CrossRef]
- Fong-Chwee, T.; Sirisena, H. Self-tuning PID controllers for dead time processes. IEEE Trans. Ind. Electron. 1988, 35, 119–125. [Google Scholar] [CrossRef]
- Besharati Rad, A.; Lo, W.L.; Tsang, K. Self-tuning PID controller using Newton-Raphson search method. IEEE Trans. Ind. Electron. 1997, 44, 717–725. [Google Scholar] [CrossRef]
- Åström, K.; Hägglund, T.; Hang, C.; Ho, W. Automatic Tuning and Adaptation for PID Controllers—A Survey. IFAC Proc. Vol. 1992, 25, 371–376. [Google Scholar] [CrossRef]
- Xing, X.F.; Li, H.Z. Modeling and Simulation the Semiconductor Lasers Diode Temperature Controlling. Adv. Mater. Res. 2011, 338, 706–708. [Google Scholar] [CrossRef]
- Cong, M.; Xu, W.; Wang, Y. Design of Temperature Controller for Laser Diode Based on DSP and Fuzzy-PID Control. In Proceedings of the 2010 International Conference on Electrical and Control Engineering, Wuhan, China, 25–27 June 2010; pp. 786–789. [Google Scholar] [CrossRef]
- Jian, Y.; Deng, H. A FPGA-based real-time particle swarm optimization for temperature control of semiconductor laser. In Proceedings of the International Conference on Optoelectronic Materials and Devices (ICOMD 2022), Chongqing, China, 16–18 December 2022; Huang, Q., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2023; Volume 12600, p. 126001S. [Google Scholar] [CrossRef]
- Chen, K.Y.; Tung, P.C.; Tsai, M.T.; Fan, Y.H. A self-tuning fuzzy PID-type controller design for unbalance compensation in an active magnetic bearing. Expert Syst. Appl. 2009, 36, 8560–8570. [Google Scholar] [CrossRef]
- Zhang, J.; Zhuang, J.; Du, H.; Wang, S. Self-organizing genetic algorithm based tuning of PID controllers. Inf. Sci. 2009, 179, 1007–1018. [Google Scholar] [CrossRef]
- Gaing, Z.L. A particle swarm optimization approach for optimum design of PID controller in AVR system. IEEE Trans. Energy Convers. 2004, 19, 384–391. [Google Scholar] [CrossRef]
- Chan, Y.F.; Moallem, M.; Wang, W. Design and Implementation of Modular FPGA-Based PID Controllers. IEEE Trans. Ind. Electron. 2007, 54, 1898–1906. [Google Scholar] [CrossRef]
- Wu, H.; Su, W.; Liu, Z. PID controllers: Design and tuning methods. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; pp. 808–813. [Google Scholar] [CrossRef]
- Borase, R.P.; Maghade, D.; Sondkar, S.; Pawar, S. A review of PID control, tuning methods and applications. Int. J. Dyn. Control 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Rahman, M.A.; Saleh, T.; Jahan, M.P.; McGarry, C.; Chaudhari, A.; Huang, R.; Tauhiduzzaman, M.; Ahmed, A.; Mahmud, A.A.; Bhuiyan, M.S.; et al. Review of Intelligence for Additive and Subtractive Manufacturing: Current Status and Future Prospects. Micromachines 2023, 14, 508. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, Y.; Li, J.; Wang, F. PID Control in the Reactor Temperature Control System Based on BP Neural Network. In Proceedings of the 2009 International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2009; Volume 1, pp. 245–248. [Google Scholar] [CrossRef]
- Aliqab, K.; Sohaib, M.A.; Ali, F.; Armghan, A.; Alsharari, M. Employment of Self-Adaptive Bayesian Neural Network for Systematic Antenna Design: Improving Wireless Networks Functionalities. Micromachines 2023, 14, 594. [Google Scholar] [CrossRef]
- Qiao, H.; Peng, W.; Jin, P.; Su, J.; Lu, H. Performance Improvement of Single-Frequency CW Laser Using a Temperature Controller Based on Machine Learning. Micromachines 2022, 13, 1047. [Google Scholar] [CrossRef] [PubMed]
- Li, C.H.; Xu, S.X.; Xie, Y.; Zhao, J. The Application of PSO-BP Neural Network PID Controller in Variable Frequency Speed Regulation System. Appl. Mech. Mater. 2014, 599, 1090–1093. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Parameter Selection in Particle Swarm Optimization. In Evolutionary Programming VII, Proceedings of the 7th International Conference, EP98, San Diego, CA, USA, 25–27 March 1998; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Li, R.; Suo, X.; Lu, E. Application of PSO-BPNN-PID Controller in Nutrient Solution EC Precise Control System: Applied Research. Sensors 2022, 22, 5515. [Google Scholar] [CrossRef]
- Åström, K.; Hägglund, T. The Future of PID Control. IFAC Proc. Vol. 2000, 33, 19–30. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, W.; Xiong, L.; Liu, H. Thermal Design and Management in High Power Semiconductor Laser Packaging. In Packaging of High Power Semiconductor Lasers; Springer: New York, NY, USA, 2015; pp. 53–88. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.Y.; Yang, Y.Y.; Huang, J.Y.; Bai, Y.R.; Zhang, Y.; Lin, X.C. Automatic compensation of thermal drift of laser beam through thermal balancing based on different linear expansions of metals. Results Phys. 2019, 13, 102201. [Google Scholar] [CrossRef]
- Peng, W.; Jin, P.; Li, F.; Su, J.; Lu, H.; Peng, K. A Review of the High-Power All-Solid-State Single-Frequency Continuous-Wave Laser. Micromachines 2021, 12, 1426. [Google Scholar] [CrossRef] [PubMed]
- Yin, Q.; Lu, H.; Su, J.; Peng, K. High power single-frequency and frequency-doubled laser with active compensation for the thermal lens effect of terbium gallium garnet crystal. Opt. Lett. 2016, 41, 2033–2036. [Google Scholar] [CrossRef]
- Chen, M.; Li, I.; Hu, C. The Driver Circuit and Focusing Lens Designed for the Laser Range-Finder. Key Eng. Mater. 2008, 364–366, 160–165. [Google Scholar] [CrossRef]
- Jin, X. Study on A High-Precision Digital Temperature-Control System for All-Solid-State Single-Frequency Green Laser. Chin. J. Lasers 2015, 42, 0902010. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Jiang, Q.; Huang, R.; Huang, Y.; Chen, S.; He, Y.; Lan, L.; Liu, C. Application of BP Neural Network Based on Genetic Algorithm Optimization in Evaluation of Power Grid Investment Risk. IEEE Access 2019, 7, 154827–154835. [Google Scholar] [CrossRef]
- Allaf, N.A. Improving the Performance of Backpropagation Neural Network Algorithm for Image Compression/Decompression System. J. Comput. Sci. 2010, 6, 1347–1354. [Google Scholar] [CrossRef]
- Lan, Y.; Yang, G.; Liu, Y.; Zhao, Y.; Wang, Z.; Li, T.; Demir, A. 808 nm broad-area laser diodes designed for high efficiency at high-temperature operation. Semicond. Sci. Technol. 2021, 36, 105012. [Google Scholar] [CrossRef]
- Bowman, S.R. High-power diode-pumped solid-state lasers. Opt. Eng. 2012, 52, 021012. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Jin, X.; Jin, P.; Su, J.; Li, F.; Lu, H. Temperature Control Performance Improvement of High-Power Laser Diode with Assistance of Machine Learning. Photonics 2025, 12, 241. https://doi.org/10.3390/photonics12030241
He Y, Jin X, Jin P, Su J, Li F, Lu H. Temperature Control Performance Improvement of High-Power Laser Diode with Assistance of Machine Learning. Photonics. 2025; 12(3):241. https://doi.org/10.3390/photonics12030241
Chicago/Turabian StyleHe, Yaohui, Xiaoli Jin, Pixian Jin, Jing Su, Fang Li, and Huadong Lu. 2025. "Temperature Control Performance Improvement of High-Power Laser Diode with Assistance of Machine Learning" Photonics 12, no. 3: 241. https://doi.org/10.3390/photonics12030241
APA StyleHe, Y., Jin, X., Jin, P., Su, J., Li, F., & Lu, H. (2025). Temperature Control Performance Improvement of High-Power Laser Diode with Assistance of Machine Learning. Photonics, 12(3), 241. https://doi.org/10.3390/photonics12030241





