Channel Characterization and Comparison in Industrial Scenario from Sub-6 GHz to Visible Light Bands for 6G
Abstract
1. Introduction
1.1. Literature Review
1.2. Contribution of This Paper
1.3. Paper Organization
2. Scenario and Ray-Tracing Simulation Setup
2.1. Industrial Scenario
2.2. Ray-Tracing Simulation Setup for Electronic Wave Bands
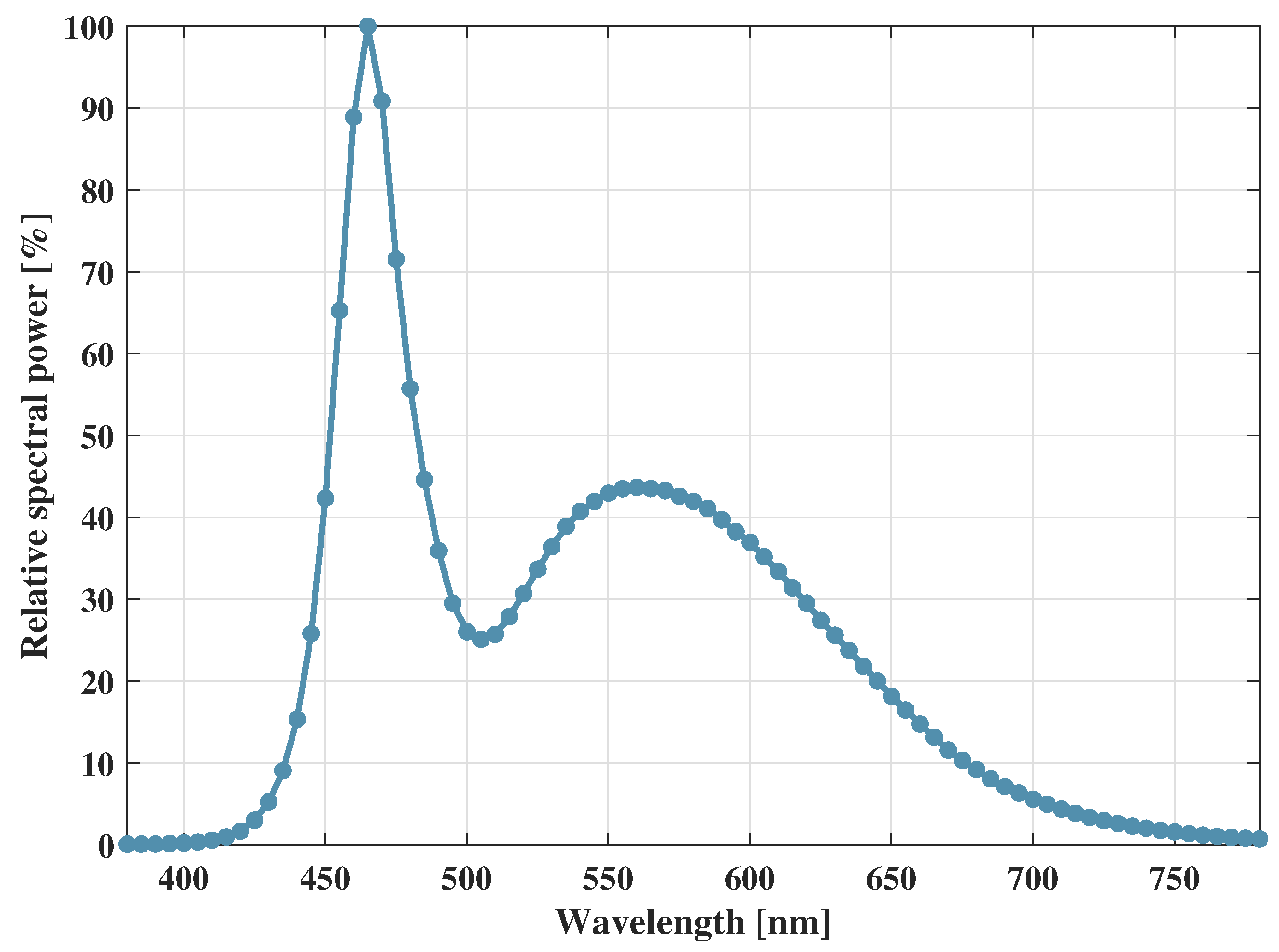
2.3. Ray-Tracing Simulation Setup for VLC Bands
3. Data Processing
4. Results and Analysis
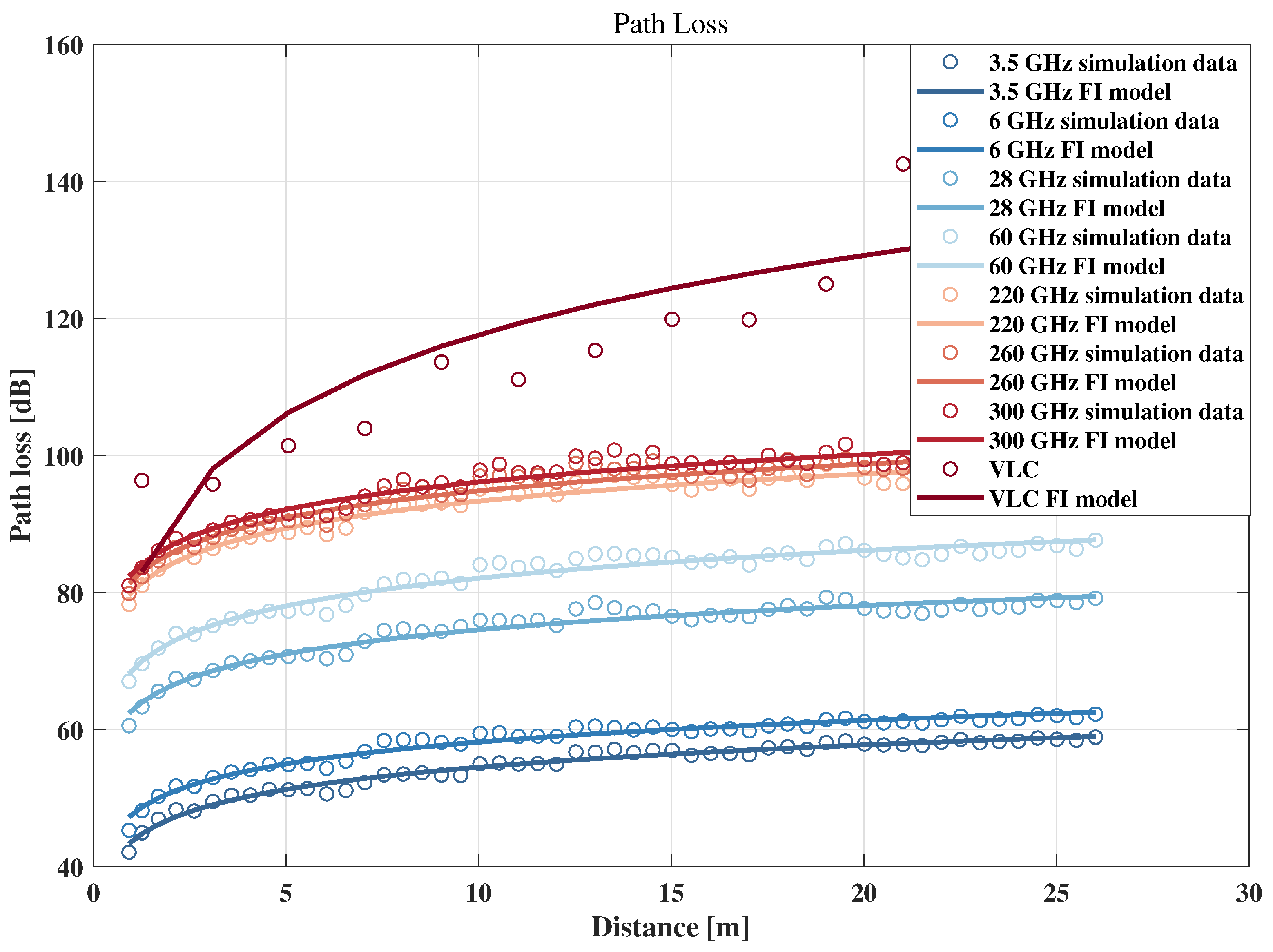
4.1. Path Loss
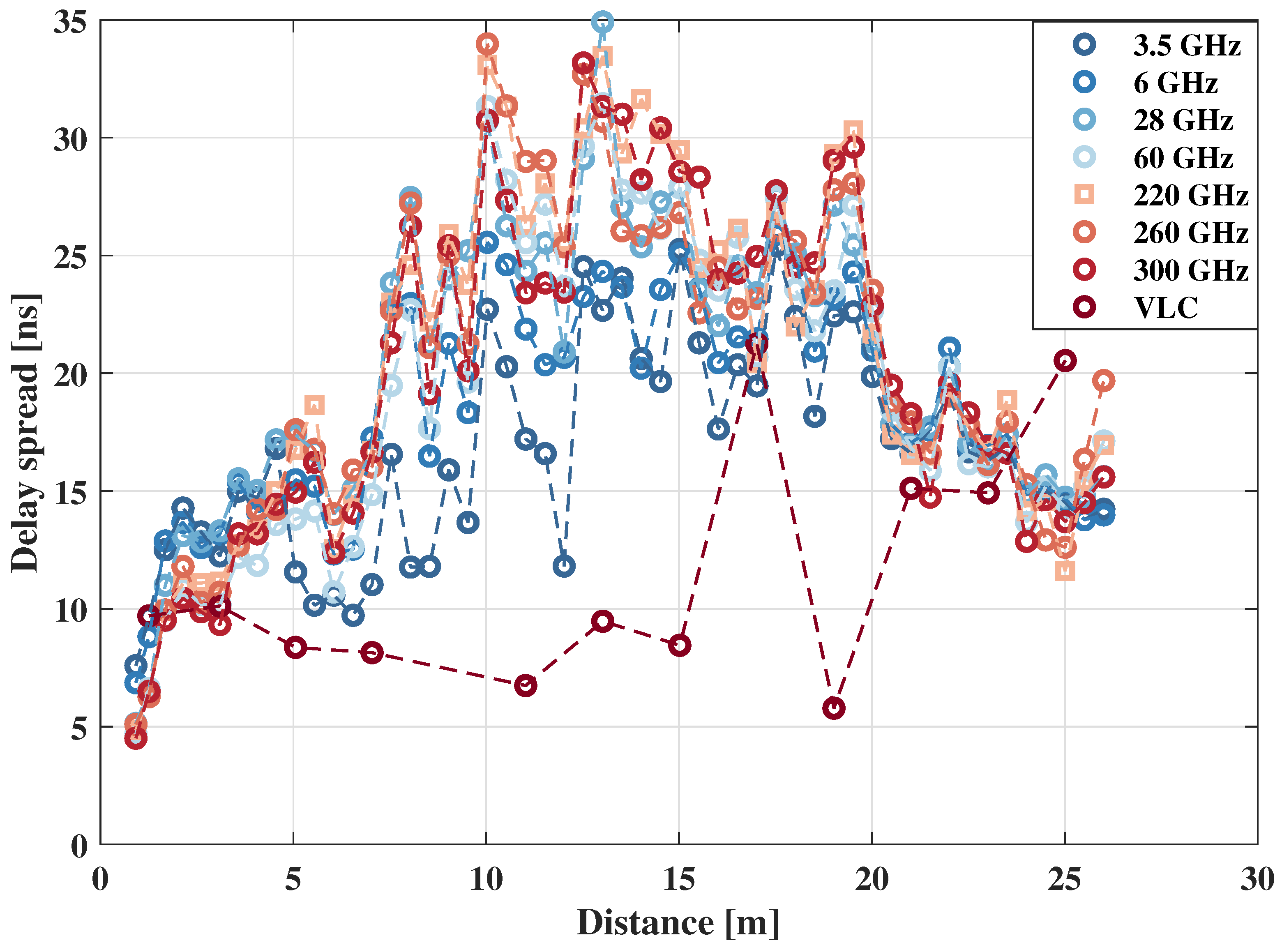
4.2. RMS Delay Spread
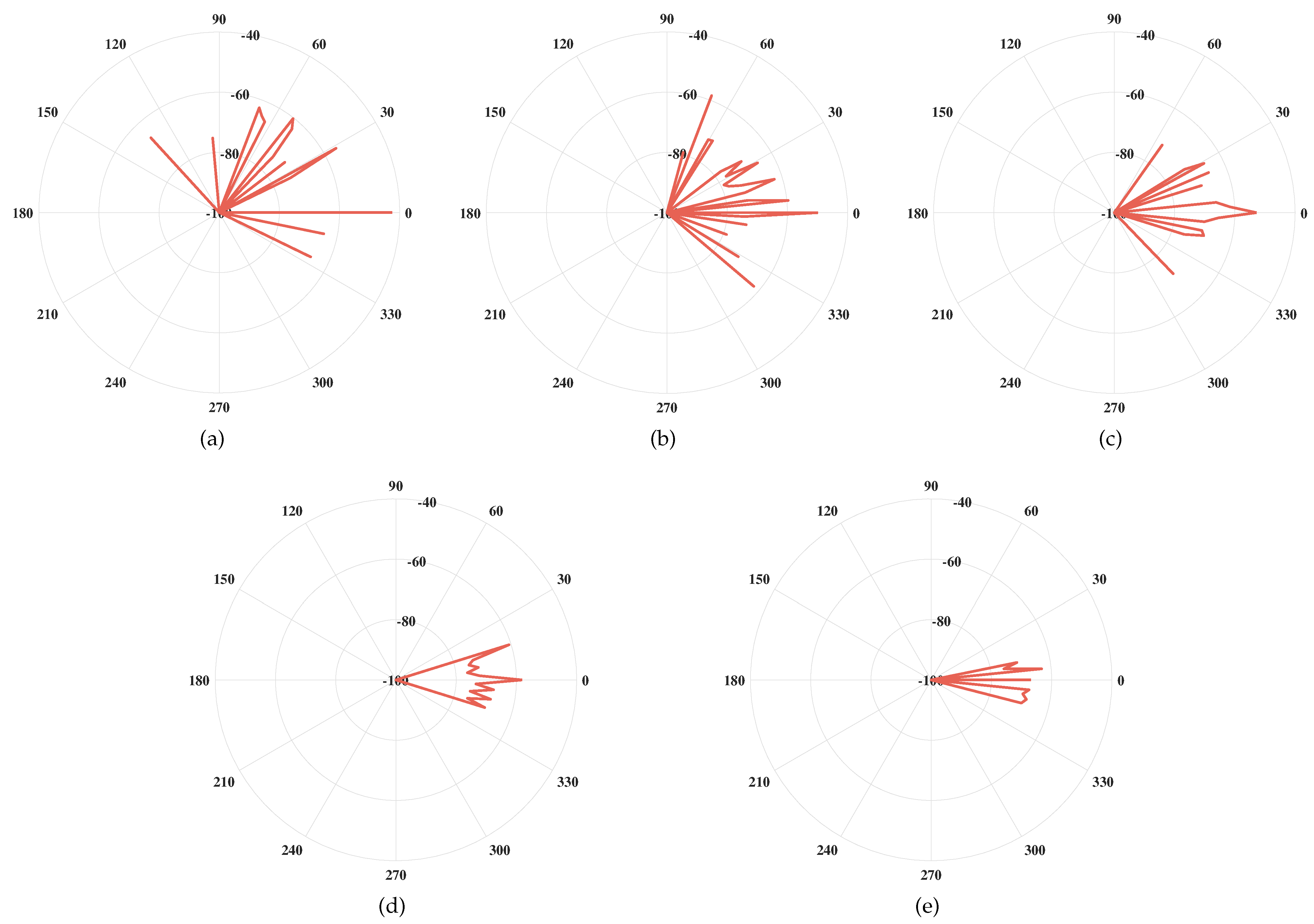
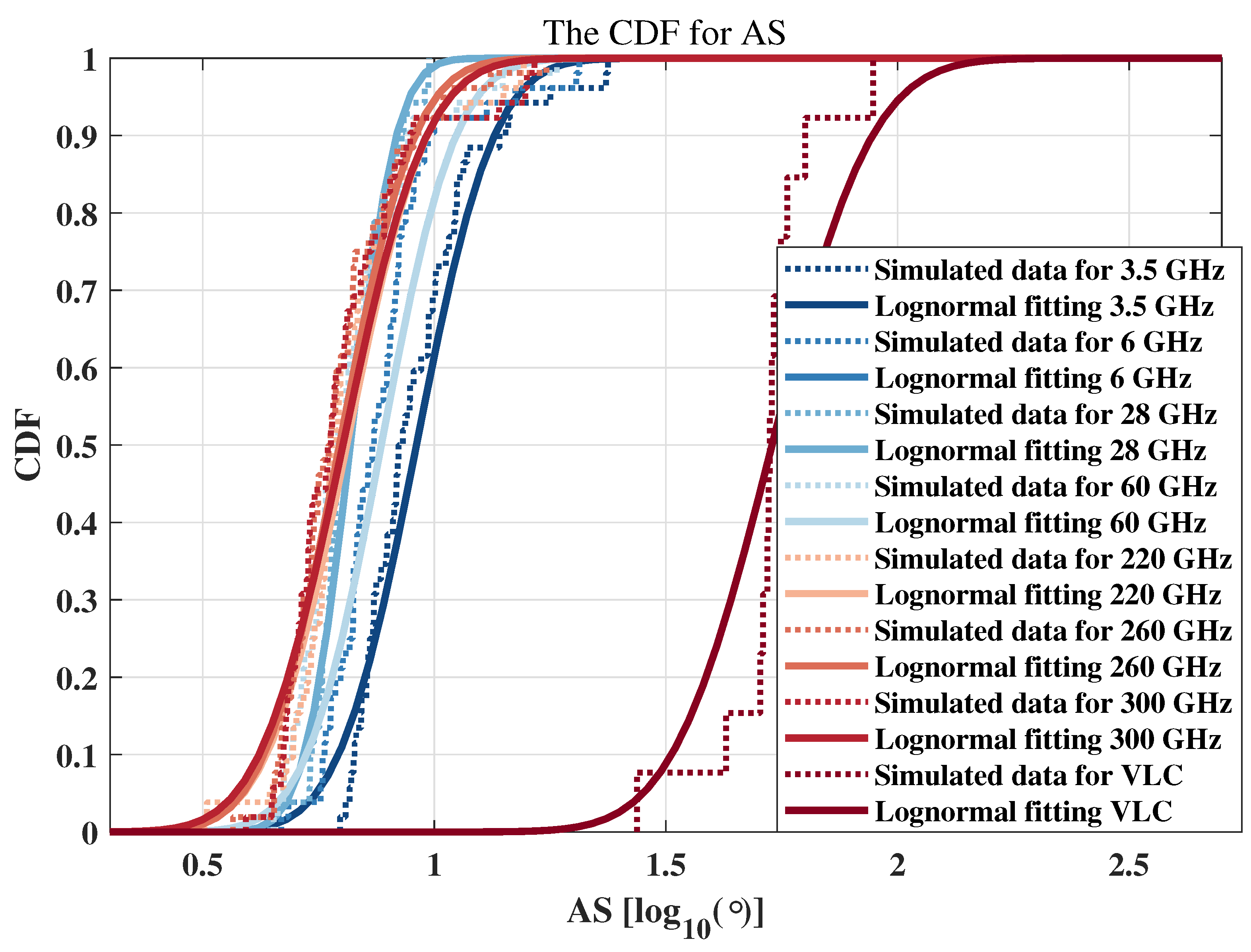
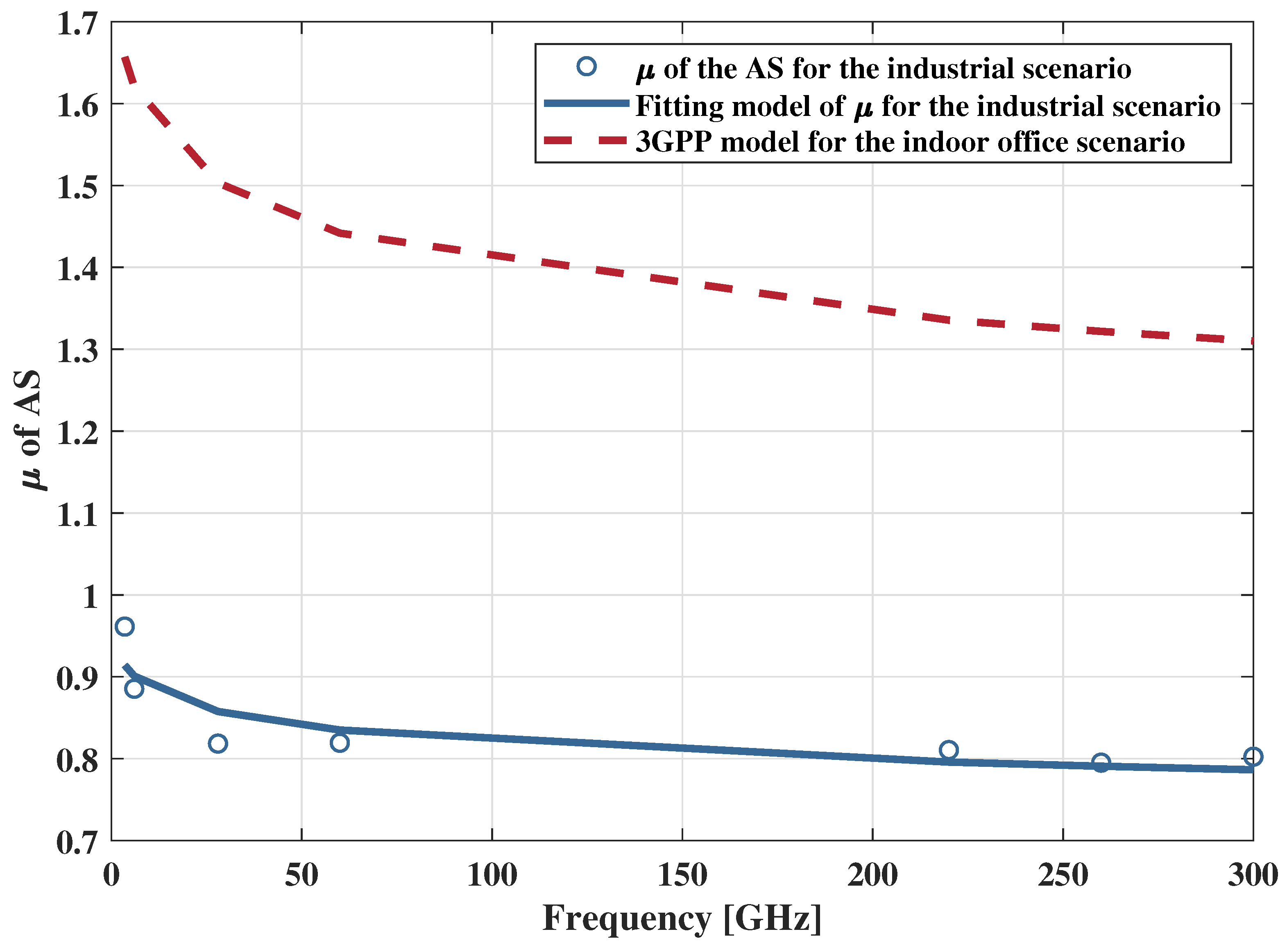
4.3. Angle Spread
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ITU-R. Framework and Overall Objectives of the Future Development of IMT for 2030 and Beyond. 2023. Available online: https://www.itu.int/dms_pub/itu-d/oth/07/31/D07310000090015PDFE.pdf (accessed on 20 January 2025).
- Tang, P.; Yin, Y.; Tong, Y.; Liu, S.; Li, L.; Jiang, T.; Wang, Q.; Chen, M. Channel Characterization and Modeling for VLC-IoE Applications in 6G: A Survey. IEEE Internet Things J. 2024, 11, 34872–34895. [Google Scholar] [CrossRef]
- Tang, P.; Zhang, J.; Xu, H.; Miao, H.; Liu, X. Preliminary perspectives on 3GPP standardization of the propagation channel model for FR3 bands for NR. Sci. China Inf. Sci. 2025, 68, 137301. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Yu, Y.; Xu, R.; Zheng, Q.; Zhang, P. 3-D MIMO: How Much Does It Meet Our Expectations Observed from Channel Measurements? IEEE J. Sel. Areas Commun. 2017, 35, 1887–1903. [Google Scholar] [CrossRef]
- Miao, H.; Zhang, J.; Tang, P.; Tian, L.; Zhao, X.; Guo, B.; Liu, G. Sub-6 GHz to mmWave for 5G-Advanced and Beyond: Channel Measurements, Characteristics and Impact on System Performance. IEEE J. Sel. Areas Commun. 2023, 41, 1945–1960. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, T.; Tang, P.; Song, Q.; Zhao, X.; Tian, L.; Zhang, J.; Liu, B. Measurement-based analysis and modeling of channel characteristics in an industrial scenario at 28 GHz. In Proceedings of the 2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall), Virtual Conference, 27 September–28 October 2021; pp. 1–5. [Google Scholar]
- Aung, S.M.Y.; Pattanaik, K.K. Path loss measurement for wireless communication in industrial environments. In Proceedings of the 2020 International Conference on Computer Science, Engineering and Applications (ICCSEA), Gunupur, India, 13–14 March 2020; pp. 1–5. [Google Scholar]
- Cebecioglu, B.; Mo, Y.K.; Dinh-Van, S.; Fowler, D.S.; Evans, A.; Sivanathan, A.; Kampert, E.; Ahmad, B.; Higgins, M.D. Sub-6 GHz channel modeling and evaluation in indoor industrial environments. IEEE Access 2022, 10, 127742–127753. [Google Scholar] [CrossRef]
- Kim, J.; Kim, C.-S.; Hong, J.-Y.; Lim, J.-S.; Chong, Y.-J. Propagation characteristics of an industrial environment channel at 4.1 GHz. In Proceedings of the 2021 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 20–22 October 2021; pp. 1530–1532. [Google Scholar]
- Solomitckii, D.; Orsino, A.; Andreev, S.; Koucheryavy, Y.; Valkama, M. Characterization of mmWave channel properties at 28 and 60 GHz in factory automation deployments. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar]
- Chizhik, D.; Du, J.; Valenzuela, R.A.; Otterbach, J.; Fuchs, R.; Koppenborg, J. Path loss and directional gain measurements at 28 GHz for factory automation. In Proceedings of the 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Atlanta, GA, USA, 7–12 July 2019; pp. 2143–2144. [Google Scholar]
- Ito, S.; Hayashi, T.; Yamazaki, K.; Nakao, M.; Sakai, S.; Kurosawa, Y.; Matsunaga, A.; Yoshida, K. Measurement and Modeling of Propagation Characteristics for an Indoor Environment in the 28 GHz-band. In Proceedings of the 2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Istanbul, Turkey, 8–11 September 2019; pp. 1–6. [Google Scholar]
- Qin, Y.; Tang, P.; Tian, L.; Lin, J.; Chang, Z.; Liu, P.; Zhang, J.; Jiang, T. Time-Varying Channel Measurement and Analysis at 105 GHz in an Indoor Factory. In Proceedings of the 2024 18th European Conference on Antennas and Propagation (EuCAP), Glasgow, UK, 17–22 March 2024; pp. 1–5. [Google Scholar]
- Ju, S.; Xing, Y.; Kanhere, O.; Rappaport, T.S. Sub-terahertz channel measurements and characterization in a factory building. In Proceedings of the ICC 2022-IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; pp. 2882–2887. [Google Scholar]
- Ju, S.; Shakya, D.; Poddar, H.; Xing, Y.; Kanhere, O.; Rappaport, T.S. 142 GHz sub-terahertz radio propagation measurements and channel characterization in factory buildings. IEEE Trans. Wirel. Commun. 2023, 23, 7127–7143. [Google Scholar] [CrossRef]
- Ju, S.; Rappaport, T.S. Statistical channel model of Wideband sub-THz radio propagation in indoor factories at 142 GHz: Towards 6G industrial wireless networks. IEEE Trans. Wirel. Commun. 2024, 23, 16316–16331. [Google Scholar] [CrossRef]
- Liao, X.; Fan, L.; Wang, Y.; Yu, Z.; Wang, G.; Chen, Y.; Zhang, J. Measurement-Based Channel Characterization in Indoor IIoT Scenarios at 220 GHz. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar]
- Schultze, A.; Schmieder, M.; Wittig, S.; Klessig, H.; Peter, M.; Keusgen, W. Angle-resolved THz channel measurements at 300 GHz in an industrial environment. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: VTC2022-Spring, Helsinki, Finland, 19–22 June 2022; pp. 1–7. [Google Scholar]
- Elesina, V.V.; Reinhardt, C.E.; Kürner, T. Channel Measurements in Workspace with Robotic Manipulators at 300 GHz and Recent Results. In Proceedings of the 2024 18th European Conference on Antennas and Propagation (EuCAP), Glasgow, UK, 17–22 March 2024; pp. 1–5. [Google Scholar]
- Dupleich, D.; Ebert, A.; Völker-Schöneberg, Y.; Löser, L.; Boban, M.; Thomä, R. Spatial/temporal characterization of propagation and blockage from measurements at sub-THz in industrial machines. In Proceedings of the 2023 17th European Conference on Antennas and Propagation (EuCAP), Florence, Italy, 26–31 March 2023; pp. 1–5. [Google Scholar]
- Uysal, M.; Miramirkhani, F.; Narmanlioglu, O.; Baykas, T.; Panayirci, E. IEEE 802.15.7r1 Reference Channel Models for Visible Light Communications. IEEE Commun. Mag. 2017, 55, 212–217. [Google Scholar] [CrossRef]
- Miramirkhani, F.; Baykas, T.; Elamassie, M.; Uysal, M. IEEE 802.11BB Reference Channel Models For Light Communications. IEEE Commun. Stand. Mag. 2023, 7, 84–89. [Google Scholar] [CrossRef]
- Tong, Y.; Tang, P.; Zhang, J.; Liu, S.; Yin, Y.; Liu, B.; Xia, L. Channel Characteristics and Link Adaption for Visible Light Communication in an Industrial Scenario. Sensors 2023, 23, 3442. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lv, Y.; Yin, X.; Duan, J. Measurement-based experimental statistical modeling of propagation channel in industrial IoT scenario. Radio Sci. 2020, 55, 1–14. [Google Scholar] [CrossRef]
- Bhatia, G.; Corre, Y.; Di Renzo, M. Tuning of ray-based channel model for 5G indoor industrial scenarios. In Proceedings of the 2023 IEEE International Mediterranean Conference on Communications and Networking (MeditCom), Dubrovnik, Croatia, 4–7 September 2023; pp. 311–316. [Google Scholar]
- Dupleich, D.; Ebert, A.; Völker-Schöneberg, Y.; Sitdikov, D.; Boban, M.; Samara, L.; Del Galdo, G.; Thomä, R. Characterization of Propagation in an Industrial Scenario from Sub-6 GHz to 300 GHz. In Proceedings of the 2023 IEEE Globecom Workshops (GC Wkshps), Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 1475–1480. [Google Scholar]
- Wang, Y.; Wang, C.; Zheng, X.; Hao, X.; Liao, X. Multi-Frequency Wireless Channel Measurements and Characterization in Indoor Industrial Scenario. IEEE Internet Things J. 2024, 11, 38455–38468. [Google Scholar] [CrossRef]
- 3rd Generation Partnership Project (3GPP). Technical Specification Group Radio Access Network; Study on Channel Model for Frequencies from 0.5 to 100 GHz. 3GPP TR 38.901. 2019. Available online: https://www.3gpp.org (accessed on 20 March 2024).
- Yuan, Z.; Lyu, Y.; Zhang, J.; Tang, P.; Liu, X.; Lin, J.; Petersen, S.S.; Fan, W. Sub-THz Ray Tracing Simulation and Experimental Validation for Indoor Scenarios. In Proceedings of the 2023 IEEE International Mediterranean Conference on Communications and Networking (MeditCom), Dubrovnik, Croatia, 4–7 September 2023; pp. 7–11. [Google Scholar]
- Miramirkhani, F.; Uysal, M. Channel Modeling and Characterization for Visible Light Communications. IEEE Photonics J. 2015, 7, 1–16. [Google Scholar] [CrossRef]
- Eldeeb, H.B.; Uysal, M.; Mana, S.M.; Hellwig, P.; Hilt, J.; Jungnickel, V. Channel modelling for light communications: Validation of ray tracing by measurements. In Proceedings of the 2020 12th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Porto, Portugal, 20–22 July 2020; pp. 1–6. [Google Scholar]
- ASTER Spectral Library—Version 2.0. Available online: http://speclib.jpl.nasa.gov (accessed on 7 September 2023).
- Yin, Y.; Tang, P.; Zhang, J.; Hu, Z.; Xia, L.; Liu, G. Multi-Wavelength Path Loss Model for Indoor VLC with Mobile Human Blockage. Electronics 2023, 12, 5036. [Google Scholar] [CrossRef]
- Tang, P.; Zhang, J.; Miao, H.; Wei, Q.; Zuo, W.; Tian, L.; Jiang, T.; Liu, G. XL-MIMO channel measurement, characterization, and modeling for 6G: A survey. Front. Inf. Technol. Electron. Eng. 2024, 25, 1627–1650. [Google Scholar] [CrossRef]
- Liu, B.; Tang, P.; Zhang, J.; Yin, Y.; Liu, G.; Xia, L. Propagation Characteristics Comparisons between mmWave and Visible Light Bands in the Conference Scenario. Photonics 2024, 9, 228. [Google Scholar] [CrossRef]
- Liu, S.; Tang, P.; Zhang, J.; Yin, Y.; Tong, Y.; Liu, B.; Liu, G.; Xia, L. Statistical channel modeling for indoor VLC communications based on channel measurements. China Commun. 2024, 21, 131–147. [Google Scholar] [CrossRef]




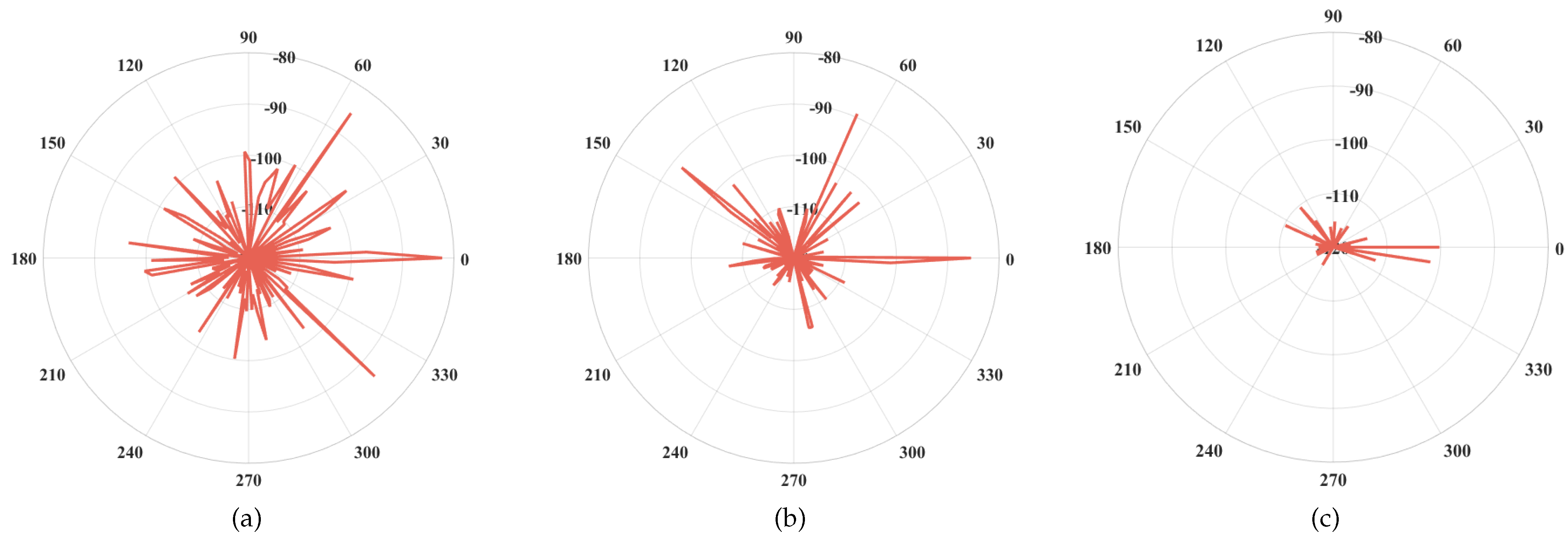
| Frequency Band | Frequency Point | Modeling Approach | Channel Characteristics | Influence Factors | Ref. |
|---|---|---|---|---|---|
| Sub-6 GHz | 2.4 GHz | Channel measurement | Path loss | Transceiver distance | [7] |
| 4.145 GHz | Channel measurement | Path loss, RMS DS | Environmental density | [8] | |
| 4.1 GHz | Channel measurement | Path loss, RMS DS | Transceiver distance, LOS and NLOS cases | [9] | |
| mmWave | 28 GHz | Channel measurement | Path loss, RMS DS, AS | Antenna height | [6] |
| 28 GHz | Ray-tracing-based simulation | Path loss, LOS probability | Environmental density | [10] | |
| 28 GHz | Channel measurement | Path loss | Transceiver distance, LOS and NLOS cases | [11] | |
| 28 GHz | Channel measurement | Path loss, RMS DS, AS | LOS and NLOS cases | [12] | |
| 105 GHz | Channel measurement | PDP, RMS DS, temporal PDP correlation coefficient | Time-varying channel | [13] | |
| 142 GHz | Channel measurement | Path loss, RMS DS, AS | Polarization characteristics | [14] | |
| 142 GHz | Channel measurement | Path loss, RMS DS, AS | Antenna transmission pattern, antenna height | [15] | |
| 142 GHz | Channel measurement | A 3-D omnidirectional multipath channel model based on clusters | LOS and NLOS cases | [16] | |
| THz | 220 GHz | Channel measurement | Path loss, RMS DS, AS, power delay angle profile | Environmental density | [17] |
| 300 GHz | Channel measurement | Path gain, path loss, RMS DS, AS | Scenario size | [18] | |
| 304.2 GHz | Channel measurement | Path gain, PDP, RMS DS | Time-invariant and time-variant settings, antenna height | [19] | |
| 300.7 GHz | Channel measurement | Received power, PDP | Penetration through glass, blockage by frame losses | [20] | |
| VLC | Ray-tracing-based simulation | The channel frequency responses, channel direct current gain, RMS DS | Comparison of visible light and infrared frequency bands | [21] | |
| Ray-tracing-based simulation | The channel frequency responses, channel direct current gain, RMS DS | Various receiving positions | [22] | ||
| Ray-tracing-based simulation | Path loss, RMS DS, AS | Antenna height | [23] | ||
| Multiple bands | 3–4 GHz and 38–40 GHz | Channel measurement | Channel gain coefficient, RMS DS, and Ricean K factor | LOS and NLOS cases | [24] |
| 3.7 GHz and 28 GHz | The Volcano ray-tracing channel simulation and channel measurement | Channel gain, RMS DS, AS | LOS and NLOS cases | [25] | |
| 6.75 GHz, 74.25 GHz, and 305.27 GHz | Channel measurement | Path loss, normalized power, DS | LOS and NLOS cases | [26] | |
| 28 GHz, 38 GHz, 132 GHz, and 220 GHz | Channel measurement | Path loss, RMS DS, AS, K factor | Scenario size | [27] | |
| Electronic Wave Band | Visible Light Band | |
|---|---|---|
| Scenario size | 33.3 m × 7.7 m × 3 m | |
| Average height of metal instruments | 1.27 m | |
| Central frequency | 3.5/6/28/60/220/260/300 GHz | White light (380–780 THz) |
| TX height | 1.60 m | |
| TX pattern | Isotropic | Isotropic-like |
| Analysis rays | ||
| Minimum relative ray intensity | ||
| Transmitter power | 1 W | |
| Radiation pattern | Specular reflection | Specular reflection 50% Lambert radiation 50% |
| RX height | 1.27 m | |
| RX pattern | Isotropic | Rectangular (10 cm) |
| Frequency/GHz | ||||
|---|---|---|---|---|
| Sub-6 GHz | 3.5 | 43.73 | 1.078 | 0.603237 |
| 6 | 47.63 | 1.054 | 0.696649 | |
| mmWave | 28 | 62.82 | 1.174 | 0.980498 |
| 60 | 68.66 | 1.343 | 1.04594 | |
| THz | 220 | 80.13 | 1.321 | 1.11161 |
| 260 | 81.79 | 1.304 | 1.22165 | |
| 300 | 82.83 | 1.33 | 1.19503 | |
| VLC | 79.25 | 3.84 | 10.1258 | |
| 3GPP | 0.5–100 GHz | - | 2.15 | 4.00 |
| Frequency/GHz | |||
|---|---|---|---|
| Sub-6 GHz | 3.5 | −7.79 | 0.12 |
| 6 | −7.75 | 0.12 | |
| mmWave | 28 | −7.72 | 0.16 |
| 60 | −7.75 | 0.18 | |
| THz | 220 | −7.72 | 0.18 |
| 260 | −7.72 | 0.17 | |
| 300 | −7.73 | 0.19 | |
| VLC | −7.93 | 0.23 | |
| Frequency/GHz | |||
|---|---|---|---|
| Sub-6 GHz | 3.5 | 0.96 | 0.13 |
| 6 | 0.89 | 0.12 | |
| mmWave | 28 | 0.82 | 0.08 |
| 60 | 0.82 | 0.12 | |
| THz | 220 | 0.81 | 0.14 |
| 260 | 0.79 | 0.13 | |
| 300 | 0.80 | 0.14 | |
| VLC | 1.73 | 0.17 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Y.; Tang, P.; Zhang, J.; Hu, Z.; Jiang, T.; Xia, L.; Liu, G. Channel Characterization and Comparison in Industrial Scenario from Sub-6 GHz to Visible Light Bands for 6G. Photonics 2025, 12, 257. https://doi.org/10.3390/photonics12030257
Yin Y, Tang P, Zhang J, Hu Z, Jiang T, Xia L, Liu G. Channel Characterization and Comparison in Industrial Scenario from Sub-6 GHz to Visible Light Bands for 6G. Photonics. 2025; 12(3):257. https://doi.org/10.3390/photonics12030257
Chicago/Turabian StyleYin, Yue, Pan Tang, Jianhua Zhang, Zheng Hu, Tao Jiang, Liang Xia, and Guangyi Liu. 2025. "Channel Characterization and Comparison in Industrial Scenario from Sub-6 GHz to Visible Light Bands for 6G" Photonics 12, no. 3: 257. https://doi.org/10.3390/photonics12030257
APA StyleYin, Y., Tang, P., Zhang, J., Hu, Z., Jiang, T., Xia, L., & Liu, G. (2025). Channel Characterization and Comparison in Industrial Scenario from Sub-6 GHz to Visible Light Bands for 6G. Photonics, 12(3), 257. https://doi.org/10.3390/photonics12030257









