Recent Advances in Integrated Vibration Sensing and Communication in Digital Subcarrier Multiplexing Systems
Abstract
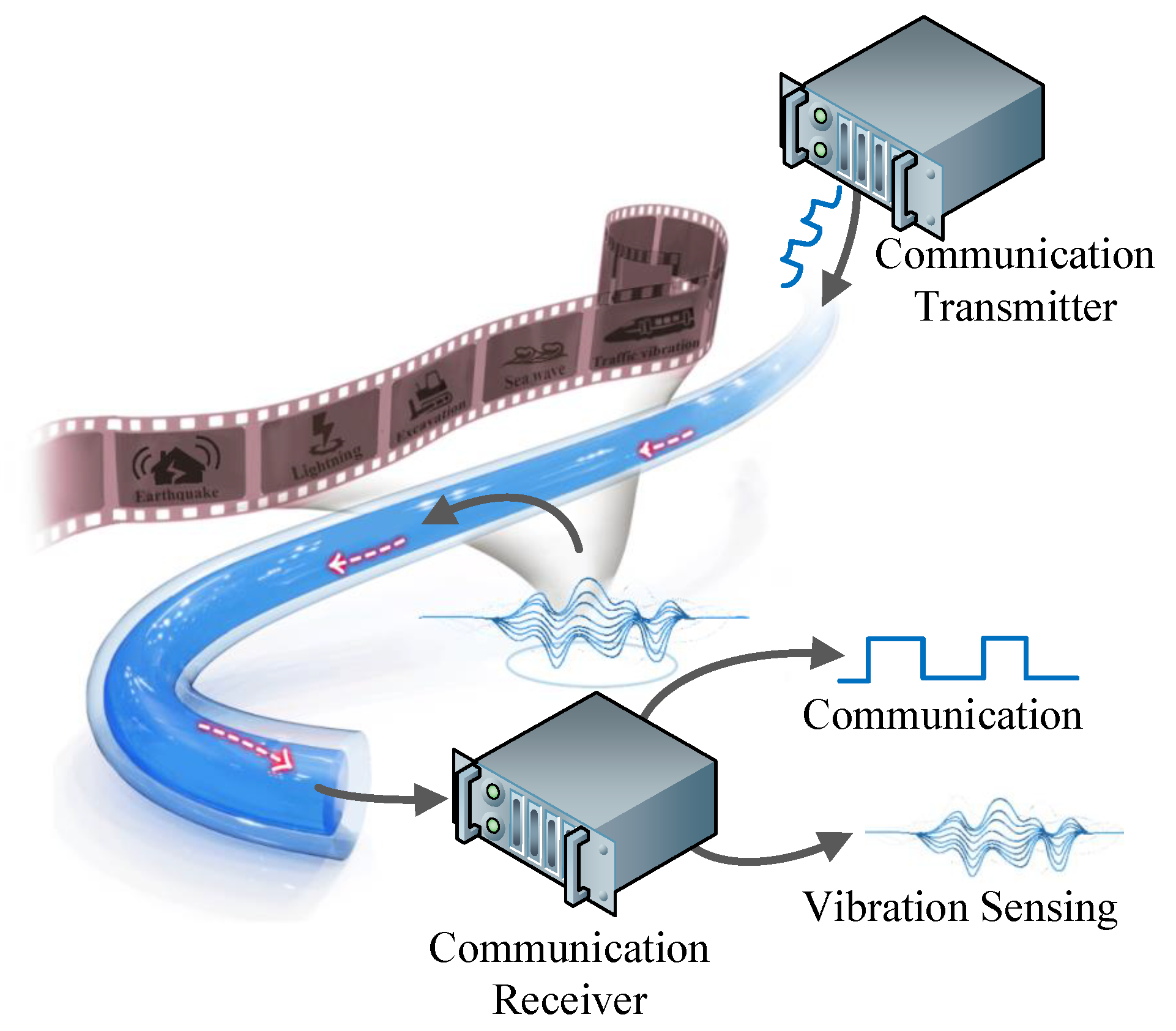
1. Introduction
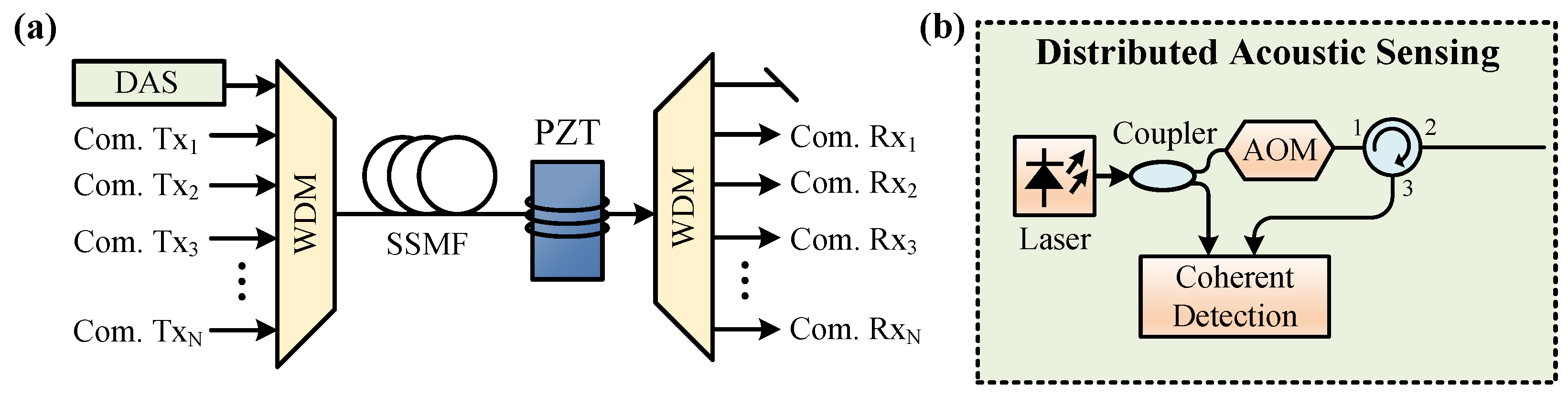
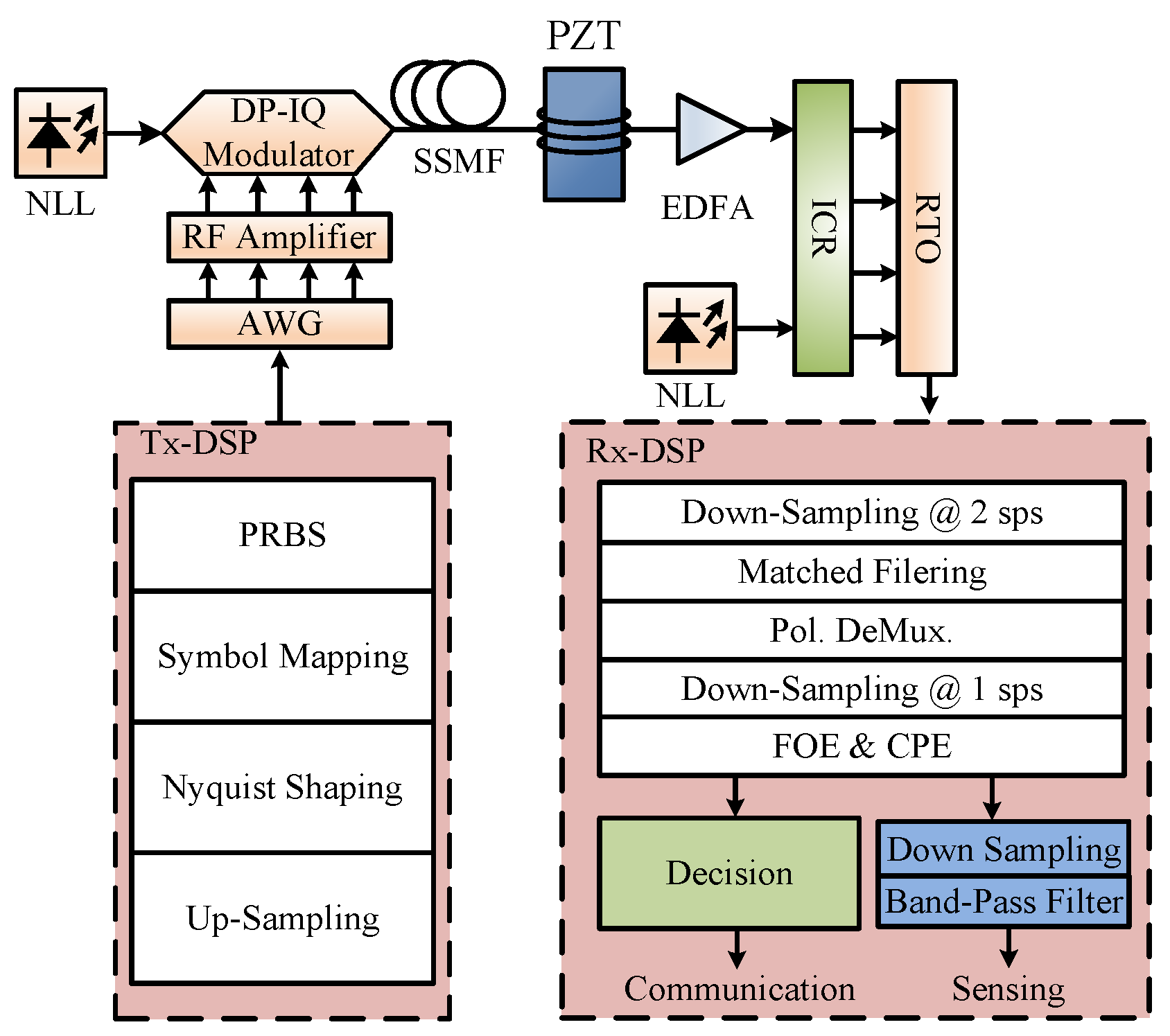
2. Integrated Sensing and Communication in Single-Carrier Systems
2.1. Back-Scattering-Based Vibration Sensing in Single-Carrier Systems
2.2. Forward-SOP-Based Vibration Sensing in Single-Carrier Systems
2.3. Forward-Phase-Based Vibration Sensing in Single-Carrier Systems
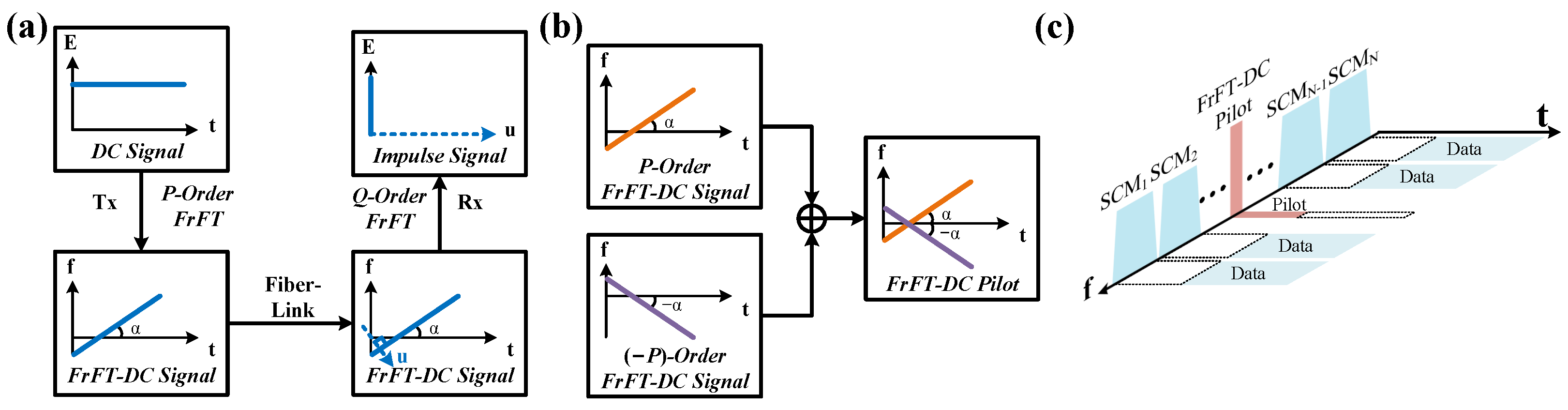
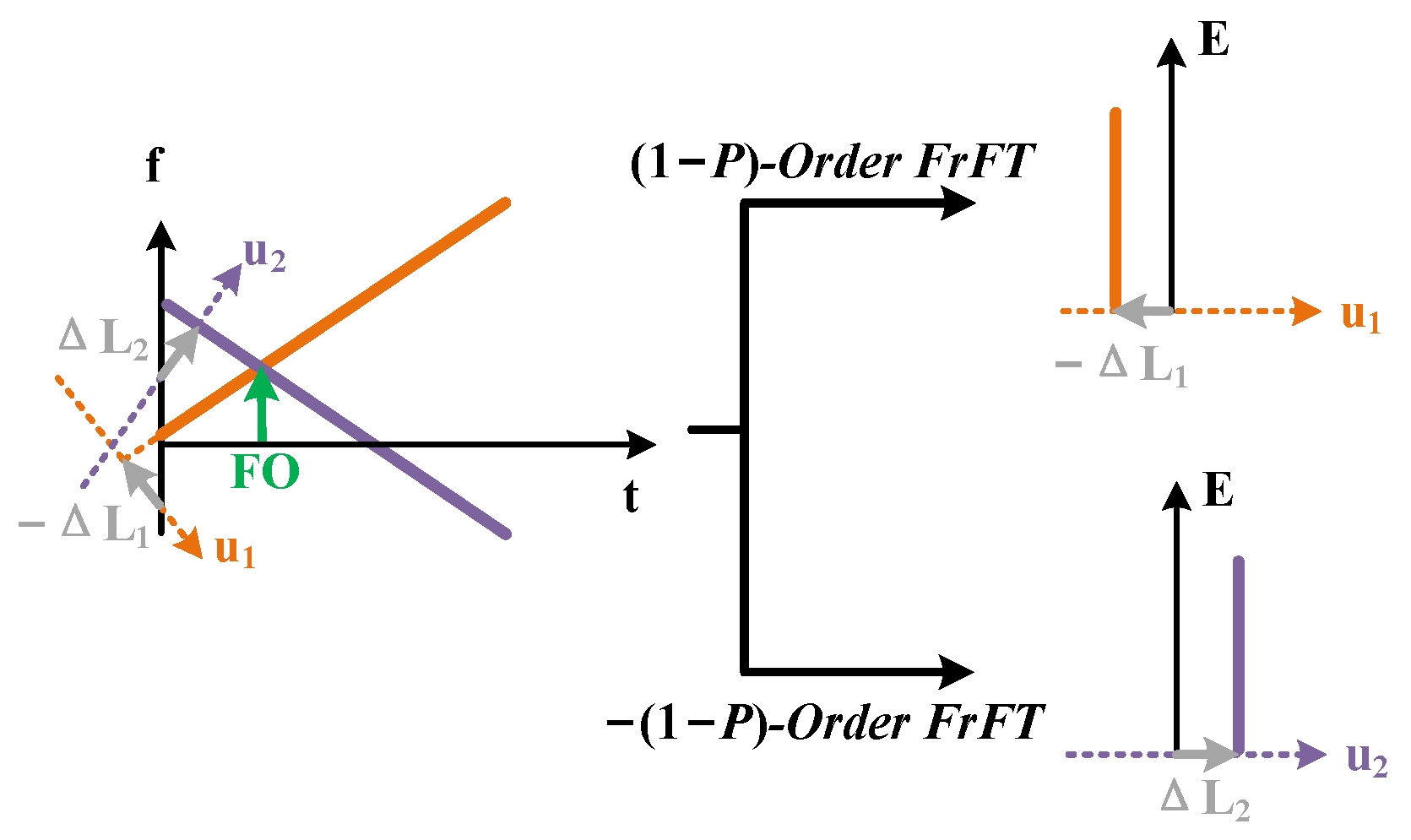
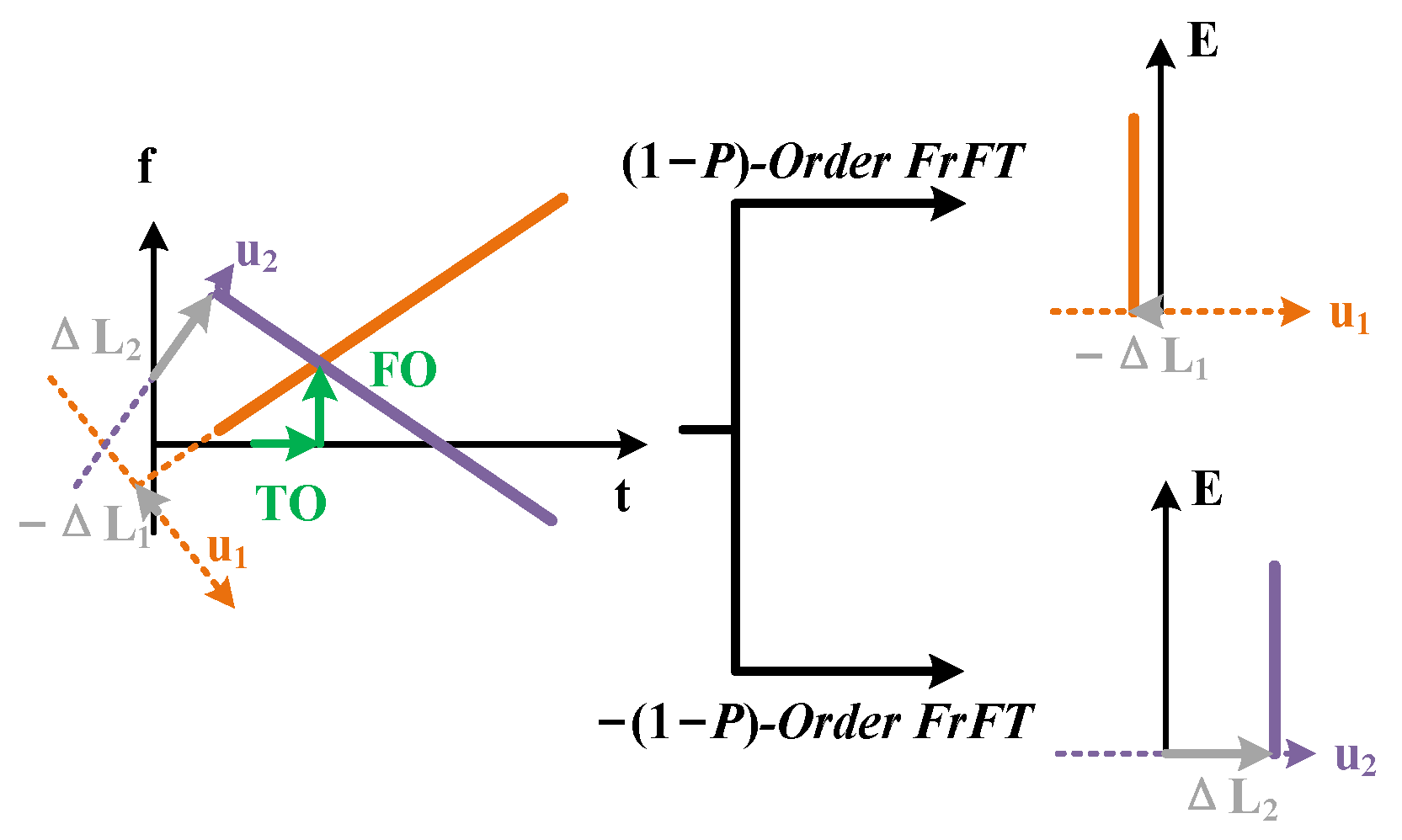
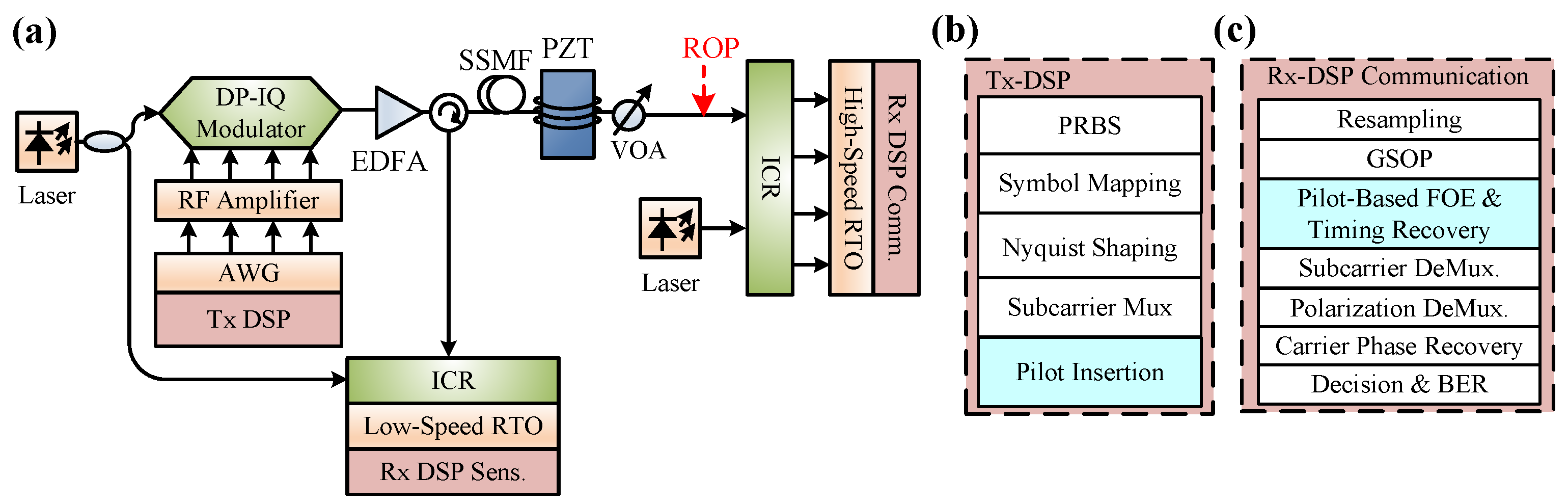
3. Integrated Sensing and Communication Based on FrFT-DC Pilot
3.1. Frequency Offset Estimation Based on FrFT-DC Pilot
3.2. Clock Recovery Based on FrFT-DC Pilot
3.3. Vibration Sensing Based on FrFT-DC Pilot
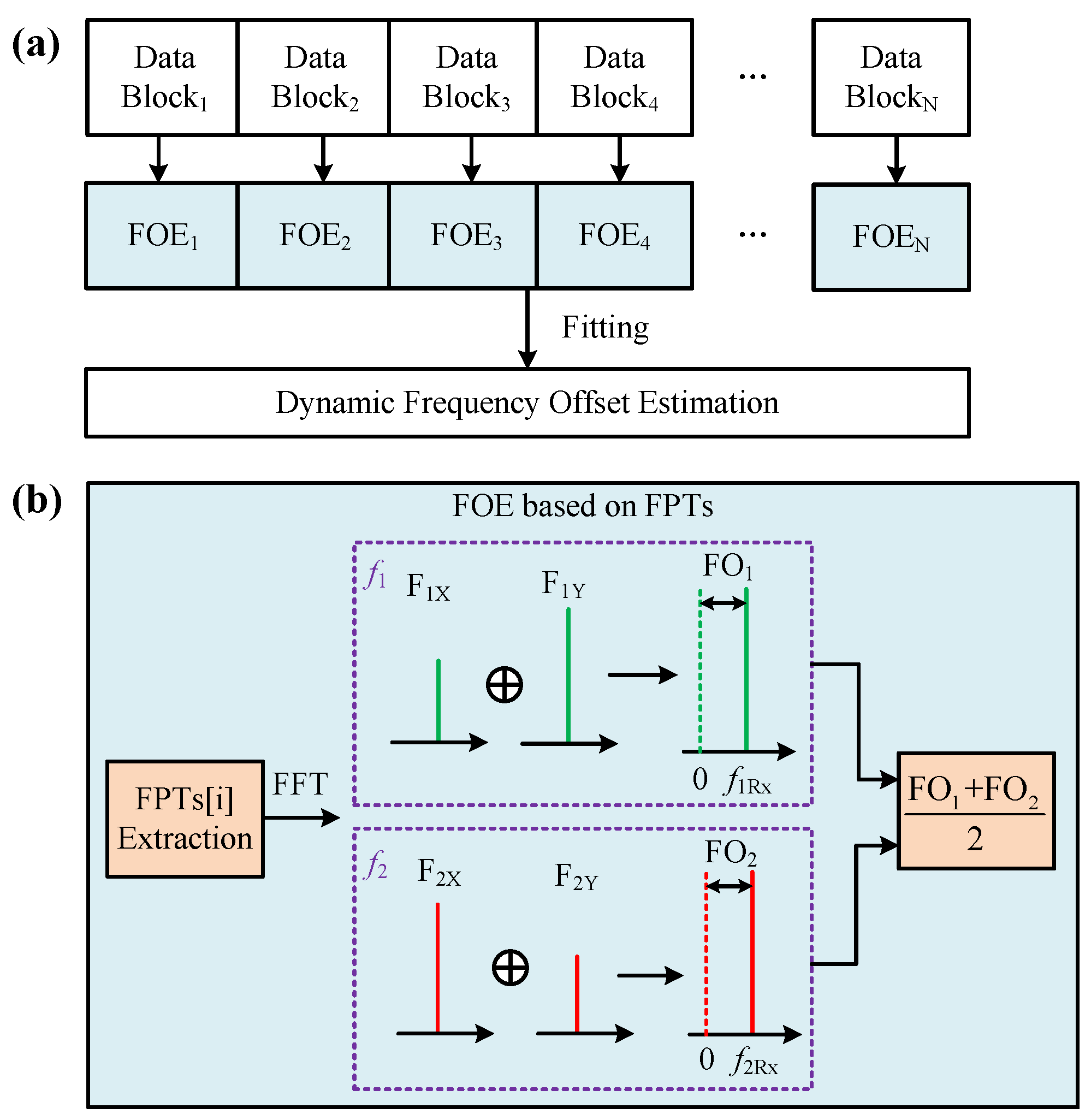
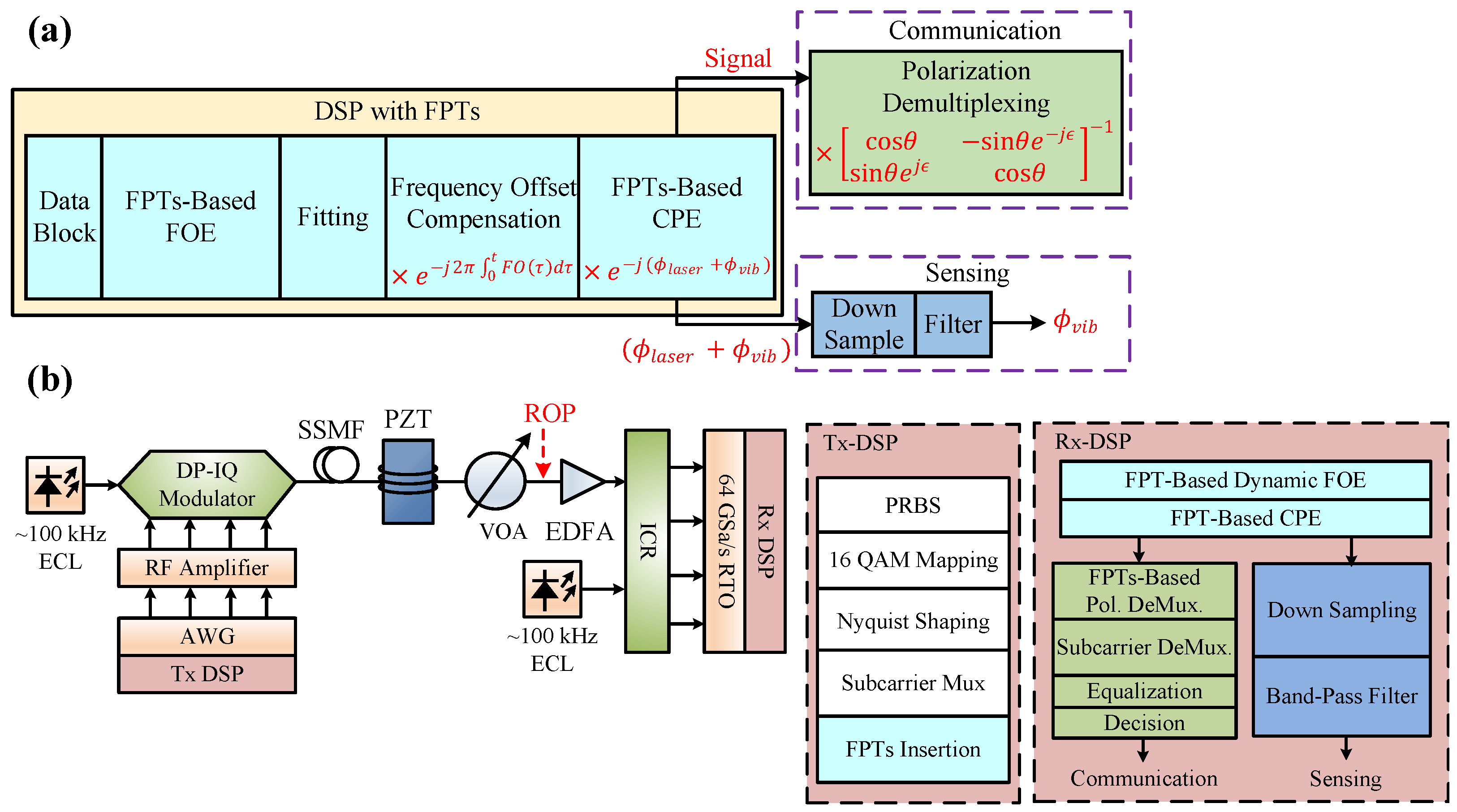
4. Integrated Sensing and Communication Based on FPTs
4.1. Frequency Offset Estimation Based on FPTs
4.2. Carrier Phase Estimation Based on FPTs
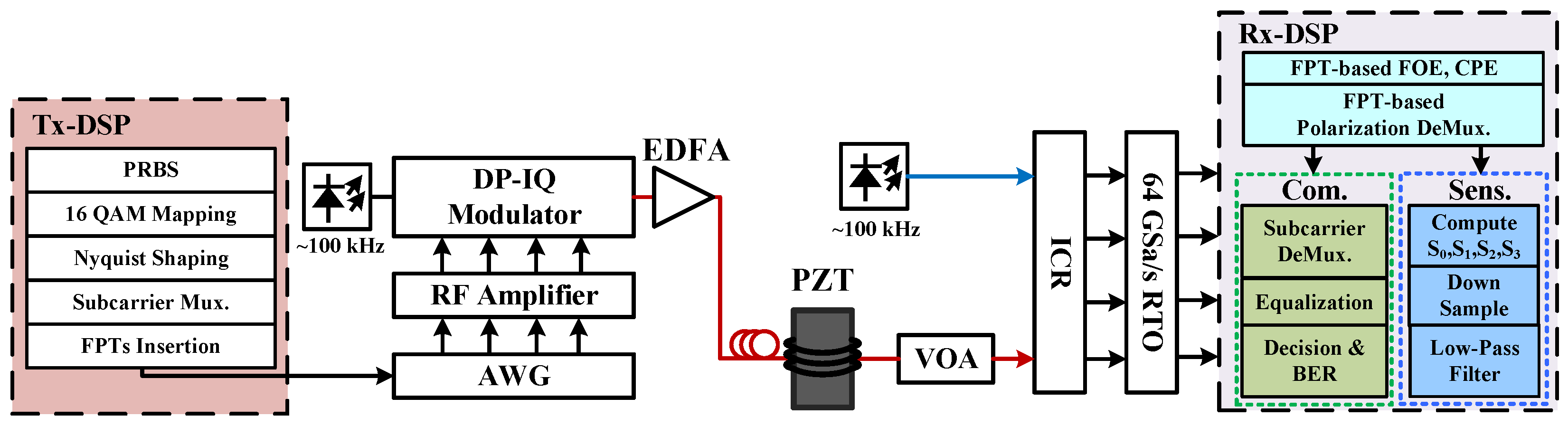
4.3. State of Polarization Tracking Based on FPTs
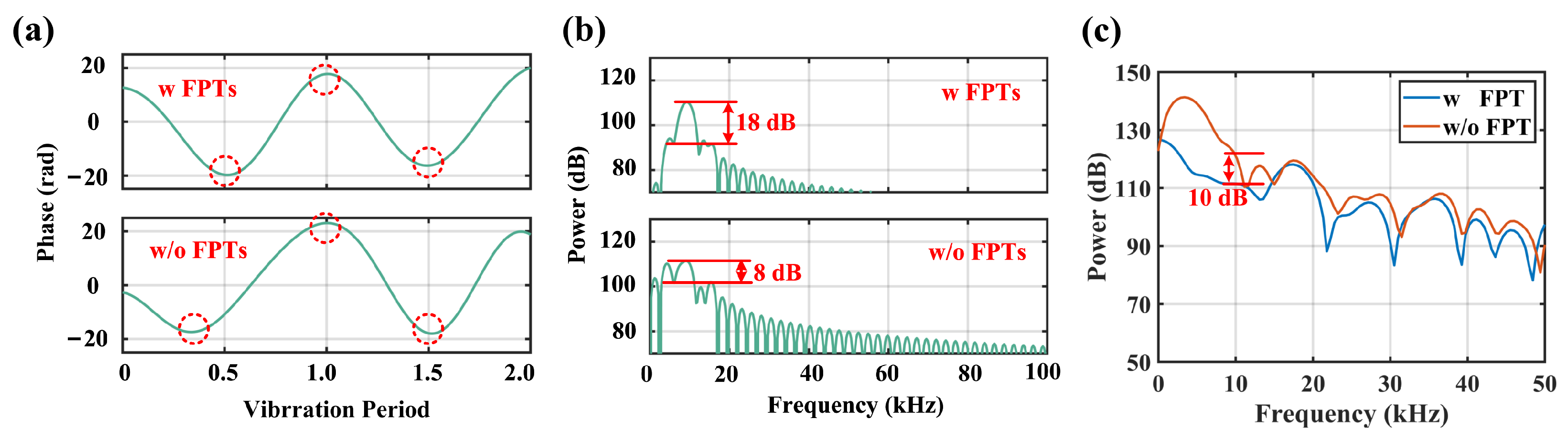
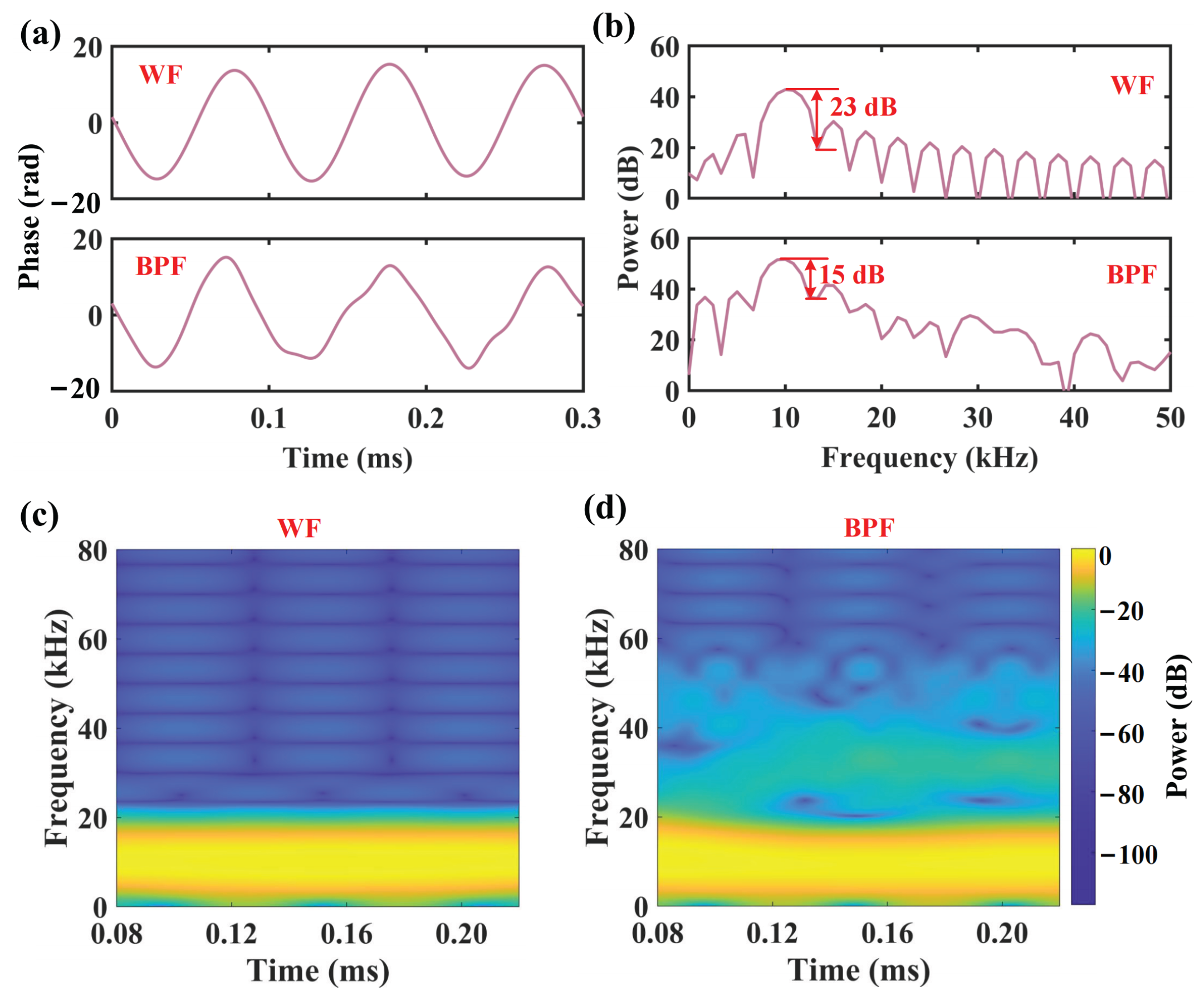
4.4. Phase-Based Vibration Sensing Using FPTs
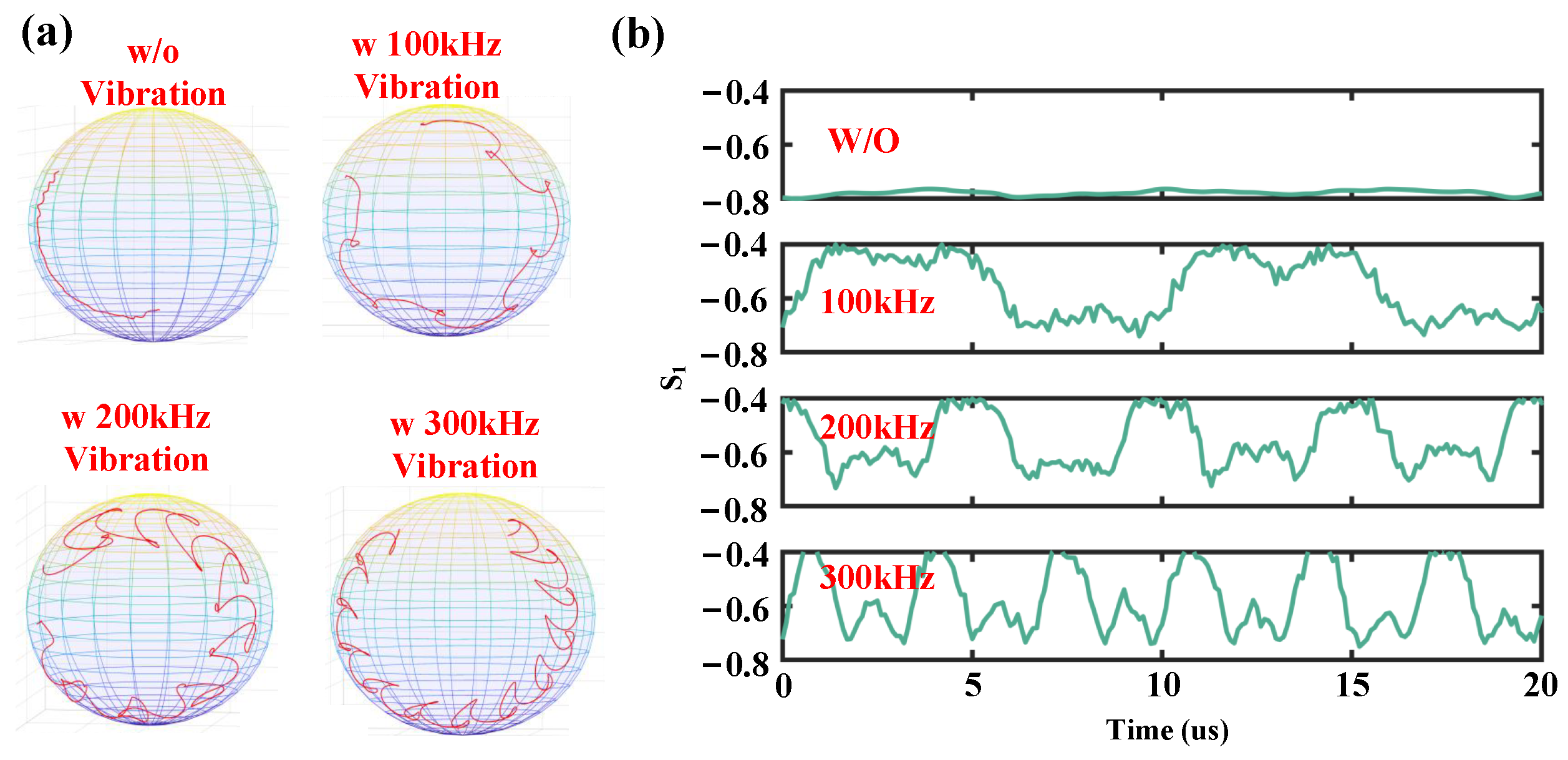
4.5. SOP-Based Vibration Sensing Using FPTs
5. Conclusions and Future Trends
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, X. Enabling optical network technologies for 5G and beyond. J. Light. Technol. 2022, 40, 358–367. [Google Scholar] [CrossRef]
- Winzer, P.J.; Neilson, D.T.; Chraplyvy, A.R. Fiber-optic transmission and networking: The previous 20 and the next 20 years. Opt. Express 2018, 26, 24190–24239. [Google Scholar] [PubMed]
- Ip, E.; Ravet, F.; Martins, H.; Huang, M.F.; Okamoto, T.; Han, S.; Narisetty, C.; Fang, J.; Huang, Y.K.; Salemi, M.; et al. Using Global Existing Fiber Networks for Environmental Sensing. Proc. IEEE 2022, 110, 1853–1888. [Google Scholar]
- Ip, E.; Huang, Y.K.; Wellbrock, G.; Xia, T.; Huang, M.F.; Wang, T.; Aono, Y. Vibration detection and localization using modified digital coherent telecom transponders. J. Light. Technol. 2022, 40, 1472–1482. [Google Scholar]
- Wang, Z.; Yang, H.; Li, Y.; Yao, Q.; Yu, T.; Zhang, C.; Liu, W.; Lin, W.; Zhang, J.; Liu, Y.; et al. Co-Route Fiber Recognition and Status Diagnosis Based on Integrated Sensing and Communication in 6G Transport Networks. IEEE Internet Things J. 2024, 11, 29348–29359. [Google Scholar]
- Zhang, M.; Wei, W.; Li, W.; He, H.; Chen, Y.; Wu, H.; Zhao, C.; Zhao, Z.; Tang, M. Endogenous BOTDA in the self-homodyne coherent detection transmission system for communication-integrated datacenter temperature monitoring. Opt. Lett. 2023, 48, 4749–4752. [Google Scholar] [CrossRef]
- Di Luch, I.; Ferrario, M.; Boffi, P.; Rizzelli, G.; Wang, H.; Gaudino, R. Demonstration of structural vibration sensing in a deployed PON infrastructure. In Proceedings of the 45th European Conference on Optical Communication (ECOC 2019), Dublin, Ireland, 22–26 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–3. [Google Scholar]
- He, H.; Jiang, L.; Pan, Y.; Yi, A.; Zou, X.; Pan, W.; Willner, A.E.; Fan, X.; He, Z.; Yan, L. Integrated sensing and communication in an optical fibre. Light. Sci. Appl. 2023, 12, 25. [Google Scholar]
- Wang, J.; Lu, L.; Wang, L.; Yan, Y.; Lau, A.P.T.; Lu, C. High-efficiency ISAC to enable sub-meter level vibration sensing for coherent fiber networks. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 24–28 March 2024; Optica Publishing Group: Washington, DC, USA, 2024; p. Tu2J-3. [Google Scholar]
- Mazur, M.; Fontaine, N.K.; Kelleher, M.; Kamalov, V.; Ryf, R.; Dallachiesa, L.; Chen, H.; Neilson, D.T.; Quinlan, F. Continuous Distributed Phase and Polarization Monitoring of Trans-Atlantic Submarine Fiber Optic Cable. In Proceedings of the 2024 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 24–28 March 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–3. [Google Scholar]
- Pellegrini, S.; Minelli, L.; Andrenacci, L.; Rizzelli, G.; Pilori, D.; Bosco, G.; Della Chiesa, L.; Crognale, C.; Piciaccia, S.; Gaudino, R. Overview on the state of polarization sensing: Application scenarios and anomaly detection algorithms. J. Opt. Commun. Netw. 2025, 17, A196–A209. [Google Scholar] [CrossRef]
- Boitier, F.; Lemaire, V.; Pesic, J.; Chavarría, L.; Layec, P.; Bigo, S.; Dutisseuil, E. Proactive fiber damage detection in real-time coherent receiver. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–3. [Google Scholar]
- Mecozzi, A.; Cantono, M.; Castellanos, J.C.; Kamalov, V.; Muller, R.; Zhan, Z. Polarization sensing using submarine optical cables. Optica 2021, 8, 788–795. [Google Scholar]
- Zhan, Z.; Cantono, M.; Kamalov, V.; Mecozzi, A.; Müller, R.; Yin, S.; Castellanos, J.C. Optical polarization–based seismic and water wave sensing on transoceanic cables. Science 2021, 371, 931–936. [Google Scholar] [CrossRef]
- Mazur, M.; Wallberg, D.; Dallachiesa, L.; Börjeson, E.; Ryf, R.; Bergroth, M.; Josefsson, B.; Fontaine, N.K.; Chen, H.; Neilson, D.T.; et al. Field trial of FPGA-based real-time sensing transceiver over 524 km of live aerial fiber. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 5–9 March 2023; Optica Publishing Group: Washington, DC, USA, 2023; p. Tu3G-4. [Google Scholar]
- Tang, J.; Li, X.; Cheng, C.; Hao, Y.; Yang, B.; Li, J.; He, Z.; Yang, Y.; Hu, W. Forward-transmission based distributed fiber sensing compatible with C+ L unidirectional communication systems. In Proceedings of the 2024 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 24–28 March 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–3. [Google Scholar]
- Carver, C.J.; Zhou, X. Polarization sensing of network health and seismic activity over a live terrestrial fiber-optic cable. Commun. Eng. 2024, 3, 91. [Google Scholar]
- Yan, Y.; Lu, L.; Wu, X.; Wang, J.; He, Y.; Chen, D.; Lu, C.; Lau, A.P.T. Simultaneous communications and vibration sensing over a single 100-km deployed fiber link by fiber interferometry. In Proceedings of the 2023 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 5–9 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–3. [Google Scholar]
- Zuo, W.; Zhou, H.; Qiao, Y.; Zhao, Y.; Ye, B. Investigation of Co-Cable Identification Based on Ultrasonic Sensing in Coherent Systems. IEEE Photonics Technol. Lett. 2023, 35, 1155–1158. [Google Scholar]
- Zhou, H.; Zuo, W.; Qiao, Y.; Zhao, Y.; Ye, B.; Bai, C.; Xu, H. Ultrasonic phase extraction method for co-cable identification in coherent optical transmission systems. Chin. Opt. Lett. 2024, 22, 100601. [Google Scholar]
- Hu, K.; Tong, F.; Lian, W.; Li, W. Model and experimental verification of SOP transient in OPGW based on direct strike lightning. Opt. Express 2023, 31, 39102–39120. [Google Scholar] [CrossRef]
- Welch, D.; Napoli, A.; Bäck, J.; Buggaveeti, S.; Castro, C.; Chase, A.; Chen, X.; Dominic, V.; Duthel, T.; Eriksson, T.A.; et al. Digital subcarrier multiplexing: Enabling software-configurable optical networks. J. Light. Technol. 2023, 41, 1175–1191. [Google Scholar] [CrossRef]
- Neves, M.S.; Lorences-Riesgo, A.; Martins, C.S.; Mumtaz, S.; Charlet, G.; Monteiro, P.P.; Guiomar, F.P. Carrier-Phase Recovery for Coherent Optical Systems: Algorithms, Challenges and Solutions. J. Light. Technol. 2024, 42, 1095–1108. [Google Scholar]
- Golani, O.; Pilori, D.; Guiomar, F.P.P.; Bosco, G.; Carena, A.; Shtaif, M. Correlated nonlinear phase-noise in multi-subcarrier systems: Modeling and mitigation. J. Light. Technol. 2019, 38, 1148–1156. [Google Scholar]
- Zhou, H.; Li, X.; Tang, M.; Wu, Q.; Chen, X.; Luo, M.; Fu, S.; Liu, D. Joint timing/frequency offset estimation and correction based on FrFT encoded training symbols for PDM CO-OFDM systems. Opt. Express 2016, 24, 28256–28269. [Google Scholar]
- Hu, Z.; Chen, Y.; Chen, J.; Li, W.; Zhang, M.; Zhao, C.; Wang, L.; Zhao, L.; Tang, M. In-Advance Joint Timing/Frequency Synchronization Using FrFT Pilot for Digital Subcarrier Multiplexing Systems. J. Light. Technol. 2024, 42, 208–218. [Google Scholar]
- Fan, L.; Yang, Y.; Cheng, C.; Gong, S.; Xiang, Q.; Zhang, Q.; Yao, Y. Hardware-Efficient, Ultra-Fast and Joint Polarization and Carrier Phase Tracking Scheme Based on Frequency Domain Pilot Tones for DSCM Systems. J. Light. Technol. 2023, 41, 1454–1463. [Google Scholar]
- Fan, L.; Yang, Y.; Gong, S.; Zhang, Q.; Yao, Y. Robust PDL Compensation and Monitoring Scheme Using Frequency Domain Pilot Tones for Coherent Digital Subcarrier Multiplexing System. J. Light. Technol. 2024, 42, 136–148. [Google Scholar]
- Fan, L.; Yang, Y.; Zhang, Q.; Gong, S.; Jia, Y.; Yao, Y. Robust, in-service, and joint monitoring of a dual-polarization transceiver IQ skew for a coherent DSCM system without channel impairment compensation. Opt. Lett. 2023, 49, 129–132. [Google Scholar]
- Hu, Z.; Zhao, C.; Chen, Y.; Zhang, M.; Chen, J.; Li, W.; Tang, M. Simultaneous distributed acoustic sensing and communication in digital subcarrier multiplexing systems. In Proceedings of the 49th European Conference on Optical Communications (ECOC 2023), Glasgow, UK, 1–5 October 2023; IET: London, UK, 2023; Volume 2023, pp. 720–723. [Google Scholar]
- Hu, Z.; Chen, Y.; Jiang, H.; Zhang, M.; Chen, J.; Li, W.; Zhao, L.; Zhao, C.; Tang, M. Enabling cost-effective high-performance vibration sensing in digital subcarrier multiplexing systems. Opt. Express 2023, 31, 32114–32125. [Google Scholar] [PubMed]
- Hu, Z.; Zhang, M.; Li, Y.; Chen, J.; Li, W.; Xiong, Y.; Zhao, L.; Zhao, C.; Tang, M. Enabling endogenous distributed acoustic sensing in a digital subcarrier coherent transmission system. Opt. Lett. 2024, 49, 3166–3169. [Google Scholar]
- Hu, Z.; Zhao, C.; Chen, Y.; Zhang, M.; Chen, J.; Li, W.; Zhao, L.; Tang, M. Enabling Endogenous DAS in P2MP Digital Subcarrier Coherent Transmission System with Enhanced Frequency Response. In Proceedings of the 2024 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 24–28 March 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–3. [Google Scholar]
- Yang, B.; Tang, J.; Cheng, C.; Fan, L.; Yang, P.; Wang, S.; Zhao, T.; Liang, J.; Gao, S.; Wei, J.; et al. Integrated Communication and Enhanced Forward Phase-based Sensing Based on Frequency-Domain Pilot Tones in DSCM Systems Using 100 kHz ECLs. J. Light. Technol. 2025, 43, 2664–2671. [Google Scholar]
- Yang, B.; Tang, J.; Cheng, C.; Fan, L.; Gao, S.; Yao, Y.; Liang, J.; Wei, J.; Yang, Y. High-fidelity and adaptive forward-phase-based vibration sensing using a Wiener filter in DSCM systems under commercial ECLs. Opt. Lett. 2025, 50, 554–557. [Google Scholar]
- Yang, B.; Tang, J.; Zhuo, Q.; Hao, Y.; Fan, L.; Wang, S.; Gao, S.; Liang, J.; Hu, W.; Yao, Y.; et al. Robust SOP-Based Vibration Sensing Integrated in DSCM System Based on Frequency-Domain Pilot Tones. In Proceedings of the Frontiers in Optics, Denver, CO, USA, 23–26 September 2024; Optica Publishing Group: Washington, DC, USA, 2024; p. FD1-6. [Google Scholar]
- Zhu, B.; Westbrook, P.; Feder, K.; Shi, Z.; Lu, P.; Dyer, R.; Sun, X.; Li, J.; Peterson, D.; DiGiovanni, D.J. Distributed Acoustic Sensing Over Passive Optical Networks Using Enhanced Scatter Fiber. In Proceedings of the Optical Fiber Communication Conference (OFC), San Diego, CA, USA, 24–28 March 2024; Optica Publishing Group: Washington, DC, USA,, 2024; p. M1K.1. [Google Scholar]
- Guerrier, S.; Dorize, C.; Pavani, H.; Mardoyan, H.; Awwad, É.; Renaudier, J. Digital Coherent Sensing over Deployed Fibers for Advanced Network Telemetry. In Proceedings of the Optical Fiber Communication Conference (OFC), San Diego, CA, USA, 24–28 March 2024; Optica Publishing Group: Washington, DC, USA, 2024; p. Tu2J.1. [Google Scholar]
- Liu, M.; Wang, J.; Chen, L.; Yu, C.; Lu, C. Integration of communication and distributed sensing over optical supervisory channel using live QPSK streams. Opt. Lett. 2025, 50, 1409–1412. [Google Scholar]
- Minelli, L.; Pellegrini, S.; Andrenacci, L.; Pilori, D.; Bosco, G.; Chiesa, L.D.; Tanzi, A.; Crognale, C.; Gaudino, R. SOP-based DSP blind anomaly detection for sensing on deployed metropolitan fibers. In Proceedings of the 49th European Conference on Optical Communications (ECOC 2023), Glasgow, UK, 1–5 October 2023; IET: London, UK, 2023; Volume 2023, pp. 519–522. [Google Scholar]
- Tomasov, A.; Dejdar, P.; Munster, P.; Horvath, T. Utilizing a State of Polarization Change Detector and Machine Learning for Enhanced Security in Fiber-Optic Networks. In Proceedings of the CLEO 2024, Charlotte, NC, USA, 5–10 May 2024; Optica Publishing Group: Washington, DC, USA, 2024; p. JTu2A.217. [Google Scholar]
- Tomasov, A.; Dejdar, P.; Munster, P.; Horvath, T.; Barcik, P.; Ros, F.D. Enhancing fiber security using a simple state of polarization analyzer and machine learning. Opt. Laser Technol. 2023, 167, 109668. [Google Scholar]
- Du, X.; Wang, Q.; Kam, P.Y. Maximum Likelihood Estimation of Wiener Phase Noise Variance in Coherent Optical Systems. J. Light. Technol. 2024, 42, 3163–3173. [Google Scholar] [CrossRef]
- Cohen, L. Time-frequency distributions-a review. Proc. IEEE 1989, 77, 941–981. [Google Scholar]
- Lian, W.; Su, X.; Hu, K.; Li, W.; Wu, B.; Zhao, H.; Huang, Y.; Zhang, S.; Wang, D.; Tong, F.; et al. Theoretical and experimental study on optical polarization states in overhead optical cables under complex weather conditions such as real lightning. Laser Phys. 2024, 35, 015101. [Google Scholar] [CrossRef]
- Zhu, R.; Rao, X.; Dai, S.; Chen, M.; Liu, G.; Liu, H.; Xu, R.; Chen, S.; Chen, G.Y.; Wang, Y. Deep Integration of Fiber-Optic Communication and Sensing Systems Using Forward-Transmission Distributed Vibration Sensing and on–off Keying. Sensors 2024, 24, 5758. [Google Scholar] [CrossRef] [PubMed]
- Ip, E.; Huang, Y.K.; Huang, M.F.; Yaman, F.; Wellbrock, G.; Xia, T.; Wang, T.; Asahi, K.; Aono, Y. DAS over 1007-km hybrid link with 10-Tb/s DP-16QAM co-propagation using frequency-diverse chirped pulses. J. Light. Technol. 2022, 41, 1077–1086. [Google Scholar] [CrossRef]
- Pang, Z.; Wang, G.; Wang, F.; Dai, H.; Li, W.; Wang, B. Fiber-based distributed sensing laser interferometer enabled by mirror-image correlation method. Adv. Photonics Nexus 2024, 3, 066007. [Google Scholar] [CrossRef]
- Hao, Y.; Yue, B.; Xu, Y.; Xiang, Q.; Fan, L.; Li, J.; Yang, Y.; Hu, W.; Li, X. Delayed Self-Heterodyne Interferometry Enabling 4.8 Tb/s Coherent Transmission and Simultaneous Vibration Sensing with 100 kHz Linewidth ECLs. In Proceedings of the 2024 Asia Communications and Photonics Conference (ACP) and International Conference on Information Photonics and Optical Communications (IPOC), Beijing, China, 2–5 November 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–4. [Google Scholar]




| Parameter | Values |
|---|---|
| FrFT order | ±0.01 |
| FrFT-DC symbol rate | 12.8 GBaud/s |
| Length of FrFT-DC sequence | 2048 symbols |
| Laser linewidth | 100 Hz |
| AWG sampling rate | 32 GSa/s |
| RTO sampling rate | 80 GSa/s |
| Communication symbol rate | 2 × 12.8 GBaud/s |
| Matched filter | RRC |
| Roll-off factor of matched filter | 0.075 |
| Length of fiber link | 10 km |
| Length of fiber used to wrap PZT | 15 m |
| Parameter | Values |
|---|---|
| Center frequencies of subcarriers | ±5 GHz, ±15 GHz |
| Bandwidth of subcarrier interval | 2 GHz |
| Laser linewidth | 100 kHz |
| AWG sampling rate | 128 GSa/s |
| RTO sampling rate | 64 GSa/s |
| Symbol rate | 4 × 8 GBaud/s |
| Matched filter | RRC |
| Roll-off factor of matched filter | 0.1 |
| Length of fiber link | 40 km |
| Center frequency of FPT at X polarization | 10 GHz |
| Center frequency of FPT at Y polarization | −10 GHz |
| Length of fiber used to wrap PZT | 5 m |
| Type | Laser Linewidth | Sensing Capability | Spatial Resolution | Communication Signal | Ref. |
|---|---|---|---|---|---|
| Back-Scattering | <100 Hz | SNR = 21.5 dB @ 1 kHz * | 4 m | PAM-4 | [8] |
| Back-Scattering | <100 Hz | SNR = 21 dB @ 800 Hz | 0.5 m | 16-QAM | [9] |
| Back-Scattering | <100 Hz | SNR = 30 dB @ 1 kHz | 5 m | DSCM 16-QAM | [31,32] |
| Forward SOP | <100 kHz | ≤ 100 kHz ** | - | QPSK | [12] |
| Forward SOP | <100 kHz | = 100 kHz | 22.04 m | QPSK | [16] |
| Forward SOP | <100 kHz | ≥ 300 kHz | - | DSCM 16-QAM | [36] |
| Forward Phase | <100 Hz | 10 Hz ≤ ≤ 2 kHz | 5 km | 16-QAM | [4] |
| Forward Phase | <100 Hz | 8.3 @ 1 kHz | 10.1 m | OOK | [46] |
| Forward Phase | <100 kHz | SNR = 19 dB @ 30 kHz | - | QPSK | [19] |
| Forward Phase | <100 kHz | SNR = 18 dB @ 10 kHz | - | DSCM 16-QAM | [34] |
| Forward Phase | <100 kHz | SNR = 23 dB @ 10 kHz | - | DSCM 16-QAM | [35] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Tang, J.; Fan, L.; Hao, Y.; Cheng, C.; Wang, S.; Gao, S.; Sun, Z.; Liang, J.; Hu, W.; et al. Recent Advances in Integrated Vibration Sensing and Communication in Digital Subcarrier Multiplexing Systems. Photonics 2025, 12, 290. https://doi.org/10.3390/photonics12030290
Yang B, Tang J, Fan L, Hao Y, Cheng C, Wang S, Gao S, Sun Z, Liang J, Hu W, et al. Recent Advances in Integrated Vibration Sensing and Communication in Digital Subcarrier Multiplexing Systems. Photonics. 2025; 12(3):290. https://doi.org/10.3390/photonics12030290
Chicago/Turabian StyleYang, Bang, Jianwei Tang, Linsheng Fan, Yaguang Hao, Chen Cheng, Shangyi Wang, Shuang Gao, Zhongliang Sun, Junpeng Liang, Weisheng Hu, and et al. 2025. "Recent Advances in Integrated Vibration Sensing and Communication in Digital Subcarrier Multiplexing Systems" Photonics 12, no. 3: 290. https://doi.org/10.3390/photonics12030290
APA StyleYang, B., Tang, J., Fan, L., Hao, Y., Cheng, C., Wang, S., Gao, S., Sun, Z., Liang, J., Hu, W., Yang, Y., & Wei, J. (2025). Recent Advances in Integrated Vibration Sensing and Communication in Digital Subcarrier Multiplexing Systems. Photonics, 12(3), 290. https://doi.org/10.3390/photonics12030290






