Broadband On-Chip Directional Coupler with Oblique Nanoslits
Abstract
:1. Introduction
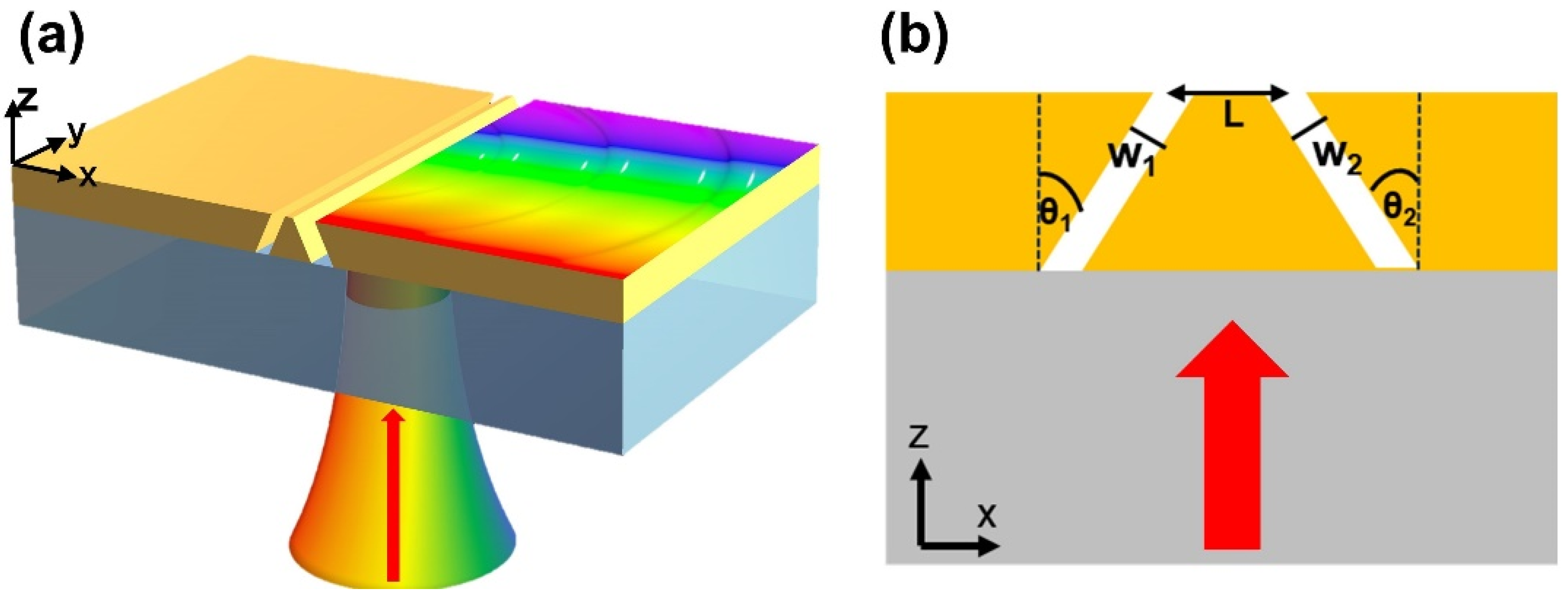
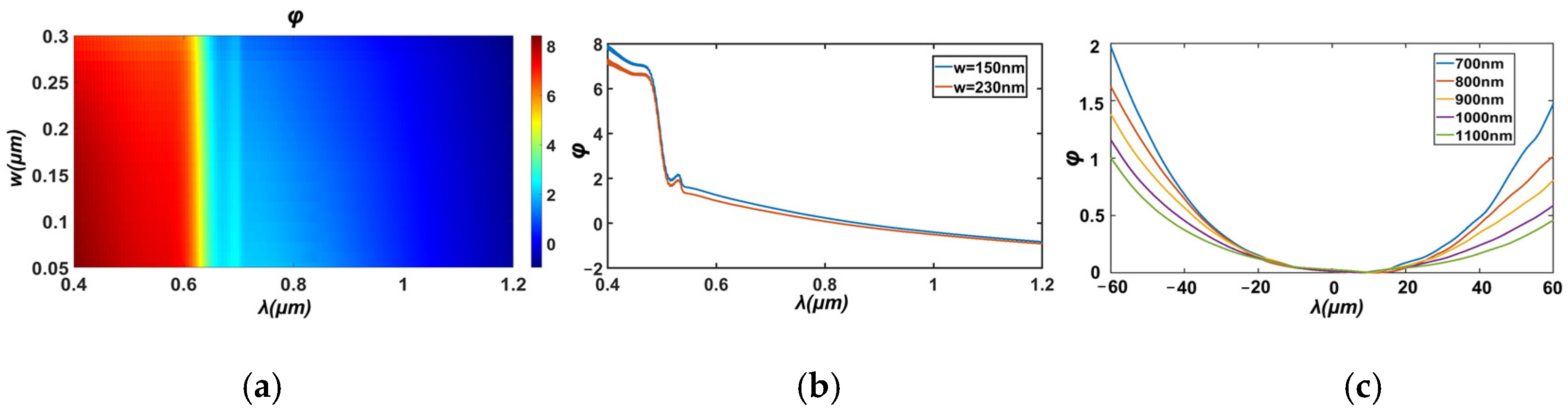
2. Theoretical Model
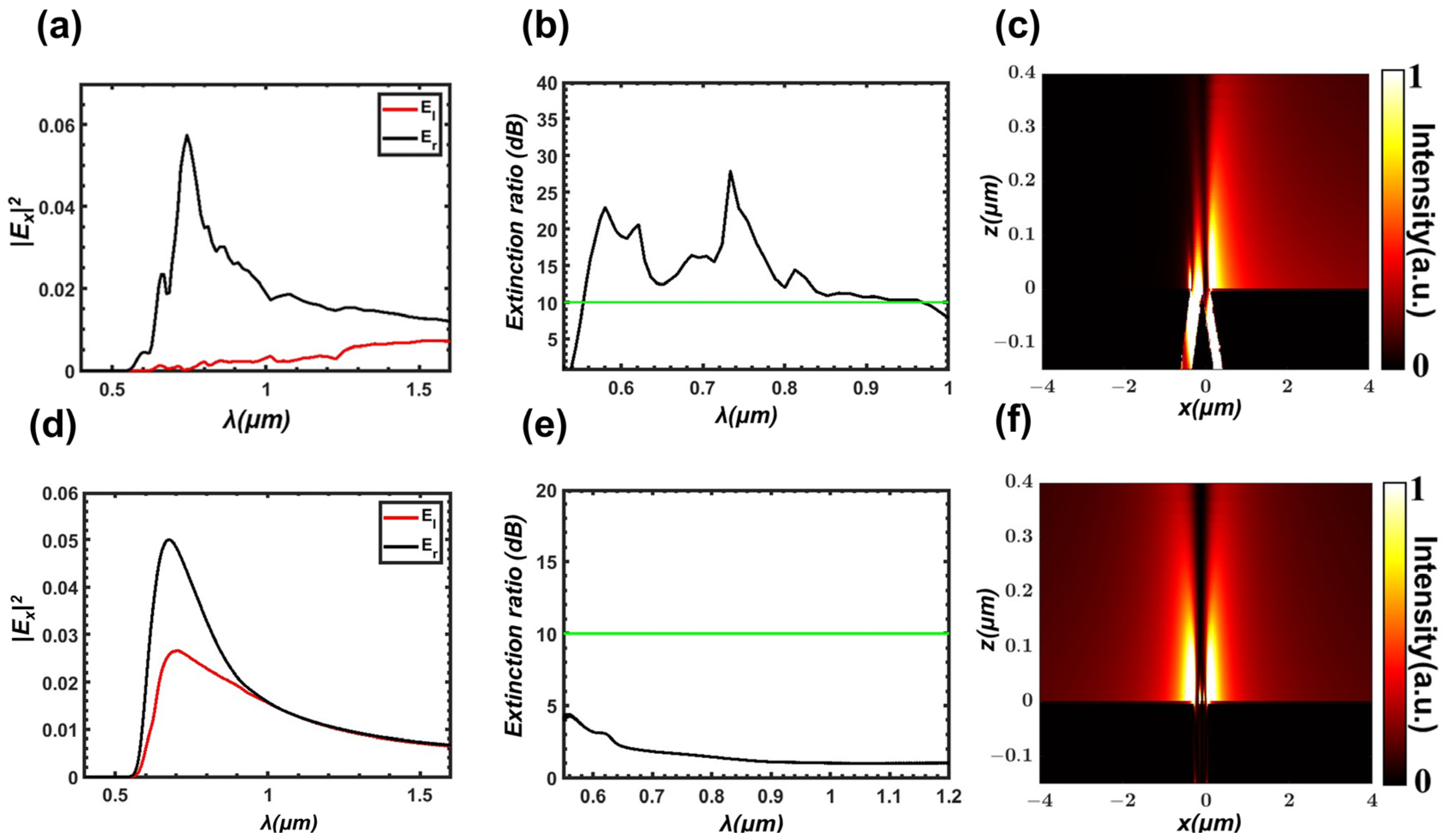
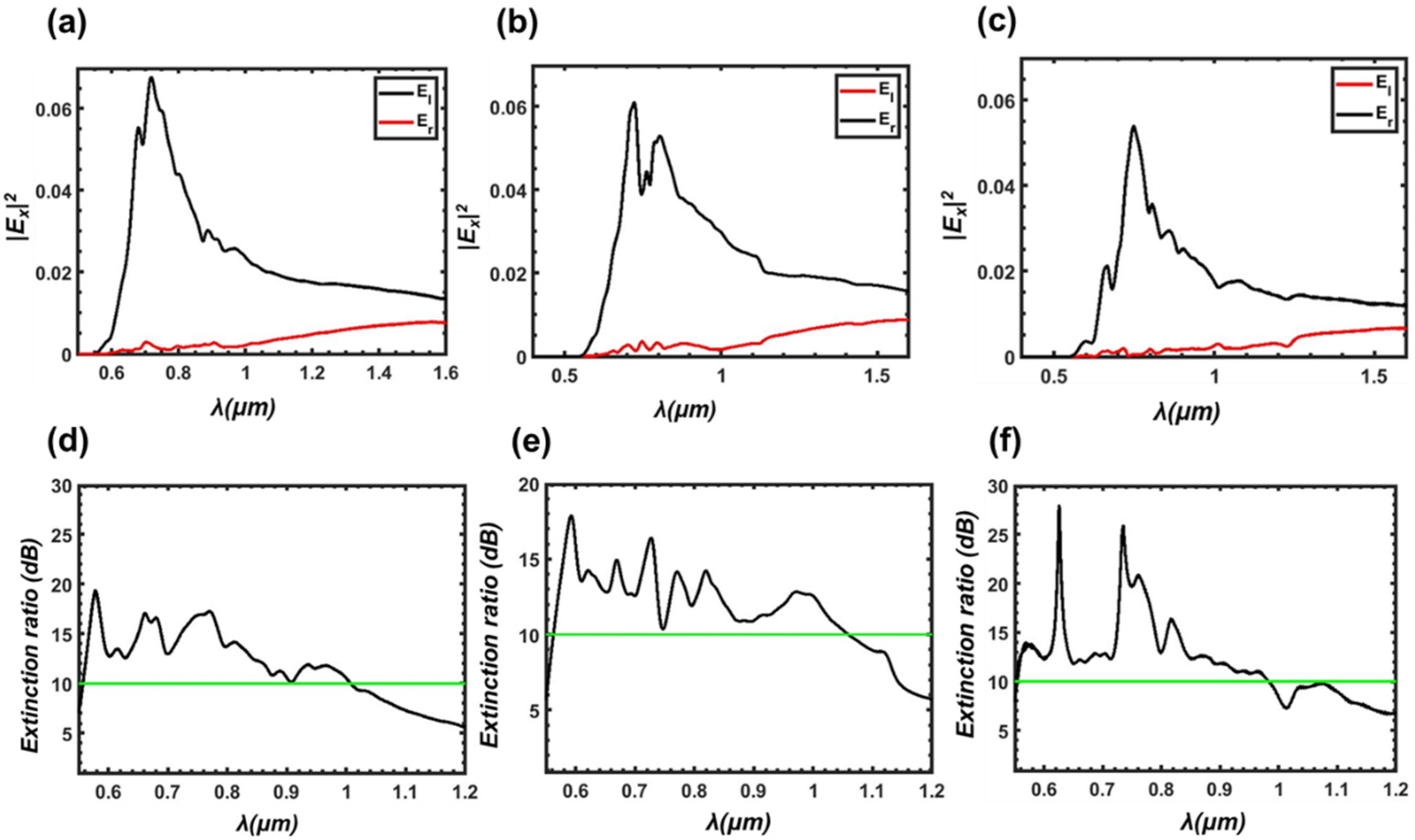
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Zhang, Y.; He, Y.; Zhu, Q.; Sun, L.; Su, Y. Compact Silicon Waveguide Mode Converter Employing Dielectric Metasurface Structure. Adv. Opt. Mater. 2019, 7, 1801191. [Google Scholar]
- Karabchevsky, A.; Katiyi, A.; Ang, A.S.; Hazan, A. On-chip nanophotonics and future challenges. Nanophotonics 2020, 9, 3733–3753. [Google Scholar]
- Tonndorf, P.; Del Pozo-Zamudio, O.; Gruhler, N.; Kern, J.; Schmidt, R.; Dmitriev, A.I.; Bakhtinov, A.P.; Tartakovskii, A.I.; Pernice, W.; Michaelis de Vasconcellos, S.; et al. On-Chip Waveguide Coupling of a Layered Semiconductor Single-Photon Source. Nano Lett. 2017, 17, 5446–5451. [Google Scholar]
- Nair, R.V.; Vijaya, R. Photonic crystal sensors: An overview. Prog. Quantum Electron. 2010, 34, 89–134. [Google Scholar]
- Novotny, L.; van Hulst, N. Antennas for light. Nat. Photon. 2011, 5, 83–90. [Google Scholar]
- Mühlschlegel, P.; Eisler, H.-J.; Martin, O.J.F.; Hecht, B.; Pohl, D.W. Resonant Optical Antennas. Science 2005, 308, 1607–1609. [Google Scholar]
- Kosako, T.; Kadoya, Y.; Hofmann, H.F. Directional control of light by a nano-optical Yagi–Uda antenna. Nat. Photon. 2010, 4, 312–315. [Google Scholar]
- Guo, R.; Decker, M.; Setzpfandt, F.; Gai, X.; Choi, D.-Y.; Kiselev, R.; Chipouline, A.; Staude, I.; Pertsch, T.; Neshev, D.N.; et al. High–bit rate ultra-compact light routing with mode-selective on-chip nanoantennas. Sci. Adv. 2017, 3, e1700007. [Google Scholar]
- Kim, I.; Jang, J.; Kim, G.; Lee, J.; Badloe, T.; Mun, J.; Rho, J. Pixelated bifunctional metasurface-driven dynamic vectorial holographic color prints for photonic security platform. Nat. Commun. 2021, 12, 3614. [Google Scholar]
- Koenderink, A.F.; Alù, A.; Polman, A. Nanophotonics: Shrinkinglight-based technology. Science 2015, 348, 516–521. [Google Scholar]
- Maier, S.A.; Kik, P.G.; Atwater, H.A.; Meltzer, S.; Harel, E.; Koel, B.E.; Requicha, A.A.G. Local detection of electromagnetic energy transport below the diffraction limit in metal nanoparticle plasmon waveguides. Nat. Mater. 2003, 2, 229–232. [Google Scholar] [CrossRef] [PubMed]
- Bozhevolnyi, S.I.; Volkov, V.S.; Devaux, E.; Laluet, J.-Y.; Ebbesen, T.W. Channel plasmon subwavelength waveguide components including interferometers and ring resonators. Nature 2006, 440, 508–511. [Google Scholar] [CrossRef] [PubMed]
- Oulton, R.F.; Sorger, V.J.; Zentgraf, T.; Ma, R.-M.; Gladden, C.; Dai, L.; Bartal, G.; Zhang, X.J. Plasmon lasers at deep subwavelength scale. Nature 2009, 461, 629–632. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.; Hoang, T.B.; Dridi, M.; Deeb, C.; Mikkelsen, M.H.; Schatz, G.C.; Odom, T.W. Real-time tunable lasing from plasmonic nanocavity arrays. Nat. Commun. 2015, 6, 6939. [Google Scholar] [CrossRef]
- Baron, A.; Devaux, E.; Rodier, J.C.; Hugonin, J.P.; Rousseau, E.; Genet, C.; Ebbesen, T.W.; Lalanne, P. Compact Antenna for Efficient and Unidirectional Launching and Decoupling of Surface Plasmons. Nano Lett. 2011, 11, 4207–4212. [Google Scholar] [CrossRef]
- Knight, M.W.; Sobhani, H.; Nordlander, P.; Halas, N.J. Photodetection with Active Optical Antennas. Science 2011, 332, 702–704. [Google Scholar] [CrossRef]
- Melikyan, A.; Alloatti, L.; Muslija, A.; Hillerkuss, D.; Schindler, P.C.; Li, J.; Palmer, R.; Korn, D.; Muehlbrandt, S.; Van Thourhout, D.; et al. High-speed plasmonic phase modulators. Nat. Photon. 2014, 8, 229–233. [Google Scholar] [CrossRef]
- Ayata, M.; Fedoryshyn, Y.; Heni, W.; Baeuerle, B.; Josten, A.; Zahner, M.; Koch, U.; Salamin, Y.; Hoessbacher, C.; Haffner, C.; et al. High-speed plasmonic modulator in a single metal layer. Science 2017, 358, 630–632. [Google Scholar] [CrossRef]
- Huang, H.; Overvig, A.C.; Xu, Y.; Malek, S.C.; Tsai, C.-C.; Alù, A.; Yu, N. Leaky-wave metasurfaces for integrated photonics. Nat. Nanotechnol. 2023, 18, 580–588. [Google Scholar] [CrossRef]
- Kabashin, A.V.; Evans, P.; Pastkovsky, S.; Hendren, W.; Wurtz, G.A.; Atkinson, R.; Pollard, R.; Podolskiy, V.A.; Zayats, A.V. Plasmonic nanorod metamaterials for biosensing. Nat. Mater. 2009, 8, 867–871. [Google Scholar] [CrossRef]
- Gao, Y.; Gan, Q.; Xin, Z.; Cheng, X.; Bartoli, F.J. Plasmonic Mach–Zehnder Interferometer for Ultrasensitive On-Chip Biosensing. ACS Nano 2011, 5, 9836–9844. [Google Scholar]
- Liu, Z.; Steele, J.M.; Srituravanich, W.; Pikus, Y.; Sun, C.; Zhang, X. Focusing Surface Plasmons with a Plasmonic Lens. Nano Lett. 2005, 5, 1726–1729. [Google Scholar] [CrossRef]
- Chen, W.; Abeysinghe, D.C.; Nelson, R.L.; Zhan, Q. Plasmonic Lens Made of Multiple Concentric Metallic Rings under Radially Polarized Illumination. Nano Lett. 2009, 9, 4320–4325. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Zhang, J. Plasmonic demultiplexer and guiding. ACS Nano 2010, 4, 6433–6438. [Google Scholar] [CrossRef]
- Li, X.; Tan, Q.; Bai, B.; Jin, G. Experimental demonstration of tunable directional excitation of surface plasmon polaritons with a subwavelength metallic double slit. Appl. Phys. Lett. 2011, 98, 251109. [Google Scholar]
- Radko, I.P.; Bozhevolnyi, S.I.; Brucoli, G.; Martin-Moreno, L.; Garcia-Vidal, F.J.; Boltasseva, A. Efficient unidirectional ridge excitation of surface plasmons. Opt. Express 2009, 17, 7228–7232. [Google Scholar] [CrossRef] [PubMed]
- López-Tejeira, F.; Rodrigo, S.G.; Martín-Moreno, L.; García-Vidal, F.J.; Devaux, E.; Ebbesen, T.W.; Krenn, J.R.; Radko, I.P.; Bozhevolnyi, S.I.; González, M.U.; et al. Efficient unidirectional nanoslit couplers for surface plasmons. Nat. Phys. 2007, 3, 324–328. [Google Scholar]
- Liu, T.; Shen, Y.; Shin, W.; Zhu, Q.; Fan, S.; Jin, C. Dislocated double-layer metal gratings: An efficient unidirectional coupler. Nano Lett. 2014, 14, 3848–3854. [Google Scholar]
- Bai, B.; Meng, X.; Laukkanen, J.; Sfez, T.; Yu, L.; Nakagawa, W.; Herzig, H.P.; Li, L.; Turunen, J. Asymmetrical excitation of surface plasmon polaritons on blazed gratings at normal incidence. Phys. Rev. B Condens. Matter 2009, 80, 1132–1136. [Google Scholar]
- Chen, J.; Li, Z.; Yue, S.; Gong, Q. Efficient unidirectional generation of surface plasmon polaritons with asymmetric single-nanoslit. Appl. Phys. Lett. 2010, 97, 041113. [Google Scholar] [CrossRef]
- Yao, W.; Liu, S.; Liao, H.; Li, Z.; Sun, C.; Chen, J.; Gong, Q. Efficient directional excitation of surface plasmons by a single-element nanoantenna. Nano Lett. 2015, 15, 3115. [Google Scholar] [PubMed]
- Chen, P.; Chen, C.; Qin, S.; Xi, J.; Huang, W.; Shi, F.; Li, K.; Liang, L.; Shi, J. Efficient planar plasmonic directional launching of linearly polarized light in a catenary metasurface. Phys. Chem. Chem. Phys. 2020, 22, 27554–27559. [Google Scholar] [PubMed]
- Yang, J.; Xiao, X.; Hu, C.; Zhang, W.; Zhou, S.; Zhang, J. Broadband surface plasmon polariton directional coupling via asymmetric optical slot nanoantenna pair. Nano Lett. 2014, 14, 704. [Google Scholar]
- Liu, J.S.; Pala, R.A.; Afshinmanesh, F.; Cai, W.; Brongersma, M.L. A submicron plasmonic dichroic splitter. Nat. Commun. 2011, 2, 525. [Google Scholar] [CrossRef] [PubMed]
- Liao, H.; Li, Z.; Chen, J.; Zhang, X.; Yue, S.; Gong, Q. A submicron broadband surface-plasmon-polariton unidirectional coupler. Sci. Rep. 2013, 3, 1918. [Google Scholar] [CrossRef]
- Xu, G.; Overvig, A.; Kasahara, Y.; Martini, E.; Maci, S.; Alù, A. Arbitrary aperture synthesis with nonlocal leaky-wave metasurface antennas. Nat. Commun. 2023, 14, 4380. [Google Scholar]
- Gupta, N.; Dhawan, A. Harnessing surface plasmon polaritons from nanogroove plasmonic lenses to enhance the EM fields around plasmonic nanoantennas. J. Opt. Soc. Am. B 2024, 41, 2247–2258. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Wang, Q.; Zhong, J.; Lei, X.; Zhan, Q. Broadband On-Chip Directional Coupler with Oblique Nanoslits. Photonics 2025, 12, 289. https://doi.org/10.3390/photonics12030289
Chen C, Wang Q, Zhong J, Lei X, Zhan Q. Broadband On-Chip Directional Coupler with Oblique Nanoslits. Photonics. 2025; 12(3):289. https://doi.org/10.3390/photonics12030289
Chicago/Turabian StyleChen, Can, Qingfang Wang, Jinzhan Zhong, Xinrui Lei, and Qiwen Zhan. 2025. "Broadband On-Chip Directional Coupler with Oblique Nanoslits" Photonics 12, no. 3: 289. https://doi.org/10.3390/photonics12030289
APA StyleChen, C., Wang, Q., Zhong, J., Lei, X., & Zhan, Q. (2025). Broadband On-Chip Directional Coupler with Oblique Nanoslits. Photonics, 12(3), 289. https://doi.org/10.3390/photonics12030289




