Adaptive Generation Method for Small Volume Easy Fabrication Freeform Unobscured Three-Mirror Systems Based on Machine Learning
Abstract
:1. Introduction
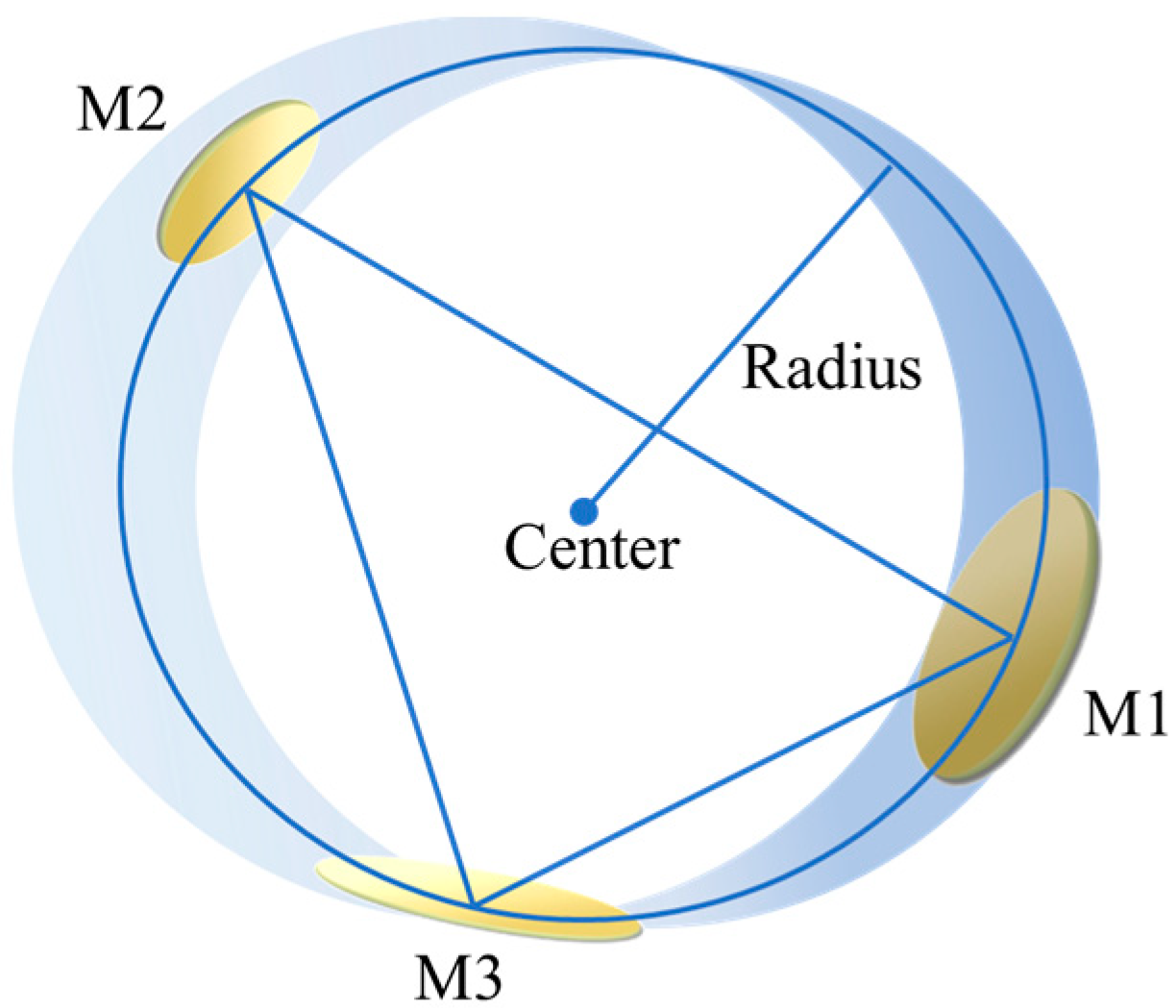
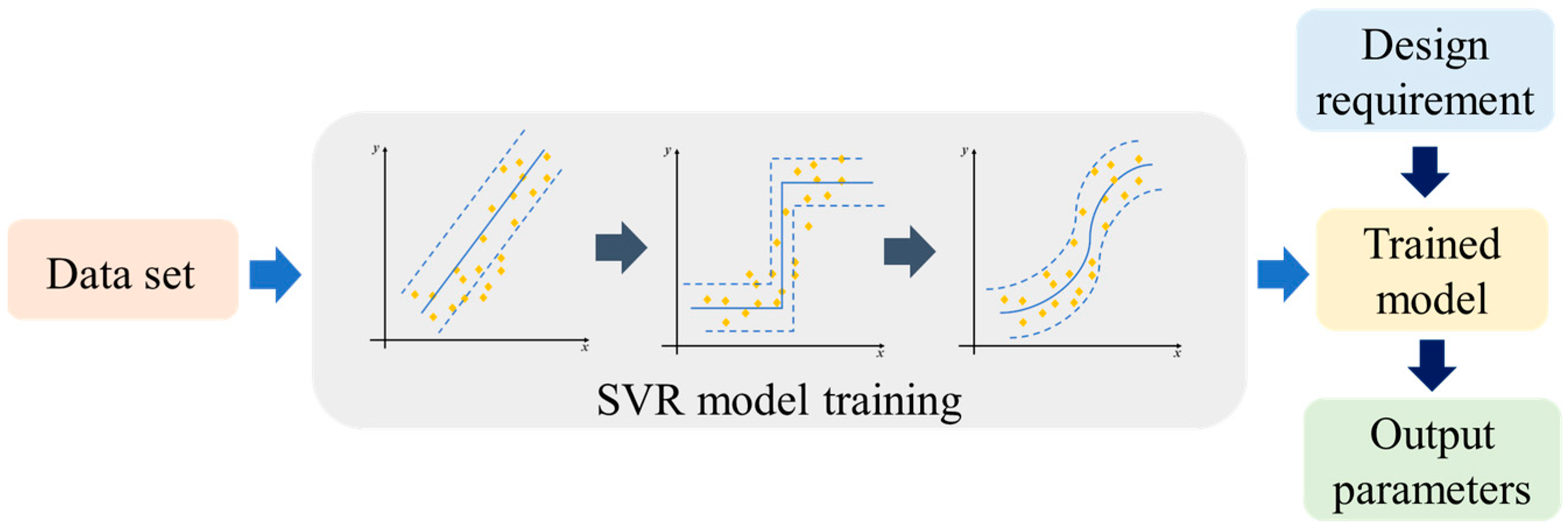
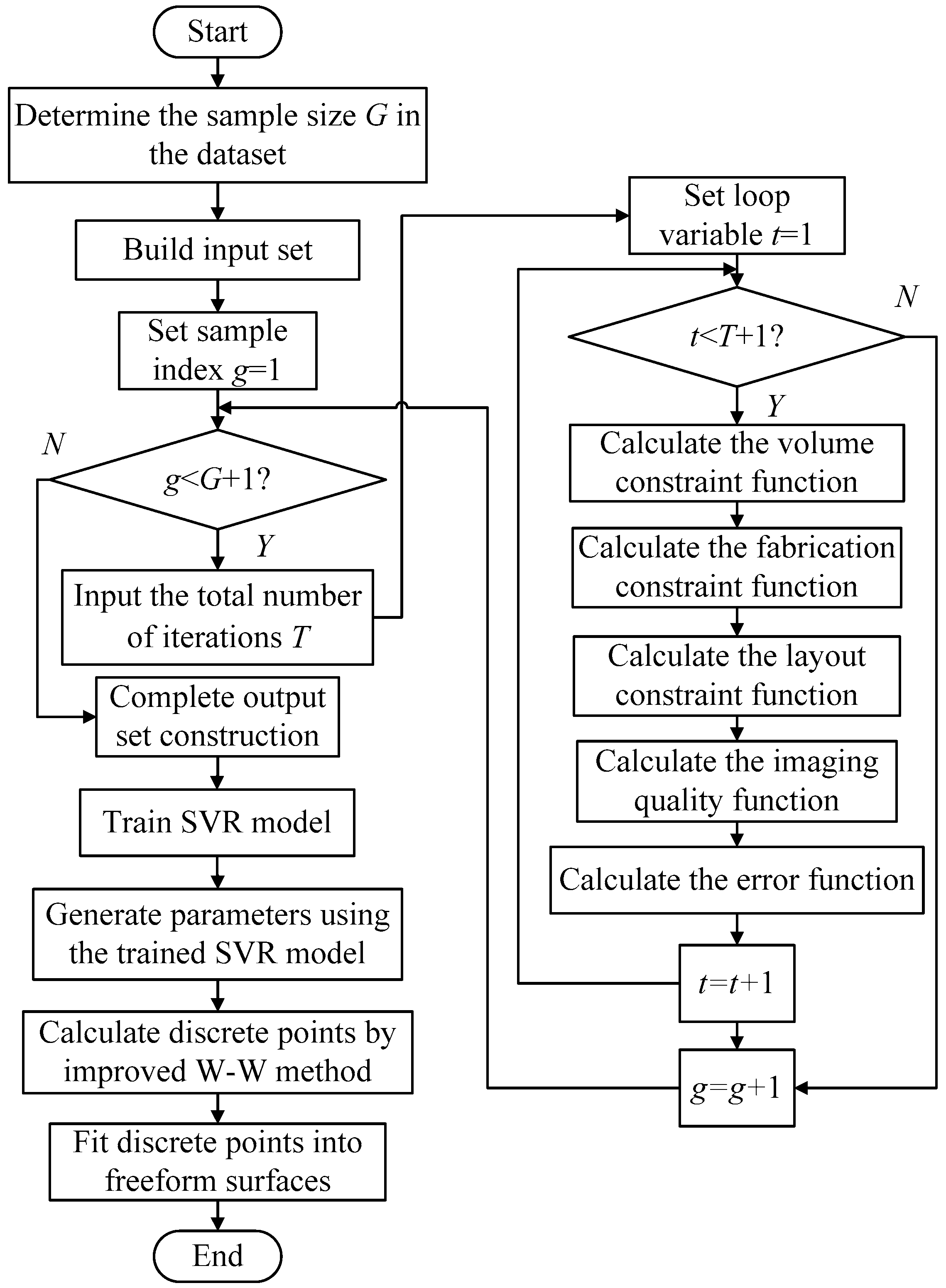
2. Design Method
3. Experiment
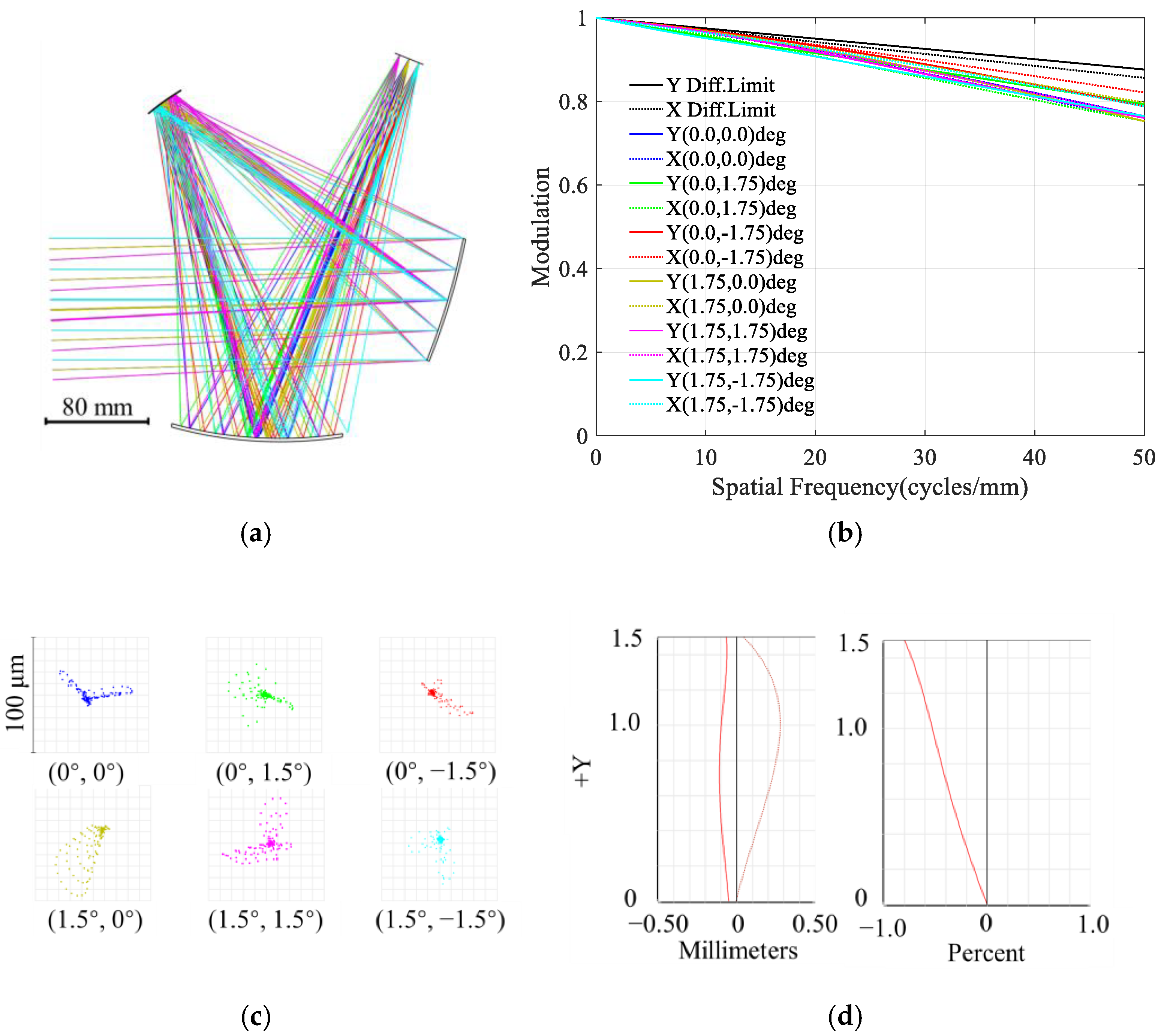
3.1. Dataset Analysis
- (1)
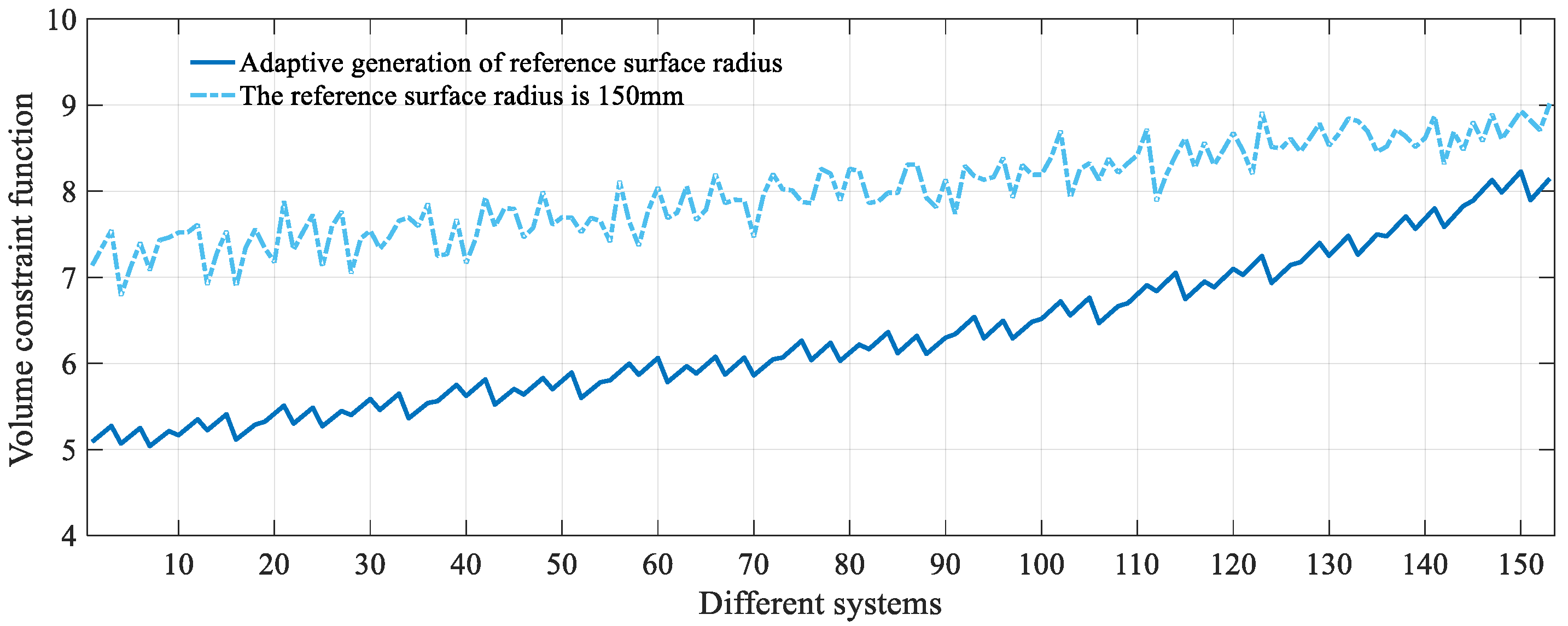
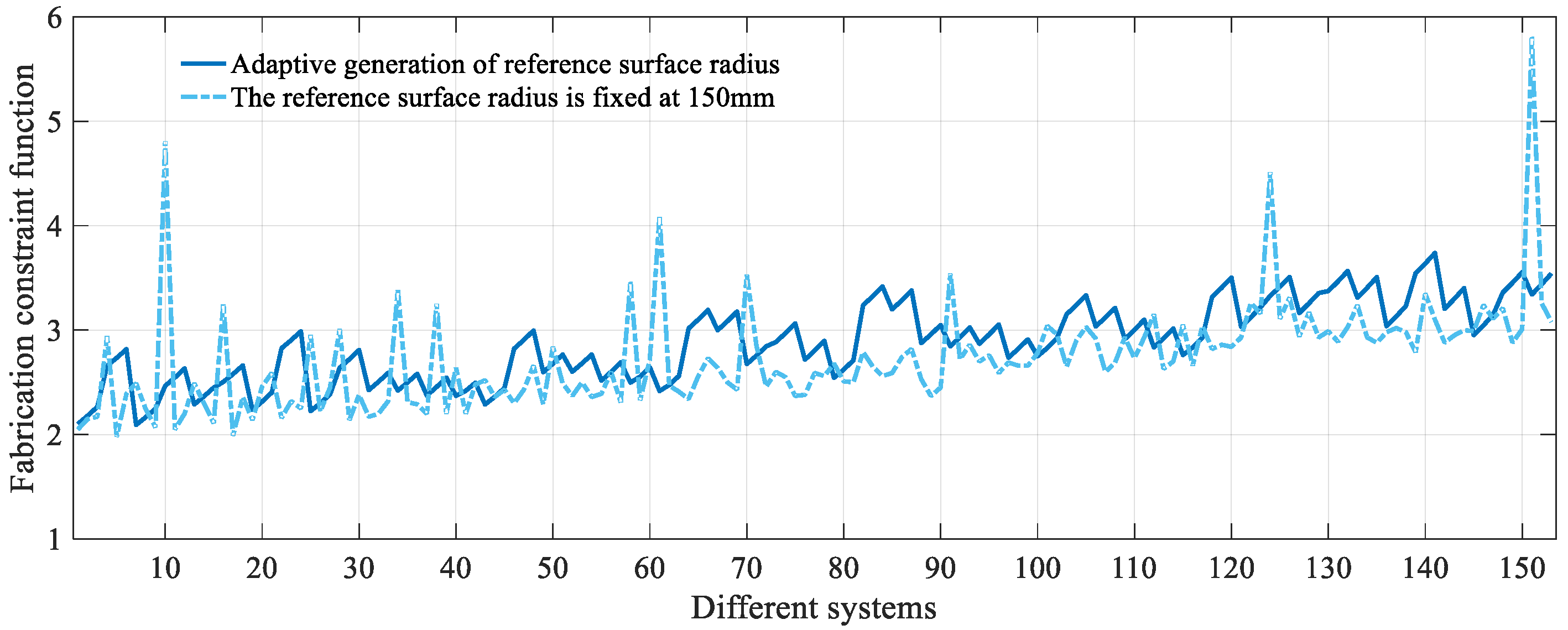
- When adaptive determination of the reference circle radius was used to construct the dataset, the mean volume of the 153 sets of unobscured three-mirror systems was found to be 6.29 L, with a maximum value of 8.23 L, a minimum value of 5.04 L, and a standard deviation of 0.84. When the radius of the reference circle was fixed at 150 mm, the mean volume, maximum value, minimum value, and standard deviation were found to be 8.00 L, 9.02 L, 6.79 L, and 0.51, respectively. When the reference circle radius was fixed, the range of volume variation was smaller, and the trend was more stable. This was due to the fixed reference circle radius, which restricted the adjustment range of distances between mirrors but also limited the possibility of achieving smaller distances between mirrors. When the method proposed in this study was used to construct the dataset, a larger variation in system volume was observed. This was because, when the system focal length was smaller, the system was better suited to a smaller reference circle radius, allowing for the possibility of obtaining smaller distances between mirrors, and thus smaller volume systems.
- (2)
- In the systems generated using the method proposed in this study for constructing the dataset, the variation range of the fabrication constraint function was found to be 2.09–3.74, with a standard deviation of 0.38 and a mean of 2.88. When the radius of the reference circle was fixed, the variation range, standard deviation, and mean of the fabrication constraint were found to be 1.98–5.82, 0.50, and 2.73, respectively. Although the mean of the fabrication constraint function for the systems obtained using the method proposed in this study was slightly higher than that of the systems obtained with a fixed reference circle radius, the variation range of the fabrication constraint function values in the systems generated by this method was smaller, with the maximum value being less than the maximum value when the reference circle radius was fixed. Furthermore, the trend was more stable. When the reference circle radius was fixed, the fluctuation of the fabrication constraint was found to be greater.
- (3)
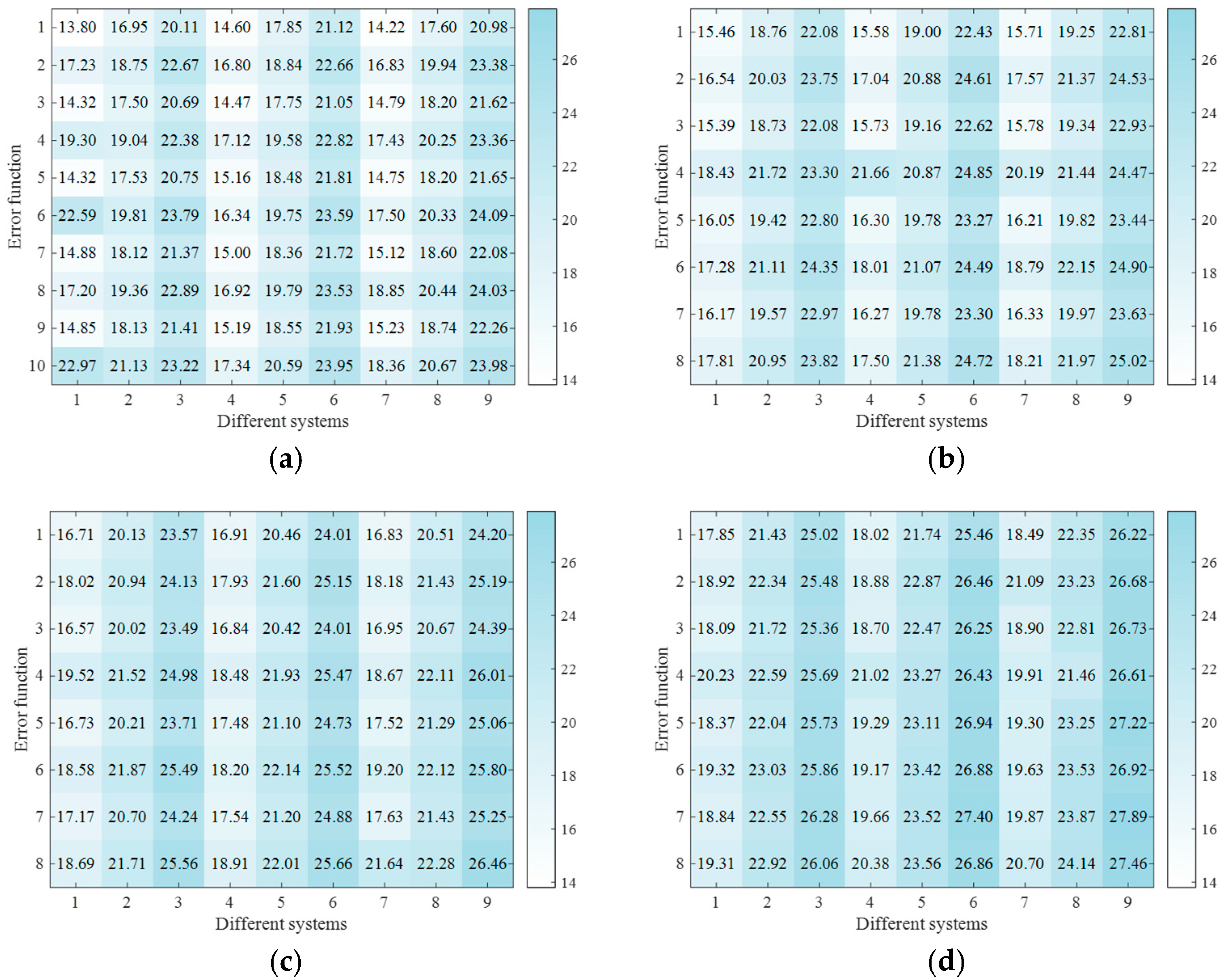
- For the systems generated using the dataset construction methods proposed in this study and with a fixed reference circle radius, the mean values of the error function were found to be 20.05 and 21.66, respectively. When the focal length was relatively short, the error values of the systems obtained using the method proposed in this study were lower, with the difference being more pronounced compared to the fixed reference circle radius method. As the focal length increased, the overall error values of the systems obtained using the proposed method continuously increased, with some individual values exceeding those of the systems obtained using the fixed reference circle radius method. This was attributed to the fact that, at larger focal lengths, the reduction in system volume often leads to a decrease in imaging quality and an increase in the fabrication constraint function values. However, the maximum overall errors obtained using the method proposed in this study and the fixed reference circle radius method were 27.89 and 27.46, respectively, with a difference of only 0.43. This indicates that the method proposed in this study still effectively balances the relationship between system volume, assembly constraints, and imaging quality.
3.2. Model Training and Testing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, T.; Xu, H.; Zhou, L.; Cheng, Y.; Wu, Z.; Shang, S.; Cheng, D.; Wang, Y. Design of a dual-focal-plane head-up display system using double freeform mirrors. Appl. Opt. 2024, 63, 8204–8211. [Google Scholar] [CrossRef]
- Xu, C.; Lai, X.; Cheng, D.; Wang, Y.; Wu, K. Automatic optical path configuration variation in off-axis mirror system design. Opt. Express 2019, 27, 15251–15261. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, T.; Lyu, X.; Cheng, D.; Wang, Y. Ultra-simplified and low-cost head-up display system enabled by freeform holographic element. Opt. Laser Technol. 2024, 178, 111253. [Google Scholar] [CrossRef]
- Xu, H.; Yang, T.; Cheng, D.; Wang, Y. Compact freeform near-eye display system design enabled by optical-digital joint optimization. Front. Phys. 2024, 12, 1440129. [Google Scholar] [CrossRef]
- Bai, X.; Xu, B.; Ju, G.; Ma, H.; Zhang, C.; Wang, S.; Xu, S. Aberration compensation strategy for the radius of curvature error of the primary mirror in off-axis three-mirror anastigmatic telescopes. Appl. Opt. 2021, 60, 6199–6212. [Google Scholar] [CrossRef]
- Ji, H.; Zhu, Z.; Tan, H.; Shan, Y.; Tan, W.; Ma, D. Design of a high-throughput telescope based on scanning an off-axis three-mirror anastigmat system. Appl. Opt. 2021, 60, 2817–2823. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, J. Automatic design method of starting points of freeform off-axis reflective imaging systems of small volume. Opt. Express 2022, 30, 7954–7967. [Google Scholar] [CrossRef]
- Qu, Z.; Zhong, X.; Zhang, K.; Wang, Y.; Li, L.; Liu, J.; Zeng, C. Automatic compact-volume design strategy for unobscured reflective optical systems based on conicoid surfaces. Opt. Commun. 2023, 533, 129304. [Google Scholar] [CrossRef]
- Rolland, J.P.; Davies, M.A.; Suleski, T.J.; Evans, C.; Bauer, A.; Lambropoulos, J.C.; Falaggis, K. Freeform optics for imaging. Optica 2021, 8, 161–176. [Google Scholar] [CrossRef]
- Li, Z.; Fang, F.; Chen, J.; Zhang, X. Machining approach of freeform optics on infrared materials via ultra-precision turning. Opt. Express 2017, 25, 2051–2062. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Fang, F.; Zhang, X.; Zeng, Z.; Zhu, L.; Yan, N. Integrated manufacture of a freeform off-axis multi-reflective imaging system without optical alignment. Opt. Express 2018, 26, 7625–7637. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Li, Z.; Zhang, X.; Fang, F. Manufacturing-constrained optical design methodology for cylindrical freeform reflective imaging system. Opt. Express 2018, 26, 22547–22562. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Sun, Y.; Chen, X.; Wang, F.; Yan, X.; Zhang, X.; Cheng, T. Design of a free-form off-axis three-mirror optical system with a low f-number based on the same substrate. Appl. Opt. 2022, 61, 7033–7040. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Wei, Y.; Chen, S.; Zhao, J. Fast starting point generation method for unobscured two-mirror imaging systems with large field-of-views. Optik 2023, 288, 171159. [Google Scholar] [CrossRef]
- Yang, T.; Cheng, D.; Wang, Y. Direct generation of starting points for freeform off-axis three-mirror imaging system design using neural network based deep-learning. Opt. Express 2019, 27, 17228–17238. [Google Scholar] [CrossRef]
- Chen, W.; Yang, T.; Cheng, D.; Wang, Y. Generating starting points for designing freeform imaging optical systems based on deep learning. Opt. Express 2021, 29, 27845–27870. [Google Scholar] [CrossRef]
- Mao, B.; Yang, T.; Xu, H.; Chen, W.; Cheng, D.; Wang, Y. FreeformNet: Fast and automatic generation of multiple-solution freeform imaging systems enabled by deep learning. Photonics Res. 2023, 11, 1408–1422. [Google Scholar] [CrossRef]
- Sun, Y.; Wei, Y.; Zhang, Y.; Zhao, J. Automated generation of easy-assembly off-axis three-mirror imaging systems based on few-shot machine learning. Appl. Opt. 2025, 64, 1068–1077. [Google Scholar] [CrossRef]
- Yang, T.; Zhu, J.; Jin, G. Compact freeform off-axis three-mirror imaging system based on the integration of primary and tertiary mirrors on one single surface. Chin. Opt. Lett. 2016, 14, 060801. [Google Scholar] [CrossRef]
- Sun, Y.; Wei, Y.; Zhao, J. Adaptive design of long-focal-length freeform off-axis reflective space cameras with lightweight and integration of primary/tertiary mirror. Front. Phys. 2024, 12, 1481131. [Google Scholar] [CrossRef]
- Sun, Y.; Wei, Y.; Di, X.; Zhao, J. Automatic generation method for long-focal-length unobscured freeform optical systems with small volume. Appl. Opt. 2024, 63, 3702–3711. [Google Scholar] [CrossRef] [PubMed]
- Gambella, C.; Ghaddar, B.; Naoum-Sawaya, J. Optimization Problems for Machine Learning: A Survey. Eur. J. Oper. Res. 2021, 290, 807–828. [Google Scholar] [CrossRef]
- Islam, M.; Park, J. Predicting PAHs removal from contaminated soil via subcritical water extraction using support vector regression. Environ. Eng. Res. 2025, 30, 240122. [Google Scholar] [CrossRef]
- Miñano, J.; Benítez, P.; Narasimhan, B. Freeform aplanatic systems as a limiting case of SMS. Opt. Express 2016, 24, 13173–13178. [Google Scholar] [CrossRef]
- Nie, Y.; Mohedano, R.; Benítez, P.; Chaves, J.; Miñano, J.C.; Thienpont, H.; Duerr, F. Multifield direct design method for ultrashort throw ratio projection optics with two tailored mirrors. Appl. Opt. 2016, 55, 3794–3800. [Google Scholar] [CrossRef]
- Yang, T.; Jin, G.; Zhu, J. Automated design of freeform imaging systems. Light Sci. Appl. 2017, 6, e17081. [Google Scholar] [CrossRef]
- Yang, T.; Zhu, J.; Wu, X.; Jin, G. Direct design of freeform surfaces and freeform imaging systems with a point-by-point three-dimensional construction-iteration method. Opt. Express 2015, 23, 10233–10246. [Google Scholar] [CrossRef]
- Zhang, B.; Jin, G.; Zhu, J. Towards automatic freeform optics design: Coarse and fine search of the three-mirror solution space. Light Sci. Appl. 2021, 10, 65. [Google Scholar] [CrossRef]
- Yang, T.; Cheng, D.; Wang, Y. Freeform imaging spectrometer design using a point-by-point design method. Appl. Opt. 2018, 57, 4718–4727. [Google Scholar] [CrossRef]
- Volatier, J.; Druart, G. Differential method for freeform optics applied to two-mirror off-axis telescope design. Opt. Lett. 2019, 44, 1174–1177. [Google Scholar] [CrossRef]
- Cheng, D.; Wang, Y.; Hua, H. Freeform optical system design with differential equations. Proc. SPIE 2010, 7849, 78490X. [Google Scholar]
- Chen, S.; Wei, Y.; Sun, Y.; Zhao, J. Design of off-axis three-mirror freeform systems based on refined W-W differential equations. Appl. Opt. 2023, 62, 3892–3903. [Google Scholar] [CrossRef]


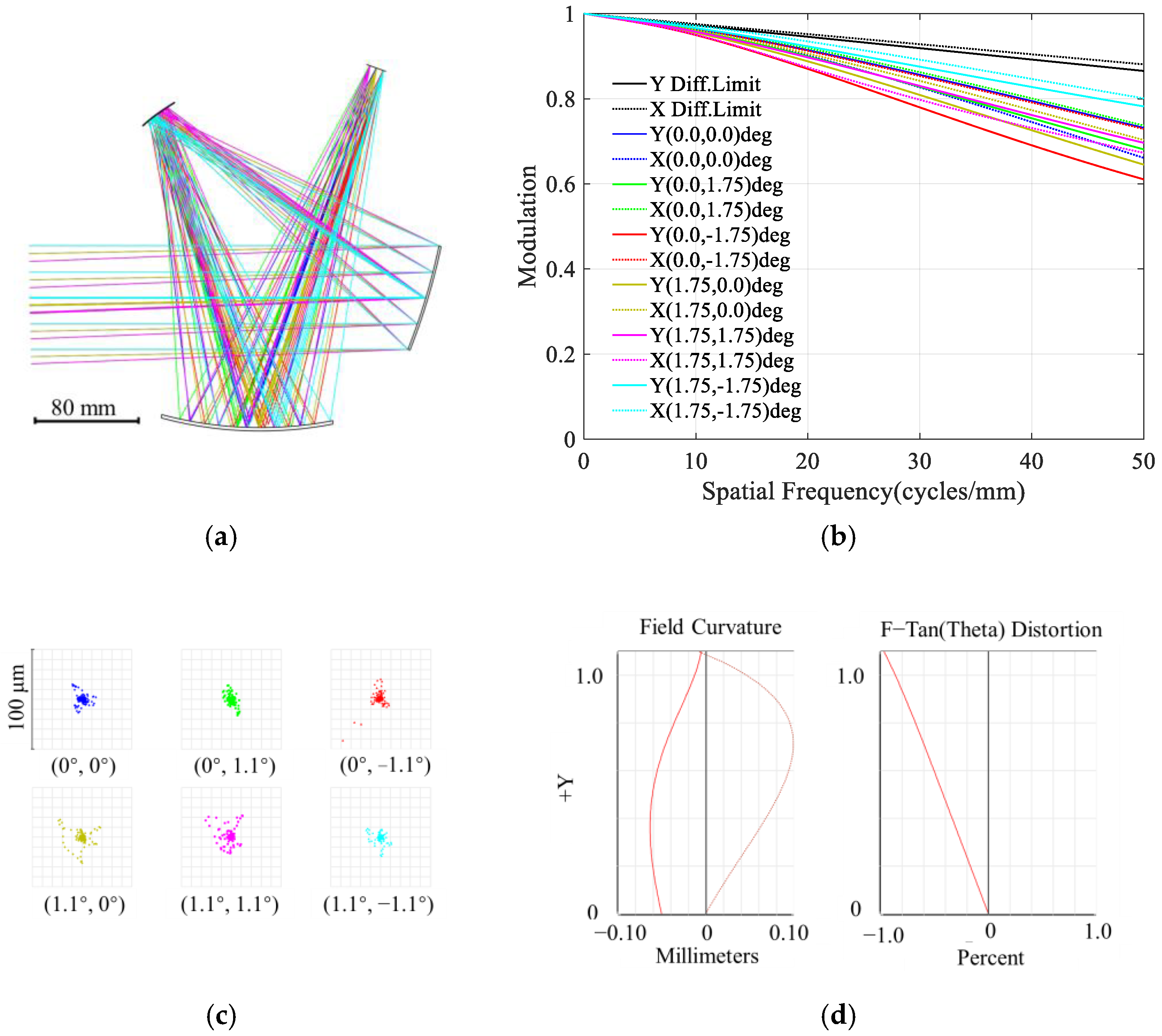
| Parameter | Specifications |
|---|---|
| Entrance pupil diameter | 80–100 mm |
| F-number | 3–3.5 |
| Field-of-view | 2° × 2°–4° × 4° |
| The number of mirrors | 3 |
| Work spectrum | 380–780 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Wei, Y.; Zhao, J. Adaptive Generation Method for Small Volume Easy Fabrication Freeform Unobscured Three-Mirror Systems Based on Machine Learning. Photonics 2025, 12, 405. https://doi.org/10.3390/photonics12050405
Sun Y, Wei Y, Zhao J. Adaptive Generation Method for Small Volume Easy Fabrication Freeform Unobscured Three-Mirror Systems Based on Machine Learning. Photonics. 2025; 12(5):405. https://doi.org/10.3390/photonics12050405
Chicago/Turabian StyleSun, Yiwei, Yangjie Wei, and Ji Zhao. 2025. "Adaptive Generation Method for Small Volume Easy Fabrication Freeform Unobscured Three-Mirror Systems Based on Machine Learning" Photonics 12, no. 5: 405. https://doi.org/10.3390/photonics12050405
APA StyleSun, Y., Wei, Y., & Zhao, J. (2025). Adaptive Generation Method for Small Volume Easy Fabrication Freeform Unobscured Three-Mirror Systems Based on Machine Learning. Photonics, 12(5), 405. https://doi.org/10.3390/photonics12050405





