Quantum Magneto-Optics in Graphene
Abstract
:1. Introduction
2. Electron Dispersion in Graphene
3. Graphene in Magnetic Fields

4. Magneto-Optic Effects in Graphene
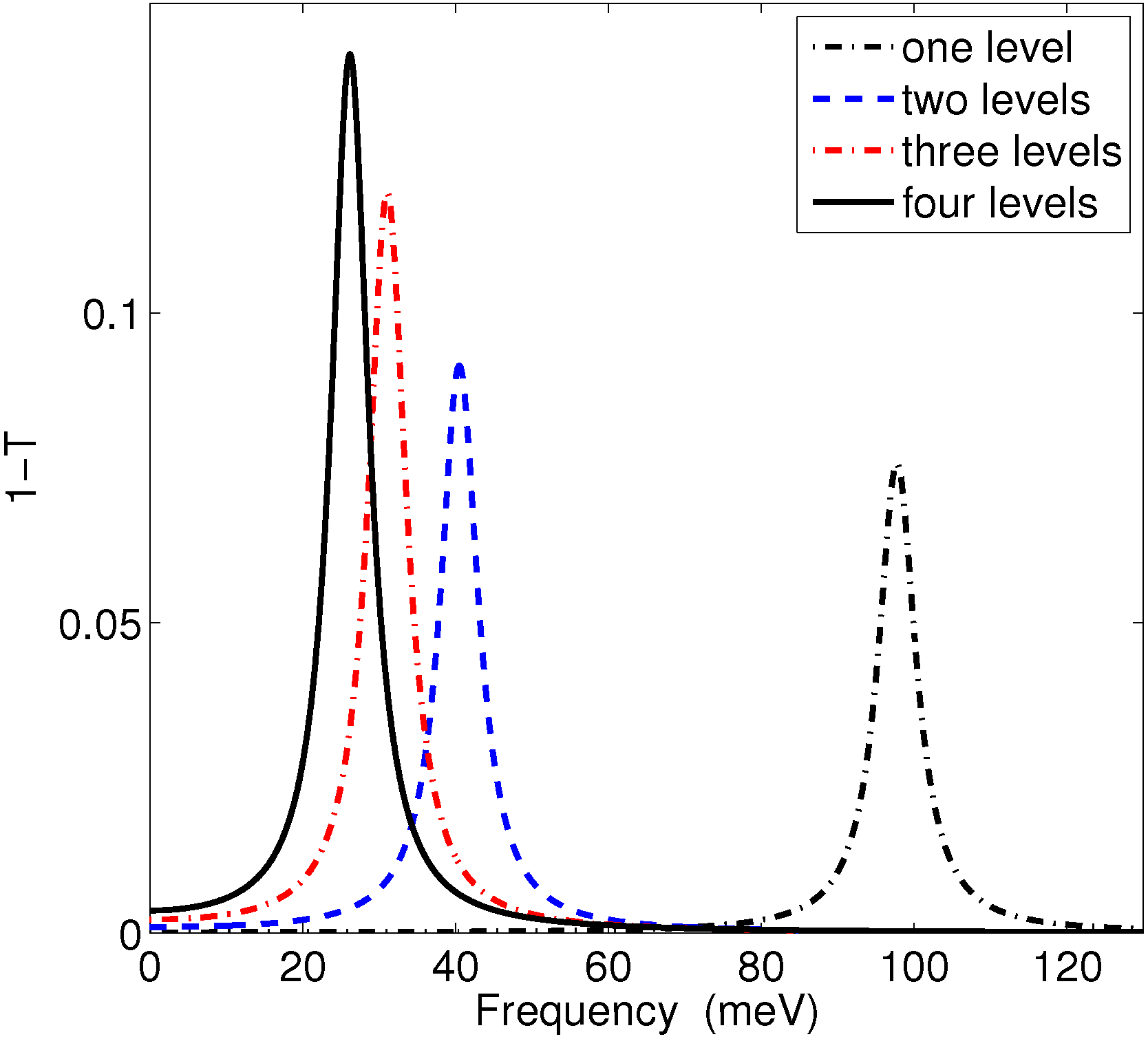

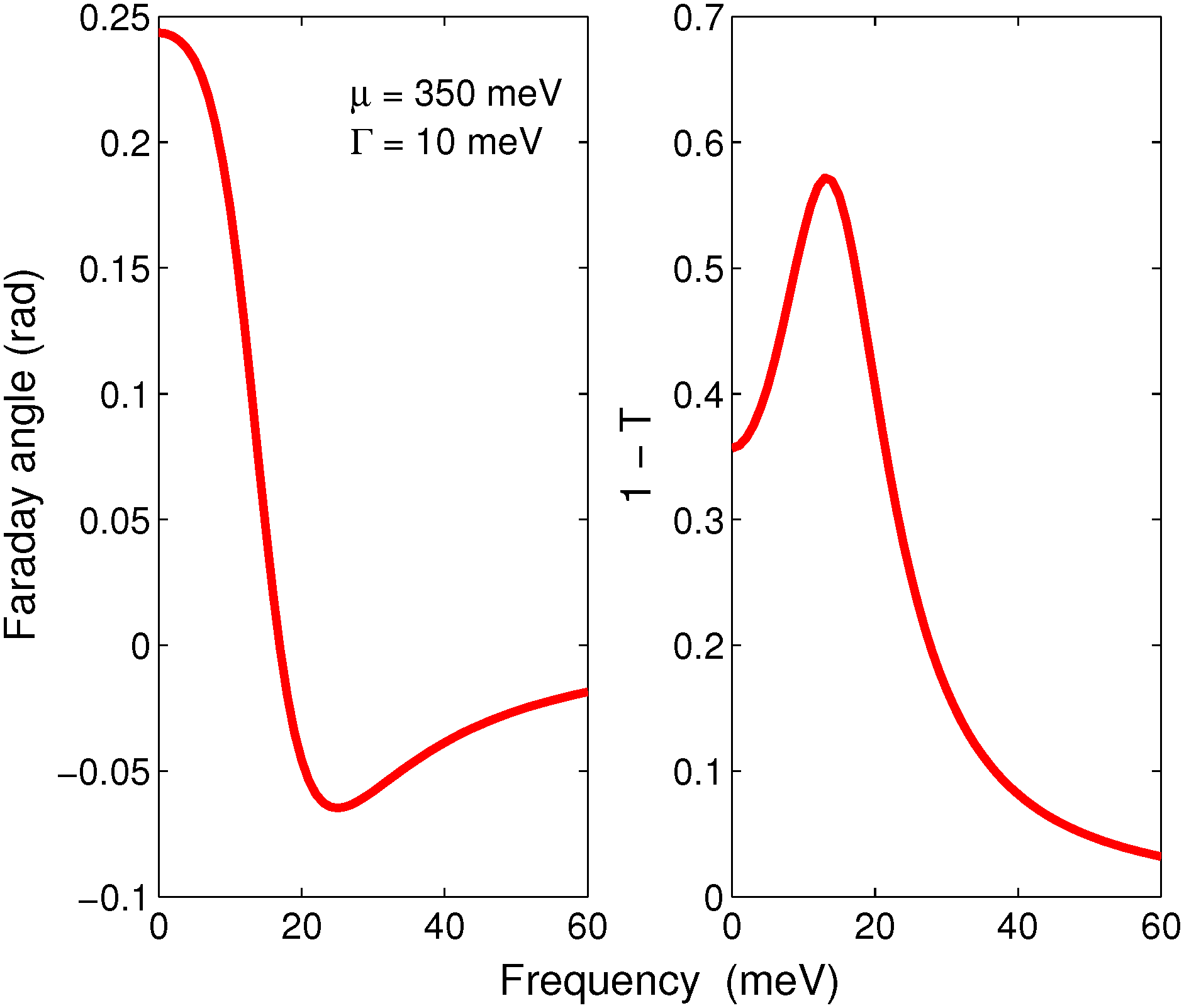
5. Discussion
Conflicts of Interest
References
- Slonchewski, J.C.; Weiss, P.R. Band Structure of Graphite. Phys. Rev. 1958, 109, 272. [Google Scholar] [CrossRef]
- Suematsu, H.; Tanuma, S.I. Cyclotron Resonances in Graphite by Using Circularly Polarized Radiation. J. Phys. Soc. Jpn. 1972, 33, 1619. [Google Scholar] [CrossRef]
- Toy, W.W.; Dresselhaus, M.S.; Dresselhaus, G. Minority carriers in graphite and the H-point magnetoreflection spectra. Phys. Rev. B 1977, 15, 4077. [Google Scholar] [CrossRef]
- Doezema, R.E.; Datars, W.R.; Schaber, H.; Van Schyndel, A. Far-infrared magnetospectroscopy of the Landau-level structure in graphite. Phys. Rev. B 1979, 19, 4224. [Google Scholar] [CrossRef]
- Mendez, E.; Misu, A.; Dresselhaus, M.S. Magnetoreflection study of graphite under pressure. Phys. Rev. B 1980, 21, 827. [Google Scholar] [CrossRef]
- Li, Z.Q.; Tsai, S.W.; Padilla, W.J.; Dordevic, S.V.; Burch, K.S.; Wang, Y.J.; Basov, D.N. Infrared probe of the anomalous magnetotransport of highly oriented pyrolytic graphite in the extreme quantum limit. Phys. Rev. B 2006, 74, 195404. [Google Scholar] [CrossRef]
- Orlita, M.; Faugeras, C.; Martinez, G.; Maude, D.K.; Sadowski, M.L.; Potemski, M. Dirac Fermions at the H Point of Graphite: Magnetotransmission Studies. Phys. Rev. Lett. 2008, 100, 136403. [Google Scholar] [CrossRef] [PubMed]
- Orlita, M.; Faugeras, C.; Schneider, J.M.; Martinez, G.; Maude, D.K.; Potemski, M. Graphite from the Viewpoint of Landau Level Spectroscopy: An Effective Graphene Bilayer and Monolayer. Phys. Rev. Lett. 2009, 102, 166401. [Google Scholar] [CrossRef] [PubMed]
- Orlita, M.; Potemski, M. Dirac electronic states in graphene systems: optical spectroscopy studies. Semicond. Sci. Technol. 2010, 25, 063001. [Google Scholar] [CrossRef]
- Crassee, I.; Levallois, J.; Walter, A. L.; Ostler, M.; Bostwick, A.; Rotenberg, E.; Seyler, T.; van der Marel, D.; Kuzmenko, A. Giant Faraday rotation in single- and multilayer graphene. Nat. Phys. 2011, 7, 48. [Google Scholar] [CrossRef]
- Kopelevich, Y.; Torres, J.H.S.; da Silva, R.R.; Mrowka, F.; Kempa, H.; Esquinazi, P. Reentrant Metallic Behavior of Graphite in the Quantum Limit. Phys. Rev. Lett. 2003, 90, 156402. [Google Scholar] [CrossRef] [PubMed]
- Luk’yanchuk, I.A.; Kopelevich, Y. Dirac and Normal Fermions in Graphite and Graphene: Implications of the Quantum Hall Effect. Phys. Rev. Lett. 2006, 97, 256801. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Zhang, Y.; Stormer, H.L.; Kim, P. Quantum Hall States near the Charge-Neutral Dirac Point in Graphene. Phys. Rev. Lett. 2007, 99, 106802. [Google Scholar] [CrossRef] [PubMed]
- Schneider, J.M.; Orlita, M.; Potemski, M.; Maude, D.K. Consistent Interpretation of the Low-Temperature Magnetotransport in Graphite Using the Slonczewski-Weiss-McClure 3D Band-Structure Calculations. Phys. Rev. Lett. 2009, 102, 166403. [Google Scholar] [CrossRef] [PubMed]
- Ramanayaka, A.N.; Mani, R.G. Transport study of the Berry phase, resistivity rule, and quantum Hall effect in graphite. Phys. Rev. B 2010, 82, 165327. [Google Scholar] [CrossRef]
- Ando, T. Magnetic Oscillation of Optical Phonon in Graphene. J. Phys. Soc. Jpn. 2007, 76, 024712. [Google Scholar] [CrossRef]
- Goerbig, M.O.; Fuchs, J.N.; Kechedzhi, K.; Fal’ko, V.I. Filling-Factor-Dependent Magnetophonon Resonance in Graphene. Phys. Rev. Lett. 2007, 99, 087402. [Google Scholar] [CrossRef] [PubMed]
- Falkovsky, L.A. Quantum magneto-optics of graphite with trigonal warping. Phys. Rev. B 2011, 84, 115414. [Google Scholar] [CrossRef]
- Li, G.; Andrei, E.Y. Observation of Landau levels of Dirac fermions in graphite. Nat. Phys. 2007, 3, 623. [Google Scholar] [CrossRef]
- Chuang, K.C.; Baker, A.M.R.; Nicholas, R.J. Magnetoabsorption study of Landau levels in graphite. Phys. Rev. B 2009, 80, 161410(R). [Google Scholar] [CrossRef]
- Zhang, L.M.; Li, Z.Q.; Basov, D.N.; Fogler, M.M.; Hao, Z.; Martin, M.C. Determination of the electronic structure of bilayer graphene from infrared spectroscopy. Phys. Rev. B 2008, 78, 235408. [Google Scholar] [CrossRef]
- Ushio, H.; Uda, T.; Uemura, Y. Theory of Cyclotron Resonance of Graphite. I. Determination of the Degree of Band Warping. J. Phys. Soc. Jpn. 1972, 33, 1551. [Google Scholar] [CrossRef]
- Nakao, K. Landau Level Structure and Magnetic Breakthrough in Graphite. J. Phys. Soc. Jpn 1976, 40, 761. [Google Scholar] [CrossRef]
- Partoens, B.; Peeters, F.M. From graphene to graphite: Electronic structure around the K point. Phys. Rev. B 2006, 74, 075404. [Google Scholar] [CrossRef]
- Grüneis, A.; Attaccalite, C.; Wirtz, L.; Shiozawa, H.; Saito, R.; Pichler, T.; Rubio, A. Tight-binding description of the quasiparticle dispersion of graphite and few-layer graphene. Phys. Rev. B 2008, 78, 205425. [Google Scholar] [CrossRef]
- Kuzmenko, A.B.; Crassee, I.; van der Marel, D.; Blake, P.; Novoselov, K.S. Determination of the gate-tunable band gap and tight-binding parameters in bilayer graphene using infrared spectroscopy. Phys. Rev. B 2009, 80, 165406. [Google Scholar] [CrossRef]
- Falkovsky, L.A.; Eksp, Z. Quasiclassical Quantization of Electrons and Holes in Bismuth in a Magnetic Field. Teor. Fiz. 1965, 49, 609. [Google Scholar]
- Dresselhaus, G. Graphite Landau levels in the presence of trigonal warping. Phys. Rev. B 1974, 10, 3602. [Google Scholar] [CrossRef]
- Elias, D.C.; Gorbachev, R.V.; Mayorov, A.S.; Morozov, S.V.; Zhukov, A.A.; Blake, P.; Ponomarenko, L.A.; Grigorieva, I.V.; Novoselov, K.S.; Guinea, F.; et al. Dirac cones reshaped by interaction effects in suspended graphene. Nat. Phys. 2011, 7, 701. [Google Scholar] [CrossRef]
- Abrikosov, A.A.; Beneslavsky, S.D. Possible Existence of Substances Intermediate Between Metals and Dielectrics. Sov. Phys. JETP 1971, 32, 699. [Google Scholar]
- Gonzalez, J.; Guinea, F.; Vozmediano, M.A.H. Non-Fermi liquid behaviour of electrons in the half-filled honeycomb lattice (A renormalization group approach). Nucl. Phys. B 1994, 424, 595. [Google Scholar] [CrossRef]
- Mishchenko, E.G. Effect of Electron-Electron Interactions on the Conductivity of Clean Graphene. Phys. Rev. Lett. 2007, 98, 216801. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falkovsky, L. Quantum Magneto-Optics in Graphene. Photonics 2015, 2, 13-20. https://doi.org/10.3390/photonics2010013
Falkovsky L. Quantum Magneto-Optics in Graphene. Photonics. 2015; 2(1):13-20. https://doi.org/10.3390/photonics2010013
Chicago/Turabian StyleFalkovsky, Leonid. 2015. "Quantum Magneto-Optics in Graphene" Photonics 2, no. 1: 13-20. https://doi.org/10.3390/photonics2010013
APA StyleFalkovsky, L. (2015). Quantum Magneto-Optics in Graphene. Photonics, 2(1), 13-20. https://doi.org/10.3390/photonics2010013



