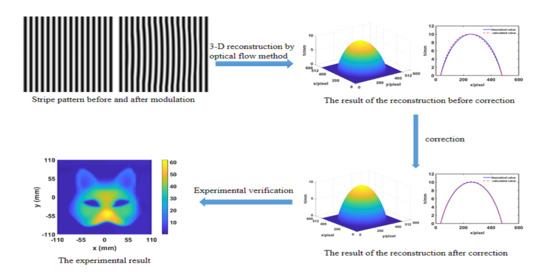
Object Shape Measurement Based on Brox Optical Flow Estimation and Its Correction Method
Abstract
1. Introduction
- Compared with existing phase measurement methods, it is simple in setup and operation. Only two frames of the image are captured and used for retrieving the height distribution.
- Compared with existing methods, it is less time consuming due to retrieving the height distribution directly. The measurement of the surface shape could be completed in less than 8 s.
- Because the optical flow method contains the time factor itself, it is more suitable for dynamic measurement.
- Compared with the existing tilt correction method, the newly proposed method is easier to implement and requires no additional operations.
- There are no strict limits to the projection pattern. Any image with varying gray values can be used for projection.
2. Principles
2.1. Introduction of the Brox Optical Flow Algorithm
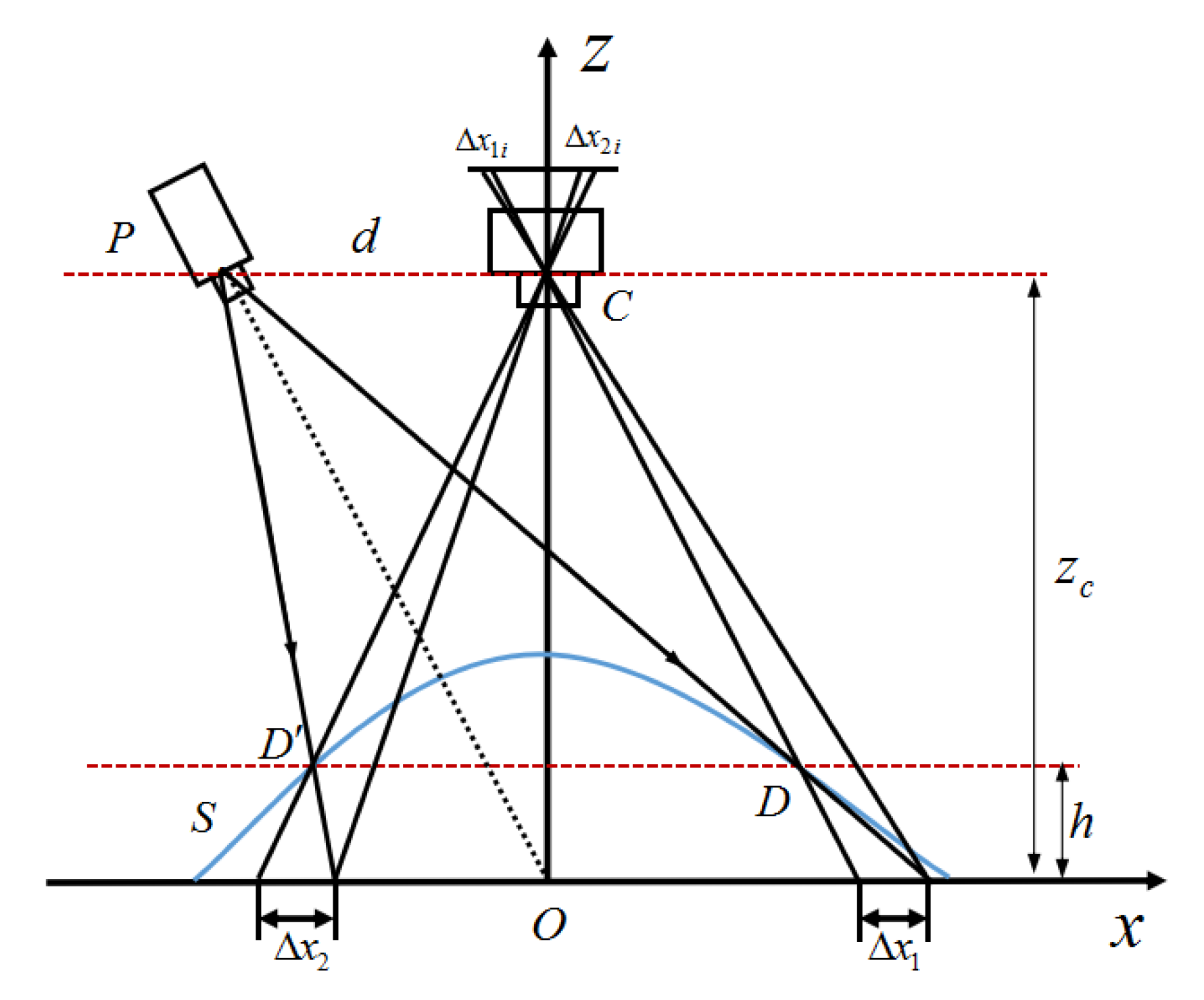
2.2. The Principle of the Surface Shape Measurement
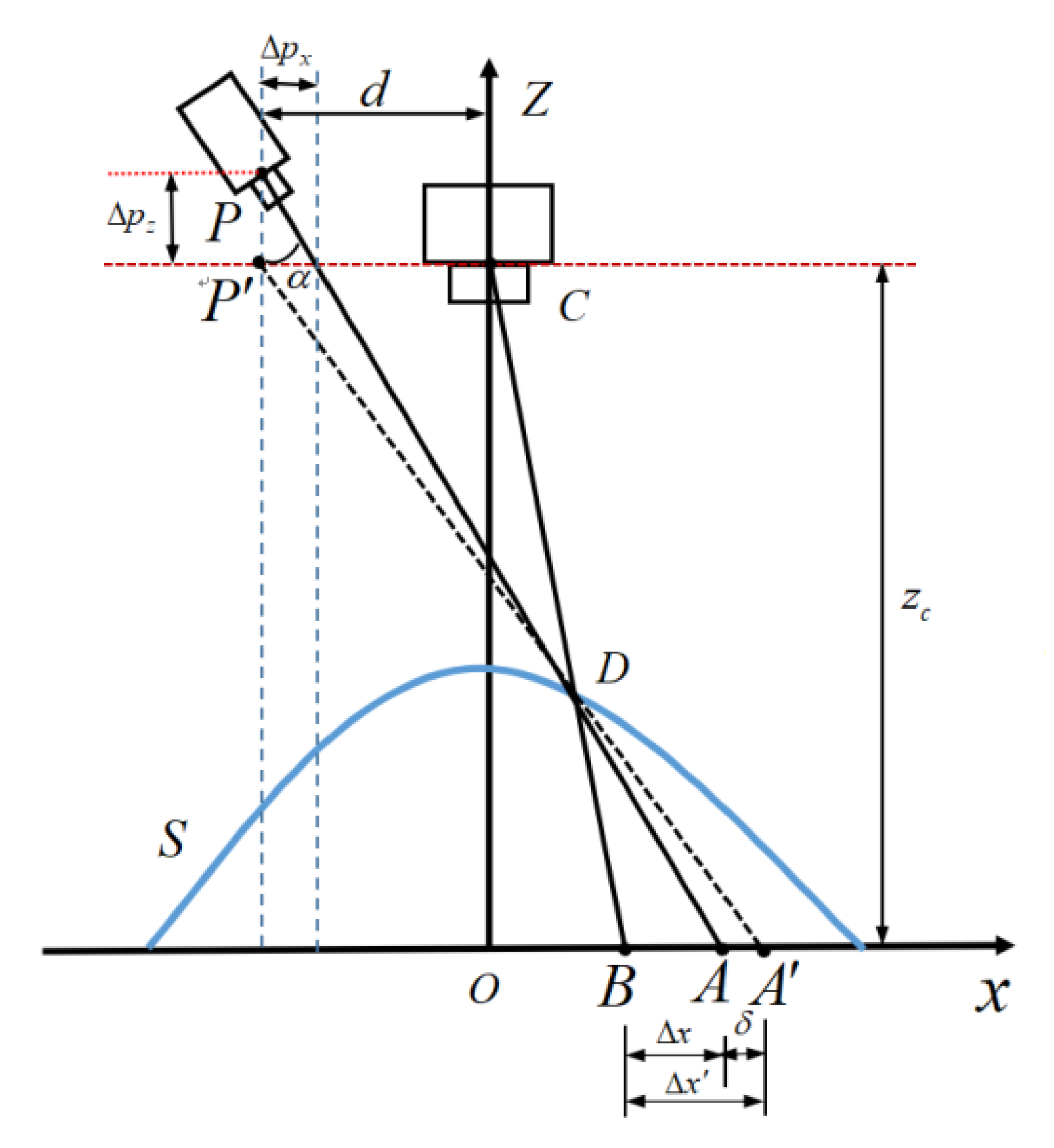
2.3. Correction Principle
3. Theoretical Simulation
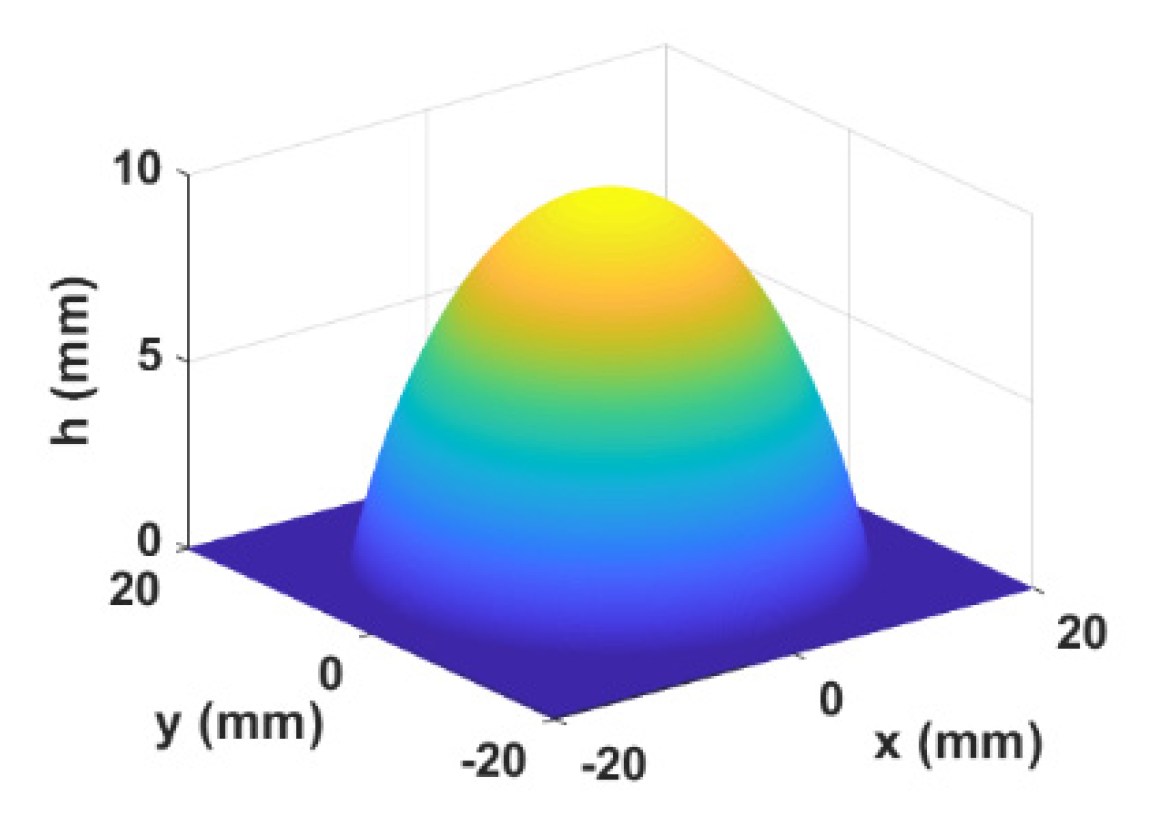
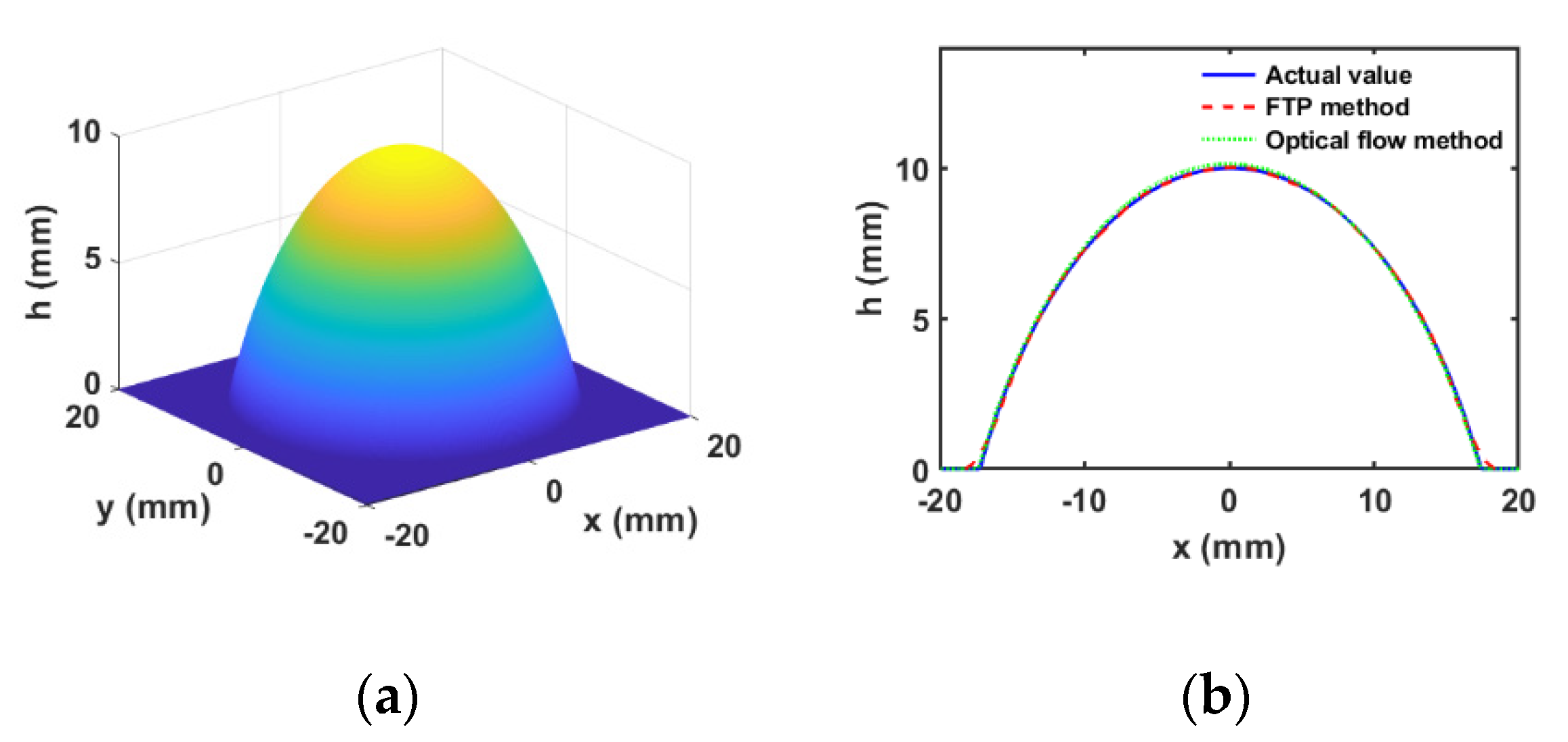
3.1. Numerical Simulation and Analysis of Surface Shape Measurement by Optical Flow Method
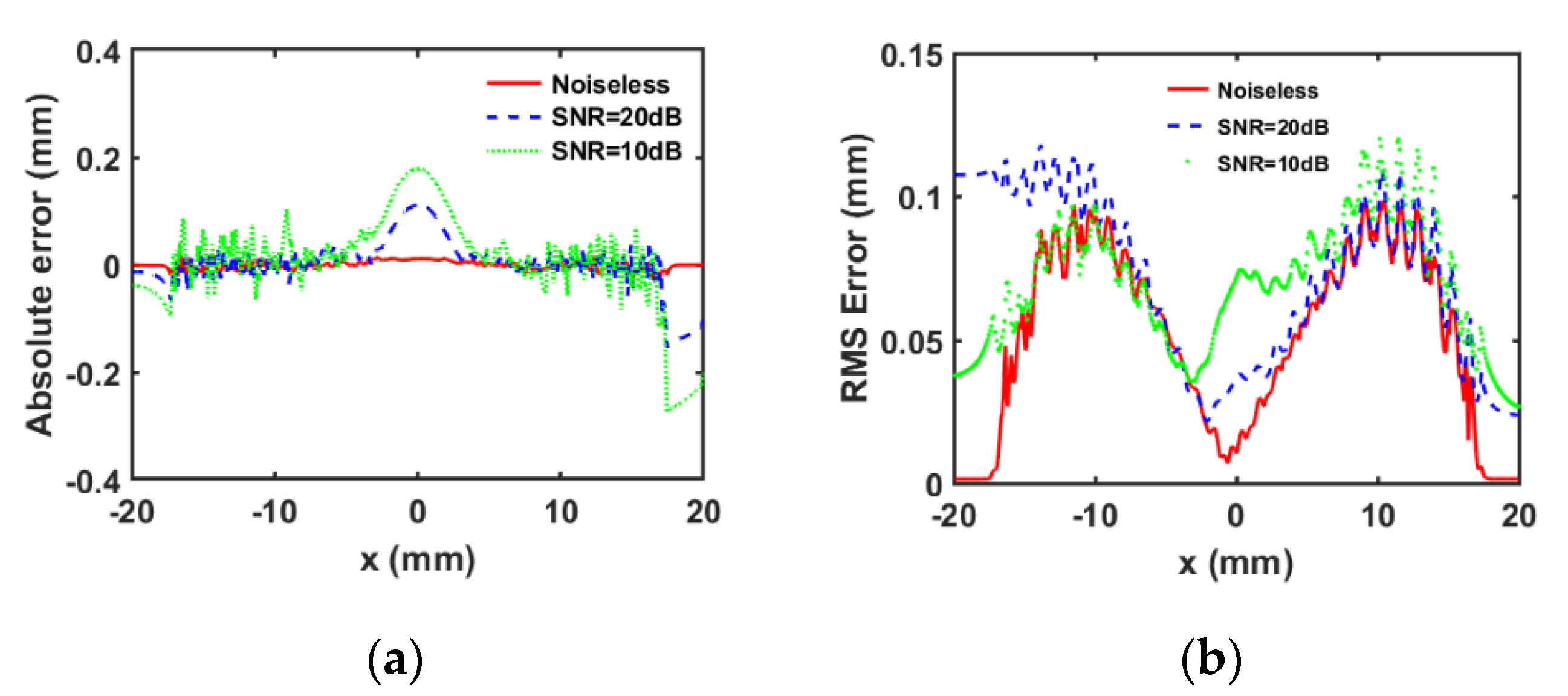
3.2. Error Correction Simulation
3.3. Sensitivity Analysis
4. Experiment
4.1. An Experiment on a Smooth Measuring Object
- Calibrating the measurement system. In order to make the effect of the correction method obvious, we set the projection distance and observation distance with large distance. Different from the optical setup parameter estimation method [17], the optical center positions of the projector and camera are calibrated by using Zhang’s calibration method [18,19]. After calibration, the distance from the projector to the reference plane is 1975.40 mm and that of the CCD sensor is 1922.80 mm. The horizontal distance between the CCD sensor and the projector is 84.50 mm. The magnification of the image is 512/220 pixel/mm. The calibration process will take about 10 min, but the following steps can be performed multiple times as long as the calibration is completed once.
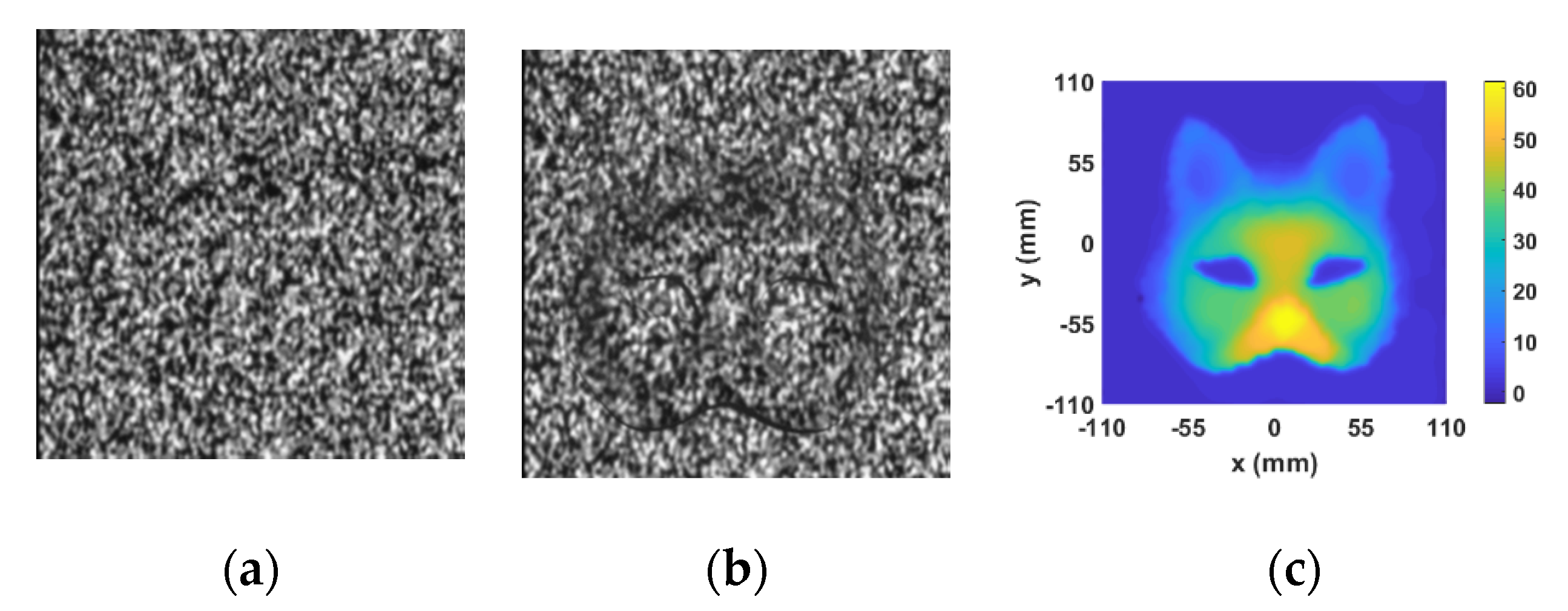
- Capturing two images. The two images before and after placing the object are recorded by an ordinary CCD sensor with the sensitive area of 768 × 576 pixels at 8-bit resolution. The captured images are shown in Figure 11. We estimate the noise level of the image by using the method proposed by Chen et al. [20]. The mean noise level of Figure 11b is 1.41 dB.
- Calculating the optical flow and height distribution. After calculating the optical flow between the two images by using the Brox method, the height distribution of the specimen can be obtained according to Equation (18)—shown in Figure 12. This step will take 6 to 10 s depending on the image size and the parameters of Brox algorithm.
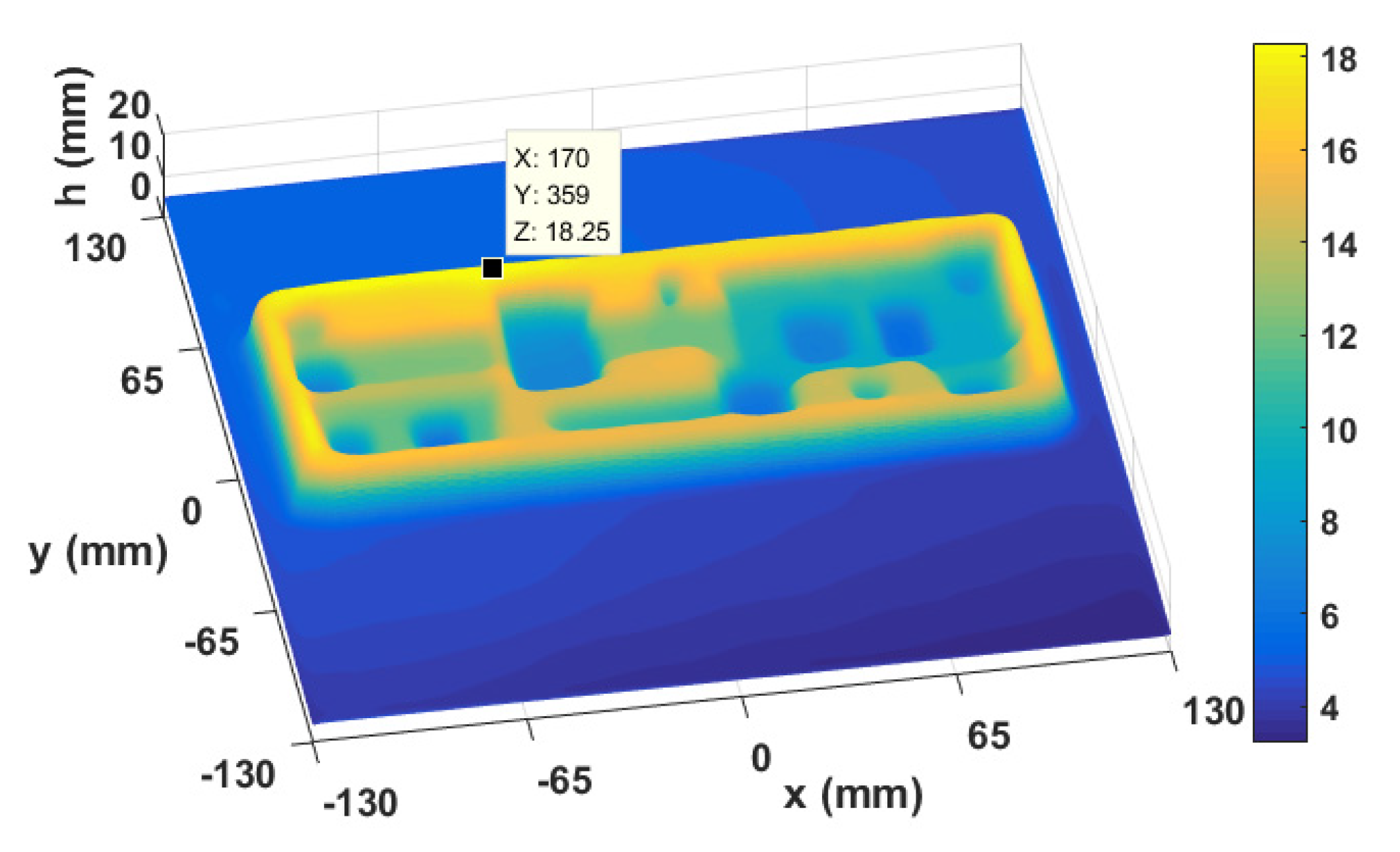
4.2. An Experiment on a Structured Object
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Godin, G.; Beraldin, J.A.; Taylor, J.; Cournoyer, L.; Rioux, M.; El-Hakim, S.; Baribeau, R.; Blais, F.; Boulanger, P.; Domey, J.; et al. Active optical 3D imaging for heritage applications. IEEE. Comput. Graph 2002, 22, 24–36. [Google Scholar] [CrossRef]
- Yue, L.; Liu, X. Application of 3D optical measurement system on quality inspection of turbine blade. In Proceedings of the 2009 16th International Conference on Industrial Engineering and Engineering Management, Beijing, China, 21–23 October 2009; pp. 1089–1092. [Google Scholar]
- Hung, Y.; Lin, L.; Shang, H.; Park, B.G. Practical three-dimensional computer vision techniques for full-field surface measurement. Opt. Eng. 2000, 39, 143. [Google Scholar] [CrossRef]
- Fitts, J.M. High-Speed 3-D Surface Measurement Surface Inspection and Reverse-CAD System. U.S. Patent 5,175,601, 29 December 1992. [Google Scholar]
- Gorthi, S.S.; Rastogi, P. Fringe projection techniques: Whither we are? Opt. Lasers Eng. 2010, 48, 133–140. [Google Scholar] [CrossRef]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Yang, F.; He, X. Two-step phase-shifting fringe projection profilometry: Intensity derivative approach. Appl. Opt. 2007, 46, 7172. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Tang, Y.; Chen, J. Three-dimensional shape measurement with an arbitrarily arranged projection moiré system. Opt. Lett. 2016, 41, 717–720. [Google Scholar] [CrossRef] [PubMed]
- Sun, P.; Dai, Q.; Tang, Y.; Lei, Z. Coordinate calculation for direct shape measurement based on optical flow. Appl. Opt. 2020, 59, 92–96. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, C.; Wang, J.; Opristescu, D.; Volk, W. Implementation and evaluation of optical flow methods for two-dimensional deformation measurement in comparison to digital image correlation. Opt. Lasers Eng. 2018, 107, 127–141. [Google Scholar] [CrossRef]
- Li, B.; Fu, Y.; Zhang, J.; Wu, H.; Zeng, Z. Period correction method of phase coding fringe. Opt. Rev. 2015, 22, 717–723. [Google Scholar] [CrossRef]
- Wang, Z.; Du, H.; Bi, H. Out-of-plane shape determination in generalized fringe projection profilometry. Opt. Express 2006, 14, 12122–12133. [Google Scholar] [CrossRef] [PubMed]
- Brox, T.; Bruhn, A.; Papenberg, N.; Weickert, J. High accuracy optical flow estimation based on a theory for warping. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2004; pp. 25–36. [Google Scholar]
- Horn, B.K.P.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Lucas, B.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence (IJCAI’), San Francisco, CA, USA, 24–28 August 1981. [Google Scholar]
- Xing-Jiang, L.; Lai-I, L. Geometric interpretation of several classical iterative methods for linear system of equations and diverse relaxation parameter of the SOR method. Appl. Math. J. Chin. Univ. 2013, 28, 269–278. [Google Scholar]
- Kofman, J. Comparison of linear and nonlinear calibration methods for phase-measuring profilometry. Opt. Eng. 2007, 46, 043601. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE. Trans. Pattern Anal. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- An, Y.; Bell, T.; Li, B.; Xu, J.; Zhang, S. Method for large-range structured light system calibration. Appl. Opt. 2016, 55, 9563–9572. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Zhu, F.; Heng, P.A. An Efficient Statistical Method for Image Noise Level Estimation. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Sun, P.; Dai, Q.; Fan, C.; Lei, Z. Object Shape Measurement Based on Brox Optical Flow Estimation and Its Correction Method. Photonics 2020, 7, 109. https://doi.org/10.3390/photonics7040109
Tang Y, Sun P, Dai Q, Fan C, Lei Z. Object Shape Measurement Based on Brox Optical Flow Estimation and Its Correction Method. Photonics. 2020; 7(4):109. https://doi.org/10.3390/photonics7040109
Chicago/Turabian StyleTang, Yuxin, Ping Sun, Qing Dai, Chao Fan, and Zhifang Lei. 2020. "Object Shape Measurement Based on Brox Optical Flow Estimation and Its Correction Method" Photonics 7, no. 4: 109. https://doi.org/10.3390/photonics7040109
APA StyleTang, Y., Sun, P., Dai, Q., Fan, C., & Lei, Z. (2020). Object Shape Measurement Based on Brox Optical Flow Estimation and Its Correction Method. Photonics, 7(4), 109. https://doi.org/10.3390/photonics7040109