Photonic Band Gaps and Resonance Modes in 2D Twisted Moiré Photonic Crystal

Abstract

The study of twisted bilayer 2D materials has revealed many interesting physics properties. A twisted moiré photonic crystal is an optical analog of twisted bilayer 2D materials. The optical properties in twisted photonic crystals have not yet been fully elucidated. In this paper, we generate 2D twisted moiré photonic crystals without physical rotation and simulate their photonic band gaps in photonic crystals formed at different twisted angles, different gradient levels, and different dielectric filling factors. At certain gradient levels, interface modes appear within the photonic band gap. The simulation reveals “tic tac toe”-like and “traffic circle”-like modes as well as ring resonance modes. These interesting discoveries in 2D twisted moiré photonic crystal may lead toward its application in integrated photonics.

1. Introduction

Reducing the dimensionality of a material system very often leads to exceptional electronic, optical, and magnetic properties because of enhanced quantum effects in reduced phase space [1]. Recently, atomically thin two-dimensional (2D) materials have been stacked layer-by-layer to create synthetic materials with entirely new properties [2]. Intensive research has been focused on moiré materials where 2D layered materials are superposed against each other with a relative twist angle [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. The formed moiré pattern at different twist angles results in a topological edge state, the formation of moiré excitons, interlayer magnetism, and fine control of the electron band structure [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. In particular, the recent discovery of superconductivity in magic-angle twisted bilayer graphene [4] has triggered another wave of research in moiré 2D materials [5,6,7,8,9,10,11,12,13,14,15,16,17,18].

Twisted moiré photonic crystal is an optical analog of twisted 2D materials while photonic crystal is a periodic dielectric structure with a modulation of the refractive index close to the operation wavelength of light [19,20,21]. The twisted bilayer photonic crystal consists of two layers of identical photonic crystal stacked into moiré patterns [19,22,23,24] that also revealed magic-angle photonic flat bands with a non-Anderson-type localization [23]. Several research groups have generated twisted photonic crystals in photorefractive crystals with a shallow refractive index modulation and have observed the localization and delocalization of light waves [25,26,27,28,29,30,31].

Moiré photonic crystals have also been fabricated by holographic fabrication through laser interference of two sets of laser beams arranged in two-cone geometry with different cone angles [31,32,33,34,35,36,37,38]. Due to the gradient pattern and super-cell in the photonic crystal, this has also been named graded photonic super-crystal [37,38,39] or graded photonic super-quasi-crystal [35]. In contrast to twisted bilayer 2D materials and twisted bilayer photonic crystal, two mutually twisted optical lattices generated by laser interference will interfere further and form a single layer twisted photonic crystal if we consider the 2D case [36].

In this paper, we show the relationship between moiré pattern and twisted holographic pattern. Due to three-dimensional (3D) feature in the formed holographic pattern, there are different modulation levels at different z-locations and, thus, different gradients in the x–y plane. We simulate the photonic band structure and resonance modes for 2D twisted photonic crystal formed at different z-locations. There are interface modes within the photonic band gap at certain z-locations. Interestingly, crossing the waveguide along the interface, ring resonator, and their combination appears at different frequencies in the simulation of electric-field intensity for resonance modes in the 2D twisted moiré photonic crystal.

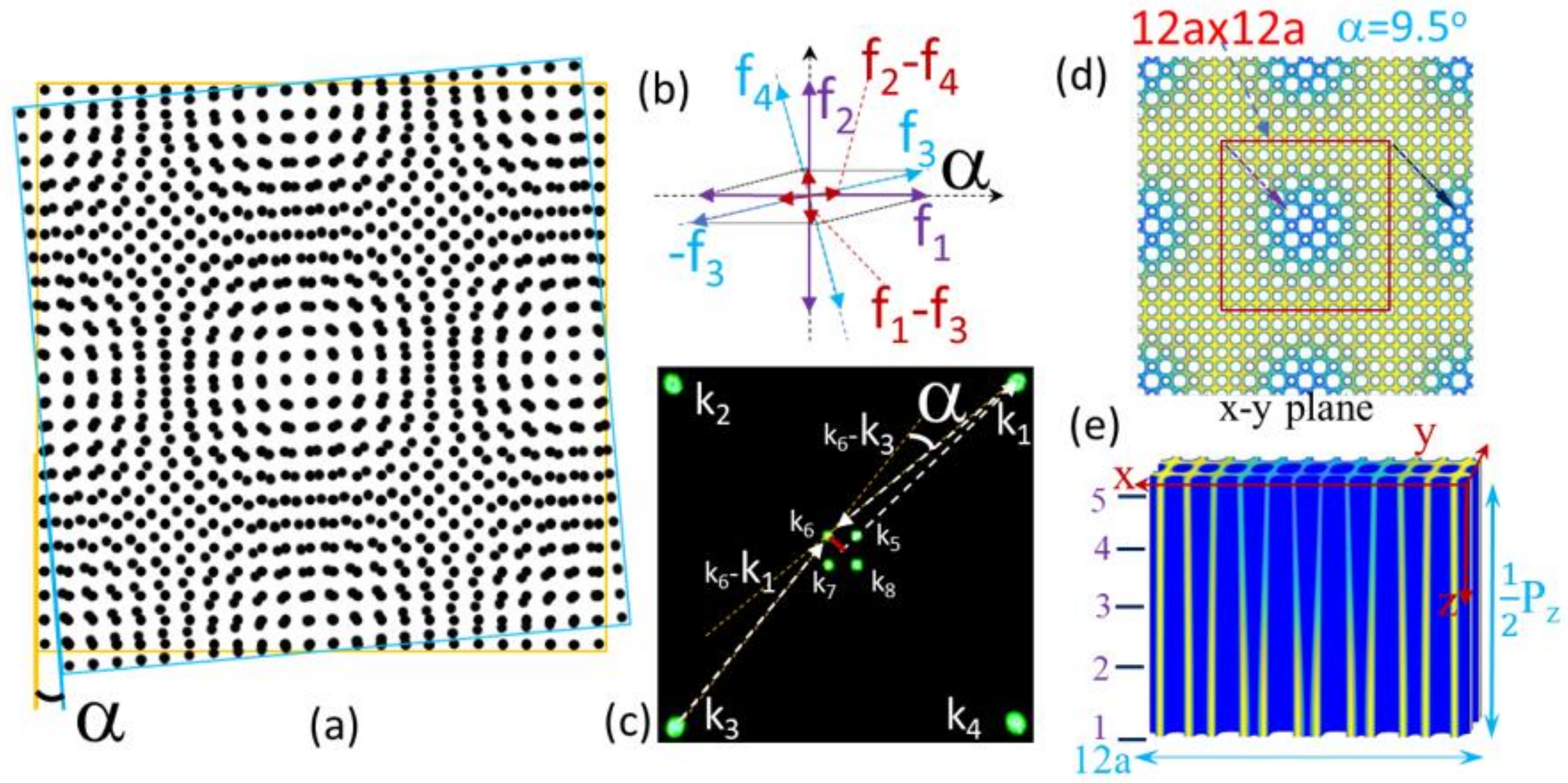
2. Design Principle from a Moiré Pattern with a Physical Rotation to a Twisted Holographic Photonic Crystal without Physical Rotations

The design principle of twisted photonic crystals comes from the analysis of reciprocal spatial and frequency (spectral) domains of the moiré pattern and the application of such an analysis to the real and reciprocal k-space in the optical lattice.

Figure 1a shows the superposition of 2D square dot patterns in the spatial domain, as an example, with a twist angle of α. The square dot pattern edged by a yellow square in Figure 1a has two fundamental frequency vectors f₁ and f₂ in the spectral domain in the Fourier transform. These two frequency vectors are perpendicular and have the same magnitude as shown in Figure 1b. The spectra of Fourier transform have …, −3f₁, −2f₁, −f₁, 0, f₁, 2f₁, 3f₁, … and −3f₂, −2f₂, −f₂, 0, f₂, 2f₂, 3f₂, …, etc. [40]. Only frequency vectors of −f₁, f₁ and −f₂, f₂ are drawn in purple arrows in Figure 1b. For the square dot pattern edged by a blue square, only frequency vectors of −f₃, f₃ and −f₄, f₄ are drawn in blue arrows in Figure 1b. The f₃ and f₄ vectors are perpendicular and have the same magnitude. The frequencies of f₁–f₃ and f₂–f₄ in Figure 1b are within the visible circle [40].

The spectra with frequencies of f₁–f₃ and f₂–f₄ represent the visible periodic component in the spatial domain in Figure 1a. The index for a moiré pattern is defined by, for example, f₁−f₃ = (1f₁ + 0f₂ − f₃ + 0f₄) => (1, 0, −1, 0) [40]. Thus, Figure 1a shows a moiré pattern with an index of (1, 0, −1, 0) and (0, 1, 0, −1) in the superposition of two square dot patterns with a twist angle of α. The moiré frequency (f₁–f₃) can be calculated by Equation (1)

$$f_1-f_3=2f_1 sin\frac{\alpha }{2}$$

(1)

A similar analysis is applied to the holographic pattern below. When eight beams (eight 532 nm green spots in Figure 1c) are overlapped through a 4f imaging system [34], these four inner beams together with four outer beams have holographic interference with an intensity I(r) calculated by Equation (2):

$$I\left(r\right)=\langle {\displaystyle \sum }_{i=1}^8{E}_i^2\left(r,t\right)\rangle +{\displaystyle \sum }_{i<j}^8{E}_i{E}_j{e}_i·e_{j}cos\left[\left(k_j-k_i\right)·r+\left({\delta }_j-{\delta }_i\right)\right]$$

(2)

where e is the electric field polarization, E is the electric field, k is the wave vector, and δ is the initial phase. The orientation of the optical lattice in real space is determined by the vector difference of (k_i–k_k) in reciprocal space. (k₁,k₂,k₃,k₄) in Figure 1c are the k-vector components in the x–y plane for outer beams and have the same magnitude while (k₅,k₆,k₇,k₈) are the k-vector components in the x–y plane for inner beams and have also the same magnitude. From Figure 1c, we can see that the k-vector difference (k₁–k₆) is twisted by a rotation angle α from (k₃–k₆).

There is the same twist angle between (k₂–k₇) and (k₄–k₇), between (k₃–k₈) and (k₁–k₈), and between (k₄–k₅) and (k₂–k₅). By analyzing the cross-section in the x–y plane of the formed 3D holographic pattern, a square optical lattice in real space due to reciprocal k-vectors of (k₁–k₆), (k₂–k₇), (k₃–k₈), and (k₄–k₅) is twisted by a rotation angle α from those by (k₃–k₆), (k₄–k₇), (k₁–k₈), and (k₂–k₅). The twist angle α is determined by the ratio of the k-vector component in th4 x–y plane of the inner beam over the outer beam in Equation (3):

$$\alpha =2 ta{n}^{-1}\left(\frac{k_6}{k_1}\right)$$

(3)

Figure 1d shows a simulated twisted 2D holographic photonic crystal in the x–y plane. A super-cell appears in the figure as indicated by red solid square. The size(s) of the super-cell is approximately determined by Equation (4):

$$s=\frac{2\pi }{k_{5}cos45-k_6\cos 135}=\frac{2\pi }{2k_{6}cos45},$$

(4)

and lattice period a is approximately calculated by Equation (5):

$$a=\frac{2\pi }{k_{1}cos45-k_2\cos 135}=\frac{2\pi }{2k_{1}cos45}.$$

(5)

Thus, the size of super-cell is related to lattice period a and twist angle α by Equation (6):

$$s=\frac{k_1}{k_6}a=\frac{a}{tan\left(\frac{\alpha }{2}\right)}$$

(6)

The period in the z-direction (P_z) of the 3D holographic pattern is determined by the z-components of inner and outer beams, k_i,z and k_o,z, respectively, in Equation (7):

$$P_z=\frac{2\pi }{k_{i,z}-k_{o,z}}.$$

(7)

Figure 1d shows simulated 2D moiré photonic crystal in the x–y plane with a twist angle of 9.5 degrees and super-cell size of 12a × 12a as indicated by the solid red square. The central area of the red square in Figure 1d is a bright region, and the others are dark regions. Figure 1e shows a 3D interference pattern with dimensions of 12a × 2a × 0.5 P_z. These two figures are inverted structures from the interference assuming a positive photoresistor is used. Figure 1d is a cross section at z = 0.17 P_z from the bottom of Figure 1e.

Thus, by arranging the two sets of interfering beams in two-cone geometry and controlling the cone angle, we are able to relate the moiré pattern to the twist photonic crystal. Those graded photonic super-crystals [31,33,34,37] generated by two-cone arrangement of the laser beam are actually 2D twisted photonic crystals.

3. Simulation Methods

We simulate photonic band gap and resonance modes for 2D twist moiré photonic crystal obtained at different z-locations of 1, 2, 3, 4, and 5 in Figure 1e and also at different iso-intensity surface by setting up the intensity threshold. In the simulation, the interference intensity function, I(r), in Equation (2) at certain z-location, is replaced by a binary Si/air structures by comparing I(r) with a threshold intensity I_th. A step function is used: ε(r) = 1 (for air) when I > I_th, and ε(r) = 12 (for Si) when I < I_th. Photonic band structures in 2D twisted moiré photonic crystal with air holes in Si were computed using the MIT Photonic Bands (MPB) software package, a fully-vectorial eigenmode solver for Maxwell’s equations [41], via the Simpetus Electromagnetic Simulation Platform from Amazon Web Services.

The spatial distribution of dielectric constants was output from MPB and is shown in top row in Figure 2 at different z-locations of 0.11, 0.23, 0.34, and 0.45 P_z in location 2, 3, 4, and 5 in Figure 1e, respectively. We also simulate cavity quality factors and electric field (E-field) intensity distributions for resonance modes in twisted photonic crystal with a thickness of 2a using the harmonic inversion function included in the MIT MEEP software [42,43] via Amazon Web Services.

4. Results

4.1. Photonic Band Structures in Twisted Photonic Crystals with Different z-Locations, Twist Angle and Threshold Intensity in the Step Function

We simulated photonic band structures in moiré photonic crystals with a twist angle of 9.5 degrees obtained at various z-locations. Figure 2a–d shows the results for TE modes in the twisted moiré photonic crystals at z = 0.11, 0.23, 0.34, and 0.45 P_z, respectively. The smaller the z-location in Figure 2, the higher the gradient level is. The shadowed areas in Figure 2a indicate the photonic crystal gaps. Figure 2a shows three photonic band gaps around frequency a/λ of 0.26–0.31, 0.4–0.42, and 0.43–0.44. With increasing z-location, the size of all three band gaps decreases and the frequency ranges of the photonic band gaps are almost same. However, interface modes (or waveguide mode for wave propagation) appear within the lowest photonic band gap in Figure 2c,d. The photonic band gap around 0.4–0.41 disappears at z-location = 0.45 P_z in Figure 2d.

Figure 3 shows the photonic band structure for TE modes in moiré photonic crystals with twist angles of 6.4, 9.5, and 18.9 degrees at a z-location around 0.4 P_z. In Figure 3a,b, the photonic band gap appears at almost the same frequency range and almost the same gap size. Interface modes appear in both Figure 3a,b. In the unit super-cell of 12a × 12a in Figure 3b, half of the lattices are inside the yellow circle (bright region). Both dark and bright regions have contribution to the formation of the photonic band gap and interface mode. An increase of the unit super-cell to 18a × 18a in Figure 3a only increases the dark region outside the yellow circle. However, almost all regions are considered as bright regions in the unit super-cell of 6a × 6a in Figure 3c.

The photonic band gap increases and the interface mode is not flat and close to the band-edge above the shadowed area in Figure 3c. Other optical properties, such as the extraction efficiency of organic light emitting diode patterned in moiré photonic crystal, reaches high performance in moiré photonic crystal with unit super-cell sizes between 9a × 9a and 14a × 14a [44]. It is not necessary to have a twisted photonic crystal with a very large unit super-cell in order to gain different properties from traditional photonic crystals. Below, we focus our research on the moiré photonic crystal with a twist angle of 9.5 degrees (super-cell of 12a × 12a).

We simulated photonic band structures for moiré photonic crystals with a twist angle of 9.5 degrees, obtained by setting the threshold I_th in the range of 16% I_max and 26% I_max in the step function and at z-locations of 0.11, 0.23, 0.34, and 0.45 P_z. Representative results for twisted photonic crystals with z = 0.11 P_z, I_th = 16% I_max, and 24% I_max are shown in Figure 4a,b, and with z = 0.34 P_z, I_th = 18% I_max, and 24% I_max in Figure 4c,d, respectively. With increasing threshold intensity, both filling fraction of dielectric materials and effective refractive index of the twisted photonic crystal will increase.

The central wavelength for the Bragg diffraction from the twisted photonic crystal will also increases. Thus, the central frequency of the photonic band gap decreases as shown in Figure 4. The band gap width also decreases with increasing the threshold intensity. By varying I_th, the bottom photonic band gap does not have an interface mode for twisted photonic crystals obtained at z = 0.11 and 0.23 P_z, and there is always an interface mode in the bottom band gap for those obtained at z = 0.34 and 0.45 P_z. However, the band gap splits and interface modes appear in the upper band gap with increasing I_th for all z locations.

4.2. Resonance Modes in Twisted Photonic Crystals at Different z-Locations

We simulate quality-factors (Q-factors) and electric-field intensity distribution for resonance modes in two moiré photonic crystals where one has no interface mode and the other has an interface mode in the bottom band gap. Figure 5a–f shows the electric-field intensity for resonance and interface modes at frequency a/λ of 0.285, 0.30, 0.39, 0.40, 0.414, and 0.42 with a Q-factor of 45,888, 2691, 1226, 6817, 2150, and 1683, respectively, for moiré photonic crystal with a twist angle of 9.5 degrees at z = 0.11 P_z.

Due to the dislocation in the bottom band gap [38] between the bright and dark regions in the moiré photonic crystal, some resonance modes appear in the bright region with a high Q-factor as shown in Figure 5a. The resonance or waveguide modes in Figure 5c–f are related to the interface modes in the upper band gap. They have a square symmetry with oscillations in the x and y directions in Figure 5c, in the diagonal direction in 5f and in both x (or y) and diagonal directions in Figure 5d,e. Figure 5g shows the Q-factors for resonance and interface modes at certain frequency locations. The purple square and red circles in the figure indicate these modes near the band gap edges or within the interface state.

Figure 6 shows the electric-field intensity distribution for interface (or waveguide) modes at frequencies a/λ of 0.272, 0.288, 0.322, and 0.422 with a Q-factor of 1481, 3260, 2046, and 3407, respectively, for moiré photonic crystal with a twist angle of 9.5 degrees at z = 0.34 P_z. Due to the small gradient in the moiré pattern at z = 0.34 P_z and interface modes within both bottom and upper band gaps, wave propagation into the moiré photonic crystal is expected. High symmetry “traffic circle”-like waveguides and ring resonators are observed in Figure 6a at a frequency a/λ of 0.272, close to the frequency for the interface mode within the bottom band gap. Figure 6b shows a ring resonator around the edge of the bright region in the moiré photonic crystal at a frequency a/λ of 0.288. Square symmetry “tic tac toe”-like wave propagation is shown in Figure 6c at a frequency a/λ of 0.322, near the gap edge of bottom band gap. The “x” shape resonance mode in Figure 6d corresponds to the interface mode within the upper band gap.

5. Discussion

Usually point or line defects are designed for the engineering of a resonance cavity or waveguide in a traditional photonic crystal. In a moiré photonic crystal with a twist angle of 9.5 degrees in Figure 6, there is an interface for light to propagate without specifically designed defects in the twisted photonic crystal. Topological properties in moiré photonic crystals need to be further studied for a potential application of topological waveguide [45,46].

The pattern inside the red square in Figure 1d with a size of 12a × 12a has been input as a unit super-cell for the simulation of the photonic band gap. The size of the air motif increases along the purple dashed arrow in a diagonal direction in the figure. However, the size of the air motif decreases along the blue dashed arrow on the right side of the square in Figure 1d. In order to have more accurate photonic band structure in the moiré photonic crystal, a unit super-cell of 24a × 24a can be used for the simulation. However, higher performance computation than the current one is needed. Even for the current simulation with a unit super-cell of 12a × 12a, a resolution of 18 is not high enough.

The simulation of electric-field intensity and Q-factors was performed in a pattern with a size of 24a × 24a for the twisted photonic crystal with a unit super-cell size of 12a × 12a in Figure 5 and Figure 6. These results include the effect of size changes in the air motif in Figure 1d.

We do not yet understand why we were not able to obtain photonic band gaps for TM modes by varying the threshold intensity and, thus, the filling fraction of dielectric materials. With increasing unit super-cell size, the number of modes increases per a frequency range in the photonic band structure. With the same unit super-cell size, the number of modes per a frequency range is same in twisted photonic crystals obtained by different z-locations in Figure 2. The central wavelength of the photonic band gap is scalable with the lattice constant of the twisted photonic crystal.

A change of the refractive index in dielectric materials in twisted photonic crystal will not only shift the central frequency of band gap but also change the band gap size. For the simulation of the photonic band gap of twisted photonic crystals in dielectric materials with a varying refractive index at different wavelengths, a MEEP program should be used [38,47]. However, the MEEP program is not good at simulating the photonic band structure at low frequencies.

6. Conclusions

We revealed the relationship between moiré patterns and twisted photonic crystals through analysis of moiré patterns in reciprocal spatial and spectral domains and holographic pattern in reciprocal spatial and wavevector spaces. The twist angle of moiré photonic crystal was calculated from the wavevector of interfering beams arranged in dual-cone geometry. We simulated a photonic band gap, electric field intensity distribution for resonance modes, and their Q-factors in twisted photonic crystals at different twist angles, different z-locations (different gradient), and different iso-intensity levels. At certain gradients in moiré twisted photonic crystals, we observed interface modes within the photonic band gap and various wave-propagation and resonances, including ring-resonators and “traffic circle”-like patterns. Further study can lead toward the application of twisted photonic crystals in integrated photonics.