Metabolic Signaling in a Theoretical Model of the Human Retinal Microcirculation
Abstract
1. Introduction
2. Materials and Methods
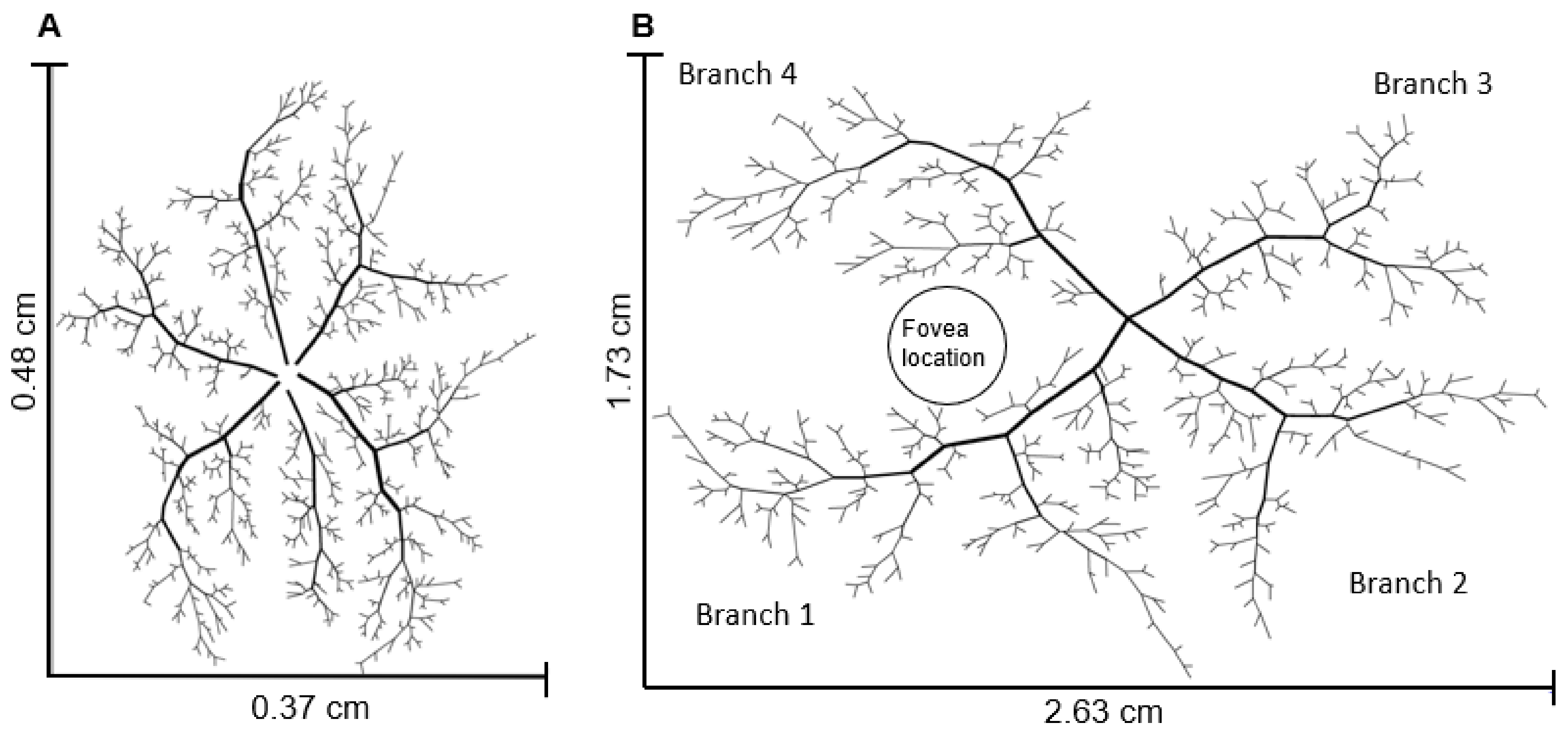
2.1. Network Geometry
2.1.1. Arteriolar Network Description
2.1.2. Capillary and Venular Network Description
2.1.3. Hybrid Model Description
2.2. Blood Flow
2.3. Oxygen Transport
2.4. Metabolic Signal Calculation
2.5. Control State for the Hybrid Model
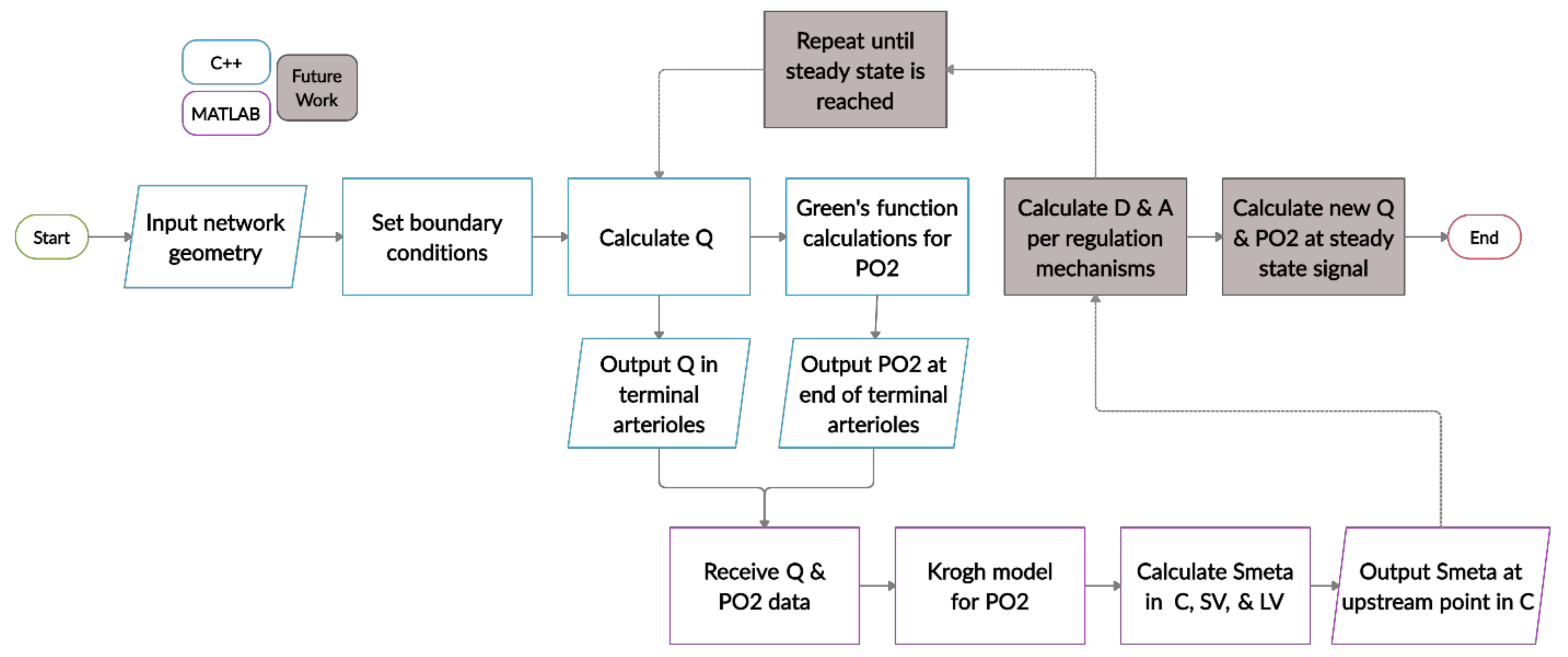
2.6. Model Algorithm and Simulations
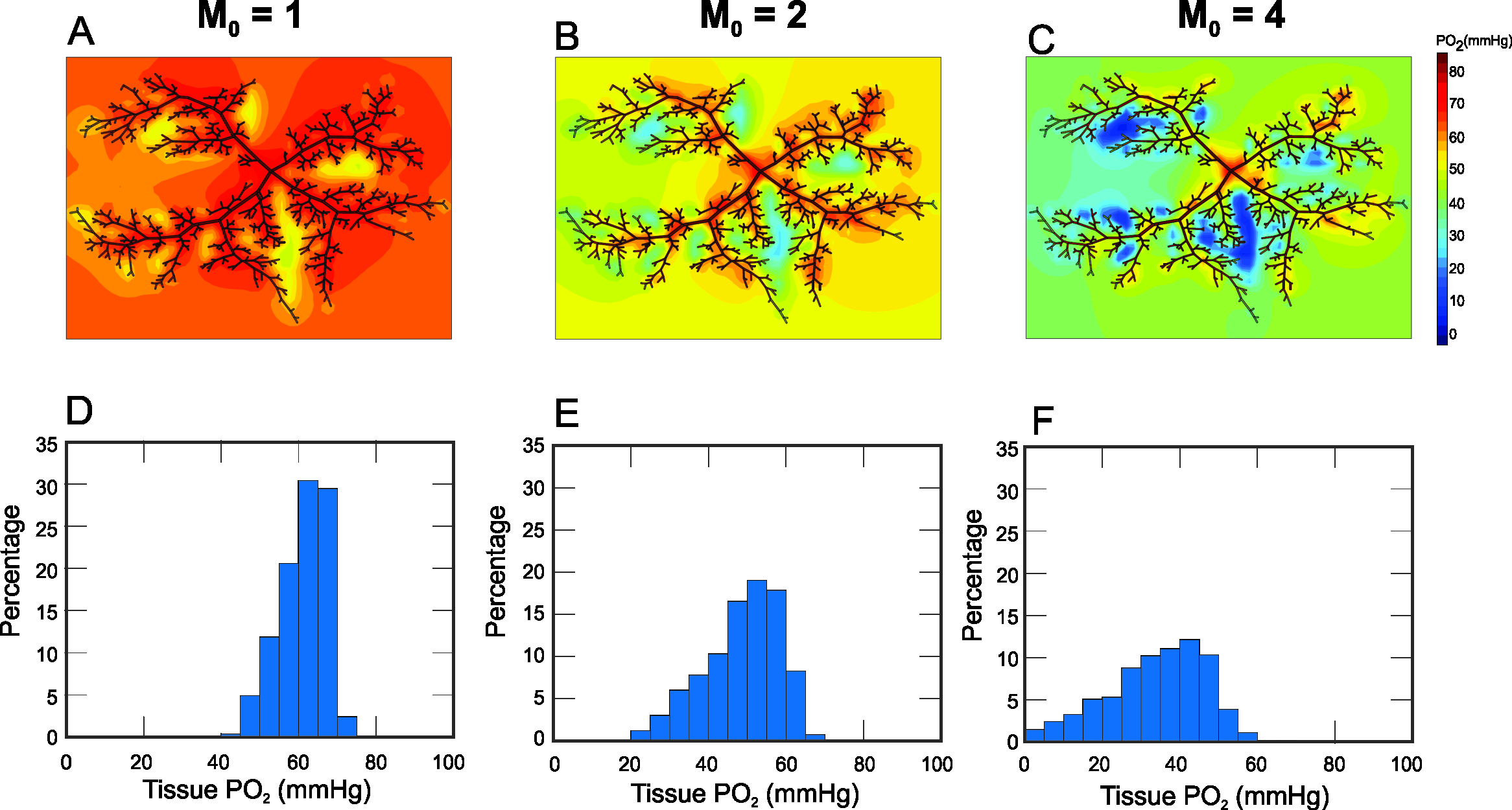
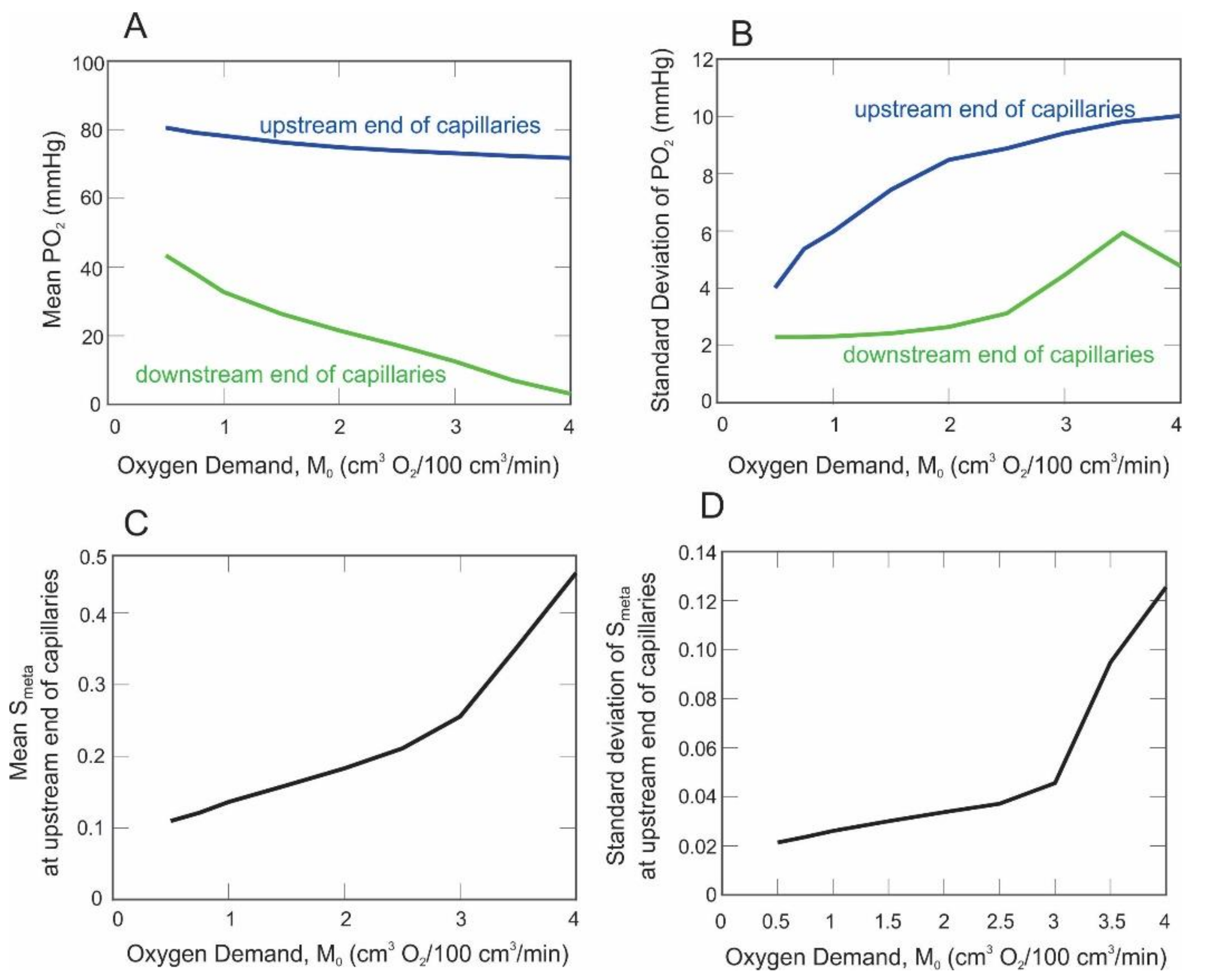
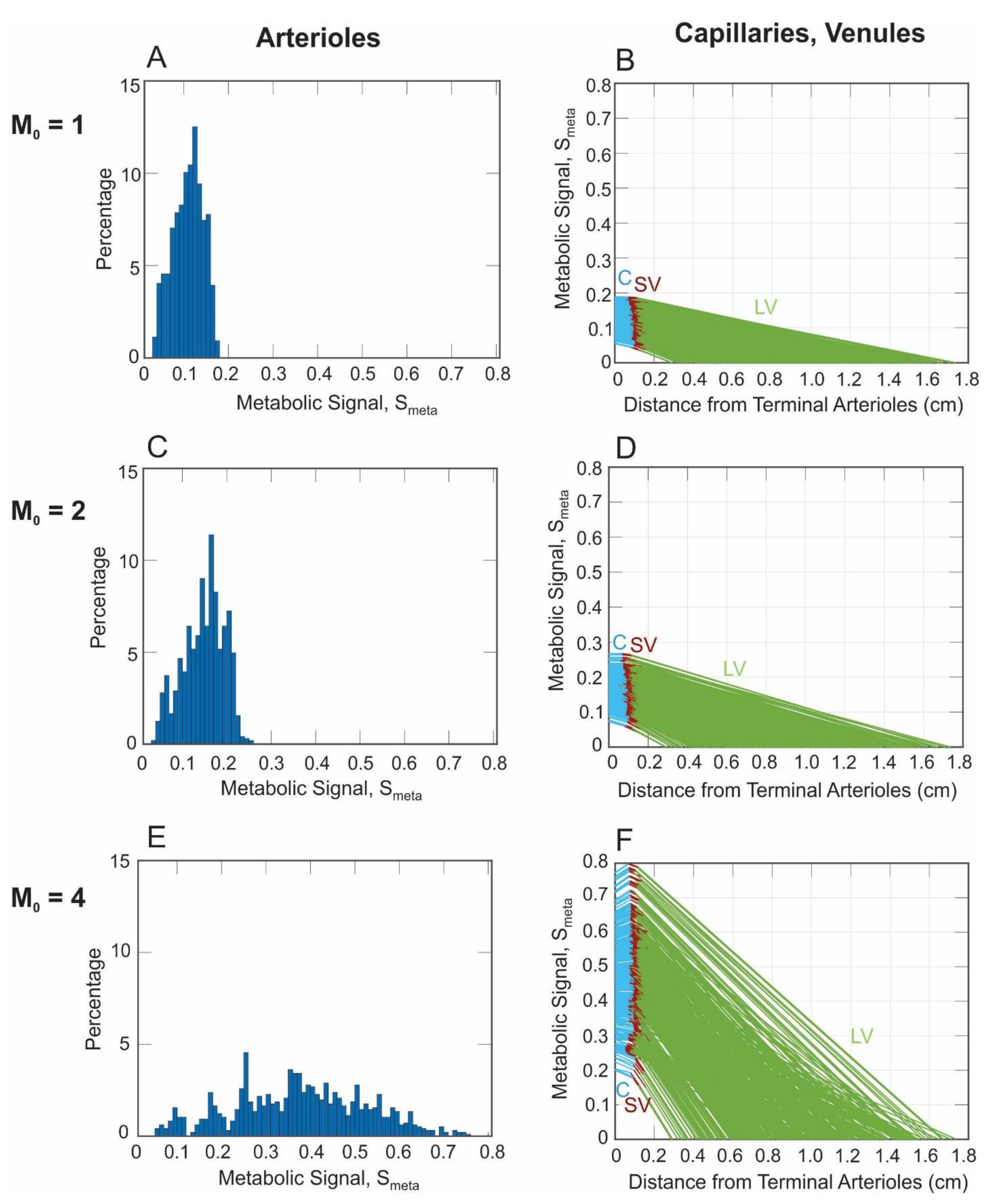
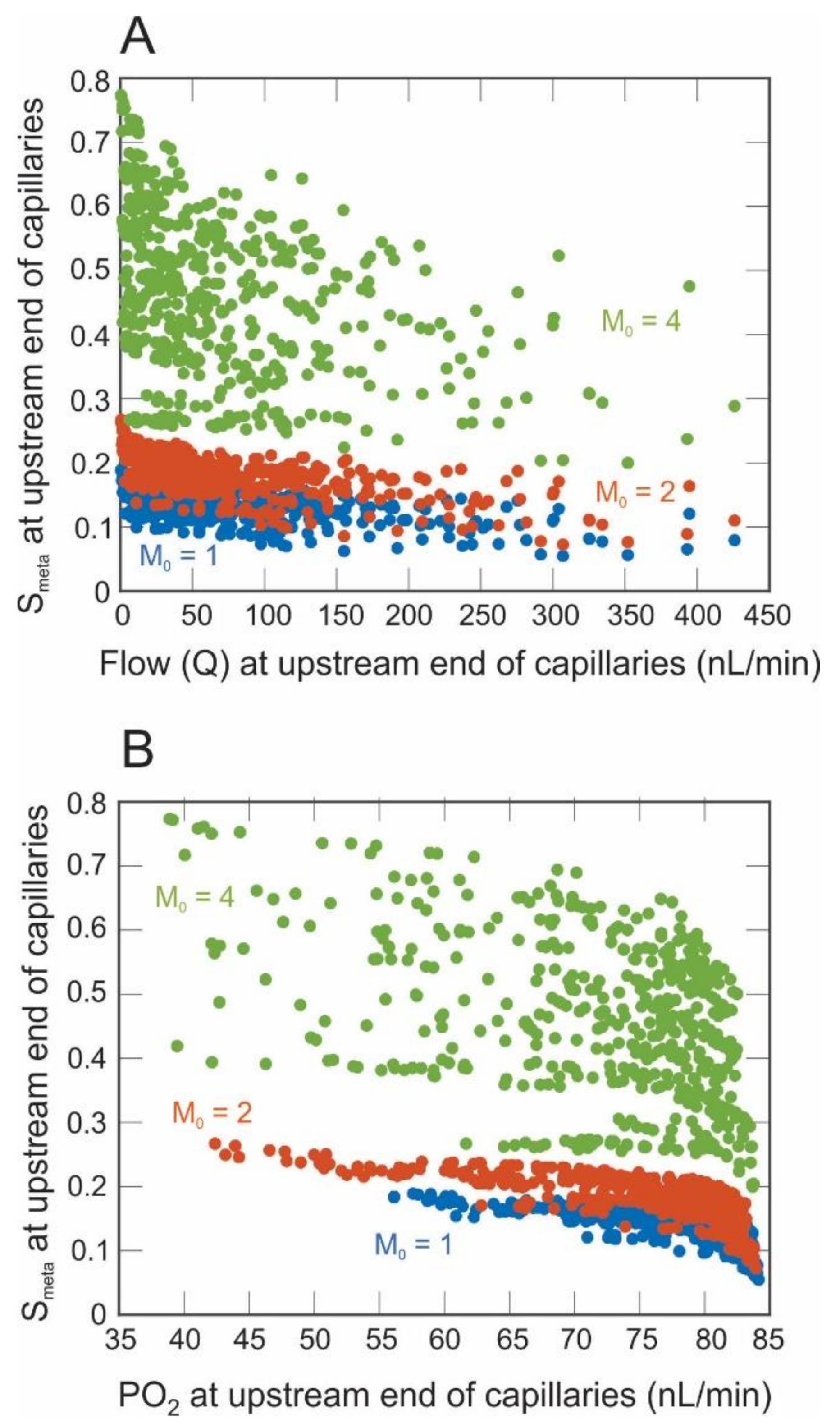
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Harris, A.; Guidoboni, G.; Siesky, B.; Mathew, S.; Vercellin, A.C.V.; Rowe, L.; Arciero, J. Ocular blood flow as a clinical observation: Value, limitations and data analysis. Prog. Retin. Eye Res. 2020, 78, 100841. [Google Scholar] [CrossRef]
- Arciero, J.; Harris, A.; Siesky, B.; Amireskandari, A.; Gershuny, V.; Pickrell, A.; Guidoboni, G. Theoretical Analysis of Vascular Regulatory Mechanisms Contributing to Retinal Blood Flow Autoregulation. Investig. Opthalmol. Vis. Sci. 2013, 54, 5584–5593. [Google Scholar] [CrossRef] [PubMed]
- Guidoboni, G.; Harris, A.; Cassani, S.; Arciero, J.; Siesky, B.; Amireskandari, A.; Tobe, L.; Egan, P.; Januleviciene, I.; Park, J. Intraocular Pressure, Blood Pressure, and Retinal Blood Flow Autoregulation: A Mathematical Model to Clarify Their Relationship and Clinical Relevance. Investig. Opthalmol. Vis. Sci. 2014, 55, 4105–4118. [Google Scholar] [CrossRef] [PubMed]
- Causin, P.; Guidoboni, G.; Malgaroli, F.; Sacco, R.; Harris, A. Blood flow mechanics and oxygen transport and delivery in the retinal microcirculation: Multiscale mathematical modeling and numerical simulation. Biomech. Model. Mechanobiol. 2015, 15, 525–542. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Wood, N.B.; Witt, N.; Hughes, A.; Thom, S.A.; Xu, X.Y. Computational Analysis of Oxygen Transport in the Retinal Arterial Network. Curr. Eye Res. 2009, 34, 945–956. [Google Scholar] [CrossRef] [PubMed]
- Carichino, L.; Harris, A.; Guidoboni, G.; Siesky, B.A.; Pinto, L.A.; Vandewalle, E.; Olafsdottir, O.B.; Hardarson, S.H.; Van Keer, K.; Stalmans, I.; et al. A theoretical investigation of the increase in venous oxygen saturation levels in advanced glaucoma patients. J. Model Ophthalmol. 2016, 1, 64–87. [Google Scholar]
- Fry, B.C.; Coburn, E.B.; Whiteman, S.; Harris, A.; Siesky, B.; Arciero, J. Predicting retinal tissue oxygenation using an image-based theoretical model. Math. Biosci. 2018, 305, 1–9. [Google Scholar] [CrossRef]
- Ganesan, P.; He, S.; Xu, H. Development of an Image-Based Network Model of Retinal Vasculature. Ann. Biomed. Eng. 2010, 38, 1566–1585. [Google Scholar] [CrossRef]
- Ganesan, P.; He, S.; Xu, H. Development of an image-based model for capillary vasculature of retina. Comput. Methods Programs Biomed. 2011, 102, 35–46. [Google Scholar] [CrossRef]
- Popovic, N.; Vujosevic, S.; Popovic, T. Regional Patterns in Retinal Microvascular Network Geometry in Health and Disease. Sci. Rep. 2019, 9, 16340. [Google Scholar] [CrossRef]
- Campbell, J.P.; Zhang, M.; Hwang, T.; Bailey, S.T.; Wilson, D.J.; Jia, Y.; Huang, D. Detailed Vascular Anatomy of the Human Retina by Projection-Resolved Optical Coherence Tomography Angiography. Sci. Rep. 2017, 7, 42201. [Google Scholar] [CrossRef]
- Heegaard, S.; Rosenberg, T.; Preising, M.; Prause, J.U.; Bek, T. An unusual retinal vascular morphology in connection with a novel AIPL1 mutation in Leber’s congenital amaurosis. Br. J. Ophthalmol. 2003, 87, 980–983. [Google Scholar] [CrossRef][Green Version]
- Van Cruchten, S.; Vrolyk, V.; Lepage, M.-F.P.; Baudon, M.; Voute, H.; Schoofs, S.; Haruna, J.; Benoit-Biancamano, M.-O.; Ruot, B.; Allegaert, K. Pre- and Postnatal Development of the Eye: A Species Comparison. Birth Defects Res. 2017, 109, 1540–1567. [Google Scholar] [CrossRef]
- Smith, A.F.; Doyeux, V.; Berg, M.; Peyrounette, M.; Haft-Javaherian, M.; LaRue, A.-E.; Slater, J.H.; Lauwers, F.; Blinder, P.; Tsai, P.; et al. Brain Capillary Networks Across Species: A few Simple Organizational Requirements Are Sufficient to Reproduce Both Structure and Function. Front. Physiol. 2019, 10, 233. [Google Scholar] [CrossRef]
- Grunwald, J.E.; Dupont, J.; Riva, C.E. Retinal haemodynamics in patients with early diabetes mellitus. Br. J. Ophthalmol. 1996, 80, 327–331. [Google Scholar] [CrossRef]
- Doblhoff-Dier, V.; Schmetterer, L.; Vilser, W.; Garhöfer, G.; Gröschl, M.; Leitgeb, R.A.; Werkmeister, R.M. Measurement of the total retinal blood flow using dual beam Fourier-domain Doppler optical coherence tomography with orthogonal detection planes. Biomed. Opt. Express 2014, 5, 630–642. [Google Scholar] [CrossRef]
- Arciero, J.C.; Carlson, B.E.; Secomb, T.W. Theoretical model of metabolic blood flow regulation: Roles of ATP release by red blood cells and conducted responses. Am. J. Physiol. Circ. Physiol. 2008, 295, H1562–H1571. [Google Scholar] [CrossRef] [PubMed]
- Pries, A.R.; Secomb, T.W. Blood flow in microvascular networks. In Handbook of Physiology: Section 2, the Cardiovascular System, Volume IV, Microcirculation; Tuma, R.F., Duran, W.N., Ley, K., Eds.; Academic Press: San Diego, CA, USA, 2008; pp. 3–36. [Google Scholar]
- Young, D. Iterative Methods for Solving Partial Difference Equations of Elliptic Type. Trans. Am. Math. Soc. 1954, 76, 92–111. [Google Scholar] [CrossRef]
- Ellsworth, M.L.; Popel, A.S.; Pittman, R.N. Assessment and impact of heterogeneities of convective oxygen transport parameters in capillaries of striated muscle: Experimental and theoretical. Microvasc. Res. 1988, 35, 341–362. [Google Scholar] [CrossRef]
- Bentley, T.B.; Meng, H.; Pittman, R.N. Temperature dependence of oxygen diffusion and consumption in mammalian striated muscle. Am. J. Physiol. Content 1993, 264, 1825–1830. [Google Scholar] [CrossRef]
- Golub, A.S.; Pittman, R.N. Oxygen dependence of respiration in rat spinotrapezius muscle in situ. Am. J. Physiol. Circ. Physiol. 2012, 303, H47–H56. [Google Scholar] [CrossRef] [PubMed]
- Hsu, R.; Secomb, T.W. A Green’s function method for analysis of oxygen delivery to tissue by microvascular networks. Math. Biosci. 1989, 96, 61–78. [Google Scholar] [CrossRef]
- Secomb, T.W.; Hsu, R.; Park, E.Y.; Dewhirst, M.W. Green’s function methods for analysis of oxygen delivery to tissue by microvascular networks. Ann. Biomed. Eng. 2004, 32, 1519–1529. [Google Scholar] [CrossRef] [PubMed]
- Fry, B.C.; Harris, A.; Siesky, B.; Arciero, J. Blood flow regulation and oxygen transport in a heterogeneous model of the mouse retina. Math. Biosci. 2020, 329, 108476. [Google Scholar] [CrossRef]
- Popel, A. Theory of oxygen transport to tissue. Crit. Rev. Biomed. Eng. 1989, 17, 257–321. [Google Scholar]
- Krogh, A. The number and distribution of capillaries in muscles with calculations of the oxygen pressure head necessary for supplying the tissue. J. Physiol. 1919, 52, 409–415. [Google Scholar] [CrossRef]
- Takahashi, T.; Nagaoka, T.; Yanagida, H.; Saitoh, T.; Kamiya, A.; Hein, T.; Kuo, L.; Yoshida, A. A mathematical model for the distribution of hemodynamic parameters in the human retinal microvascular network. J. Biorheol. 2009, 23, 77–86. [Google Scholar] [CrossRef]
- Broadway, D.C. Visual field testing for glaucoma—A practical guide. Community Eye Health 2012, 25, 66–70. [Google Scholar]
- Yousefi, S.; Sakai, H.; Murata, H.; Fujino, Y.; Garway-Heath, D.; Weinreb, R.; Asaoka, R. Asymmetric Patterns of Visual Field Defect in Primary Open-Angle and Primary Angle-Closure Glaucoma. Investig. Opthalmol. Vis. Sci. 2018, 59, 1279–1287. [Google Scholar] [CrossRef]
- Kim, J.M.; Kyung, H.; Shim, S.H.; Azarbod, P.; Caprioli, J. Location of Initial Visual Field Defects in Glaucoma and Their Modes of Deterioration. Investig. Opthalmol. Vis. Sci. 2015, 56, 7956–7962. [Google Scholar] [CrossRef]
- Carlson, B.E.; Arciero, J.C.; Secomb, T.W. Theoretical model of blood flow autoregulation: Roles of myogenic, shear-dependent, and metabolic responses. Am. J. Physiol. Heart Circ. Physiol. 2008, 295, H1572–H1579. [Google Scholar] [CrossRef] [PubMed]

| Description | C | SV | LV |
|---|---|---|---|
| Diameter, D (μm) | 6 | 29.5 | 137.3 |
| Wall shear stress, τ (dyn/cm2) | 15 | 15.6 | 14.7 |
| Pressure Drop, ΔP (mmHg) | 6 | 0.3 | 2.7 |
| Number of segments, n | 340 | 1 | 0.008 |
| Length, L (cm) | 0.080 | 0.032 | 0.854 |
| Viscosity, µ (cP) | 9.05 | 2.28 | 2.39 |
| Flow, Q (cm3/s) | 3.5110−9 | 1.1910−6 | 1.5210−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arciero, J.; Fry, B.; Albright, A.; Mattingly, G.; Scanlon, H.; Abernathy, M.; Siesky, B.; Vercellin, A.V.; Harris, A. Metabolic Signaling in a Theoretical Model of the Human Retinal Microcirculation. Photonics 2021, 8, 409. https://doi.org/10.3390/photonics8100409
Arciero J, Fry B, Albright A, Mattingly G, Scanlon H, Abernathy M, Siesky B, Vercellin AV, Harris A. Metabolic Signaling in a Theoretical Model of the Human Retinal Microcirculation. Photonics. 2021; 8(10):409. https://doi.org/10.3390/photonics8100409
Chicago/Turabian StyleArciero, Julia, Brendan Fry, Amanda Albright, Grace Mattingly, Hannah Scanlon, Mandy Abernathy, Brent Siesky, Alice Verticchio Vercellin, and Alon Harris. 2021. "Metabolic Signaling in a Theoretical Model of the Human Retinal Microcirculation" Photonics 8, no. 10: 409. https://doi.org/10.3390/photonics8100409
APA StyleArciero, J., Fry, B., Albright, A., Mattingly, G., Scanlon, H., Abernathy, M., Siesky, B., Vercellin, A. V., & Harris, A. (2021). Metabolic Signaling in a Theoretical Model of the Human Retinal Microcirculation. Photonics, 8(10), 409. https://doi.org/10.3390/photonics8100409








