An Infrared DoLP Model Considering the Radiation Coupling Effect
Abstract
:1. Introduction
2. Materials and Methods
2.1. pBRDF Model
2.2. DoLP Model Considering the RCE
2.2.1. Reflection DoLP Model of Rough Surface
2.2.2. Radiation DoLP Model of Rough Surface
2.2.3. Infrared DoLP Model of Rough Surface
3. Results
3.1. Simulation
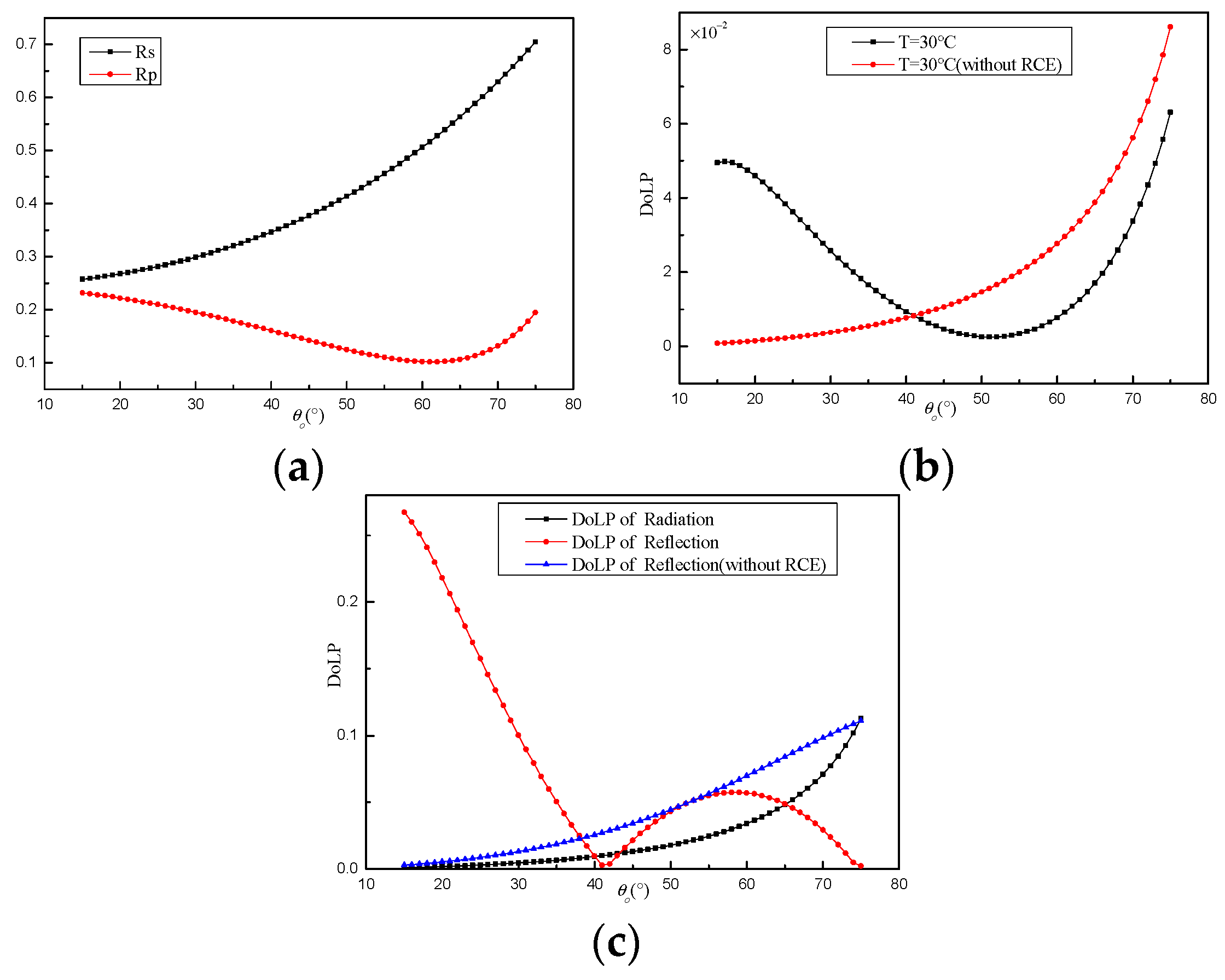
3.1.1. Influence of RCE on the DoLP of Object
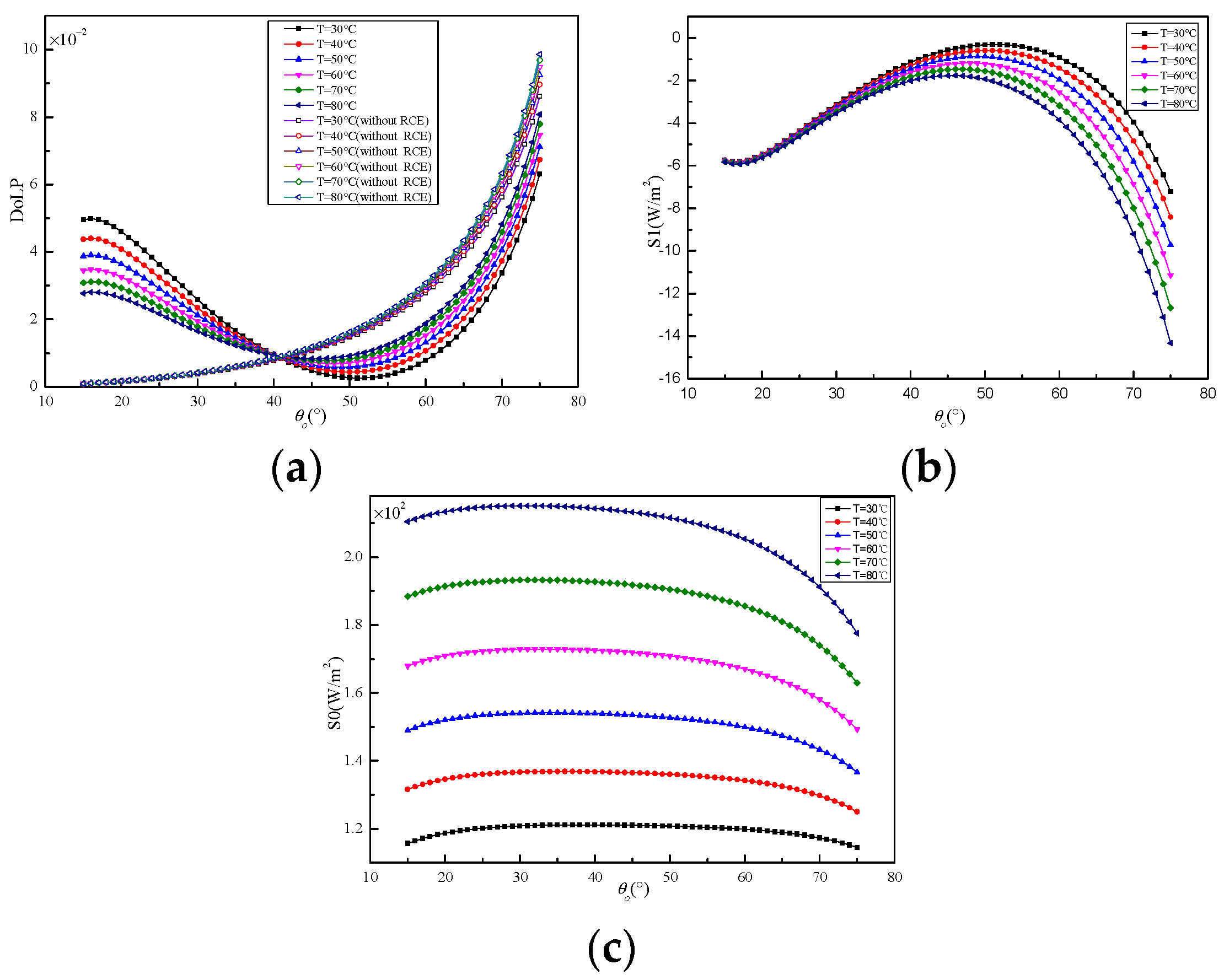
3.1.2. Influence of Object Temperature on the DoLP of Object
3.1.3. Influence of Surface Roughness on the DoLP of Object
3.2. Experimental Verification
3.2.1. The Experimental Setup
3.2.2. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hioki, S.; Riedi, J.; Djellali, M.S. A study of polarimetric error induced by satellite motion: Application to the 3MI and similar sensors. Atmos. Meas. Tech. 2021, 14, 1801–1816. [Google Scholar] [CrossRef]
- Li, S.; Jiao, J.; Wang, C. Research on Polarized Multi-Spectral System and Fusion Algorithm for Remote Sensing of Vegetation Status at Night. Remote Sens 2021, 13, 3510. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, Y.C.; Shen, Y.F.; Ding, J.; Zhang, M.; Mao, Z. Polarized Remote Inversion of the Refractive Index of Marine Spilled Oil From PARASOL Images Under Sunglint. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2710–2719. [Google Scholar] [CrossRef]
- Yang, M.; Xu, W.; Sun, Z.; Wu, H.; Tian, Y.; Li, L. Mid-wave infrared polarization imaging system for detecting moving scene. Opt. Lett. 2020, 45, 5884–5887. [Google Scholar] [CrossRef] [PubMed]
- Ren, K.; Lv, Y.Y.; Gu, G.H.; Chen, Q. Calculation method of multiangle polarization measurement for oil spill detection. Appl. Opt. 2019, 58, 3317–3324. [Google Scholar] [CrossRef]
- Zhang, J.H.; Zhang, Y.; Shi, Z.G. Enhancement of dim targets in a sea background based on long-wave infrared polarization features. IET Image Process. 2018, 12, 2042–2050. [Google Scholar] [CrossRef]
- Xue, F.D.; Jin, W.Q.; Qiu, S.; Yang, J. Airborne optical polarization imaging for observation of submarine Kelvin wakes on the sea surface: Imaging chain and simulation. ISPRS J. Photogramm. Remote Sens. 2021, 178, 136–154. [Google Scholar] [CrossRef]
- Tyo, J.S.; Ratliff, B.M.; Boger, J.K.; Black, W.T.; Bowers, D.L.; Fetrow, M.P. The effects of thermal equilibrium and contrast in LWIR Polarimetric images. Opt. Express 2007, 15, 15161–15167. [Google Scholar] [CrossRef]
- Felton, M.; Gurton, K.P.; Pezzaniti, J.L.; Chenault, D.B.; Roth, L.E. Measured comparison of the crossover periods for mid- and long-wave IR (MWIR and LWIR) polarimetric and conventional thermal imagery. Opt. Express 2010, 18, 15704–15713. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.Z.; Shi, Z.L.; Feng, B. An Infrared DoLP Computational Model considering Surroundings Irradiance. Infrared Phys. Technol. 2019, 106, 103043. [Google Scholar] [CrossRef]
- Flynn, D.S.; Alexander, C. Polarized surface scattering expressed in terms of a bidirectional reflectance distribution function matrix. Opt. Eng. 1995, 34, 1646–1650. [Google Scholar]
- Priest, R.G.; Germer, T.A. Polarimetric BRDF in the Microfacet Model: Theory and Measurements. In Proceedings of the 2000 Meeting of the Military Sensing Symposia Specialty Group on Passive Sensors, Ann Arbor, MI, USA, 1 May 2000. [Google Scholar]
- Torrance, K.E.; Sparrow, E.M. Theory for off-specular reflection from roughened surfaces. J. Opt. Soc. Am. A 1967, 57, 1105–1114. [Google Scholar] [CrossRef]
- Hyde, M.W.; Schmidt, J.D.; Havrilla, M.J. A geometrical optics polarimetric bidirectional reflectance distribution function for dielectric and metallic surfaces. Opt. Express 2009, 17, 22138–22153. [Google Scholar] [CrossRef]
- Feng, W.W.; Wei, Q.N. A scatterometer for measuring the polarized bidirectional reflectance distribution function of painted surfaces. Infrared Phys. Technol. 2008, 51, 559–563. [Google Scholar]
- Liu, Y.L.; Yu, K.; Liu, Z.L.; Zhao, Y.J.; Liu, Y.F. Polarized BRDF measurement of steel E235B in the near-infrared region: Based on a self-designed instrument with absolute measuring method. Infrared Phys. Technol. 2018, 91, 78–84. [Google Scholar] [CrossRef]
- Jordan, D.L.; Lewis, G. Measurements of the effect of surface roughness on the polarization state of thermally emitted radiation. Opt. Lett. 1994, 19, 692–694. [Google Scholar] [CrossRef] [PubMed]
- Wolff, L.B.; Lundberg, A.; Tang, R. Image understanding from thermal emission polarization. In Proceedings of the 1998 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Santa Barbara, CA, USA, 25 June 1998. [Google Scholar]
- Gurton, K.P.; Dahmani, R. Effect of surface roughness and complex indices of refraction on polarized thermal emission. Appl. Opt. 2005, 44, 5361–5367. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Han, J.T.; Li, J.C.; Yang, W.P.; Gong, T. Characteristics analysis of infrared polarization for several typical artificial objects. In Proceedings of the SPIE The International Society for Optical Engineering, Amsterdam, The Netherlands, 23 October 2014. [Google Scholar]
- Liu, F.; Shao, X.P.; Gao, Y.; Li, B.X.; Han, P.L.; Li, G. Polarization characteristics of objects in long-wave infrared range. J. Opt. Soc. Am. A 2016, 33, 237–243. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, J.P.; Wang, K.; Xu, R. Polarized BRDF for coatings based on three-component assumption. Opt. Commun. 2017, 384, 118–124. [Google Scholar] [CrossRef]
- Cheng, Y.Y.; Wang, Y.X.; Niu, Y.Y.; Zhao, Z.R. Concealed object enhancement using multi-polarization information for passive millimeter and terahertz wave security screening. Opt. Express 2020, 28, 6350–6366. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Y.; Li, Z. Optical Polarization Characteristics of Low-Earth-Orbit Space Targets. J. Korean Phys. Soc. 2020, 76, 311–317. [Google Scholar] [CrossRef]
- Su, J.L.; Wu, H.F.; Li, P.F.; Hu, Y.; Hu, F. Detection for ship by dual-polarization imaging radiometer. Opt. Express 2021, 29, 27830–27844. [Google Scholar] [CrossRef]
- Tuo, H.N.; Shi, G.C.; Luo, X.L. Detection Method of Ship Target Infrared Polarization Image. In Proceedings of the 7th International Conference on Computer-Aided Design, Manufacturing, Modeling and Simulation (CDMMS 2020), Busan, Korea, 14–15 November 2020. [Google Scholar]
- Zhang, X.F.; Nie, X.F.; Du, Z.Q. Target polarization characteristics analysis and detection in complex background. In Proceedings of the 2021 International Conference on Electrical, Electronics and Computing Technology (EECT 2021), Xiamen, China, 26–28 March 2021. [Google Scholar]
- Wei, M.; Zhang, Y.; Shi, Z.G.; Zhang, Y.; Liu, P.J. Analysis of visible/infrared polarization characteristics of small UAV with complex background of buildings. In Proceedings of the Third International Conference on Image, Video Processing and Artificial Intelligence, Shanghai, China, 21–23 August 2020. [Google Scholar]
- Zhang, J.H.; Zhang, Y.; Shi, Z.G. Study and modeling of infrared polarization characteristics based on sea scene in long wave band. J. Infrared Millim. Waves 2018, 37, 586–594. [Google Scholar]
- Gil, J.J.; Ossikovski, R. Polarized Light and the Mueller Matrix Approach, 1st ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 107–109. [Google Scholar]
- Thilak, V.; Voelz, D.G.; Creusere, C.D. Polarization-based index of refraction and reflection angle estimation for remote sensing applications. Appl. Opt. 2007, 46, 7527–7536. [Google Scholar] [CrossRef] [Green Version]
- Resnick, A.; Persons, C.; Lindquist, G. Polarized emissivity and Kirchhoff’s law. Appl. Opt. 1999, 38, 1384–1387. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, D.; Liu, L.; Liu, L.; Ming, R.; Wu, S.; Zhang, J. An Infrared DoLP Model Considering the Radiation Coupling Effect. Photonics 2021, 8, 546. https://doi.org/10.3390/photonics8120546
Su D, Liu L, Liu L, Ming R, Wu S, Zhang J. An Infrared DoLP Model Considering the Radiation Coupling Effect. Photonics. 2021; 8(12):546. https://doi.org/10.3390/photonics8120546
Chicago/Turabian StyleSu, Dezhi, Liang Liu, Lingshun Liu, Ruilong Ming, Shiyong Wu, and Jilei Zhang. 2021. "An Infrared DoLP Model Considering the Radiation Coupling Effect" Photonics 8, no. 12: 546. https://doi.org/10.3390/photonics8120546
APA StyleSu, D., Liu, L., Liu, L., Ming, R., Wu, S., & Zhang, J. (2021). An Infrared DoLP Model Considering the Radiation Coupling Effect. Photonics, 8(12), 546. https://doi.org/10.3390/photonics8120546



