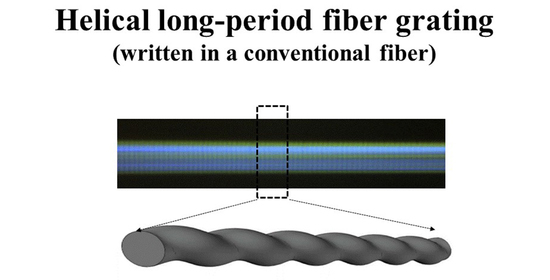
Advances on Mode-Coupling Theories, Fabrication Techniques, and Applications of the Helical Long-Period Fiber Gratings: A Review
Abstract
:1. Introduction
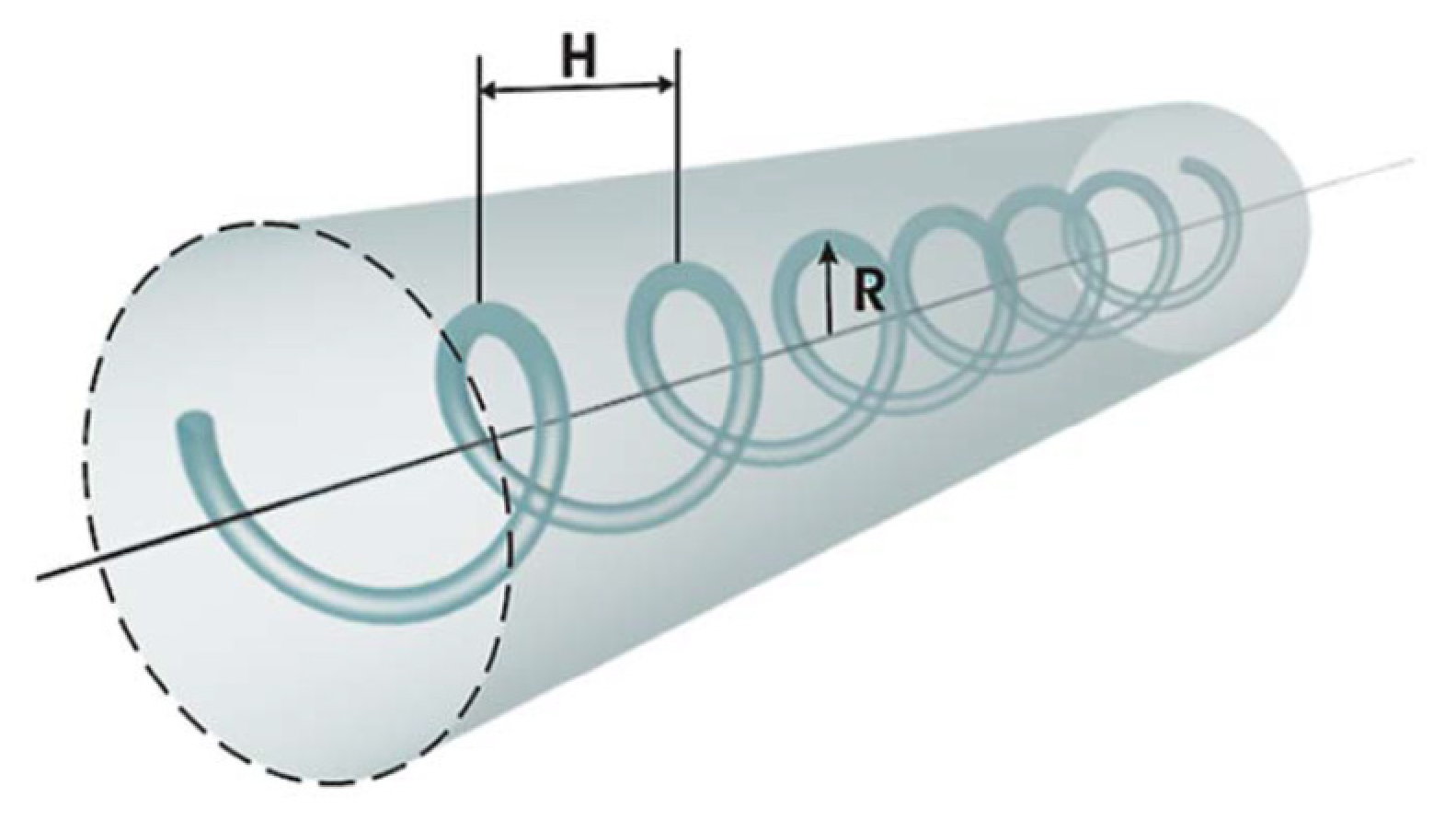
2. Mode-Couplings in HLPGs
2.1. Mode-Coupled Theory Based on the Perturbation Analysis
2.2. The Geometrical Transformation and Full-Vector Finite-Element Beam Propagation Method
2.3. Mode-Selection Rules of the HLPGs Obtained by Using the Fourier Expansion Method
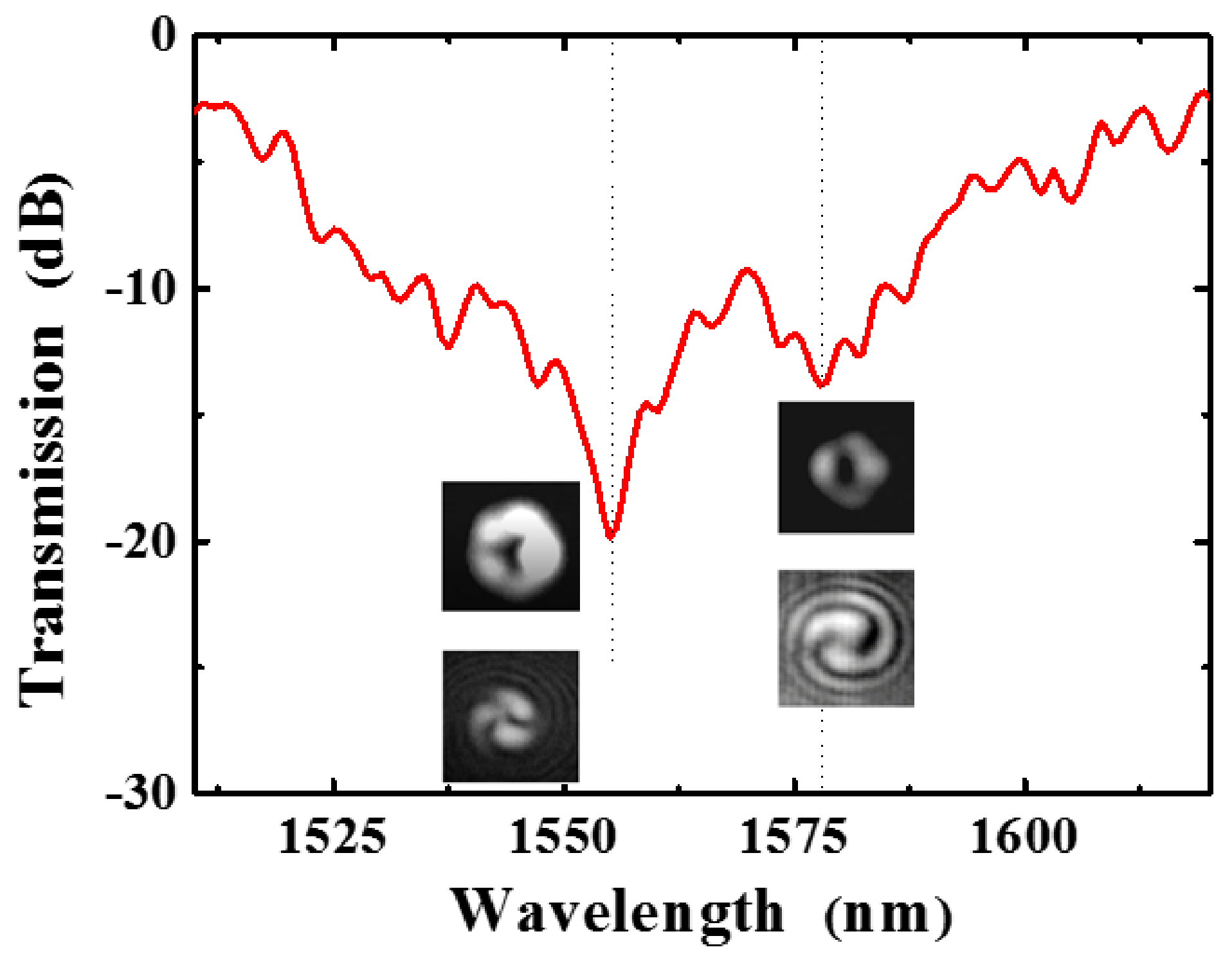
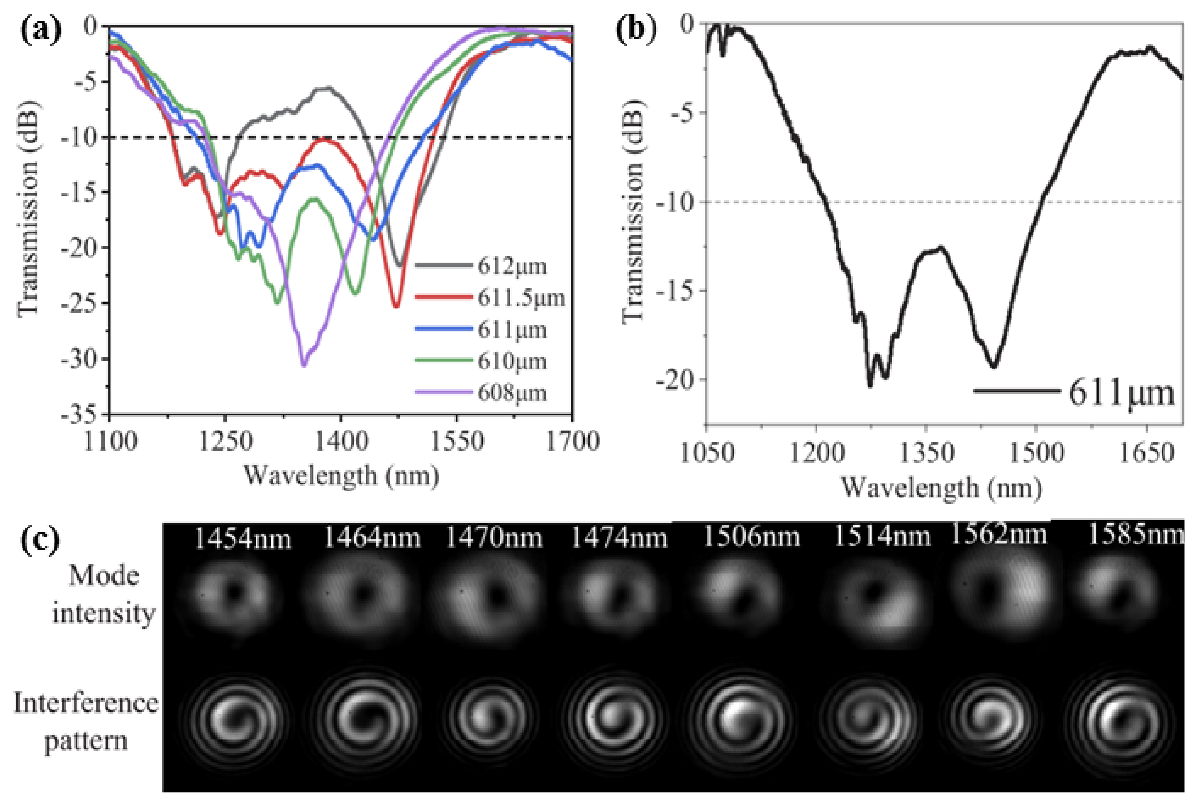
2.4. Validation of the Mode-Selection Rules Obeyed in Single-Helix HLPGs
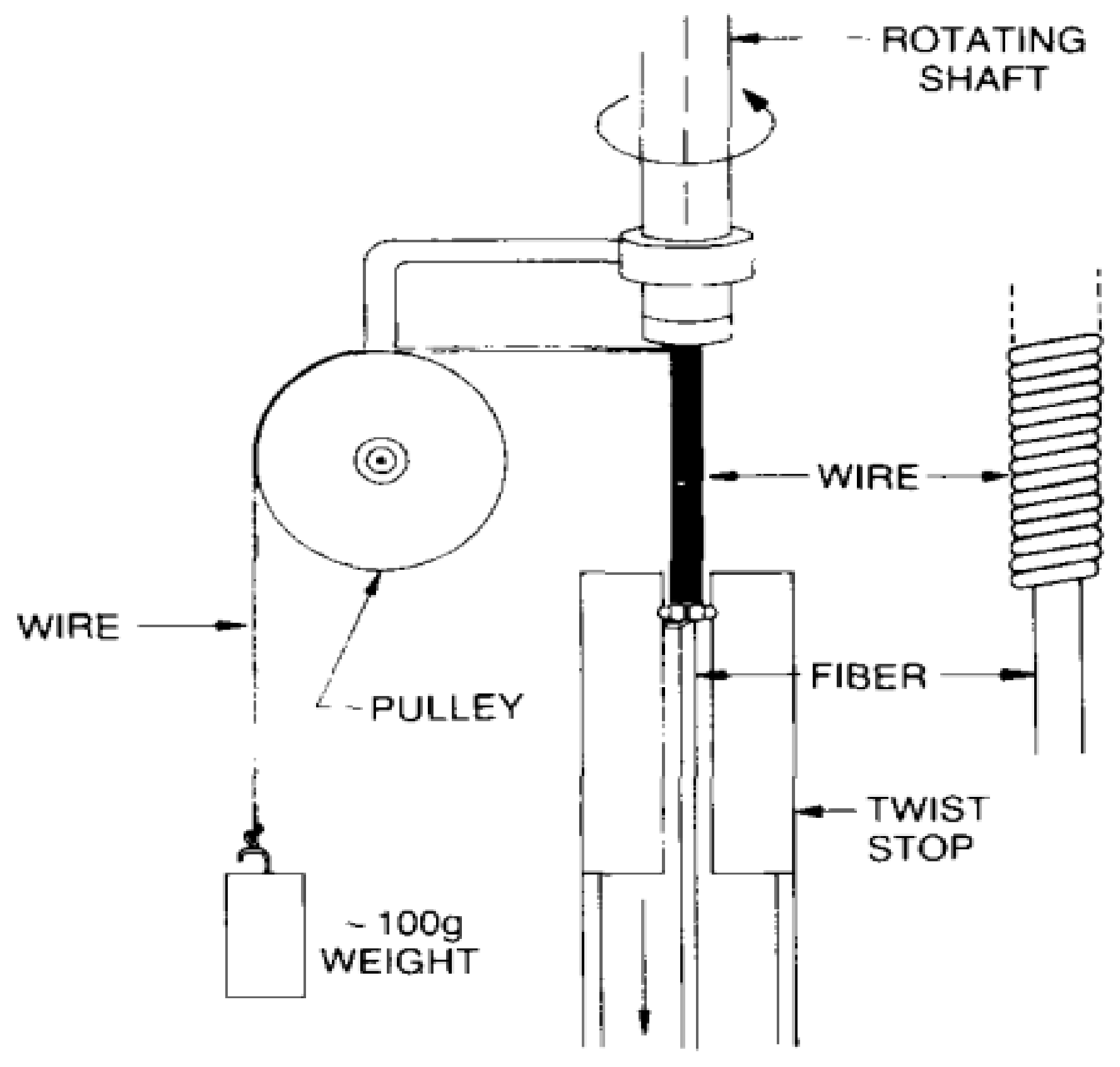
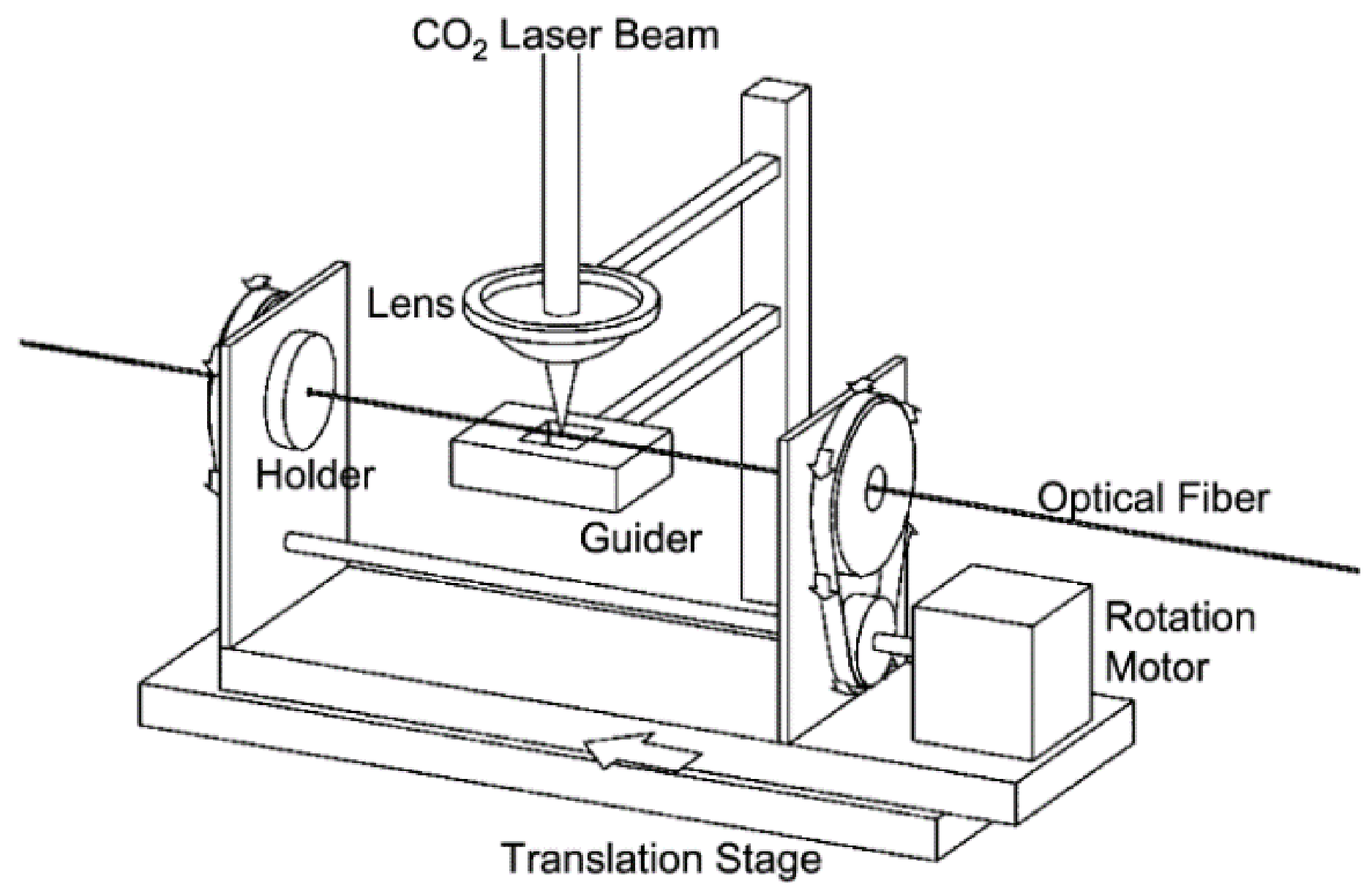
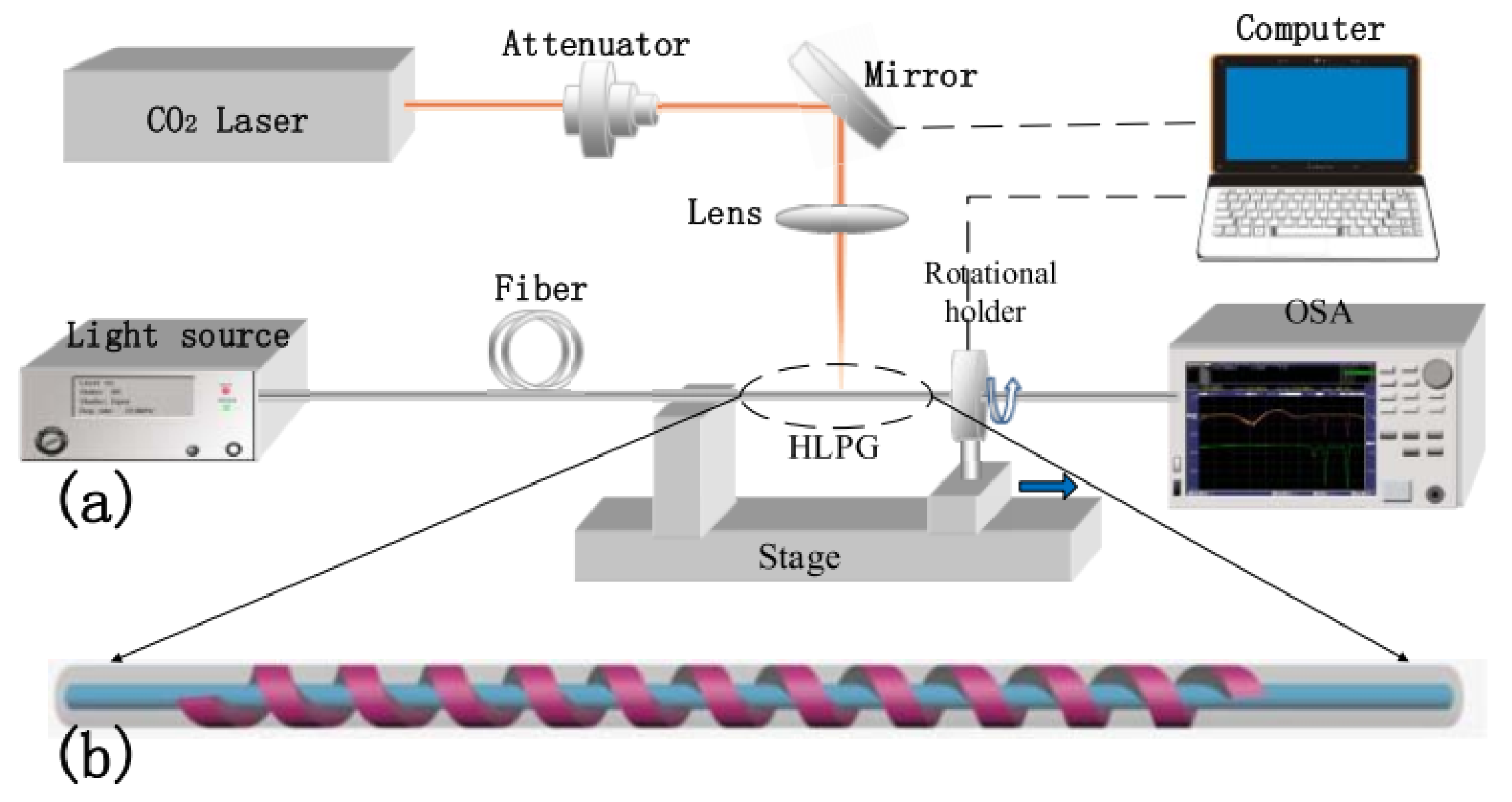
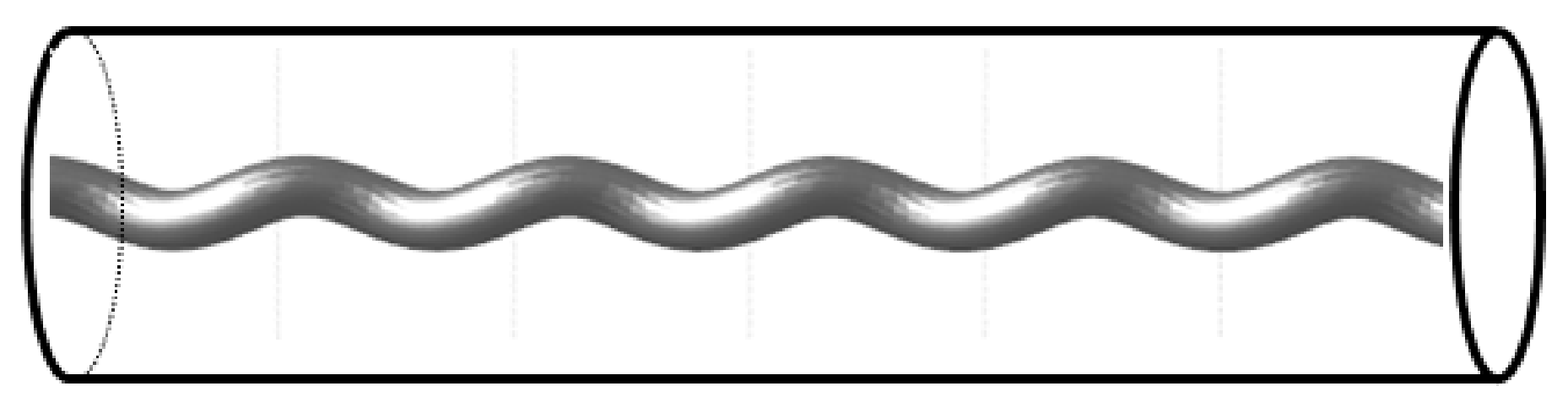
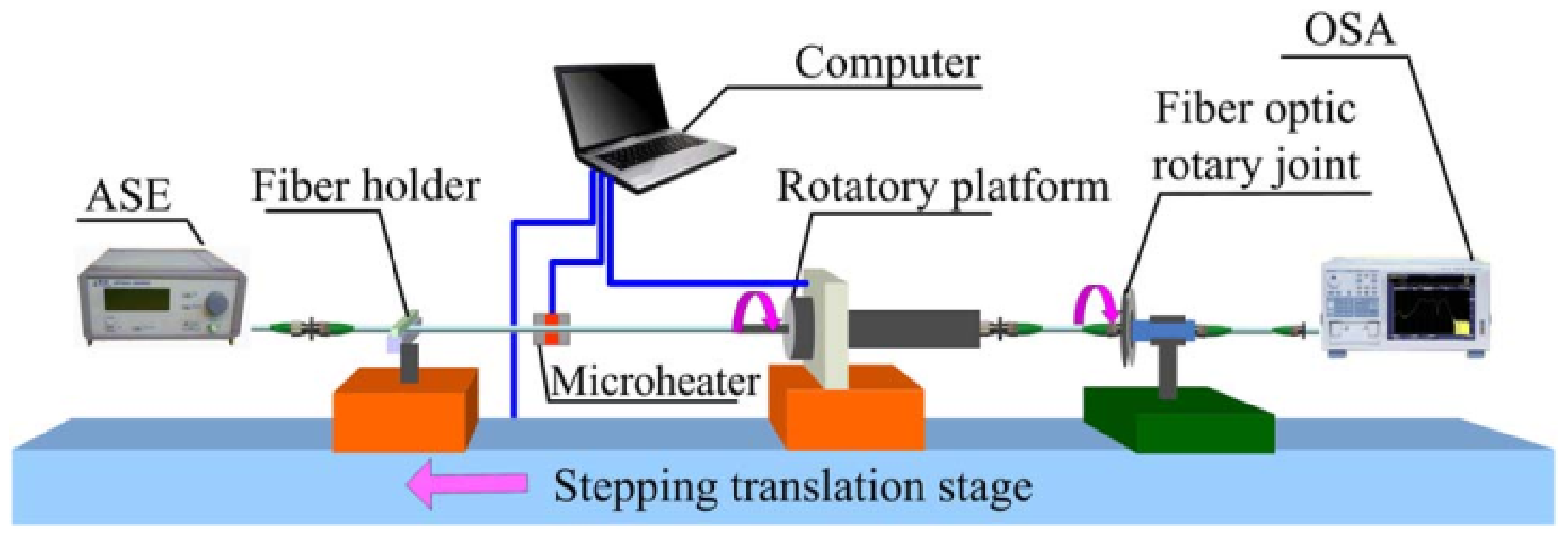
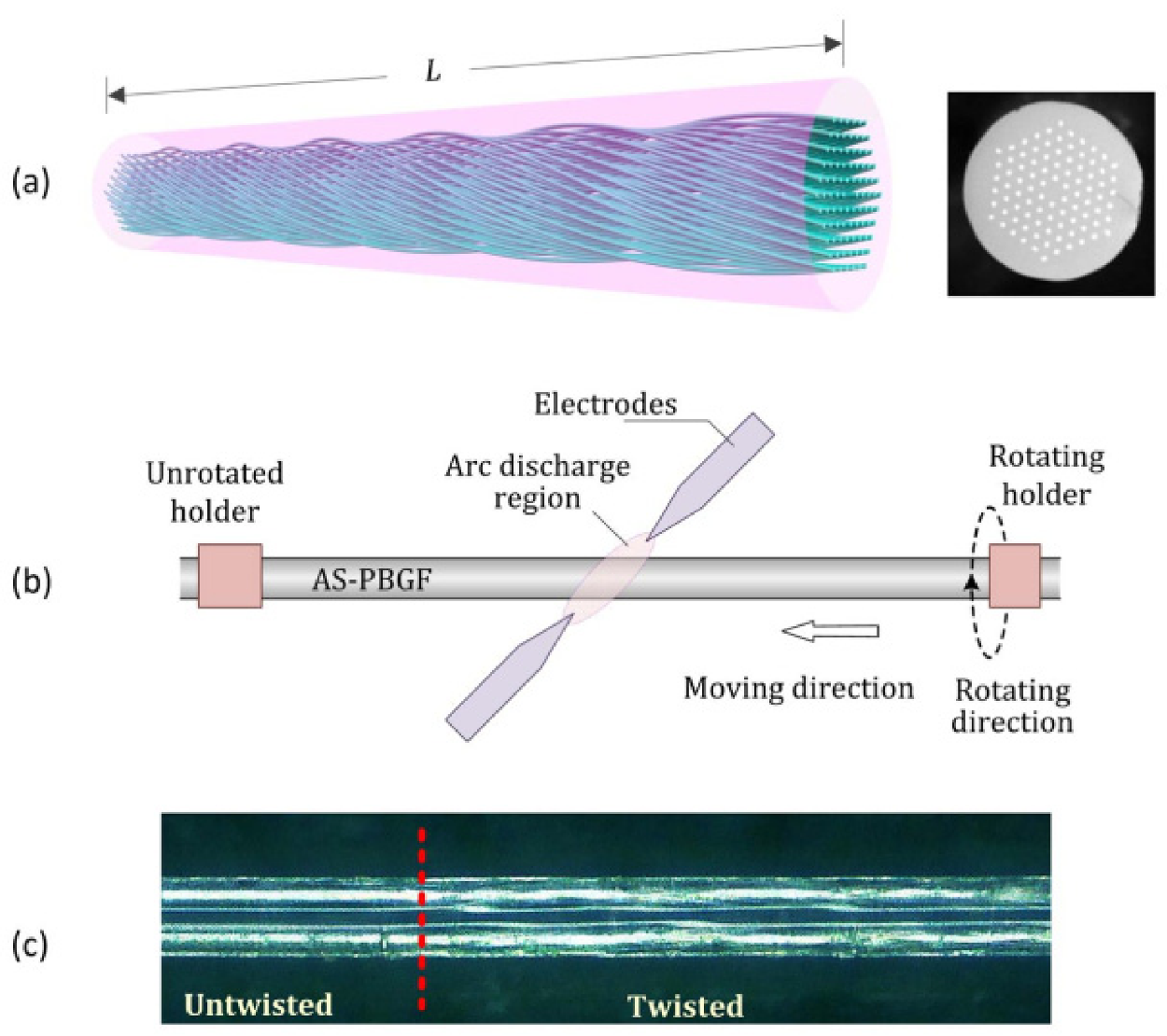
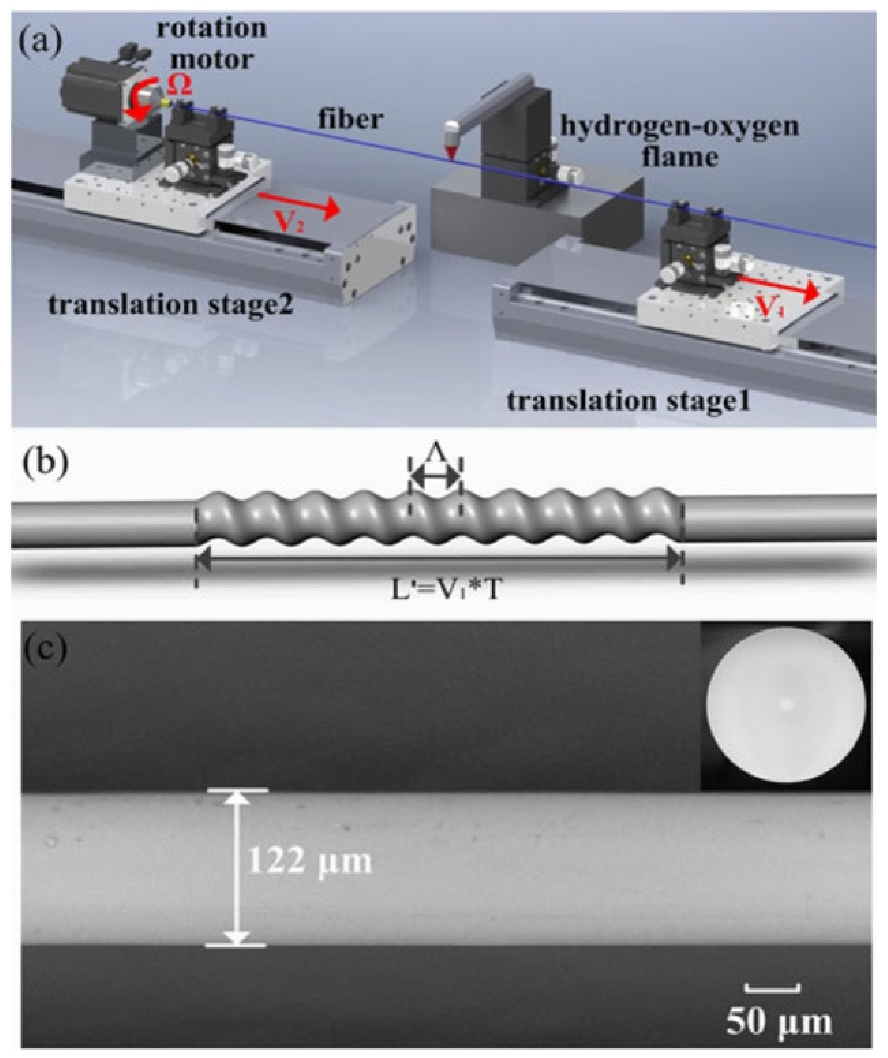
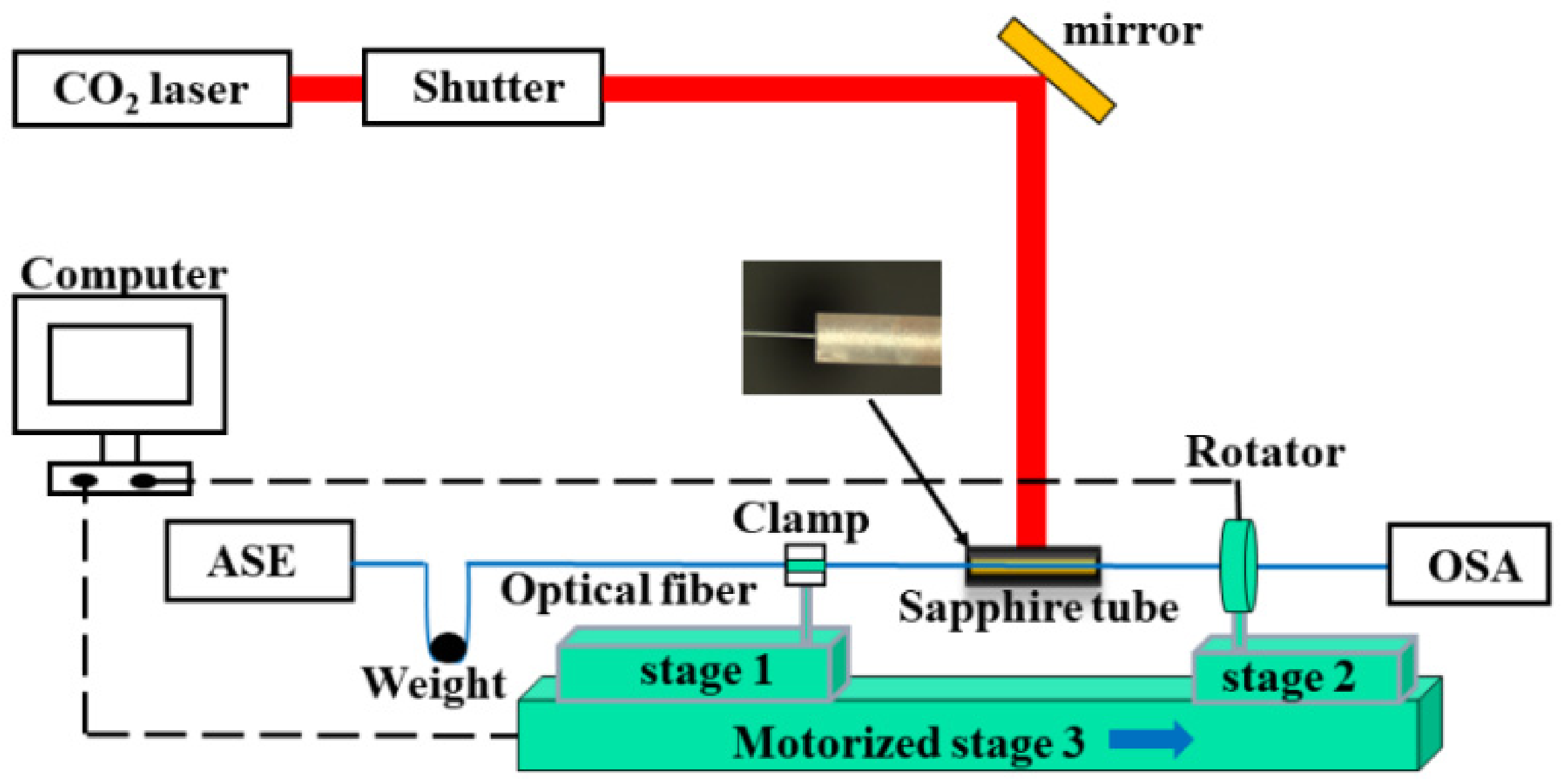
3. Fabrication Techniques for the HLPGs
4. Applications of the HLPGs
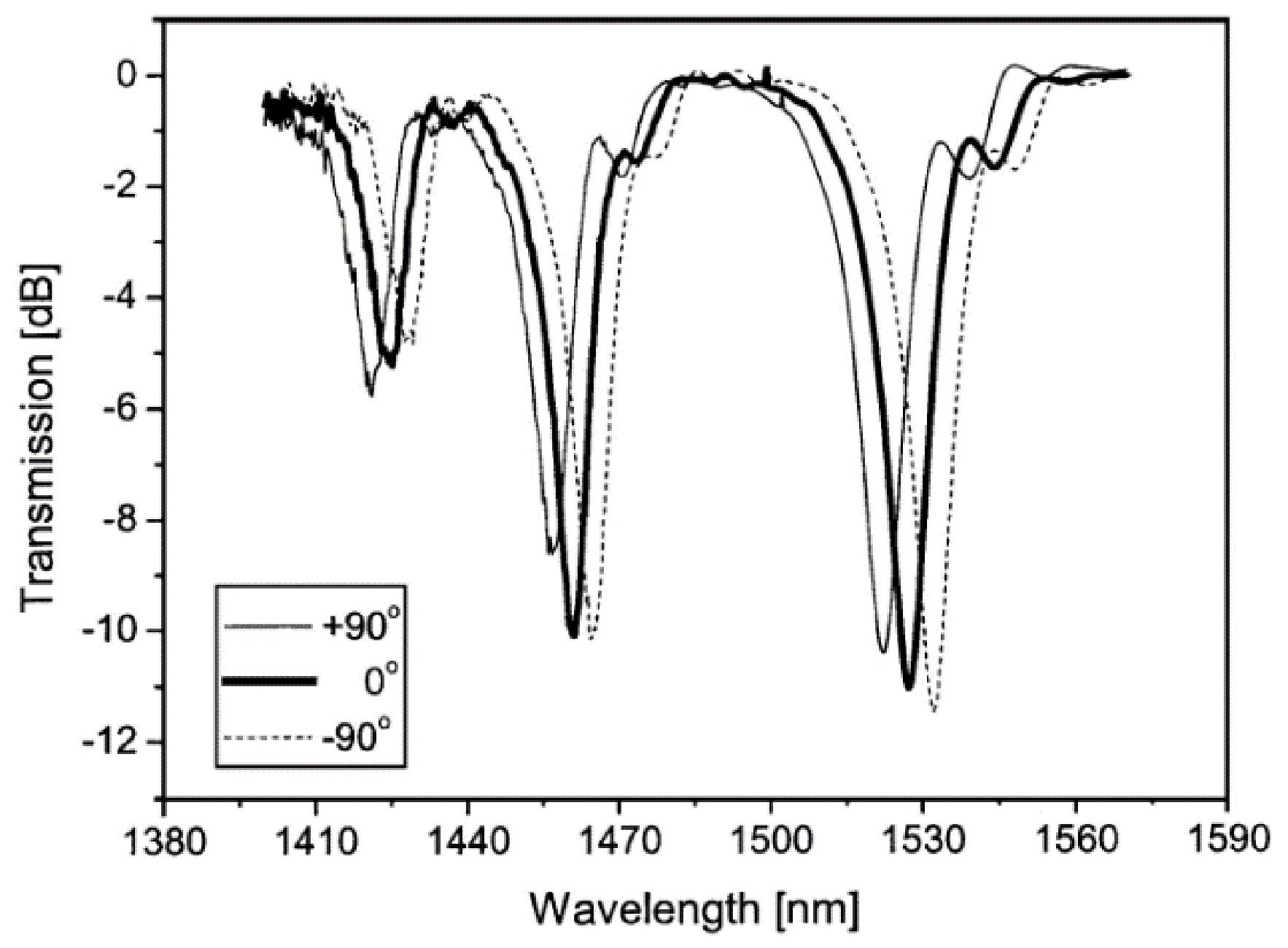
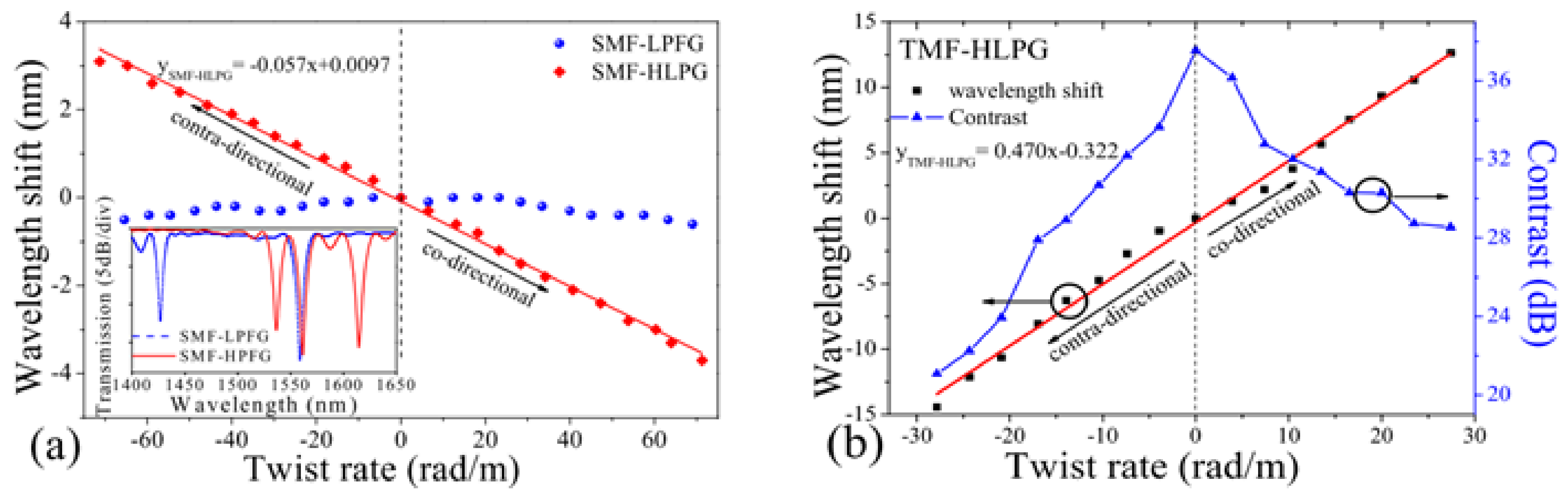
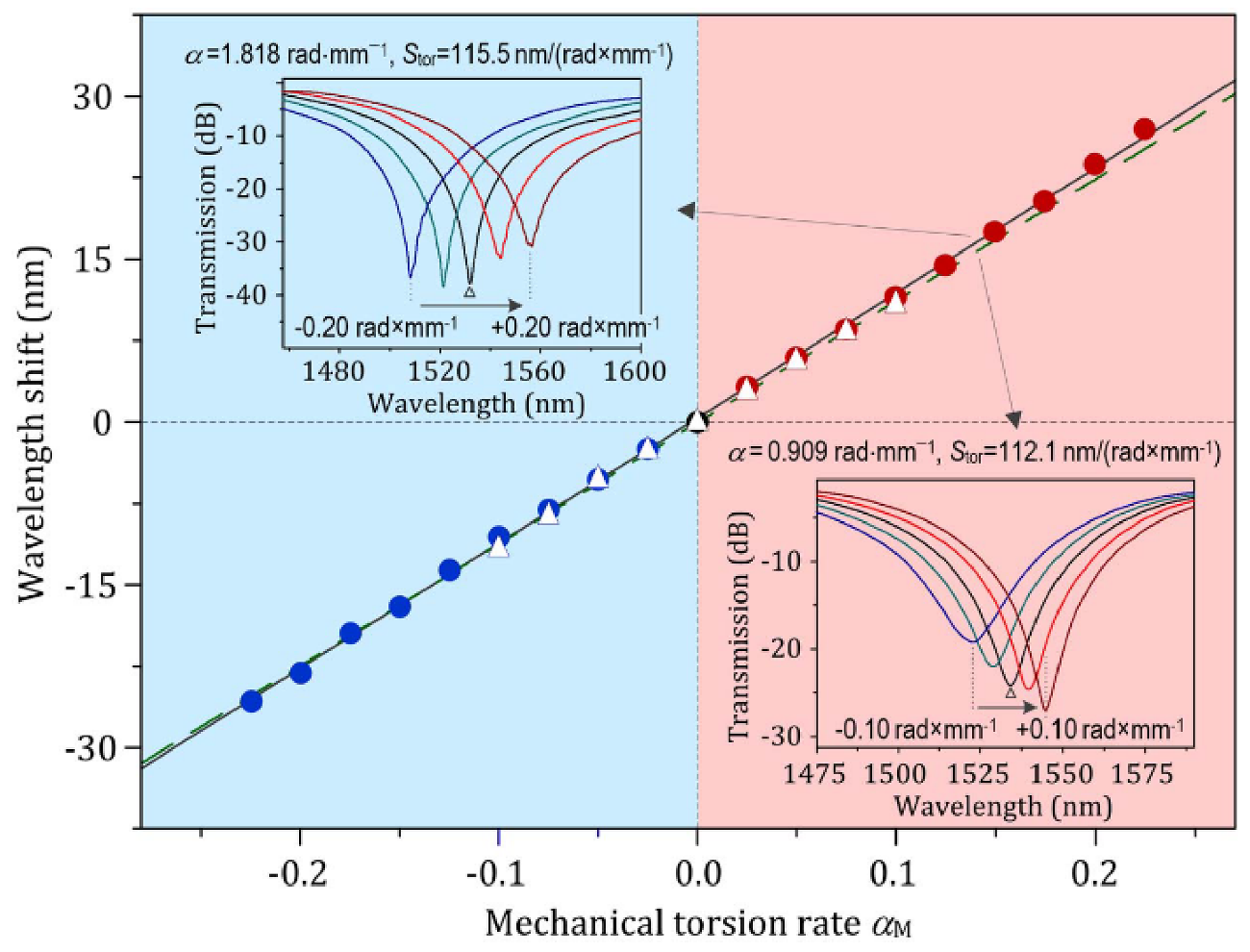
4.1. Applications of the HLPGs to Torsion Sensors
4.2. Applications to All-Fiber Circular Polarization Filter, All-Fiber Band-Rejection Filter, and All-Fiber Circular-Birefringent/Circular-Dichromatic Components
4.2.1. All-Fiber Circular Polarization Filter
4.2.2. All-Fiber Flat-Top Band-Rejection Filter
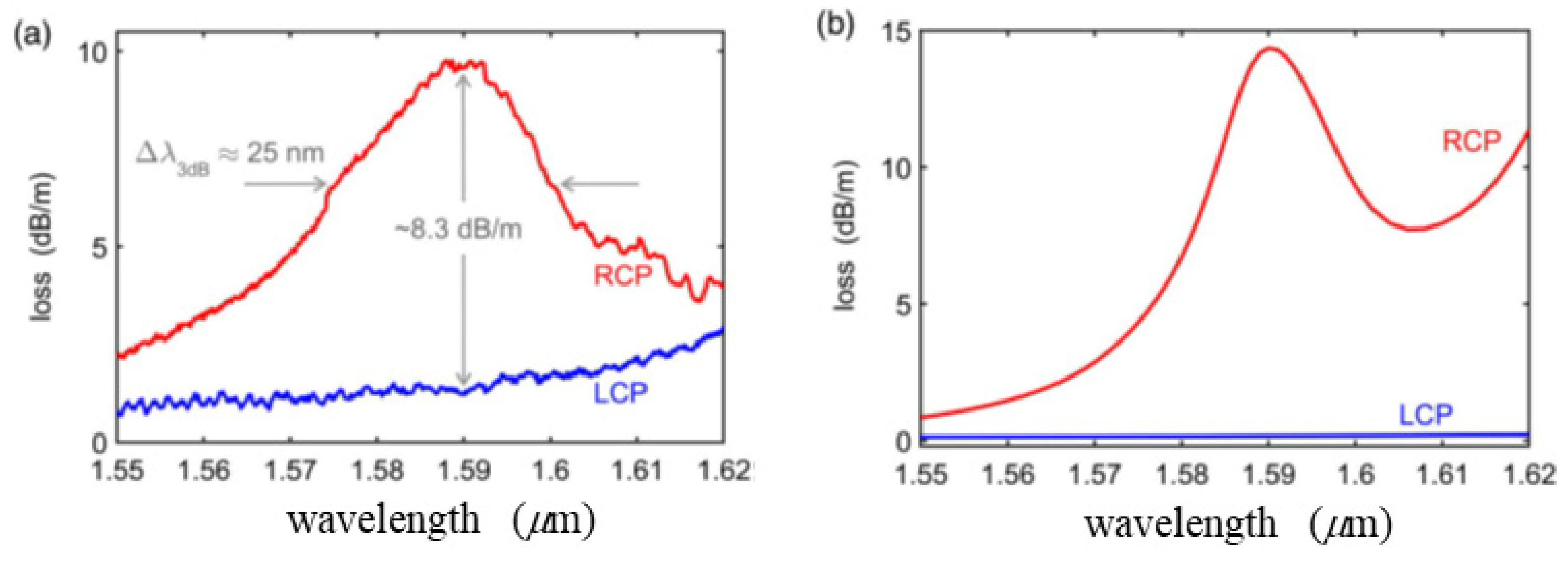
4.2.3. Optical Activity in HLPG and Its Potential Applications
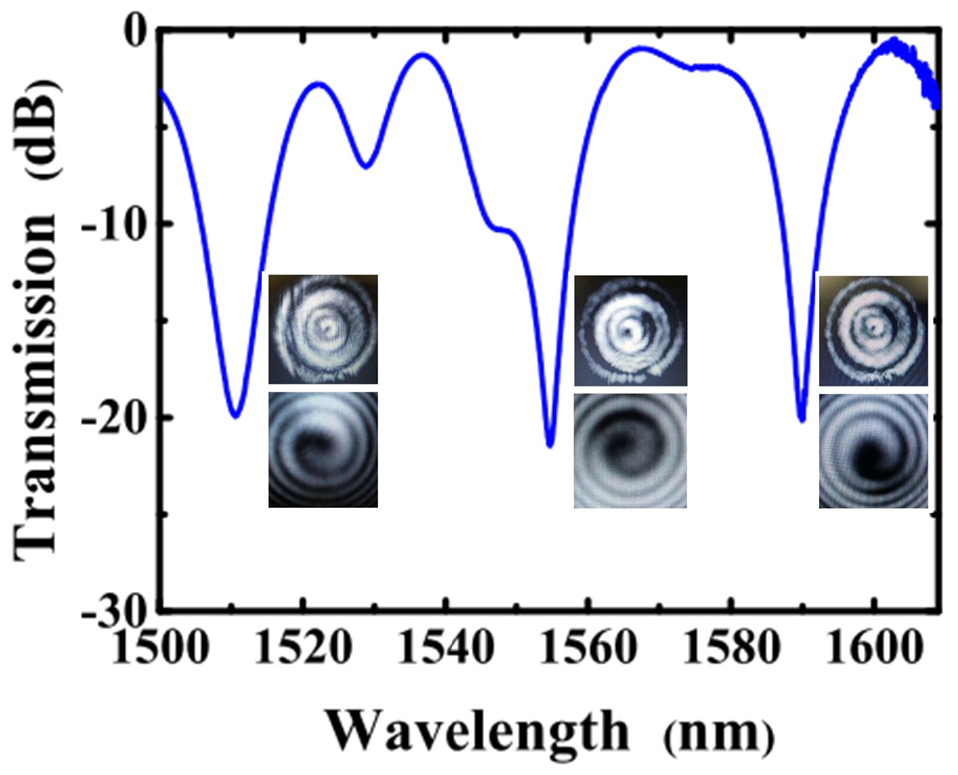
4.3. Applications of the HLPGs to All-Fiber OAM Mode Converters
5. Conclusions and Prospects
Author Contributions
Funding
Conflicts of Interest
References
- Urich, R.; and Simon, A. Polarization optics of twisted single-mode fibres. Appl. Opt. 1979, 18, 2241–2251. [Google Scholar] [CrossRef] [PubMed]
- Barlow, A.; Ramskov-Hansen, J.; Payne, D. Birefringence and polarization mode-dispersion in spun single-mode fibers. Appl. Opt. 1981, 20, 2962–2968. [Google Scholar] [CrossRef] [PubMed]
- Pool, C.D.; Townsend, C.D.; Nelson, K.T. Helical-grating two-mode fiber spatial-mode coupler. J. Lightwave Technol. 1991, 9, 598–604. [Google Scholar] [CrossRef]
- Lee, K. Coupling analysis of spiral fiber gratings. Opt. Commun. 2001, 198, 317–324. [Google Scholar] [CrossRef]
- Kopp, V.I.; Genack, A.Z. Double-helix chiral fibers. Opt. Lett. 2003, 28, 1876–1878. [Google Scholar] [CrossRef]
- Kopp, V.I.; Churikov, V.M.; Singer, J.; Chao, N.; Neugroschl, D.; Genack, A.Z. Chiral fiber gratings. Science 2004, 305, 74–75. [Google Scholar] [CrossRef]
- Churikov, V.M.; Kopp, V.I.; Genack, A.Z. Chiral diffraction gratings in twisted microstructured fibers. Opt. Lett. 2010, 35, 342–344. [Google Scholar] [CrossRef]
- Kopp, V.I.; Park, J.P.; Wlodawski, M.; Singer, J.; Neugroschl, D.; Genack, A.Z. Chiral Fibers: Microformed optical waveguides for polarization control, sensing, coupling, amplification, and switching. J. Lightwave Technol. 2014, 32, 605–613. [Google Scholar] [CrossRef]
- Wong, G.; Kang, M.; Lee, H.; Biancalana, F.; Conti, C.; Weiss, T.; Russell, P. Excitation of orbital angular momentum resonances in helically twisted photonic crystal fiber. Science 2012, 337, 446–449. [Google Scholar] [CrossRef]
- Beravat, R.; Wong, G.; Frosz, M.; Xi, X.; Russell, P. Twist-induced guidance in coreless photonic crystal fiber: A helical channel for light. Sci. Adv. 2016, 2, e1601421. [Google Scholar] [CrossRef] [Green Version]
- Russell, P.; Beravat, R.; Wong, G. Helically twisted photonic crystal fibres. Phil. Trans. R. Soc. A 2017, 375, 20150440. [Google Scholar] [CrossRef]
- Ren, K.; Ren, L.; Liang, J.; Kong, X.; Ju, H.; Xu, Y.; Wu, Z. Online fabrication scheme of helical long-period fiber grating for liquid-level sensing. Appl. Opt. 2016, 55, 9675–9679. [Google Scholar] [CrossRef]
- Xian, L.; Wang, P.; Li, H. Power-interrogated and simultaneous measurement of temperature and torsion using paired helical long period fiber gratings with opposite helicities. Opt. Express 2014, 22, 20260–20267. [Google Scholar] [CrossRef]
- Wang, P.; Li, H. Helical long-period grating formed in a thinned fiber and its application to a refractometric sensor. Appl. Opt. 2016, 55, 1430–1434. [Google Scholar] [CrossRef]
- Fu, C.; Liu, S.; Bai, Z.; He, J.; Liao, C.; Wang, Y.; Li, Z.; Zhang, Y.; Yang, K.; Yu, B.; et al. Orbital angular momentum mode converter based on helical long period fiber grating inscribed by hydrogen–oxygen flame. J. Lightwave Technol. 2018, 36, 1683–1688. [Google Scholar] [CrossRef]
- Fu, C.; Liu, S.; Wang, Y.; Bai, Z.; He, J.; Liao, C.; Zhang, Y.; Zhang, F.; Yu, B.; Gao, S.; et al. High-order orbital angular momentum mode generator based on twisted photonic crystal fiber. Opt. Lett. 2018, 43, 1786–1789. [Google Scholar] [CrossRef] [Green Version]
- Oh, S.; Lee, K.R.; Paek, U.C.; Chung, Y. Fabrication of helical long-period fiber gratings by use of a CO2 laser. Opt. Lett. 2004, 29, 1464–1466. [Google Scholar] [CrossRef]
- Ivanov, V. Fabrication of long-period fiber gratings by twisting a standard single-mode fiber. Opt. Lett. 2005, 30, 3290–3292. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Cao, X.; Wang, T. High sensitivity chiral long-period grating sensors written in the twisted fiber. IEEE Sens. J. 2016, 16, 4253–4257. [Google Scholar] [CrossRef]
- Cao, X.; Liu, Y.; Zhang, L.; Zhao, Y.; Wang, T. Characteristics of chiral long-period fiber gratings written in the twisted two-mode fiber by CO2 laser. Appl. Opt. 2017, 56, 5167–5171. [Google Scholar] [CrossRef]
- Sun, B.; Wei, W.; Liao, C.; Zhang, L.; Zhang, Z.; Chen, M.; Wang, Y. Automatic arc discharge-induced helical long period fiber gratings and its sensing applications. IEEE Photonics Technol. Lett. 2017, 29, 873–876. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Fan, P.; Sun, L.; Wu, C.; Guan, B. Few-period helically twisted all-solid photonic bandgap fibers. Opt. Lett. 2018, 43, 655–658. [Google Scholar] [CrossRef]
- Alexeyev, C.; Yavorsky, M. Generation and conversion of optical vortices in long-period helical core optical fibers. Phy. Rev. A 2008, 78, 043828. [Google Scholar] [CrossRef]
- Alexeyev, C.; Fadeyeva, T.; Lapin, B.; Yavorsky, M. Generation and conversion of optical vortices in long-period twisted elliptical fibers. Appl. Opt. 2012, 51, C193–C197. [Google Scholar] [CrossRef] [Green Version]
- Alexeyev, C.; Alexeyev, A.; Lapin, B.; Milione, G.; Yavorsky, M. Spin-orbit-interaction-induced generation of optical vortices in multihelicoidal fibers. Phy. Rev. A 2013, 88, 063814. [Google Scholar] [CrossRef]
- Xu, H.; Yang, L. Conversion of orbital angular momentum of light in chiral fiber gratings. Opt. Lett. 2013, 38, 1978–1980. [Google Scholar] [CrossRef]
- Shvets, G.; Trendafilov, S.; Kopp, V.I.; Neugroschl, D.; Genack, A.Z. Polarization properties of chiral fiber gratings. J. Opt. A, Pure Appl. Opt. 2009, 11, 074007. [Google Scholar] [CrossRef]
- Erdogan, T. Cladding-mode resonances in short- and long period fiber grating filters. J. Opt. Soc. Am. A 1997, 14, 1760–1773. [Google Scholar] [CrossRef]
- Qian, J.; Su, J.; Xue, L.; Yang, L. Coupled-mode analysis for chiral fiber long-period gratings using local mode approach. J. Quantum. Electron. 2012, 48, 49–55. [Google Scholar] [CrossRef]
- Xu, H.; Yang, L.; Han, Z.; Qian, J. Higher-order mode couplings in double-helix chiral long-period fiber gratings. Opt. Comm. 2013, 201, 207–214. [Google Scholar] [CrossRef]
- Ma, X.; Liu, C.; Chang, G.; Galvanauskas, A. Angular-momentum coupled optical waves in chirally-coupled-core fibers. Opt. Express 2011, 19, 26515–26528. [Google Scholar] [CrossRef] [PubMed]
- Napiorkowski, M.; Urbanczyk, W. Rigorous simulations of a helical core fiber by the use of transformation optics formalism. Opt. Express 2014, 22, 23108–23120. [Google Scholar] [CrossRef] [PubMed]
- Napiorkowski, M.; Urbanczyk, W. Rigorous simulations of coupling between core and cladding modes in a double-helix fiber. Opt. Lett. 2015, 40, 3324–3327. [Google Scholar] [CrossRef] [PubMed]
- Nicolet, A.; Zolla, F.; Guenneau, S. Modelling of twisted optical waveguides with edge elements. Eur. Phys. J. Appl. Phys. 2004, 28, 153–157. [Google Scholar] [CrossRef]
- Nicolet, A.; Zolla, F.; Agha, Y.; Guenneau, S. Geometrical transformations and equivalent materials in computational electromagnetism. COMPEL 2008, 27, 806–819. [Google Scholar] [CrossRef]
- Napiorkowski, M.; Urbanczyk, W. Coupling between core and cladding modes in a helical core fiber with large core offset. J. Opt. 2016, 18, 055601. [Google Scholar] [CrossRef]
- Napiorkowski, M.; Urbanczyk, W. Role of symmetry in mode coupling in twisted microstructured optical fibers. Opt. Lett. 2018, 43, 395–398. [Google Scholar] [CrossRef]
- Zolnacz, K.; Napiorkowski, M.; Kiczor, A.; Makara, M.; Mergo, P.; Urbanczyk, W. Bend-induced long period grating in a helical core fiber. Opt. Lett. 2020, 45, 1595–1598. [Google Scholar] [CrossRef]
- Xi, X.; Wong, G.; Frosz, M.; Babic, F.; Ahmed, G.; Jiang, X.; Euser, T.; Russell, P. Orbital-angular-momentum-preserving helical Bloch modes in twisted photonic crystal fiber. Optica 2014, 1, 165–169. [Google Scholar] [CrossRef]
- Roth, P.; Wong, G.; Frosz, M.; Ahmed, G.; Russell, P. Full-field characterization of helical Bloch modes guided in twisted coreless photonic crystal fiber. Opt. Lett. 2019, 44, 5049–5052. [Google Scholar] [CrossRef]
- Fujisawa, T.; Sato, T.; Saitoh, K. Full-vector finite-element beam propagation method for helicoidal waveguides and its application to twisted photonic crystal fibers. J. Lightwave Technol. 2017, 14, 2894–2901. [Google Scholar] [CrossRef]
- Fujisawa, T.; Saitoh, K. Off-axis core transmission characteristics of helically twisted photonic crystal fibers. Opt. Lett. 2018, 43, 4935–4938. [Google Scholar] [CrossRef]
- Nakano, S.; Fujisawa, T.; Saitoh, K. The effect of core offset on the mode converting characteristics in twisted single mode fibers. J. Lightwave Technol. 2019, 37, 5479–5485. [Google Scholar] [CrossRef]
- Erdogan, T. Fiber grating spectra. J. Lightwave Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef] [Green Version]
- Grubsky, V.; Skorucak, A.; Starodubov, D.S.; Feinberg, J. Fabrication of long-period fiber gratings with no harmonics. IEEE Photon. Technol. Lett. 1999, 11, 87–89. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, P.; Yamakawa, T.; Li, H. All-fiber second-order orbital angular momentum generator based on a single-helix helical fiber grating. Opt. Lett. 2019, 44, 5370–5373. [Google Scholar] [CrossRef]
- Detani, T.; Zhao, H.; Wang, P.; Suzuki, T.; Li, H. Simultaneous generation of the second- and third-order OAM modes by using a high-order helical long-period fiber grating. Opt. Lett. 2021, 46, 949–952. [Google Scholar] [CrossRef]
- Zhao, H.; Li, H. Enhancing the azimuthal mode couplings in a helical fiber grating by using phase sampling. IEEE Photonics Technol. Lett. 2018, 30, 630–633. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, H.; Detani, T.; Tsuyuki, Y.; Li, H. Demonstration of the mode-selection rules obeyed in a single-helix helical long-period fiber grating. Opt. Lett. 2020, 45, 1846–1849. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Zhao, Y.; Wang, T. High sensitivity twist sensor based on helical long-period grating written in two-mode fiber. IEEE Photon. Technol. Lett. 2016, 28, 1629–1632. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, Y.; Huang, L.; Mou, C. Double cladding fiber chiral long-period grating-based directional torsion sensor. IEEE Photon. Technol. Lett. 2019, 31, 1522–1525. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, Y.; Zhao, Y.; Mou, C.; Wang, T. Helical long-period gratings inscribed in polarization-maintaining fibers by CO2 laser. J. Lightwave Technol. 2019, 37, 889–897. [Google Scholar] [CrossRef]
- Shen, X.; Hu, X.; Yang, L.; Dai, N.; Wu, J.; Zhang, F.; Peng, J.; Li, H.; Li, J. Helical long-period grating manufactured with a CO2 laser on multicore fiber. Opt. Express 2017, 25, 10405–10412. [Google Scholar]
- Kong, X.; Ren, K.; Ren, L.; Liang, J.; Ju, H. Chiral long-period gratings: Fabrication, highly sensitive torsion sensing, and tunable single-band filtering. Appl. Opt. 2017, 56, 4702–4707. [Google Scholar] [CrossRef]
- Ren, K.; Ren, L.; Liang, J.; Kong, X.; Ju, H.; Wu, Z. Online and efficient fabrication of helical long-period fiber gratings. IEEE Photon. Technol. Lett. 2017, 29, 1175–1178. [Google Scholar]
- Zhang, Y.; Bai, Z.; Fu, C.; Liu, S.; Tang, J.; Yu, J.; Liao, C.; Wang, Y.; He, J.; Wang, Y. Polarization-independent orbital angular momentum generator based on a chiral fiber grating. Opt. Lett. 2019, 44, 61–64. [Google Scholar] [CrossRef]
- Sumetsky, M.; Dulashko, Y.; Hale, A. Fabrication and study of bent and coiled free silica nanowires: Self-coupling microloop optical interferometer. Opt. Express 2004, 12, 3521–3531. [Google Scholar] [CrossRef]
- Inoue, G.; Wang, P.; Li, H. Flat-top band-rejection filter based on two successively-cascaded helical fiber gratings. Opt. Express 2016, 24, 5442–5447. [Google Scholar] [CrossRef]
- Zhu, C.; Zhao, H.; Wang, P.; Subramanian, R.; Li, H. Enhanced flat-top band-rejection filter based on reflective helical long-period fiber gratings. IEEE Photon. Technol. Lett. 2017, 29, 964–967. [Google Scholar] [CrossRef]
- Zhu, C.; Zhao, H.; Li, H. Mode-couplings in two cascaded helical long-period fibre gratings and their application to polarization-insensitive band-rejection filter. Opt. Commun. 2018, 423, 81–85. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, H.; Yamakawa, T.; Li, H. Polarization-independent flat-top band-rejection filter based on the phase-modulated HLPG. IEEE Photon. Technol. Lett. 2020, 32, 170–173. [Google Scholar] [CrossRef]
- Wang, P.; Ramanathan, S.; Zhu, C.; Zhao, H.; Li, H. Phase-shifted helical long-period fiber grating and its characterization by using the microscopic imaging method. Opt. Express 2017, 25, 7402–7407. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Wang, P.; Zhu, C.; Ramanathan, S.; Li, H. Analysis for the phase-diffusion effect in a phase-shifted helical long-period fiber grating and its pre-compensation. Opt. Express 2017, 25, 19085–19093. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Ishikami, S.; Wang, P.; Zhao, H.; Li, H. Multichannel helical long-period fiber gratings based on the phase-only sampling. Opt. Express 2019, 27, 2281–2291. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Yamakawa, T.; Zhao, H.; Li, H. All-fiber circular polarization filter realized by using helical long-period fiber gratings. IEEE Photon. Technol. Lett. 2018, 30, 1905–1908. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, P.; Zhao, H.; Mizushima, R.; Ishikami, S.; Li, H. DC-sampled helical fiber grating and its application to multi-channel OAM generator. IEEE Photon. Technol. Lett. 2019, 31, 1445–1448. [Google Scholar] [CrossRef]
- Mizushima, R.; Detani, T.; Zhu, C.; Wang, P.; Zhao, H.; Li, H. The superimposed multi-channel helical long-period fiber grating and its application to multi-channel OAM mode generator. IEEE J. Lightwave Technol. 2021, in press. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, H.; Detani, T.; Li, H. Simultaneous generation of the first- and second-order OAM using the cascaded HLPGs. IEEE Photon. Technol. Lett. 2020, 32, 685–688. [Google Scholar] [CrossRef]
- Budinski, V.; Donlagic, D. Fiber-optic sensors for measurements of torsion, twist and rotation: A Review. Sensors 2017, 17, 443. [Google Scholar] [CrossRef] [Green Version]
- Fu, C.; Wang, Y.; Liu, S.; Bai, Z.; Liao, C.; He, J.; Wang, Y. Recent progress in fabrications and applications of heating-induced long period fiber gratings. Sensors 2019, 19, 4473. [Google Scholar] [CrossRef] [Green Version]
- Xi, X.; Wong, G.; Weiss, T.; Russell, P. Measuring mechanical strain and twist using helical photonic crystal fiber. Opt. Lett. 2013, 38, 5401–5404. [Google Scholar] [CrossRef]
- Subramanian, R.; Zhu, C.; Zhao, H.; Li, H. Torsion, strain, and temperature sensor based on helical long-period fiber gratings. IEEE Photon. Technol. Lett. 2018, 30, 327–330. [Google Scholar] [CrossRef]
- Kopp, V.I.; Churikov, V.M.; Genack, A.Z. Synchronization of optical polarization conversion and scattering in chiral fibers. Opt. Lett. 2006, 31, 571–573. [Google Scholar] [CrossRef]
- Yang, L.; Xue, L.; Li, C.; Su, J.; Qian, J. Adiabatic circular polarizer based on chiral fiber grating. Opt. Express 2011, 19, 2251–2256. [Google Scholar] [CrossRef]
- Fu, C.; Wang, Y.; Bai, Z.; Liu, S.; Zhang, Y.; Li, Z. Twist-direction-dependent orbital angular momentum generator based on inflation-assisted helical photonic crystal fiber. Opt. Lett. 2019, 44, 459–462. [Google Scholar] [CrossRef]
- Zhao, H.; Zhu, C.; Subramanian, R.; Li, H. Comprehensive analysis for the consecutively cascaded single-helix long-period fiber gratings with opposite helicities. IEEE J. Quantum. Electron. 2018, 54, 6800606. [Google Scholar] [CrossRef]
- Usuga-Restrepo, J.; Guimaraes, W.; Franco, M. All-fiber circular polarization beam splitter based on helically twisted twin-core photonic crystal fiber coupler. Opt. Fiber Technol. 2020, 58, 102285. [Google Scholar] [CrossRef]
- Shin, W.; Yu, B.; Noh, Y.; Lee, Z.; Ko, K.; Oh, K. Bandwidth-tunable band-rejection filter based on helicoidal fiber grating pair grating of opposite helicities. Opt. Lett. 2007, 32, 1214–1216. [Google Scholar] [CrossRef]
- Bassett, I.M. Design principle for a circularly birefringent optical fiber. Opt. Lett. 1988, 13, 844–846. [Google Scholar] [CrossRef]
- Xi, X.; Weiss, T.; Wong, G.; Biancalana, F.; Barnett, S.; Padgett, M.; Russell, P. Optical activity in twisted solid-core photonic crystal fibers. Phys. Rev. Lett. 2013, 110, 143903. [Google Scholar] [CrossRef] [Green Version]
- Weiss, T.; Wong, G.; Biancalana, F.; Barnett, S.; Xi, X.; Russell, P. Topological Zeeman effect and circular birefringence in twisted photonic crystal fibers. J. Opt. Soc. Am. B 2013, 30, 2921–2927. [Google Scholar] [CrossRef] [Green Version]
- Wong, G.; Xi, X.; Frosz, M.; Russell, P. Enhanced optical activity and circular dichroism in twisted photonic crystal fiber. Opt. Lett. 2015, 40, 4639–4642. [Google Scholar] [CrossRef]
- Nakano, S.; Fujisawa, T.; Sato, T.; Saitoh, K. Beam propagation analysis of optical activity and circular dichroism in helically twisted photonic crystal fiber. Jpn. J. Appl. Phys. 2018, 57, 08PF06. [Google Scholar] [CrossRef]
- Roth, P.; Chen, Y.; Gunendi, M.C.; Beravat, R.; Edavalath, N.; Frosz, M.; Ahmed, G.; Wong, G.; Russell, P. Strong circular dichroism for the HE11 mode in twisted single-ring hollow-core photonic crystal fiber. Optica 2018, 5, 1315–1321. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Coerwinkel, R.; Kristensen, M.; Woerdman, J.P. Helical-wavefront laser beams produced with a spiral phase plate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Leach, J.; Jack, B.; Romero, J.; Jha, A.K.; Yao, A.M.; Franke-Arnold, S.; Ireland, D.G.; Boyd, R.W.; Barnett, S.M.; Padgett, M.J. Quantum correlations in optical angle–orbital angular momentum variables. Science 2010, 329, 662–665. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [Green Version]
- Dashti, P.; Alhassen, F.; Lee, H. Observation of orbital angular momentum transfer between acoustic and optical vortices in optical fiber. Phys. Rev. Lett. 2006, 96, 043604. [Google Scholar] [CrossRef] [PubMed]
- Fang, L.; Wang, J. Flexible generation/conversion/exchange of fiber-guided orbital angular momentum modes using helical gratings. Opt. Lett. 2015, 40, 4010–4013. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, X.; Liu, Y.; Liu, Z.; Mou, C. All-fiber bandwidth tunable ultra-broadband mode converters based on long-period fiber gratings and helical long-period gratings. Opt. Express 2020, 28, 11990–12000. [Google Scholar] [CrossRef] [PubMed]
- Bai, Z.; Wang, Y.; Zhang, Y.; Fu, C.; Liu, S.; Li, M.; Liao, C.; Wang, Y.; He, J. Helical long-period fiber gratings as wavelength-tunable orbital angular momentum mode generators. IEEE Photonics Technol. Lett. 2020, 32, 418–421. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, M.; Li, H. Modal-dispersion effects on the spectra of the helical long-period fiber grating-based components. Opt. Commun. 2020, 457, 124708. [Google Scholar] [CrossRef]
- Ren, K.; Cheng, M.; Ren, L.; Jiang, Y.; Han, D.; Wang, Y.; Dong, J.; Liu, J.; Yang, L.; Xi, Z. Ultra-broadband conversion of OAM mode near the dispersion turning point in helical fiber gratings. OSA Continuum 2020, 3, 77–87. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, A.; Xu, L.; Zhang, X.; Sun, B.; Gu, C.; Ming, H. Generation of optical vortices using a helical fiber Bragg grating. J. Lightwave Technol. 2014, 32, 605–612. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, A.; Chen, R.; Zhou, Y.; Ming, H.; Zhan, Q. Generation and conversion of higher order optical vortices in optical fiber with helical fiber Bragg gratings. J. Lightwave Technol. 2016, 34, 2413–2418. [Google Scholar] [CrossRef]









| ccSHLPG (l = 1) | cSHLPG (l = −1) | ||
|---|---|---|---|
| Core | Cladding | Core | Cladding |
| HE11+ | HE24+ | HE11+ | TE04/TM04 |
| HE11− | TE04/TM04 | HE11− | HE24− |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Li, H. Advances on Mode-Coupling Theories, Fabrication Techniques, and Applications of the Helical Long-Period Fiber Gratings: A Review. Photonics 2021, 8, 106. https://doi.org/10.3390/photonics8040106
Zhao H, Li H. Advances on Mode-Coupling Theories, Fabrication Techniques, and Applications of the Helical Long-Period Fiber Gratings: A Review. Photonics. 2021; 8(4):106. https://doi.org/10.3390/photonics8040106
Chicago/Turabian StyleZhao, Hua, and Hongpu Li. 2021. "Advances on Mode-Coupling Theories, Fabrication Techniques, and Applications of the Helical Long-Period Fiber Gratings: A Review" Photonics 8, no. 4: 106. https://doi.org/10.3390/photonics8040106
APA StyleZhao, H., & Li, H. (2021). Advances on Mode-Coupling Theories, Fabrication Techniques, and Applications of the Helical Long-Period Fiber Gratings: A Review. Photonics, 8(4), 106. https://doi.org/10.3390/photonics8040106