Progress on Studies of Beams Carrying Twist
Abstract
:1. Introduction
2. The Twist Phase and the Twisting Phase
3. Properties of Various Types of Beams That Carry Twist Phase
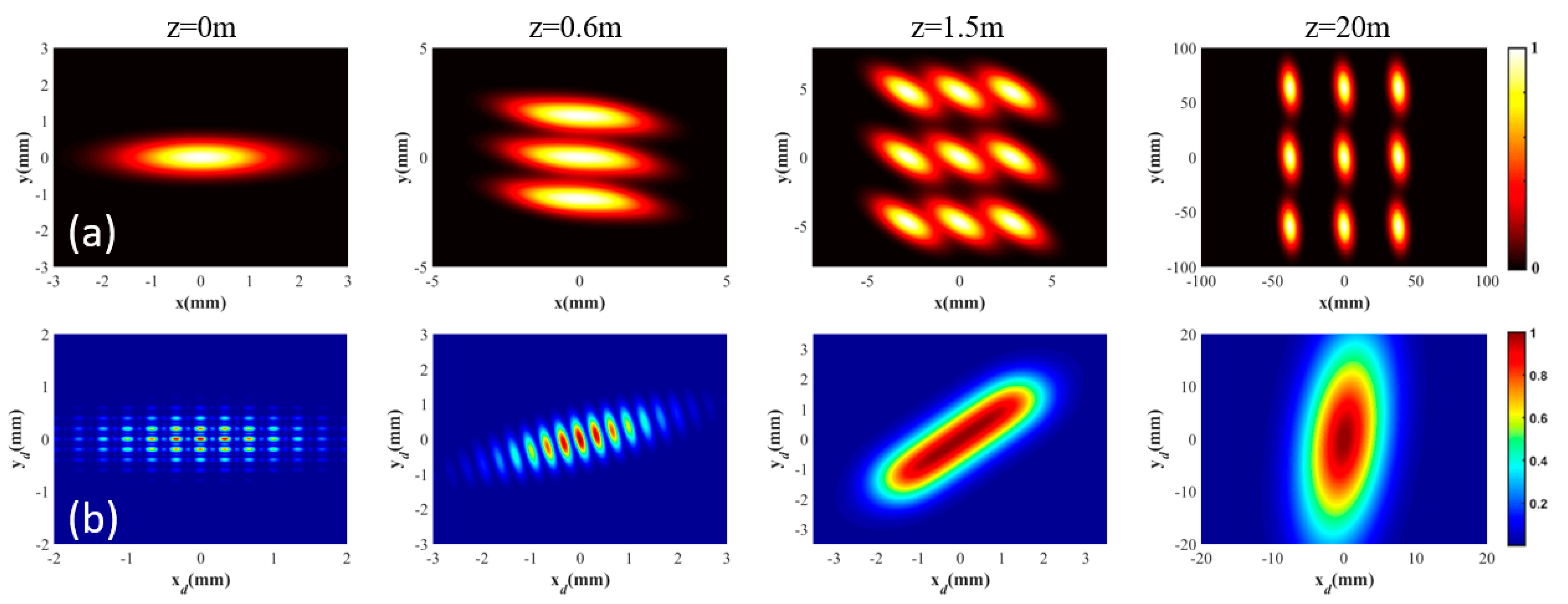
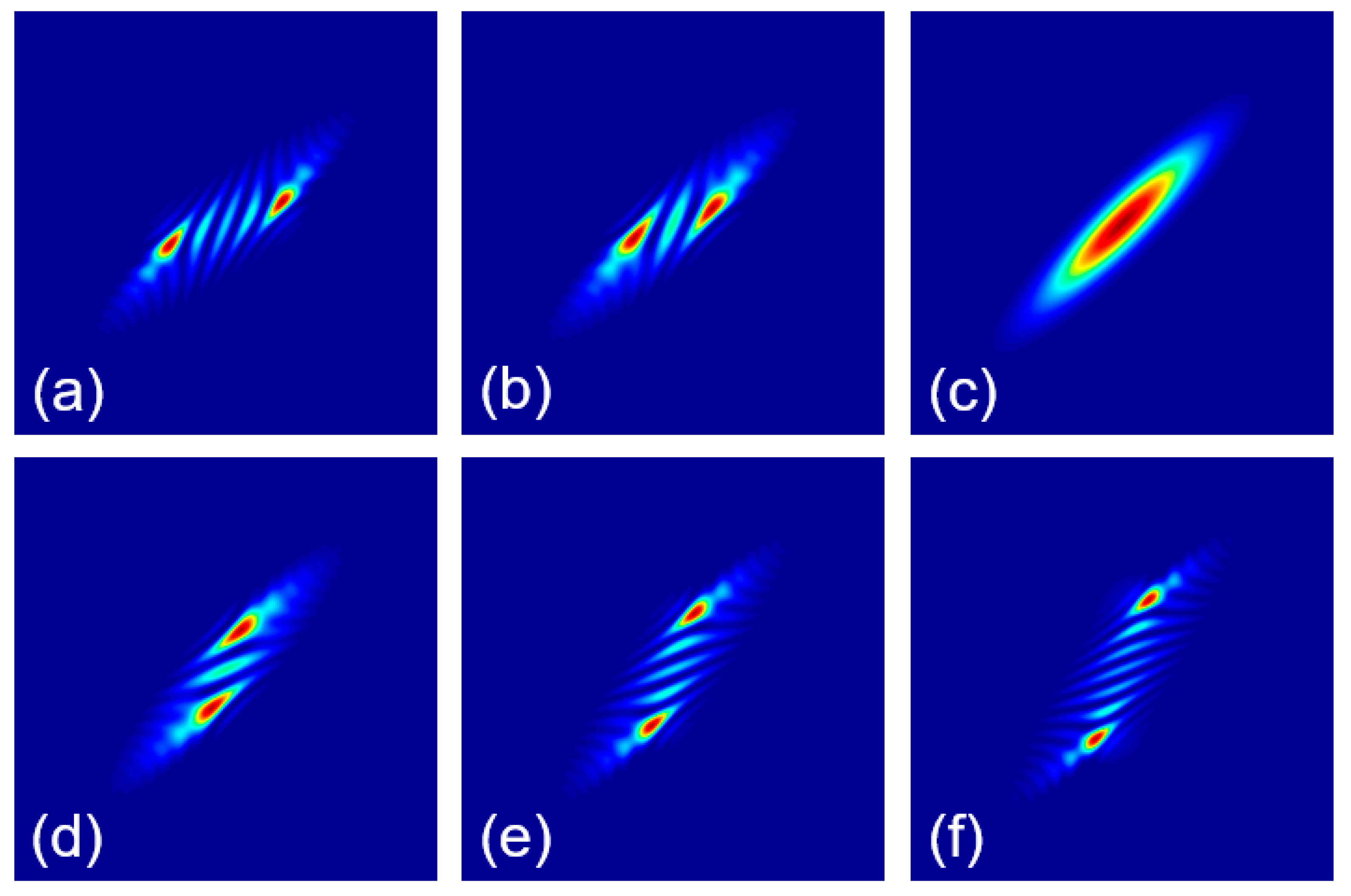
3.1. Twisted Gaussian Schell-Model Array (TGSMA) Beams
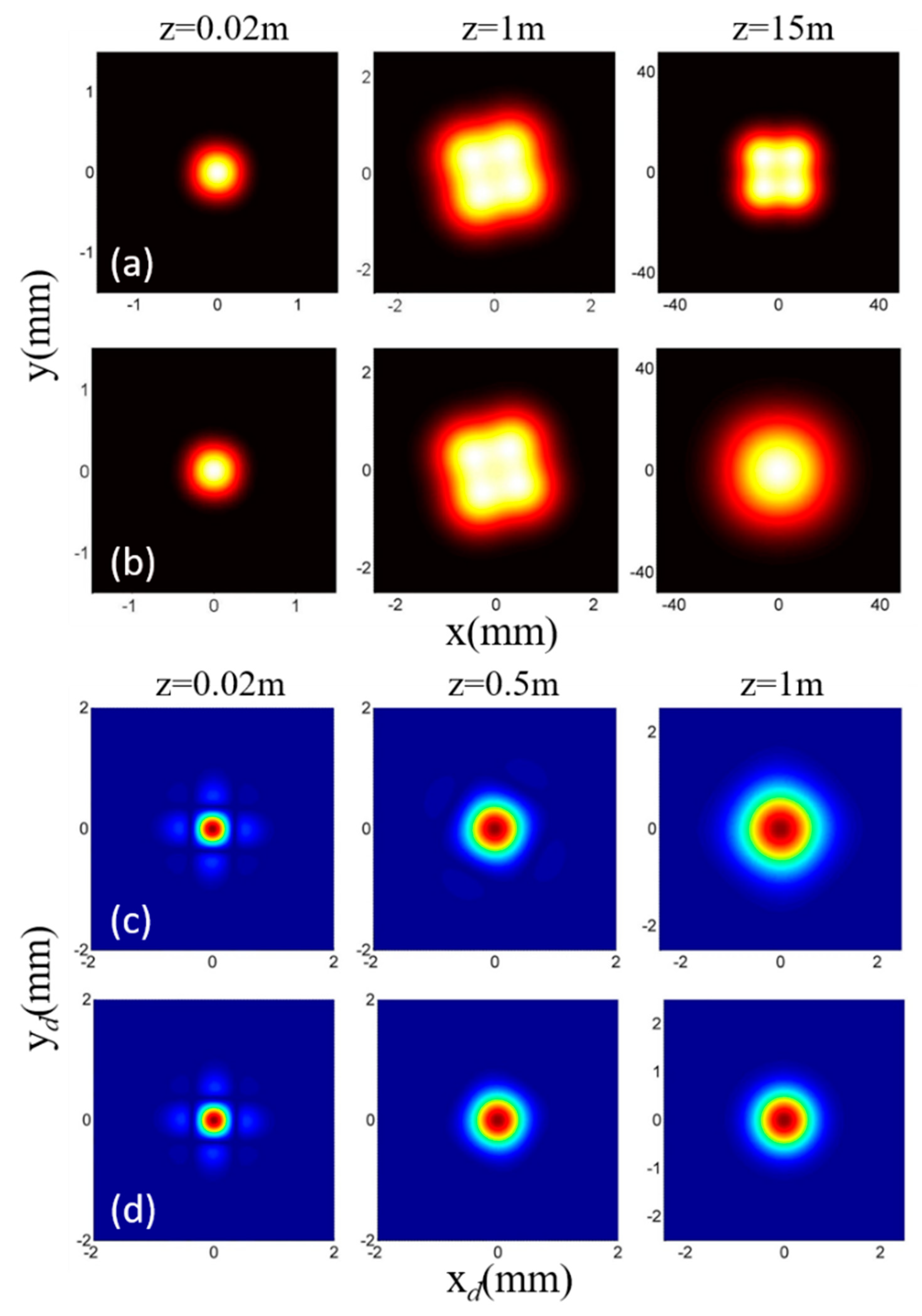
3.2. Twisted Rectangular Multi-Gaussian Schell-Model (TRMGSM) Beam
3.3. Electromagnetic Twisted Gaussian Schell-Model Array (EM TGSMA) Beam
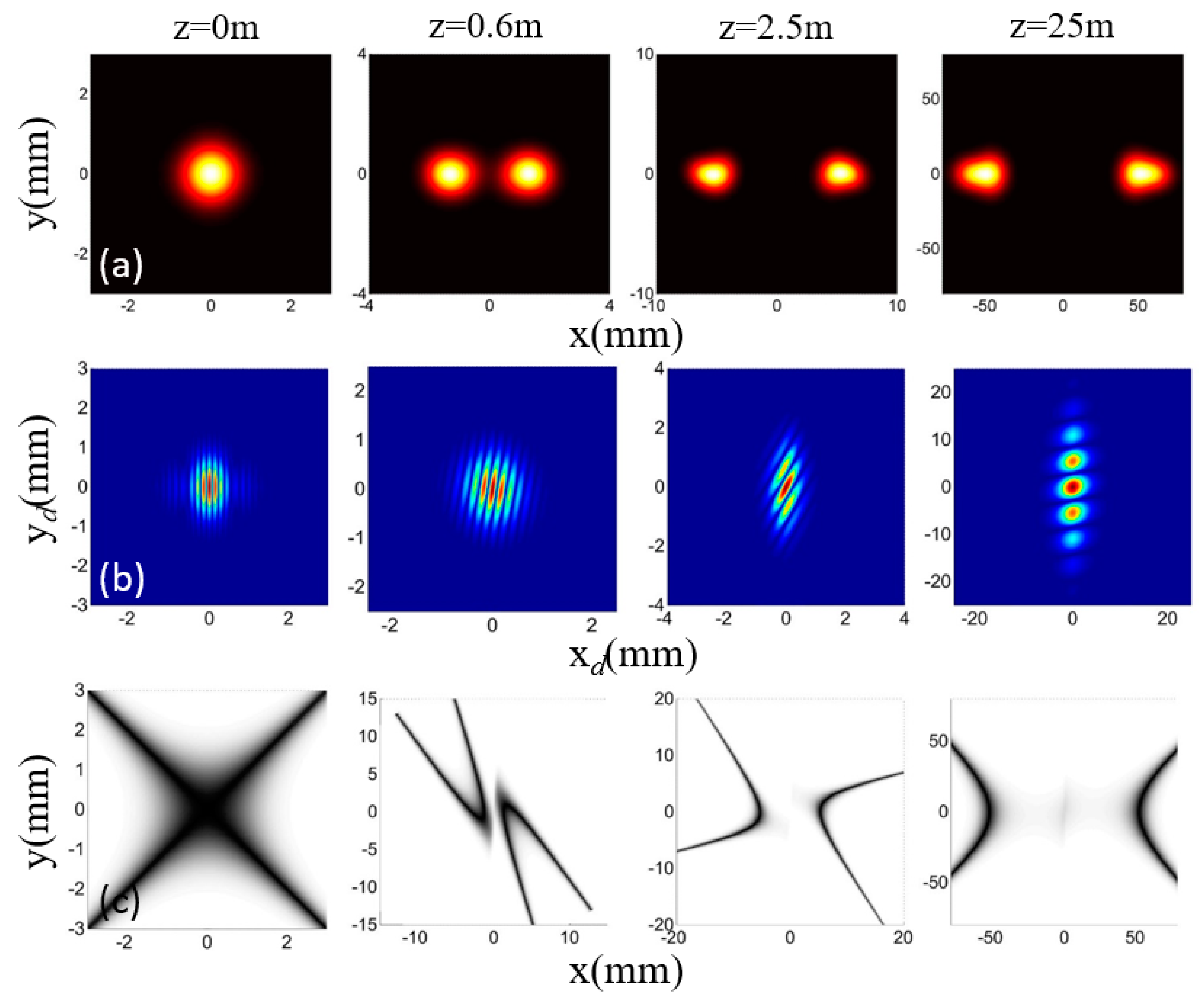
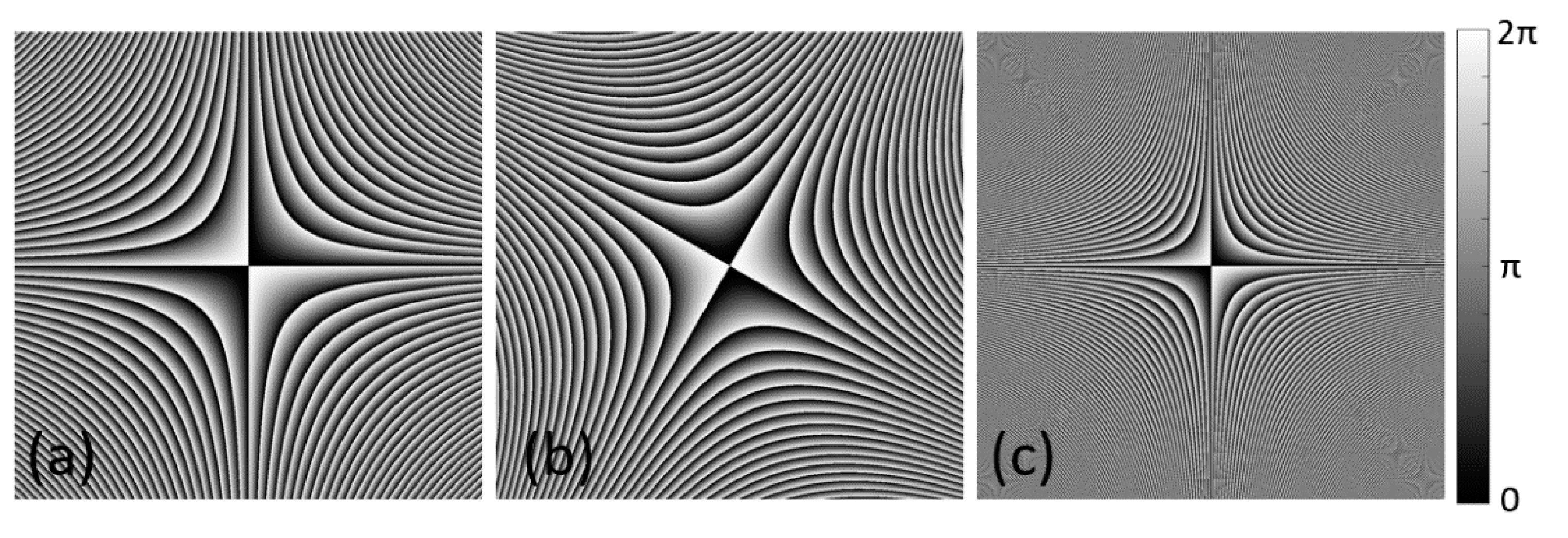
3.4. Beams with High-Order Twist Phase
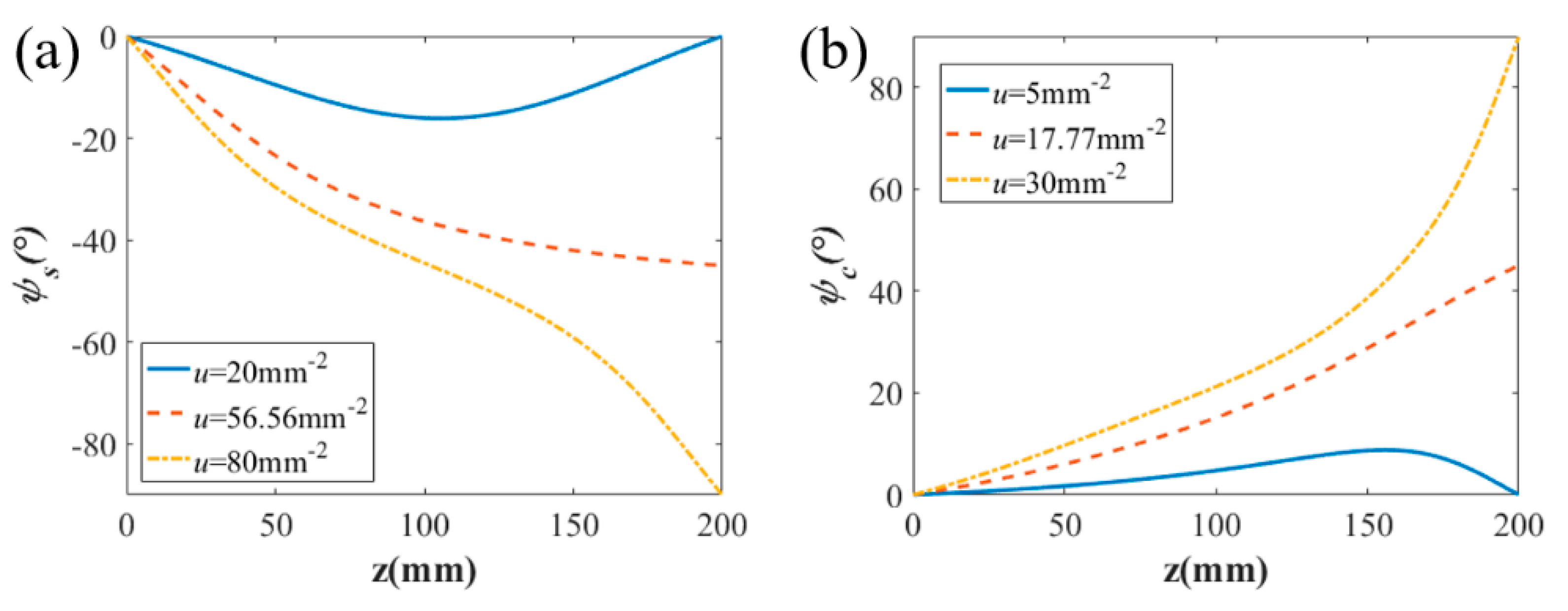
4. Effect of the Twisting Phase on Beams
4.1. The Twisting Phase in Completely Coherent Beams
4.2. The Twisting Phase in Partially Coherent Beams
4.3. The Twisting Phase in Optical Trapping Rayleigh Particles
5. Summary and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Simon, R.; Mukunda, N. Twisted Gaussian Schell-model beams. J. Opt. Soc. Am. A 1993, 10, 95–109. [Google Scholar] [CrossRef]
- Simon, R.; Sundar, K.; Mukunda, N. Twisted Gaussian Schell-model beams. I. Symmetry structure and normal-mode spectrum. J. Opt. Soc. Am. A 1993, 10, 2008–2016. [Google Scholar] [CrossRef]
- Sundar, K.; Simon, R.; Mukunda, N. Twisted Gaussian Schell-model beams. II. Spectrum analysis and propagation characteristics. J. Opt. Soc. Am. A 1993, 10, 2017–2023. [Google Scholar] [CrossRef]
- Friberg, A.T.; Tervonen, E.; Turunen, J. Focusing of twisted gaussian Schell-model beams. Opt. Commun. 1994, 106, 127–132. [Google Scholar] [CrossRef]
- Simon, R.; Friberg, A.T.; Wolf, E. Transfer of radiance by twisted Gaussian Schell-model beams in paraxial systems. Pure Appl. Opt. 1996, 5, 331–343. [Google Scholar] [CrossRef]
- Gori, F.; Bagini, V.; Santarsiero, M.; Frezza, F. Coherent and Partially Coherent Twisting Beams. Opt. Rev. 1994, 1, 143–145. [Google Scholar] [CrossRef]
- Ambrosini, D.; Bagini, V.; Gori, F.; Santarsiero, M. Twisted Gaussian Schell-model Beams: A Superposition Model. J. Mod. Opt. 1994, 41, 1391–1399. [Google Scholar] [CrossRef]
- Friberg, A.T.; Tervonen, E.; Turunen, J. Interpretation and experimental demonstration of twisted Gaussian Schell-model beams. J. Opt. Soc. Am. A 1994, 11, 1818–1826. [Google Scholar] [CrossRef]
- Lin, Q.; Cai, Y. Tensor ABCD law for partially coherent twisted anisotropic Gaussian-Schell model beams. Opt. Lett. 2002, 27, 216–218. [Google Scholar] [CrossRef] [PubMed]
- Mei, Z.; Korotkova, O. Random sources for rotating spectral densities. Opt. Lett. 2017, 42, 255–258. [Google Scholar] [CrossRef]
- Simon, R.; Mukunda, N. Twist phase in Gaussian-beam optics. J. Opt. Soc. Am. A 1998, 15, 2373–2382. [Google Scholar] [CrossRef]
- Ponomarenko, S.A. Twisted Gaussian Schell-model solitons. Phys. Rev. E 2001, 64, 036618. [Google Scholar] [CrossRef]
- Shukri, M.A.; Alkelly, A.A.; Alarify, Y.S. Spatial correlation properties of twisted partially coherent light focused by diffractive axicons. J. Opt. Soc. Am. A 2012, 29, 2019–2027. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Santarsiero, M. Twisted Gaussian Schell-model beams as series of partially coherent modified Bessel-Gauss beams. Opt. Lett. 2015, 40, 1587–1590. [Google Scholar] [CrossRef]
- Serna, J.; Movilla, J.M. Orbital angular momentum of partially coherent beams. Opt. Lett. 2001, 26, 405–407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, S.M.; Gbur, G. Angular momentum conservation in partially coherent wave fields. Phys. Rev. A 2012, 86, 043814. [Google Scholar] [CrossRef]
- Cai, Y.; Zhu, S. Orbital angular moment of a partially coherent beam propagating through an astigmatic ABCD optical system with loss or gain. Opt. Lett. 2014, 39, 1968–1971. [Google Scholar] [CrossRef] [PubMed]
- Borghi, R.; Gori, F.; Guattari, G.; Santarsiero, M. Twisted Schell-model beams with axial symmetry. Opt. Lett. 2015, 40, 4504–4507. [Google Scholar] [CrossRef]
- Riccardo, B. Twisting partially coherent light. Opt. Lett. 2018, 43, 1627. [Google Scholar]
- Gori, F.; Santarsiero, M. Devising genuine twisted cross-spectral densities. Opt. Lett. 2018, 43, 595–598. [Google Scholar] [CrossRef]
- Wu, G. Propagation properties of a radially polarized partially coherent twisted beam in free space. J. Opt. Soc. Am. A 2016, 33, 345–350. [Google Scholar] [CrossRef]
- Mei, Z.; Korotkova, O. Twisted EM beams with structured correlations. Opt. Lett. 2018, 43, 3905–3908. [Google Scholar] [CrossRef] [PubMed]
- Wan, L.; Zhao, D. Twisted Gaussian Schell-model array beams. Opt. Lett. 2018, 43, 3554–3557. [Google Scholar] [CrossRef] [PubMed]
- Wan, L.; Zhao, D. Generalized partially coherent beams with nonseparable phases. Opt. Lett. 2019, 44, 4714–4717. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Liu, L.; Wang, F.; Popov, S.; Cai, Y. Twisted Laguerre-Gaussian Schell-model beam and its orbital angular moment. Opt. Express 2018, 26, 33956–33969. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zhao, D. Statistical properties of electromagnetic twisted Gaussian Schell-model array beams during propagation. Opt. Express 2019, 27, 19624–19632. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Zhao, D. Elliptical Laguerre Gaussian Schell-model beams with a twist in random media. Opt. Express 2019, 27, 30044–30054. [Google Scholar] [CrossRef]
- Luo, M.; Zhao, D. Twisted anisotropic electromagnetic beams with Laguerre Gaussian-Schell model correlation. Opt. Express 2020, 28, 31360–31372. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Yuan, C.; Ji, X.; Wang, T. Ring-shaped twisted Gaussian Schell-model array beams. J. Opt. Soc. Am. A 2020, 37, 444–449. [Google Scholar] [CrossRef]
- Hyde, M.W. Twisted space-frequency and space-time partially coherent beams. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef]
- Wang, H.; Peng, X.; Liu, L.; Wang, F.; Cai, Y.; Ponomarenko, S.A. Generating bona fide twisted Gaussian Schell-model beams. Opt. Lett. 2019, 44, 3709–3712. [Google Scholar] [CrossRef]
- Tian, C.; Zhu, S.; Huang, H.; Cai, Y.; Li, Z. Customizing twisted Schell-model beams. Opt. Lett. 2020, 45, 5880–5883. [Google Scholar] [CrossRef]
- Cai, Y.; He, S. Propagation of a partially coherent twisted anisotropic Gaussian Schell-model beam in a turbulent atmosphere. Appl. Phys. Lett. 2006, 89, 041117. [Google Scholar] [CrossRef]
- Wang, F.; Cai, Y. Second-order statistics of a twisted Gaussian Schell-model beam in turbulent atmosphere. Opt. Express 2010, 18, 24661–24672. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Cai, Y.; Eyyuboglu, H.T.; Baykal, Y. Twist phase-induced reduction in scintillation of a partially coherent beam in turbulent atmosphere. Opt. Lett. 2012, 37, 184–186. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Liu, L.; Cai, Y.; Baykal, Y. Statistical properties of a radially polarized twisted Gaussian Schell-model beam in an underwater turbulent medium. J. Opt. Soc. Am. A 2017, 34, 133–139. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, D. Propagation properties of a twisted rectangular multi-Gaussian Schell-model beam in free space and oceanic turbulence. Appl. Opt. 2018, 57, 8978–8983. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Huang, H.; Chen, Y.; Wang, H.; Zhu, S.; Li, Z.; Cai, Y. Twisted partially coherent array sources and their transmission in anisotropic turbulence. Opt. Express 2018, 20, 25974–25988. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Lin, Q.; Korotkova, O. Ghost imaging with twisted Gaussian Schell-model beam. Opt. Express 2009, 17, 2453–2464. [Google Scholar] [CrossRef]
- Zhao, C.; Cai, Y.; Korotkova, O. Radiation force of scalar and electromagnetic twisted Gaussian Schell-model beams. Opt. Express 2009, 17, 21472–21487. [Google Scholar] [CrossRef]
- Tong, Z.; Korotkova, O. Beyond the classical Rayleigh limit with twisted light. Opt. Lett. 2012, 37, 2595–2597. [Google Scholar] [CrossRef]
- Peng, X.; Wang, H.; Liu, L.; Wang, F.; Popov, S.; Cai, Y. Self-reconstruction of twisted Laguerre-Gaussian Schell-model beams partially blocked by an opaque obstacle. Opt. Express 2020, 28, 31510–31523. [Google Scholar] [CrossRef]
- Wan, L.; Zhao, D. Controllable rotating Gaussian Schell-model beams. Opt. Lett. 2019, 44, 735–738. [Google Scholar] [CrossRef] [PubMed]
- Abramochkin, E.; Volostnikov, V. Beam Transformations and Nontransformed Beams. Opt. Commun. 1991, 83, 123–135. [Google Scholar] [CrossRef]
- Abramochkin, E.G.; Volostnikov, V.G. Generalized Gaussian beams. J. Opt. A Pure Appl. Opt. 2004, 6, S157–S161. [Google Scholar] [CrossRef]
- Courtial, J.; Dholakia, K.; Allen, L.; Padgett, M.J. Gaussian beams with very high orbital angular momentum. Opt. Commun. 1997, 144, 210–213. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Astigmatic transforms of an optical vortex for measurement of its topological charge. Appl. Opt. 2017, 56, 4095–4104. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Astigmatic laser beams with a large orbital angular momentum. Opt. Express 2018, 26, 141–156. [Google Scholar] [CrossRef]
- Ponomarenko, S.A. A class of partially coherent beams carrying optical vortices. JOSA A 2001, 18, 150–156. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhao, D. Effect of the astigmatic phase on the intensity of nonsingular beams during propagation. Laser Phys. 2020, 30, 015003. [Google Scholar] [CrossRef]
- Shen, D.; Zhao, D. Measuring the topological charge of optical vortices with a twisting phase. Opt. Lett. 2019, 44, 2334–2337. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, D. Experimental generation of a kind of reversal rotating beams. Opt Express 2020, 28, 2884–2894. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yan, H.; Zhao, D. Optical trapping Rayleigh particles with a twist effect. Opt. Lasers Eng. 2020, 130, 106101. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef] [Green Version]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Mei, Z.; Zhao, D.; Korotkova, O.; Mao, Y. Gaussian Schell-model arrays. Opt. Lett. 2015, 40, 5662–5665. [Google Scholar] [CrossRef]
- Ma, L.; Ponomarenko, S.A. Optical coherence gratings and lattices. Opt. Lett. 2014, 39, 6656–6659. [Google Scholar] [CrossRef]
- Wan, L.; Zhao, D. Optical coherence grids and their propagation characteristics. Opt. Express 2018, 26, 2168–2180. [Google Scholar] [CrossRef] [PubMed]
- Nikishov, V.V.; Nikishov, V.I. Spectrum of Turbulent Fluctuations of the Sea-Water Refraction Index. Int. J. Fluid Mech. Res. 2000, 27, 82–98. [Google Scholar] [CrossRef]
- Thorpe, S.A. An Introduction to Ocean Turbulence; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Wolf, E. Correlation-induced changes in the degree of polarization, the degree of coherence, and the spectrum of random electromagnetic beams on propagation. Opt. Lett. 2003, 28, 1078–1080. [Google Scholar] [CrossRef]
- Gbur, G. Singular Optics; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Voelz, D.G. Computational Fourier Optics: A MATLAB Tutorial; SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Lajunen, H.; Saastamoinen, T. Propagation characteristics of partially coherent beams with spatially varying correlations. Opt. Lett. 2011, 36, 4104–4106. [Google Scholar] [CrossRef]
- Peng, Y.; Gan, X.-T.; Ju, P.; Wang, Y.-D.; Zhao, J.-L. Measuring Topological Charges of Optical Vortices with Multi-Singularity Using a Cylindrical Lens. Chin. Phys. Lett. 2015, 32, 024201. [Google Scholar] [CrossRef]
- Wang, F.; Liang, C.; Yuan, Y.; Cai, Y. Generalized multi-Gaussian correlated Schell-model beam: From theory to experiment. Opt. Express 2014, 22, 23456–23464. [Google Scholar] [CrossRef] [PubMed]
- Harada, Y.; Asakura, T. Radiation forces on a dielectric sphere in the Rayleigh scattering regime. Opt. Commun. 1996, 124, 529–541. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wan, L.; Zhou, Y.; Zhang, Y.; Zhao, D. Progress on Studies of Beams Carrying Twist. Photonics 2021, 8, 92. https://doi.org/10.3390/photonics8040092
Liu Z, Wan L, Zhou Y, Zhang Y, Zhao D. Progress on Studies of Beams Carrying Twist. Photonics. 2021; 8(4):92. https://doi.org/10.3390/photonics8040092
Chicago/Turabian StyleLiu, Zhenglin, Lipeng Wan, Yujie Zhou, Yao Zhang, and Daomu Zhao. 2021. "Progress on Studies of Beams Carrying Twist" Photonics 8, no. 4: 92. https://doi.org/10.3390/photonics8040092
APA StyleLiu, Z., Wan, L., Zhou, Y., Zhang, Y., & Zhao, D. (2021). Progress on Studies of Beams Carrying Twist. Photonics, 8(4), 92. https://doi.org/10.3390/photonics8040092




