Metasurface Holography in the Microwave Regime
Abstract
1. Introduction
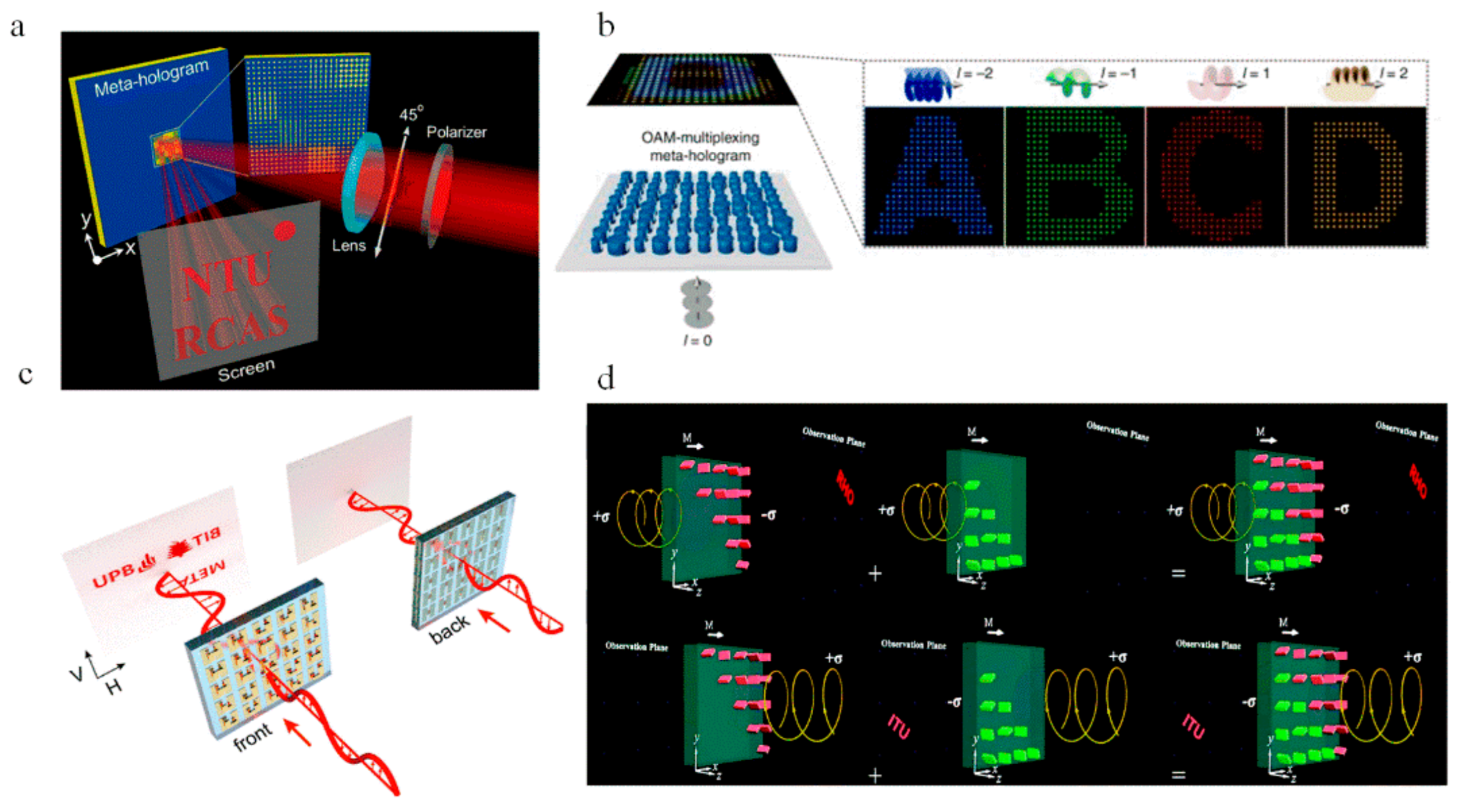
2. Optical Metasurface Holography
3. Microwave Metasurface Hologram
3.1. Realization of Microwave Metasurface Holography
3.2. Polarization-Multiplexed Metasurface Holograms
3.3. Frequency-Multiplexed Metasurface Holograms
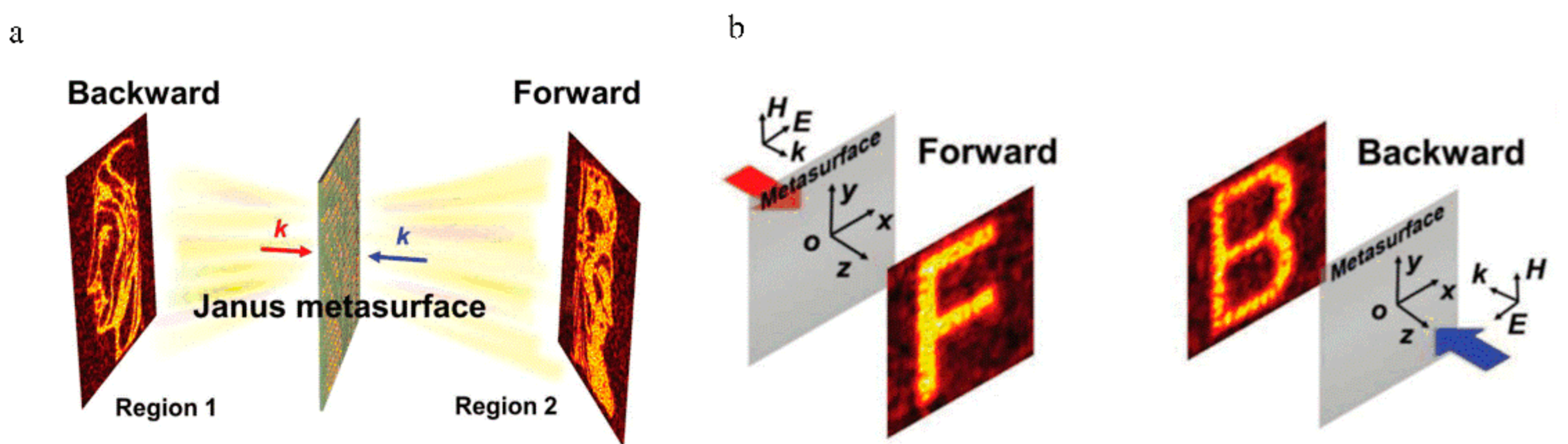
3.4. Space Asymmetric Propagation Hologram
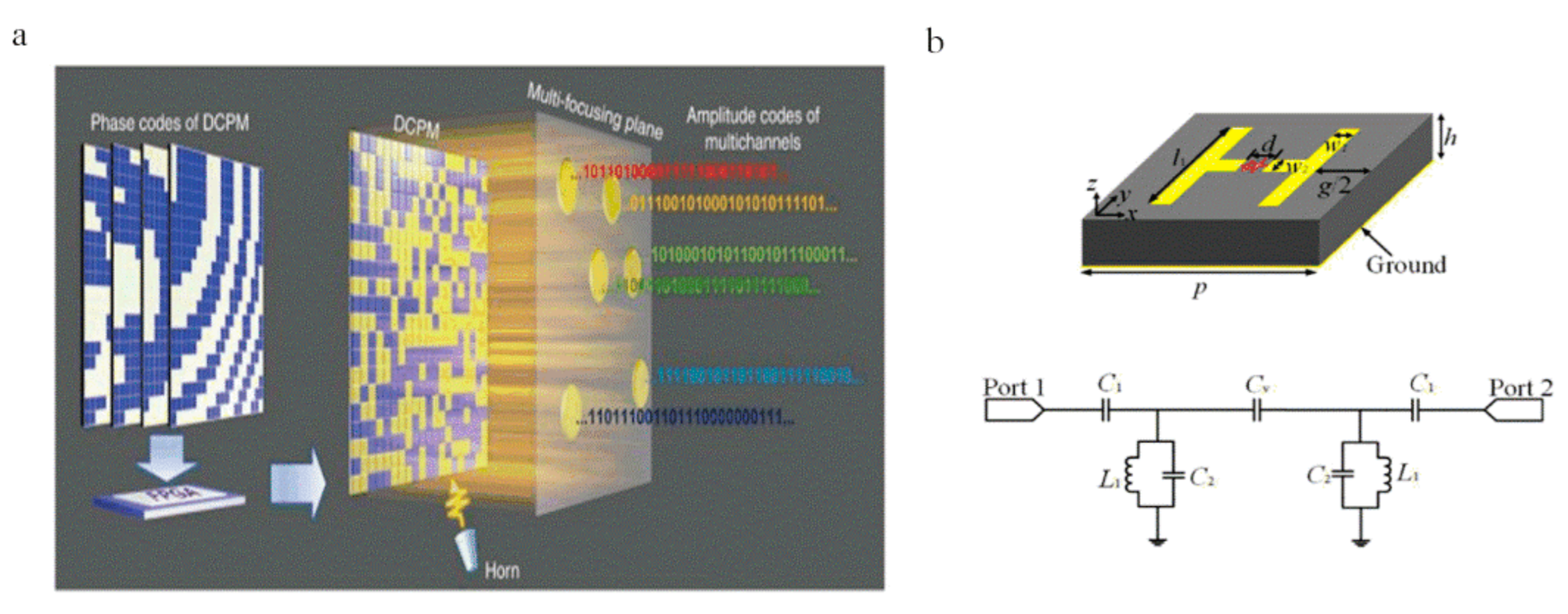
3.5. Reconfigurable Metasurface Holograms
4. Perspective in Metasurface Holography
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gabor, D. A new microscope principle. Nature 1948, 161, 777. [Google Scholar] [CrossRef]
- Maiman, T.H. Stimulated Optical Radiation in Ruby. Nature 1960. [Google Scholar] [CrossRef]
- Gabor. Microscopy by Reconstructed Wave Fronts: II. Proc. Phys. Soc. 1951, 64, 449–469. [Google Scholar] [CrossRef]
- Sirat, G.Y.; Paz, F.; Agronik, G. Conoscopic holography. Proc. SPIE Int. Soc. Opt. Eng. 2005, 10, 11–16. [Google Scholar]
- Miao, J.; Charalambous, P.; Kirz, J. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 1999, 400, 342–344. [Google Scholar] [CrossRef]
- Mertz, L.; Young, N.O. Fresnel transformations of images. SPIE Milest. Ser. MS 1996, 128, 44–49. [Google Scholar]
- Kim, S.G.; Lee, B.; Kim, E.S. Resolution analysis of incoherent triangular holography. Appl. Opt. 2001, 40, 4672–4678. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.; Brooker, G. Digital spatially incoherent Fresnel holography. Opt. Lett. 2007, 32, 912–914. [Google Scholar] [CrossRef]
- Rosen, J.; Brooker, G. Fluorescence incoherent color holography. Opt. Express 2007, 15, 2244–2250. [Google Scholar] [CrossRef] [PubMed]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography—A new type of incoherent digital holograms. Opt. Express 2016, 24, 12430–12441. [Google Scholar] [CrossRef]
- Hong, J.; Kim, M.K. Resolution Enhancement of Incoherent Digital Holography using the Super Resolution Image Reconstruction Technique. In Digital Holographic Optical Processing; OSA Techinal Digest (CD): Kohala Coast, HI, USA, 2013; p. DTh1A.3. [Google Scholar]
- Siegel, N.; Storrie, B.; Bruce, M.; Brooker, G. CINCH (confocal incoherent correlation holography) super resolution fluorescence microscopy based upon FINCH (Fresnel incoherent correlation holography). Proc. SPIE Int. Soc. Opt. Eng. 2015, 9336. [Google Scholar] [CrossRef]
- Kim, M.K. Full color natural light holographic camera. Opt. Express 2013, 21, 9636–9642. [Google Scholar] [CrossRef]
- Barbastathis, G.; Balberg, M.; Brady, D.J. Confocal microscopy with a volume holographic filter. Opt. Lett. 1999, 24, 811–813. [Google Scholar] [CrossRef]
- Lohmann, A.W.; Paris, D.P. Binary Fraunhofer Holograms, Generated by Computer. App. Opt. 1967, 6, 1739–1748. [Google Scholar] [CrossRef]
- Shimobaba, T.; Kakue, T.; Ito, T. Review of Fast Algorithms and Hardware Implementations on Computer Holography. IEEE Trans. Ind. Inf. 2016, 12, 1611–1622. [Google Scholar] [CrossRef]
- Brown, B.R.; Lohmann, A.W. Complex Spatial Filtering with Binary Masks. App. Opt. 1966, 5. [Google Scholar] [CrossRef]
- Hutton, G. Fast-Fourier-transform holography: Recent results. Opt. Lett. 1978, 3, 30–32. [Google Scholar] [CrossRef] [PubMed]
- Faklis, D.; Michael, G. Spectral properties of multi order diffractive lenses. App. Opt. 1995, 34, 2462–2468. [Google Scholar] [CrossRef] [PubMed]
- Barlev, O.; Golub, M.A. Multifunctional binary diffractive optical elements for structured light projectors. Opt. Express 2018, 26, 21092–21107. [Google Scholar] [CrossRef]
- Roberts, D. Polarization-independent diffractive waveplate optics. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018. [Google Scholar]
- Zhan, T.; Xiong, J.; Lee, Y.H. Polarization-independent Pancharatnam-Berry phase lens system. Opt. Express 2018, 26, 35026–35033. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Mei, S.; Huang, K.; Qiu, C.W. Advances in Full Control of Electromagnetic Waves with Metasurfaces. Adv. Opt. Mater. 2016, 4, 818–833. [Google Scholar] [CrossRef]
- Hsiao, H.-H.; Chu, C.H.; Tsai, D.P. Fundamentals and Applications of Metasurfaces. Small Methods 2017, 1. [Google Scholar] [CrossRef]
- Ding, F.; Pors, A.; Bozhevolnyi, S.I. Gradient metasurfaces: A review of fundamentals and applications. Rep. Prog. Phys. 2017, 81, 26401. [Google Scholar] [CrossRef]
- Chen, S.; Li, Z.; Zhang, Y.; Cheng, H.; Tian, J. Phase Manipulation of Electromagnetic Waves with Metasurfaces and Its Applications in Nanophotonics. Adv. Opt. Mater. 2018, 6. [Google Scholar] [CrossRef]
- Sung, J.; Lee, G.-Y.; Lee, B. Progresses in the practical metasurface for holography and lens. Nanophotonics 2019, 8, 1701–1718. [Google Scholar] [CrossRef]
- Genevet, P.; Capasso, F.; Aieta, F.; Khorasaninejad, M.; Devlin, R. Recent advances in planar optics: From plasmonic to dielectric metasurfaces. Optica 2017, 4, 139–152. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, W.; Moitra, P.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation. Nano Lett. 2014, 14, 1394–1399. [Google Scholar] [CrossRef]
- Huang, K.; Liu, H.; Restuccia, S.; Mehmood, M.Q.; Mei, S.T.; Giovannini, D.; Danner, A.; Padgett, M.J.; Teng, J.H.; Qiu, C.W. Spiniform phase-encoded metagratings entangling arbitrary rational-order orbital angular momentum. Light. Sci. Appl. 2018, 7. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, X.; Gao, J. Spin-Selective Second-Harmonic Vortex Beam Generation with Babinet-Inverted Plasmonic Metasurfaces. Adv. Opt. Mater. 2018, 6. [Google Scholar] [CrossRef]
- Pégard, N.C.; Fleischer, J.W. Optimizing holographic data storage using a fractional Fourier transform. Opt. Lett. 2011, 36, 2551–2553. [Google Scholar] [CrossRef]
- Goh, X.M.; Zheng, Y.; Tan, S.J.; Zhang, L.; Kumar, K.; Qiu, C.W.; Yang, J.K. Three-dimensional plasmonic stereoscopic prints in full colour. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef]
- Jin, L.; Dong, Z.; Mei, S.; Yu, Y.F.; Wei, Z.; Pan, Z.; Rezaei, S.D.; Li, X.; Kuznetsov, A.I.; Kivshar, Y.S.; et al. Noninterleaved Metasurface for (2(6)-1) Spin- and Wavelength-Encoded Holograms. Nano Lett. 2018, 18, 8016–8024. [Google Scholar] [CrossRef]
- Liu, H.C.; Yang, B.; Guo, Q.; Shi, J.; Guan, C.; Zheng, G.; Mühlenbernd, H.; Li, G.; Zentgraf, T.; Zhang, S. Single-pixel computational ghost imaging with helicity-dependent metasurface hologram. Sci. Adv. 2017, 3, e1701477. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sanjeev, V.; Khorasaninejad, M.; Shi, Z.; Lee, E.; Capasso, F. A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 2018, 13, 220–226. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.C.; Lai, Y.C.; Chen, M.K.; Kuo, H.Y.; Chen, B.H.; Chen, Y.H.; Huang, T.T.; Wang, J.H.; et al. A broadband achromatic metalens in the visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.C.; Lai, Y.C.; Hung Chu, C.; Chen, J.W.; Lu, S.H.; Chen, J.; Xu, B.; Kuan, C.H.; et al. Broadband achromatic optical metasurface devices. Nat. Commun. 2017, 8, 187. [Google Scholar] [CrossRef]
- Ma, Z.; Li, Y.; Li, Y.; Gong, Y.; Maier, S.A.; Hong, M. All-dielectric planar chiral metasurface with gradient geometric phase. Opt. Express 2018, 26, 6067–6078. [Google Scholar] [CrossRef]
- Pan, C.; Ren, M.; Li, Q.; Fan, S.; Xu, J. Broadband asymmetric transmission of optical waves from spiral plasmonic metamaterials. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Bao, Y.; Yu, Y.; Xu, H.; Lin, Q.; Wang, Y.; Li, J.; Zhou, Z.-K.; Wang, X.-H. Coherent Pixel Design of Metasurfaces for Multidimensional Optical Control of Multiple Printing-Image Switching and Encoding. Adv. Funct. Mater. 2018, 28. [Google Scholar] [CrossRef]
- Minovich, A.E.; Miroshnichenko, A.E.; Bykov, A.Y.; Murzina, T.V.; Neshev, D.N.; Kivshar, Y.S. Functional and nonlinear optical metasurfaces. Laser Photonics Rev. 2015, 9, 195–213. [Google Scholar] [CrossRef]
- Xiao, Y.; Qian, H.; Liu, Z. Nonlinear Metasurface Based on Giant Optical Kerr Response of Gold Quantum Wells. ACS Photonics 2018, 5, 1654–1659. [Google Scholar] [CrossRef]
- Li, G.; Wu, L.; Li, K.F.; Chen, S.; Schlickriede, C.; Xu, Z.; Huang, S.; Li, W.; Liu, Y.; Pun, E.Y.B.; et al. Nonlinear Metasurface for Simultaneous Control of Spin and Orbital Angular Momentum in Second Harmonic Generation. Nano Lett. 2017, 17, 7974–7979. [Google Scholar] [CrossRef]
- Hasman, E.; Kleiner, V.; Biener, G. Polarization dependent focusing lens by use of quantized Pancharatnam–Berry phase diffractive optics. Appl. Phys. Lett. 2003, 82, 328–330. [Google Scholar] [CrossRef]
- Bomzon, Z.; Biener, G.; Kleiner, V. Space-variant Pancharatnam-Berry phase optical elements with computer-generated subwavelength gratings. Opt. Lett. 2002, 27, 1141–1143. [Google Scholar] [CrossRef]
- Ding, X.; Monticone, F.; Zhang, K.; Zhang, L.; Gao, D.; Burokur, S.N.; de Lustrac, A.; Wu, Q.; Qiu, C.-W. Ultrathin Pancharatnam-Berry metasurface with maximal cross-polarization efficiency. Adv. Mater. 2015, 27, 1195–1200. [Google Scholar] [CrossRef] [PubMed]
- Wen, D.; Yue, F.; Li, G.; Zheng, G.; Chan, K.; Chen, S.; Chen, M.; Li, K.F.; Wong, P.W.; Cheah, K.W.; et al. Helicity multiplexed broadband metasurface holograms. Nat. Commun. 2015, 6, 8241. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Ambrosio, A.; Kanhaiya, P.; Capasso, F. Broadband and chiral binary dielectric meta-holograms. Sci. Adv. 2016, 2, e1501258. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Zhang, H.; Chen, S.; Bai, B.; Tan, Q.; Jin, G.; Cheah, K.-W.; Qiu, C.-W.; et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 2013, 4, 4. [Google Scholar] [CrossRef]
- Zheng, G.; Muhlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, J.; Wang, Y.; Pu, M.; Li, X.; Zhao, Z.; Gao, P.; Wang, C.; Luo, X. Metasurface-based broadband hologram with high tolerance to fabrication errors. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Zhao, W.; Jiang, H.; Liu, B.; Song, J.; Jiang, Y.; Tang, C.; Li, J. Dielectric Huygens’ Metasurface for High-Efficiency Hologram Operating in Transmission Mode. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Zhou, F.; Liu, Y.; Cai, W. Plasmonic holographic imaging with V-shaped nanoantenna array. Opt. Express 2013, 21, 4348–4354. [Google Scholar] [CrossRef] [PubMed]
- Overvig, A.C.; Shrestha, S.; Malek, S.C.; Lu, M.; Stein, A.; Zheng, C.; Yu, N. Dielectric metasurfaces for complete and independent control of the optical amplitude and phase. Light. Sci. Appl. 2019, 8, 1–12. [Google Scholar] [CrossRef]
- Jiang, Q.; Cao, L.; Huang, L.; He, Z.; Jin, G. A complex-amplitude hologram using an ultra-thin dielectric metasurface. Nanoscale 2020, 12, 24162–24168. [Google Scholar] [CrossRef]
- Ni, X.; Kildishev, A.V.; Shalaev, V.M. Metasurface holograms for visible light. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, X.; Kenney, M.; Su, X.; Xu, N.; Ouyang, C.; Shi, Y.; Han, J.; Zhang, W.; Zhang, S. Broadband Metasurfaces with Simultaneous Control of Phase and Amplitude. Adv. Mater. 2014, 26, 5031–5036. [Google Scholar] [CrossRef]
- Song, E.-Y.; Lee, G.-Y.; Park, H.; Lee, K.; Kim, J.; Hong, J.; Kim, H.; Lee, B. Compact Generation of Airy Beams with C-Aperture Metasurface. Adv. Opt. Mater. 2017, 5, 5. [Google Scholar] [CrossRef]
- Lee, G.-Y.; Yoon, G.; Lee, S.-Y.; Yun, H.; Cho, J.; Lee, K.; Kim, H.; Rho, J.; Lee, B. Complete amplitude and phase control of light using broadband holographic metasurfaces. Nanoscale 2018, 10, 4237–4245. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.; Xu, Y.; Gu, J.; Li, Y.; Tian, Z.; Singh, R.; Zhang, S.; Han, J.; Zhang, W. Broadband metasurface holograms: Toward complete phase and amplitude engineering. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Chong, K.E.; Wang, L.; Staude, I.; James, A.R.; Dominguez, J.; Liu, S.; Subramania, G.S.; Decker, M.; Neshev, D.N.; Brener, I.; et al. Efficient Polarization-Insensitive Complex Wavefront Control Using Huygens’ Metasurfaces Based on Dielectric Resonant Meta-atoms. ACS Photonics 2016, 3, 514–519. [Google Scholar] [CrossRef]
- Song, X.; Huang, L.; Tang, C.; Li, J.; Li, X.; Liu, J.; Wang, Y.; Zentgraf, T. Selective Diffraction with Complex Amplitude Modulation by Dielectric Metasurfaces. Adv. Opt. Mater. 2018, 6. [Google Scholar] [CrossRef]
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 2015, 10, 937–943. [Google Scholar] [CrossRef]
- Wan, W.; Gao, J.; Yang, X. Full-Color Plasmonic Metasurface Holograms. ACS Nano 2016, 10, 10671–10680. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, X.; Gao, J. Spin-controlled wavefront shaping with plasmonic chiral geometric metasurfaces. Light. Sci. Appl. 2018, 7, 1–10. [Google Scholar] [CrossRef]
- Huang, L.; Mühlenbernd, H.; Li, X.; Song, X.; Bai, B.; Wang, Y.; Zentgraf, T. Broadband Hybrid Holographic Multiplexing with Geometric Metasurfaces. Adv. Mater. 2015, 27, 6444–6449. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, S.; Yue, W.; Xu, Q.; Zhang, W. Direct polarization measurement using a multiplexed Pancharatnam-Berry meta-hologram. Optica 2019, 6. [Google Scholar] [CrossRef]
- Wang, B.; Dong, F.; Yang, D.; Song, Z.; Xu, L.; Chu, W.; Gong, Q.; Li, Y. Polarization-controlled color-tunable holograms with dielectric metasurfaces. Optica 2017, 4, 1368–1371. [Google Scholar] [CrossRef]
- Chen, W.T.; Yang, K.-Y.; Wang, C.-M.; Huang, Y.-W.; Sun, G.; Chiang, I.-D.; Liao, C.Y.; Hsu, W.-L.; Lin, H.T.; Sun, S.; et al. High-Efficiency Broadband Meta-Hologram with Polarization-Controlled Dual Images. Nano Lett. 2014, 14, 225–230. [Google Scholar] [CrossRef]
- Mueller, J.P.B.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface Polarization Optics: Independent Phase Control of Arbitrary Orthogonal States of Polarization. Phys. Rev. Lett. 2017, 118. [Google Scholar] [CrossRef]
- Wei, Q.; Huang, L.; Li, X.; Liu, J.; Wang, Y. Broadband Multiplane Holography Based on Plasmonic Metasurface. Adv. Opt. Mater. 2017, 5, 5. [Google Scholar] [CrossRef]
- Walther, B.; Helgert, C.; Rockstuhl, C.; Setzpfandt, F.; Eilenberger, F.; Kley, E.B.; Lederer, F.; Tünnermann, A.; Pertsch, T. Spatial and Spectral Light Shaping with Metamaterials. Adv. Mater. 2012. [Google Scholar] [CrossRef]
- Franklin, D.; Modak, S.; Vázquez-Guardado, A.; Safaei, A.; Chanda, D. Covert infrared image encoding through imprinted plasmonic cavities. Light. Sci. Appl. 2018, 7, 1–8. [Google Scholar] [CrossRef]
- Shi, Z.; Khorasaninejad, M.; Huang, Y.-W.; Roques-Carmes, C.; Zhu, A.Y.; Chen, W.T.; Sanjeev, V.; Ding, Z.-W.; Tamagnone, M.; Chaudhary, K.; et al. Single-Layer Metasurface with Controllable Multiwavelength Functions. Nano Lett. 2018, 18, 2420–2427. [Google Scholar] [CrossRef]
- Li, X.; Ren, H.; Chen, X.; Liu, J.; Li, Q.; Li, C.; Xue, G.; Jia, J.; Cao, L.; Sahu, A.; et al. Athermally photoreduced graphene oxides for three-dimensional holographic images. Nat. Commun. 2015, 6, 6984. [Google Scholar] [CrossRef]
- Kamali, S.M.; Arbabi, E.; Arbabi, A.; Horie, Y.; Faraji-Dana, M.; Faraon, A. Angle-Multiplexed Metasurfaces: Encoding Independent Wavefronts in a Single Metasurface under Different Illumination Angles. Phys. Rev. X 2017, 7, 7. [Google Scholar] [CrossRef]
- Deng, J.; Yang, Y.; Tao, J.; Deng, L.; Liu, D.; Guan, Z.; Li, G.; Li, Z.; Yu, S.; Zheng, G.; et al. Spatial Frequency Multiplexed Meta-Holography and Meta-Nanoprinting. ACS Nano 2019, 13, 9237–9246. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Wang, Y.; Fan, X.; Jiao, B.; Li, T.; Shang, C.; Zeng, C.; Deng, L.; Xiong, W.; Xia, J.; et al. Dynamic 3D meta-holography in visible range with large frame number and high frame rate. Sci. Adv. 2020, 6, eaba8595. [Google Scholar] [CrossRef]
- Ren, H.; Briere, G.; Fang, X.; Ni, P.; Sawant, R.; Héron, S.; Chenot, S.; Vézian, S.; Damilano, B.; Brändli, V.; et al. Metasurface orbital angular momentum holography. Nat. Commun. 2019, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Jin, L.; Huang, Y.W.; Jin, Z.; Devlin, R.C.; Dong, Z.; Mei, S.; Jiang, M.; Chen, W.T.; Wei, Z.; Liu, H.; et al. Dielectric multi-momentum meta-transformer in the visible. Nat. Commun. 2019, 10, 4789. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Ren, H.; Gu, M. Orbital angular momentum holography for high-security encryption. Nat. Photonics 2020, 14, 102–108. [Google Scholar] [CrossRef]
- Zhou, H.; Sain, B.; Wang, Y.; Schlickriede, C.; Zhao, R.; Zhang, X.; Wei, Q.; Li, X.; Huang, L.; Zentgraf, T. Polarization-Encrypted Orbital Angular Momentum Multiplexed Metasurface Holography. ACS Nano 2020, 14, 5553–5559. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Fang, X.; Jang, J.; Bürger, J.; Rho, J.; Maier, S.A. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nat. Nanotechnol. 2020, 15, 948–955. [Google Scholar] [CrossRef]
- Frese, D.; Wei, Q.; Wang, Y.; Huang, L.; Zentgraf, T. Nonreciprocal Asymmetric Polarization Encryption by Layered Plasmonic Metasurfaces. Nano Lett. 2019, 19, 3976–3980. [Google Scholar] [CrossRef] [PubMed]
- Ansari, M.A.; Kim, I.; Rukhlenko, I.D.; Zubair, M.; Yerci, S.; Tauqeer, T.; Mehmood, M.Q.; Rho, J. Engineering spin and antiferromagnetic resonances to realize an efficient direction-multiplexed visible meta-hologram. Nanoscale Horizons 2019, 5, 57–64. [Google Scholar] [CrossRef]
- Ansari, M.A.; Kim, I.; Lee, D.; Waseem, M.H.; Zubair, M.; Mahmood, N.; Badloe, T.; Yerci, S.; Tauqeer, T.; Mehmood, M.Q.; et al. A Spin-Encoded All-Dielectric Metahologram for Visible Light. Laser Photonics Rev. 2019, 13. [Google Scholar] [CrossRef]
- Kim, T.; Yu, E.S.; Bae, Y.G.; Lee, J.; Kim, I.S.; Chung, S.; Lee, S.Y.; Ryu, Y.S. Asymmetric optical camouflage: Tuneable reflective colour accompanied by the optical Janus effect. Light Sci. Appl. 2020, 9, 175. [Google Scholar] [CrossRef]
- Deng, Z.-L.; Deng, J.; Zhuang, X.; Wang, S.; Li, K.; Wang, Y.; Chi, Y.; Ye, X.; Xu, J.; Wang, G.P.; et al. Diatomic Metasurface for Vectorial Holography. Nano Lett. 2018, 18, 2885–2892. [Google Scholar] [CrossRef]
- Arbabi, E.; Kamali, S.M.; Arbabi, A.; Faraon, A. Vectorial Holograms with a Dielectric Metasurface: Ultimate Polarization Pattern Generation. ACS Photon. 2019, 6, 2712–2718. [Google Scholar] [CrossRef]
- Ren, H.; Shao, W.; Li, Y.; Salim, F.; Gu, M. Three-dimensional vectorial holography based on machine learning inverse design. Sci. Adv. 2020, 6, eaaz4261. [Google Scholar] [CrossRef]
- Wan, X.; Zhang, Q.; Chen, T.Y.; Zhang, L.; Xu, W.; Huang, H.; Xiao, C.K.; Xiao, Q.; Cui, T.J. Multichannel direct transmissions of near-field information. Light. Sci. Appl. 2019, 8, 1–8. [Google Scholar] [CrossRef]
- Kuang, Z.; Hao, Y.; Xumin, D.; Qun, W. Experimental validation of active holographic metasurface for electrically beam steering. Opt. Express 2018, 26. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, K.; Ding, X.; Wu, Q. A Dual-Beam Leaky-Wave Antenna Based on Squarely Modulated Reactance Surface. Appl. Sci. 2020, 10, 962. [Google Scholar] [CrossRef]
- Elsherbiny, M.; Fathy, A.E.; Rosen, A.; Ayers, G.; Perlow, S.M. Holographic Antenna Concept, Analysis, and Parameters. IEEE Trans. Antennas Propag. 2004, 52, 830–839. [Google Scholar] [CrossRef]
- Sutinjo, A.; Okoniewski, M.; Johnston, R.H. A Holographic Antenna Approach for Surface Wave Control in Microstrip Antenna Applications. IEEE Trans. Antennas Propag. 2010, 58, 675–682. [Google Scholar] [CrossRef]
- Pandi, S.; Balanis, C.A.; Birtcher, C.R. Design of Scalar Impedance Holographic Metasurfaces for Antenna Beam Formation With Desired Polarization. IEEE Trans. Antennas Propag. 2015, 63, 3016–3024. [Google Scholar] [CrossRef]
- Sutinjo, A.; Okoniewski, M. A Surface Wave Holographic Antenna for Broadside Radiation Excited by a Traveling Wave Patch Array. IEEE Trans. Antennas Propag. 2010, 59, 297–300. [Google Scholar] [CrossRef]
- Martinez-Ros, A.J.; Gomez-Tornero, J.L.; Goussetis, G. Holographic Pattern Synthesis with Modulated Substrate Integrated Waveguide Line-Source Leaky-Wave Antennas. IEEE Trans. Antennas Propag. 2013, 61, 3466–3474. [Google Scholar] [CrossRef]
- Wang, Y.; Guan, C.; Ding, X.; Zhang, K.; Ratni, B.; Burokur, S.N.; Gu, X.; Wu, Q. Multi-focus hologram utilizing Pancha-ratnam-Berry phase elements based metamirror. Opt. Lett. 2019, 44, 2189–2192. [Google Scholar] [CrossRef]
- Wang, Y.; Guan, C.; Li, H.; Ding, X.; Zhang, K.; Wang, J.; Burokur, S.N.; Liu, J.; Wu, Q. Dual-Polarized Tri-Channel Encrypted Holography Based on Geometric Phase Metasurface. Adv. Photonics Res. 2020, 1, 2000022. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.B.; Shen, J.L.; Cui, T.J. Low-Profile Electromagnetic Holography by Using Coding Fabry–Perot Type Metasurface with In-Plane Feeding. Adv. Opt. Mater. 2020, 8. [Google Scholar] [CrossRef]
- Wu, J.W.; Wang, Z.X.; Fang, Z.Q.; Liang, J.C.; Fu, X.; Liu, J.F.; Wu, H.T.; Bao, D.; Miao, L.; Zhou, X.Y.; et al. Full-State Synthesis of Electromagnetic Fields using High Efficiency Phase-Only Metasurfaces. Adv. Funct. Mater. 2020, 30, 30. [Google Scholar] [CrossRef]
- Zhu, B.O.; Feng, Y. Passive Metasurface for Reflectionless and Arbitary Control of Electromagnetic Wave Transmission. IEEE Trans. Antennas Propag. 2015, 63, 5500–5511. [Google Scholar] [CrossRef]
- Wang, Z.; Ding, X.; Zhang, K.; Ratni, B.; Burokur, S.N.; Gu, X.; Wu, Q. Huygens Metasurface Holograms with the Modulation of Focal Energy Distribution. Adv. Opt. Mater. 2018, 6. [Google Scholar] [CrossRef]
- Ding, X.; Wang, Z.; Liu, S.; Zhang, K.; Wu, Q. Polarization-multiplexed Huygens metasurface holography. Opt. Lett. 2020, 45, 5488–5491. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Ding, X.; Zhao, W.; Zhang, K.; Li, H.; Ratni, B.; Burokur, S.N.; Wu, Q. Three-Dimensional Microwave Holography Based on Broadband Huygens’ Metasurface. Phys. Rev. Appl. 2020, 13, 13. [Google Scholar] [CrossRef]
- Ding, X.; Wang, Z.; Hu, G.; Liu, J.; Zhang, K.; Li, H.; Ratni, B.; Burokur, S.N.; Wu, Q.; Tan, J.; et al. Metasurface holographic image projection based on mathematical properties of Fourier transform. PhotoniX 2020, 1, 1–12. [Google Scholar] [CrossRef]
- Ding, X.; Wang, Z.; Guan, C.; Liu, S.; Zhang, K.; Gu, X.; Wu, Q. Spatial Rotation Operations on Huygens Metasurface Hologram in Microwave Regime. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Guan, C.; Liu, J.; Ding, X.; Wang, Z.; Zhang, K.; Li, H.; Jin, M.; Burokur, S.N.; Wu, Q. Dual-polarized multiplexed meta-holograms utilizing coding metasurface. Nanophotonics 2020, 9, 3605–3613. [Google Scholar] [CrossRef]
- Wang, Z.X.; Wu, J.W.; Wu, L.W.; Gou, Y.; Ma, H.F.; Cheng, Q.; Cui, T.J. High Efficiency Polarization-Encoded Holograms with Ultrathin Bilayer Spin-Decoupled Information Metasurfaces. Adv. Opt. Mater. 2020, 9. [Google Scholar] [CrossRef]
- Shang, G.; Li, H.; Wang, Z.; Zhang, K.; Burokur, S.N.; Liu, J.; Wu, Q.; Ding, X.; Ding, X. Coding metasurface holography with polarization-multiplexed functionality. J. Appl. Phys. 2021, 129. [Google Scholar] [CrossRef]
- Guan, C.; Ding, X.; Wang, Z.; Zhang, K.; Jin, M.; Burokur, S.N.; Wu, Q. Helicity-switched hologram utilizing a polarization-free multi-bit coding metasurface. Opt. Express 2020, 28, 22669–22678. [Google Scholar] [CrossRef]
- Xu, H.; Hu, G.; Jiang, M.; Tang, S.; Wang, Y.; Wang, C.; Huang, Y.; Ling, X.; Liu, H.; Zhou, J. Wavevector and Frequency Multiplexing Performed by a Spin-Decoupled Multichannel Metasurface. Adv. Mater. Technol. 2019, 5, 5. [Google Scholar] [CrossRef]
- Iqbal, S.; Rajabalipanah, H.; Zhang, L.; Qiang, X.; Abdolali, A.; Cui, T.J. Frequency-multiplexed pure-phase microwave meta-holograms using bi-spectral 2-bit coding metasurfaces. Nanophotonics 2020, 9, 703–714. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, Z.; Huang, Y.; Ma, X.; Pu, M.; Guo, Y.; Li, X.; Luo, X. Asymmetric Transmission and Wavefront Manipulation toward Dual-Frequency Meta-Holograms. ACS Photonics 2019, 6, 1541–1546. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, R.Y.; Bai, G.D.; Wu, H.T.; Ma, Q.; Chen, X.Q.; Cui, T.J. Transmission-Reflection-Integrated Multifunctional Coding Metasurface for Full-Space Controls of Electromagnetic Waves. Adv. Funct. Mater. 2018, 28. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, G.; Xu, H.X.; Zhang, X.; Li, H.P. Helicity-Dependent Multifunctional Metasurfaces for Full-Space Wave Control. Adv. Opt. Mater. 2020, 8. [Google Scholar] [CrossRef]
- Chen, K.; Ding, G.; Hu, G.; Jin, Z.; Zhao, J.; Feng, Y.; Jiang, T.; Alù, A.; Qiu, C. Directional Janus Metasurface. Adv. Mater. 2019, 32, e1906352. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Feng, Y.; Monticone, F.; Zhao, J.; Zhu, B.; Jiang, T.; Zhang, L.; Kim, Y.; Ding, X.; Zhang, S.; et al. A Reconfigurable Active Huygens’ Metalens. Adv. Mater. 2017, 29, 29. [Google Scholar] [CrossRef]
- Ratni, B.; Wang, Z.; Zhang, K.; Ding, X.; de Lustrac, A.; Piau, G.-P.; Burokur, S.N. Dynamically Controlling Spatial Energy Distribution with a Holographic Metamirror for Adaptive Focusing. Phys. Rev. Appl. 2020, 13. [Google Scholar] [CrossRef]
- Li, L.; Jun Cui, T.; Ji, W.; Liu, S.; Ding, J.; Wan, X.; Bo Li, Y.; Jiang, M.; Qiu, C.W.; Zhang, S. Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun. 2017, 8, 197. [Google Scholar] [CrossRef]
- Wu, L.W.; Ma, H.F.; Wu, R.Y.; Xiao, Q.; Gou, Y.; Wang, M.; Wang, Z.X.; Bao, L.; Wang, H.L.; Qing, Y.M.; et al. Transmission-Reflection Controls and Polarization Controls of Electromagnetic Holograms by a Reconfigurable Anisotropic Digital Coding Metasurface. Adv. Opt. Mater. 2020, 8. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, G.; Wang, Z.; Li, H.; Zhang, K.; Wu, Q.; Burokur, S.N.; Ding, X. Metasurface Holography in the Microwave Regime. Photonics 2021, 8, 135. https://doi.org/10.3390/photonics8050135
Shang G, Wang Z, Li H, Zhang K, Wu Q, Burokur SN, Ding X. Metasurface Holography in the Microwave Regime. Photonics. 2021; 8(5):135. https://doi.org/10.3390/photonics8050135
Chicago/Turabian StyleShang, Guanyu, Zhuochao Wang, Haoyu Li, Kuang Zhang, Qun Wu, Shah Nawaz Burokur, and Xumin Ding. 2021. "Metasurface Holography in the Microwave Regime" Photonics 8, no. 5: 135. https://doi.org/10.3390/photonics8050135
APA StyleShang, G., Wang, Z., Li, H., Zhang, K., Wu, Q., Burokur, S. N., & Ding, X. (2021). Metasurface Holography in the Microwave Regime. Photonics, 8(5), 135. https://doi.org/10.3390/photonics8050135








