Investigation of Composite Structure with Dual Fabry–Perot Cavities for Temperature and Pressure Sensing
Abstract
:1. Introduction
2. Sensing Principle and Fabrication Process
2.1. Sensing Principle
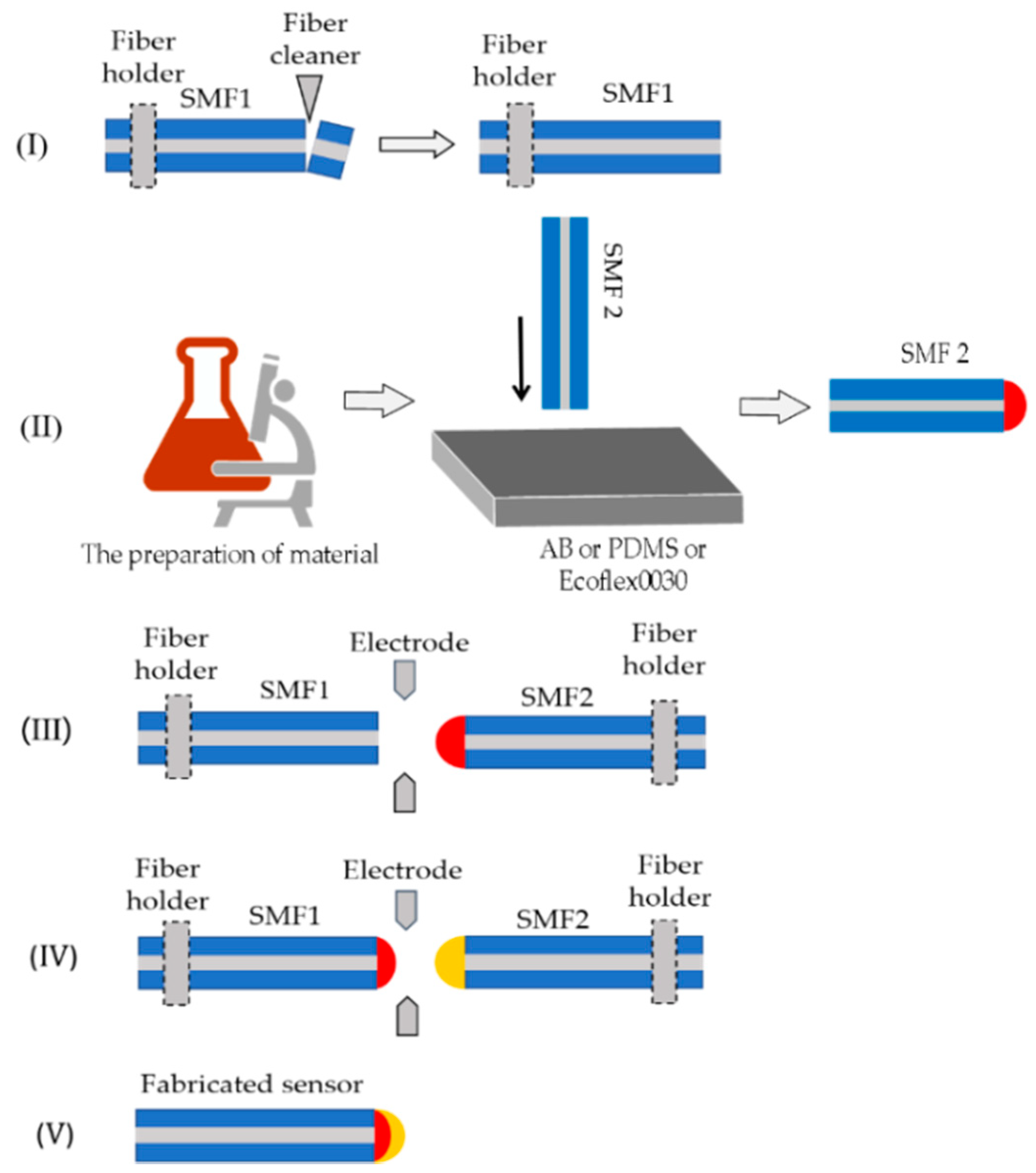
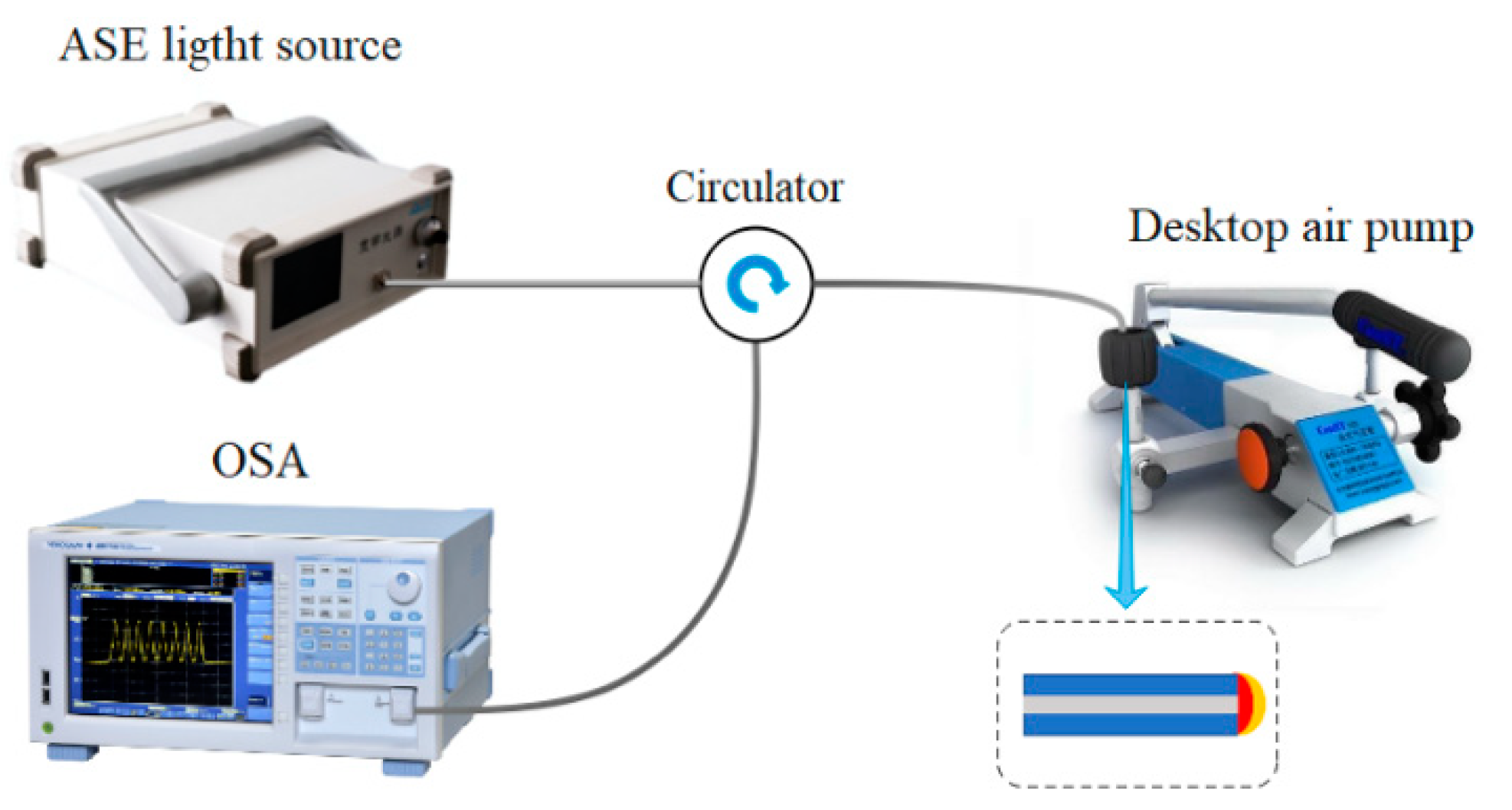
2.2. Fabrication Process
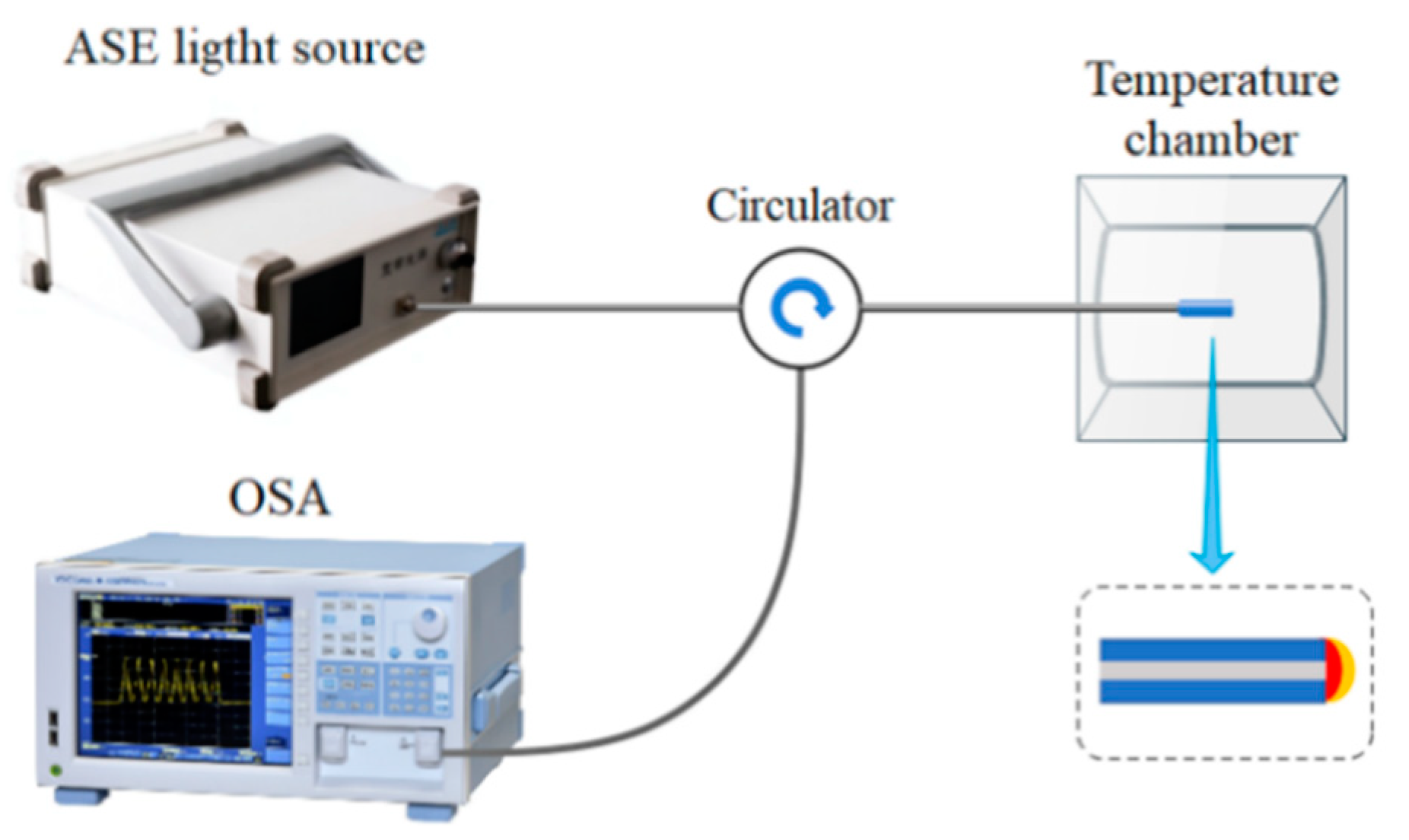
3. Experimental Results and Analysis
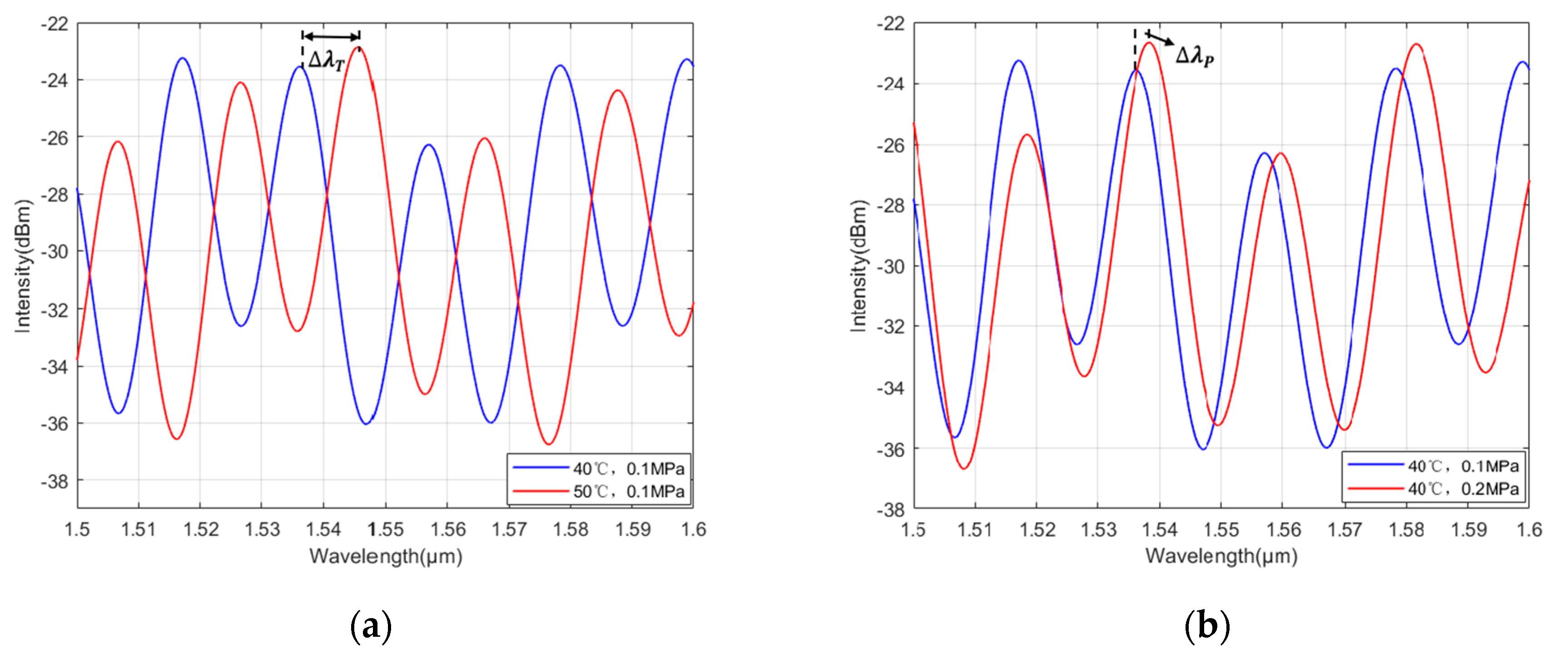
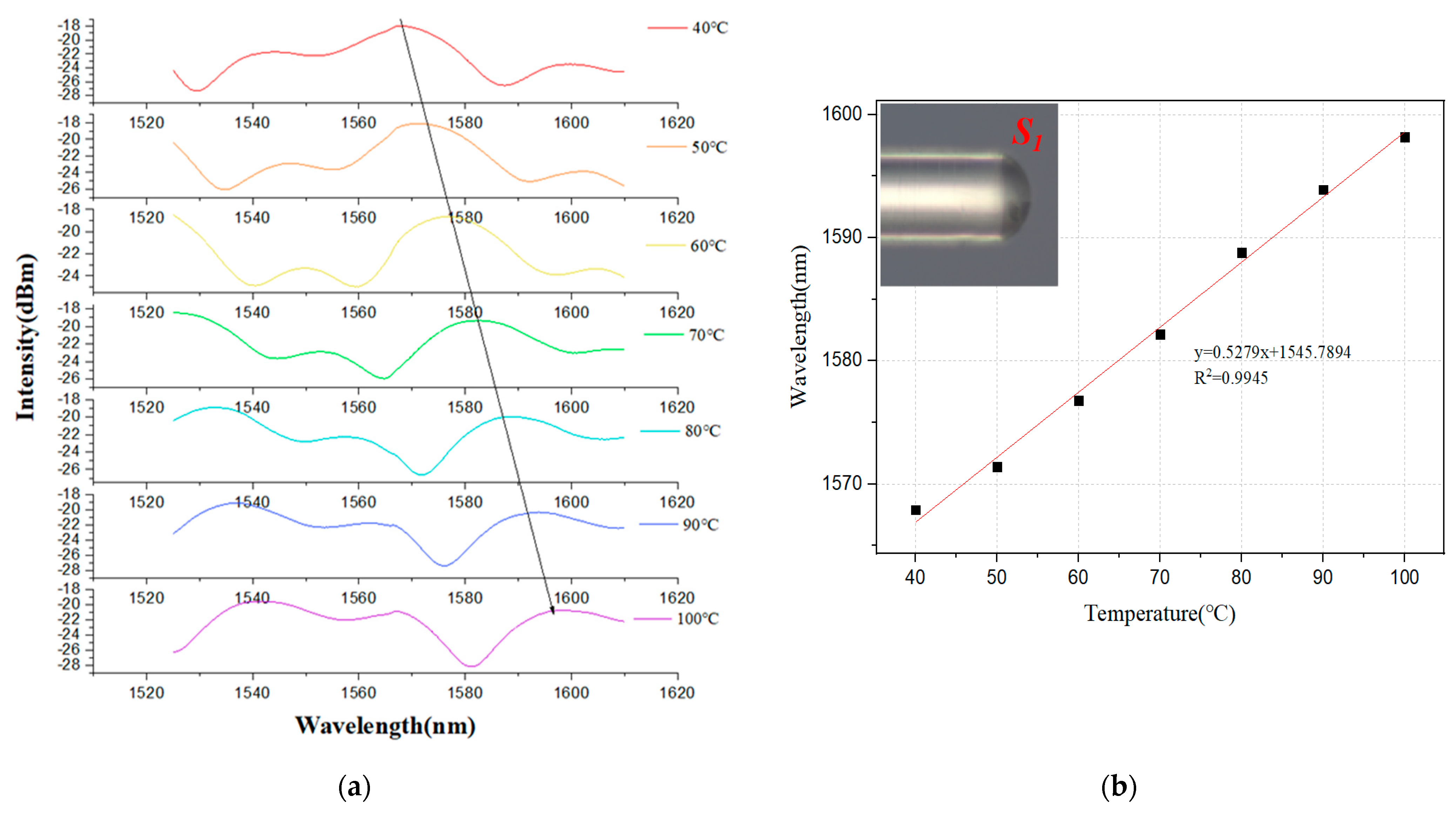
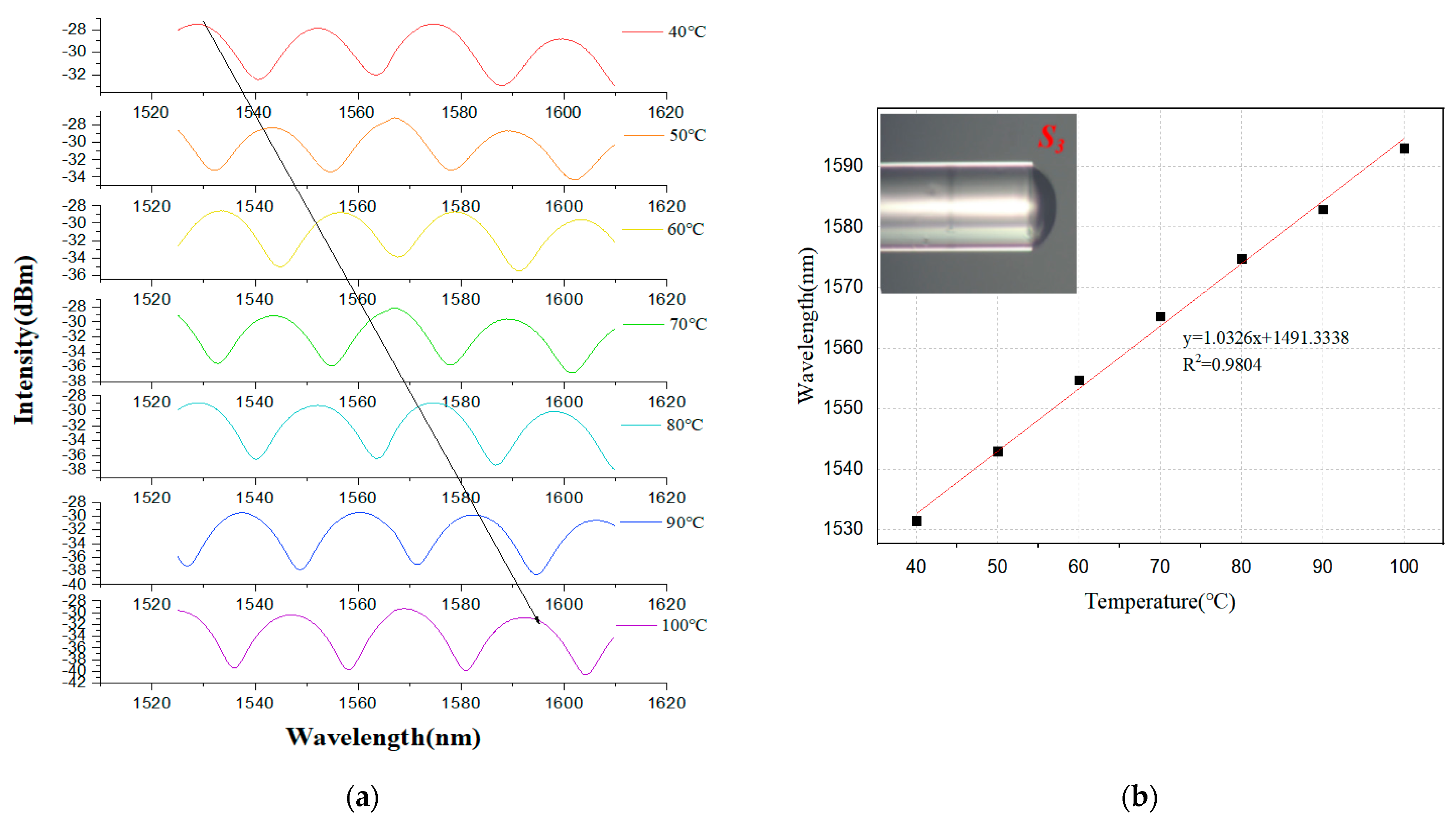
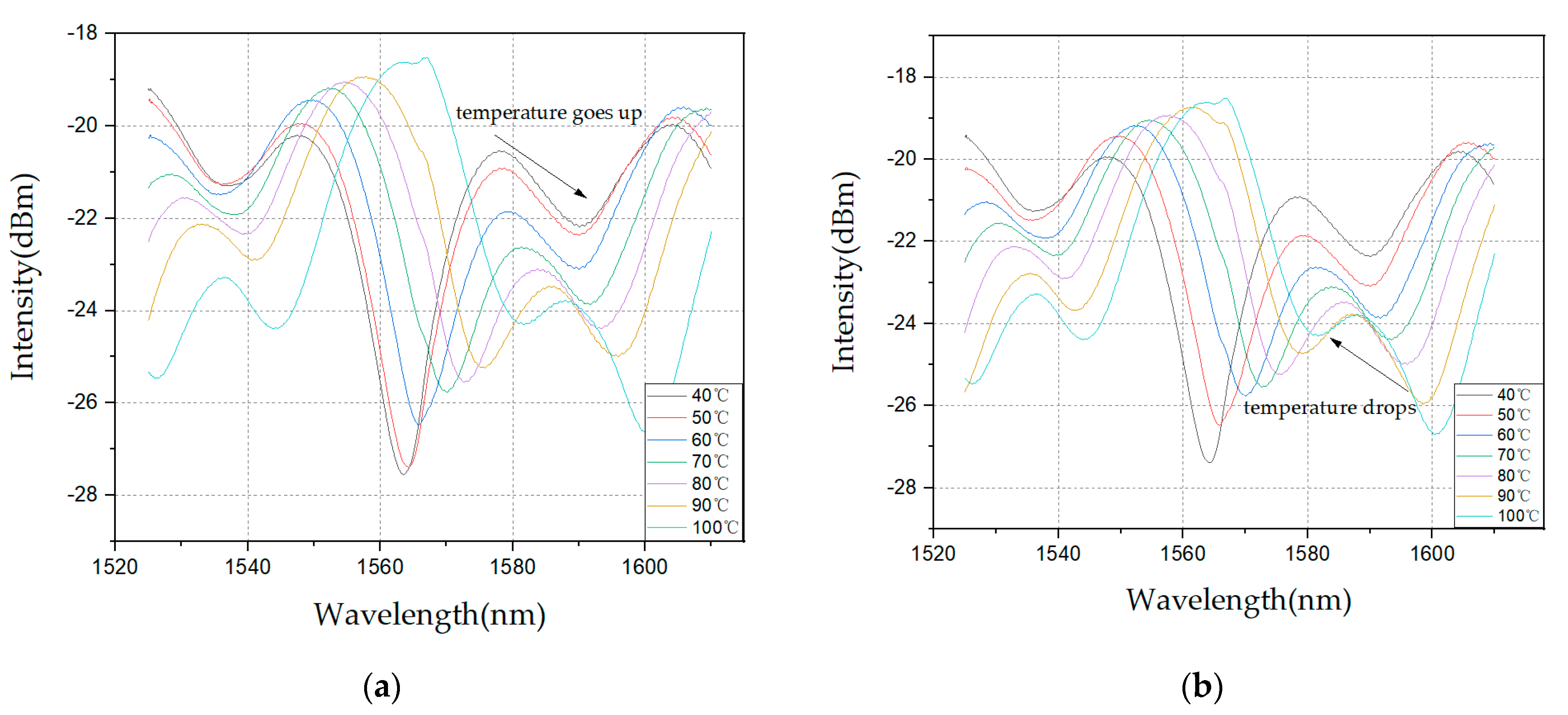
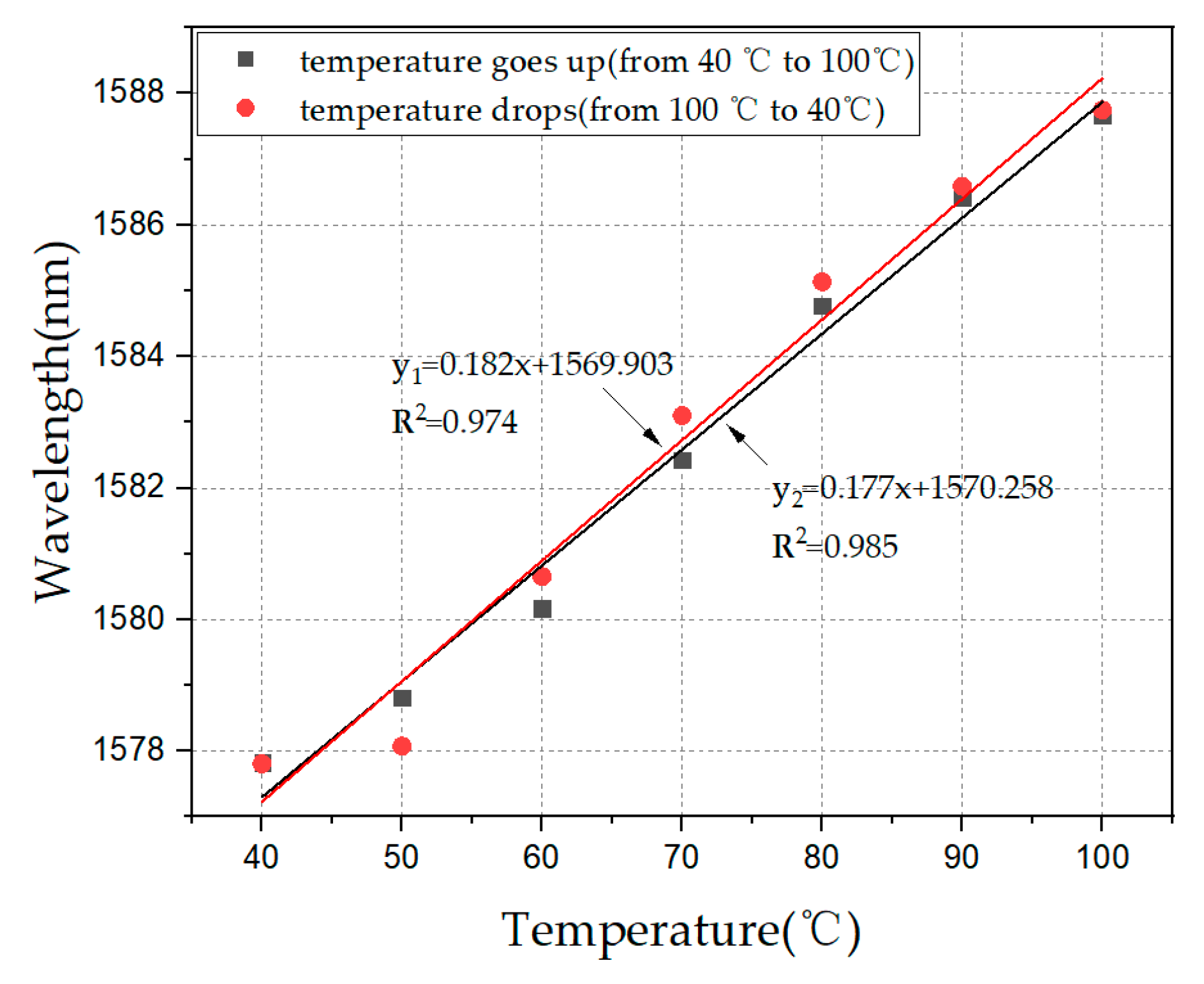
3.1. Temperature Sensitivity Analysis
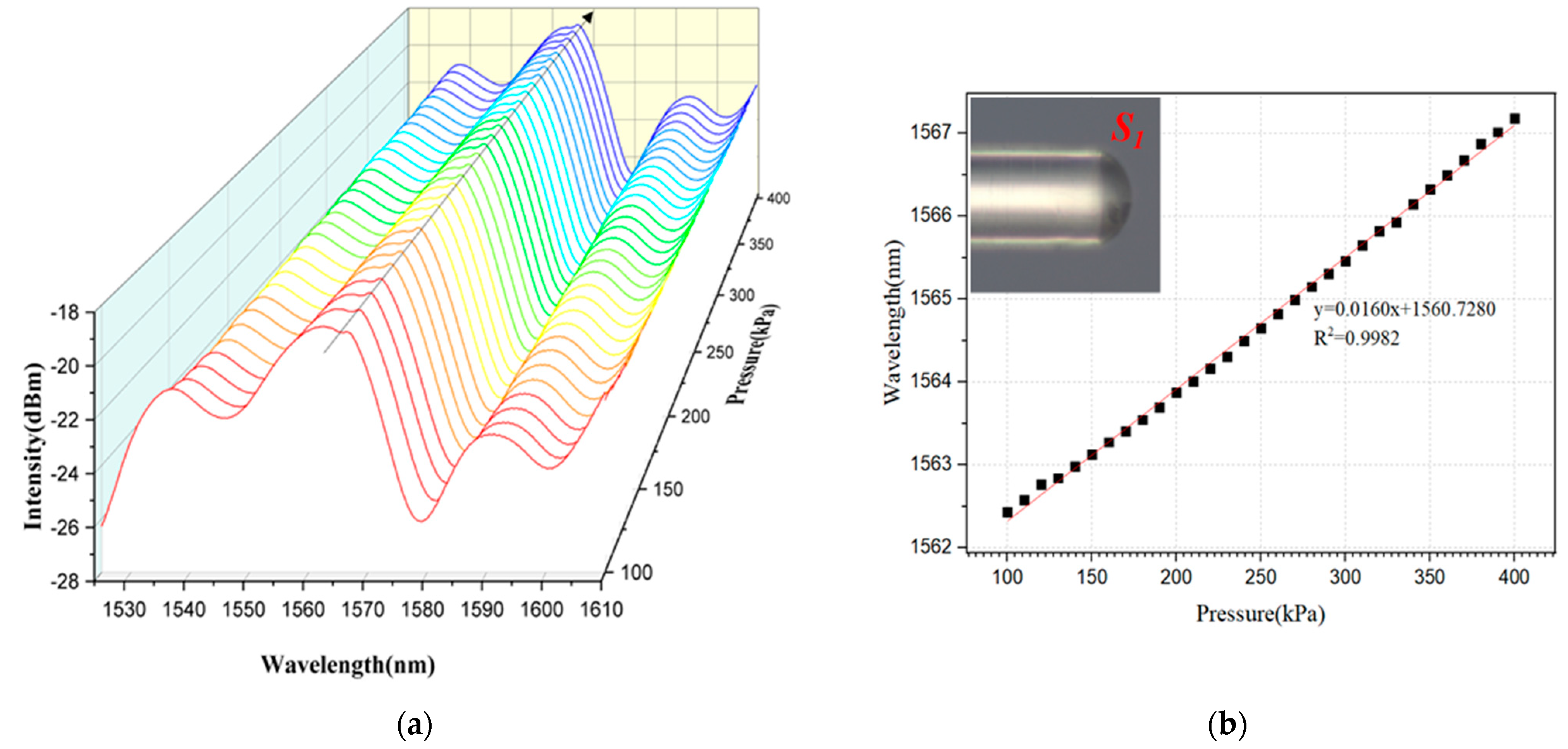
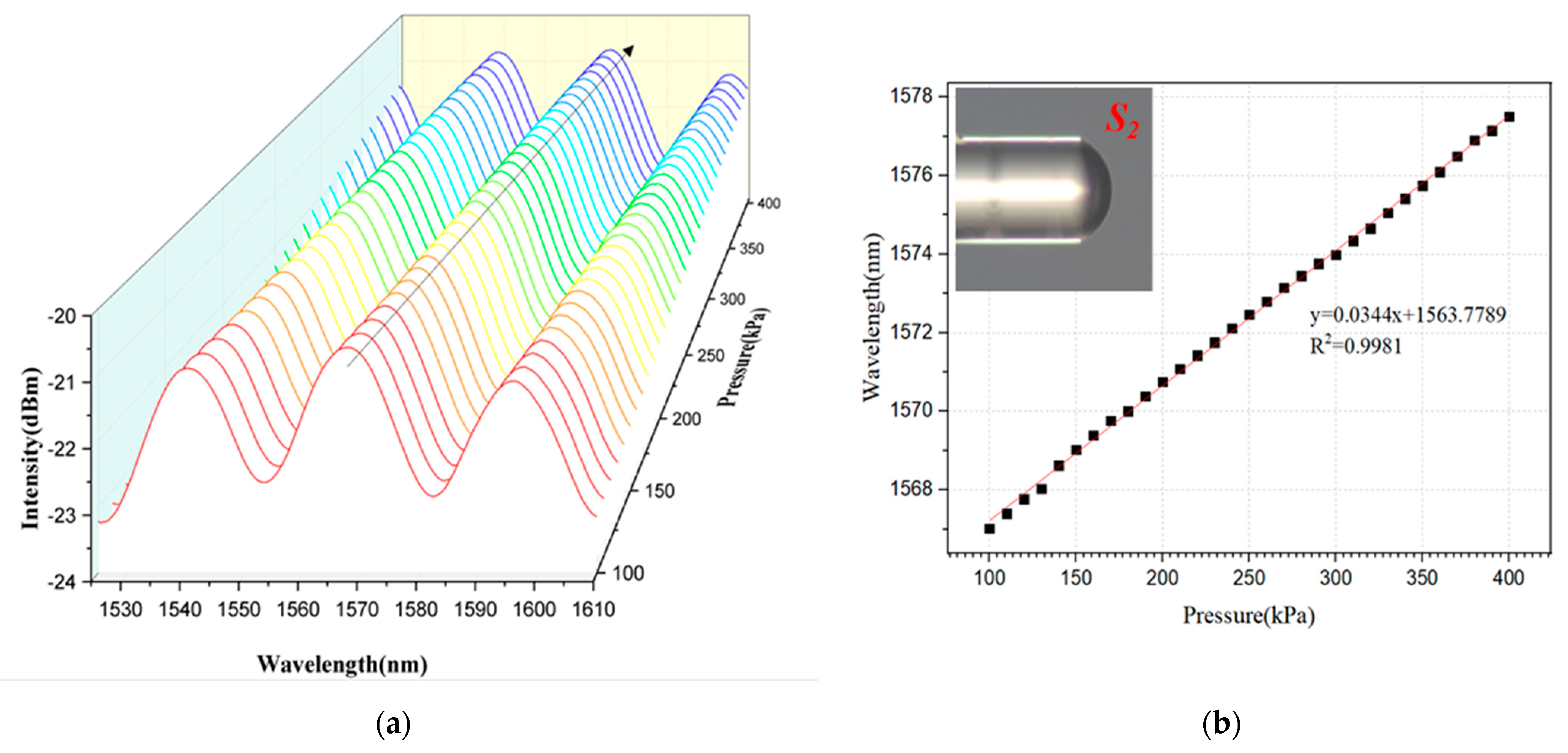
3.2. Pressure Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, T.; He, X.; Ran, Z.; Xie, Z.; Rao, Y.; Qiao, X.; He, Z.; He, P. Highly Integrated All-Fiber FP/FBG Sensor for Accurate Measurement of Strain under High Temperature. Materials 2018, 11, 1867. [Google Scholar] [CrossRef] [Green Version]
- Zawisza, R.; Eftimov, T.; Mikulic, P.; Bock, W.J.; Jaroszewicz, L.R. Ambient Refractive-Index Measurement with Simultaneous Temperature Monitoring Based on a Dual-Resonance Long-Period Grating Inside a Fiber Loop Mirror Structure. Sensors 2018, 18, 2370. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Luo, J.; Liu, S.; Chen, Y.; Huang, B.; Liao, C.; Wang, Y. A Probe-Shaped Sensor With FBG and Fiber-Tip Bubble for Pressure and Temperature Sensing. Photonics Sens. 2021, 1–7. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, M.; Wang, D.N.; Liu, S.; Lu, P. Fiber in-line Mach-Zehnder interferometer fabricated by femtosecond laser micromachining for refractive index measurement with high sensitivity. J. Opt. Soc. Am. B 2010, 27, 370–374. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Yang, D.; Wang, Y.; Zhang, T.; Shao, M.; Yu, D.; Fu, H.; Jia, Z. Fabrication of dual-parameter fiber-optic sensor by cascading FBG with FPI for simultaneous measurement of temperature and gas pressure. Opt. Commun. 2019, 443, 166–171. [Google Scholar] [CrossRef]
- Monfared, Y.E.; Liang, C.; Khosravi, R.; Kacerovska, B.; Yang, S. Selectively toluene-filled photonic crystal fiber Sagnac interferometer with high sensitivity for temperature sensing applications. Results Phys. 2019, 13, 102297. [Google Scholar] [CrossRef]
- Yin, J.; Liu, T.; Jiang, J.; Liu, K.; Wang, S.; Qin, Z.; Zou, S. Batch-Producible Fiber-Optic Fabry–Pérot Sensor for Simultaneous Pressure and Temperature Sensing. IEEE Photonics Technol. Lett. 2014, 26, 2070–2073. [Google Scholar] [CrossRef]
- Bae, H.; Yun, D.; Liu, H.; Olson, D.A.; Yu, M. Hybrid Miniature Fabry–Perot Sensor with Dual Optical Cavities for Simultaneous Pressure and Temperature Measurements. J. Lightwave Technol. 2014, 32, 1585–1593. [Google Scholar] [CrossRef]
- Gao, H.; Jiang, Y.; Cui, Y.; Zhang, L.; Jia, J.; Hu, J. Dual-Cavity Fabry–Perot Interferometric Sensors for the Simultaneous Measurement of High Temperature and High Pressure. IEEE Sens. J. 2018, 18, 10028–10033. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, Y.; Gao, H.; Jia, J.; Cui, Y.; Wang, S.; Hu, J. Simultaneous Measurements of Temperature and Pressure With a Dual-Cavity Fabry–Perot Sensor. IEEE Photonics Technol. Lett. 2018, 31, 106–109. [Google Scholar] [CrossRef]
- Chen, M.-Q.; Zhao, Y.; Xia, F.; Peng, Y.; Tong, R.-J. High sensitivity temperature sensor based on fiber air-microbubble Fabry-Perot interferometer with PDMS-filled hollow-core fiber. Sens. Actuators A Phys. 2018, 275, 60–66. [Google Scholar] [CrossRef]
- Bai, Y.; Qi, Y.; Dong, Y.; Jian, S. Highly Sensitive Temperature and Pressure Sensor Based on Fabry–Perot Interference. IEEE Photonics Technol. Lett. 2016, 28, 2471–2474. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Yang, D.; Wu, J.; Zhang, T.; Yu, D.; Zhenan, J.; Fu, H.; Jia, Z. Hollow-Core Fiber-Based All-Fiber FPI Sensor for Simultaneous Measurement of Air Pressure and Temperature. IEEE Sens. J. 2019, 19, 11236–11241. [Google Scholar] [CrossRef]
- Pevec, S.; Donlagic, D. Miniature all-fiber Fabry-Perot sensor for simultaneous measurement of pressure and temperature. Appl. Opt. 2012, 51, 4536–4541. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Yan, G.; Wang, C.; Lian, Z.; Chen, X.; He, S. FBG Incorporated Side-open Fabry-Perot Cavity for Simultaneous Gas Pressure and Temperature Measurements. J. Lightwave Technol. 2016, 34, 1. [Google Scholar] [CrossRef]
- Zhang, W.; Zhuang, W.; Dong, M.; Zhu, L.; Meng, F. Dual-Parameter Optical Fiber Sensor for Temperature and Pressure Discrimination Featuring Cascaded Tapered-FBG and Ball-EFPI. IEEE Sens. J. 2019, 19, 5645–5652. [Google Scholar] [CrossRef]
- Sun, B.; Wang, Y.; Qu, J.; Liao, C.; Yin, G.; He, J.; Zhou, J.; Tang, J.; Liu, S.; Li, Z.; et al. Simultaneous measurement of pressure and temperature by employing Fabry-Perot interferometer based on pendant polymer droplet. Opt. Express 2015, 23, 1906–1911. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Liu, Y.M.; Wang, D.N.; Li, J.Q. Fiber Fabry–Pérot Interferometer for Measurement of Gas Pressure and Temperature. J. Lightwave Technol. 2016, 34, 4920–4925. [Google Scholar] [CrossRef]
- Fu, D.; Liu, X.; Shang, J.; Sun, W.; Liu, Y. A Simple, Highly Sensitive Fiber Sensor for Simultaneous Measurement of Pressure and Temperature. IEEE Photonics Technol. Lett. 2020, 32, 747–750. [Google Scholar] [CrossRef]
- Ge, M.; Li, Y.; Han, Y.; Xia, Z.; Guo, Z.; Gao, J.; Qu, S. High-sensitivity double-parameter sensor based on the fibre-tip Fabry–Pérot interferometer. J. Mod. Opt. 2016, 64, 1–5. [Google Scholar] [CrossRef]
- Kangpeng, Z.; Wei, H.; Wen, Z.; Mingli, D.; Lianqing, Z. A Dual-parameter Fabry–Perot Interferometer Sensor Based on Single Mode-Photonic Crystal-Multimode Fiber Structure. Instrum. Exp. Tech. 2019, 62, 426–431. [Google Scholar] [CrossRef]
- Liu, X.; Gang, T.; Tong, R.; Qiao, X.; Zuo, C.; Bai, X.; Bian, C.; Hu, M. Air-coupled fiber Fabry-Perot ultrasonic sensor formed by diaphragm for seismic physical model imaging. Optik 2018, 168, 794–799. [Google Scholar] [CrossRef]
- Kanawade, R.; Kumar, A.; Pawar, D.; Vairagi, K.; Late, D.; Sarkar, S.; Sinha, R.K.; Mondal, S. Negative axicon tip-based fiber optic interferometer cavity sensor for volatile gas sensing. Opt. Express 2019, 27, 7277–7290. [Google Scholar] [CrossRef] [PubMed]
- Park, C.-S.; Joo, K.-I.; Kang, S.-W.; Kim, H.-R. A PDMS-Coated Optical Fiber Bragg Grating Sensor for Enhancing Temperature Sensitivity. J. Opt. Soc. Korea 2011, 15, 329–334. [Google Scholar] [CrossRef]
- Yu, T. Study on Mechanical Properties and Bonding of PDMS in Flexible Electrons. Master’s Thesis, Yangzhou University, Yangzhou, China, 2017. [Google Scholar]
- Ren, X.; Chen, J.; Xu, F.; Nie, M. Study on Bilayer-Microstructure Flexible Strain Sensors Based on Carbon Nanotubes. Chin. J. Sens. Actuators 2019, 32, 654–657. [Google Scholar]
- Zhang, Z.; Ping, Z.; Peng, L.; Sun, F. Thermo-optic coefficients of polymers for optical waveguide applications. Polymer 2006, 47, 4893–4896. [Google Scholar] [CrossRef]
- Li, J.; Gai, L.; Li, H.; Hu, H. A high sensitivity temperature sensor based on packaged microfibre knot resonator. Sens. Actuators A Phys. 2017, 263, 369–372. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Li, Y. Modeling and Analysis of Soft Pneumatic Actuator with Symmetrical Chambers Used for Bionic Robotic Fish. Soft Robot. 2020, 7, 168–178. [Google Scholar] [CrossRef]
- Gao, H.; Jiang, Y.; Zhang, L.; Cui, Y.; Jiang, Y.; Jia, J.; Jiang, L. Antiresonant mechanism based self-temperature-calibrated fiber optic Fabry–Perot gas pressure sensors. Opt. Express 2019, 27, 22181–22189. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Jia, P.; Liu, J.; Fang, G.; Li, Z.; Hong, Y.-P.; Liang, T.; Xiong, J. Diaphragm-Free Fiber-Optic Fabry-Perot Interferometric Gas Pressure Sensor for High Temperature Application. Sensors 2018, 18, 1011. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Zhang, T.; Wang, Y.; Yang, D.; Liu, X.; Fu, H.; Jia, Z. Simultaneous measurement of gas pressure and temperature with integrated optical fiber FPI sensor based on in-fiber micro-cavity and fiber-tip. Opt. Fiber Technol. 2018, 46, 77–82. [Google Scholar] [CrossRef]
- Chen, D.; Hu, G.; Chen, L. Pressure/Temperature Sensor Based on a Dual-Core Photonic Crystal Fiber. In Proceedings of the Asia Communications & Photonics Conference & Exhibition. International Society for Optics and Photonics, Shanghai, China, 14 November 2011. [Google Scholar] [CrossRef]




| PDMS | Ecoflex0030 Silicone Rubber | Epoxy Resin AB | |
|---|---|---|---|
| Thermo–optic coefficient (°C−1) | |||
| Thermal expansion coefficient (m/m°C) | |||
| Refractive index (RIU) | 1.418 | 1.41–1.53 | 1.45–1.52 |
| Young’s modulus (MPa) | 5 | 2 | 21,250 |
| Poisson’s ratio | 0.46 | 0.369 | 0.25 |
| Tensile strength (psi) | 200 |
| Composite Structure | Material | Thickness |
|---|---|---|
| Material 1: AB | 32 | |
| Material 2: PDMS | 11 | |
| Material 1: Ecoflex0030 | 31 | |
| Material 2: PDMS | 10 | |
| Material 1: PDMS | 28 | |
| Material 2: Ecoflex0030 | 12 |
| Sensor Structure | Temperature Sensitivity | Pressure Sensitivity | Simultaneous | Ref. |
|---|---|---|---|---|
| FBG cascade FPI | 223.4 pm/°C | 24.99 pm/kPa | Yes | 2019 [5] |
| Hybrid Miniature FPI with Dual Optical Cavities | 2.9 nm/°C | 12.2nm/kPa | Yes | 2014 [8] |
| SMF-SMF-HCF-CF | 19.8nm/°C | 98pm/kPa | Yes | 2018 [9] |
| Dual-cavity FPI with Cascade Hollow-core Fibers | 17 nm/°C | 1.336 nm/kPa | No | 2018 [11] |
| Hollow-Core Fiber-Based All-Fiber FPI | 9.22 pm/°C | 1.05 pm/kPa | Yes | 2019 [13] |
| FBG incorporated FPI | 0.871 pm/°C | 4.071 pm/MPa | Yes | 2016 [15] |
| FPI based on Pendant Polymer Droplet | 249 pm/°C | 1.130 pm/kPa | Yes | 2015 [17] |
| FPI embedded with Microspheres | 7.1 pm/°C | 2.126 pm/kPa | Yes | 2016 [18] |
| SMF-HCF-SMF | 0.584 nm/°C | 3.884 pm/kPa | No | 2019 [30] |
| Diaphragm-Free Fiber-Optic FPI | 14.8 pm/°C | 4.28 pm/kPa | No | 2018 [31] |
| FPI based on In-fiber Micro-cavity and Fiber-tip | 0.0108 nm/°C | 4.158 pm/kPa | Yes | 2018 [32] |
| A Dual-Core Photonic Crystal Fiber Sensor | 20.7 pm/°C | −3.47 pm/MPa | No | 2011 [33] |
| Composite Structure with Dual FP Cavities | 528 pm/°C 540 pm/°C 1033 pm/°C | : 16.0 pm/kPa 34.6 pm/kPa 30.2 pm/kPa | No | Our work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, L.; Liu, S.; Wu, D.; Wang, W.; Song, M.; Wang, G.; Huang, M. Investigation of Composite Structure with Dual Fabry–Perot Cavities for Temperature and Pressure Sensing. Photonics 2021, 8, 138. https://doi.org/10.3390/photonics8050138
Wang J, Li L, Liu S, Wu D, Wang W, Song M, Wang G, Huang M. Investigation of Composite Structure with Dual Fabry–Perot Cavities for Temperature and Pressure Sensing. Photonics. 2021; 8(5):138. https://doi.org/10.3390/photonics8050138
Chicago/Turabian StyleWang, Jun, Long Li, Shuaicheng Liu, Diyang Wu, Wei Wang, Ming Song, Guanjun Wang, and Mengxing Huang. 2021. "Investigation of Composite Structure with Dual Fabry–Perot Cavities for Temperature and Pressure Sensing" Photonics 8, no. 5: 138. https://doi.org/10.3390/photonics8050138
APA StyleWang, J., Li, L., Liu, S., Wu, D., Wang, W., Song, M., Wang, G., & Huang, M. (2021). Investigation of Composite Structure with Dual Fabry–Perot Cavities for Temperature and Pressure Sensing. Photonics, 8(5), 138. https://doi.org/10.3390/photonics8050138





