Free-Space Nonreciprocal Transmission Based on Nonlinear Coupled Fano Metasurfaces
Abstract
1. Introduction
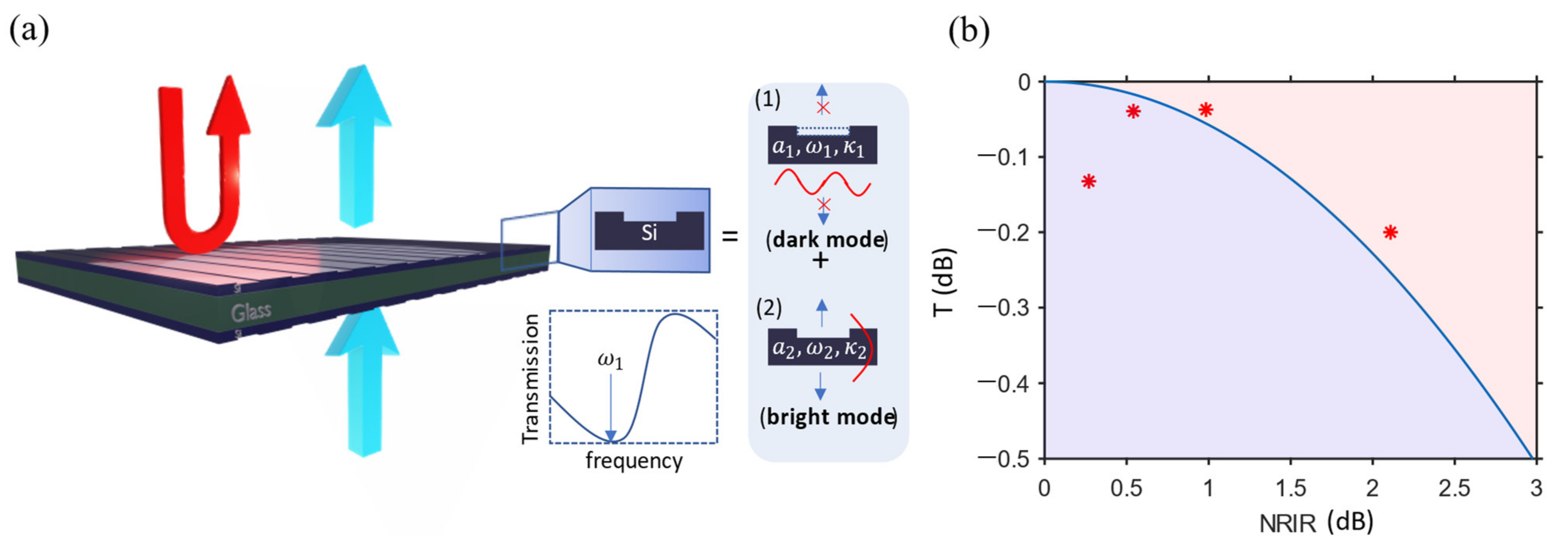
2. Principle of Operation of Nonlinearity-Based Nonreciprocal Devices Based on Coupled Fano Metasurfaces
3. Practical Implementations (for the Numerical Analysis, Please See Section ‘Full Wave Numerical Simulation’)
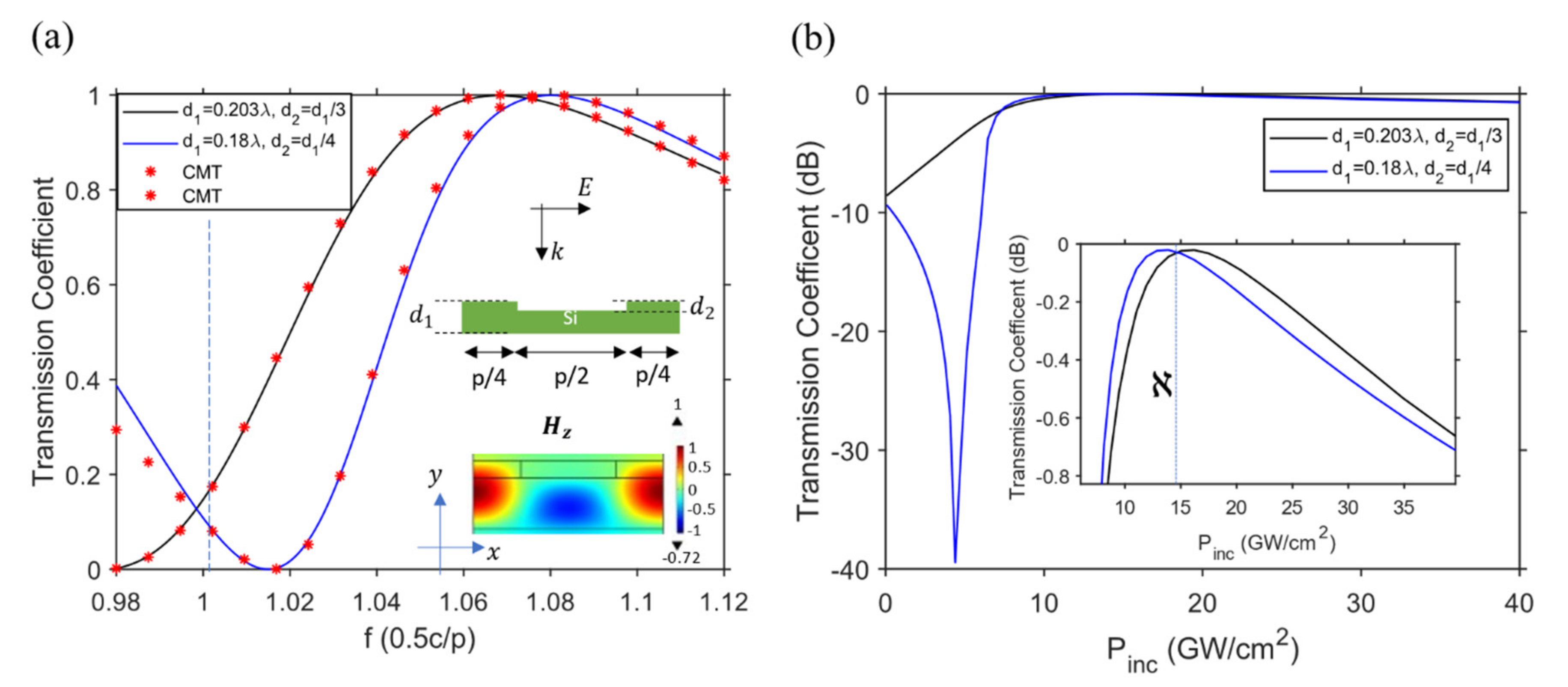
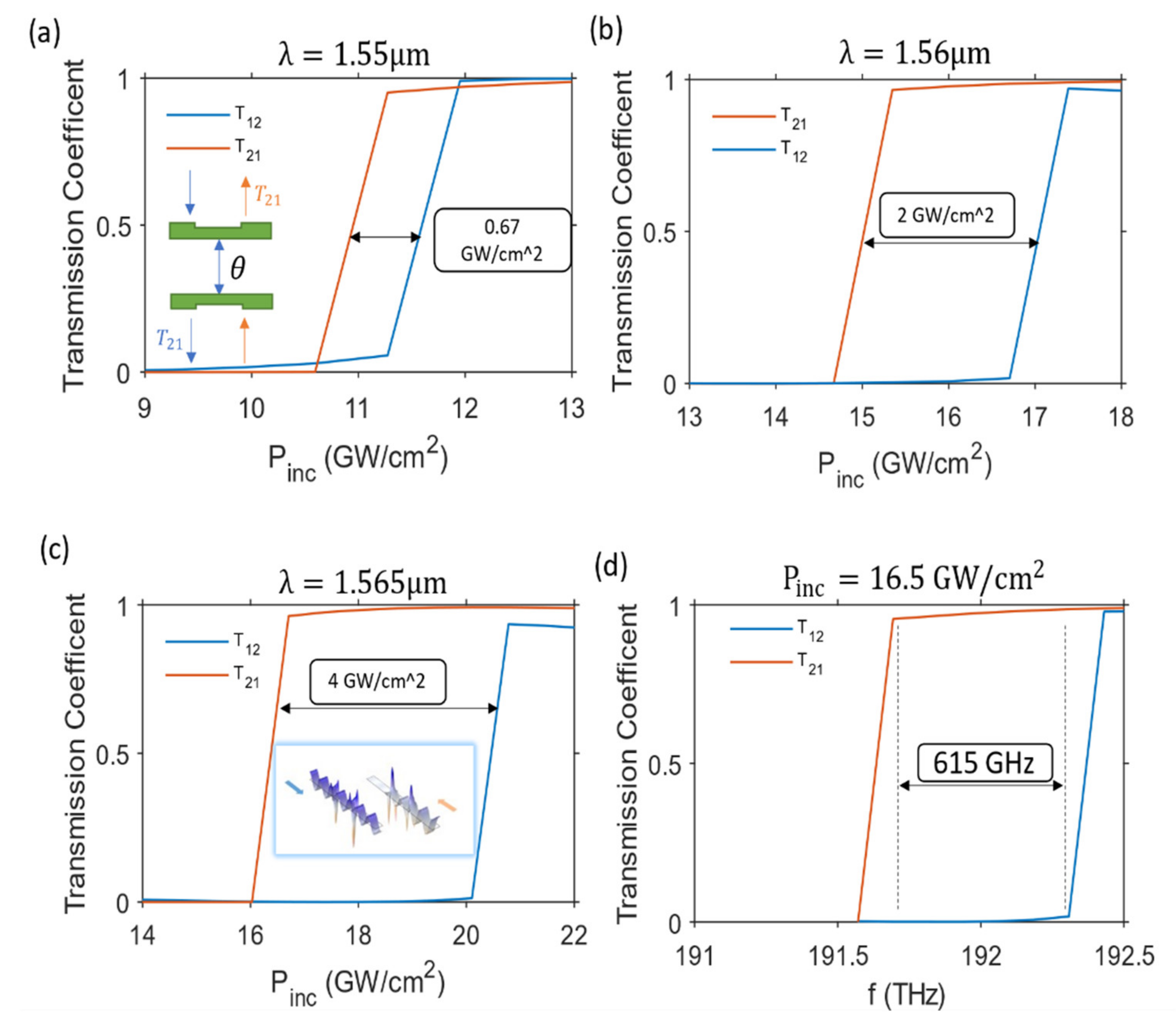
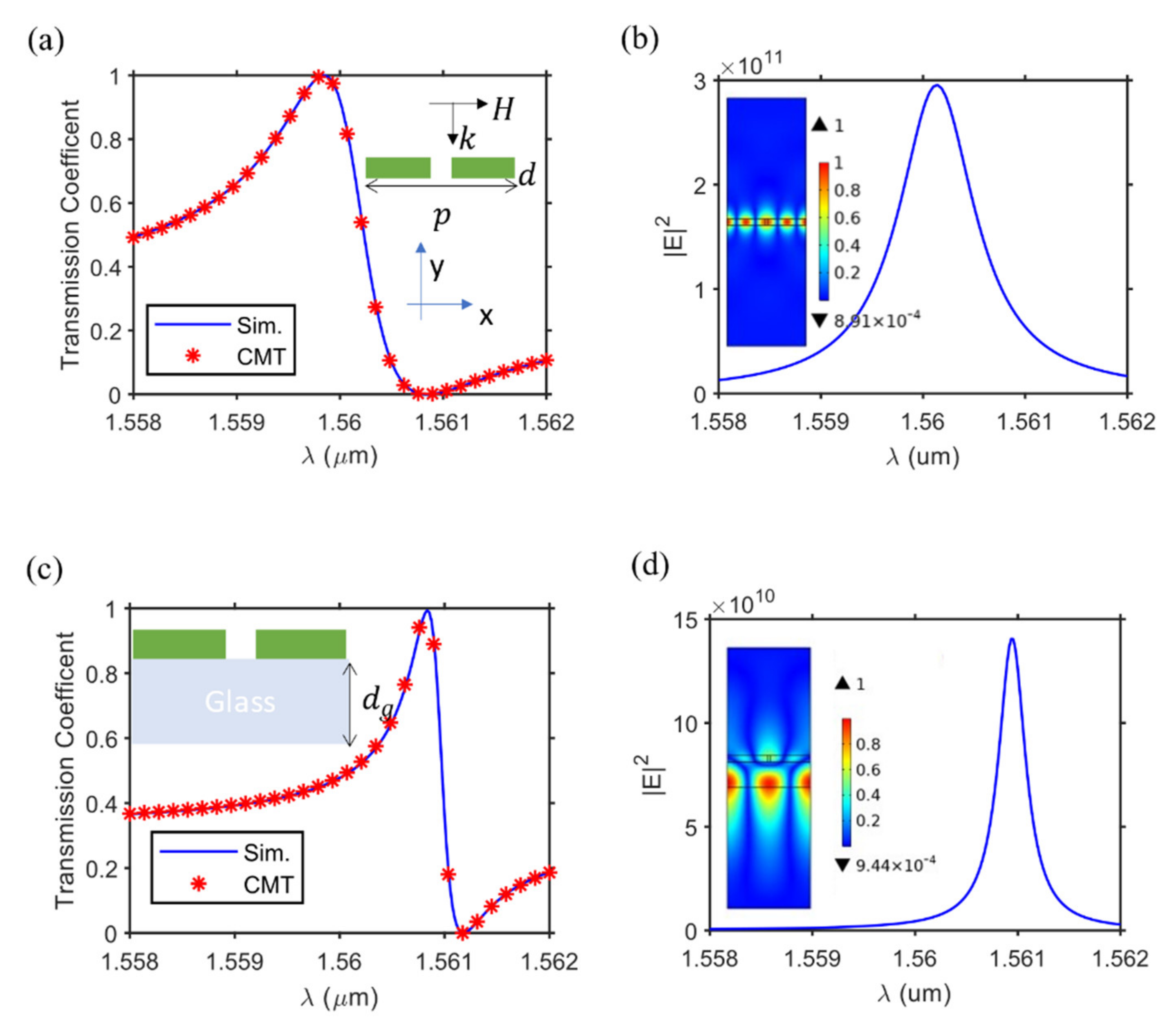
3.1. Low Quality Factor Resonators
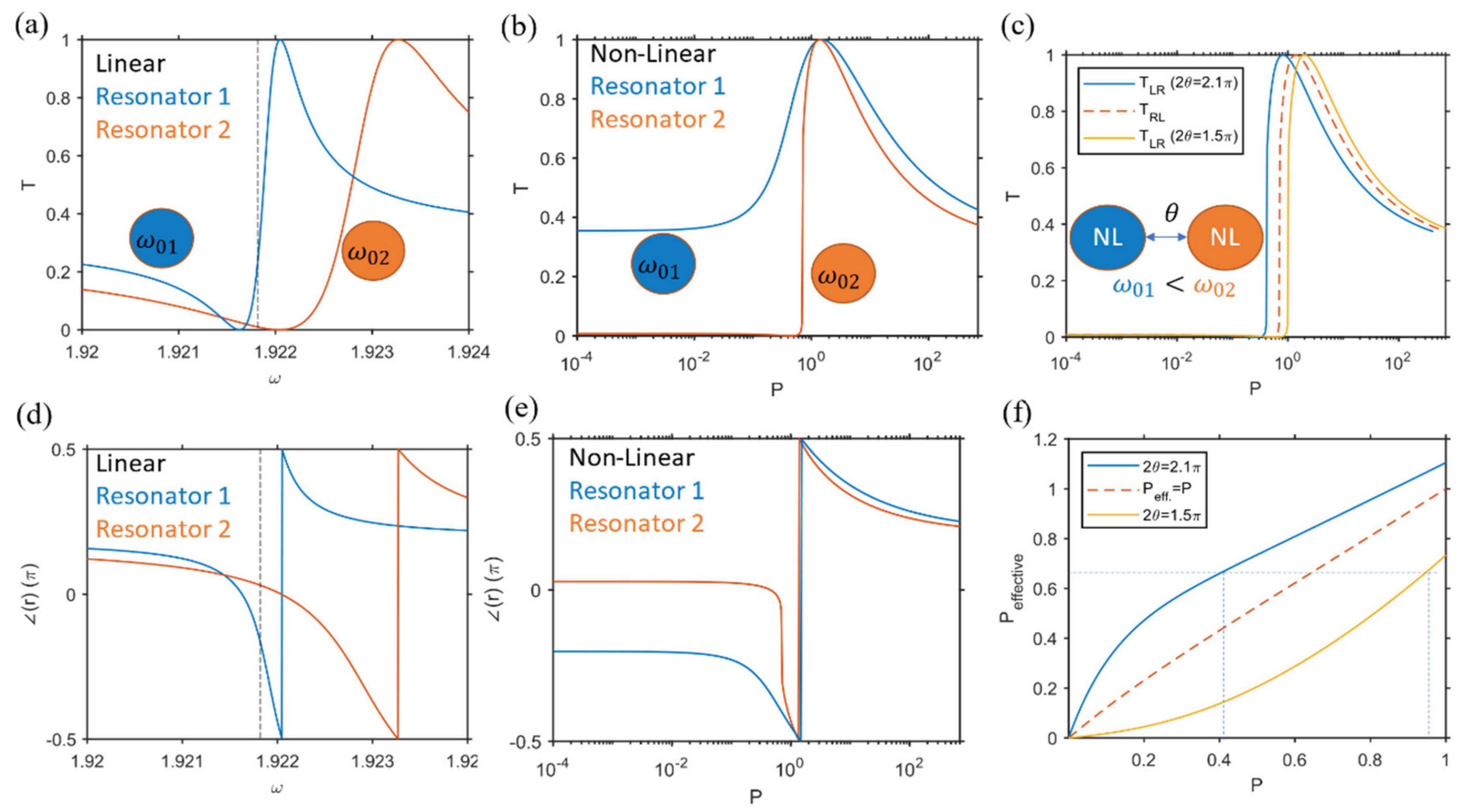
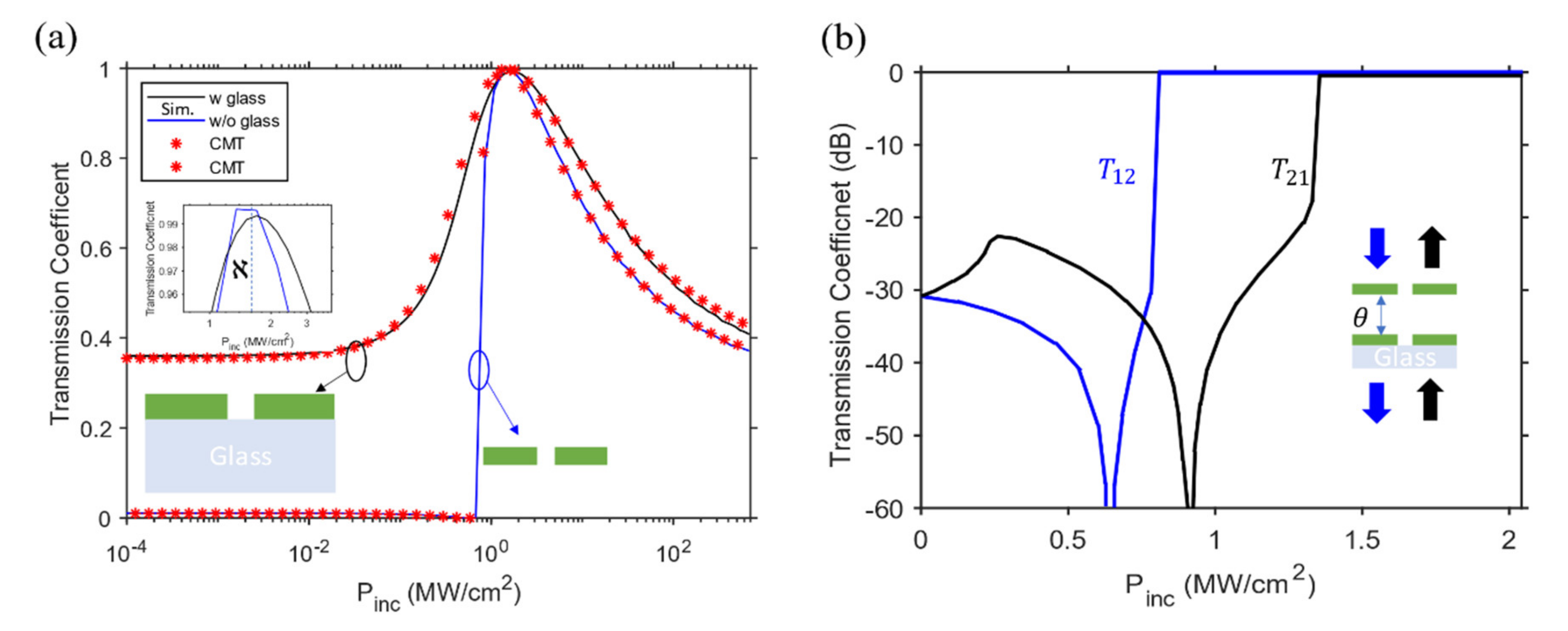
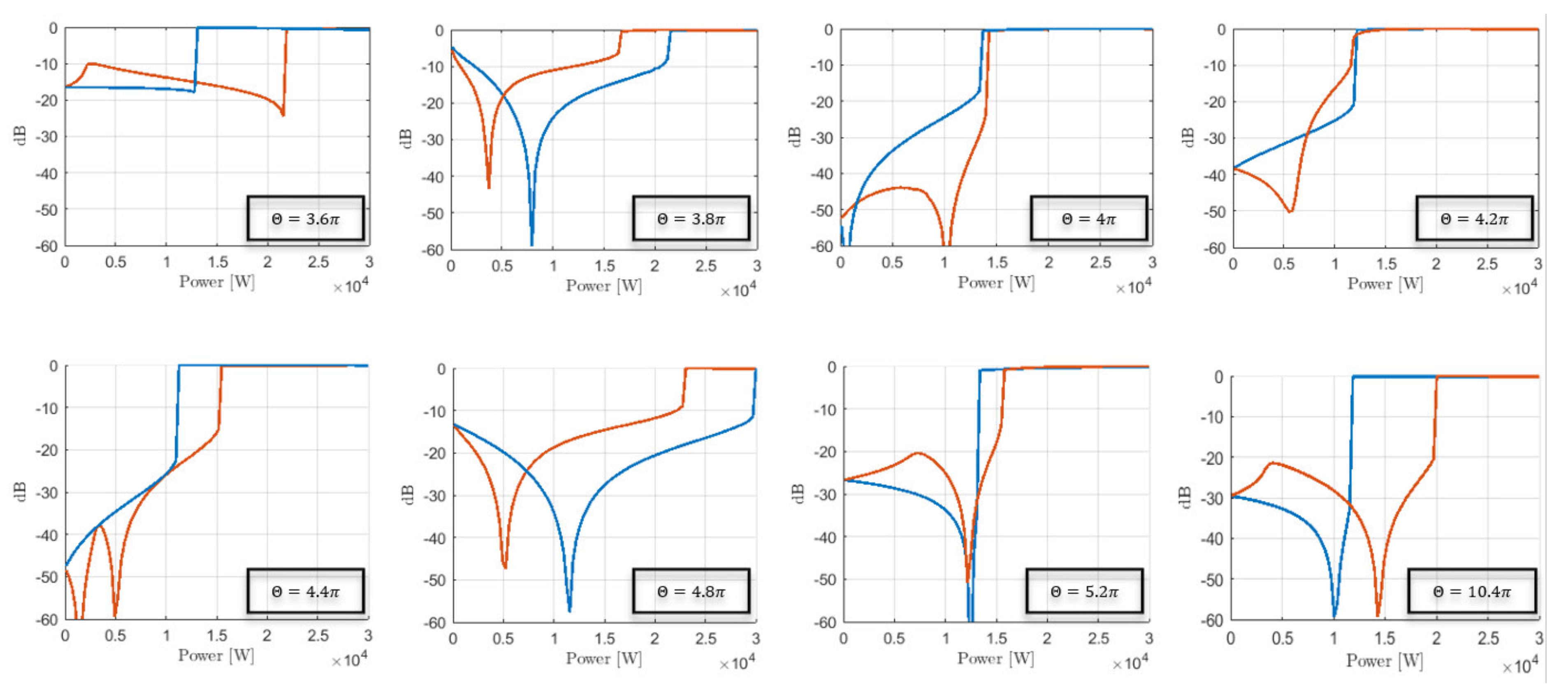
3.2. High Quality Factor Resonators
4. Conclusions
5. Materials and Methods
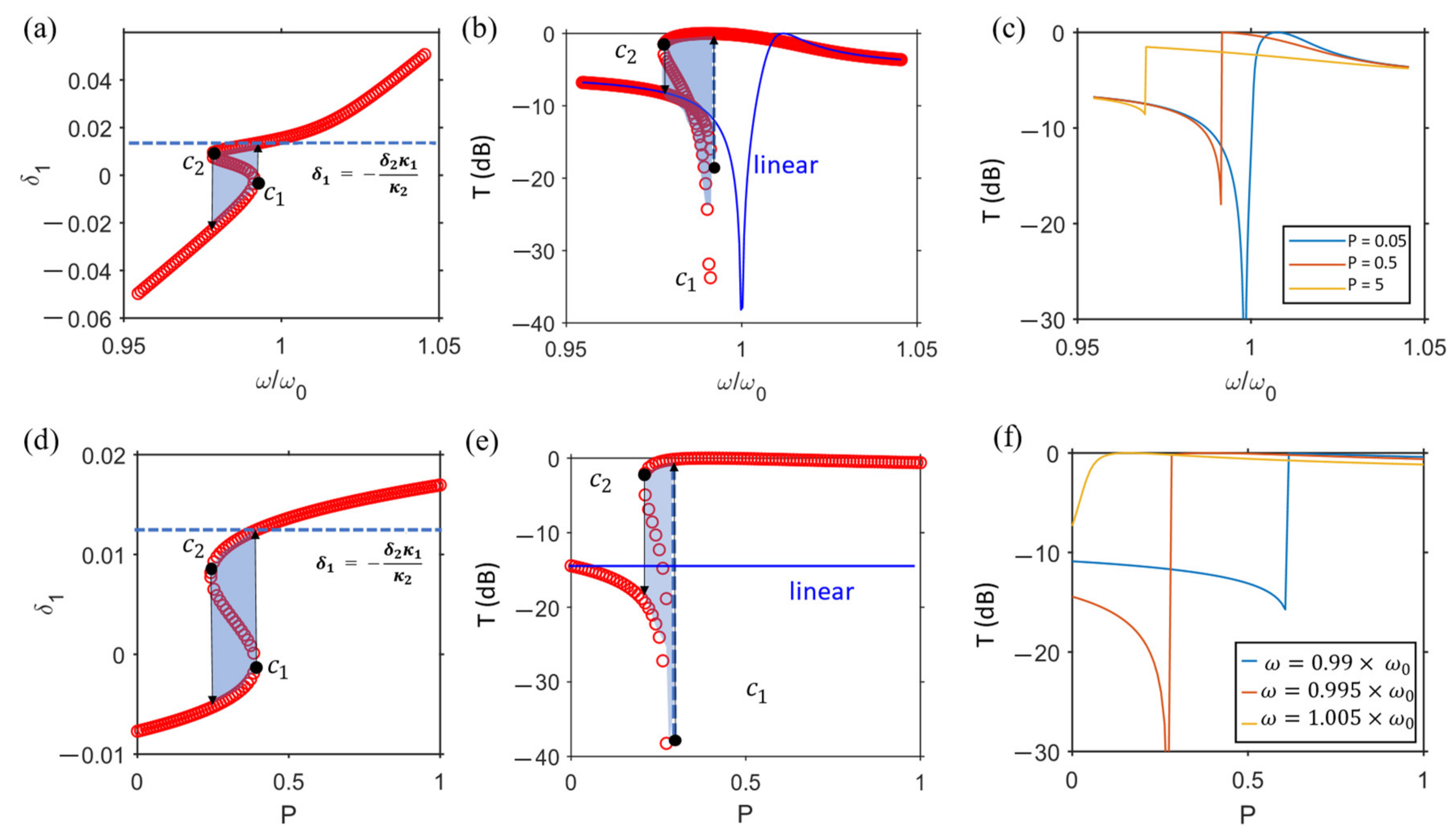
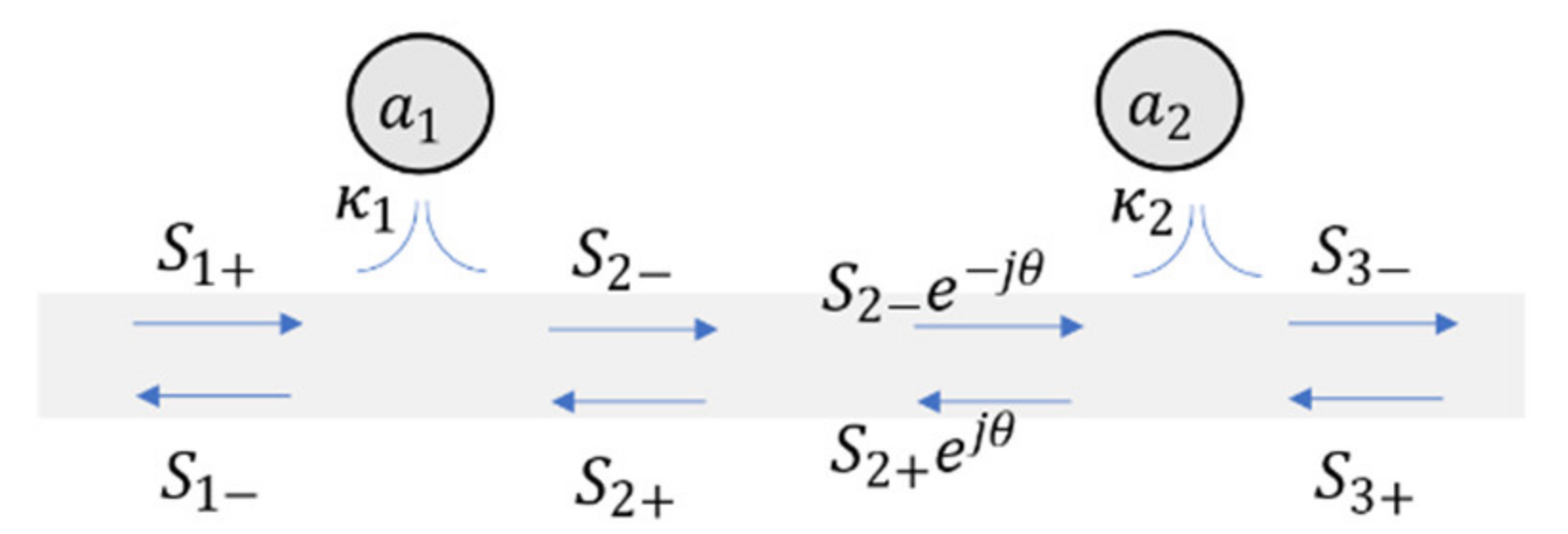
5.1. Coupled Mode Theory
5.2. Nonlinear Bistability
5.3. Bistability Condition
5.4. Effective Power of Coupled Nonlinear Fano Resonators
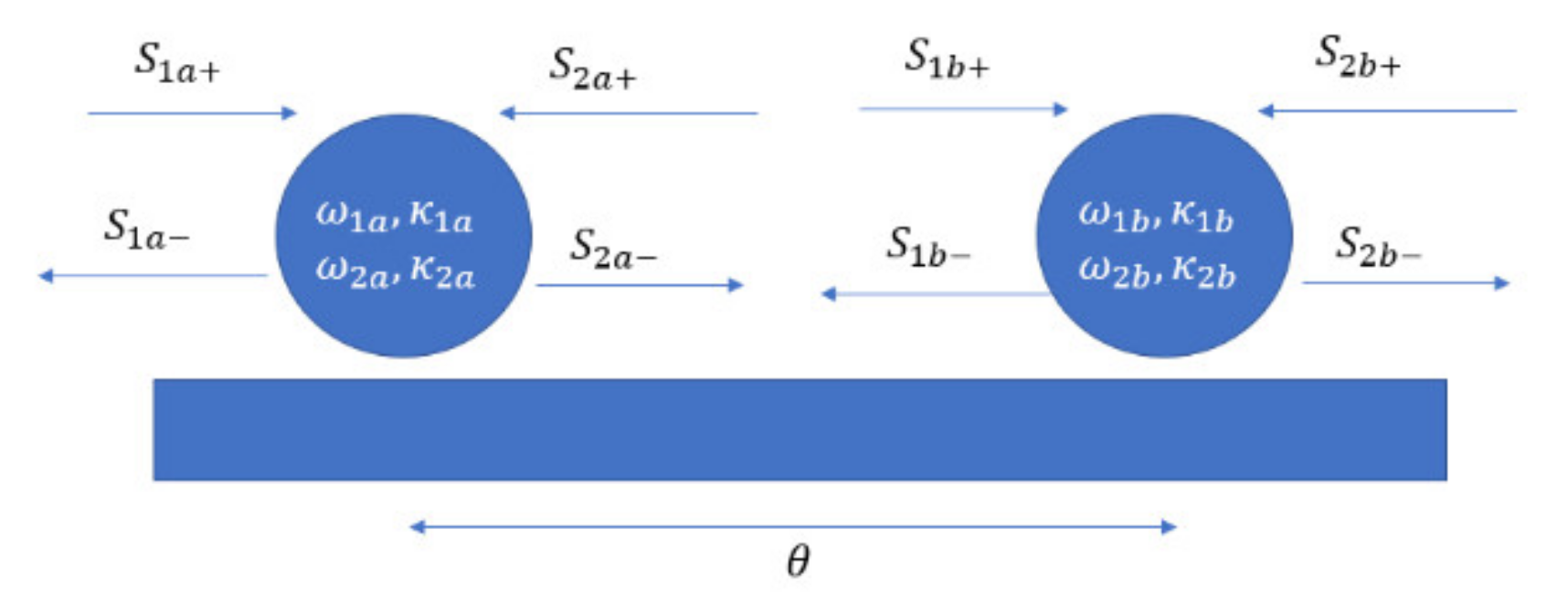
5.5. Fano Resonator Parameters for Figure 3, Figure 4, Figure 6 and Figure 7
5.6. Full Wave Numerical Simulation (We Used Full Wave Numerical Simulation to Obtain the Results in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8)
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, Y.; Chen, Y.; Hu, H.; Xue, W.; Yvind, K.; Mork, J. Nonreciprocal transmission in a nonlinear photonic-crystal Fano structure with broken symmetry: Nonreciprocal transmission in a nonlinear Fano structure. Laser Photonics Rev. 2015, 9, 241–247. [Google Scholar] [CrossRef]
- Yang, K.Y.; Skarda, J.; Cotrufo, M.; Dutt, A.; Ahn, G.H.; Sawaby, M.; Vercruysse, D.; Arbabian, A.; Fan, S.; Alù, A.; et al. Inverse-designed non-reciprocal pulse router for chip-based LiDAR. Nat. Photonics 2020, 14, 369–374. [Google Scholar] [CrossRef]
- Shoji, Y.; Mizumoto, T.; Yokoi, H.; Hsieh, I.-W.; Osgood, R.M., Jr. Magneto-optical isolator with silicon waveguides fabricated by direct bonding. Appl. Phys. Lett. 2008, 92, 071117. [Google Scholar] [CrossRef]
- Tien, M.-C.; Mizumoto, T.; Pintus, P.; Kromer, H.; Bowers, J.E. Silicon ring isolators with bonded nonreciprocal magneto-optic garnets. Opt. Express 2011, 19, 11740–11745. [Google Scholar] [CrossRef] [PubMed]
- Sounas, D.L.; Alù, A. Non-reciprocal photonics based on time modulation. Nat. Photonics 2017, 11, 774–783. [Google Scholar] [CrossRef]
- Fleury, R.; Sounas, D.L.; Sieck, C.F.; Haberman, M.R.; Alù, A. Sound Isolation and Giant Linear Nonreciprocity in a Compact Acoustic Circulator. Science 2014, 343, 516–519. [Google Scholar] [CrossRef]
- Kord, A.; Tymchenko, M.; Sounas, D.L.; Krishnaswamy, H.; Alu, A. CMOS Integrated Magnetless Circulators Based on Spatiotemporal Modulation Angular-Momentum Biasing. IEEE Trans. Microw. Theory Tech. 2019, 67, 2649–2662. [Google Scholar] [CrossRef]
- Estep, N.A.; Sounas, D.L.; Soric, J.; Alù, A. Magnetic-free non-reciprocity and isolation based on parametrically modulated coupled-resonator loops. Nat. Phys. 2014, 10, 923–927. [Google Scholar] [CrossRef]
- Correas-Serrano, D.; Alù, A.; Gomez-Diaz, J.S. Magnetic-free nonreciprocal photonic platform based on time-modulated graphene capacitors. Phys. Rev. B 2018, 98, 165428. [Google Scholar] [CrossRef]
- Doerr, C.R.; Chen, L.; Vermeulen, D. Silicon photonics broadband modulation-based isolator. Opt. Express 2014, 22, 4493–4498. [Google Scholar] [CrossRef]
- Taravati, S.; Eleftheriades, G.V. Full-Duplex Nonreciprocal Beam Steering by Time-Modulated Phase-Gradient Metasurfaces. Phys. Rev. Appl. 2020, 14, 014027. [Google Scholar] [CrossRef]
- Hadad, Y.; Soric, J.C.; Alu, A. Breaking temporal symmetries for emission and absorption. Proc. Natl. Acad. Sci. USA 2016, 113, 3471–3475. [Google Scholar] [CrossRef]
- Zang, J.; Correas-Serrano, D.; Do, J.; Liu, X.; Alvarez-Melcon, A.; Gomez-Diaz, J. Nonreciprocal Wavefront Engineering with Time-Modulated Gradient Metasurfaces. Phys. Rev. Appl. 2019, 11, 054054. [Google Scholar] [CrossRef]
- Guo, X.; Ding, Y.; Duan, Y.; Ni, X. Nonreciprocal metasurface with space–time phase modulation. Light Sci. Appl. 2019, 8, 1–9. [Google Scholar] [CrossRef]
- Williamson, B.I.A.D.; Minkov, M.; Dutt, A.; Wang, J.; Song, A.Y.; Fan, S. Integrated Nonreciprocal Photonic Devices with Dynamic Modulation. Proc. IEEE 2020, 108, 1759–1784. [Google Scholar] [CrossRef]
- Kord, A.; Sounas, D.L.; Alu, A. Differential magnetless circulator using modulated bandstop filters. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS), Honololu, HI, USA, 4–9 June 2017; pp. 384–387. [Google Scholar]
- Wang, Z.; Wang, J.; Zhang, B.; Huangfu, J.; Joannopoulos, J.D.; Soljačić, M.; Ran, L. Gyrotropic response in the absence of a bias field. Proc. Natl. Acad. Sci. USA 2012, 109, 13194–13197. [Google Scholar] [CrossRef]
- Taravati, S.; Khan, B.A.; Gupta, S.; Achouri, K.; Caloz, C. Nonreciprocal Nongyrotropic Magnetless Metasurface. IEEE Trans. Antennas Propag. 2017, 65, 3589–3597. [Google Scholar] [CrossRef]
- Taravati, S.; Eleftheriades, G.V. Programmable nonreciprocal meta-prism. Sci. Rep. 2021, 11, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Ma, Q.; Chen, L.; Jing, H.B.; Hong, Q.R.; Cui, H.Y.; Liu, Y.; Li, L.; Cui, T.J. Controllable and Programmable Nonreciprocity Based on Detachable Digital Coding Metasurface. Adv. Opt. Mater. 2019, 7, 1901285. [Google Scholar] [CrossRef]
- Krasnok, A.; Tymchenko, M.; Alù, A. Nonlinear metasurfaces: A paradigm shift in nonlinear optics. Mater. Today 2018, 21, 8–21. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic Press: San Diego, CA, USA, 2008. [Google Scholar]
- Jin, B.; Argyropoulos, C. Self-Induced Passive Nonreciprocal Transmission by Nonlinear Bifacial Dielectric Metasurfaces. Phys. Rev. Appl. 2020, 13, 054056. [Google Scholar] [CrossRef]
- Lawrence, M.; Barton, D.R., 3rd; Dionne, J.A. Nonreciprocal flat optics with silicon metasurfaces. Nano Lett. 2018, 18, 1104–1109. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Miroshnichenko, A.E. Reconfigurable nonreciprocity with a nonlinear Fano diode. Phys. Rev. B 2014, 89, 134306. [Google Scholar] [CrossRef]
- Balanis, C.A. Advanced Engineering Electromagnetics, 2nd ed.; John Wiley & Sons: Chichester, UK, 2012. [Google Scholar]
- Sounas, D.L.; Alù, A. Fundamental bounds on the operation of Fano nonlinear isolators. Phys. Rev. B 2018, 97, 115431. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; John Wiley & Sons: Nashville, TN, USA, 2012. [Google Scholar]
- Fernandes, D.E.; Silveirinha, M.G. Asymmetric Transmission and Isolation in Nonlinear Devices: Why They Are Different. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1953–1957. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, Z.; Fan, S. Limitations of nonlinear optical isolators due to dynamic reciprocity. Nat. Photonics 2015, 9, 388–392. [Google Scholar] [CrossRef]
- Sounas, D.L.; Alu, A. Nonreciprocity Based on Nonlinear Resonances. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1958–1962. [Google Scholar] [CrossRef]
- Ishimaru, A. Unidirectional Waves in Anisotropic Media and the Resolution of the Thermodynamic Paradox; Technical Report 69; Air Force Cambridge Research Laboratories: Bedford, MA, USA, 1962. [Google Scholar]
- Caloz, C.; Alù, A.; Tretyakov, S.; Sounas, D.; Achouri, K.; Deck-Léger, Z.-L. Electromagnetic Nonreciprocity. Phys. Rev. Appl. 2018, 10, 047001. [Google Scholar] [CrossRef]
- Sounas, D.L.; Soric, J.; Alù, A. Broadband passive isolators based on coupled nonlinear resonances. Nat. Electron. 2018, 1, 113–119. [Google Scholar] [CrossRef]
- Xu, L.; Kamali, K.Z.; Huang, L.; Rahmani, M.; Smirnov, A.; Camacho-Morales, R.; Ma, Y.; Zhang, G.; Woolley, M.; Neshev, D.; et al. Dynamic Nonlinear Image Tuning through Magnetic Dipole Quasi-BIC Ultrathin Resonators. Adv. Sci. 2019, 6, 1802119. [Google Scholar] [CrossRef]
- Wu, F.; Wu, J.; Guo, Z.; Jiang, H.; Sun, Y.; Li, Y.; Ren, J.; Chen, H. Giant Enhancement of the Goos-Hänchen Shift Assisted by Quasibound States in the Continuum. Phys. Rev. Appl. 2019, 12, 014028. [Google Scholar] [CrossRef]
- Li, S.; Zhou, C.; Liu, T.; Xiao, S. Symmetry-protected bound states in the continuum supported by all-dielectric metasurfaces. Phys. Rev. A 2019, 100, 063803. [Google Scholar] [CrossRef]
- Tian, J.; Li, Q.; Belov, P.A.; Sinha, R.K.; Qian, W.; Qiu, M. High-Q All-Dielectric Metasurface: Super and Suppressed Optical Absorption. ACS Photonics 2020, 7, 1436–1443. [Google Scholar] [CrossRef]
- Overvig, A.; Yu, N.; Alù, A. Chiral Quasi-Bound States in the Continuum. Phys. Rev. Lett. 2021, 126, 073001. [Google Scholar] [CrossRef] [PubMed]
- Overvig, A.; Alù, A. Wavefront-selective Fano resonant metasurfaces. Adv. Photonics 2021, 3, 026002. [Google Scholar] [CrossRef]
- Wang, X.; Duan, J.; Chen, W.; Zhou, C.; Liu, T.; Xiao, S. Controlling light absorption of graphene at critical coupling through magnetic dipole quasi-bound states in the continuum resonance. Phys. Rev. B 2020, 102, 155432. [Google Scholar] [CrossRef]
- Haus, H.A. Waves and Fields in Optoelectronics; Prentice Hall: Old Tappan, NJ, USA, 1983. [Google Scholar]
- Zhang, K.; Huang, Y.; Miroshnichenko, A.E.; Gao, L. Tunable Optical Bistability and Tristability in Nonlinear Graphene-Wrapped Nanospheres. J. Phys. Chem. C 2017, 121, 11804–11810. [Google Scholar] [CrossRef]
- Sounas, D.L.; Alù, A. Time-Reversal Symmetry Bounds on the Electromagnetic Response of Asymmetric Structures. Phys. Rev. Lett. 2017, 118, 154302. [Google Scholar] [CrossRef] [PubMed]
- Mekawy, A.; Alù, A. Giant midinfrared nonlinearity based on multiple quantum well polaritonic metasurfaces. Nanophotonics 2020, 10, 667–678. [Google Scholar] [CrossRef]
- Huang, D.; Pintus, P.; Zhang, C.; Morton, P.; Shoji, Y.; Mizumoto, T.; Bowers, J.E. Dynamically reconfigurable integrated optical circulators. Optica 2016, 4, 23–30. [Google Scholar] [CrossRef]
- Sun, Y.; Tong, Y.-W.; Xue, C.-H.; Ding, Y.-Q.; Li, Y.-H.; Jiang, H.; Chen, H. Electromagnetic diode based on nonlinear electromagnetically induced transparency in metamaterials. Appl. Phys. Lett. 2013, 103, 091904. [Google Scholar] [CrossRef]
- Yu, J.; Park, S.; Hwang, I.; Kim, D.; Jung, J.; Lee, J. Third-Harmonic Generation from Plasmonic Metasurfaces Coupled to Intersubband Transitions. Adv. Opt. Mater. 2019, 7, 1801510. [Google Scholar] [CrossRef]
- Lee, J.; Tymchenko, M.; Argyropoulos, C.; Chen, P.Y.; Lu, F.; Demmerle, F.; Boehm, G.; Amann, M.; Alù, A.; Belkin, M.A. Giant nonlinear response from plasmonic metasurfaces coupled to intersubband transitions. Nature 2014, 511, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Reed, G.T.; Knights, A.P. Knights, Silicon Photonics: An Introduction; John Wiley & Sons: Nashville, TN, USA, 2008. [Google Scholar]
- Vakulenko, A.; Kiriushechkina, S.; Li, M.; Zhirihin, D.; Ni, X.; Guddala, S.; Korobkin, D.; Alù, A.; Khanikaev, A.B. Direct visualization of topological transitions and higher-order topological states in photonic metasurfaces. arXiv 2019, arXiv:1911.11110. [Google Scholar]
- Zangeneh-Nejad, F.; Fleury, R. Topological Fano Resonances. Phys. Rev. Lett. 2019, 122, 014301. [Google Scholar] [CrossRef] [PubMed]

| Work | Breaking Reciprocity Due to: | Bandwidth/Center Frequency | Modulation Frequency (mf) or Total Gain of the Amplifiers (tga) or Kerr Nonlinearity Coefficient | Thickness/Wavelength | Pump Power Per Unit Cell or Signal Power/Intensity | Isolation (or Transmission Contrast) at Best Insertion Loss | Frequency Conversion/Programmable | ||
|---|---|---|---|---|---|---|---|---|---|
| [11] | Time modulation | NA/ 5.28 [GHz] | MF | 50 [MHz] | 2.54 [mm]/56.8 [mm] | Modulation signal power or intensity | NA | NA | No/yes |
| [13] | 0.3 [GHz]/ 8.97 [GHz] | 370 [MHz] or 600 [MHz] | 2 [mm]/33.33 [mm] | 10 dBm or 1 V | 5 dB loss, isolation of 30 dB | Yes/yes | |||
| [14] | 5.77 [THz]/ 348.8 [THz] | 2.8 [THz] | 400 [nm]/860 [nm] | 15 GW/cm2 | NA | Yes/yes | |||
| [17] | Unidirectional gain amplifiers | 6 [MHz]/ 944 [MHz] ¥ | TGA | 0 dB | 31.7 [mm]/317 [mm] | DC power of each amplifier in one layer, number of layers | NA, 2 | Isolation of −1.5 dB assuming 0 dB insertion loss ¥ | No/yes |
| [18] | 0.17 [GHz]/ 5.9 [GHz] | 20 dB | 1.7 [mm]/50.8 [mm] | 0.18 [W], 2 | 17 dB transmission gain and 10 dB loss correspond to 27 dB. | ||||
| [19] | 0.25 [GHz]/ 5.875 [GHz] | 10 dB- 30 dB | 1.82 [mm]/51 [mm] | 0.1–0.2 [W] £, 2 | 20 dB transmission gain and 20 dB loss correspond to 40 dB isolation | ||||
| [20] | 0.05 [GHz]/ 5.5 [GHz] | 20 dB | 2.1 [mm]/54.54 [mm] | 0.1 [W], 2 | 13 dB of transmission gain and 32 dB isolation | ||||
| [23] | Kerr nonlinearity | NA | (m2/V2) | 0.1 [um]/1.5 [um] | Signal intensity | 5 kW/cm2 | −17 dB at −1.2 dB over 4.77 dB * | No/no | |
| [24] | (2.7–6.15) [um]/1.53 [um] | (1.5–2) MW/cm2 | Isolation of −25.4 dB at insertion loss of −0.46 dB over NRIR of 2.79 dB ** Isolation of −35.7 dB at insertion loss of −0.41 dB over NRIR of 1.5 dB *** Isolation of −15.2 dB at −0.044 dB over NRIR of 1.52 dB ****¿ | ||||||
| This work | 0.6 [THz]/ 192 [THz] | (1.33–5.334) [um]/1.56 [um] | (16.8–0.001) GW/cm2 | −56 dB at −0.04 dB, −65 dB at −0.2 dB | |||||
| Structure 1 () () are normalized by () | |||||
| Structure 2 () () are normalized by () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mekawy, A.; Sounas, D.L.; Alù, A. Free-Space Nonreciprocal Transmission Based on Nonlinear Coupled Fano Metasurfaces. Photonics 2021, 8, 139. https://doi.org/10.3390/photonics8050139
Mekawy A, Sounas DL, Alù A. Free-Space Nonreciprocal Transmission Based on Nonlinear Coupled Fano Metasurfaces. Photonics. 2021; 8(5):139. https://doi.org/10.3390/photonics8050139
Chicago/Turabian StyleMekawy, Ahmed, Dimitrios L. Sounas, and Andrea Alù. 2021. "Free-Space Nonreciprocal Transmission Based on Nonlinear Coupled Fano Metasurfaces" Photonics 8, no. 5: 139. https://doi.org/10.3390/photonics8050139
APA StyleMekawy, A., Sounas, D. L., & Alù, A. (2021). Free-Space Nonreciprocal Transmission Based on Nonlinear Coupled Fano Metasurfaces. Photonics, 8(5), 139. https://doi.org/10.3390/photonics8050139





