Color Digital Holography Based on Generalized Phase-Shifting Algorithm with Monitoring Phase-Shift
Abstract
:1. Introduction
2. Color Phase-Shifting Digital Holography with Bayer Color Filter
3. Generalized Phase-Shifting Algorithm with Monitoring Phase-Shift
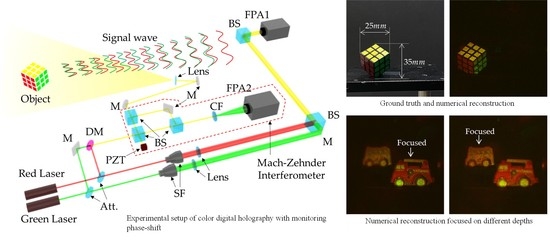
4. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Desse, J.M.; Picart, P. Digital color holography for analyzing unsteady wake flows. In New Techniques in Digital Holography; Picart, P., Ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2015; pp. 107–136. [Google Scholar]
- Kozacki, T.; Chlipala, M.; Makowski, P.L. Color Fourier orthoscopic holography with laser capture and an LED display. Opt. Express 2018, 26, 12144–12158. [Google Scholar] [CrossRef]
- Hu, Y.; Luo, X.; Chen, Y.; Liu, Q.; Li, X.; Wang, Y.; Liu, N.; Duan, H. 3D-Integrated metasurfaces for full-color holography. Light Sci. Appl. 2019, 8, 1–9. [Google Scholar] [CrossRef]
- Javidi, B.; Moon, I.; Yeom, S.; Carapezza, E. Three-dimensional imaging and recognition of microorganism using single-exposure on-line (SEOL) digital holography. Opt. Express 2005, 13, 4492–4506. [Google Scholar] [CrossRef]
- Zakrisson, J.; Schedin, S.; Andersson, M. Cell shape identification using digital holographic microscopy. Appl. Opt. 2015, 54, 7442–7448. [Google Scholar] [CrossRef] [Green Version]
- Han, J.-H.; Li, R.-P.; Liu, J.-H.; Hai, F.-S.; Huang, M.-J. Two-step phase shifting differential-recording digital holographic microscopy. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.K. Full color natural light holographic camera. Opt. Express 2013, 21, 9636–9642. [Google Scholar] [CrossRef]
- Javidi, B.; Tajahuerce, E. Three-dimensional object recognition by use of digital holography. Opt. Lett. 2000, 25, 610–612. [Google Scholar] [CrossRef] [PubMed]
- Schnars, U.; Jüptner, W.P. Digital recording and numerical reconstruction of holograms. Meas. Sci. Technol. 2002, 13, R85. [Google Scholar] [CrossRef]
- Yamaguchi, I.; Zhang, T. Phase-shifting digital holography. Opt. Lett. 1997, 22, 1268–1270. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, I.; Matsumura, T.; Kato, J.I. Phase-shifting color digital holography. Opt. Lett. 2002, 27, 1108–1110. [Google Scholar] [CrossRef]
- Kato, J.I.; Yamaguchi, I.; Matsumura, T. Multicolor digital holography with an achromatic phase shifter. Opt. Lett. 2002, 27, 1403–1405. [Google Scholar] [CrossRef]
- Nomura, T.; Shinomura, K. Generalized sequential four-step phase-shifting color digital holography. Appl. Opt. 2017, 56, 6851–6854. [Google Scholar] [CrossRef]
- Tahara, T.; Otani, R.; Takaki, Y. Wavelength-selective phase-shifting digital holography: Color three-dimensional imaging ability in relation to bit depth of wavelength-multiplexed holograms. Appl. Sci. 2018, 8, 2410. [Google Scholar] [CrossRef] [Green Version]
- Kakue, T.; Tahara, T.; Ito, K.; Shimozato, Y.; Awatsuji, Y.; Nishio, K.; Matoba, O. Parallel phase-shifting color digital holography using two phase shifts. Appl. Opt. 2009, 48, H244–H250. [Google Scholar] [CrossRef] [PubMed]
- Han, G.S.; Kim, S.W. Numerical correction of reference phases in phase-shifting interferometry by iterative least squares fitting. Appl. Opt. 1994, 33, 7321–7325. [Google Scholar] [CrossRef] [PubMed]
- Schmit, J.; Creath, K. Extended averaging technique for derivation of error-compensating algorithms phase-shifting interferometry. Appl. Opt. 1995, 34, 3610–3619. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, X.; Gramaglia, M.; Yeazell, J.A. Phase-shifting interferometry with uncalibrated phase shifts. Appl. Opt. 2000, 39, 585–591. [Google Scholar] [CrossRef] [PubMed]
- Yoshikawa, N.; Shiratori, T.; Kajihara, K. Robust phase-shift estimation method for statistical generalized phase-shifting digital holography. Opt. Express 2014, 22, 14155–14165. [Google Scholar] [CrossRef]
- Cai, L.Z.; Liu, Q.; Yang, X.L. Generalized phase-shifting interferometry with arbitrary unknown phase steps for diffraction objects. Opt. Lett. 2004, 29, 183–185. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.Z.; Liu, Q.; Yang, X.L. Phase-shift extraction and wave-front reconstruction in phase-shifting interferometry with arbitrary phase steps. Opt. Lett. 2003, 28, 1808–1810. [Google Scholar] [CrossRef] [PubMed]
- Hahn, J.; Kim, H.; Cho, S.W.; Lee, B. Phase-shifting interferometry with genetic algorithm-based twin image noise elimination. Appl. Opt. 2008, 47, 4068–4076. [Google Scholar] [CrossRef] [PubMed]
- Lim, S.; Choi, K.; Hahn, J.; Marks, D.L.; Brady, D.J. Image-based registration for synthetic aperture holography. Opt. Express 2011, 19, 11716–11731. [Google Scholar] [CrossRef] [PubMed]
- Xia, P.; Wang, Q.; Ri, S.; Tsuda, H. Calibrated phase-shifting digital holographic microscope using a sampling moiré technique. Appl. Sci. 2018, 8, 706. [Google Scholar] [CrossRef] [Green Version]
- Hahn, J.; Kim, H.; Lee, B. Optimization of the spatial light modulation with twisted nematic liquid crystals by a genetic algorithm. Appl. Opt. 2008, 47, D87–D95. [Google Scholar] [CrossRef] [PubMed]
- Hahn, J.; Kim, H. Uncertainty-managed phase-shifting digital holography. Opt. Lett. 2012, 37, 4492–4494. [Google Scholar] [CrossRef]








| Step | 1st | 2nd | 3rd | 4th |
|---|---|---|---|---|
| Driving Voltage (V) | 1.7 | 3.4 | 5.1 | 6.8 |
| 532 nm (rad) | 0 | 0.5639π | 1.1617π | 1.7156π |
| 633 nm (rad) | 0 | 0.4739π | 0.9763π | 1.4418π |
| Step | 1st | 2nd | 3rd | 4th |
|---|---|---|---|---|
| Driving Voltage (V) | 1.75 | 3.5 | 5.25 | 7 |
| 532 nm (rad) | 0 | 0.5895π | 1.1680π | 1.7376π |
| 633 nm (rad) | 0 | 0.4954π | 0.9816π | 1.4604π |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, M.; Jeon, H.; Lim, S.; Hahn, J. Color Digital Holography Based on Generalized Phase-Shifting Algorithm with Monitoring Phase-Shift. Photonics 2021, 8, 241. https://doi.org/10.3390/photonics8070241
Jung M, Jeon H, Lim S, Hahn J. Color Digital Holography Based on Generalized Phase-Shifting Algorithm with Monitoring Phase-Shift. Photonics. 2021; 8(7):241. https://doi.org/10.3390/photonics8070241
Chicago/Turabian StyleJung, Minwoo, Hosung Jeon, Sungjin Lim, and Joonku Hahn. 2021. "Color Digital Holography Based on Generalized Phase-Shifting Algorithm with Monitoring Phase-Shift" Photonics 8, no. 7: 241. https://doi.org/10.3390/photonics8070241
APA StyleJung, M., Jeon, H., Lim, S., & Hahn, J. (2021). Color Digital Holography Based on Generalized Phase-Shifting Algorithm with Monitoring Phase-Shift. Photonics, 8(7), 241. https://doi.org/10.3390/photonics8070241