Design and Analysis of Trench-Assisted Low-Bending-Loss Large-Mode-Field-Area Multi-Core Fiber with an Air Hole

Abstract

In this paper, a trench-assisted low-bending-loss large-mode-field-area multi-core fiber with air hole is proposed, which can achieve dual-mode transmission. The influence of structural parameters on fiber performance is analyzed systematically, and the structure of the trench, with a lower refractive index than the cladding, is also analyzed and optimized. By adjusting the structural parameters, the effective mode field area of the fundamental mode can reach 2003.24 um² at 1550 nm, and when the bending radius is 1 cm, the bending loss is 2.57 × 10⁻³ dB/m. The practical implementation of the proposed fiber is feasible using existing fabrication technology and is applicable to the transmission of large-capacity optical communication systems and high-power lasers.

1. Introduction

The advent of the “Internet +” era and the 5G era have put forward higher requirements for the high speed and high bandwidth of optical communication networks. Ultra-high-speed, large-capacity, and ultra-long-distance transmission has become the future trend. The conventional single-mode single-core fiber (SM-SCF) is gradually approaching its 100 Tb/s transmission limit due to the limitation of the nonlinear effect [1]. The rapid development of communication technologies such as wavelength division multiplexing (WDM) and polarization multiplexing (PDM) enables mode division multiplexing (MDM) based on few-mode fibers to be used to increase channel transmission capacity [2]. Increasing the mode field area can reduce the nonlinear effect of the fiber, but it will also increase the number of transmittable modes in the fiber and bring about bending loss. Therefore, low-bending loss and large-mode area few-mode fibers have important research significance in high-power optical communication devices [3].

In recent years, fiber lasers have developed rapidly. In order to overcome the limitation of fiber laser power improvements such as the fiber nonlinear effect and fiber damage, the method of increasing the mode field area can be used to overcome the nonlinear effect. The strong coupling multi-core fiber (MCF) increases the mode field area (MFA) of the fiber by introducing the lateral coupling of the core, thereby reducing the nonlinear effect. Therefore, it is often used in fiber lasers and amplifiers [4]. But multi-core fibers have a higher bending loss [5]. However, the reduction of the bending loss (BL) is conducive to improving the stability and output efficiency of the fiber laser source [6,7]. Adding air holes and a trench in cladding can effectively reduce the bending loss.

Commonly used fiber structures for achieving a large mode field and low bending loss include: photonic crystal fiber, trench-assisted fiber, and multi-core fiber. The photonic crystal fiber has a large mode field area and good bending resistance. However, the structure is complex and asymmetric, and the technological level is high and welding is difficult. Usually, the effective mode field area can reach 794 um², and the bending loss is 0.064 dB/m, when the bending radius is 15 cm [8]. The trench-assisted fiber has good bending resistance. However, due to process limitations, the width and depth of the submerged layer will be limited. The fiber can not only support ultra-low bending loss (0.052 dB/turn when bending radius R = 5 mm), but also support an effective mode field area of up to 260 um² at a working wavelength of 1.55 um [9,10].

Multi-core optical fiber has the characteristics of a symmetrical structure distribution, simple design, flexible parameter adjustment, and large mode field area. However, large mode field multi-core optical fiber often has a higher bending loss. The fiber can generally transmit with a low bending loss (less than 1.0 dB/m when the bending radius R = 0.34 m), and the effective area is as high as 1331 um² [11,12,13,14,15].

There is a mutually restrictive relationship between the bending loss of the optical fiber and the mode field diameter (mode field area). The smaller the mode field diameter, the better the light can be confined, thus reducing the bending loss of the fiber. But if the mode field diameter of the fiber is too small, there will be serious nonlinear effects under high power conditions [16]. Therefore, the two must be considered comprehensively.

A trench-assisted low-bending-loss large-mode-field-area multi-core fiber (TA-LBL-LMFA MCF) with an air hole structure is proposed in this paper that can realize dual-mode transmission. The MFA of the fundamental mode of the fiber can reach 2003.24 um². When the bending radius is 1 cm, BL can be as low as 2.57 × 10⁻³ dB/m. Using the existing fabrication techniques, the practical implementation of the proposed fiber is feasible.

2. Optical Fiber Structure and Theoretical Analysis

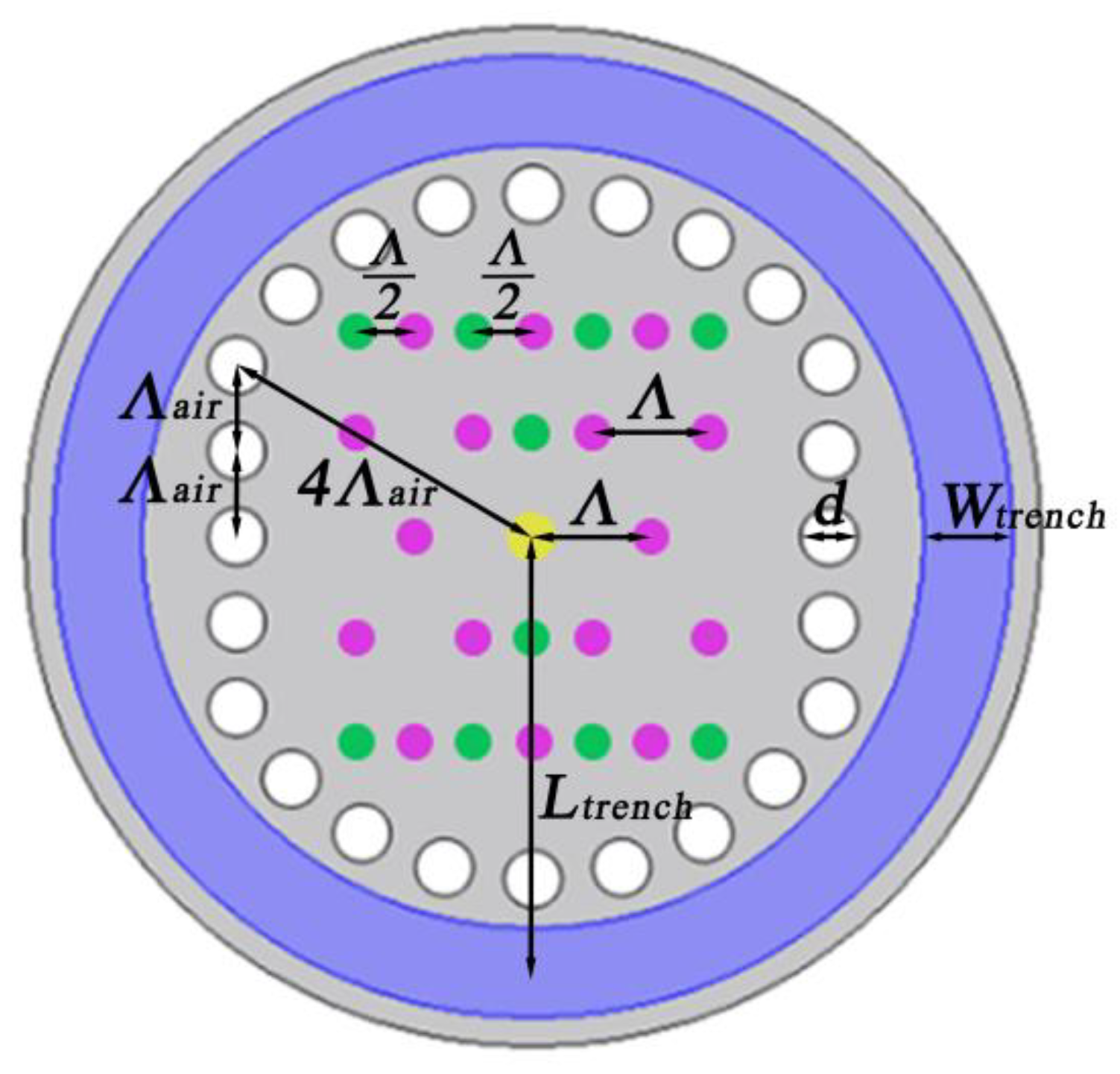
The fiber structure is shown in Figure 1. The yellow part is the central core and the gray part is the silica cladding. The blue part is a trench with a lower refractive index (RI) than the cladding. This structure adds 10 cores (green part) to the traditional hexagonal 19-core optical fiber structure (pink part), removes the cores on both sides of the 19-core optical fiber, and adds air holes and a trench in the cladding. The green part, yellow part, and pink part constitute the core area.

The diameter of the fiber cladding is d_clad = 125 um, the refractive index of the fiber cladding n_clad = 1.444, the refractive index of the air hole is the refractive index of air n_air = 1.000, the refractive index of the central core is n_center, and the refractive index of the other cores is n_core. The refractive index difference between the center core and the cladding is Δn_center = n_center − n_clad; Δn = n_core − n_clad is the refractive index difference between the core and the cladding; Λ is the distance between the core and the core, Λ_air = 14 um is the spacing between the air holes, and d_center is the diameter of the central core. The diameter of the other cores is d, the diameter of the air hole is d_air = 7 um, and the refractive index of the trench is n_trench. Δn₁ = n_clad − n_trench, which is the refractive index difference between cladding and the trench; W_trench is the thickness of the trench layer, and L_trench is the distance between the trench layer and the central core. The structural parameters are composed of seven parameters: Λ, d, Δn, d_center, Δn_cneter, W_trench, and L_trench.

This paper is mainly based on the finite element method (FEM) software to analyze the fiber structure [17].

The refractive index of the beam propagating in a specific mode changes with the wavelength and the geometric structure of the waveguide. This is called the effective refractive index n_eff of the mode. The conduction of specific mode in optical fiber needs to satisfy the conduction mode condition of the optical waveguide theory: n_eff < n_clad < n_core. Otherwise, the mode will be cut off and does not exist in the fiber. The effective refractive index n_eff calculation formula can be expressed as [18]:

$$n_{eff}=Re\left(\frac{\beta }{k_0}\right).$$

(1)

Among these figures, β is the propagation constant, the Re is the real part of the whole, the wave number in vacuum is k₀ = 2π/λ, and λ is the working wavelength.

The electromagnetic field of each mode along the cross section of the fiber is called the mode field. An optical fiber with a large mode field area can suppress the nonlinear effect in the optical fiber. The effective mode field area A_eff can be expressed as [19]:

$$A_{eff}=\frac{\int {\left(E{E}^{*}dA\right)}^2}{\int {\left(E{E}^{*}\right)}^{2}dA}$$

(2)

where E represents the electric field of the mode, and E* represents the conjugate complex number of the electric field of the mode.

When the fiber is bent in the positive direction of the x-axis, and the equivalent refractive index distribution of the fiber cross-section is [20]:

$$n\left(x,y\right)=n_0\left(x,y\right)\sqrt{1+\frac{2x}{R_{eff}}}.$$

(3)

Among them, n(x, y) is the equivalent refractive index of the fiber after bending, and n₀(x, y) is the initial refractive index of the fiber. R is the bending radius of the optical fiber along the positive x-axis. When the elastic optical correction factor is introduced, the equivalent bending radius R_eff = 1.28R.

The calculation formula of fiber bending loss α can be expressed as [20]:

$$a=-\frac{20\pi }{ln10}IM\left(\beta \right)\approx -8.686\frac{2\pi }{\lambda }IM\left(n_{eff}\right)$$

(4)

where IM represents the imaginary part, and n_eff represents the effective refractive index of the fiber.

3. Analysis and Optimization of Optical Fiber Structure Parameters

The fiber structure can effectively destroy the circular symmetrical structure of the traditional 19-core optical fiber. It cuts off the higher-order modes (TE₀₁, TM₀₁), leaving two degenerate fundamental modes (HE₁₁) and second-order modes (HE₂₁), as shown in Figure 2. In addition, the 10 fiber cores increase the lateral coupling of the fiber, which significantly increases the mode field area of the fiber. The effective refractive index of the cladding is reduced by adding air holes and grooves in the cladding. As a result, the refractive index difference between the core and the cladding is increased, and the BL is significantly reduced.

3.1. Analysis of Three Structural Parameters Λ, d, and Δn

For this paper, we conducted research on the basis of strict dual-mode transmission. Λ, d, and Δn three structural parameters were analyzed. The working wavelength λ was set at 1550 nm, and the initial structure parameter was set as Λ = 15 um, d = 3 um, Δn = 0.003, d_center = d, Δn_center = 0.003, W_trench = 5.5 um, L_trench = 52 um, Δn₁= 0.004.

The result of analyzing the influence of the structural parameter Λ on n_eff and A_eff is shown in Figure 3. To realize dual-mode transmission and cut high-order modes of optical fiber, its effective refractive index should be less than n_clad. Figure 3a shows that the transmission mode can be adjusted by modifying Λ. If dual-mode transmission is to be realized, Λ should be greater than or equal to 11.5 um. Figure 3b shows that as Λ goes from 10 um to 15 um, the A_eff of HE₁₁ grows from 1451 um² to 2201 um² and then drops to 1996 um², and finally reaches the maximum value at 14.5 um; in addition, the A_eff of HE₂₁ grows from 1219 um² to 1717 um². From the above discussion, it can be concluded that 14.5 um is the best choice for Λ.

When Λ is 14.5 um, the results of analyzing the influence of structure parameter d on n_eff and A_eff are shown in Figure 4. Figure 4a shows that as d increases, the effective refractive index of each mode also increases. If d is less than or equal to 3.3 um, then the fiber realizes dual-mode transmission. It can be seen from Figure 4b that as d increases to 3.4 um, the A_eff of HE₁₁ rises to the maximum value of 2032 um², and the A_eff of HE₂₁ decreases from 1706 um² to 1616 um². However, due to the limitation of dual-mode transmission conditions, d is the most suitable to be 3.3 um. At this time, the A_eff of HE₁₁ is 2029 um², and the A_eff of HE₂₁ is 1632 um². Optical fiber can achieve dual-mode transmission, but also has a large A_eff.

When d is 3.3 um, the effect of Δn on n_eff and A_eff is shown in Figure 5. Figure 5a shows that with the increase of Δn, the neff of TE₀₁ and TM₀₁ also increase. In order to ensure dual-mode transmission, Δn should be less than or equal to 0.00315. It can be seen from Figure 5b that the maximum A_eff of HE₁₁ at 3.1 um is 2031 um² for Δn, and the A_eff of HE₂₁ at this time is 1622 um². In order to ensure that the fundamental mode obtains a larger mode field area, Δn is selected as 0.003.

3.2. Analysis of Structural Parameters of Central Core

In order to enhance the core’s ability to confine light, the central core diameter d_center is increased to reduce the central core refractive index Δn_center, thereby reducing the bending loss. This part analyzes the d_center and Δn_center structure parameters of the center core and initializes the center core structure parameters to Δn_center = 0.001 and d_center = 3 um.

Based on the optimization of the above structural parameters, the influence of d_center on n_eff and A_eff is studied, as shown in Figure 6. Figure 6a shows that the effective refractive index of the higher-order modes TE₀₁, TM₀₁ is around 1.444, intersecting with ncl at 7.2 um. To ensure dual-mode transmission, d_center should be less than 7.2 um. As shown in Figure 6b, HE₁₁ has the largest A_eff at 4.8 um in d_center, which is about 2039 um² and the A_eff of HE₂₁ has been stable around 1622 um², so 4.8 um is the best choice for d_center.

When the d_center is 4.8 um, the influence of Δn_center on n_eff and A_eff is shown in Figure 7. Figure 7a shows that TE₀₁, TM₀₁, and ncl intersect at 0.002. To ensure dual-mode transmission, Δn_center must be restricted within 0.002.

The greater the refractive index of the central core of the optical fiber, the stronger its ability to confine light, but the mode field area will decrease. It can be seen from Figure 7b that when Δn_center exceeds 0.002, the A_eff of HE₁₁ decreases rapidly. The A_eff of HE₂₁ is stable at 1622 um², and the A_eff of HE₁₁ is 2002 um² at 0.002. Δn_center is selected as 0.002 as the best, which not only has a large mode field area, but also has a better ability to bind light.

4. Bending Characteristic Analysis

This part studies the effect of R on the A_eff and BL of HE₁₁ and HE₂₁ when the working wavelength is 1550 nm.

When the bending radius is 1.5 cm, the mode field and electric field will deviate from the core area to the direction of the trench as shown in Figure 8, resulting in a reduction in the mode field area and an increase in the bending loss. In order to prevent the electric field from deviating to the trench, a circle of air holes is added in the middle of the cladding. The air holes have a lower refractive index, which can effectively prevent the electric field from deviating to the trench. At the same time, it reduces the refractive index of the cladding and the bending loss is reduced.

The two polarization states of a mode have the same changing trend and similar size, so the two polarization states are almost overlapped. Figure 9a shows that when R increases from 1 cm to 19 cm, the A_eff of HE₁₁ and HE₂₁ will also increase. After the bending radius is greater than 11 cm, the A_eff of HE₁₁ and HE₂₁ tends to be stable, around 2100 um² and 1600 um². Figure 9b shows that as R increases from 1 cm to 6 cm, the BL of HE₁₁ and HE₂₁ will also decrease. When the bending radius is 1.5 cm, the BL of the two modes is less than 10⁻³ dB/m. The fiber has very low bending loss. In the case of no bending, the A_eff of HE₁₁ is 2003.24 um² and the A_eff of HE₂₁ is 1686.71 um². Therefore, the optical fiber has good bending insensitivity.

Table 1. A comparison table with other recent work and literature.

Article	Description
[21]	Mode area of 2622 um2 at a bend radius of 20 cm can be achieved. Bending loss can be reduced to about 0.092 dB/m at 1550 nm.
[17]	When the bending radius is 20 cm, the effective mode area of the fiber can reach 914 um2 at 1.06 um, and loss ratio between lowest-HOMs and fundamental mode is larger than 100.
[22]	Mode field area of the fundamental mode can reach 1916.042 um2 at 1550 nm., and when the bending radius is 1.4 cm, the bending loss is 2.96 × 10−3 dB/m.
This article	Mode field area of the fundamental mode can reach 2003.24 um2, and when the bending radius is 1 cm, the bending loss is 2.57 × 10−3 dB/m at 1550 nm.

is a comparison table between this article and other recent work and literature.

5. Structural Optimization of the Trench

Adding trench in the cladding can effectively reduce the bending loss of the optical fiber and improve the bending resistance of the optical fiber. However, the bending loss of the optical fiber and the mode field area are mutually restrictive, so the two parts must be taken into consideration at the same time in the design. In order to balance the relationship between the bending loss and the mode field area, this paper defines the performance factor PI [23] of the fiber, and the expression is:

$$PI=\frac{BL}{A_{eff}}.$$

(5)

PI is used to measure the trade-off between BL and A_eff. When A_eff increases and BL decreases, PI will decrease, and the comprehensive performance of the fiber will be better.

This section provides analysis and optimization of the L_trench and Δn₁ parameters of the trench. We used PI to evaluate the comprehensive performance of the optical fiber. W_trench has little effect on the A_eff of each mode, and the larger the thickness, the smaller the bending loss. Therefore, the larger the W_trench, the better the comprehensive performance of the fiber. However, W_trench is limited by the diameter of the cladding layer to a maximum of 5.5 um.

When the W_trench is 5.5 um, the influence of the L_trench on the A_eff and PI of the fiber under the condition of a 1.5 cm bending radius is shown in Figure 10. From Figure 10a, it can be seen that the A_eff of HE₁₁ drops rapidly at 53.9 um, and the A_eff of HE₂₁ slightly rises. When the L_trench exceeds 53.8 um, the trench will exceed the cladding and the structure will be disordered, resulting in a sudden change in the curve. It can be seen from Figure 10b that with the increase of L_trench, the PI of HE₁₁ first drops and then rises rapidly, with a minimum value at 53.8 um, while the PI of HE₂₁ is relatively stable. So, at 53.8 um, the fiber has the best comprehensive performance.

When L_trench is 53.8 um, the influence of Δn₁ on N_eff and PI is shown in Figure 11. Figure 11a shows that with the increase of Δn₁, A_eff of the two modes firstly decreases, then increases, and finally stabilizes. In Figure 11b, the PI of the fiber decreases with the increase of Δn₁. This indicates that the larger the Δn₁, the better the comprehensive performance of the fiber. Due to the limitation of the manufacturing process, Δn₁ cannot be too large, and is usually set to 0.004.

In summary, the final optimized parameters are as follows: Λ = 14.5 um, d = 33 um, Δn = 0.0031, d_center = 4.8 um, Δn_center = 0.002, W_trench = 5.5um, L_trench = 53.8 um, Δn₁ = 0.004.

6. Conclusions

A dual-mode TA-LBL-LMFA MCF with air hole structure is investigated in this paper. By removing the core on both sides of the traditional 19-core fiber, the fiber can destroy the circular symmetry structure of traditional 19-core fiber and cut off the high-order modes TE₀₁ and TM₀₁ with circular symmetry. Adding a circle of air holes at the periphery of the core area can confine the mode field in the core area effectively. Also, adding a trench that is lower than the refractive index of the cladding at the periphery of the air hole can effectively reduce the BL. The introduction of 10 cores into the silica region between the 19 cores increases the lateral coupling in the core area and increases the mode field area. In this way, a large mode field dual-mode transmission with low bending loss is realized. Λ = 14.5 um, d = 33 um, Δn = 0.0031, d_center = 4.8 um, Δn_center = 0.002, W_trench = 5.5 um, L_trench = 53.8 um, and Δn₁ = 0.004 are the optimized parameters. At this time, the A_eff of the optical fiber HE₁₁ can reach 2003.24 um². When the bending radius R is 1 cm, the bending loss BL is 2.57 × 10⁻³ dB/m. Potential applications are anticipated in the transmission of large-capacity optical communication systems and high-power lasers.