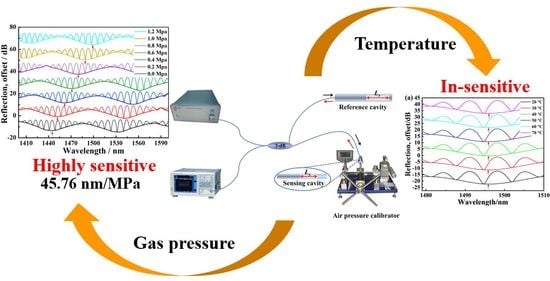
High Sensitivity Fiber Gas Pressure Sensor with Two Separated Fabry–Pérot Interferometers Based on the Vernier Effect
Abstract
:1. Introduction
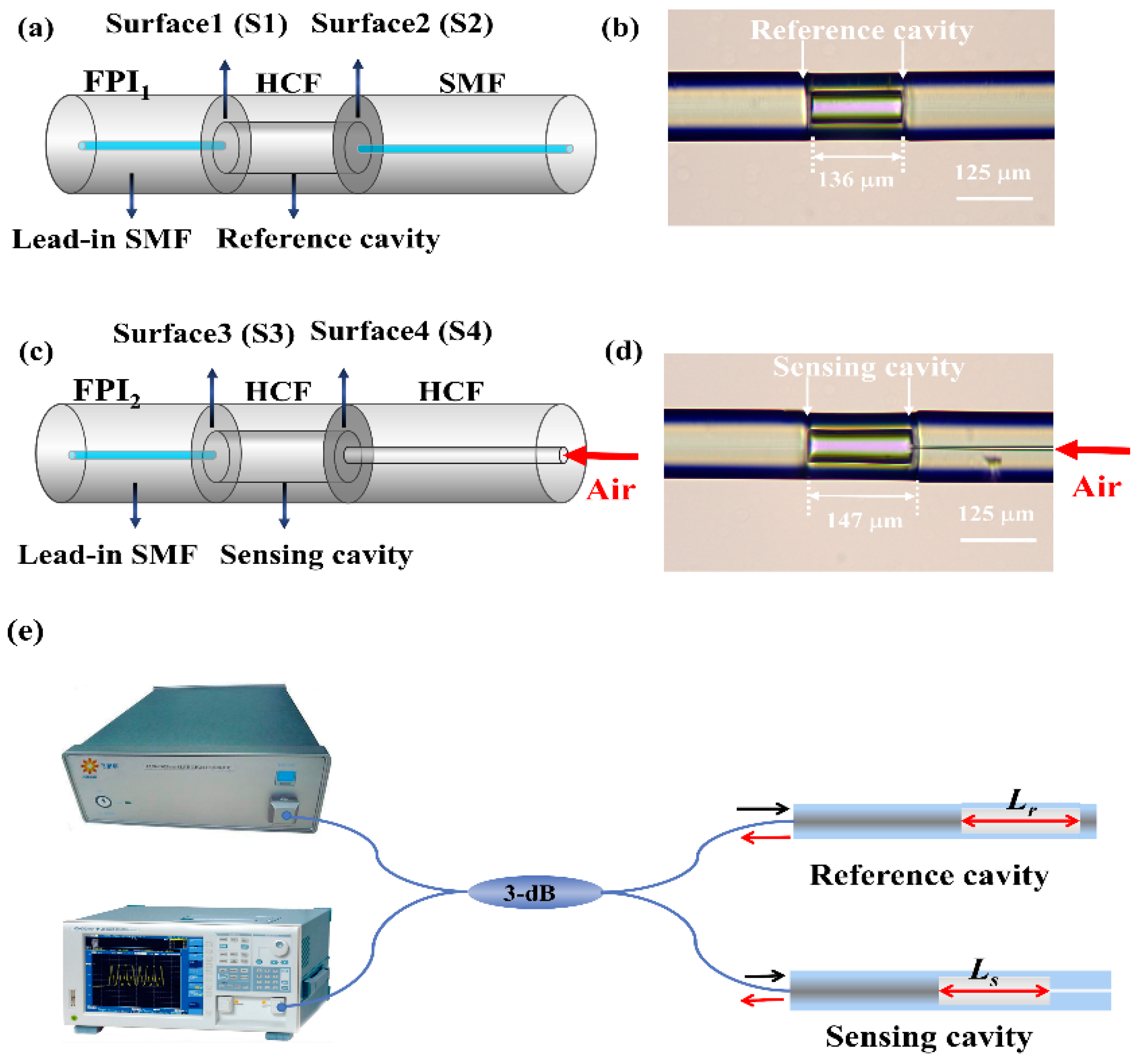
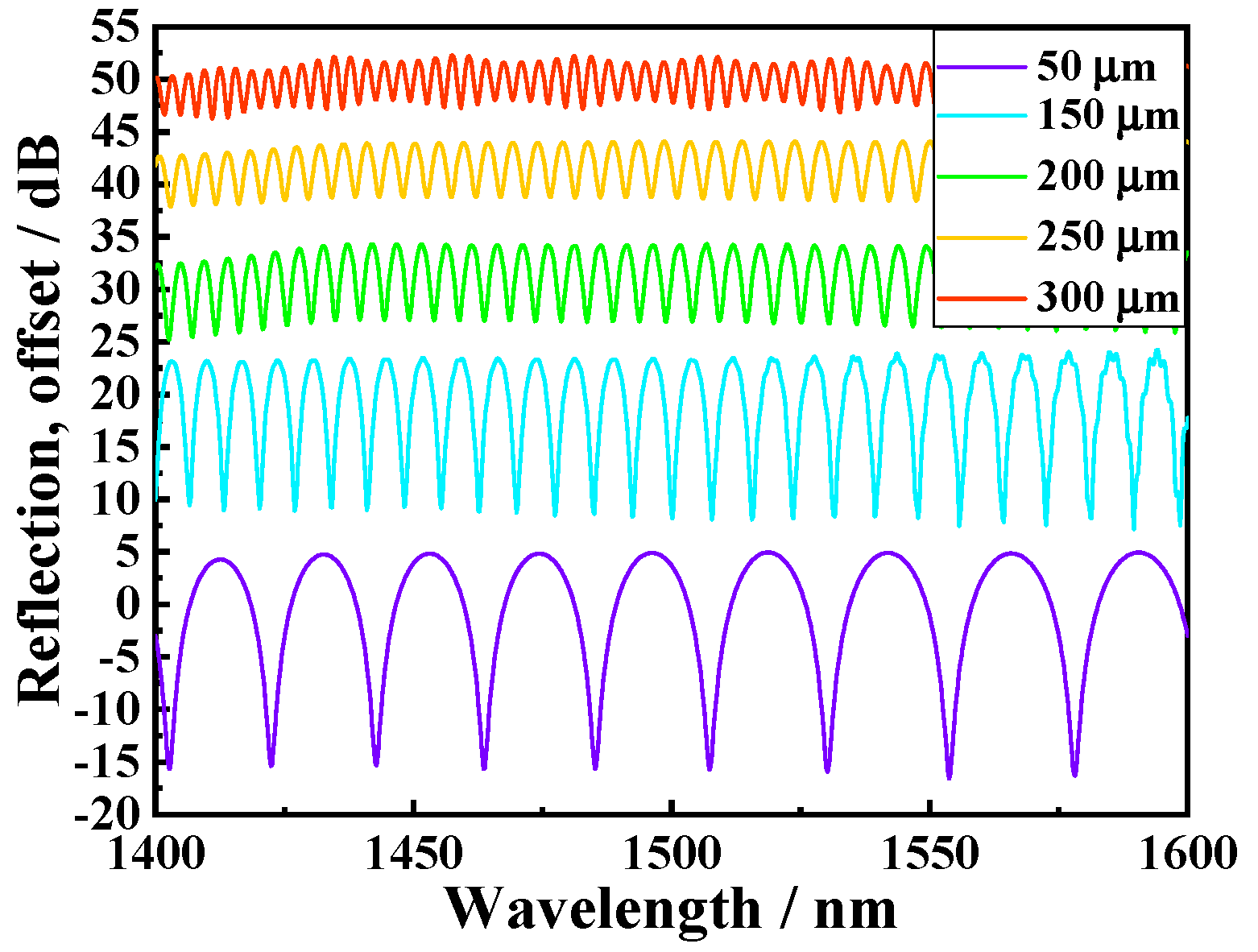
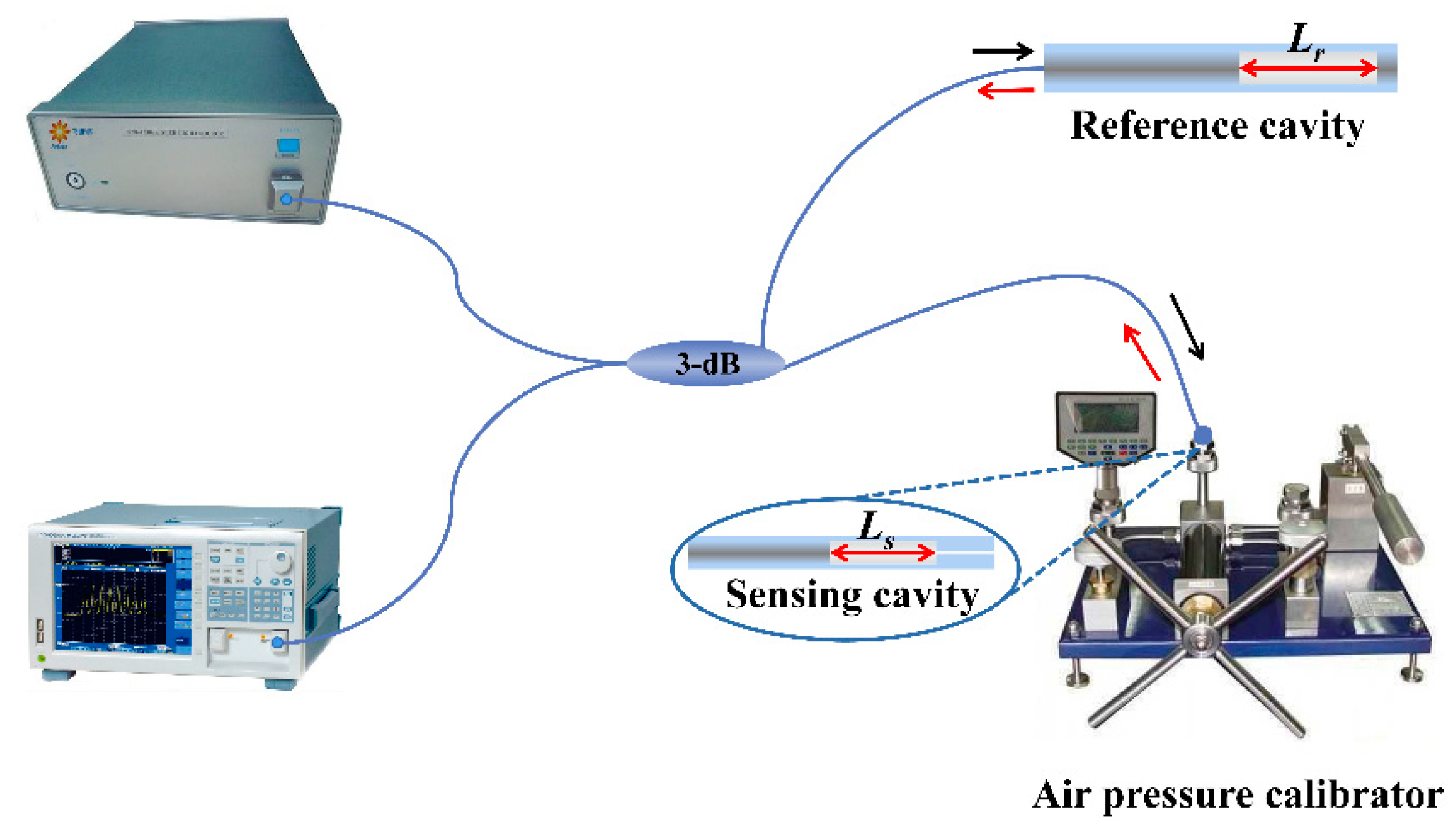
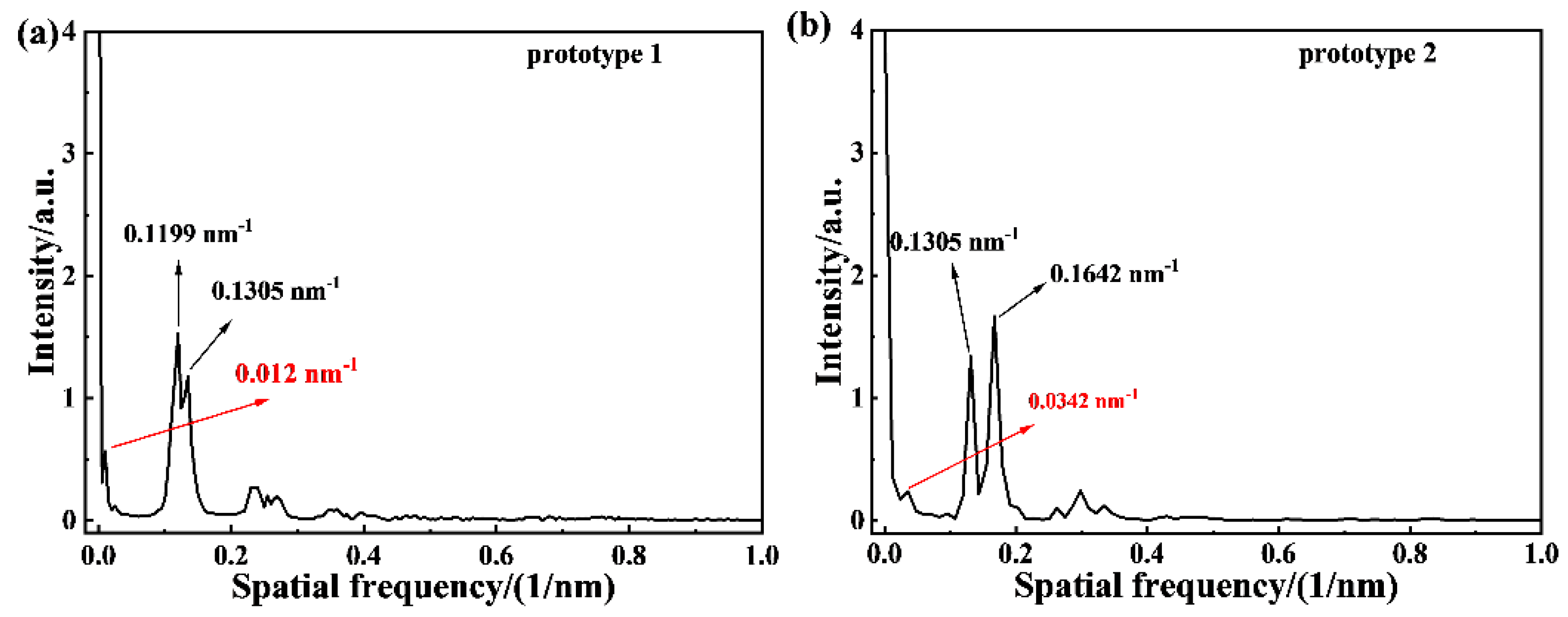
2. Fabrication and Principle
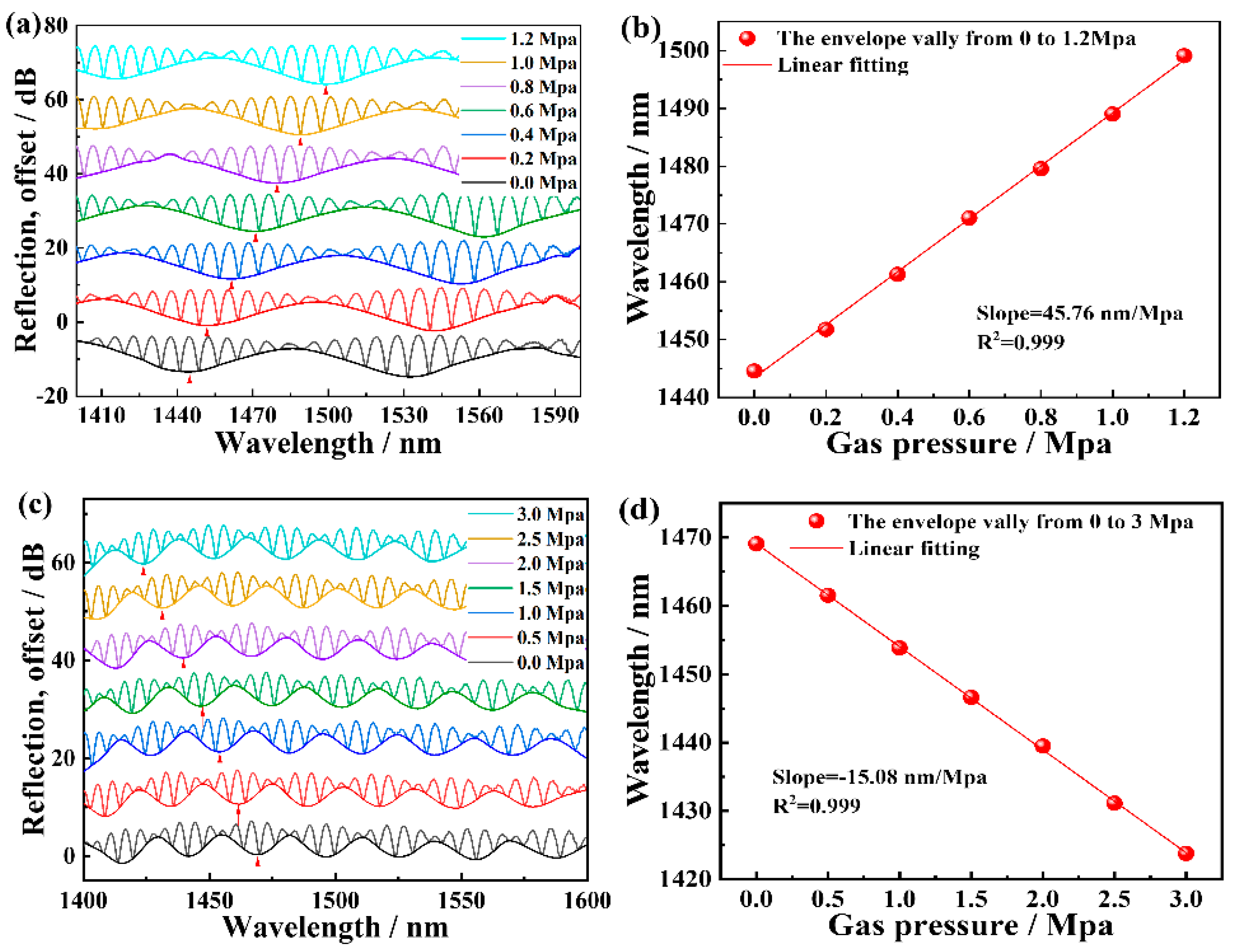
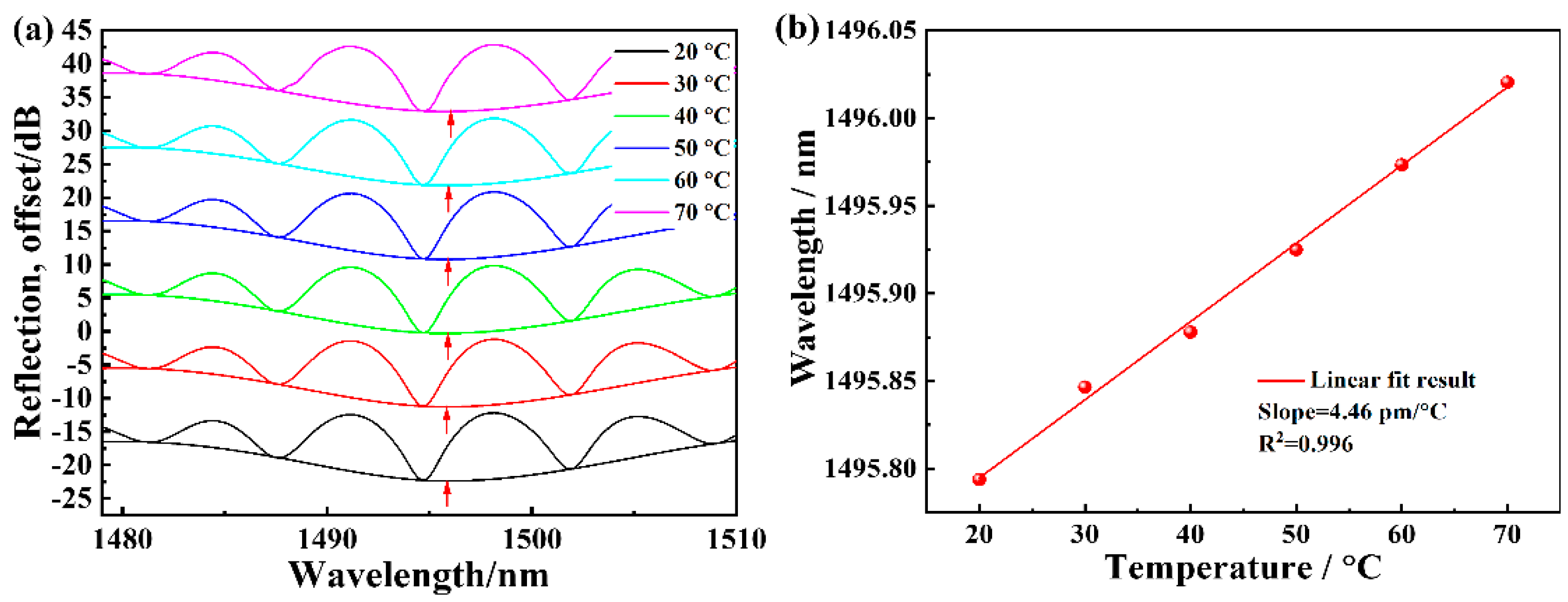
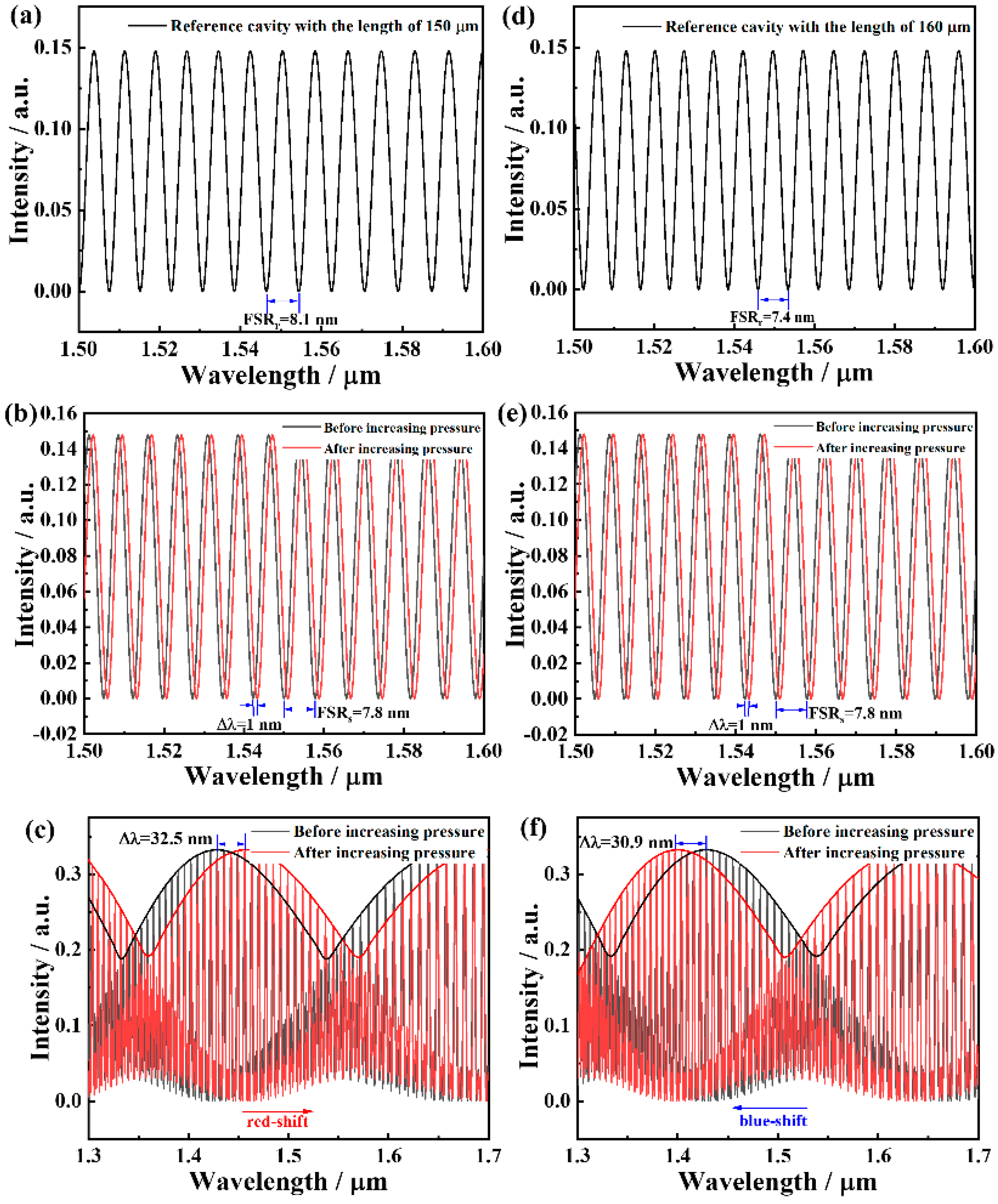
3. Experimental Results
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, C.; Fu, H.Y.; Qureshi, K.K.; Guan, B.O.; Tam, H.Y. High-pressure and high-temperature characteristics of a Fabry-Perot interferometer based on photonic crystal fiber. Opt. Lett. 2011, 36, 412–414. [Google Scholar] [CrossRef] [Green Version]
- Dong, Q.; Bae, H.; Zhang, Z.; Chen, Y.; Wen, Z.; Olson, D.A.; Yu, M.; Liu, H. Miniature Fiber Optic Acoustic Pressure Sensors with Air-Backed Graphene Diaphragms. J. Vib. Acoust. 2019, 141, 041003. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Chen, M.Q.; Xia, F.R.; Lv, Q. Small in-fiber Fabry-Perot low-frequency acoustic pressure sensor with PDMS diaphragm embedded in hollow-core fiber. Sens. Actuators A 2018, 270, 162–169. [Google Scholar] [CrossRef]
- Gu, Z.; Xu, Y.; Gao, K. Optical fiber long-period grating with solgel coating for gas sensor. Opt. Lett. 2006, 31, 2405–2407. [Google Scholar] [CrossRef] [PubMed]
- Jian, T.; Yin, G.; Shen, L. CO2 laser writing of long period fiber grating in air-core photonic bandgap fiber as gas pressure sensor. In Proceedings of the 2015 Optoelectronics Global Conference (OGC), Shenzhen, China, 29–31 August 2015. [Google Scholar]
- Stephens, A.F.; Busch, A.; Salamonsen, R.F.; Gregory, S.D.; Tansley, G.D. A novel fibre Bragg grating pressure sensor for rotary ventricular assist devices. Sens. Actuators A 2019, 295, 474–482. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, Z.D.; Wen, X.Y.; Zhang, D.S. A diaphragm-type fiber Bragg grating pressure sensor with temperature compensation. Measurement 2013, 46, 1041–1046. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, S.; Meng, F.Y.; Song, Y.M.; Zhu, L.Q. Compact Mach-Zehnder interferometer based on processed hollow-core fiber for gas pressure sensing. J. Nano-Photonics 2019, 13, 036013. [Google Scholar] [CrossRef]
- Li, Z.Y.; Liao, C.R.; Wang, Y.P.; Lu, L.; Wang, D.N.; Dong, X.P.; Liu, S.; Wang, Q.; Yang, K.M.; Zhou, J.T. Highly-sensitive gas pressure sensor using twin-core fiber based in-line Mach-Zehnder interferometer. Opt. Express 2015, 23, 6673–6678. [Google Scholar] [CrossRef]
- Silva, S.; Coelho, L.; Frazão, O. An all-fiber Fabry-Pérot interferometer for pressure sensing in different gaseous environments. Measurement 2014, 47, 418–421. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, Q.; Peng, W. Fiber-optic Fabry-Perot pressure sensor for down-hole application. Opt. Lasers Eng. 2019, 121, 289–299. [Google Scholar] [CrossRef]
- Xu, B.; Wang, C.; Wang, D.N.; Liu, Y.M.; Li, Y. Fiber-tip gas pressure sensor based on dual capillaries. Opt. Express 2015, 23, 23484–23492. [Google Scholar] [CrossRef]
- Gao, H.C.; Jiang, Y.; Zhang, L.C.; Yi, C.; Jiang, Y.; Jia, J.S.; Liang, J. Anti-resonant mechanism based self-temperature-calibrated fiber optic Fabry-Perot gas pressure sensors. Opt. Express 2019, 27, 22181–22189. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Yin, G.L.; Liao, C.R.; Liu, S.; Li, Z.Y.; Zhong, X.Y.; Wang, Q.; Zhao, J.; Yang, K.M.; Wang, Y.P. High-sensitivity gas pressure Sensor based on Fabry-Pérot interferometer with a side-opened channel in hollow-core photonic bandgap fiber. IEEE Photonics J. 2015, 7, 6803307. [Google Scholar] [CrossRef]
- Hou, M.X.; Zhu, F.; Wang, Y.; Wang, Y.P.; Liao, C.R.; Liu, S.; Lu, P.X. Anti-resonant reflecting guidance mechanism in hollow-core fiber for gas pressure sensing. Opt. Express 2016, 24, 27890–27898. [Google Scholar] [CrossRef] [Green Version]
- Xiao, G.Z.; Adnet, A.; Zhang, Z.Y.; Lu, Z.G.; Grover, C.P. Fiber optic Fabry-Perot interferometer gas pressure sensors embedded in pressure fittings. Microw. Opt. Technol. Lett. 2004, 42, 486–489. [Google Scholar] [CrossRef]
- Zhao, C.L.; Hou, L.Y.; Kang, J.; Mao, B.N.; Shen, C.Y. High-sensitivity hydraulic pressure sensor based on Fabry-Perot interferometer filled with polydimethylsiloxane film. Rev. Sci. Instrum. 2019, 90, 095002. [Google Scholar] [CrossRef]
- Liao, C.R.; Liu, S.; Xu, L.; Wang, C.; Wang, Y.P.; Li, Z.Y.; Wang, Q.; Wang, D.N. Sub-micron silica diaphragm-based fiber-tip Fabry-Perot interferometer for pressure measurement. Opt. Lett. 2014, 39, 2827–2830. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cui, Q.; Thakur, P.; Rablau, C.; Avrutsky, L. Miniature optical fiber pressure sensor with exfoliated graphene diaphragm. IEEE Sens. J. 2019, 19, 5621–5631. [Google Scholar] [CrossRef]
- Wang, J.; Li, L.; Liu, S.; Wu, D.; Wang, W.; Song, M.; Wang, G.; Huang, M. Investigation of composite structure with dual Fabry–Perot cavities for temperature and pressure sensing. Photonics 2021, 8, 138. [Google Scholar] [CrossRef]
- Lin, H.F.; Liu, F.F.; Guo, H.Y.; Zhou, A.; Dai, Y.T. Ultra-highly sensitive gas pressure sensor based on dual side-hole fiber interferometers with Vernier effect. Opt. Express 2018, 26, 28763–28772. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.X.; Zhang, W.G.; Kong, L.X.; Yan, T.Y.; Geng, P.C.; Wang, B. High-sensitivity gas pressure Fabry–Perot fiber probe with micro-channel based on Vernier Effect. J. Lightwave Technol. 2019, 37, 3444–3451. [Google Scholar] [CrossRef]
- Zhou, P.; Liao, C.R.; Li, Z.Y.; Liu, S.; Wang, Y.P. In-fiber cascaded F-P interferometer fabricated by chemical-assisted femtosecond laser micromachining for micro-fluidic sensing. J. Lightwave Technol. 2019, 37, 3214–3221. [Google Scholar] [CrossRef]
- Nan, T.; Liu, B.; Wu, Y.F.; Wang, J.F.; Mao, Y.Y.; Zhao, L.L.; Sun, T.T.; Wang, J. Ultrasensitive strain sensor based on Vernier-effect improved parallel structured fiber-optic Fabry-Perot interferometer. Opt. Express 2019, 27, 17239–17250. [Google Scholar] [CrossRef] [PubMed]
- Liao, H.; Lu, P.; Fu, X.; Jiang, X.Y.; Ni, W.J.; Liu, D.M.; Zhang, J.S. Sensitivity amplification of fiber-optic in-line Mach–Zehnder interferometer sensors with modified Vernier-effect. Opt. Express 2017, 25, 26898–26909. [Google Scholar] [CrossRef]
- Bhardwaj, V.; Singh, V.K. Fabrication and characterization of cascaded tapered Mach-Zehnder interferometer for refractive index sensing. Sens. Actuators A-Phys. 2016, 244, 30–34. [Google Scholar] [CrossRef]
- Yang, Y.Q.; Wang, Y.G.; Zhao, Y.X.; Jiang, J.X.; He, X.J.; Yang, W.L.; Zhu, Z.H.; Gao, W.; Li, L.J. Sensitivity-enhanced temperature sensor by hybrid cascaded configuration of a Sagnac loop and a F-P cavity. Opt. Express 2017, 25, 33290–33296. [Google Scholar] [CrossRef]
- Wu, B.; Zhao, C.; Xu, B.; Li, Y. Optical fiber hydrogen sensor with single Sagnac interferometer loop based on vernier effect. Sens. Actuators B Chem. 2018, 255, 3011–3016. [Google Scholar] [CrossRef]
- Seyfari, A.K.; Bahadoran, M.; Honarasa, G. Design of micro-optical pressure sensor using cascaded ring resonator. In Proceedings of the Iranian Nano Photonic Conference, Terhran, Iran, 22 March 2021. [Google Scholar]
- Lin, H.F.; Liu, F.F.; Dai, Y.T.; Zhou, A. Cascaded fiber Mach–Zehnder interferometers for sensitivity-enhanced gas pressure measurement. IEEE Sens. J. 2019, 19, 2581–2586. [Google Scholar] [CrossRef]
- Chen, P.; Dai, Y.T.; Zhang, D.S.; Wen, X.Y.; Yang, M.H. Cascaded-cavity Fabry-Perot interferometric gas pressure sensor based on Vernier Effect. Sensors 2018, 18, 3677. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.S.; Ye, W.H.; Jiang, C.; Sun, S.M. High sensitivity gas pressure sensor based on two parallel-connected Fabry–Perot interferometers and Vernier effect. Meas. Sci. Technol. 2021, 32, 125124. [Google Scholar] [CrossRef]
- He, H.Y.; Liu, Y.; Liao, Y.Y.; Lang, C.P.; Li, Y.; Qu, S.L. Simple fiber-optic sensor for simultaneous and sensitive measurement of high pressure and high temperature based on the silica capillary tube. Opt. Express 2019, 27, 25777–25788. [Google Scholar] [CrossRef]
- Fu, X.H.; Liu, L.X.; Huang, S.M.; Fu, G.W.; Jin, W.; Bi, W.H. Simultaneous measurement of temperature and refractive index with F–P microcavity sensor based on graded-index few mode fiber. Opt. Commun. 2020, 455, 124577. [Google Scholar] [CrossRef]
- Birch, K.P.; Downs, M.J. An Updated Edlén Equation for the Refractive Index of Air. Metrologia 1993, 30, 155–162. [Google Scholar] [CrossRef]
- Wei, X.Y.; Song, X.K.; Li, C.; Hou, L.T.; Li, Z.J.; Li, Y.; Ran, L.L. Optical fiber gas pressure sensor based on Polydimethylsiloxane microcavity. J. Lightwave Technol. 2021, 39, 2988–2993. [Google Scholar] [CrossRef]
- Hou, L.T.; Zhang, X.D.; Yang, J.R.; Kang, J.; Ran, L.L. Simultaneous measurement of refractive index and temperature based on half-tapered SMS fiber structure with fringe-visibility difference demodulation method. Opt. Commun. 2019, 433, 252–255. [Google Scholar] [CrossRef]
- Qi, Y.F.; Cong, B.T.; Liu, Z.M.; Gong, C.B.; Li, F.K.; Hu, T.N.; Liu, Y.Y. All-fiber sensitivity-enhanced pressure sensor based on Sagnac and F-P interferometer. Optik 2021, 243, 167359. [Google Scholar] [CrossRef]
- Pan, R.; Yang, W.L.; Li, L.J.; Yang, Y.Q.; Yu, X.Y.; Fan, J.Y.; Yu, S.; Xiong, Y.L.; Zhang, L.J. High-sensitive fiber-optic pressure sensor based on Fabry-Perot interferometer filled with ultraviolet glue film and Vernier effect. Opt. Fiber Technol. 2021, 69, 102710. [Google Scholar] [CrossRef]


| Structures | Sensitivity | Temperature Crosstalk | Linear Response Range | Fabrication | Refs. |
|---|---|---|---|---|---|
| Side-opened channel structure Anti-resonant | 4.24 nm/MPa | - | 0–2 MPa | Fs | [14] |
| Reflecting guidance with single-HCF | 3.59 nm/MPa | 7.5 KPa/°C | 0–2 MPa | Fs | [15] |
| Single-FPI with sub-micron silica diaphragm | 1.036 nm/MPa | 0.96 KPa/°C | 0–2 MPa | Coating | [18] |
| Dual FP cavities with composite diaphragm | 30.2 nm/MPa | - | 0–0.4 MPa | Coating | [20] |
| Cascaded MZIs with a micro-machined air cavity in SMS * | 82.131 nm/MPa | 0.647 KPa/°C | 0–0.7 Mpa | Fs | [30] |
| Cascaded FPIs in a glass capillary tube * | 86.64 nm/MPa | 5.18 KPa/°C | 0–0.6 MPa | Fs | [31] |
| Parallel-connected FPIs with gas hole * | 47.76 nm/MPa | 5.1 KPa/°C | 0–0.45 MPa | Fs | [32] |
| Separated structures using SI and FPI with a silver film * | 31.73 nm/MPa | - | 0–1.6 MPa | Coating | [38] |
| Paralleled FPIs with a thin layer of UV glue * | −38.3 nm/MPa | - | 0.1–0.7 MPa | Coating | [39] |
| Paralleled FPIs with HCF * | 45.76 nm/MPa | 0.097 KPa/°C | 0–3 MPa | Arc discharge | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Hou, L.; Wei, X.; Su, H.; Li, C.; Li, Y.; Ran, L. High Sensitivity Fiber Gas Pressure Sensor with Two Separated Fabry–Pérot Interferometers Based on the Vernier Effect. Photonics 2022, 9, 31. https://doi.org/10.3390/photonics9010031
Song X, Hou L, Wei X, Su H, Li C, Li Y, Ran L. High Sensitivity Fiber Gas Pressure Sensor with Two Separated Fabry–Pérot Interferometers Based on the Vernier Effect. Photonics. 2022; 9(1):31. https://doi.org/10.3390/photonics9010031
Chicago/Turabian StyleSong, Xiaokang, Liangtao Hou, Xiangyu Wei, Hang Su, Chang Li, Yan Li, and Lingling Ran. 2022. "High Sensitivity Fiber Gas Pressure Sensor with Two Separated Fabry–Pérot Interferometers Based on the Vernier Effect" Photonics 9, no. 1: 31. https://doi.org/10.3390/photonics9010031
APA StyleSong, X., Hou, L., Wei, X., Su, H., Li, C., Li, Y., & Ran, L. (2022). High Sensitivity Fiber Gas Pressure Sensor with Two Separated Fabry–Pérot Interferometers Based on the Vernier Effect. Photonics, 9(1), 31. https://doi.org/10.3390/photonics9010031