Electro-Optic Modulation of Higher-Order Poincaré Beam Based on Nonlinear Optical Crystal
Abstract
:1. Introduction
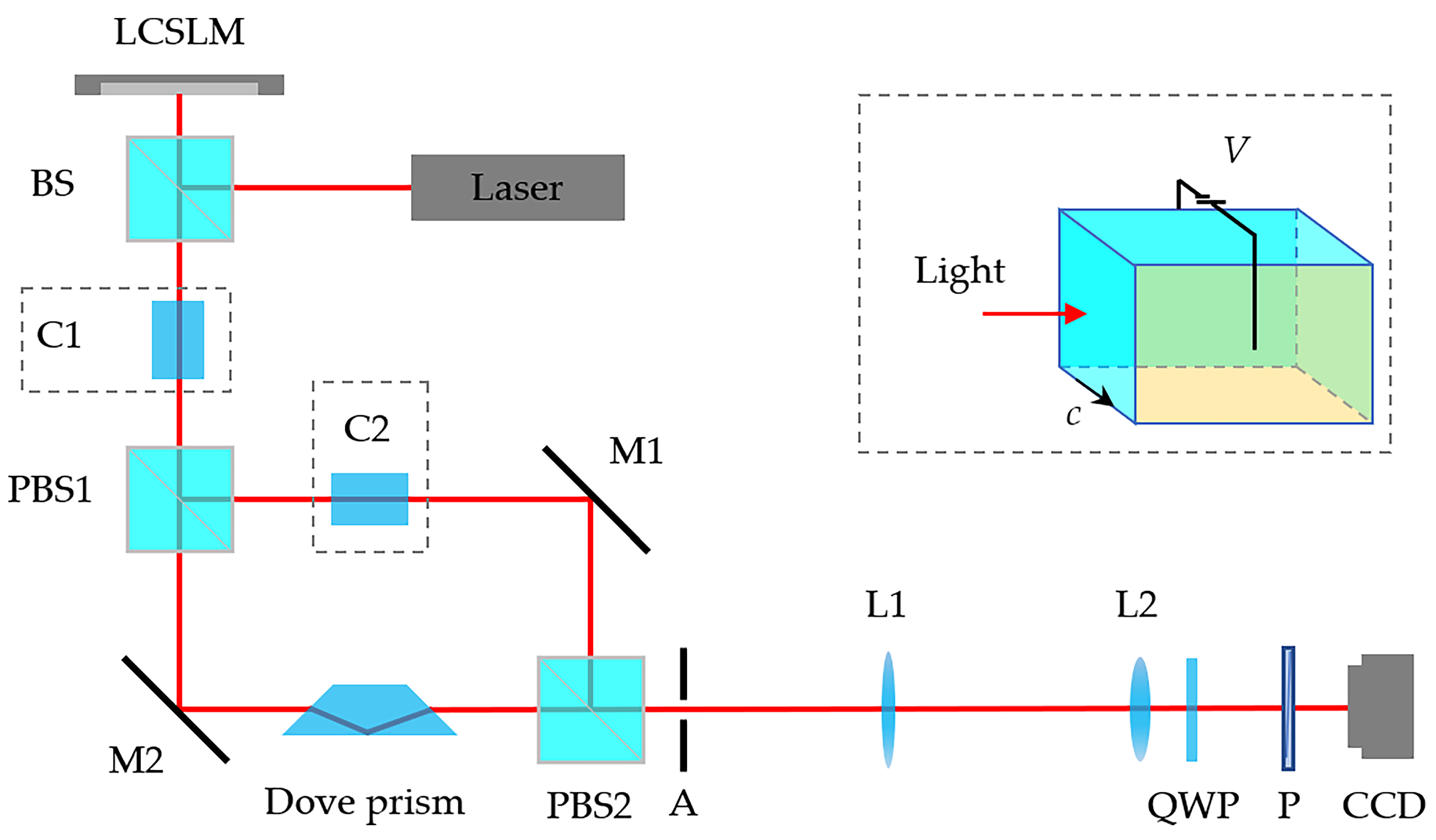
2. Method and Experimental Setup
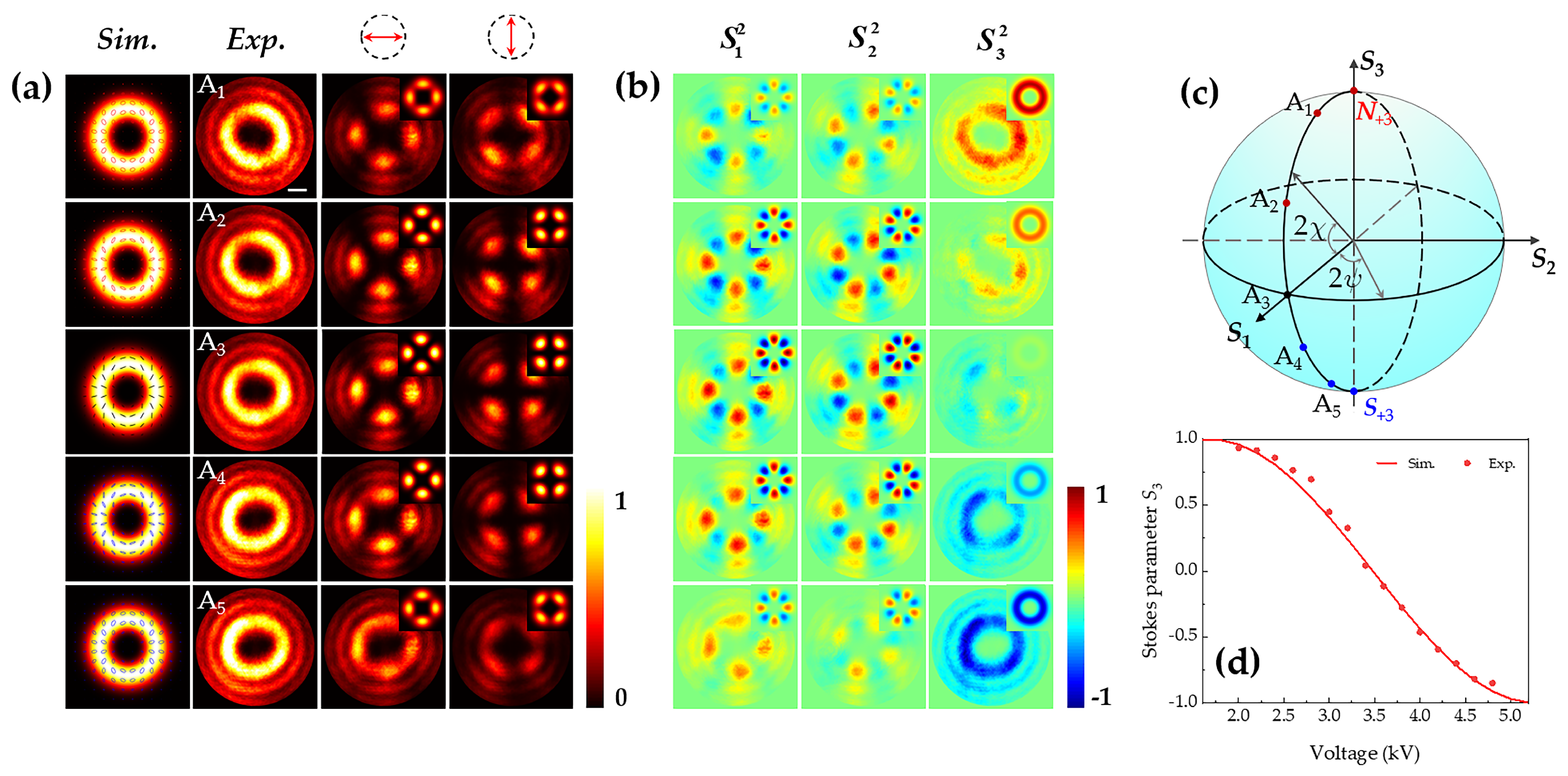
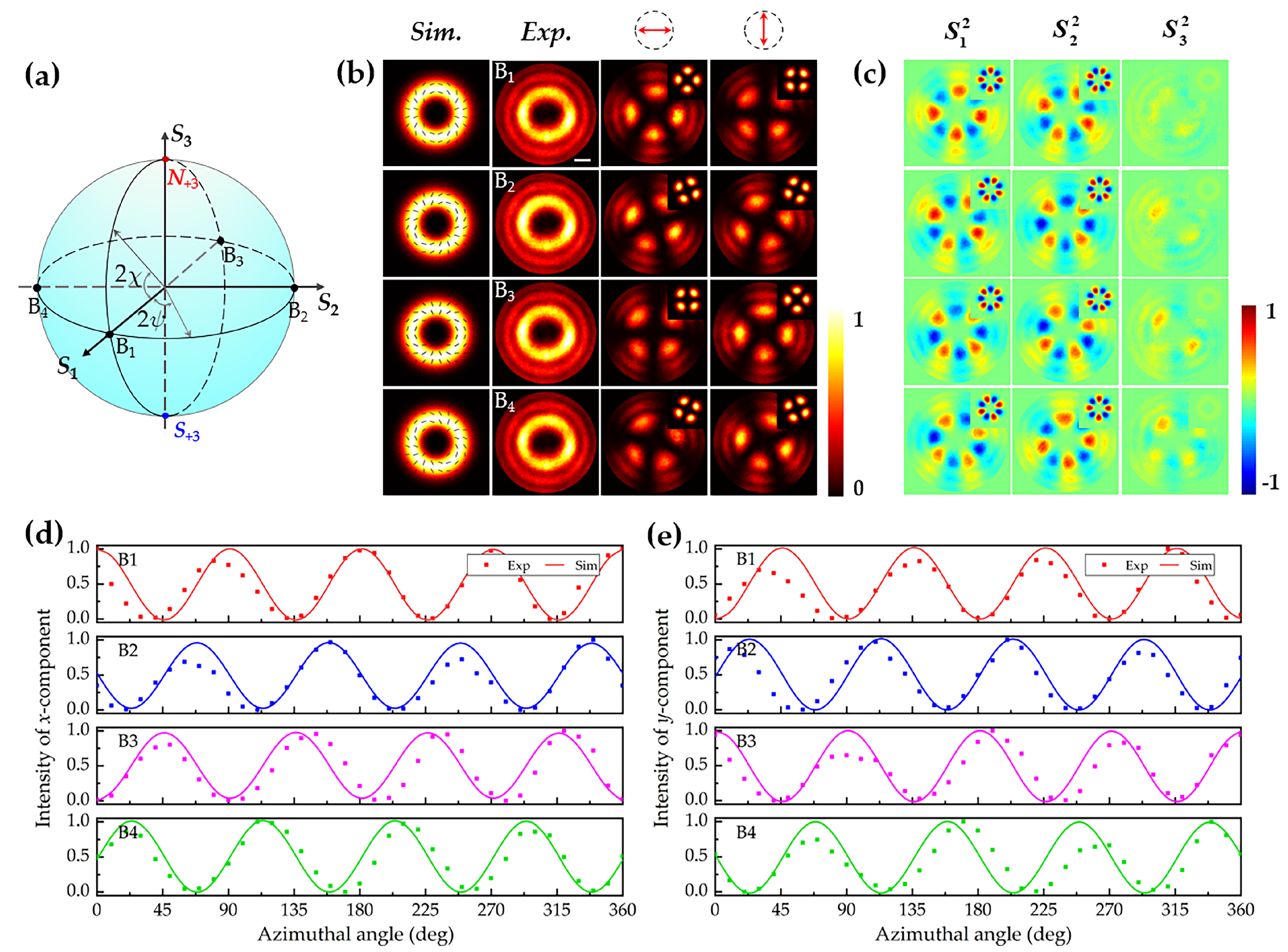
3. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photon. 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Chen, J.; Wan, C.; Zhan, Q. Vectorial optical fields: Recent advances and future prospects. Sci. Bull. 2018, 63, 54–74. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Du, L.; Xin, Z.; Si, G.; Yang, A.; Lei, T.; Lin, J.; Yuan, X. Polarization-to-phase coupling at a structured surface for plasmonic structured illumination microscopy. Laser Photon. Rev. 2018, 12, 1800148. [Google Scholar] [CrossRef]
- Yoshida, M.; Kozawa, Y.; Sato, S. Subtraction imaging by the combination of higher-order vector beams for enhanced spatial resolution. Opt. Lett. 2019, 44, 883–886. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wan, C.; Chong, A.; Zhan, Q. Subwavelength focusing of a spatio-temporal wave packet with transverse orbital angular momentum. Opt. Express 2020, 28, 18472–18478. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J.; Bai, C.; Zhang, D.; Zhan, Q. Dynamical generation of multiple focal spot pairs with controllable position and polarization. Opt. Express 2020, 28, 26706–26716. [Google Scholar] [CrossRef]
- Salakhutdinov, V.; Sondermann, M.; Carbone, L.; Giacobino, E.; Bramati, A.; Leuchs, G. Optical trapping of nanoparticles by full solid-angle focusing. Optica 2016, 3, 1181–1186. [Google Scholar] [CrossRef]
- Kozawa, Y.; Sato, S. Optical trapping of micrometer-sized dielectric particles by cylindrical vector beams. Opt. Express 2010, 18, 10828–10833. [Google Scholar] [CrossRef] [PubMed]
- Drevinskas, R.; Zhang, J.; Beresna, M.; Gecevičius, M.; Kazanskii, A.G.; Svirko, Y.P.; Kazansky, P.G. Laser material processing with tightly focused cylindrical vector beams. Appl. Phys. Lett. 2016, 108, 221107. [Google Scholar] [CrossRef] [Green Version]
- Xian, M.; Xu, Y.; Ouyang, X.; Cao, Y.; Lan, S.; Li, X. Segmented cylindrical vector beams for massively-encoded optical data storage. Sci. Bull. 2020, 65, 2072–2079. [Google Scholar] [CrossRef]
- Wang, C.; Yang, B.; Cheng, M.; Cheng, S.; Liu, J.; Xiao, J.; Ye, H.; Li, Y.; Fan, D.; Chen, S. Cylindrical vector beam multiplexing for radio-over-fiber communication with dielectric metasurfaces. Opt. Express 2020, 28, 38666–38681. [Google Scholar] [CrossRef]
- Lai, W.J.; Lim, B.C.; Phua, P.B.; Tiaw, K.S.; Teo, H.H.; Hong, M.H. Generation of radially polarized beam with a segmented spiral varying retarder. Opt. Express 2008, 16, 15694–15699. [Google Scholar] [CrossRef] [PubMed]
- Li, S.M.; Qian, S.X.; Kong, L.J.; Ren, Z.C.; Li, Y.; Tu, C.; Wang, H.T. An efficient and robust scheme for controlling the states of polarization in a Sagnac interferometric configuration. Europhys. Lett. 2014, 105, 64006. [Google Scholar] [CrossRef]
- Kozawa, Y.; Sato, S. Generation of a radially polarized laser beam by use of a conical Brewster prism. Opt. Lett. 2005, 30, 3063–3065. [Google Scholar] [CrossRef]
- Chen, P.; Ji, W.; Wei, B.Y.; Hu, W.; Chigrinov, V.; Lu, Y.Q. Generation of arbitrary vector beams with liquid crystal polarization converters and vector-photoaligned q-plates. Appl. Phys. Lett. 2015, 107, 241102. [Google Scholar] [CrossRef]
- Lou, S.; Zhou, Y.; Yuan, Y.; Lin, T.; Fan, F.; Wang, X.; Huang, H.; Wen, S. Generation of arbitrary vector vortex beams on hybrid-order Poincaré; sphere based on liquid crystal device. Opt. Express 2019, 27, 8596–8604. [Google Scholar] [CrossRef]
- Wang, D.; Liu, T.; Zhou, Y.; Zheng, X.; Sun, S.; He, Q.; Zhou, L. High-efficiency metadevices for bifunctional generations of vectorial optical fields. Nanophotonics 2021, 10, 685–695. [Google Scholar] [CrossRef]
- Milione, G.; Evans, S.; Nolan, D.A.; Alfano, R.R. Higher Order Pancharatnam-Berry Phase and the Angular Momentum of Light. Phys. Rev. Lett. 2012, 108, 190401. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Zhou, X.; Liu, Y.; Ling, X.; Luo, H.; Wen, S. Generation of arbitrary cylindrical vector beams on the higher order Poincaré sphere. Opt. Lett. 2014, 39, 5274–5276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, C.; Zhang, Y.; Ma, L.; Zhang, Y.; Li, Z.; Zhang, R.; Zeng, X.; Zhan, Z.; He, C.; Ren, X.; et al. Flexible generation of higher-order Poincaré beams with high efficiency by manipulating the two eigenstates of polarized optical vortices. Opt. Express 2020, 28, 10618–10632. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, Z.; Ding, J.; Wang, H.T. Single ultra-high-definition spatial light modulator enabling highly efficient generation of fully structured vector beams. Appl. Opt. 2019, 58, 6591–6596. [Google Scholar] [CrossRef] [PubMed]
- Mellado-Villaseñor, G.; Aguirre-Olivas, D.; Arrizón, V. Generation of vector beams using synthetic phase holograms. J. Opt. Soc. Am. A 2021, 38, 1094–1103. [Google Scholar] [CrossRef]
- Liu, S.; Qi, S.; Zhang, Y.; Li, P.; Wu, D.; Han, L.; Zhao, J. Highly efficient generation of arbitrary vector beams with tunable polarization, phase, and amplitude. Photon. Res. 2018, 6, 228–233. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, Y.; Han, L.; Yue, Q.; Guo, C. Generation of arbitrary vector beams based on a single spatial light modulator and a thin-film polarization splitting cubic. Chin. Opt. Lett. 2016, 14, 122601. [Google Scholar] [CrossRef]
- Holleczek, A.; Aiello, A.; Gabriel, C.; Marquardt, C.; Leuchs, G. Classical and quantum properties of cylindrically polarized states of light. Opt. Express 2011, 19, 9714–9736. [Google Scholar] [CrossRef] [Green Version]
- Milione, G.; Sztul, H.I.; Nolan, D.A.; Alfano, R.R. Higher-order Poincaré sphere, Stokes parameters, and the angular momentum of light. Phys. Rev. Lett. 2011, 107, 053601. [Google Scholar] [CrossRef] [PubMed]
- Nikogosyan, D. Nonlinear Optical Crystals: A Complete Survey; Springer: New York, NY, USA, 2006. [Google Scholar]
- Boyd, R. Nonlinear Optics; Elsevier Science: Hoboken, NJ, USA, 2020. [Google Scholar]
- Sun, Z.; Cui, Z.; Sun, M.; Yuan, Y.; Li, Q.; Liu, D.; Zhu, J. Electro-optic coefficient measurement of a K(H1−xDx)2PO4 crystal based on χ(2) nonlinear optical technology. Opt. Express 2021, 29, 2647–2657. [Google Scholar] [CrossRef]
- Goodman, J. Introduction to Fourier Optics; McGraw-Hill Physical and Quantum Electronics Series; W. H. Freeman: New York, NY, USA, 2005. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, L.; Li, Z.; Chen, C.; Sun, X.; Zhang, J.; Liu, D. Electro-Optic Modulation of Higher-Order Poincaré Beam Based on Nonlinear Optical Crystal. Photonics 2022, 9, 41. https://doi.org/10.3390/photonics9010041
Han L, Li Z, Chen C, Sun X, Zhang J, Liu D. Electro-Optic Modulation of Higher-Order Poincaré Beam Based on Nonlinear Optical Crystal. Photonics. 2022; 9(1):41. https://doi.org/10.3390/photonics9010041
Chicago/Turabian StyleHan, Lu, Zhan Li, Chao Chen, Xin Sun, Junyong Zhang, and Dean Liu. 2022. "Electro-Optic Modulation of Higher-Order Poincaré Beam Based on Nonlinear Optical Crystal" Photonics 9, no. 1: 41. https://doi.org/10.3390/photonics9010041




