Suppression of Pulse Intensity Dependent Dispersion during Nonlinear Spectral Broadening with Intermediate Compression for Passive CEP Stable Pulse Generation
Abstract
:1. Introduction
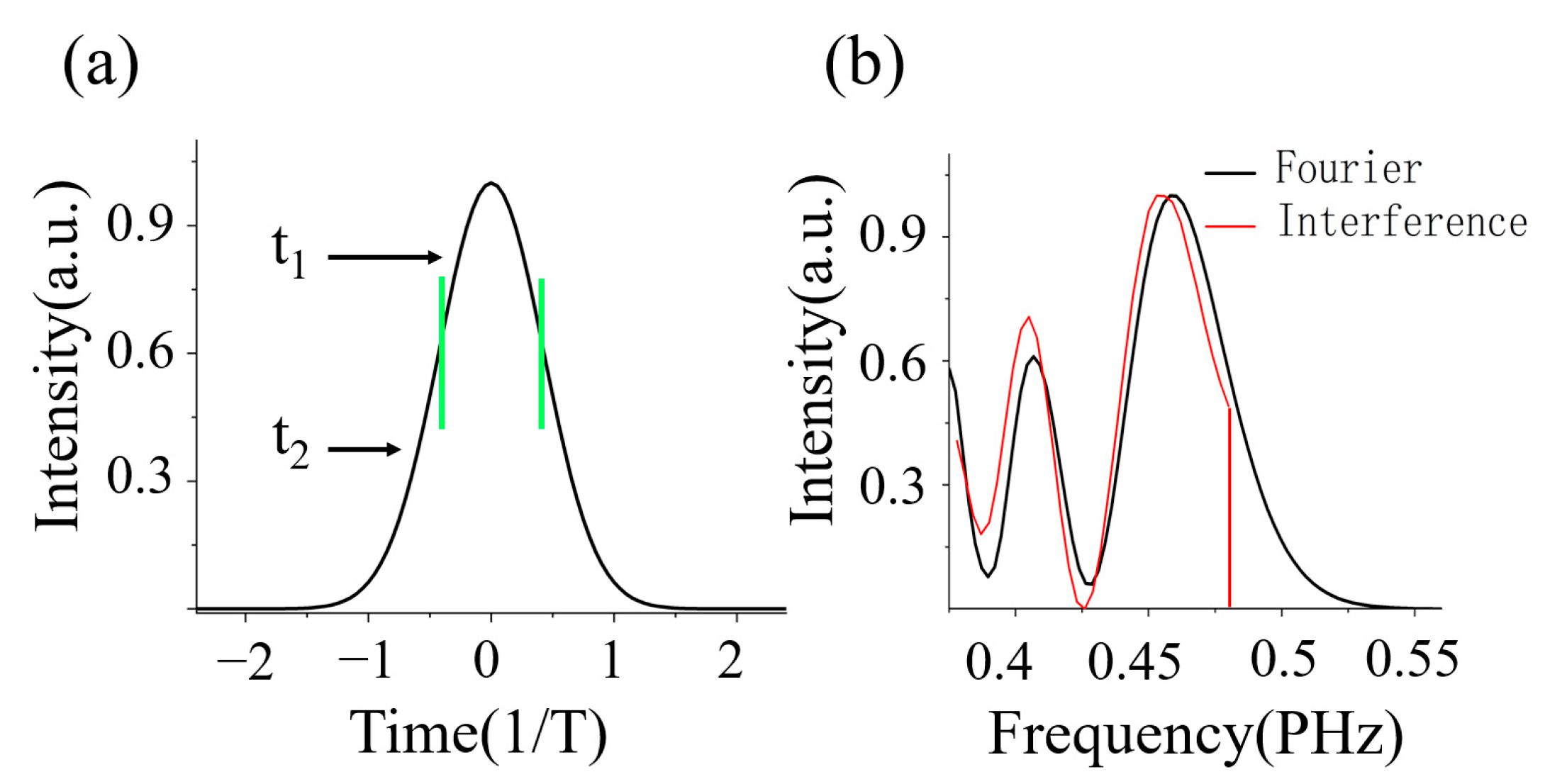
2. Theoretical Methods
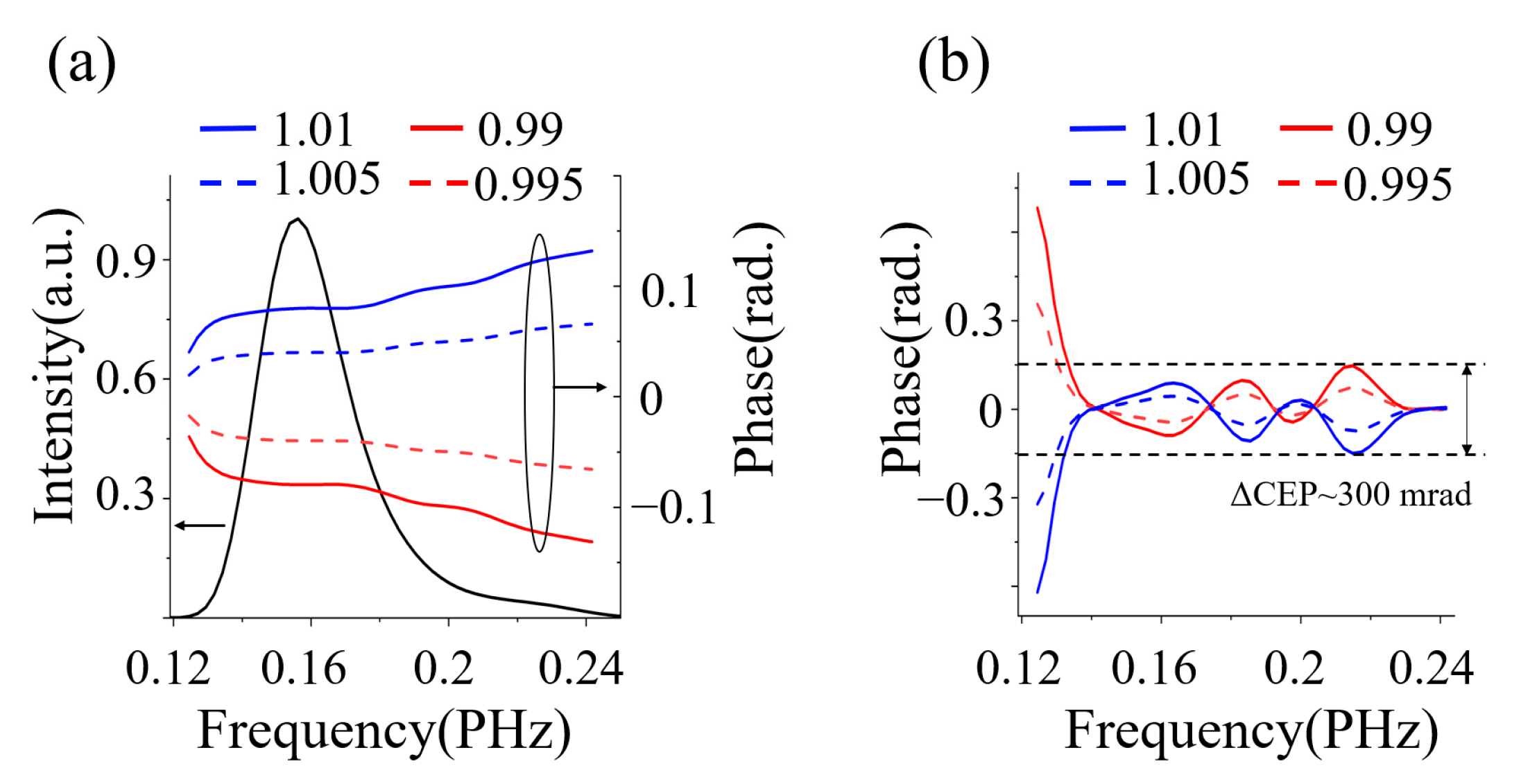
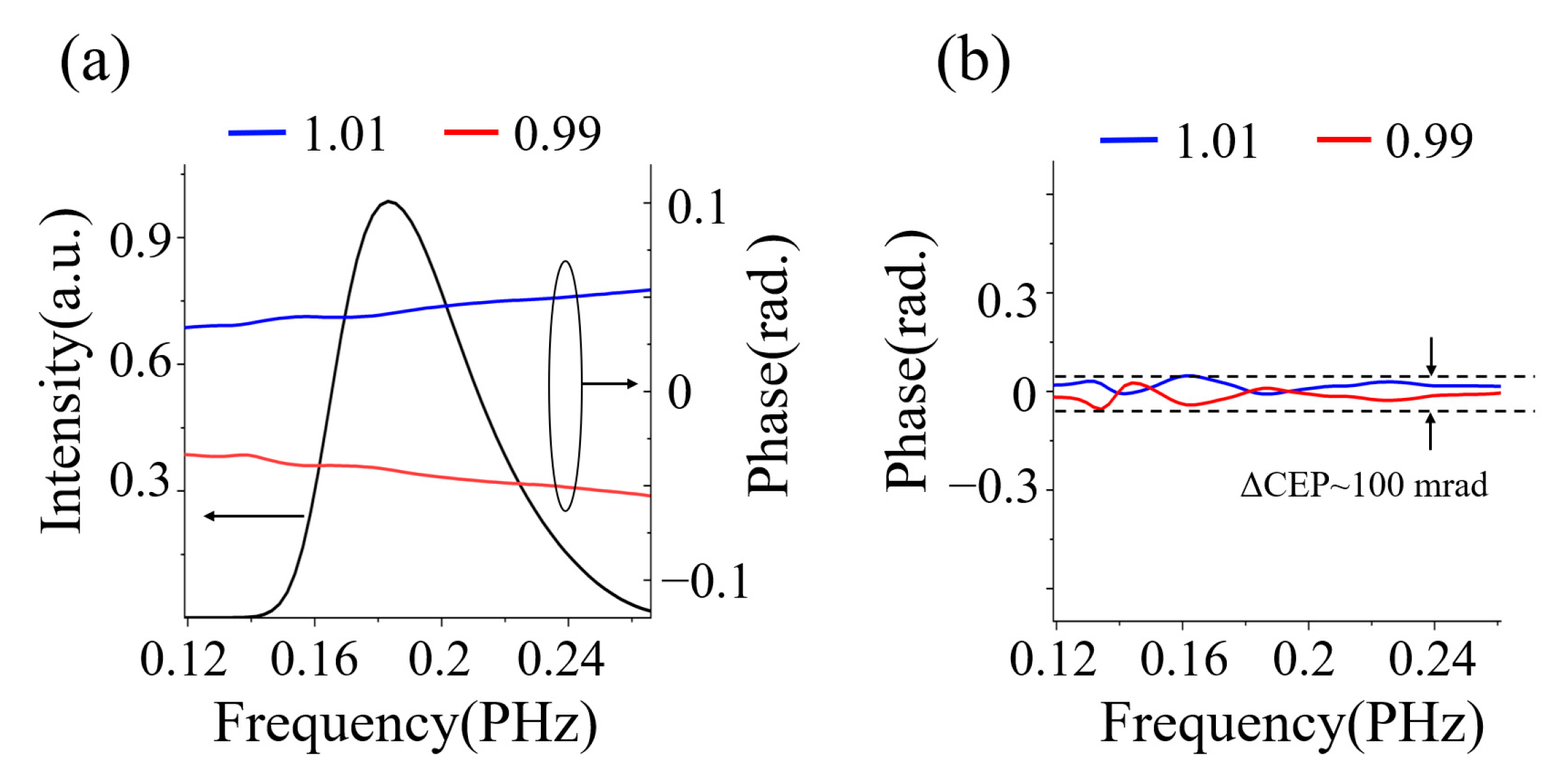
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kling, M.F.; Rauschenberger, J.; Verhoef, A.J.; Hasović, E.; Uphues, T.; Milošević, D.B.; Muller, H.G.; Vrakking, M.J.J. Imaging of carrier-envelope phase effects in above-threshold ionization with intense few-cycle laser fields. New J. Phys. 2008, 10, 025024. [Google Scholar] [CrossRef] [Green Version]
- Piglosiewicz, B.; Schmidt, S.; Park, D.J.; Vogelsang, J.; Grosz, P.; Manzoni, C.; Farinello, P.; Cerullo, G.; Lienau, C. Carrier-envelope phase effects on the strong-field photoemission of electrons from metallic nanostructures. Nat. Photonics 2014, 8, 37–42. [Google Scholar] [CrossRef] [Green Version]
- Rácz, P.; Irvine, S.; Lenner, M.; Mitrofanov, A.; Baltuška, A.; Elezzabi, A.; Dombi, P. Strong-field plasmonic electron acceleration with few-cycle, phase-stabilized laser pulses. Appl. Phys. Lett. 2011, 98, 111116. [Google Scholar] [CrossRef]
- Corkum, P.B.; Krausz, F. Attosecond science. Nat. Phys. 2007, 3, 381–387. [Google Scholar] [CrossRef]
- Xue, B.; Tamaru, Y.; Fu, Y.; Yuan, H.; Lan, P.; Mücke, O.D.; Suda, A.; Midorikawa, K.; Takahashi, E.J. A Custom-Tailored Multi-TW Optical Electric Field for Gigawatt Soft-X-ray Isolated Attosecond Pulses. Ultrafast Sci. 2021, 2021, 9828026. [Google Scholar] [CrossRef]
- Hoflund, M.; Peschel, J.; Plach, M.; Dacasa, H.; Veyrinas, K.; Constant, E.; Smorenburg, P.; Wikmark, H.; Maclot, S.; Guo, C.; et al. Focusing Properties of High-Order Harmonics. Ultrafast Sci. 2021, 2021, 9797453. [Google Scholar] [CrossRef]
- Manzoni, C.; Cerullo, G.; Silvestri, S.D. Ultrabroadband self-phase-stabilized pulses by difference-frequency generation. Opt. Lett. 2004, 29, 2668–2670. [Google Scholar] [CrossRef]
- Thiré, N.; Maksimenka, R.; Kiss, B.; Ferchaud, C.; Gitzinger, G.; Pinoteau, T.; Jousselin, H.; Jarosch, S.; Bizouard, P.; Pietro, V.D.; et al. Highly stable, 15 W, few-cycle, 65 mrad CEP-noise mid-IR OPCPA for statistical physics. Opt. Express 2018, 26, 26907–26915. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Li, J.; Ren, X.; Zhao, K.; Wu, Y.; Cunningham, E.; Chang, Z. High-efficiency optical parametric chirped-pulse amplifier in BiB3O6 for generation of 3 mJ, two-cycle, carrier-envelope-phase-stable pulses at 1.7 μm. Opt. Lett. 2016, 41, 1142–1145. [Google Scholar] [CrossRef] [PubMed]
- Ishii, N.; Xia, P.; Kanai, T.; Itatani, J. Optical parametric amplification of carrier-envelope phase-stabilized mid-infrared pulses generated by intra-pulse difference frequency generation. Opt. Express 2019, 27, 11447–11454. [Google Scholar] [CrossRef]
- Huang, H.; Hu, C.; He, H.; Teng, H.; Li, Z.; Zhao, K.; Wei, Z. Broadband mid-infrared pulse via intra-pulse difference frequency generation based on supercontinuum from multiple thin plates. Chin. Phys. B 2019, 28, 114203. [Google Scholar] [CrossRef]
- Kanda, N.; Ishii, N.; Itatani, J.; Matsunaga, R. Optical parametric amplification of phase-stable terahertz-to-mid-infrared pulses studied in the time domain. Opt. Express 2021, 29, 3479–3489. [Google Scholar] [CrossRef]
- Kaumanns, M.; Pervak, V.; Kormin, D.; Leshchenko, V.; Kessel, A.; Ueffing, M.; Chen, Y.; Nubbemeyer, T. Multipass spectral broadening of 18 mJ pulses compressible from 1.3 ps to 41 fs. Opt. Lett. 2018, 43, 5877–5880. [Google Scholar] [CrossRef]
- Viotti, A.; Seidel, M.; Escoto, E.; Rajhans, S.; Leemans, W.P.; Hartl, I.; Heyl, C.M. Multi-pass cells for post-compression of ultrashort laser pulses. Optica 2022, 9, 197–216. [Google Scholar] [CrossRef]
- Baltuška, A.; Fuji, T.; Kobayashi, T. Controlling the Carrier-Envelope Phase of Ultrashort Light Pulses with Optical Parametric Amplifiers. Phys. Rev. Lett. 2022, 88, 133901. [Google Scholar] [CrossRef]
- Raabe, N.; Feng, T.; Witting, T.; Demircan, A.; Brée, C.; Steinmeyer, G. Role of Intrapulse Coherence in Carrier-Envelope Phase Stabilization. Phys. Rev. Lett. 2017, 119, 123901. [Google Scholar] [CrossRef]
- Ishii, N.; Kaneshima, K.; Kanai, T.; Watanabe, S.; Itatani, J. Generation of ultrashort intense optical pulses at 1.6 μm from a bismuth triborate-based optical parametric chirped pulse amplifier with carrier-envelope phase stabilization. J. Opt. 2015, 17, 094001. [Google Scholar] [CrossRef]
- Seidel, M.; Balla, P.; Li, C.; Arisholm, G.; Winkelmann, L.; Hartl, I.; Heyl, C.M. Factor 30 Pulse Compression by Hybrid Multipass Multiplate Spectral Broadening. Ultrafast Sci. 2022, 2022, 9754919. [Google Scholar] [CrossRef]
- Daher, N.; Guichard, F.; Jolly, S.W.; Délen, X.; Quéré, F.; Hanna, M.; Georges, P. Multipass cells: 1D numerical model and investigation of spatio-spectral couplings at high nonlinearity. J. Opt. Soc. Am. B 2020, 37, 993–999. [Google Scholar] [CrossRef]
- He, P.; Liu, Y.; Zhao, K.; Teng, H.; He, X.; Huang, P.; Huang, H.; Zhong, S.; Jiang, Y.; Fang, S.; et al. High-efficiency supercontinuum generation in solid thin plates at 0.1 TW level. Opt. Lett. 2017, 42, 474–477. [Google Scholar] [CrossRef] [PubMed]
- Couairon, A.; Brambilla, E.; Corti, T.; Majus, D.; Ramirez-Gongora, O.J.; Kolesiket, M. Practitioner’s guide to laser pulse propagation models and simulation. Eur. Phys. J. Spec. Top. 2011, 199, 5–76. [Google Scholar] [CrossRef]
- Finot, C.; Chaussard, F.; Boscolo, S. Simple guidelines to predict self-phase modulation patterns. J. Opt. Soc. Am. B 2018, 35, 3143–3152. [Google Scholar] [CrossRef] [Green Version]
- Haider, Z. Simulation of white light generation and near light bullets using a novel numerical technique. Commun. Nonlinear Sci. Numer. Simulat. 2018, 54, 356–376. [Google Scholar]
- Robert, W.B. Nonlinear Optics, 3rd ed.; Academic Press: Burlington, VT, USA, 2008; pp. 105–108. [Google Scholar]
- Meenkyo, S.; Khurelbaatar, T.; Sambit, M.; Matthias, K.; Dongeon, K. High-contrast, intense single-cycle pulses from an all thin-solid-plate setup. Opt. Lett. 2020, 45, 367–370. [Google Scholar]
- Julius, H.; Lucas, R.; Igor, A.A.; Aline, V.; Marie, O.; Jaismeen, K.; Zhao, C.; Rodrigo, L.; Jérôme, F. Waveform Control of Relativistic Electron Dynamics in Laser-Plasma Acceleration. Phys. Rev. X 2022, 12, 011036. [Google Scholar]
- Tsai, M.; Liang, A.; Tsai, C.; Lai, P.; Lin, M.; Chen, M. Nonlinear compression toward high-energy single-cycle pulses by cascaded focus and compression. Sci. Adv. 2022, 8, eabo1945. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Cao, H.; Wang, Y.; Zhao, W.; Fu, Y. Suppression of Pulse Intensity Dependent Dispersion during Nonlinear Spectral Broadening with Intermediate Compression for Passive CEP Stable Pulse Generation. Photonics 2022, 9, 761. https://doi.org/10.3390/photonics9100761
Wang H, Cao H, Wang Y, Zhao W, Fu Y. Suppression of Pulse Intensity Dependent Dispersion during Nonlinear Spectral Broadening with Intermediate Compression for Passive CEP Stable Pulse Generation. Photonics. 2022; 9(10):761. https://doi.org/10.3390/photonics9100761
Chicago/Turabian StyleWang, Hushan, Huabao Cao, Yishan Wang, Wei Zhao, and Yuxi Fu. 2022. "Suppression of Pulse Intensity Dependent Dispersion during Nonlinear Spectral Broadening with Intermediate Compression for Passive CEP Stable Pulse Generation" Photonics 9, no. 10: 761. https://doi.org/10.3390/photonics9100761
APA StyleWang, H., Cao, H., Wang, Y., Zhao, W., & Fu, Y. (2022). Suppression of Pulse Intensity Dependent Dispersion during Nonlinear Spectral Broadening with Intermediate Compression for Passive CEP Stable Pulse Generation. Photonics, 9(10), 761. https://doi.org/10.3390/photonics9100761



