Numerical Simulations of the Influence on the Temperature Fields of Large-Sized Nd-Glass Slab with Designed Edge-Cladding Materials, Methods, and Structures

Abstract

The good cladding of a large-sized Nd-doped phosphate glass slab as a laser amplifier requires not only the amplified spontaneous emission and parasitic oscillation to be fully absorbed, to hold up the small signal gain coefficient of the Nd ions, but also the absorbed heat energy to be appropriately dissipated to extend a uniform temperature field for the larger laser beam aperture of the edge-cladded Nd–glass slab. In the present work, numerical simulations were performed based on the developed feasible edge-cladding designs for a 786 × 436 × 40 mm³ Nd–glass slab, including the following alterations: optical absorptivity, quantum-dot absorption centers, ceramics with higher thermal diffusivity, glasses with lower and higher specific heat values, 3D printing edge-cladding methods, double-deck edge-cladding structure with transparent strips as a buffer layer, and thickening of the edge-cladding. All of these designed edge-cladding materials, methods, and structures satisfy both requirements of sufficiently absorbing and precisely matching with the refractive index, as emphasized by the edge-cladding for the Nd–glass. Some of the designed edge-claddings resulted in a much more uniform temperature field than the composite polymer–glass edge-cladding as the standard for comparison, which could be utilized to extend the effective laser aperture of the Nd–glass slab, thus being beneficial to the laser beam size and laser energy in the optics recycle loop strategy.

1. Introduction

Edge-cladding has long been an effective way to suppress transverse amplified spontaneous emission and parasitic oscillations, which severely affect the magnitude and spatial distribution of the inversion occurring in laser media with a large laser gain [1]. Only when these media are edge-cladded when designed can much more laser pulse energy be extracted from the media. Using these cladded media, the developed high-energy and high-power laser systems can be exploited to support ignition science [2] and unprecedented extreme physics [3], in which diverse edge-cladding methods and materials have been used.

The absorptive solder glass cladding method [4,5] was used to suppress bulk and surface parasitic oscillations, which limited the energy storage in earlier large-aperture Nd–glass disk lasers. Later, the application of liquid edge-cladding [5] to a 200 mm-aperture Nd–glass disk laser increased the energy storage capability by ~20% over the solder glass cladding. In the 1980s, bubbles were found at the cladding interface, and the theoretical reflectivity in the geometric limit was studied to establish realistic limits for the allowable bubble size and number density while using monolithic edge-cladding [6]. The maximum allowable interfacial reflectivity [6] was dictated in one section of the comprehensive specifications by the Lawrence Livermore National Laboratory, and the composite polymer–glass edge-cladding method for large Nd–glass disks and slabs was invented to prevent edge reflections [7] from causing parasitic oscillations, in which the key specification is a closely matched index of refraction. Without using an index-matching material, it is desirable to have a film attached to the reflective surface to bring about suppression of the total internal reflections [8]. Since entering the 21st Century, some new edge-cladding methods have been developed, such as roughening peripheral edges [9] and processing the gain medium edge into an arris [10,11]. In recent years, an inorganic edge-cladding method based on hydroxide catalysis bonding was proposed [12,13] for large-aperture Nd–glass slabs.

With regard to edge-cladding materials, a sealing glass with a low melting point, whose softening point is at least 100 °C lower than the transition point of the laser glass, was invented for earlier Nd–glasses [14]. To reduce residual bubbles, a glass with a low fusing temperature and high expansion coefficient was invented [15]. Later, to avoid the time and expense associated with edge-cladding, silicone rubbers were utilized [16]. Since the 1990s, thermally induced strains have been a concern, and near-zero expansion glass–ceramic cladding materials have been developed [17,18,19]. Either for the previously developed edge-cladding methods [4,5,6,7,8] or the new edge-cladding methods [9,10,11,12,13] developed in recent years, the corresponding edge-cladding material should be provided individually for a certain method [20]. One of the most important design aspects is to choose a lower [14] or a higher [15] absorption coefficient depending on the concentration of the absorption center in the edge-cladding material. For Nd–glasses lasing at ~1 μm, the utilized edge-cladding material with a matched refractive index must have the advantage that it is capable of containing a large amount of transition elements and an infrared absorbing center such as V, Fe, or Cu [14,15,20].

Actually, Nd–glass is not the only material that requires the development of edge-cladding methods and materials. In recent years, the transverse amplified spontaneous emission of a 235 mm-diameter Ti:sapphire crystal amplifier was suppressed using index-matching liquid edge-cladding [3,21]. A roughly 50 mm-diameter Yb:YAG crystal or ceramic was edge-cladded with Cr:YAG light-absorbing ceramics, which were effective in suppressing parasitic oscillations in high-pulse-energy disk lasers [22,23,24]. Even the traditional Nd:YAG with a diameter as small as 14 mm should also be edge-cladded with the optimal Cr,Ca:YAG to avoid the decrease in conversion [25], whereas Nd–glass is of a size as large as 786 × 436 × 40 mm³, and the stimulated emission cross-section is higher than 3.8 × 10⁻²⁰ cm². A more satisfactory edge-cladding method or material is of great importance for Nd–glass laser amplifier slabs to achieve a better performance in practical applications. Although the edge-cladding process for the Nd–glass slab mainly depends on if there exist feasible edge-cladding materials and corresponding methods are developed, it is worth pointing out that some earlier research on the edge-cladding structures for Yb:YAG crystals, such as placing undoped YAG between the gain medium and the clad [26], multilayer cladding with variable absorption [27], provides successful experience for an important reference.

To sustain the high fluence operation of the National Ignition Facility’s laser based on Nd–glass, which is the world’s largest laser at the Lawrence Livermore National Laboratory, the optics recycle loop strategy [28] is implemented to raise the laser operating point above the UV damage threshold, thus keeping the energy that is delivered to the target at around 1.8 MJ. Before the size of any damage site is such that action is needed to prevent that site from growing to an unrepairable size, a small spot blocker generated by a programmable spatial shaper should be electronically placed to shadow (i.e., mask [29]) the damage site and prevent further growth. Since the fluence threshold of the fused silica final optics is only 4 J/cm², significantly less than the required operating fluence of 9 J/cm², additional spot blockers should be added as additional damage sites occur. When the laser beam area covered by spot blockers becomes a significant fraction of the total beam, it will impact the laser energy that can be delivered to the target [28], which is a special emphasis [29] and a key parameter for scientific ignition experiments [2]. At this time, it is desirable to enlarge the laser beam area so that the loop can continue to routinely employ laser energy and fluence that would otherwise have been unachievable [28]. However, whether the laser beam can be enlarged or not mainly depends on the adopted edge-cladding, since the enlarged area must be located in the edge-cladding region near the edge-cladding interface.

More than ~30% of the heat energy generated in flashlamp pumping will be deposited in the edge-cladding strips, whose volume is only ~8% of a Nd–glass amplifier slab. The average energy density in the edge-cladding strips is about 3.8–8-times as high as that in Nd–glass. As a result, a significant amount of energy will be transferred through the interface to the edge-cladding region, the peripheral region of pure Nd–glass slabs. In this paper, the temperature field distributed in the edge-cladding region was simulated under the conditions of adopting diverse cladding methods and materials. A total of twelve alterations were divided into four groups, as follows: (1) decreasing the absorption coefficient or deposited energy; (2) adopting new edge-cladding materials with higher or lower thermal diffusivity or specific heat; (3) adopting 3D printing as a new edge-cladding method with more precise adjustment of the doping concentration, similar to the multilayer cladding with variable absorption for Yb:YAG crystals [27]; (4) increasing the thickness of the edge-cladding strip, or adopting a double-deck structure with a nonabsorbent base by new edge-cladding materials, such as the structure placing undoped YAG between the Yb:YAG crystal and the clad [26]. These alterations are analyzed in the following Section 3.2, Section 3.3, Section 3.4 and Section 3.5.

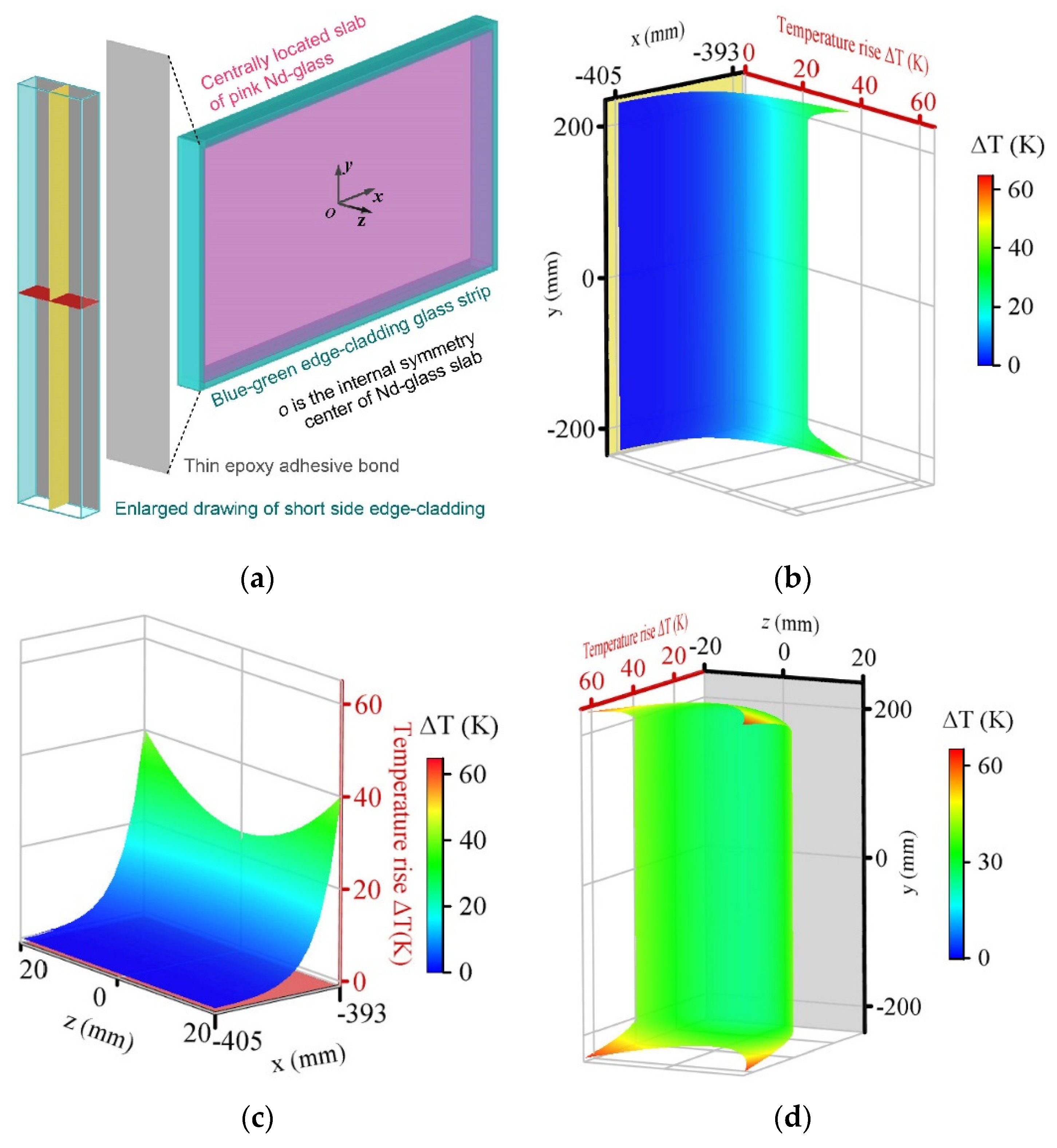
2. Modeling and Simulation

COMSOL Multiphysics 5.6 was utilized to numerically simulate the thermal behavior in the rectangular slab of a Nd–glass laser amplifier, whose schematic diagram is shown in Figure 1a, taking the incenter as the coordinate origin. Using the composite polymer–glass edge-cladding method [7], a pure Nd–glass slab with a size of 786 × 436 × 40 mm³ can be edge-cladded using two pairs of edge-cladding strips, both with a thickness of ~12 mm [30]. By cladding the longer peripheral sides of the pure Nd–glass slab using one pair of longer strips with a size of 786 × 40 × 12 mm³ and then the shorter sides using another pair of shorter strips with a size of 460 × 40 × 12 mm³, a Nd–glass laser amplifier slab with a final size of 810 × 460 × 40 mm³ can be used in lasers such as those of the National Ignition Facility (US) [30], Laser MegaJoule (France) [30], and ShenGuang (China) [31]. Different types of Nd-doped glasses are or will be adopted in the facilities, and each of them needs a corresponding type of edge-cladding material. No matter what type of material is adopted, its refractive index at the Nd laser wavelength must be matched with that of the Nd–glass adopted. From the aspect of index matching, it is also required that the interface layer matches with both the Nd–glass and the edge-cladding material. Such an interface layer with a thickness [7] smaller than 25 μm (the thickness was set to 15 μm in the simulation) can be used as a strong adhesive bond between the Nd–glass and edge-cladding glass, as shown in Figure 1a. In the composite polymer–glass edge-cladding method [7], one of the reasons for selecting epoxy as the bonding agent is that its refractive index can be adjusted to the desired value. If well matched, the amplified spontaneous emission and parasitic oscillation will pass through the epoxy interface without any reflection until they are fully absorbed by the edge-cladding material.

N41-type Cu-containing edge-cladding glass was chosen for the N41-type Nd–glass, whose absorption coefficient at the Nd laser wavelength can be adjusted to 7.5 cm⁻¹. Since the cladding interface temperature resulting from the cladding absorptivity of 7.5 cm⁻¹ is somewhat high [7] and especially since there really needs to be enough absorptivity to ensure full absorption, an absorption coefficient of 5 cm⁻¹ was used so that all of the following simulated edge-claddings can maximize the laser gain of the Nd–glass. On the other hand, it should be noted that, even if there is a uniform distribution of the absorption coefficient over the edge-cladding glass, the deposited energy will be distributed nonuniformly. Firstly, obeying the Bouguer–Lambert–Beer law, Figure 1b shows the absorbed energy is deposited exponentially along the x-axis of the edge-cladding thickness direction. Then, along the z-axis of the Nd–glass thickness direction, the parasitic oscillation is stronger near the surface regions of the Nd–glass slab, where it absorbs higher flashlamp pumping energy. This means that more energy is absorbed and deposited in the lateral-side surface regions of the edge-cladding glass strips, as shown in Figure 1c. As for the four corner regions, the energy they absorb is the spontaneous emission amplified along the diagonal line of the rectangular Nd–glass slab. Since the diagonal line is the longest optical path, more energy is absorbed and deposited in the corner regions, as shown in Figure 1b,d. For the same reason, the short-side edge-cladding strip will absorb much more energy than the long-side strip.

The total absorbed energy does not vary according to the same flashlamp pumping energy if the size of the pure Nd–glass slab is not changed. By calculation according to the average temperatures determined experimentally [32,33], the average maximum energy densities deposited in the pure Nd–glass slab, in the long- and short-side edge-cladding strips, are 1.3 J/cm³, 5.0 J/cm³, and 10 J/cm³. The data were adopted to establish the initial heat conditions within the cladded laser amplifier slab on the basis of the absorption and pumping mechanism as stated above, and especially the edge-cladding structures and the absorption coefficients adopted. Figure 1b–d are the standard conditions based on the standard composite polymer–glass edge-cladding structure and 5 cm⁻¹ absorptivity. The corresponding initial conditions for the diverse cladding structures and materials adopted, as shown in Section 3, were preset before the simulation.

Numerical simulations were carried out using COMSOL to solve the governing equation of heat diffusion [34,35], in which the “solid heat transfer” module and “transient analysis” mode were selected to simulate the temperature fields after flashlamp pumping. The governing equation of the transient heat transfer process in the laser amplifier slab is:

$$\frac{\partial T\left(x,y,z,t\right)}{\partial t}=\frac{k}{\rho C_p}\left(\frac{{\partial }^{2}T\left(x,y,z,t\right)}{\partial x^2}+\frac{{\partial }^{2}T\left(x,y,z,t\right)}{\partial y^2}+\frac{{\partial }^{2}T\left(x,y,z,t\right)}{\partial z^2}\right)$$

(1)

In Equation (1), T(x, y, z, t) is the time-dependent three-dimensional spatial temperature distribution function of the laser slab. k, ρ, and C_p are the thermal conductivity, density, and specific heat of the glass, respectively.

In the pumping cavity, the outer surfaces of the edge-cladded slab, as shown in Figure 1a, are subjected to ambient gas at a temperature of 293.15 K, which is assumed to be a constant during the thermal recovery. The initial condition of the laser amplifier slab can be expressed as:

$$T\left(x,y,z,t=0\right)=T_0\left(x,y,z\right)$$

(2)

In Equation (2), T₀(x, y, z) is the initial temperature distribution function of the laser slab, which is depicted in Figure 1b–d.

At the initial time of recovery, the temperatures distributed over the edge-cladding strips and Nd–glass slab are raised on the basis of a 293.15 K uniform background. Then, the temperature field is determined by internal heat conduction in the cladded slab and external heat transfer through convection and radiation with the environment. Since the edge-cladded slab is shielded with a frame mask, two large-aperture surfaces of the Nd–glass slab can still be applied to the multi-pass laser beam, but the surfaces of the four edge-cladding strips on the peripheral sides of the Nd–glass slab are shielded. Thus, two boundary conditions for the Nd–glass aperture surfaces and edge-cladding strip surfaces are adopted [34,35], which are directly related to the surface heat transfer coefficients [36], 2 W/m²K for the cladding strips and 3 W/m²K for the Nd–glass slab. The boundary conditions of the Nd–glass surfaces and the edge-cladding surfaces of the laser amplifier slab were set as the third type heat transfer boundary conditions, and the equations are:

$$\begin{gathered} {\left.-k\frac{\partial T\left(x,y,z,t\right)}{\partial n}\right|}_s=h_s\left[T\left(x,y,z,t\right)\left|{}_s\right.-T_{ext}\right] \\ {\left.-k\frac{\partial T\left(x,y,z,t\right)}{\partial n}\right|}_e=h_e\left[T\left(x,y,z,t\right)\left|{}_e\right.-T_{ext}\right] \end{gathered}$$

(3)

In Equation (3), s represents the surface of the Nd–glass, and e represents the surface of the edge-cladding. n is the normal direction of the surfaces. h is the heat transfer coefficient for the combined mode of convection and radiation heat transfer, and T_ext means the ambient temperature. The heat conduction between the frame mask and the long-side edge-cladding strip at the bottom of the slab, where there are smaller structural elements holding the slab, was neglected in the following simulations.

To check the simulation accuracy, hexahedral meshes increasing from 3906 to 101,885 were chosen to satisfy the mesh independency, while setting the relative tolerance to 10⁻⁶. Finally, the number of 46,800 elements was selected for discretizing both the Nd–glass slab and the edge-cladding glass strips. Especially for the epoxy interface in between, a finer mesh [37] was applied to the ten thinner layers on both sides. With a stretching factor of 1.1, the 1 mm element thickness was increased by 10% layer by layer. The epoxy interface itself was simulated by a thermally thin approximation [37] considering the heat flux perpendicular to the epoxy interface, which is described by the thermal diffusivity (0.11 mm²/s), specific heat (1.5 J/gK), and density (1.2 g/cm³) [38]. Compared with the N41-type glass, in terms of thermal diffusivity (0.3 mm²/s), specific heat (0.77 J/gK), and density (2.6 g/cm³), it can be found that all of the materials used in the cladded slab are of a lower thermal conductivity.

3. Results and Discussion

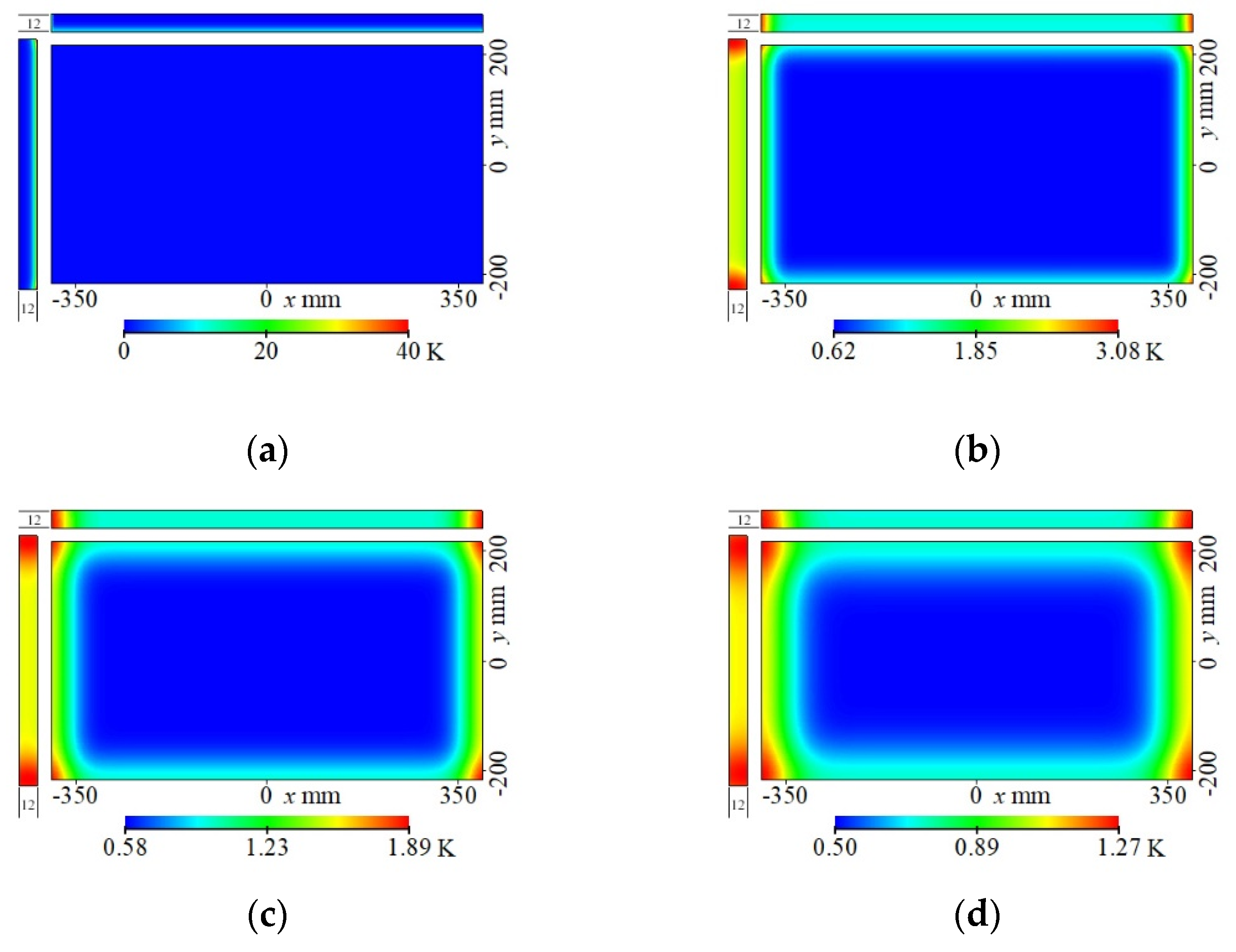
3.1. Temperature Field Evolution for Standard Edge-Cladding

On the basis of a standard composite polymer–glass edge-cladding and its resulting 15 μm epoxy interface and by using N41-type edge-cladding glass with a standard thickness of 12 mm and a standard absorption coefficient of 5 cm⁻¹, the N41-type Nd–glass laser amplifier slab was cladded and then installed in the pumping cavity. Immediately after pumping, i.e., at 0 min, as shown in Figure 2a, the energy deposited in the edge-cladding strips will be transferred through the interface into the Nd–glass slab, and concurrently, the energies deposited close to both of the aperture surfaces of the Nd–glass will be transferred toward the midplane of xy (z = 0). Due to the lower thermal conductivity, it is quite difficult to release the heat energy distributed on the midplane into the environment. Since the midplane field distribution that eventually evolves will decide the thermal distortion, the laser beam quality, and thus, the size of the beam aperture, the temperature rises on the midplane are used to reflect the temperature field evolution.

The evolution after ten minutes, as shown in Figure 2b, shows that high-temperature fields appear in the peripheral regions of the Nd–glass slab, as 82% or 78% of the energy in the long- or short-side edge-cladding strips enters into the Nd–glass slab during this first ten minutes. In particular, the high-temperature field is much wider in the regions close to the short-side edge-cladding than in those close to the long-side edge-cladding. Obviously, the short-side cladding will exert a much greater influence on the temperature field of the Nd–glass slab, especially in the edge-cladding region close to the short-side edge-cladding, which will be the focus in the comparison with other cladding methods or materials in the following sections. The reason for these phenomena is that the energy absorbed by the short side is from the spontaneous emission and parasitic oscillation amplified along the long-side direction, which is also in agreement with the determined average temperatures for the short- and long-side edge-cladding strips [32,33].

Due to a similar reason, more energy is deposited at both the ends of each edge-cladding strip, which comes from the diagonal direction. These heat energies at the four edge-cladding corner regions do not enter into the Nd–glass directly or immediately. They firstly need some time to be transferred inside the strips and then passed through the epoxy interface. After 30 min of evolution, as shown in Figure 2c, higher-temperature fields emerge at the four corners of the Nd–glass itself. With further evolution to 60 (Figure 2d), 120 (Figure 2e), and 180 (Figure 2f) minutes, the high-temperature area in each corner is expanded, and its core is slightly shifted away from the epoxy interfaces. On the other hand, it can be seen from the color bars in Figure 2 that, from 10 min to 180 min, the temperature in the central region of the Nd–glass slab decreased from 0.62 K to 0.30 K, and the temperature in the edge-cladding regions of the Nd–glass slab decreased basically from 0.92 K to 0.47 K.

With the decreasing temperatures, the temperature gradients in the Nd–glass slab should also be decreased, which reflects the trend towards a uniform temperature field. Along the z-axis of the thickness direction for the Nd–glass slab, the temperature difference between the incenter and the center on the aperture surface is as small as 0.01 K at 274 min. However, along the xy midplane, as shown in Figure 2g, the maximum temperature difference is still as large as 0.1 K, and there exist apparent demarcation lines, which indicate a sudden change in temperature. Especially in the central region, the approximately elliptical region with a 0.21 K lower temperature shrunk, which means that the laser beam quality will be affected by such nonuniformity of the temperature field and that further thermal recovery is still needed.

After evolving for 406 min, as shown in Figure 2h, this elliptical region disappeared since the temperature at the central point decreased to 0.12 K. However, instead, a much larger rectangular 0.13 K temperature region appeared, covering most of the aperture surface. At this time, the z-direction temperature difference between the incenter and the surface center, as well as the maximum temperature difference along the xy plane further decreased from 0.01 K and 0.1 K to 0.006 K and 0.04 K, respectively. In particular, the average temperature rise of the Nd–glass slab lowered down to 0.13 K, which was interpreted to be the allowable temperature difference between the slab average temperature and the environment temperature set by the National Ignition Facility [32]. According to the numerical evolutions in Figure 2, the thermal recovery of the edge-cladded Nd–glass slab can be achieved after 406 min, which is in agreement with the measured result that the thermal recovery takes place in no more than 7 h [32].

Even if such a recovery is achieved after a long time, it does not mean the laser beam is not affected by thermal distortion, but most of the 786 × 436 mm² aperture can be used for the designed clear aperture [39] of 400 × 400 mm². Although the 786 mm length of the long side can support 420 mm at the Brewster angle [40], the laser beam size propagation is only between 360 and 373 mm [39]. It can be seen very clearly from Figure 2h that, for each short-side edge-cladding, there are two large, spindle-shaped high-temperature cores close to the interface, which are caused by the energy from the short-side edge-cladding strip. These four high-temperature cores are the thermal sources resulting in the temperature gradient in the 400 × 400 mm² aperture. During the thermal recovery from 274 min (Figure 2g) to 406 min (Figure 2h), the core position is shifted inward and further limits the beam size. As large an aperture as possible could be utilized for a laser beam with a better quality and less accumulative effect, as long as these heat energies in the four high-temperature cores are dissipated out of the edge-cladded slab. However, complete temperature recovery will be much slower and must be disturbed by practical gas cooling, which cannot be avoided. By adopting diverse edge-cladding methods, structures, and materials and by comparing with the thermal recovery process of the standard composite polymer–glass edge-cladding as shown in Figure 2, numerical simulations were performed to seek a more uniform temperature field for a larger beam size and a higher laser energy.

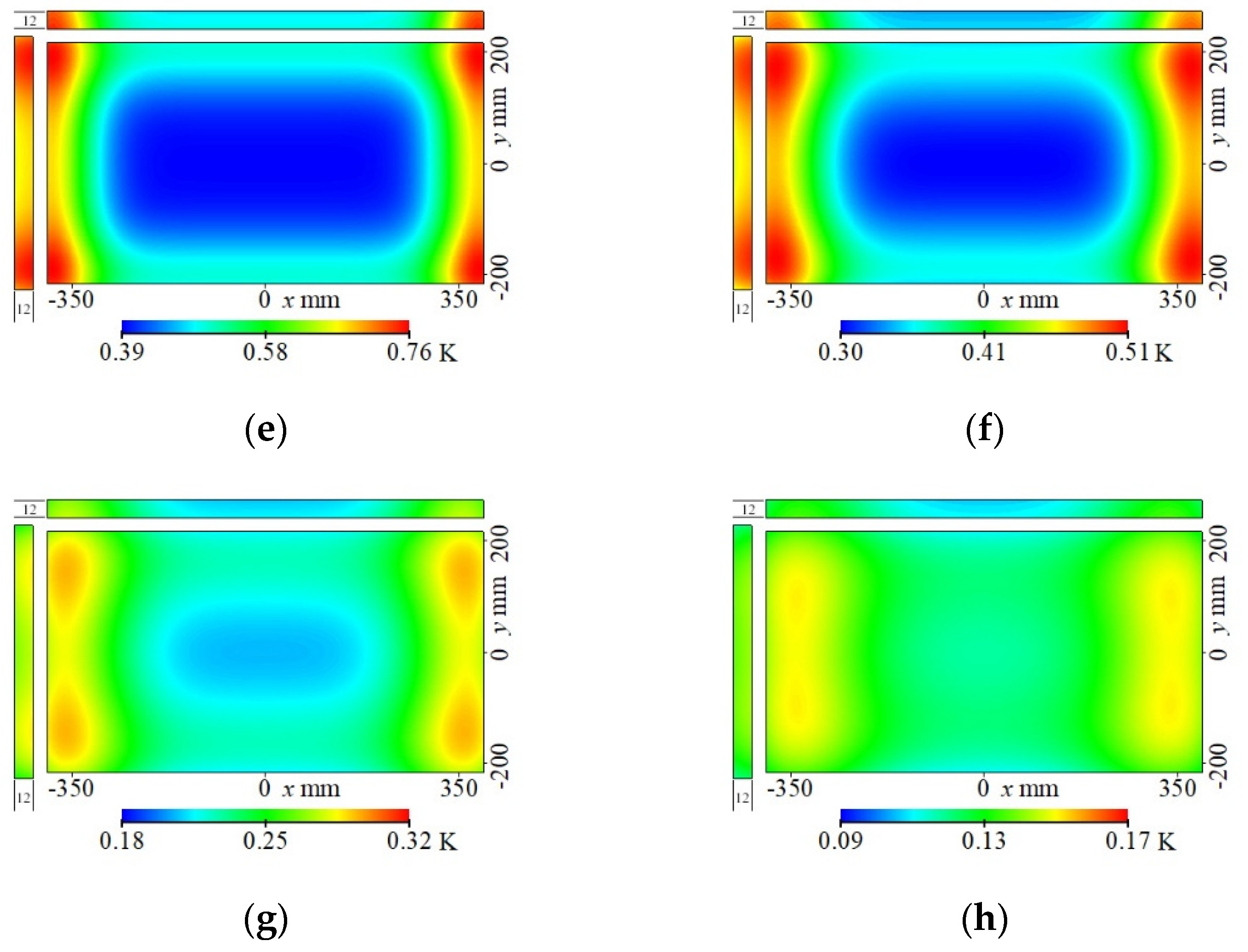
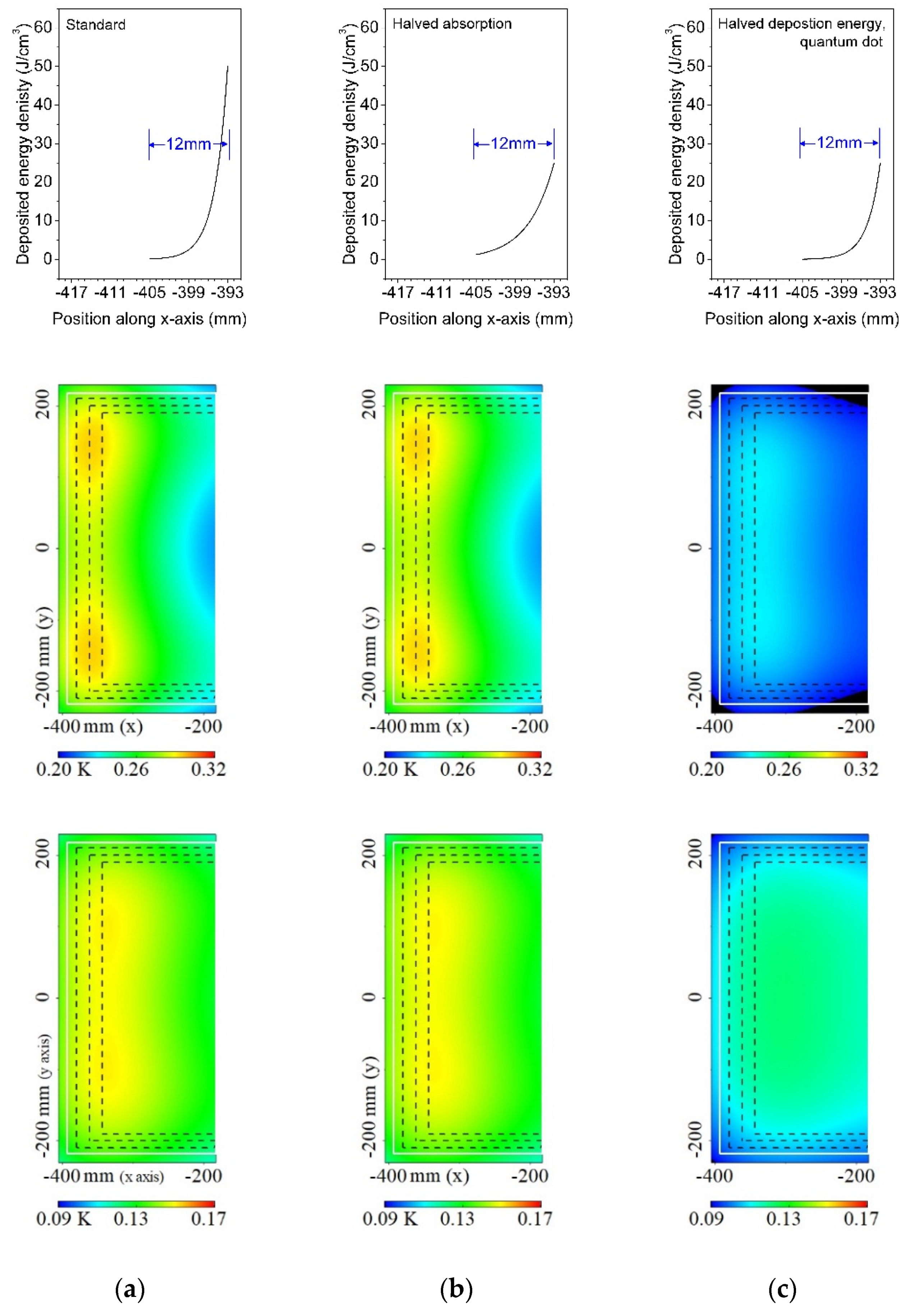
3.2. Edge-Cladding by Halving the Absorption Coefficient and Deposition Energy

A uniform temperature field mainly depends on the heat energies deposited in the short-side edge-cladding strips, including their magnitude and distribution. Even if the total amount of the absorbed energy is not changed, it can be distributed in different ways by adjusting the absorptivity of the cladding strips. If it is desired to halve the standard 5 cm⁻¹ absorption coefficient to 2.5 cm⁻¹, this can be achieved by simply halving the concentration of copper in the cladding strip [7]. Although the concentration and absorptivity are distributed uniformly, the absorbed energy will be distributed exponentially along the thickness direction of the cladding strip, obeying the Bouguer–Lambert–Beer law. In the case of 2.5 cm⁻¹, the absorbed energy is almost the same as that with 5.0 cm⁻¹, but some of the energy is not deposited close to the epoxy interface and redistributed towards the outer surface of the edge-cladding strip, as shown in Figure 3b. After a long period of thermal recovery, the temperature field is still almost the same as that with 5.0 cm⁻¹; in view of this, it seems impossible to improve the temperature field greatly by singly decreasing the absorption coefficient. Thereafter, the absorption coefficient remained as 5 cm⁻¹ or the equivalent absorptivity level for new edge-cladding materials and methods. In Section 3.4, a new cladding method is suggested to push the energy deposition towards the outer surface more, far away from the epoxy polymer interface and the Nd–glass slab.

If the size of the Nd-glass slab and the corresponding pumping energy are not changed, the absorbed energy from the amplified spontaneous emission and parasitic oscillation cannot be changed. As the absorption center, divalent copper can absorb in the range from visible to near infrared, but it cannot emit, which means all of the absorbed energy will be deposited as heat energy. Semiconductor colloidal quantum dots have been studied during the past three decades, not only due to academic interest, but also due to their practical applications. PbS and PbSe quantum dots of IV–VI semiconductors [41], with band gaps near 1 eV, could be taken as absorption centers for a 1053 nm laser of Nd-glass, while they can be embedded in a phosphate glass matrix [42]. The quantum dots can not only absorb around 1053 nm, but can also emit far above 1053 nm with quantum efficiencies [43] of 45–55%, which means half of the energy will not be reabsorbed by the Nd–glass and will also not be deposited in the edge-cladding glass. When doping quantum dots instead of copper ions, the deposited heat energy is only half of the standard, as shown in Figure 3c. After the same thermal recovery time, not only are the temperatures decreased more, but also the temperature field is more uniform. As shown in Figure 3a of the standard cladding, the two high-temperature cores close to the short-side edge-cladding cannot even allow a 380 mm aperture. However, as shown in Figure 3c, these high-temperature cores are dissipated. It seems that, by using quantum dots, the edge-cladding can even support a 420 mm aperture because the absorbed heat energy is halved.

Although half of the absorbed energy cannot be reabsorbed when using quantum dots, this part must be deposited in the pumping cavity, whose thermal disturbance to the Nd–glass slab and the gas environment is neglected. In particular, it should be pointed out that the refractive index of PbSe is very large [44], almost three-times that of Nd–glass. Such index unmatching is a problem for residual reflectivity, notably on the cladding interface. If the residual reflectivity is increased from 10⁻⁴, the laser gain coefficient of the Nd–glass amplifier will be decreased [45]. Despite this problem, it is found that one of the advantages of removing half of the deposited energy is that the time to reverse the heat flux direction is moved up, as indicated in Figure 4.

In the first minute of the thermal recovery, the average heat fluxes through the short-side edge-cladding epoxy interface are larger, especially for the standard edge-cladding. For the edge-cladding using the halved absorptivity, some of the energy is redistributed far away from the epoxy interface, and the thermal transfer is slowed. It behaves almost the same as the edge-cladding using quantum dots in the first minute, as indicated in Figure 4, but their final temperature fields are totally different, as indicated in Figure 3b,c. It is found from Figure 4 that the heat is always transferred from the edge-cladding strip to the Nd-glass slab with negative heat fluxes from 0 to 84 min for the edge-cladding using the halved absorptivity. Until 84 min, as with the standard edge-cladding, the heat starts to be transferred reversely from the Nd-glass to the edge-cladding strip with positive heat fluxes. Meanwhile, for the cladding with the removal of half of the deposition energy, the transition point at which the heat flux direction is reversed is brought forward from 84 min to 58 min, which means more time can be utilized to dissipate more heat energy in the Nd-glass slab to the cladding strip. Seeing that the distribution of the deposition energy in the edge-cladding strip can advance the transition point, such a point should also be related to the properties of the edge-cladding strip material used.

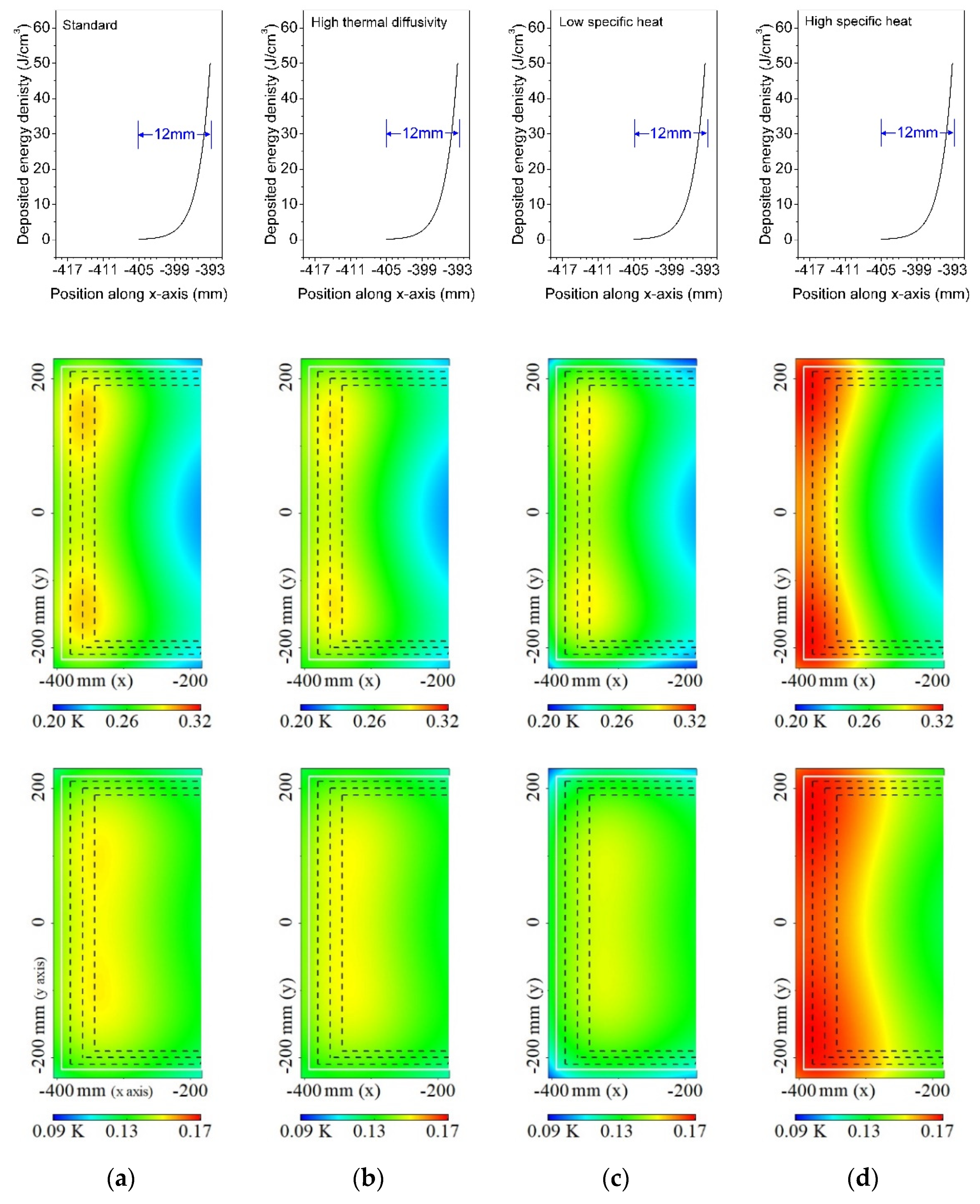
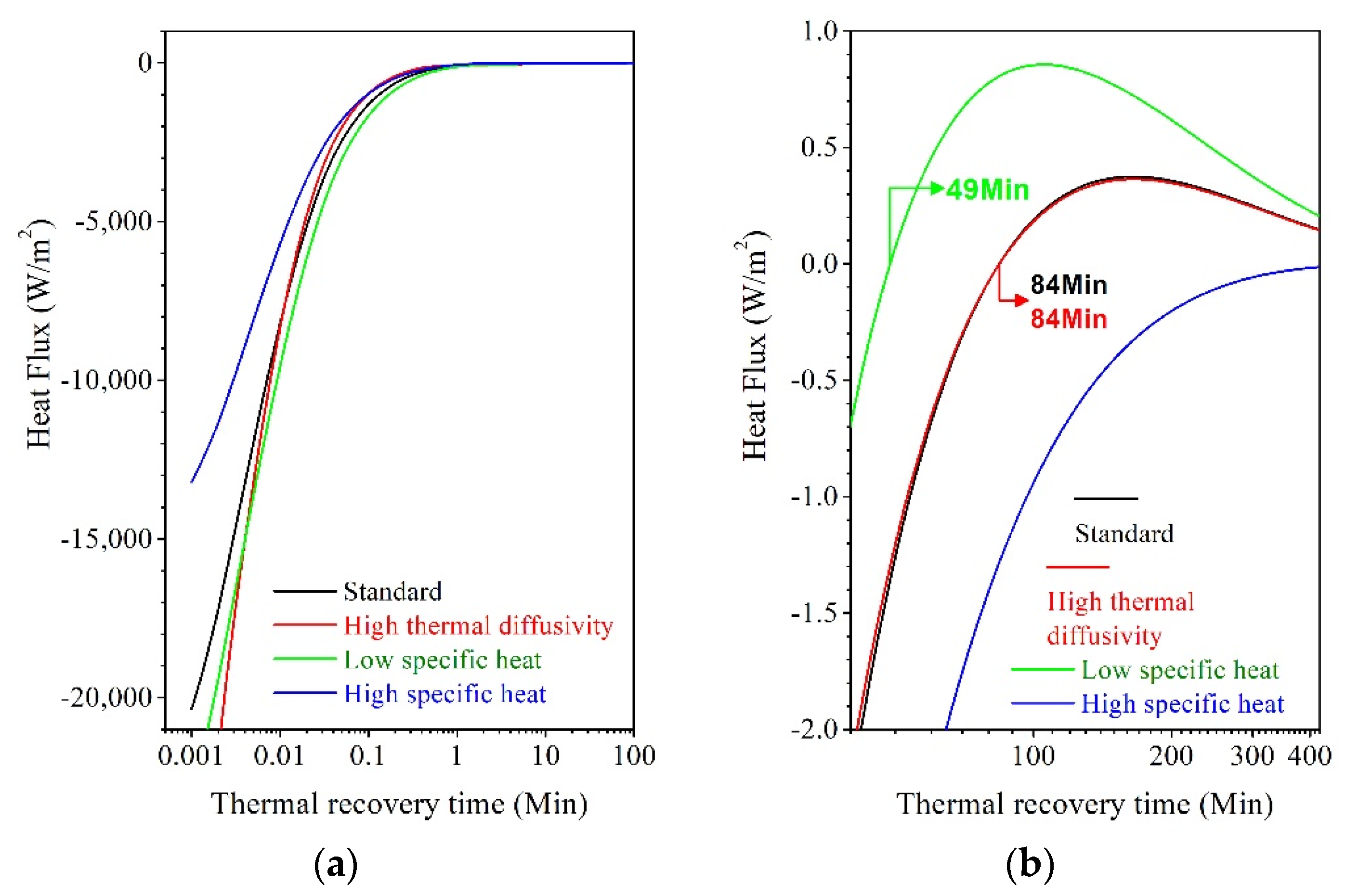
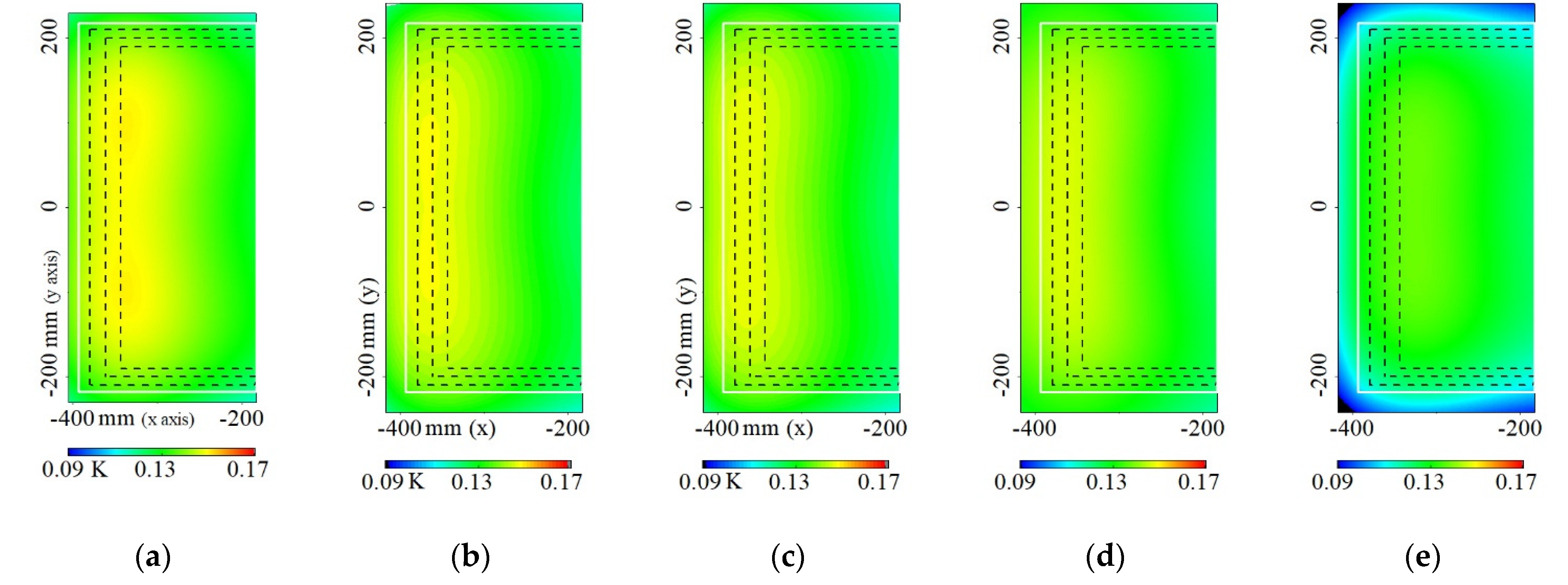
3.3. Edge-Cladding Using Materials with Higher Thermal Diffusivity and Higher and Lower Specific Heat

The thermal diffusivity and specific heat of the edge-cladding material were studied to see if they can improve the thermal transfer and recovery by advancing the transition point, under conditions with the same distribution of the deposition energy, as indicated in Figure 5. If the thermal diffusivity of the cladding material is lower, the corresponding thermal conductivity is lower. Additionally, if the heat energy in the edge-cladding strip cannot be dissipated more easily, the remaining heat will affect the temperature field of the cladding region in the Nd–glass slab. In the following simulations, edge-cladding materials with higher thermal diffusivity, as well as lower and higher specific heat values were considered.

Glass–ceramics [19] doped with copper or iron are generally suitable for absorbing light in the wavelength range above 0.8 μm, whose composition is almost the same as that of the low-expansion glass–ceramic Zerodur^®. While the basic general composition of the Zerodur^® material is based on 55.42SiO₂-24.99Al₂O₃-7.31P₂O₅, the refractive index [19] is about 1.54, somewhat larger than the 1.51 of the N41-type Nd–glass. Since the contents [19] of P₂O₅ and Al₂O₃ can be adjusted between 0 and 10 wt% and 15 and 30 wt%, respectively, the refractive index can be decreased to 1.51, well matching with that of the N41-type glass. Such a silicate glass–ceramic with a higher content of P₂O₅ and a lower content of Al₂O₃ can be applied to the cladding material of the Nd–glass slab [19]. As Zerodur^® almost has an identical composition, its thermal parameters were adopted [46]. The thermal diffusivity of 0.7 mm²/s is more than two-times the 0.3 mm²/s of N41, and the specific heat of 0.8 J/gK is similar to the 0.77 J/gK of N41-type phosphate glass.

The specific heat of phosphate glass is known to vary with its multiple compositions, not only depending on P₂O₅. For the 60P₂O₅-20Na₂O-18CaO-2Al₂O₃ (all in wt%) base glass, its specific heat [47] is 0.7 J/gK. By adding 20 wt% CoO into the base glass, the specific heat can be increased to higher than 1.2 J/gK. On this basis, further adding 1 wt% CuO results in a specific heat of less than 0.5 J/gK. On the other hand, the refractive index [47] of the base glass is about 1.44. After adding CoO and further adding CuO, it is increased to ~1.58 and ~1.57, somewhat larger than the 1.51 of the N41-type glass. It is reported that, with a decreasing CaO content in 45P₂O₅-(50-x)Na₂O-xCaO-5SrO (x = 20 − 35, in mol%) glass, the refractive index is decreased [48] from 1.57 to 1.45. For 60P₂O₅-20Na₂O-18CaO-2Al₂O₃ (in wt%) glass [47], by decreasing CaO and increasing P₂O₅, the refractive index can be decreased more. Since the Na₂O content is fixed, which possesses a higher factor contributing to specific heat, and the amount of the increasing P₂O₅ can be offset by that of the decreasing CaO, the specific heat of the modified base glass can almost be retained. Regarding glass with a specific heat of [47] less than 0.5 J/gK or higher than 1.2 J/gK, 0.45 J/gK or 1.2 J/gK were, respectively, adopted. The former can be adjusted by slightly decreasing CoO, while the latter can be adjusted by decreasing CoO and slightly increasing CuO, which is beneficial to decrease the refractive index to satisfy the index matching. Their thermal diffusivity is 0.24 or 0.23 mm²/s without largely changing [47].

In the case of cladding the Nd–glass slab using the standard composite polymer–glass cladding method, but utilizing the edge-cladding glass with high thermal diffusivity or with a lower or higher specific heat, the temperature field evolutions were simulated and shown in Figure 5, and the corresponding heat fluxes through the short-side edge-cladding epoxy interface are shown in Figure 6.

It can be seen from Figure 6 that the higher thermal diffusivity does not advance the transition point of 84 min, as with the standard, at which the heat flux is reversed to dissipate the heat energy in the Nd–glass. Although the heat flux before ~1 s (0.015 min) is greater than that of the standard, the flux becomes smaller from 0.015 to 1 min and then almost equals the flux of the standard. According to the calculation, both total amounts of heat energy, from the edge-cladding strip to the Nd–glass slab and from the slab to the strip, are similar, but slightly smaller than the standard. It can be observed from Figure 5b that the two high-temperature cores become blurred, since the central core region with 0.151 K for the standard cladding disappears. Such a uniform field is not only related to the transfer process between the edge-cladding strip and Nd–glass slab, but also due to the high thermal diffusivity of the strip. Slightly more energy is transferred by fast conduction and dissipated from the strip surfaces. The energy left in the strip and transferred to the Nd–glass slab decreases.

In contrast, slightly more heat energy is transferred from the strip to the slab when the standard N41-type edge-cladding glass strip is replaced by the glass with lower specific heat. As seen in Figure 6, the heat flux is larger than that of the standard edge-cladding before 6 min and only slightly smaller from 6 to 48 min. On the other hand, the lower specific heat does advance the transition point, from the 84 min of the standard to 49 min. According to the calculation, the heat energy transferred from the Nd–glass slab to the strip with lower specific heat is more than two-times that from the standard edge-cladding. As a result, it can be seen from Figure 5c that the two high-temperature cores almost disappear since the central core region with 0.147 K almost disappears. Compared with the standard and the edge-cladding using glass with high thermal diffusivity, the edge-cladding using glass with a lower specific heat results in a much more uniform temperature field, almost without a temperature gradient.

The above simulations indicate that the cladded Nd–glass slab can support a uniform aperture of even 420 mm when using a material with high thermal diffusivity or low specific heat as the edge-cladding material. As for the glass with high specific heat, its edge-cladding results in a much wider high-temperature region covering both sides of the epoxy interface. In particular, with the thermal recovery, the high-temperature region extends inward and cannot even support an aperture of less than 360 mm. In the following numerical simulations, only lower specific heat and higher thermal diffusivity will be considered.

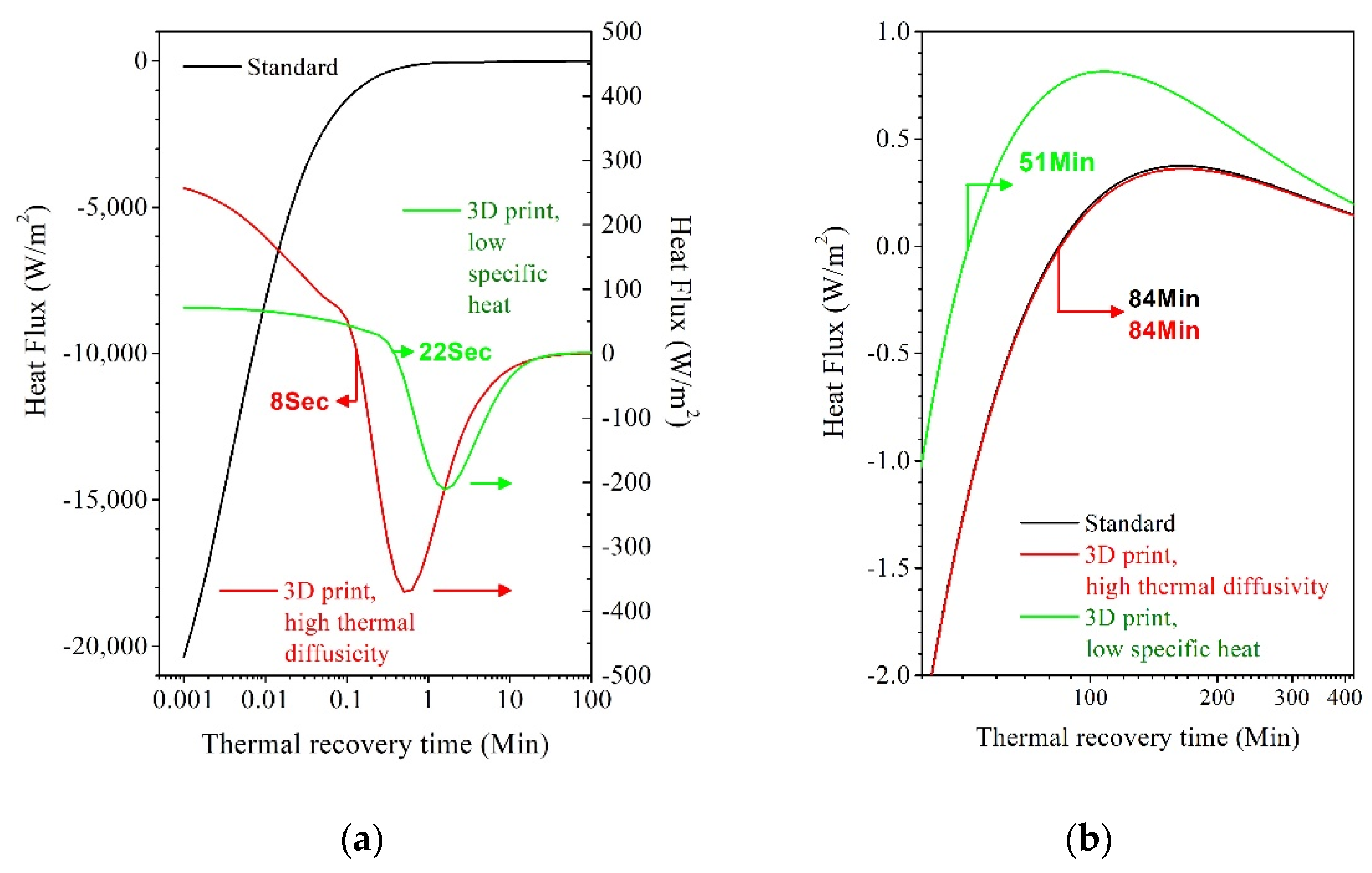
3.4. Edge-Cladding by 3D Printing

As analyzed in Section 3.3, higher thermal diffusivity can result in fast conduction so that slightly more energy can be transferred to the outer surface far away from the epoxy interface. If some or all of the heat energy could be deposited in the region close to the outer surface of the edge-cladding strip, which is also beneficial to avoid the degradation of the epoxy interface, this should result in the same effect that more energy can be dissipated directly from the surface. It is similar to the multilayer cladding for Yb:YAG crystals [27], in which the absorption values are properly designed to overcome the radial thermal gradients in disk amplifiers. To achieve such a purpose, the 3D printing technique is proposed as the edge-cladding method for the Nd–glass amplifier slab by using silicate glass–ceramics with high thermal diffusivity or phosphate glass with low specific heat, although this is a difficult task.

Three-dimensional-printed glasses [49] are limited in their chemical compositions and suffer from a lower printing resolution. The development of 3D printing technologies that broaden the compositional design space and improve the resolution of printed objects is the key to advancing the practical applications. It took more than two decades for the first 3D-printed transparent silicate glasses to emerge [50]. If 3D printing leads to white, porous, and non-transparent glass, this material cannot be used as an edge-cladding material [45] since the residual reflectivity will be larger due to bubbles and voids. Until recently, it was reported that transparent phosphate glasses can be 3D-printed with preserved optical properties [51]. Purely inorganic glass compositions have been successfully extruded and directly deposited layer by layer with 0.1 mm resolution. If 3D printing leads to millimeter resolution [51], this will not be enough to achieve the purpose proposed above, since the doping concentration cannot be controlled finely with a poor layer resolution.

As shown in Figure 7, the edge-cladding strip could be fictitiously divided into two parts along the thickness direction. The first 8 mm part toward the epoxy interface and Nd–glass will be printed on the basis of the index-matched host of the glass–ceramic with high thermal diffusivity or the glass with low specific heat, which are assumed to not have any doping of the 1053 nm absorption center, such as with copper. There is no heat energy deposited in this first part. For the remaining 4 mm part, it will be 3D-printed using both the glass–ceramic and the glass containing copper. At this stage, the layer resolution of 3D printing plays an important role in establishing a programmed copper concentration gradient according to a quartic power function. As shown in Figure 7, the heat energy deposited in this part can be adjusted layer by layer as programmed. As proposed above, the purpose of this is to ensure that the heat energy is deposited far away from the epoxy interface. If necessary, the conventional quartic power function can be altered so that the heat energy will be deposited on the outer surface region.

Compared with the standard, the edge-cladding by printing, either with the glass–ceramic with high thermal diffusivity or the glass with low specific heat, will result in a more uniform temperature field, as shown in Figure 7. However, the uniformity due to the lower specific heat (Figure 7c) is significantly improved compared to that due to the high thermal diffusivity (Figure 7b) and also that due to the low specific heat without utilizing 3D printing (Figure 5c). It can be seen from Figure 7c that the two high-temperature cores fully disappear since the central core region with 0.143 K fully disappears, which means less heat energy is left in the Nd–glass slab. Actually, 3D printing using glass with low specific heat advances the transition point greatly from the 84 min of the standard to 51 min. Moreover, such a 3D-printed edge-cladding can produce an 8 mm region without any heat deposition. Thus, in the initial 22 s, the heat is transferred from the Nd–glass slab to the edge-cladding strip, not vice versa. Since there are two time ranges in which the heat energy is dissipated in the Nd–glass slab, the temperature field becomes much more uniform. However, it should be noted that the 3D-printed edge-cladding using glass with low specific heat mainly depends on if a material can be found, which should possess the three properties of sufficient index matching, lower specific heat, and the absence of copper. The specific heat of 0.7 J/gK is decreased to 0.45 J/gK when copper oxide is added into the base glass [47]; otherwise, the specific heat remains almost the same as that of the N41-type glass. If the first 8 mm part of the edge-cladding strip is 3D-printed using N41-type cladding glass with medium specific heat, the temperature field will not be very good, as shown in Figure 7c, but it will still be better than that of the standard, as shown in Figure 7a, and the 3D-printed edge-cladding using the glass–ceramic with higher thermal diffusivity, as shown in Figure 7b.

The edge-cladding produced by combining 3D printing with a glass–ceramic with higher thermal diffusivity does not fully accomplish the proposed purpose, although its resulting temperature field, as shown in Figure 7b, is much better than that of the standard, as shown in Figure 7a. Compared with the standard, some of the heat energy deposited in the Nd–glass is transferred to the edge-cladding strip in the initial 8 s, as indicated in Figure 8. Due to fast conduction, this time range is not as long as the 22 s of 3D printing with glass with lower specific heat, which results in a more uniform temperature field, as shown in Figure 7c. Compared with the edge-cladding using only the glass–ceramic with higher thermal diffusivity without 3D printing, the two blurred high-temperature cores (Figure 5b) do not further disappear when later combining with 3D printing, as shown in Figure 7b. In both cases, either with (Figure 8) or without 3D printing (Figure 6), the transition points of 84 min are not brought forward, remaining the same as the 84 min of the standard. In spite of this, it can be observed clearly that, during the thermal recovery from 274 min (self-equilibration state) to 406 min (slab equilibration state), the centers of the two high-temperature cores are shifted inward from the line of the 400 mm aperture to the line of the 380 mm aperture, as shown in Figure 7b. This implies that, if the first 8 mm part toward the epoxy interface and Nd–glass is thickened, the centers of these two high-temperature cores will be shifted outward so that a larger aperture can be applied.

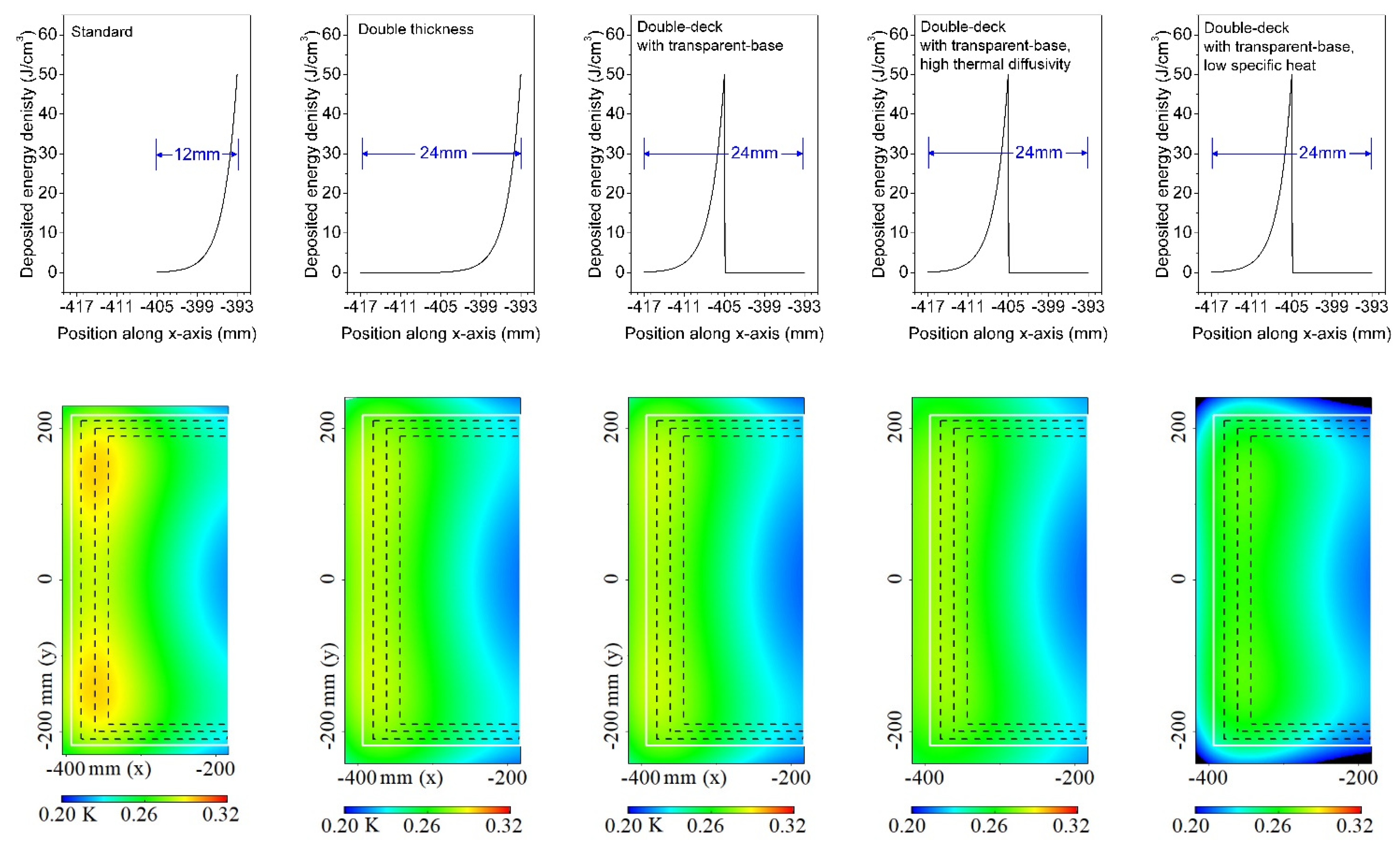
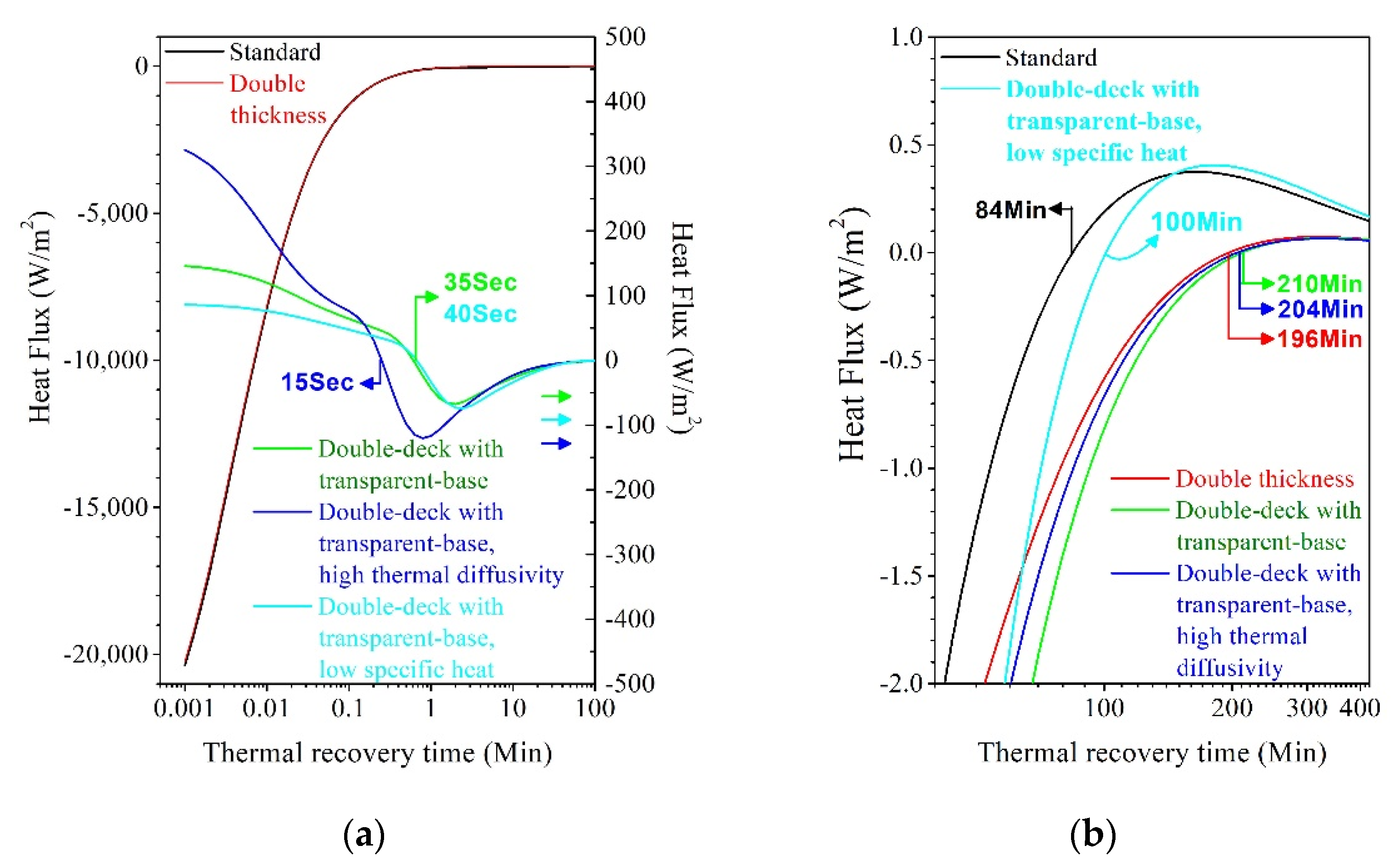
3.5. Edge-Cladding with Double Thickness and Double-Deck Structure

When using 3D printing to prepare cladding strips with the thickness increased from 12 to 24 mm, as proposed in Section 3.4, low-cost and time-efficient manufacturing is required [51] since nearly 83% of the cladding strip, the transparent portion, is not required to be 3D-printed. In view of the high performance–cost ratio [7], as well as the low risk [52] of damaging the Nd–glass slab, the composite polymer–glass edge-cladding method is still the first choice for the edge-cladding of large-sized Nd–glass slabs. To imitate a structure overlaid with doped and non-doped glass, the composite polymer–glass edge-cladding method can be performed in two steps. Such a structure is just like the layout used for Yb:YAG crystals [26], in which 1.25 mm-thick undoped YAG is placed between the gain medium and the clad. A transparent glass strip of 12 mm thickness is firstly cladded as the base on the peripheral surfaces of the Nd–glass slab, and then, a doped glass strip of 12 mm thickness is finally cladded on the transparent strip. Although such a two-step cladding means the first time’s epoxy interface will be cured again by heating up to 80 °C for about 4 h [7], it was demonstrated by our previous experiences [53] that there is no degradation of the epoxy polymer used. The so-produced double-deck cladding structure is not only similar to the structure produced by 3D printing, but also increases the thickness of the edge-cladding to 24 mm. Because the transparent glass strip is between the Nd–glass slab and the doped glass strip, the doped strip must be located deep in the frame mask. There will be no chance to absorb the flashlamp pumping energy, and no extra heat energy will be deposited in the double-deck edge-cladding, which will be beneficial for the temperature field of the Nd–glass slab. On the other hand, while the temperature of the doped glass strip is raised instantly as it absorbs the amplified spontaneous emission and parasitic oscillation, it expands, interacting with the Nd–glass slab. Now, the transparent strip in the double-deck edge-cladding can act as an important buffer layer to the expansion and will be of great importance to thermal distortion, beam steering, and focusability in the edge-cladding region of the Nd–glass slab, which are the main concerns of the high-power laser beams of the National Ignition Facility [30], Laser MegaJoule [30], and ShenGuang [31].

To construct a double-deck edge-cladding structure, the transparent glass and its parallel doped glass were produced, with the same base glass composition. Then, they were applied to the edge-cladding of the same size of Nd–glass slab, using a pair of transparent and doped glass strips made from N41-type glass, as shown in Figure 9c, a glass–ceramic with high thermal diffusivity, as shown in Figure 9d, and glass with low specific heat, as shown in Figure 9e. It can be seen in Figure 9 that there is no heat in the transparent strip close to the Nd–glass slab. As for the doped strip, the absorptivity can be adjusted to 5 cm⁻¹ by doping the corresponding copper contents for the three base glasses, while the deposited energies are the same. Among them, the double-deck edge-cladding using the glass with low specific heat results in the most uniform temperature field since the temperatures are not higher than 0.139 K, as shown in Figure 9e. Nevertheless, the transparent strip with lower specific heat should be further developed, as stated in Section 3.4. In this case, even if the transparent glass strips are replaced by the transparent N41-type glass with medium specific heat, the result also shows a much more uniform temperature field, which means such a double-deck structure is very efficient. Since the thickness of all three double-deck cladding structures is increased to 24 mm, their transition points are all postponed beyond the 84 min of the 12 mm standard, as shown in Figure 10. For the double-deck cladding using the glass with low specific heat, its transition still occurs at the earliest 100 min. There should be enough time to dissipate the heat in the Nd–glass slab. As for the cases of the N41-type glass and the glass–ceramic with high thermal diffusivity, their transition points are, respectively, at 210 and 204 min. Although there is less time to dissipate in the final stage of the thermal recovery, some of the energy in the Nd–glass slab can be dissipated in the initial stage. As shown in Figure 10, the initial dissipation period of 40 s is the longest among the three, resulting from the double-deck edge-cladding using the glass with lower specific heat.

When adopting the glass–ceramic with high thermal diffusivity for the double-deck edge-cladding, the temperature field, as shown in Figure 9d, is more uniform than that of the 12 mm edge-cladding produced by 3D printing, as shown in Figure 7b, or using the composite polymer–glass cladding method with the glass–ceramic with higher thermal diffusivity, as shown in Figure 5b. Even when adopting the N41-type glass for such a double-deck edge-cladding, as shown in Figure 9c, the temperature field is also more uniform than that of the 12 mm standard, as shown in Figure 9a. As shown in Figure 10, during the initial 15 to 35 s, some of the heat energy in the Nd–glass slab can be transferred to the double-deck edge-cladding strips. Since the thickness of the transparent strip is larger than that of the non-absorbing region produced by 3D printing, more capacity can be used to store the heat from the Nd–glass slab. The initial period to dissipate the heat energy in the Nd–glass slab is longer than that of the 3D-printed edge-cladding, so more energy can be dissipated to the double-deck cladding strips, resulting in a more uniform temperature field in which the two high-temperature cores almost disappear since the central core regions with 0.147 K and 0.144 K almost disappear, as shown in Figure 9c,d.

It should be pointed out that the edge-cladding will be applied to at least 3072 Nd–glass slabs [30] or even more [30,31], and a trade-off edge-cladding would consider both the performance and the cost [53]. In view of this point, the double-deck edge-cladding structure will cost slightly more and involve more working time, but it is important to note that the performance of such a structure is the best and worth considering. On the other hand, it was demonstrated that continuous melting produces a good yield of high-quality cladding glass [53] and has a lower manufacturing cost. By not adopting the double-deck structure, but keeping its thickness of 24 mm, such a thicker edge-cladding for Nd–glass slabs can be applied only once using the standard composite polymer–glass edge-cladding method [7]. Even when a glass–ceramic with high thermal diffusivity or glass with low specific heat is not adopted, the thicker edge-cladding of 24 mm can perform well when just adopting N41-type cladding glass, which can be continuously melted, just like N41-type Nd–glass [54]. Compared with the 12 mm standard, as shown in Figure 9a, the edge-cladding with a double thickness of 24 mm shows a more uniform temperature field, as shown in Figure 9b. It can be seen that the two high-temperature cores are much more blurred since the central core region with 0.151 K for the standard cladding disappears, and the temperature field can even be compared to the uniform temperature field of the double-deck structure using the N41-type transparent and doped glass strips, as shown in Figure 9c. In particular, the comparison between Figure 9a,b clearly indicates that the centers of the two high-temperature cores are shifted from the 380 mm aperture line (Figure 9a) to the 400 mm aperture line (Figure 9b) while only increasing the cladding thickness from 12 mm to 24 mm. In general, either with or without the double-deck structure, the temperature field is more uniform than that of the 12 mm standard, provided the thickness of the edge-cladding is increased to 24 mm. This can be observed clearly not only in the lower four temperature fields at 406 min (slab equilibration state), but also in the middle four fields at 274 min (self-equilibration state), as shown in Figure 9b–e. Moreover, regarding the 24 mm double-thickness edge-cladding without a double-deck structure, as shown in Figure 9b, even if the thickness is decreased from 24 mm, i.e., the edge-cladding is applied only once with a copper-containing N41-type cladding glass strip of 18 mm, the simulated temperature field is also significantly improved compared to that of the standard, as shown in Figure 9a. This temperature field is not as good as that shown in Figure 9b, but it can still support a larger aperture. For the 360–373 mm laser beam [39], even if the practical laser aperture is enlarged only by 2.5 mm, additional spot blockers can be added [29] in the laser beam without impacting the beam area and laser energy that can be delivered to the target [28]. For the National Ignition Facility [30], Laser MegaJoule [30], and ShenGuang [31], it is of great importance to sustain continuous operation above the UV damage threshold using the optics recycle loop strategy [28].

4. Conclusions

Numerical simulations were carried out, taking the standard composite polymer–glass edge-cladding as the criterion, to compare the temperature fields resulting from diverse absorptivity, absorption centers, thermal parameters, cladding methods, and structures for the edge-cladding of a Nd–glass slab. Changing only the absorptivity of the edge-cladding glass, without decreasing the deposited heat energy in the cladding glass, does not improve the temperature field in the edge-cladding region of the Nd–glass slab. Taking advantage of quantum dots as absorption centers to decrease the deposited heat energy can improve the temperature field enormously, although this still requires further development and validation. Using a glass–ceramic with high thermal diffusivity or glass with low specific heat instead of N41-type cladding glass is beneficial to the temperature field. Although further improvements are necessary, glass–ceramics or glasses are proposed for 3D printing. Both without doping and with gradient doping from the epoxy interface to the outer surfaces, as designed in the 3D-printed edge-cladding, the resulting temperature fields are much more uniform than those produced by the standard composite polymer–glass method, although the 3D cladding method will cost more and take up more working hours. To achieve a high performance–cost ratio, the double-deck edge-cladding structure was proposed, composed of a pair of transparent and absorbent strips, which are made of N41-type edge-cladding glass, a glass–ceramic with high thermal diffusivity or glass with low specific heat, without doping of the transparent strips and with doping of the absorbent strips. The temperature fields resulting from the double-deck edge-cladding structure with the transparent strips as a buffer layer are much more uniform, although such a method needs to be performed in two steps. Even when adopting the standard method only once, but increasing the thickness of the N41-type edge-cladding glass from 12 mm to 18–24 mm, the resulting temperature field is not as uniform as that of 24 mm double-deck structures, but still much more uniform than that using the 12 mm standard method, which can still support a larger aperture. It was proven by the simulations that the cladding designed using new absorption centers, cladding materials, cladding methods, and cladding structures can be adopted to improve the temperature field in the edge-cladding region of the Nd–glass slab. The results obtained are not only beneficial to developing more suitable edge-claddings and making full use of the 400 mm laser aperture of the 786 × 436 × 40 mm³ Nd–glass slab [39], but also referential to the edge-cladding of the recently developed 215 × 120 × 10 mm³ Nd–glass split-slab [55], to pursue better laser performances on beam quality, beam energy, and beam pointing.