Relaxation of Beam Irradiation Accuracy of Cooperative Optical Wireless Power Transmission in Terms of Fly Eye Module with Beam Confinement Mechanism
Abstract
:1. Introduction
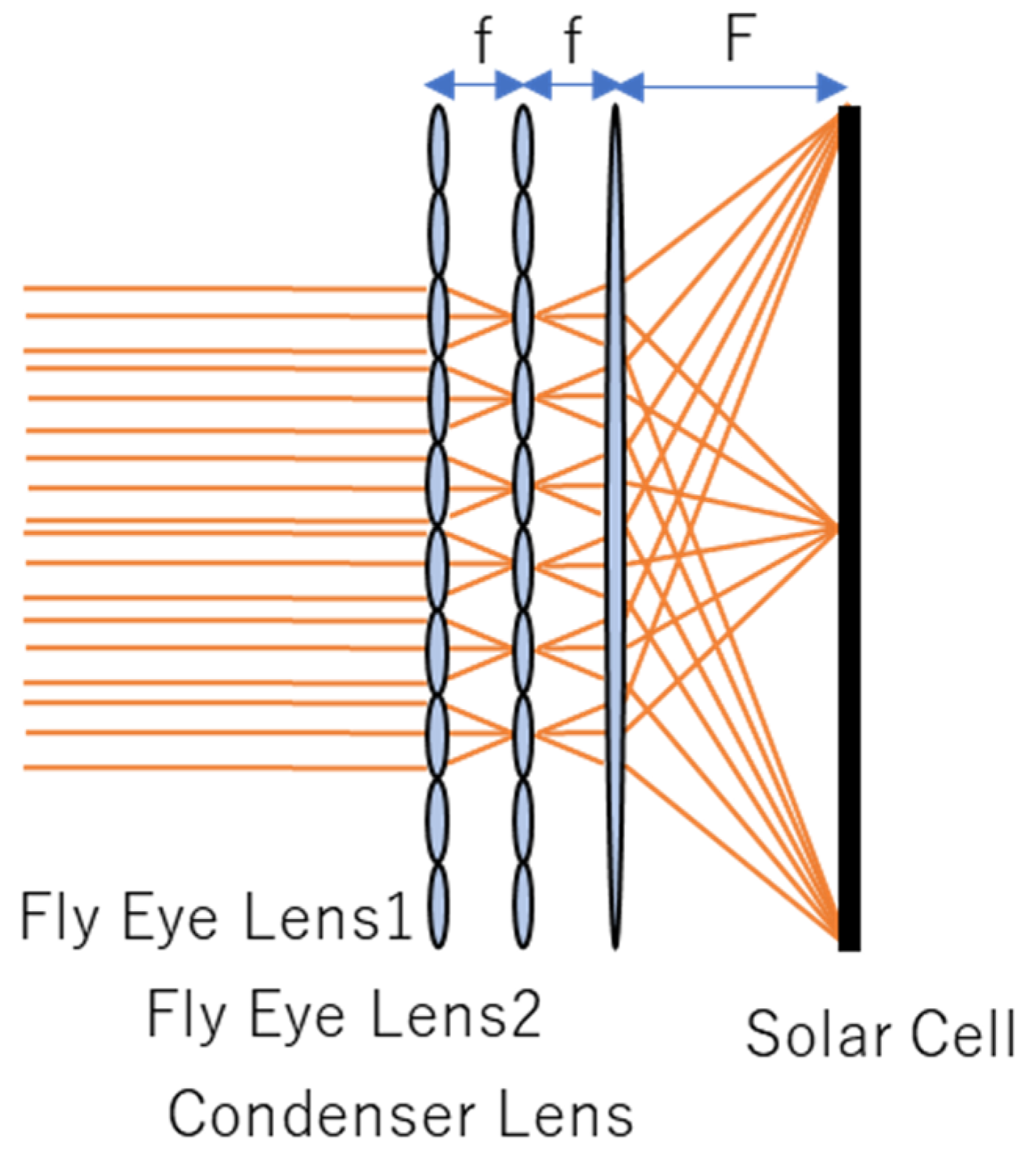
2. Fly Eye Module Model
3. Cooperative OWPT with the Fly Eye Module
3.1. Geometrical, Optical Configuration of the Analysis
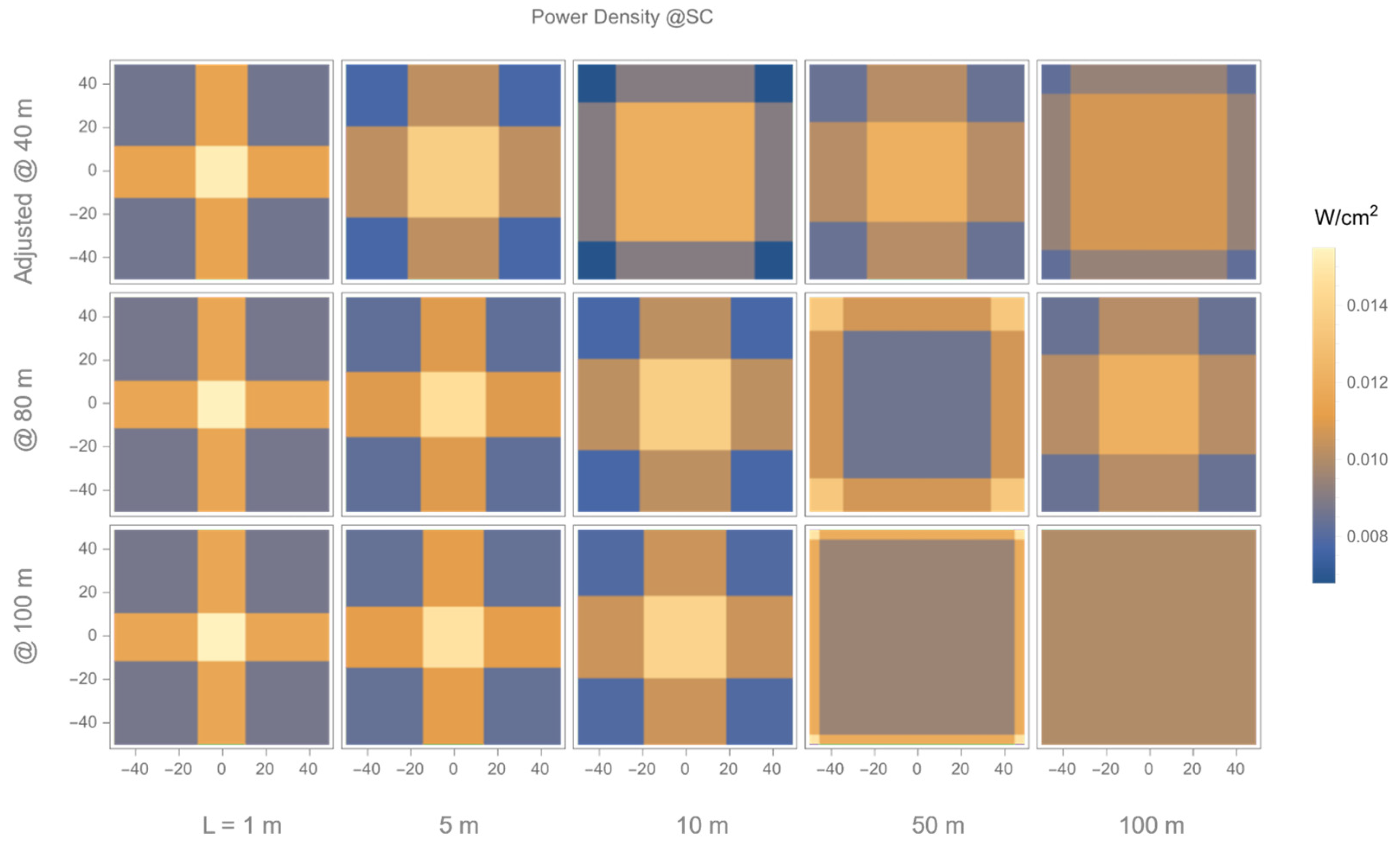
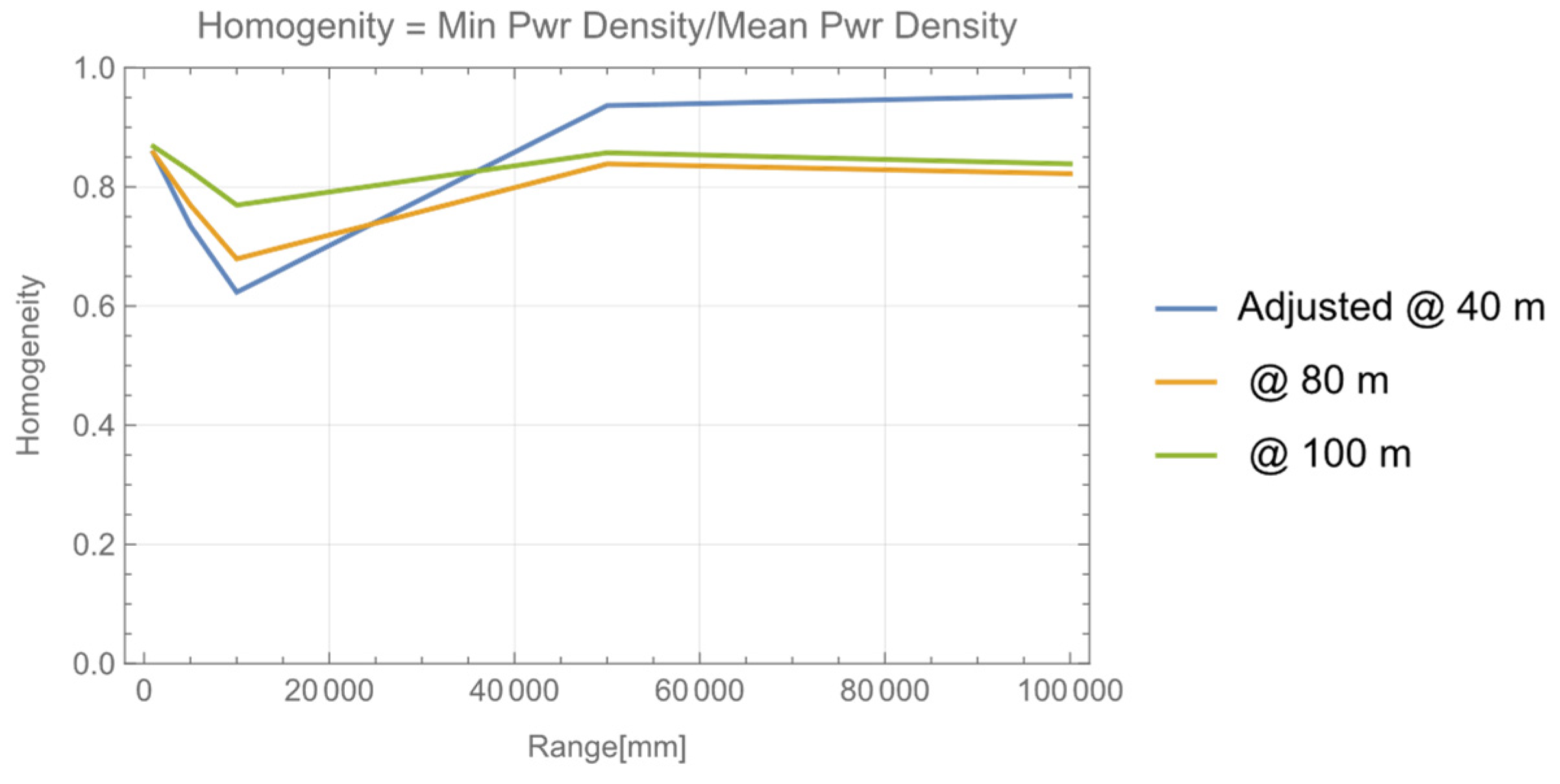
3.2. Power Generation Ratio, Homogenization by Fly Eye Module
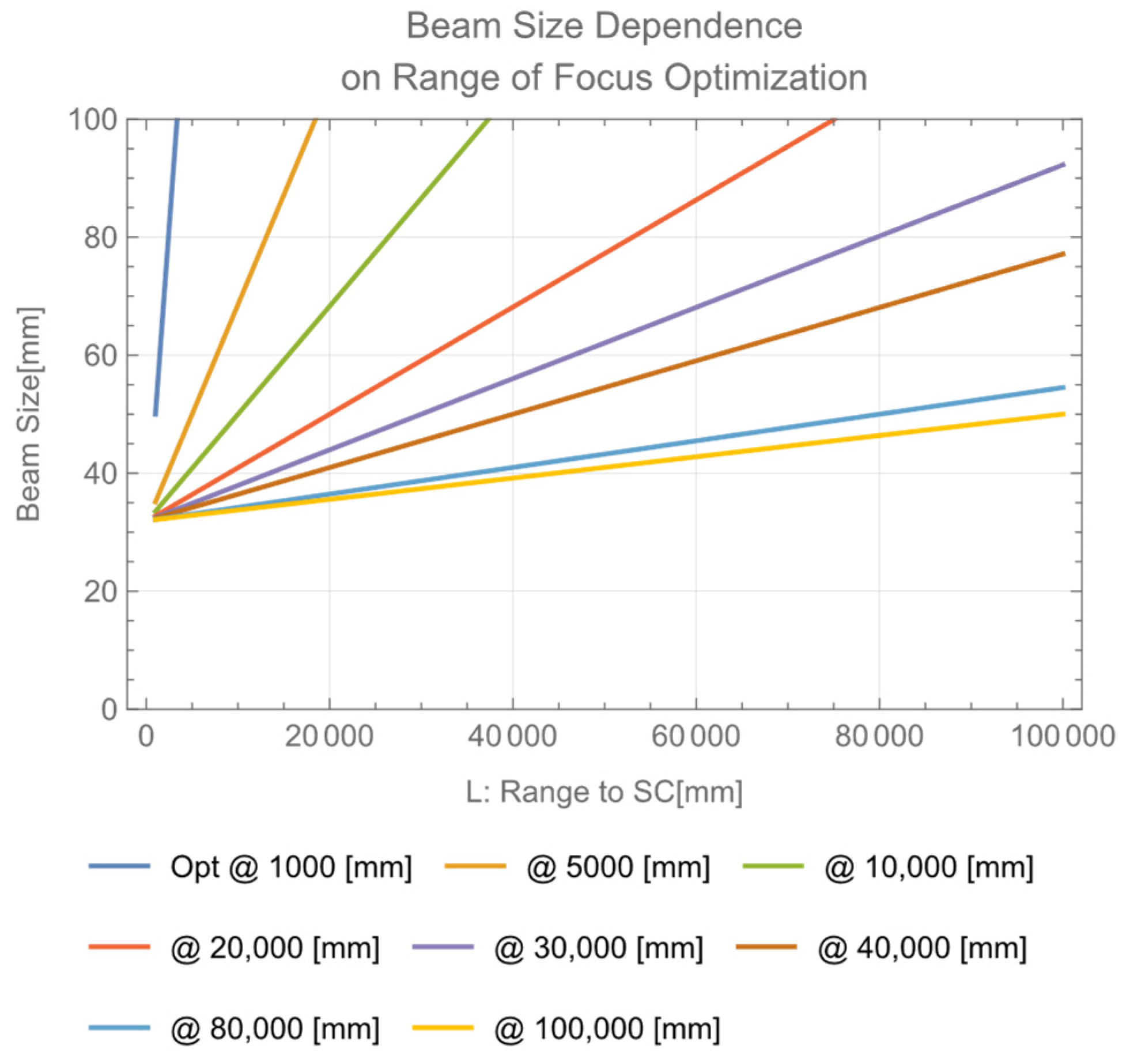
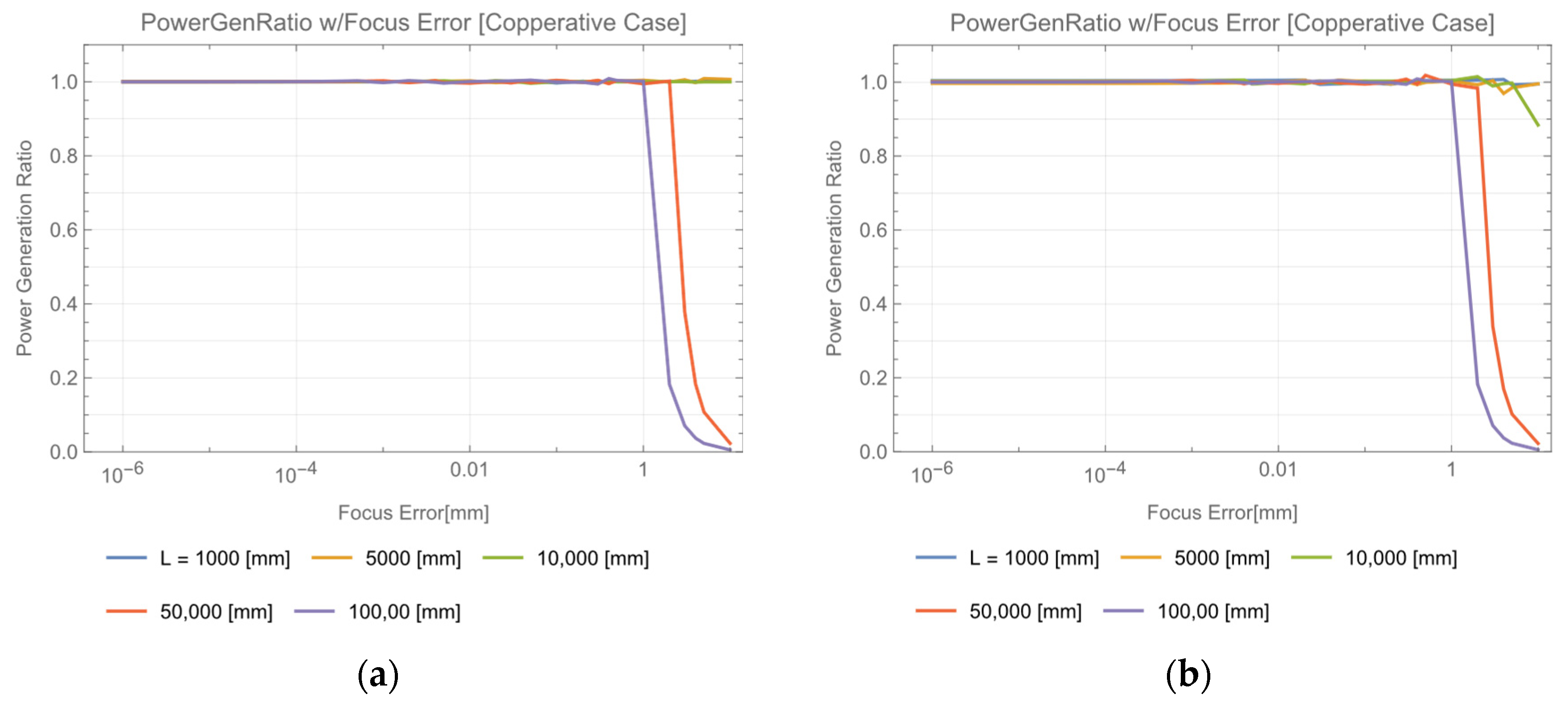
4. Requirement for Focus Adjustment of Transmitter Beam Expander
5. Requirement for Beam Alignment
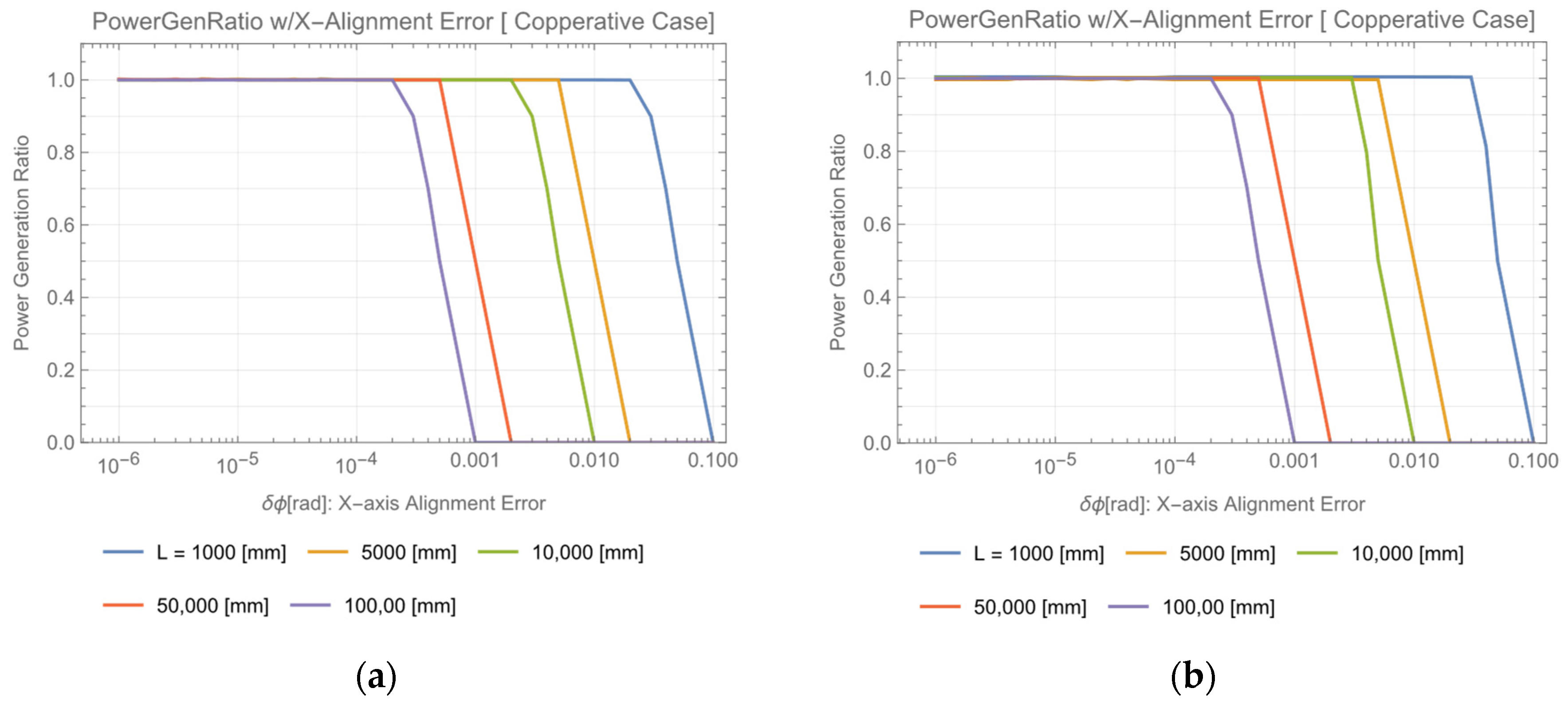
5.1. X(Y) Direction Beam Alignment
5.2. Rotational Alignment around Beam Direction
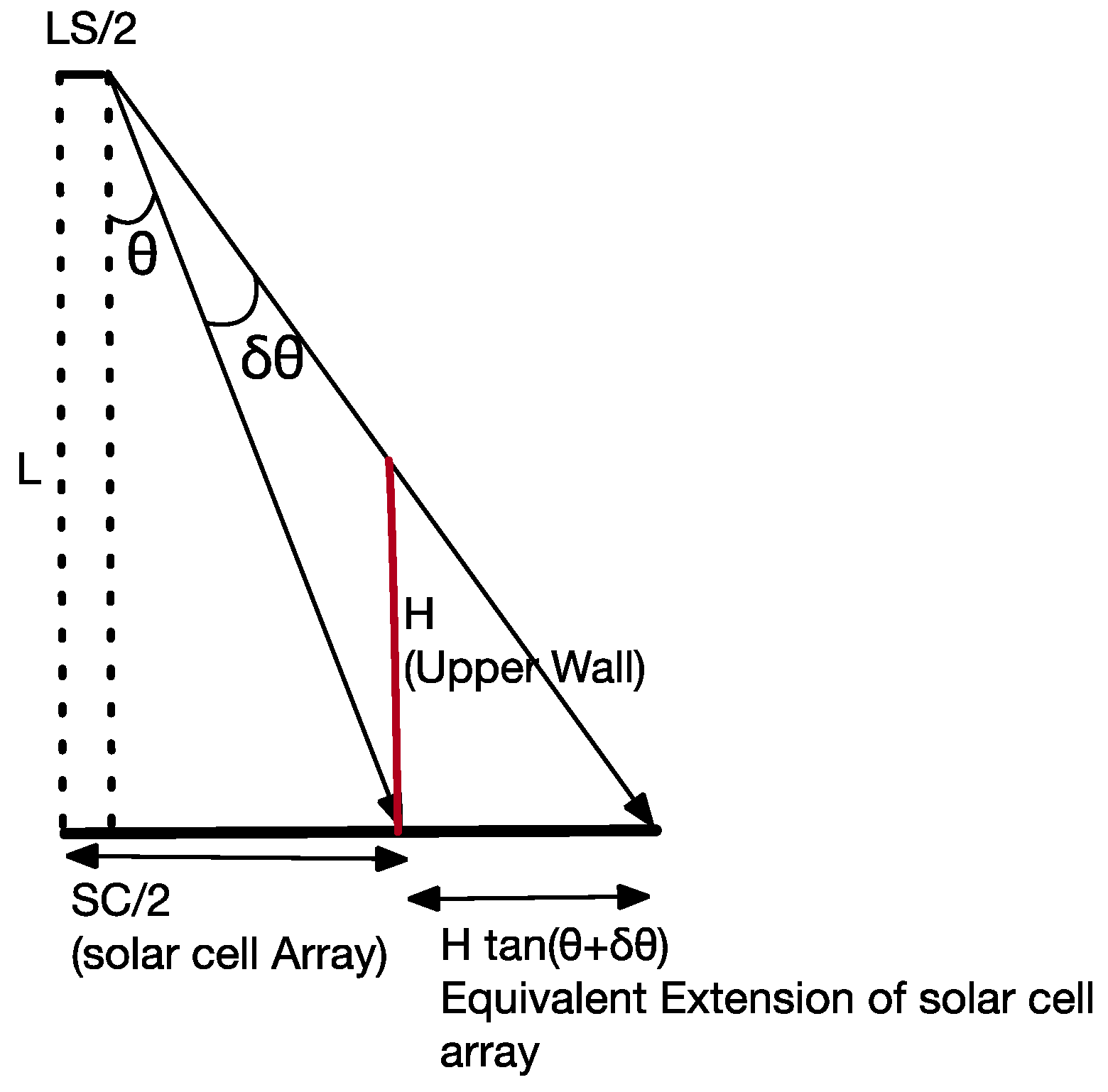
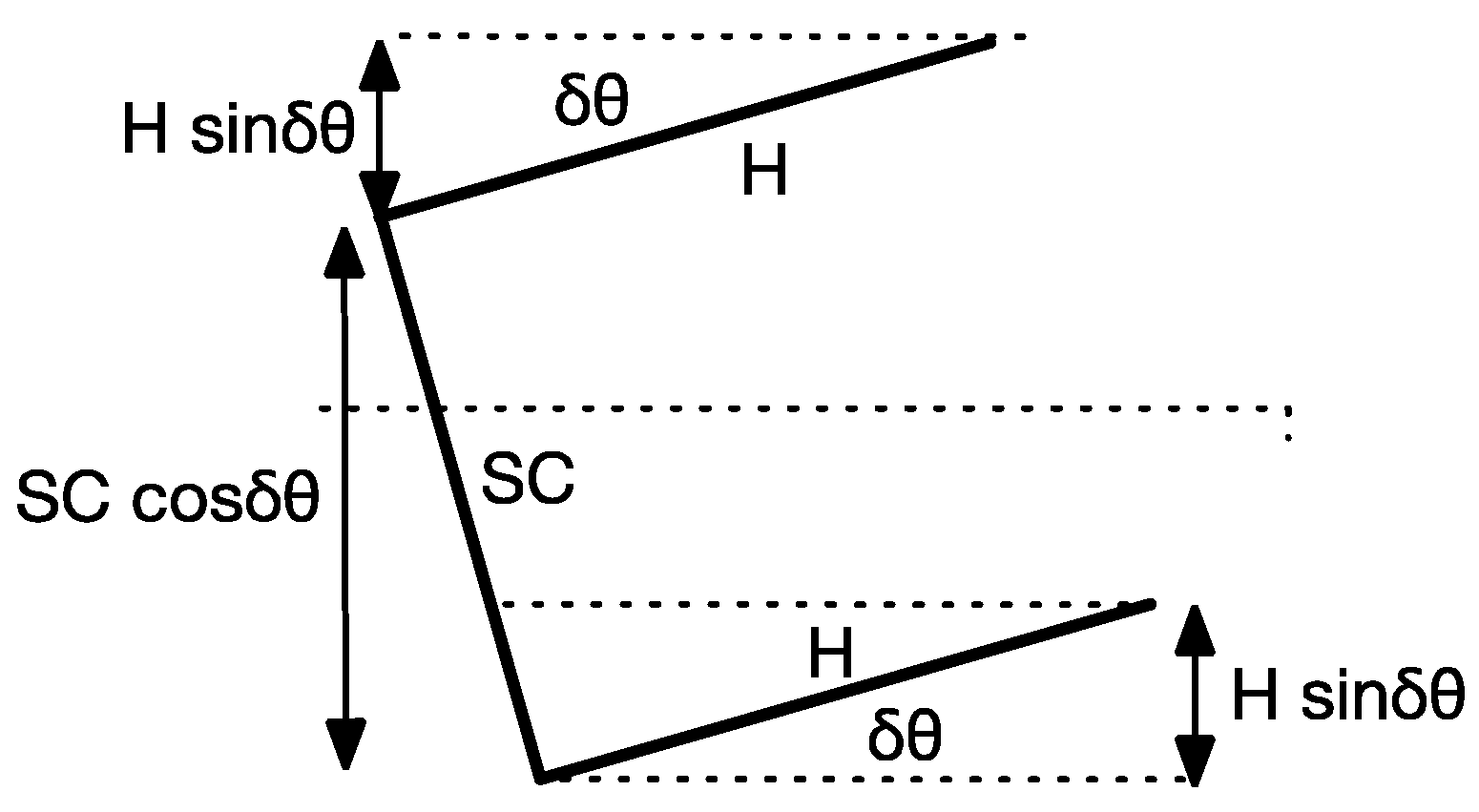
6. Requirement for Tilt of Solar Cell and Beam Energy Confinement in the Fly Eye Module
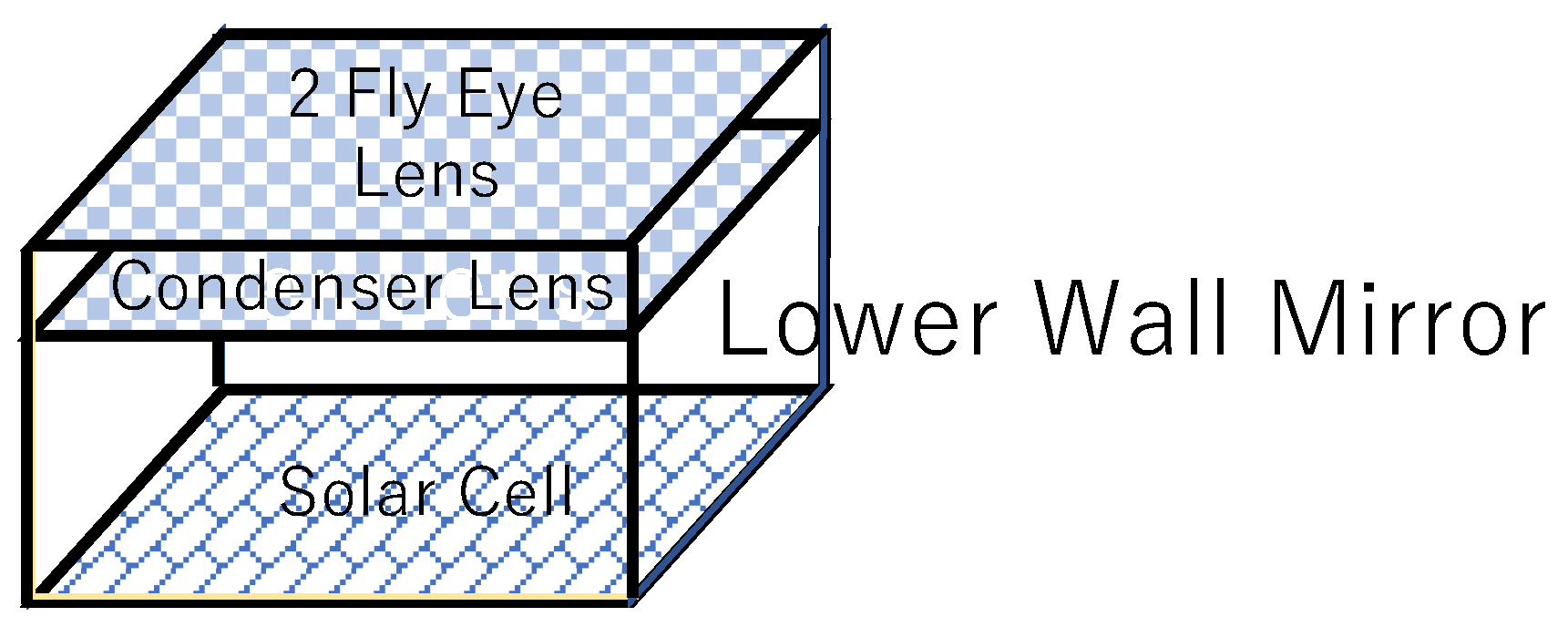
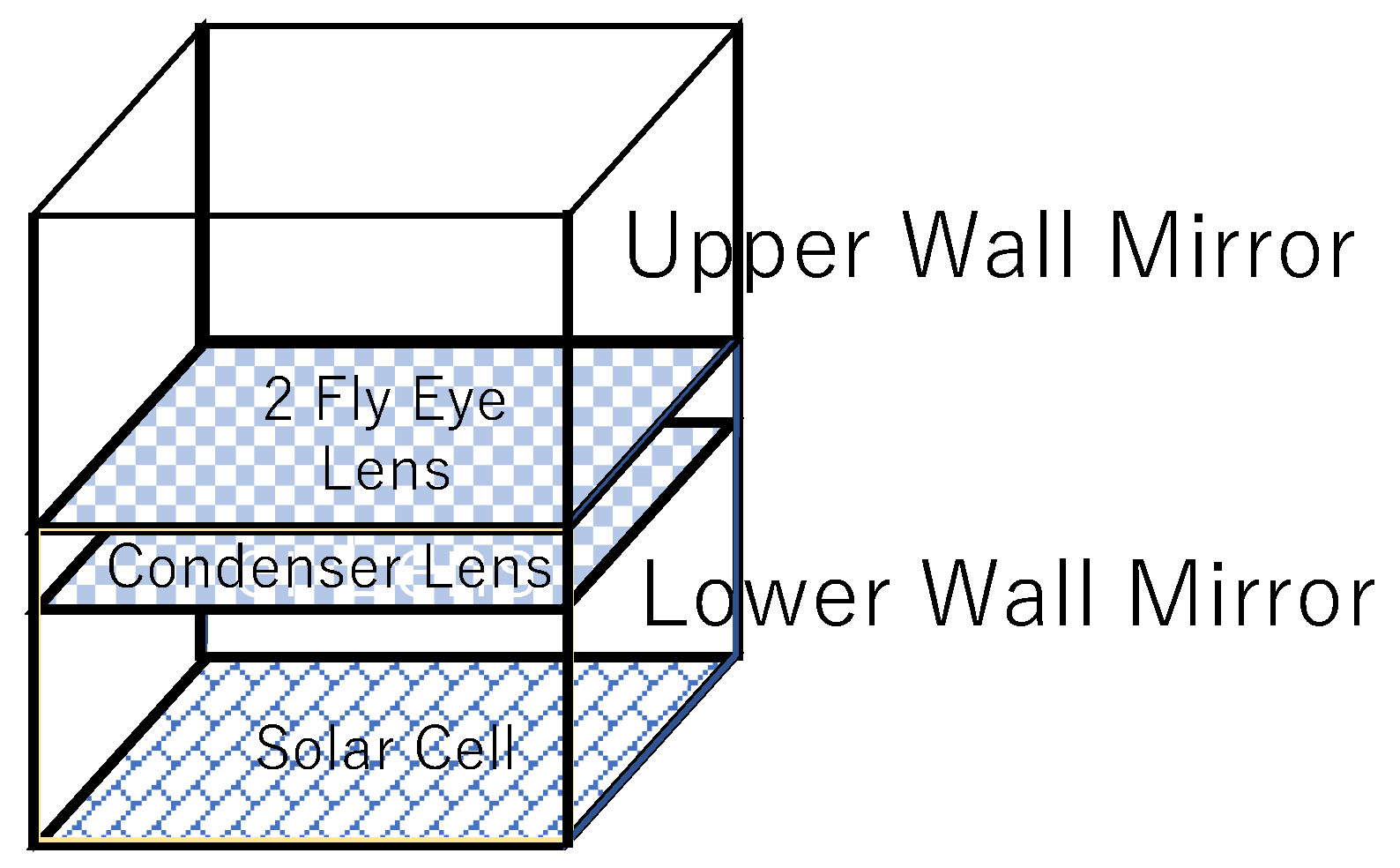
6.1. Upper Wall Mirror, Lower Wall Mirror Configurations
6.2. Beam Acceptance Angle and Beam Confinement Effect in Fly Eye Module with Uppwe/Lower Wall Mirror
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Frolova, E.; Dobroskok, N.; Morozov, A. Critical Review of Wireless Electromagnetic Power Transmission Methods; Atlantis Press International B.V: Saint-Petersburg, Russia, 2022. [Google Scholar] [CrossRef]
- Kurooka, K.; Honda, T.; Komazawa, Y.; Warigaya, R.; Uchida, S. A 46.7% Efficient GaInP Photonic Power Converter under High-Power 638 Nm Laser Uniform Irradiation of 1.5 W/cm2. Appl. Phys. Express 2022, 15, 062003. [Google Scholar] [CrossRef]
- Peng, Y.S.; Yao, M.H.; Liu, Z.M.; Tu, J.L.; Cao, Q.J.; Gong, S.F.; Hu, Y.T.; Zhou, S.L. Numerical Investigation on Performance of Ultra-Thin GaAs Solar Cells Enabled with Frontal Surface Pyramid Array. J. Phys. D Appl. Phys. 2022, 55, 245105. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Tumen-Ulzii, G.; Matsushima, T.; Adachi, C. Performance Analysis of a Perovskite-Based Thing-to-Thing Optical Wireless Power Transfer System. IEEE Photonics J. 2022, 14, 1–8. [Google Scholar] [CrossRef]
- Hassan, M.R. Theory of Dronized Laser Source for Next Generation of Optical Wireless Power Transmission. IEEE J. Select. Top. Quantum Electron. 2022, 28, 1–9. [Google Scholar] [CrossRef]
- Setiawan Putra, A.W.; Tanizawa, M.; Maruyama, T. Optical Wireless Power Transmission Using Si Photovoltaic through Air, Water, and Skin. IEEE Photon. Technol. Lett. 2019, 31, 157–160. [Google Scholar] [CrossRef]
- Rathod, Y.; Hughes, L. Simulating the Charging of Electric Vehicles by Laser. Procedia Comput. Sci. 2019, 155, 527–534. [Google Scholar] [CrossRef]
- Iyer, V.; Bayati, E.; Nandakumar, R.; Majumdar, A.; Gollakota, S. Charging a Smartphone across a Room Using Lasers. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2018, 1, 1–21. [Google Scholar] [CrossRef]
- Baraskar, A.; Yoshimura, Y.; Nagasaki, S.; Hanada, T. Space Solar Power Satellite for the Moon and Mars Mission. J. Space Saf. Eng. 2022, 9, 96–105. [Google Scholar] [CrossRef]
- Lee, N.; Blanchard, J.T.; Kawamura, K.; Weldon, B.; Ying, M.; Young, S.A.; Close, S. Supporting Uranus Exploration with Deployable ChipSat Probes. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA & Virtual, 3–7 January 2022; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2022. [Google Scholar] [CrossRef]
- Landis, G.A. Laser Power Beaming for Lunar Polar Exploration. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, Virtual Event, 24–28 August 2020; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. [Google Scholar] [CrossRef]
- Atul, A. A Study on Space-Based Solar Power System. IOSR-JESTFT 2015, 1, 1–3. [Google Scholar]
- Mori, M.; Kagawa, H.; Saito, Y. Summary of Studies on Space Solar Power Systems of Japan Aerospace Exploration Agency (JAXA). Acta Astronaut. 2006, 59, 132–138. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Y.; He, X.; Luo, B.; Mai, R. Research and Application of Capacitive Power Transfer System: A Review. Electronics 2022, 11, 1158. [Google Scholar] [CrossRef]
- Setiawan Putra, A.W.; Kato, H.; Maruyama, T. Infrared LED Marker for Target Recognition in Indoor and Outdoor Applications of Optical Wireless Power Transmission System. Jpn. J. Appl. Phys. 2020, 59, SOOD06. [Google Scholar] [CrossRef]
- Takeda, K.; Kawashima, N. 1.2 km Laser Energy Transmission for the Lunar Rover Model to Explore the Ice on the Moon. Space Technol. Jpn. Jpn. Soc. Aeronaut. Space Sci. 2004, 3, 45–48. [Google Scholar] [CrossRef]
- Takeda, K.; Kawashima, N. 100 m Laser Energy Transportation Experiment to a Model Rover to Explore the Ice on the Moon. J. Jpn. Soc. Aeronaut. Space Sci. 2003, 51, 393–396. [Google Scholar] [CrossRef]
- Mukherjee, J.; Wulfken, W.; Hartje, H.; Steinsiek, F.; Perren, M.; Sweeney, S.J. Demonstration of Eye-Safe (1550 Nm) Terrestrial Laser Power Beaming at 30 m and Subsequent Conversion into Electrical Power Using Dedicated Photovoltaics. In Proceedings of the 2013 IEEE 39th Photovoltaic Specialists Conference (PVSC), Tampa, FL, USA, 16–21 June 2013; pp. 1074–1076. [Google Scholar] [CrossRef]
- PowerLight Technologies. Available online: https://powerlighttech.com/ (accessed on 23 May 2022).
- The Wireless Power Company. Wi-Charge. Available online: https://www.wi-charge.com (accessed on 9 May 2022).
- Kim, S.-M. Optical Beamforming for Communication and Power Transmission. SPIE Newsroom, 6 February 2014. [Google Scholar] [CrossRef] [Green Version]
- Asaba, K.; Miyamoto, T. System Level Requirement Analysis of Beam Alignment and Shaping for Optical Wireless Power Transmission System by Semi–Empirical Simulation. Photonics 2022, 9, 452. [Google Scholar] [CrossRef]
- Kakeya, H.; Sawada, S.; Ueda, Y.; Kurokawa, T. Integral Volumetric Imaging with Dual Layer Fly-Eye Lenses. Opt. Express 2012, 20, 1963. [Google Scholar] [CrossRef]
- Mori, N. Design of Projection System for Optical Wireless Power Transmission Using Multiple Laser Light Sources, Fly-Eye Lenses, and Zoom Lens. In Proceedings of the 1st Optical Wireless and Fiber Power Transmission Conference (OWPT2019), Yokohama, Japan, 23–25 April 2019; OWPT-3-02. [Google Scholar]
- Katsuta, Y.; Miyamoto, T. Design, Simulation and Characterization of Fly-Eye Lens System for Optical Wireless Power Transmission. Jpn. J. Appl. Phys. 2019, 58, SJJE02. [Google Scholar] [CrossRef]
- Tai, Y.; Miyamoto, T. Experimental Configuration of Fly-eye Lens Based Underwater Optical Wireless Power Transmission. In Proceedings of the 4th Optical Wireless and Fiber Power Transmission Conference (OWPT2022), OWPT-3-02, Online, Japan, 18–21 April 2022. [Google Scholar]
- Tang, J.; Matsunaga, K.; Miyamoto, T. Numerical Analysis of Power Generation Characteristics in Beam Irradiation Control of Indoor OWPT System. Opt. Rev. 2020, 27, 170–176. [Google Scholar] [CrossRef]
- Wagner, L.; Bett, A.W.; Helmers, H. On the alignment tolerance of photovoltaic laser power converters. Optik 2017, 131, 287–291. [Google Scholar] [CrossRef]
- Alsaigh, R.E.; Bauer, R.; Lavery, M.P.J. Multi-Element Lenslet Array for Efficient Solar Collection at Extreme Angles of Incidence. Sci. Rep. 2020, 10, 8741. [Google Scholar] [CrossRef]
- Takeda, Y.; Iizuka, H.; Mizuno, S.; Hasegawa, K.; Ichikawa, T.; Ito, H.; Kajino, T.; Ichiki, A.; Motohiro, T. Silicon Photovoltaic Cells Coupled with Solar-Pumped Fiber Lasers Emitting at 1064 nm. J. Appl. Phys. 2014, 116, 014501. [Google Scholar] [CrossRef]






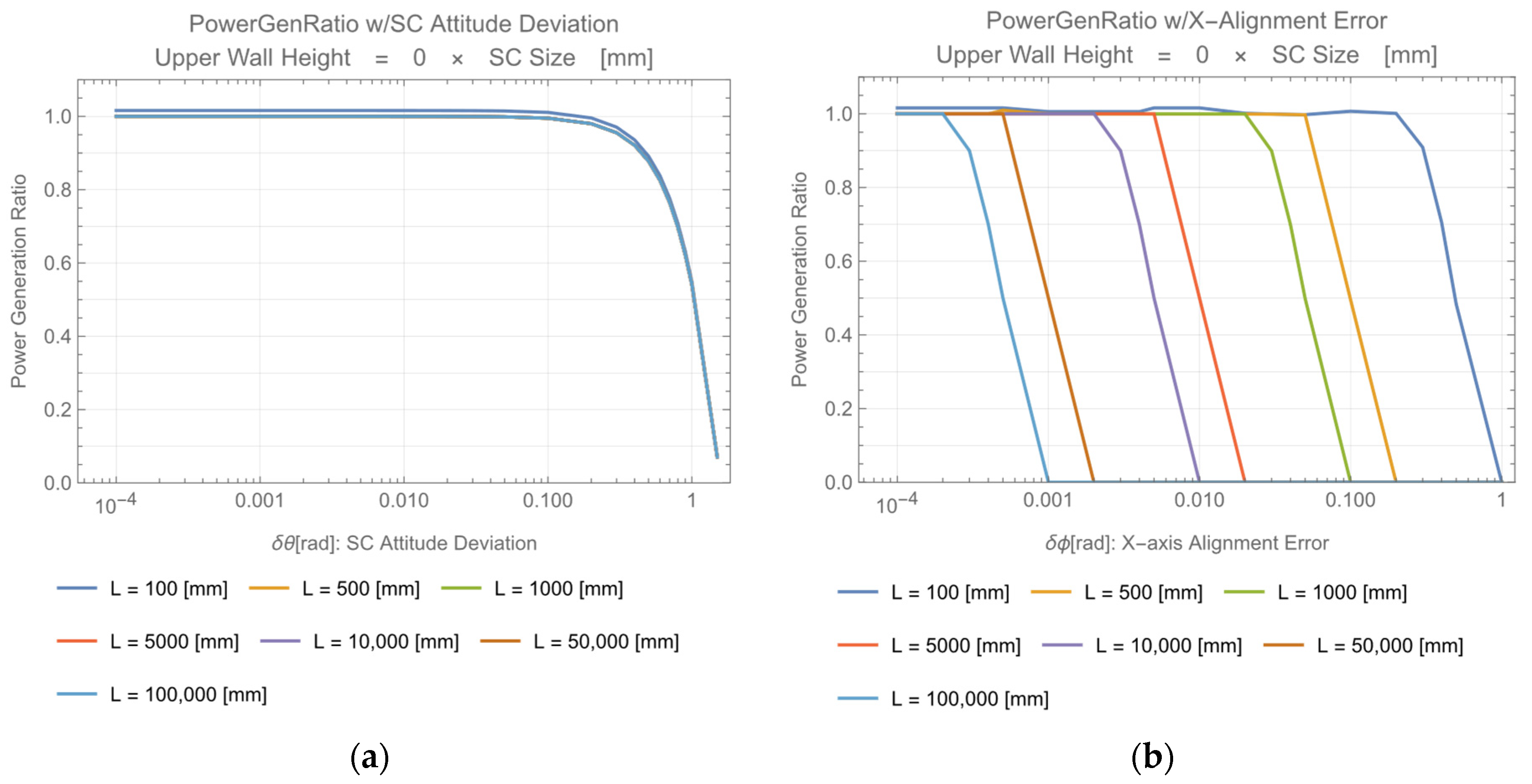
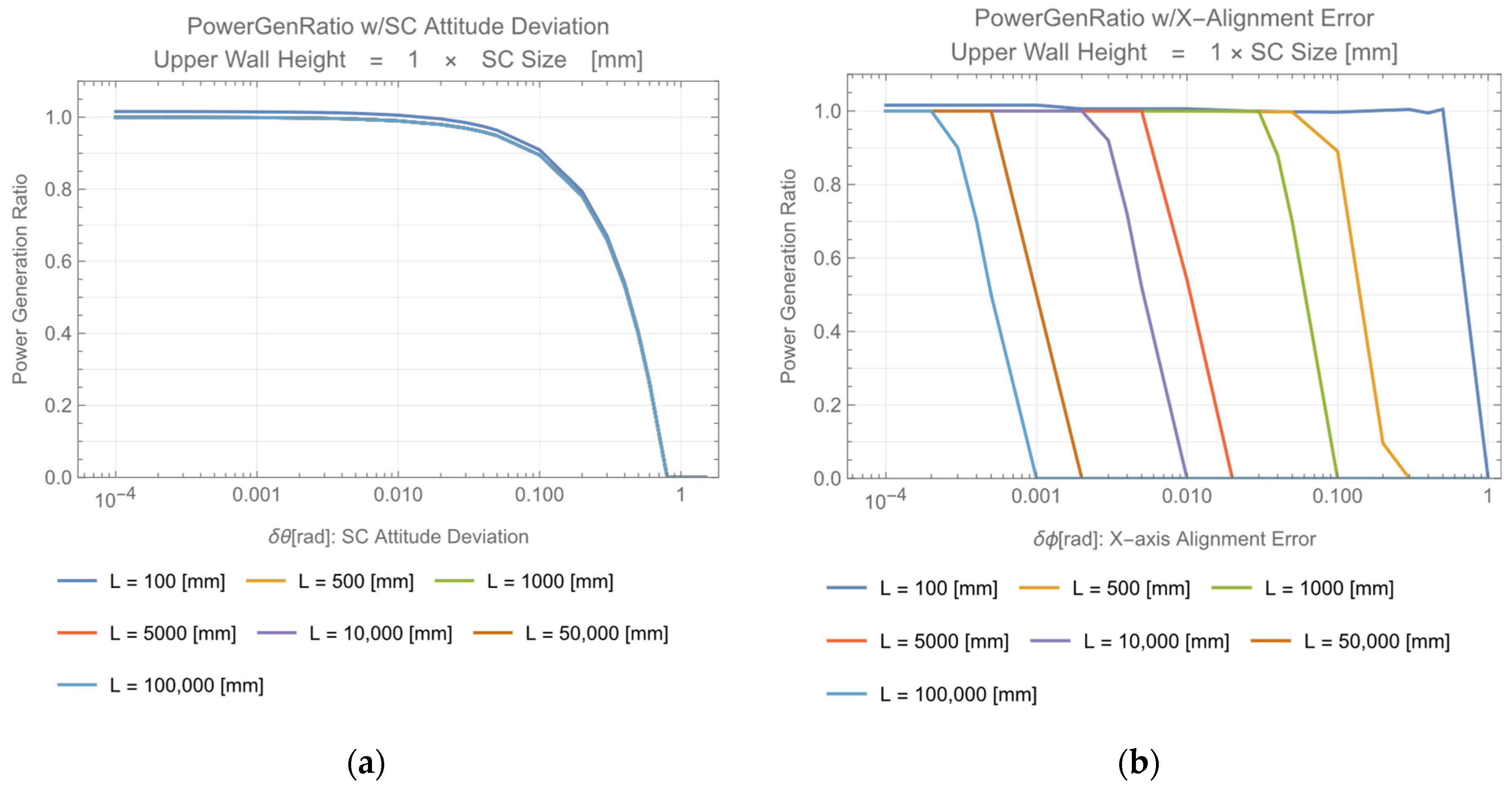
| Configuration | Upper Wall Height | Requirement for Incident Angle | Requirement for X(Y) Deviation |
|---|---|---|---|
| Wall-Less (with neither lower wall nor upper wall mirror | 0 | 245 mrad | 340 mrad (L = 0.1 m) |
| 34 mrad (L = 1 m) | |||
| 3.4 mrad (L = 10 m) | |||
| 0.32 mrad (L = 100 m) | |||
| Lower-Wall Mirror (lower mirror only) | 0 | 499 mrad | 340 mrad (L = 0.1 m) |
| 34 mrad (L = 1 m) | |||
| 3.4 mrad (L = 10 m) | |||
| 0.32 mrad (L = 100 m) | |||
| Two-Wall Mirror (both upper wall and lower wall) | SC | 180 mrad | 606 mrad (L = 0.1 m) |
| 117 mrad (L = 1 m) | |||
| 4.2 mrad (L = 10 m) | |||
| 0.36 mrad (L = 100 m) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asaba, K.; Miyamoto, T. Relaxation of Beam Irradiation Accuracy of Cooperative Optical Wireless Power Transmission in Terms of Fly Eye Module with Beam Confinement Mechanism. Photonics 2022, 9, 995. https://doi.org/10.3390/photonics9120995
Asaba K, Miyamoto T. Relaxation of Beam Irradiation Accuracy of Cooperative Optical Wireless Power Transmission in Terms of Fly Eye Module with Beam Confinement Mechanism. Photonics. 2022; 9(12):995. https://doi.org/10.3390/photonics9120995
Chicago/Turabian StyleAsaba, Kaoru, and Tomoyuki Miyamoto. 2022. "Relaxation of Beam Irradiation Accuracy of Cooperative Optical Wireless Power Transmission in Terms of Fly Eye Module with Beam Confinement Mechanism" Photonics 9, no. 12: 995. https://doi.org/10.3390/photonics9120995
APA StyleAsaba, K., & Miyamoto, T. (2022). Relaxation of Beam Irradiation Accuracy of Cooperative Optical Wireless Power Transmission in Terms of Fly Eye Module with Beam Confinement Mechanism. Photonics, 9(12), 995. https://doi.org/10.3390/photonics9120995





