Performance of Surface Plasmon Resonance Sensors Using Copper/Copper Oxide Films: Influence of Thicknesses and Optical Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Determination of Thicknesses and Optical Properties
- In the model of optical properties, we replace the Drude–Lorentz two-terms model of dispersion by a sum of partial fraction functions for fitting copper and copper oxide properties as a function of the photon energy ( and , respectively). is the order of the partial fractions model, also called the complex-conjugate pole-residue pair model [16]. is actually the number of poles in the function (see Equation (5)).
- We replace the two-steps method using first the bulk properties by a single multi-objective method, involving the error of fit and the relative difference between the optical properties we found and the bulk material properties. The purpose is to decrease the computational time.
- To achieve the fitting, we use three metaheuristic methods: Particle Swarm Method (PSO), Genetic Algorithm (GA), and Artificial Bee Colony method (ABC), with Gradient (GR) or Nelder–Mead simplex (NM) hybridization. Actually, metaheuristics are more or less efficient for achieving optimization, depending on the dimension of the problem (the number of input parameters of the model that have to be found) and on the topology of the objective function: the error of fit. Moreover, many realizations of the metaheuristics must be analyzed carefully to numerically characterize the stability of the solution and, hopefully, its uniqueness.
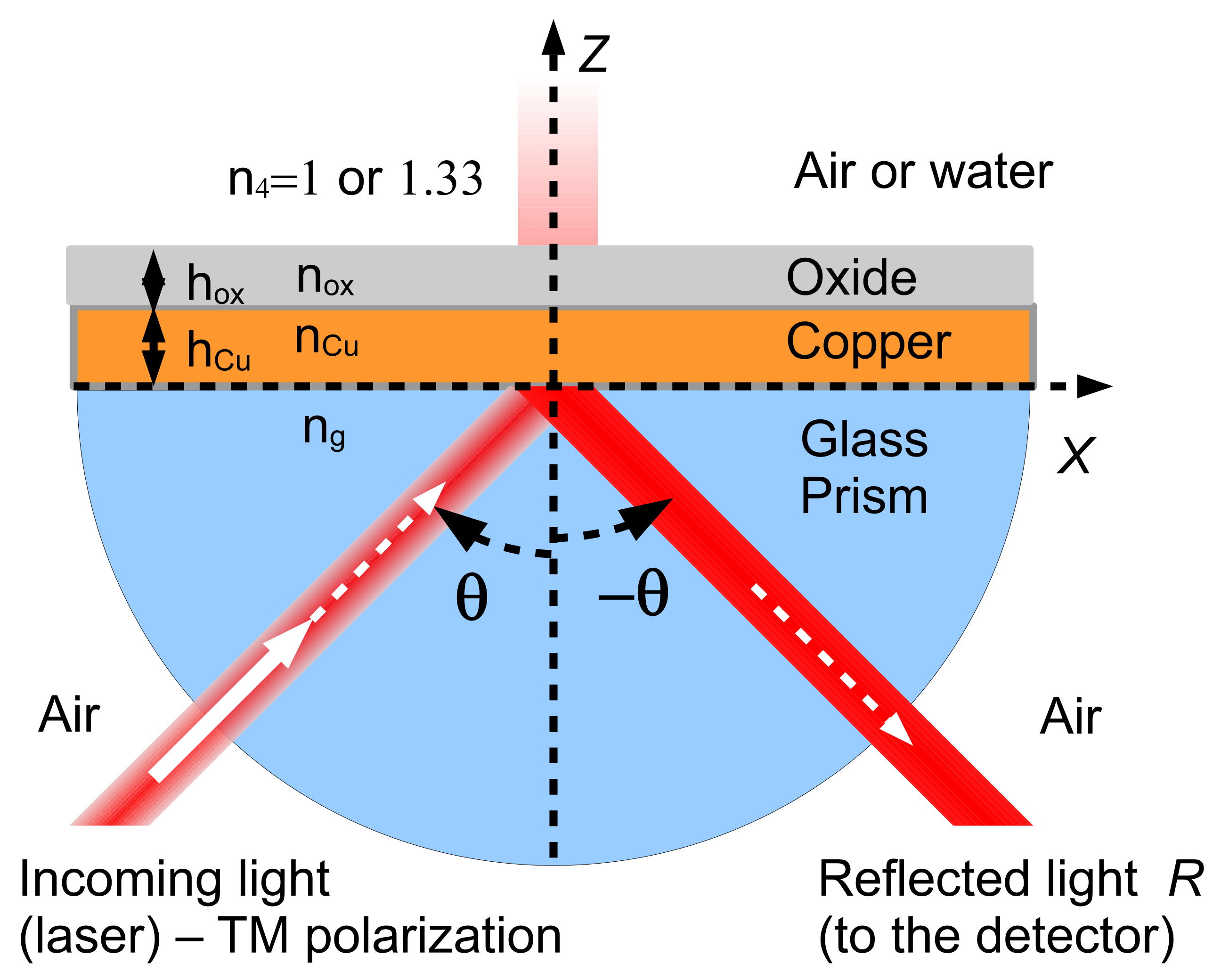
2.2. The SPR Model
2.3. Performance of the SPR Sensor
2.3.1. Sensitivity
2.3.2. Full Width at Half Maximum
2.3.3. Figure of Merit
2.4. Optimal Thicknesses
2.5. Investigated Samples
- Copper and copper oxide thicknesses are globally in agreement with those obtained from experimental measurements (see Appendix B).
- The real part of the relative permittivity of copper is smaller than the bulk one for almost all samples. The imaginary part of the relative permittivity of copper is about twice the bulk one. The mean value of over the samples with nm is (standard deviation ) compared to [29].
- The real part and the imaginary parts of the relative permittivity of oxide are close to that of the bulk, except for full oxidized samples for which both parts decrease. This behavior is probably due to air inclusion in oxide (the grain size of oxide can reach 80 nm, see Appendix B). The mean value of over the samples with nm is (standard deviation ) compared to and [29]. If we suppose a chemical mix of both oxides, we deduce that oxide may be made of 76% Cu2O and 24% CuO. This result was confirmed by XPS measurements [14,30]. The decrease in the real part of the oxide permittivity may also be due to air inclusion in oxide.
- For samples with roughness varying from 2 to 14 nm [14], the electromagnetic model of generalized Fresnel coefficients could be accurate enough. The quality of absorbance fitting shown in Figure A1, Figure A2, Figure A3, Figure A4, Figure A5, Figure A6, Figure A7, Figure A8, Figure A9, Figure A10 and Figure A11 confirms the validity of the model, which can therefore be used to model the SPR.
3. Results
3.1. Dry Case
3.2. Wet Case
4. Discussion
4.1. Cu-Oxide-SPR Performance
4.2. Optimal Thicknesses
5. Conclusions
- Production series of samples with controlled annealing under low temperature;
- Characterization of samples (measurement of thickness and optical properties) from absorbance curves, for example;
- Characterization of samples in angular interaction mode;
- Fit of the SPR signal to verify the optical properties;
- Selection of the best sample and verification at regular time intervals that the thicknesses and optical properties remain the same.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIM | Angular Interrogation Mode |
| ABC | Artificial Bee Colony |
| EM | Evolutionary Method |
| FOM | Figure of Merit |
| FWHM | full width at half maximum |
| GR | method of gradient descent |
| NM | Nelder–Mead Simplex Method |
| PSO | Particle Swarm Optimization |
| SPR | Surface Plasmon Resonance |
Appendix A. The Samples Preparation
| Annealing Time (Min) | Temperature ( C) | Reference Name of Data |
|---|---|---|
| 0 | 20 | A0XYnmCut0 |
| 22 | 120 | A0XYnm22min120 |
| 72 | 120 | A0XYnm72min120 |
| 102 | 120 | A0XYnm102min120 |
| 160 | 120 | A0XYnm160min120 |
| 10 | 120 | A0XYnm190min120 |
| 240 | 130 | A0XYnm240min130 |
| 600 | 130 | A0XYnm600min130 |
| 900 | 170 | A0XYnm900lin170 |
| 910 | 170 | A0XYnm910min170 |
Appendix B. Measurement of Thicknesses
| Sample | SEM | AFM | MAI | SE | UV-Vis-NIR |
|---|---|---|---|---|---|
| A010nmCut0 | − | 11 ± 3 | 7.2 ± 0.1 | 11.0 ± 0.2 | 9.8 ± 0.2 |
| − | 0.2 ± 0.1 | 3.4 ± 0.2 | 1.8 ± 1.1 | ||
| A030nmCut0 | − | 31 ± 5 | 28.2 ± 0.1 | 38.7 ± 1.3 | 30.0 ± 0.1 |
| − | 2.9 ± 0.1 | 3.7 ± 0.2 | 0.0 ± 0.7 | ||
| A050nmCut0 | − | 51 ± 8 | − | − | 50.0 ± 0.1 |
| − | − | 5 ± 0.9 | 0.1 ± 0.2 | ||
| A010nm900min170 | 34 ± 7 | 26 ± 3 | 5.6 ± 0.1 | 0.9 ± 0.4 | 1.2 ± 0.5 |
| 19.6± 0.1 | 20.3 ± 3.1 | 19.7 ± 1.6 | |||
| A030nm900min170 | 104 ± 29 | 98 ± 23 | 4.9 ± 0.1 | 0.3 ± 1.4 | 0.6 ± 4.2 |
| 84.6 ± 0.1 | 63.1 ± 7.4 | 44.8 ± 6.6 | |||
| A050nm900min170 | 136 ± 15 | 142 ± 30 | − | 0 ± 7.9 | 0.0 ± 0.6 |
| − | 87.3 ± 3.7 | 89.6 ± 4.4 | |||
| − | − |
Appendix C. Method of Fitting and Results
Appendix C.1. Metaheuristics for UV-Visible-NIR Absorbance Fitting
- PSO: the parameters are moved along a vector of translation, which is the sum of three vectors [37,38,39,40]. More details are given in Reference [38]:
- —
- A uniform random contribution of the difference between the N parameter sets at the previous step of the evolutionary loop and the global best position of this swarm (weight ).
- —
- A uniform random contribution of the difference between the N parameter sets at the previous step of the evolutionary loop and their best positions obtained in all the previous steps (weight ).
- —
- A linearly decreasing contribution of the previous translation vector, with weight ranging from 0.99 at the beginning of the evolutionary loop to 0.43 at the maximum number of iterations.
If the value of the multi-objective function is better than that obtained at the previous step of the evolutionary loop, then the best parameter set is updated for the next step. Classical PSO without hybridization was used to analyze aluminum oxidation from Turbadar experimental data [41] in the Kretschmann configuration. The strong dependence of Aluminum optical properties as a function of its nanometric thickness was demonstrated. - GA: the input parameters are varied by using crossover, mutation and selection operators [38,40,42].
- —
- The crossover operator calculates the mean value of each parameter of two randomly selected sets. The crossover operates on parameter set.
- —
- The mutation operator modifies each parameter by adding a normally distributed random vector with zero expectation and self-adaption variance [43]. The mutation operates on a parameter set.
- —
- The N parameter sets that result from the crossover, and mutation operators are evaluated.
- —
- The selection operator keeps the N best solutions among these parameter sets and the best set, obtained at the previous step of the evolutionary loop according to an elitist strategy [43].
- ABC: the parameter sets are divided into two families of size . Specific operators are applied to these two families. The parameter set is updated by adding a translation vector [48]. More details on ABC can be found in [49].
- —
- First family: the translation vector is a uniform random contribution of the difference between the parameter set and another randomly picked one from the same family. The multi-objective function is evaluated and the family is updated with a parameter set for improved values of the multi-objective function. A probability of attraction of these parameter sets is calculated to promote the best to guide the second family sets [48].
- —
- Second family: the translation vector is the uniform random contribution of the difference between the parameter set and a random pickup of the most attractive parameter sets of the first family.
Appendix C.2. The Domain of Search
Appendix C.3. The Multi-Objective Function
Appendix C.4. Detailed Results of Fitting
Appendix C.4.1. Sample of Initial Copper Thickness nm
| Sample | F | Method | ||||
|---|---|---|---|---|---|---|
| (nm) | (nm) | at eV | at eV | |||
| A010nmCut0 | 9.8 | 1.8 | −12.5 + 3.6 | 8.2 + 1.2 | 7.9× 10 | EM + NM |
| (0.2) | (1.1) | (0.5 + 0.5) | (0.4 + 0.5) | (5 × 10) | ||
| 37%, 63%, 0%, 100%, 0 | ||||||
| A010nm22min120 | 9.7 | 2.8 | −11.9 + 3.3 | 8.2 + 1.3 | 5.1 × 10 | ABC + NM |
| (0.2) | (1.2) | (0.5 + 0.5) | (0.4 + 0.5) | (1 × 10) | ||
| 100%, 0%, 0%, 100%, 0 | ||||||
| A010nm72min120 | 9.6 | 2.8 | −12.5 + 3.6 | 7.8 + 1.1 | 7.1 × 10 | ABC + NM |
| (0.3) | (1.4) | (0.7 + 0.5) | (0.5 + 0.4) | (8 × 10) | ||
| 43%, 57%, 0%, 100%, 0 | ||||||
| A010nm102min120 | 9.5 | 3.2 | −14.1 + 3.2 | 7.7 + 1.0 | 8.0 × 10 | ABC + NM |
| (0.3) | (1.5) | (0.8+0.5) | (0.5 + 0.4) | (7 × 10) | ||
| 100%, 0%, 0%, 100%, 0 | ||||||
| A010nm160min120 | 8.7 | 4.9 | −15.4 + 4.8 | 8.0 + 1.0 | 1.1 × 10 | EM + NM |
| (0.5) | (1.0) | (1.1 + 1.0) | (1.1 + 0.5) | (6 × 10) | ||
| 36%, 45%, 19%, 100%, 0 | ||||||
| A010nm190min120 | 8.5 | 6.9 | −14.8 + 5.6 | 7.5 + 1.2 | 9.3 × 10 | EM + NM |
| (0.5) | (1.1) | (1.2 + 1.0) | (1.1 + 0.5) | (6 × 10) | ||
| 60%, 40%, 0%, 100%, 0 | ||||||
| A010nm240min130 | 2.6 | 16.7 | −11.1 + 3.4 | 9.6 + 0.6 | 6.2 × 10 | EM + NM |
| (0.7) | (1.1) | (0.4 + 0.6) | (0.3 + 0.2) | (5 × 10) | ||
| 24%, 29%, 47%, 92%, 8 | ||||||
| A010nm600min130 | 1.9 | 17.9 | −11.2 + 3.2 | 8.6 + 0.1 | 7.6 × 10 | ABC + NM |
| (0.5) | (0.9) | (0.5 + 0.5) | (0.4 + 0.0) | (5 × 10) | ||
| 50%, 22%, 28%, 100%, 0 | ||||||
| A010nm900min170 | 1.2 | 18.5 | −14.2 + 4.2 | 8.5 + 0.0 | 1.6 × 10 | PSO + NM |
| (0.5) | (1.5) | (1.1 + 1.5) | (0.7 + 0.1) | (5 × 10) | ||
| 25%, 44%, 31%, 100%, 0 | ||||||
| A010nm910min170 | 0.7 | 18.7 | −11.0+3.3 | 8.3 + 0.0 | 6.4 × 10 | ABC + NM |
| (0.5) | (1.0) | (0.6 + 0.6) | (0.4 + 0.0) | (8 × 10) | ||
| 56%, 16%, 28%, 100%, 0 | ||||||

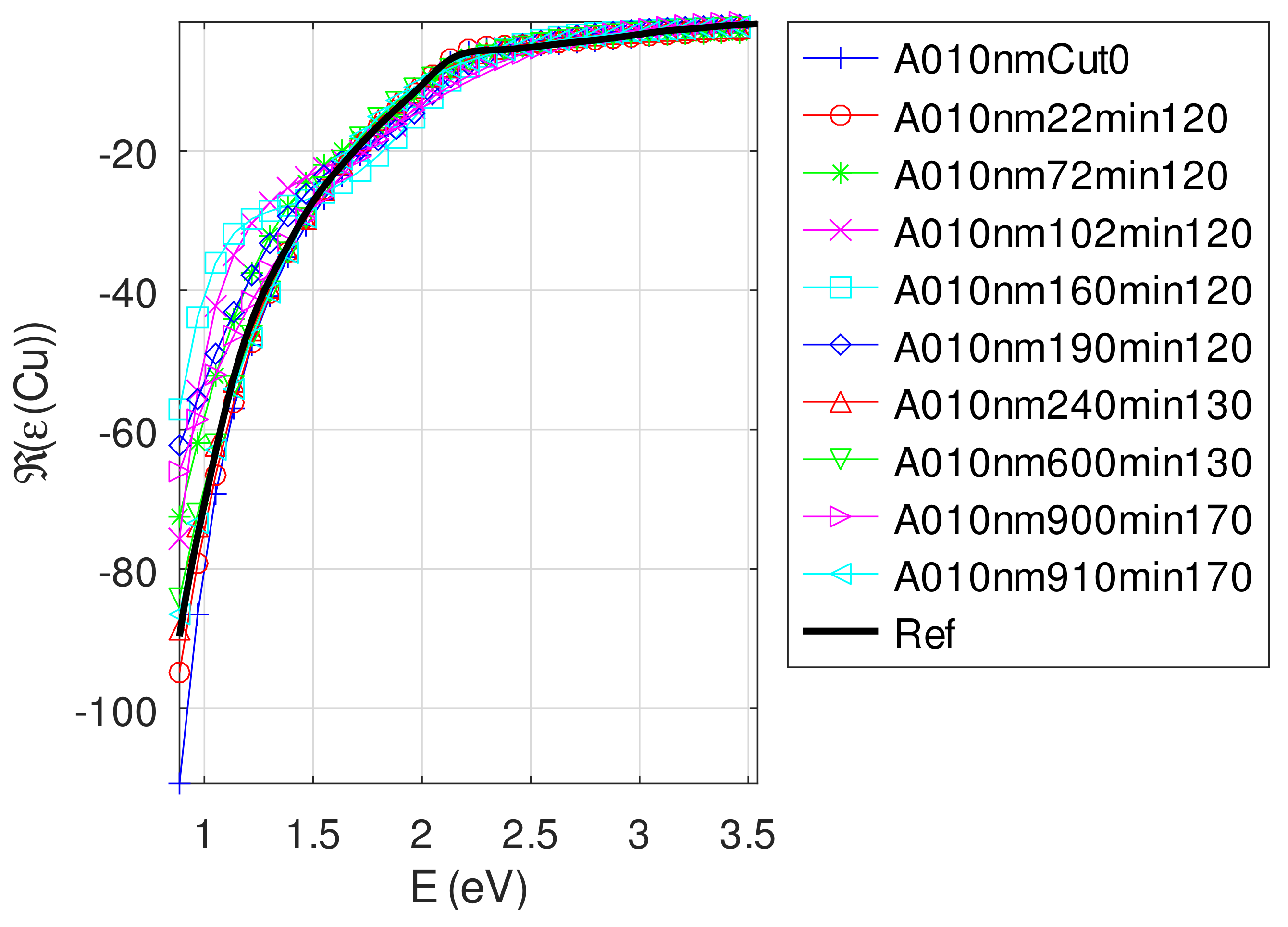



Appendix C.4.2. Sample of Initial Copper Thickness nm
| Sample | F | Method | ||||
|---|---|---|---|---|---|---|
| (nm) | (nm) | at eV | at eV | |||
| A030nmCut0 | 30.0 | 0.0 | −14.1 + 2.7 | 8.3 + 1.2 | 8.7 × 10 | ABC + NM |
| (0.1) | (0.7) | (0.5 + 0.6) | (0.2 + 0.3) | (4 × 10) | ||
| 62%, 38%, 0%, 100%, 0 | ||||||
| A030nm22min120 | 29.9 | 0.1 | −13.3 + 2.8 | 8.6 + 0.7 | 7.9 × 10 | ABC + NM |
| (0.1) | (0.5) | (0.5 + 0.5) | (0.3 + 0.3) | (8 × 10) | ||
| 42%, 50%, 8%, 100%, 0 | ||||||
| A030nm72min120 | 29.5 | 1.0 | −12.5 + 2.9 | 8.2 + 1.0 | 6.2 × 10 | EM + NM |
| (0.3) | (0.5) | (0.4 + 0.4) | (0.3 + 0.3) | (4 × 10) | ||
| 44%, 56%, 0%, 100%, 0 | ||||||
| A030nm102min120 | 29.4 | 1.0 | −13.0 + 2.0 | 8.1 + 1.1 | 5.2 × 10 | EM + NM |
| (0.4) | (0.7) | (0.5 + 0.3) | (0.3 + 0.2) | (5 × 10) | ||
| 14%, 86%, 0%, 100%, 0 | ||||||
| A030nm160min120 | 28.2 | 3.1 | −12.8 + 3.1 | 8.3 + 0.5 | 4.9 × 10 | ABC + NM |
| (0.6) | (1.0) | (0.5 + 0.5) | (0.3 + 0.3) | (5 × 10) | ||
| 17%, 83%, 0%, 100%, 0 | ||||||
| A030nm190min120 | 27.9 | 3.5 | −13.5 + 2.9 | 8.4 + 0.6 | 4.8 × 10 | ABC + NM |
| (0.7) | (1.2) | (0.5 + 0.5) | (0.3 + 0.3) | (5 × 10) | ||
| 50%, 50%, 0%, 100%, 0 | ||||||
| A030nm240min130 | 21.2 | 14.5 | −11.3 + 8.2 | 7.7 + 1.3 | 1.1 × 10 | EM + NM |
| (1.5) | (2.4) | (1.1 + 1.5) | (0.9 + 1.1) | (5 × 10) | ||
| 9%, 70%, 21%, 100%, 0 | ||||||
| A030nm600min130 | 20.1 | 16.6 | −15.9 + 6.8 | 7.7 + 0.6 | 1.2 × 10 | EM + NM |
| (1.2) | (2.2) | (0.9 + 0.8) | (0.9 + 0.6) | (5 × 10) | ||
| 18%, 57%, 25%, 100%, 0 | ||||||
| A030nm900min170 | 0.6 | 44.8 | −10.2 + 2.2 | 7.0 + 0.0 | 1.1 × 10 | EM + NM |
| (4.2) | (6.6) | (0.9 + 1.0) | (1.1 + 0.8) | (5 × 10) | ||
| 4%, 96%, 0%, 100%, 0 | ||||||
| A030nm910min170 | 0.4 | 45.8 | −11.5 + 3.1 | 7.1 + 0.0 | 1.1 × 10 | EM + NM |
| (4.2) | (6.6) | (0.9 + 1.0) | (1.1 + 0.8) | (5 × 10) | ||
| 0%, 40%, 60%, 100%, 0 | ||||||
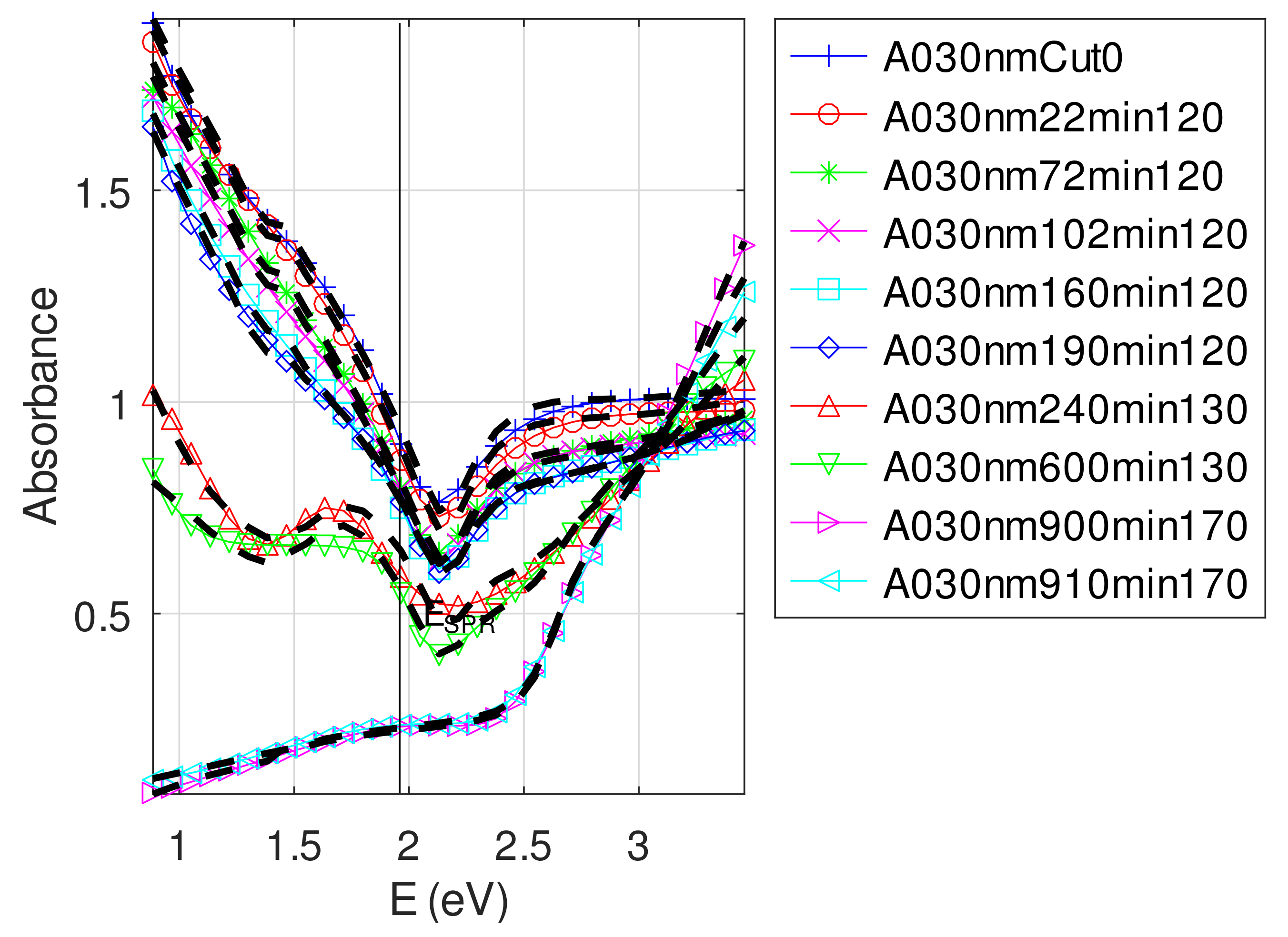
| Sample | F | Method | ||||
|---|---|---|---|---|---|---|
| (nm) | (nm) | at eV | at eV | |||
| A050nmCut0 | 50.0 | 0.1 | −15.4 + 2.0 | 7.9 + 1.0 | 1.0 × 10 | EM + NM |
| (0.1) | (0.2) | (0.5 + 0.4) | (0.4 + 0.3) | (5 × 10) | ||
| 38%, 62%, 0%, 100%, 0 | ||||||
| A050nm22min120 | 49.8 | 0.1 | −14.6 + 1.8 | 8.2 + 0.8 | 9.3 × 10 | EM + NM |
| (0.1) | (0.2) | (0.4 + 0.4) | (0.3 + 0.3) | (9 × 10) | ||
| 26%, 48%, 26%, 100%, 0 | ||||||
| A050nm72min120 | 49.8 | 0.6 | −14.2 + 2.2 | 8.3 + 0.9 | 7.0 × 10 | EM + NM |
| (0.3) | (0.3) | (0.4 + 0.4) | (0.3 + 0.3) | (4 × 10) | ||
| 33%, 51%, 15%, 100%, 0 | ||||||
| A050nm102min120 | 49.8 | 0.6 | −13.2 + 2.3 | 8.8 + 0.5 | 5.7 × 10 | EM + NM |
| (0.3) | (0.3) | (0.3 + 0.5) | (0.3 + 0.3) | (7 × 10) | ||
| 33%, 56%, 11%, 100%, 0 | ||||||
| A050nm160min120 | 49.2 | 1.6 | −12.5 + 2.3 | 8.4 + 0.8 | 5.6 × 10 | EM + NM |
| (0.5) | (0.6) | (0.4 + 0.4) | (0.3 + 0.2) | (4 × 10) | ||
| 38%, 59%, 3%, 100%, 0 | ||||||
| A050nm190min120 | 49.1 | 1.8 | −12.2 + 2.3 | 8.3 + 0.7 | 5.5 × 10 | EM + NM |
| (0.5) | (0.6) | (0.4 + 0.4) | (0.3 + 0.2) | (3 × 10) | ||
| 43%, 57%, 0%, 100%, 0 | ||||||
| A050nm240min130 | 42.1 | 14.1 | −13.7 + 2.6 | 7.4 + 1.3 | 7.1 × 10 | PSO + NM |
| (3.0) | (5.5) | (0.8 + 0.7) | (0.4 + 0.4) | (9 × 10) | ||
| 0%, 38%, 62%, 100%, 0 | ||||||
| A050nm600min130 | 39.0 | 19.0 | −14.4 + 3.5 | 8.1 + 1.4 | 8.4 × 10 | PSO + NM |
| (3.8) | (6.7) | (1.0 + 0.8) | (0.3 + 0.7) | (1 × 10) | ||
| 29%, 31%, 40%, 97%, 3 | ||||||
| A050nm900min170 | 0.4 | 81.9 | −9.1 + 2.3 | 6.1 + 0.1 | 1.4 × 10 | EM + NM |
| (0.6) | (4.6) | (0.9 + 1.1) | (0.5 + 0.1) | (1 × 10) | ||
| 7%, 83%, 11%, 100%, 0 | ||||||
| A050nm910min170 | 0.0 | 89.6 | −11.5 + 2.8 | 6.6 + 0.3 | 1.4 × 10 | ABC + NM |
| (0.6) | (4.4) | (0.8 + 1.1) | (0.5 + 0.1) | (8 × 10) | ||
| 97%, 0%, 3%, 100%, 0 | ||||||
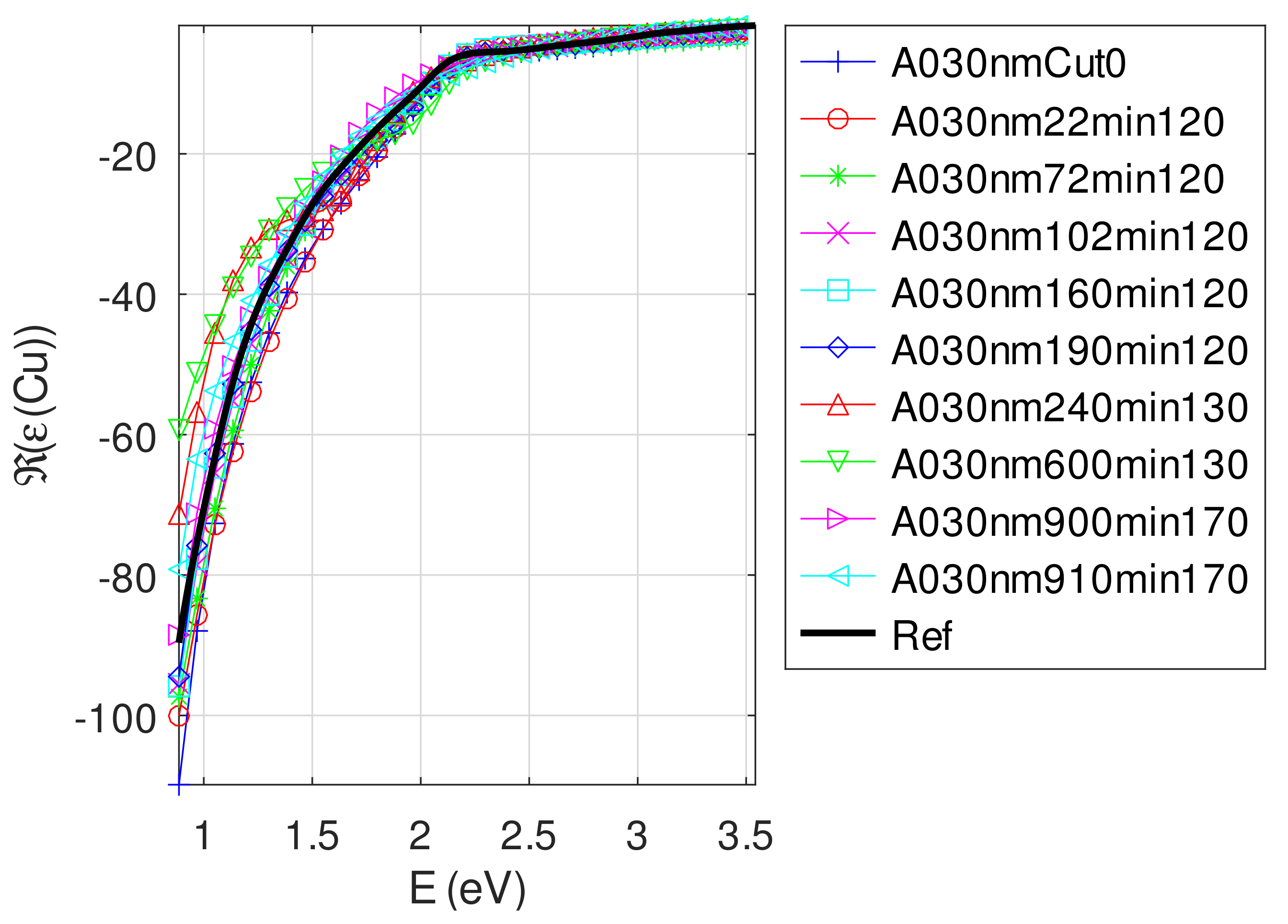



Appendix C.4.3. Sample of Initial Copper Thickness nm


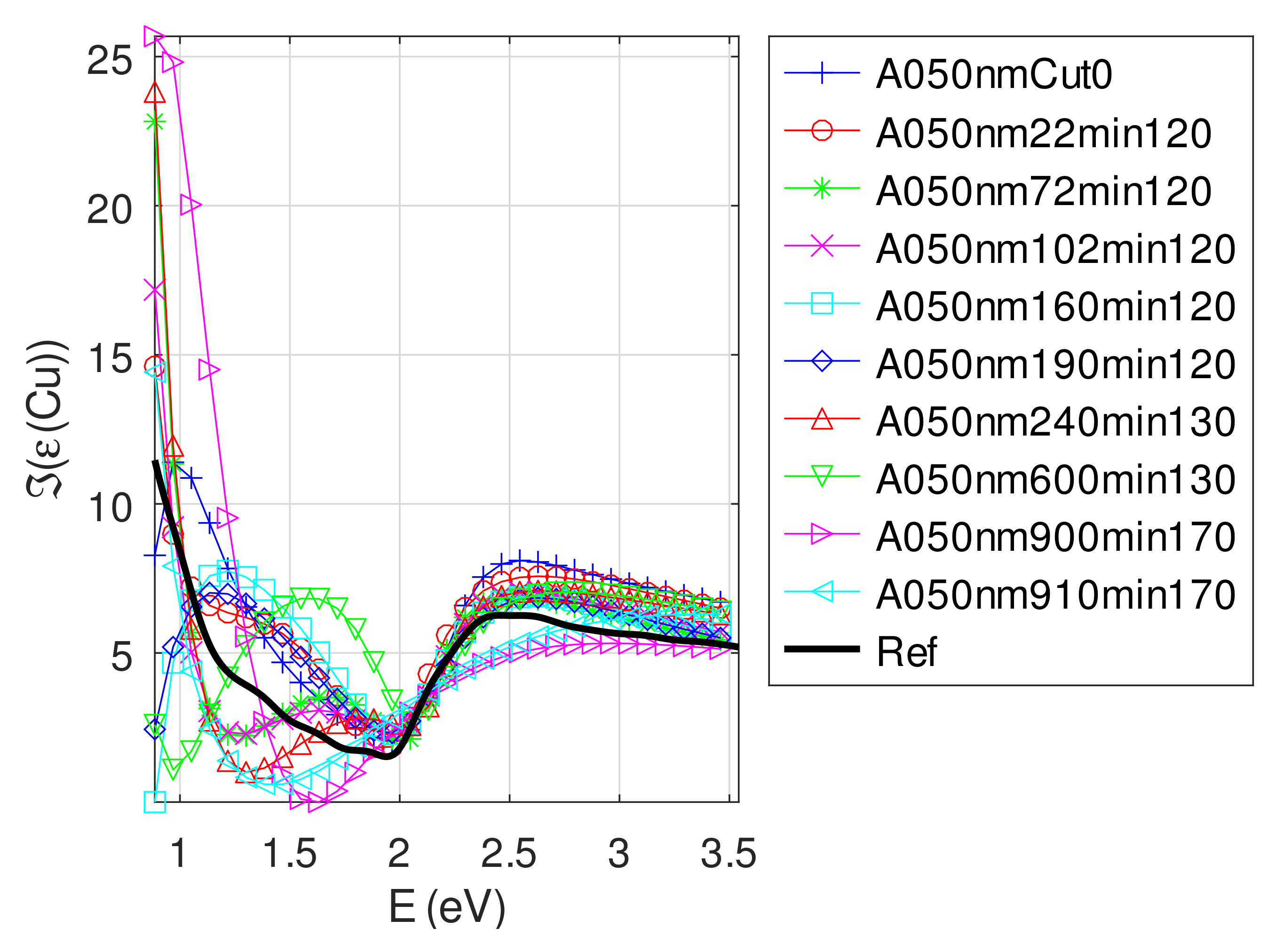
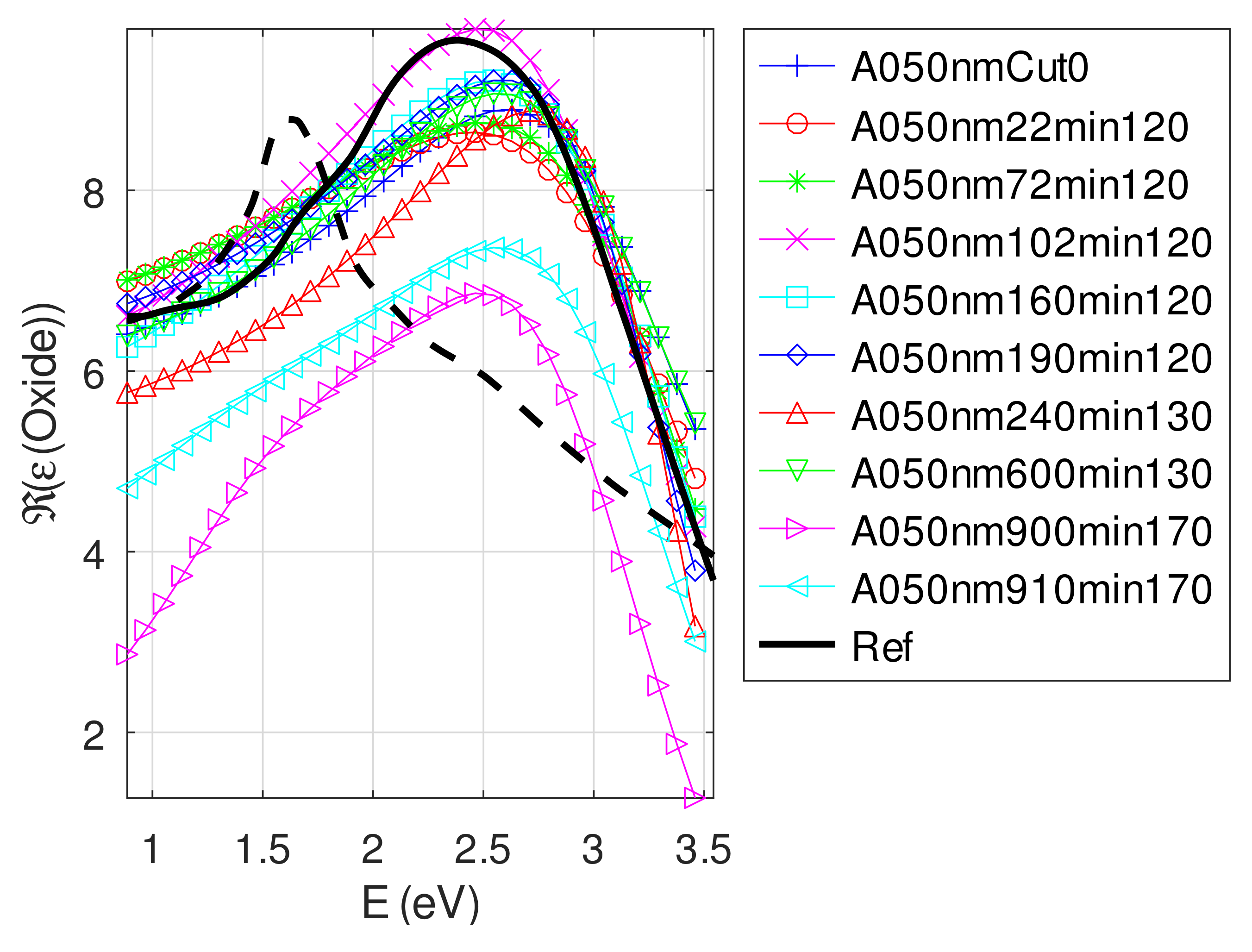
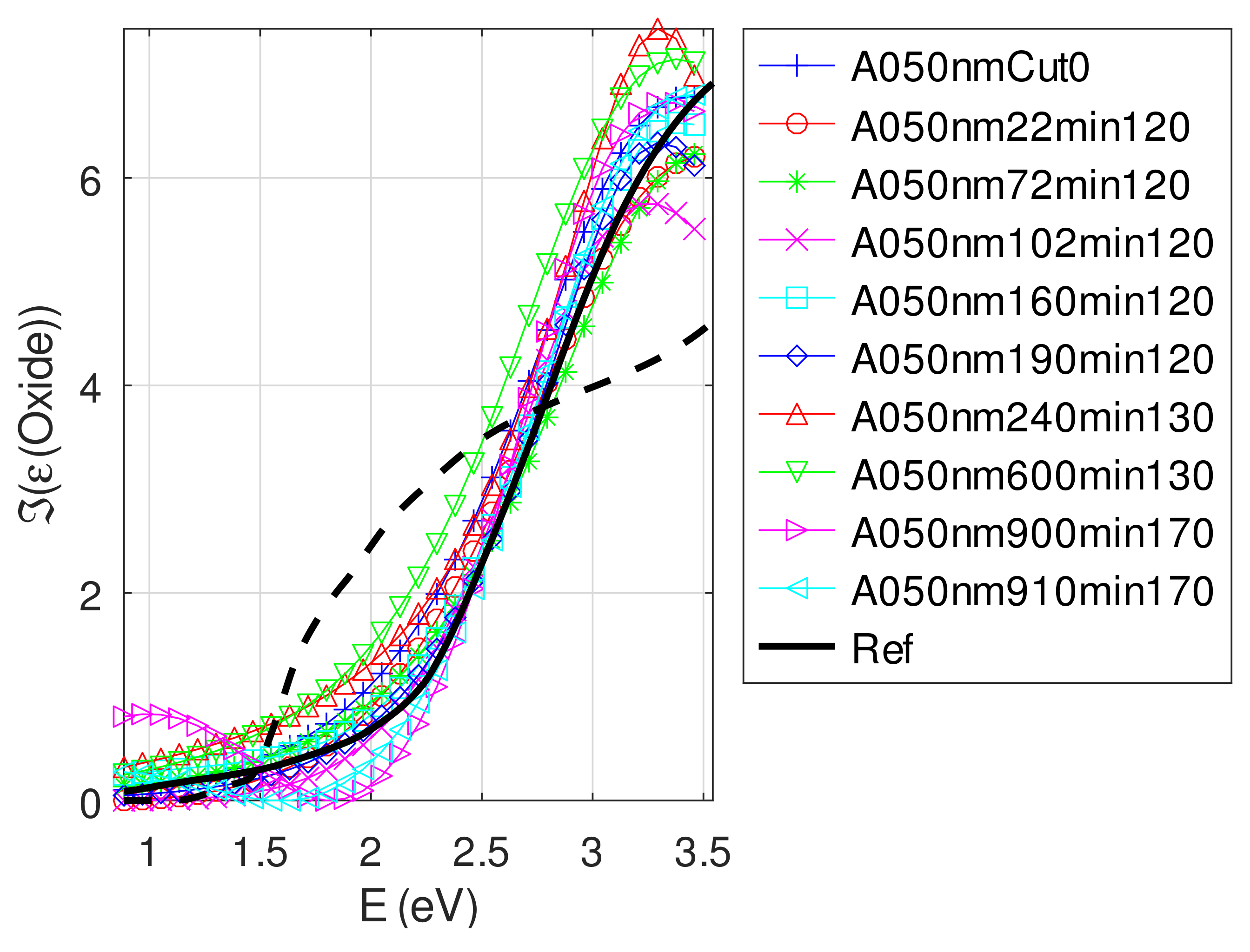
Appendix C.5. Discussion on the Resolution of the Inverse Problem: The Fitting of UV-Visible-NIR Absorbance Curves
References
- Kretschmann, E.; Raether, H. Radiative Decay of Nonradiative Surface Plasmons Excited by Light. Z. Naturforsch. A 1968, 23A, 2135–2136. [Google Scholar] [CrossRef]
- Ahn, H.; Song, H.; Choi, J.R.; Kim, K. A Localized Surface Plasmon Resonance Sensor Using Double-Metal-Complex Nanostructures and a Review of Recent Approaches. Sensors 2018, 18, 98. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Z.; Zhao, X.; Lin, C.; Chen, S.; Yin, L.; Ding, Y. Figure of merit enhancement of surface plasmon resonance sensors using absentee layer. Appl. Opt. 2016, 55, 6832–6835. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.Q.; Zhao, X.; Lin, C.Y.; Chen, S.J.; Ding, Y.C.; Chen, Z.Y. Figure of Merit Enhancement of a Surface Plasmon Resonance Sensor Using a Low-Refractive-Index Porous Silica Film. Sensors 2017, 17, 1846. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.Y.; Lee, T.W.; Kim, W.K.; Kim, B.S.; Park, J.H.; Bae, J.S.; Cho, Y.C.; Kim, J.; Oh, M.W.; et al. Fabrication of high-quality single-crystal Cu thin films using radio-frequency sputtering. Sci. Rep. 2014, 4, 6230. [Google Scholar] [CrossRef] [Green Version]
- Tripathi, A.; Dixit, T.; Agrawal, J.; Singh, V. Bandgap engineering in CuO nanostructures: Dual-band, broadband, and UV-C photodetectors. Appl. Phys. Lett. 2020, 116, 111102. [Google Scholar] [CrossRef]
- Editorial Feature of AEO Nano. Copper (Cu) Nanoparticles-Properties, Applications. Available online: https://www.azonano.com/article.aspx?ArticleID=3271 (accessed on 9 May 2021).
- Kesarwani, R.; Khare, A. Surface plasmon resonance and nonlinear optical behavior of pulsed laser-deposited semitransparent nanostructured copper thin films. Appl. Phys. B 2018, 124, 116. [Google Scholar] [CrossRef]
- Rodrigues, E.P.; Oliveira, L.C.; Silva, M.L.F.; Moreira, C.S.; Lima, A.M.N. Surface Plasmon Resonance Sensing Characteristics of Thin Copper and Gold Films in Aqueous and Gaseous Interfaces. IEEE Sens. J. 2020, 20, 7701–7710. [Google Scholar] [CrossRef]
- Stebunov, Y.V.; Yakubovsky, D.I.; Fedyanin, D.Y.; Arsenin, A.V.; Volkov, V.S. Superior Sensitivity of Copper-Based Plasmonic Biosensors. Langmuir 2018, 34, 4681–4687. [Google Scholar] [CrossRef] [Green Version]
- Granito, C.; Wilde, J.; Petty, M.; Houghton, S.; Iredale, P. Toluene vapour sensing using copper and nickel phthalocyanine Langmuir-Blodgett films. Thin Solid Films 1996, 284–285, 98–101. [Google Scholar] [CrossRef]
- Homola, J.; Yee, S.S.; Gauglitz, G. Surface Plasmon Resonance Sensors Review. Sens. Actuators B 1999, 54, 3–15. [Google Scholar] [CrossRef]
- Murali, D.S.; Kumar, S.; Choudhary, R.J.; Wadikar, A.D.; Jain, M.K.; Subrahmanyam, A. Synthesis of Cu2O from CuO thin films: Optical and electrical properties. Int. Adv. Eng. Res. Sci. (IJAERS) 2015, 5, 047143. [Google Scholar] [CrossRef]
- Cakir, D. Enhanced Raman Signatures on Copper Based-Materials. Ph.D. Thesis, Univesité de Montpellier, Montpellier, France, 2017. [Google Scholar]
- Barchiesi, D.; Cakir, D.; Grosges, T.; Fréty, N.; Anglaret, E. Recovering effective thicknesses and optical properties of copper and copper oxide layers from absorbance measurements. Opt. Mater. 2019, 91, 138–146. [Google Scholar] [CrossRef]
- Han, L.; Zhou, D.; Li, K.; Xun, l.; Huang, W.P. A Rational-Fraction Dispersion Model for Efficient Simulation of Dispersive Material in FDTD Method. J. Light. Technol. 2012, 30, 2216–2225. [Google Scholar] [CrossRef]
- Michalski, K.A. On the Low-Order Partial-Fraction Fitting of Dielectric Functions at Optical Wavelengths. IEEE Trans. Antennas Propag. 2013, 61, 6128–6135. [Google Scholar] [CrossRef]
- Gharbi, T.; Barchiesi, D.; Kessentini, S.; Maalej, R. Fitting optical properties of metals by Drude-Lorentz and partial-fraction models in the [0.5;/,6] eV range. Opt. Mater. Express 2020, 10, 1129–1162. [Google Scholar] [CrossRef]
- Barchiesi, D.; Otto, A. Excitations of surface plasmon polaritons by attenuated total reflection, revisited. Riv. Nuovo C. 2013, 36, 173–209. [Google Scholar]
- Barchiesi, D.; Kremer, E.; Mai, V.P.; Grosges, T. A Poincaré’s Approach for Plasmonics The Plasmon Localization. J. Microsc. 2008, 229, 525–532. [Google Scholar] [CrossRef]
- Barchiesi, D.; Lidgi-Guigui, N.; Lamy de la Chapelle, M. Functionalization Layer Influence on the Sensitivity of Surface Plasmon Resonance (SPR) Biosensor. Opt. Commun. 2012, 285, 1619–1623. [Google Scholar] [CrossRef]
- Salvi, J.; Barchiesi, D. Measurement of thicknesses and optical properties of thin films from Surface Plasmon Resonance (SPR). Appl. Phys. A 2014, 115, 245–255. [Google Scholar] [CrossRef]
- Kessentini, S.; Barchiesi, D. Nanostructured Biosensors Influence of Adhesion Layer, Roughness and Size on the LSPR A Parametric Study. In State of the Art in Biosensors-General Aspects; Rinken, T., Ed.; INTECH Open Access: London, UK, 2013; Chapter 12; pp. 311–330. ISBN 978-953-51-1004-0. [Google Scholar]
- Colas, F.; Barchiesi, D.; Kessentini, S.; Toury, T.; Lamy de la Chapelle, M. Comparison of adhesion layers of gold on silicate glasses for SERS detection. J. Opt. 2015, 17, 114010. [Google Scholar] [CrossRef] [Green Version]
- Barchiesi, D. A classroom theory of the surface plasmon polariton. Eur. J. Phys. 2012, 33, 1345–1357. [Google Scholar] [CrossRef]
- Lecaruyer, P.; Canva, M.; Rolland, J. Metallic Film Optimization in a Surface Plasmon Resonance Biosensor by the Extended Rouard Method. Appl. Opt. 2007, 46, 2361–2369. [Google Scholar] [CrossRef] [PubMed]
- Barchiesi, D. Improved method based on S matrix for the optimization of SPR biosensors. Opt. Commun. 2013, 286, 23–29. [Google Scholar] [CrossRef]
- Barchiesi, D. Numerical retrieval of thin aluminium layer properties from SPR experimental data. Opt. Express 2012, 20, 9064–9078. [Google Scholar] [CrossRef]
- Software Spectra, I. Optical Data from Sopra SA. Available online: http://www.sspectra.com/sopra.html (accessed on 9 May 2021).
- Ramirez, M.; Henneken, L.; Virtanen, S. Oxidation kinetics of thin copper films and wetting behaviour of copper and Organic Solderability Preservatives (OSP) with lead-free solder. Appl. Surf. Sci. 2011, 257, 6481–6488. [Google Scholar] [CrossRef]
- Shanidand, M.; Abdul Khadar, M.; Sathe, V.G. Fröhlich interaction and associated resonance enhancement in nanostructured copper oxide films. J. Raman Spectrosc. 2011, 42, 1769–1773. [Google Scholar] [CrossRef]
- Figueiredo, V.; Elangovan, E.; Goncalves, G.; Barquinha, P.; Pereira, L.; Franco, N.; Alves, E.; Martins, R.; Fortunato, E. Effect of post-annealing on the properties of copper oxide thin films obtained from the oxidation of evaporated metallic copper. Appl. Surf. Sci. 2008, 254, 3949–3954. [Google Scholar] [CrossRef]
- Gao, W.; Hong, H.; He, J.; Thomas, A.; Chan, L.; Li, S. Oxidation behaviour of Cu thin films on Si wafer at 175–400 °C. Mater. Lett. 2001, 51, 78–84. [Google Scholar] [CrossRef]
- Iijima, J.; Lim, J.W.; Hong, H.S.; Suzuki, S.; Mimura, K.; Isshiki, M. Native oxidation of ultra high purity Cu bulk and thin films. Appl. Surf. Sci. 2006, 253, 2825–2829. [Google Scholar] [CrossRef]
- Cabrera, N.; Mott, N.F. Theory of the oxidation of metals. Rep. Prog. Phys. 1949, 12, 163. [Google Scholar] [CrossRef]
- Mugwang’a, F.; Karimi, P.; Njoroge, W.; Omayio, O.; Waita, S. Optical characterization of Copper Oxide thin films prepared by reactive dc magnetron sputtering for solar cell applications. Int. J. Thin Film Sci. Technol. 2012, 2, 15–24. [Google Scholar]
- Shi, Y.; Eberhart, R.C. A modified particle swarm optimizer. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC’98), Anchorage, Alaska, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Rahmat-Samii, Y. Genetic algorithm (GA) and particle swarm optimization (PSO) in engineering electromagnetics. In Proceedings of the 17th International Conference on Applied Electromagnetics and Communications, Dubrovnik, Republika Hrvatska, 1–3 October 2003; pp. 1–5. [Google Scholar] [CrossRef]
- Robinson, J.; Rahmat-Samii, Y. Particle swarm optimization in electromagnetics. IEEE Trans. Antennas Propag. 2004, 52, 397–407. [Google Scholar] [CrossRef]
- Barchiesi, D. Numerical optimization of plasmonic biosensors. In New Perspectives in Biosensors Technology and Applications; Serra, P.A., Ed.; INTECH Open Access: London, UK, 2011; Chapter 5; pp. 105–126. ISBN 978-953-307-448-1. [Google Scholar]
- Turbadar, T. Complete Absorption of Light by Thin Metal Films. Proc. Phys. Soc. 1959, 73, 40–44. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; Michigan University: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Bäck, T.; Hammel, U.; Schwefel, H.P. Evolutionary Computation Comments on the History and Current State. IEEE Trans. Evol. Comput. 1997, 1, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Macías, D.; Vial, A.; Barchiesi, D. Evolution Strategies Approach for the Solution of an Inverse Problem in Near-Field Optics. In Lecture Notes in Computer Science (6e European Workshop on Evolutionary Computation in Image Analysis and Signal Processing); Raidl, G., Cagnoni, S., Branke, J., Corne, D.W., Drechsler, R., Jin, Y., Johnson, C., Machado, P., Marchiori, E., Rothlauf, F., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3005/2004, pp. 329–338. [Google Scholar]
- Johnson, J.; Rahmat-Samii, V. Genetic algorithms in engineering electromagnetics. IEEE Antennas Propag. Mag. 1997, 39, 7–21. [Google Scholar] [CrossRef] [Green Version]
- Rahmat-Samii, Y.; Michielssen, E. Electromagnetic Optimization by Genetic Algorithms, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Macías, D.; Vial, A.; Barchiesi, D. Application of Evolution Strategies for the Solution of an Inverse Problem in Near-Field Optics. J. Opt. Soc. Am. A 2004, 21, 1465–1471. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report tr06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Zaman, M.; Gaffar, M.; Alam, M.M.; Mamun, S.; Matin, M. Synthesis of Antenna Arrays Using Artificial Bee Colony Optimization Algorithm. Int. J. Microw. Opt. Technol. 2011, 6, 234–241. [Google Scholar]
- Kessentini, S.; Naãs, I. Absolute versus stochastic stability of the artificial bee colony in synchronous and sequential modes. Natural Comput. 2021, 20, 443–470. [Google Scholar] [CrossRef]
- Chiandussi, G.; Codegone, M.; Ferrero, S.; Varesio, F. Comparison of multi-objective optimization methodologies for engineering applications. Comput. Math. Appl. 2012, 63, 912–942. [Google Scholar] [CrossRef] [Green Version]
- Jiang, M.; Luo, Y.P.; Yang, S.Y. Stochastic convergence analysis and parameter selection of the standard particle swarm optimization algorithm. Inf. Process. Lett. 2007, 102, 8–16. [Google Scholar] [CrossRef]
- Trelea, I.C. The particle swarm optimization algorithm convergence analysis and parameter selection. Inf. Process. Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Barchiesi, D.; Grosges, T. Propagation of uncertainties and applications in numerical modeling: Tutorial. J. Opt. Soc. Am. A 2017, 34, 1602–1619. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Korzhavyi, P.A.; Johansson, B. Literature Review on the Properties of Cuprous Oxide Cu2O and the Process of Copper Oxidation; Technical Report SKB TR-11-08, Svensk Kärnbränslehantering AB; Swedish Nuclear Fueland Waste Management Co.: Stockholm, Sweden, 2011. [Google Scholar]
- Alhassan, W.A.A.; Wadi, I.A. Determination of Optical Energy Gap fo rCopper oxide at Different Temperatures. Int. Adv. Eng. Res. Sci. (IJAERS) 2018, 5, 255–258. [Google Scholar] [CrossRef]
- Wang, Y.; Lany, S.; Ghanbaja, J.; Fagot-Revurat, Y.; Chen, Y.P.; Soldera, F.; Horwat, D.; Mücklich, F.; Pierson, J.F. Electronic structures of Cu2O, Cu4O3, and CuO: A joint experimental and theoretical study. Phys. Rev. B 2016, 94, 245418. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.Z.; Sharangpani, R.; Tay, S.P. Kinetic investigation of copper film oxidation by spectroscopic ellipsometry and reflectometry. J. Vac. Sci. Technol. A 2000, 18, 2527–2532. [Google Scholar] [CrossRef]



| FWHM | FOM | FOM | FOM | |||||
|---|---|---|---|---|---|---|---|---|
| Bulk | ox. Free | |||||||
| (nm) | () | (/RIU) | (RIU) | (RIU) | (RIU) | |||
| 49.1 | −12.2 + 2.3 | |||||||
| 1.8 | 8.3 + 0.7 | 46.8 | 0.08 | 3.2 | 67.5 | 20.9 (0.0) | 27.8 | 25.8 |
| 49.2 | −12. + 2.3 | |||||||
| 1.6 | 8.4 + 0.8 | 46.7 | 0.08 | 2.8 | 67.0 | 23.5 (0.0) | 28.6 | 28.5 |
| 49.8 | −13.2 + 2.3 | |||||||
| 0.6 | 8.8 + 0.5 | 46.2 | 0.09 | 2.1 | 65.0 | 31.2 (5.5) | 32.9 | 33.5 |
| 49.8 | −14. + 2.2 | |||||||
| 0.6 | 8.3 + 0.9 | 46.0 | 0.10 | 1.5 | 63.9 | 41.4 (0.0) | 33.1 | 44.2 |
| 49.8 | −14.6 + 1.8 | |||||||
| 0.1 | 8.2 + 0.8 | 45.8 | 0.07 | 1.1 | 63.4 | 57.3 (0.5) | 34.9 | 57.7 |
| 50.0 | −15.4 + 2.0 | |||||||
| 0.1 | 7.9 + 1.0 | 45.6 | 0.11 | 1.1 | 62.7 | 58.5 (0.0) | 35.1 | 59.3 |
| FWHM | FOM | FOM | FOM | |||||
|---|---|---|---|---|---|---|---|---|
| Bulk | ox. Free | |||||||
| (nm) | () | (/RIU) | (RIU) | (RIU) | (RIU) | |||
| 27.9 | −13.5 + 2.9 | |||||||
| 3.5 | 8.4 + 0.6 | 81.4 | 0.04 | 11.1 | 258.0 | 23.3 (1.1) | 9.5 | 19.1 |
| 28.2 | −12.8 + 3.1 | |||||||
| 3.1 | 8.3 + 0.5 | 81.4 | 0.03 | 11.3 | 253.0 | 22.4 (1.0) | 10.1 | 18.7 |
| 29.4 | −13.0 + 2.0 | |||||||
| 1.0 | 8.1 + 1.1 | 78.6 | 0.11 | 10.0 | 231.4 | 23.1 (1.0) | 5.8 | 22.1 |
| 29.5 | −12.5 + 2.9 | |||||||
| 1.0 | 8.2 + 1.0 | 78.9 | 0.04 | 10.9 | 229.6 | 21.1 (0.0) | 5.9 | 20.0 |
| 29.9 | −13.3 + 2.8 | |||||||
| 0.1 | 8.6 + 0.7 | 77.3 | 0.06 | 10.3 | 214.5 | 20.8 (0.2) | 10.1 | 20.8 |
| 30.0 | −14.1 + 2.7 | |||||||
| 0.0 | 8.3 + 1.2 | 76.8 | 0.06 | 9.9 | 210.7 | 21.4 (0.0) | 5.9 | 21.3 |
| 49.1 | −12.2 + 2.3 | |||||||
| 1.8 | 8.3 + 0.7 | 83.3 | 0.26 | 8.7 | 200.2 | 22.9 (0.0) | 11.9 | 34.4 |
| 49.2 | −12.5 + 2.3 | |||||||
| 1.6 | 8.4 + 0.8 | 82.8 | 0.23 | 8.6 | 252.8 | 29.2 (0.0) | 16.4 | 35.5 |
| 49.8 | −13.2 + 2.3 | |||||||
| 0.6 | 8.8 + 0.5 | 80.3 | 0.15 | 8.3 | 305.7 | 36.8 (2.1) | 38.7 | 36.5 |
| 49.8 | −13.2 + 2.3 | |||||||
| 0.6 | 8.8 + 0.5 | 80.3 | 0.15 | 8.3 | 305.7 | 36.8 (2.1) | 38.7 | 36.5 |
| 49.8 | −14.2 + 2.2 | |||||||
| 0.6 | 8.3 + 0.9 | 78.9 | 0.13 | 7.3 | 292.6 | 40.0 (0.0) | 39.4 | 40.2 |
| 49.8 | −14.6 + 1.8 | |||||||
| 0.1 | 8.2 + 0.8 | 77.8 | 0.08 | 5.9 | 277.7 | 47.2 (0.6) | 43.7 | 47.3 |
| 50.0 | −15.4 + 2.0 | |||||||
| 0.1 | 7.9+1.0 | 77.0 | 0.11 | 5.7 | 262.2 | 45.7 (0.0) | 43.7 | 45.8 |
| (nm) | (nm) | / | ||||
|---|---|---|---|---|---|---|
| Top 1% | ||||||
| 28.1 (5.6) | 14.9 (9.5) | 0.003 (0.003) | 73.7 (26.2) | 23.7 (6.3) | 3.3 (1.5) | 3.1 (1.8) |
| Top 1% | ||||||
| 31.9 (11.6) | 51.0 (5.9) | 1 (0) | 0.0 (0.0) | 90.0 (0.0) | 0.0 (0.0) | 0.0 (0.0) |
| Top 1% | ||||||
| 31.9 (11.5) | 50.3 (7.7) | 1 (0.1) | 1.4 (10.7) | 88.9 (8.5) | 0.1 (0.5) | 0.0 (0.0) |
| Top 1% | ||||||
| 46.0 (3.9) | 1.0 (0.0) | 0.1 (0.05) | 65.4 (0.6) | 5.5 (0.3) | 12.0 (0.5) | 14.5 (3.2) |
| Top 1% | ||||||
| 46.2 (1.7) | 1.0 (0.0) | 0.1 (0.02) | 65.2 (0.6) | 5.2 (0.1) | 12.5 (0.0) | 14.9 (1.4) |
| Top 1% | ||||||
| 54.1 (4.0) | 16.9 (0.3) | 0.3 (0.05) | 125.0 (0.5) | 30.1 (0.6) | 4.2 (0.1) | 30.9 (2.3) |
| (nm) | (nm) | / | ||||
|---|---|---|---|---|---|---|
| Top 1% | ||||||
| 24.8 (7.2) | 6.5 (4.9) | 0.004 (0.003) | 199.5 (62.8) | 10.7 (1.4) | 18.2 (4.0) | 3.6 (2.0) |
| Top 1% | ||||||
| 31.9 (11.5) | 50.4 (7.4) | 1 (0.06) | 0.9 (14.8) | 89.7 (4.7) | 0.1 (1.3) | 0.0 (0.0) |
| Top 1% | ||||||
| 42.7 (17.0) | 35.0 (15.3) | 1 (0) | 0.0 (0.0) | 90.0 (0.0) | 0.0 (0.0) | 24.5 (18.2) |
| Top 1% | ||||||
| 10.9 (0.9) | 17.9 (1.3) | 0.03 (0.03) | 49.3 (30.8) | 7.4 (0.3) | 6.7 (4.2) | 9.8 (6.5) |
| Top 1% | ||||||
| 43.5 (1.9) | 1.0 (0.0) | 0.1 (0.04) | 265.5 (0.8) | 11.0 (0.0) | 24.1 (0.1) | 27.3 (4.4) |
| Top 1% | ||||||
| 44.0 (2.2) | 1.0 (0.0) | 0.1 (0.05) | 265.4 (0.8) | 11.0 (0.0) | 24.0 (0.1) | 28.4 (5.0) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barchiesi, D.; Gharbi, T.; Cakir, D.; Anglaret, E.; Fréty, N.; Kessentini, S.; Maâlej, R. Performance of Surface Plasmon Resonance Sensors Using Copper/Copper Oxide Films: Influence of Thicknesses and Optical Properties. Photonics 2022, 9, 104. https://doi.org/10.3390/photonics9020104
Barchiesi D, Gharbi T, Cakir D, Anglaret E, Fréty N, Kessentini S, Maâlej R. Performance of Surface Plasmon Resonance Sensors Using Copper/Copper Oxide Films: Influence of Thicknesses and Optical Properties. Photonics. 2022; 9(2):104. https://doi.org/10.3390/photonics9020104
Chicago/Turabian StyleBarchiesi, Dominique, Tasnim Gharbi, Deniz Cakir, Eric Anglaret, Nicole Fréty, Sameh Kessentini, and Ramzi Maâlej. 2022. "Performance of Surface Plasmon Resonance Sensors Using Copper/Copper Oxide Films: Influence of Thicknesses and Optical Properties" Photonics 9, no. 2: 104. https://doi.org/10.3390/photonics9020104
APA StyleBarchiesi, D., Gharbi, T., Cakir, D., Anglaret, E., Fréty, N., Kessentini, S., & Maâlej, R. (2022). Performance of Surface Plasmon Resonance Sensors Using Copper/Copper Oxide Films: Influence of Thicknesses and Optical Properties. Photonics, 9(2), 104. https://doi.org/10.3390/photonics9020104






