Correction of Spatial Nonuniformity in Spectroradiometer Field-of-View Using a Concentric-Circles Method
Abstract
:1. Introduction
2. Calibration Scheme for FOV Nonuniformity
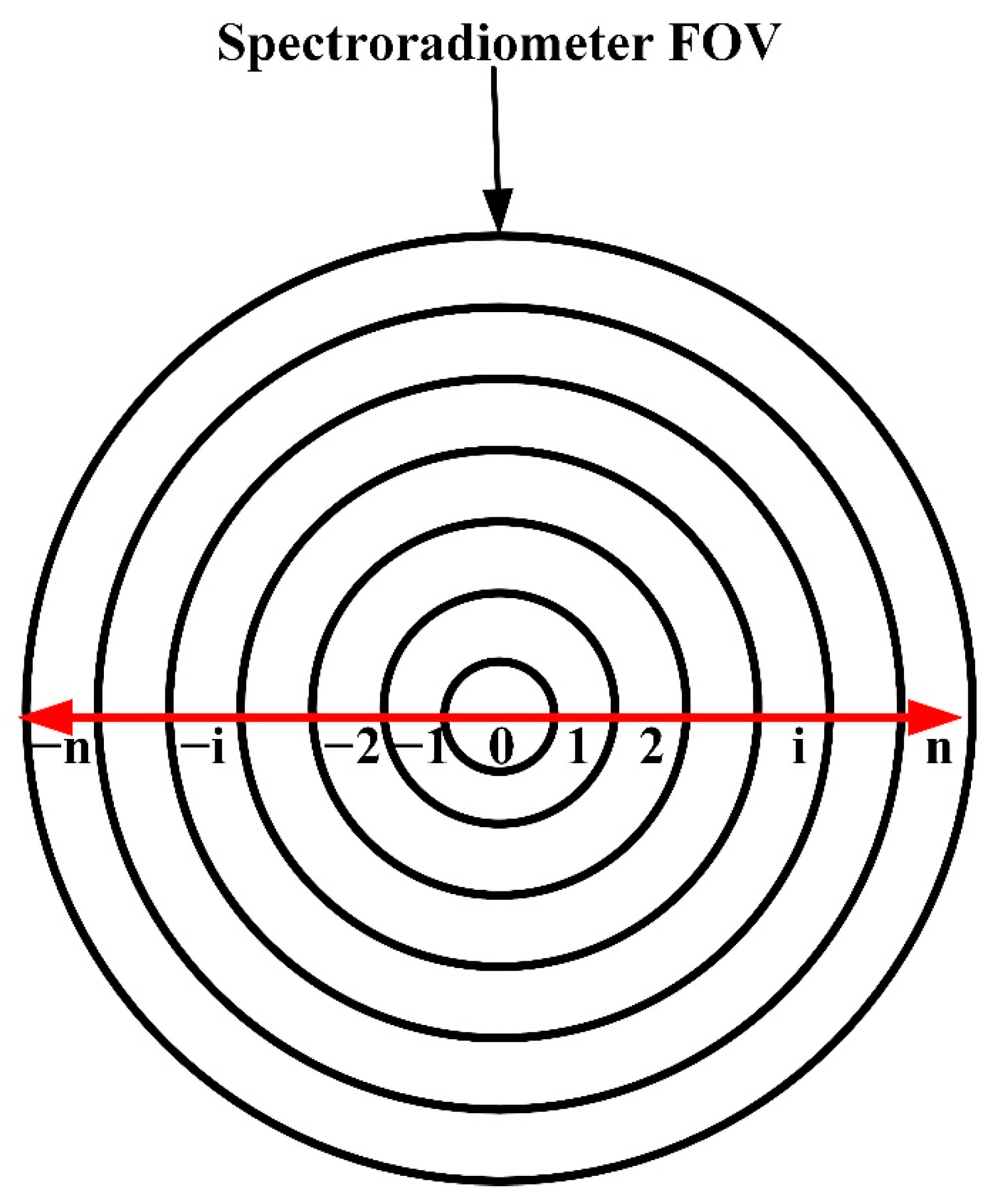
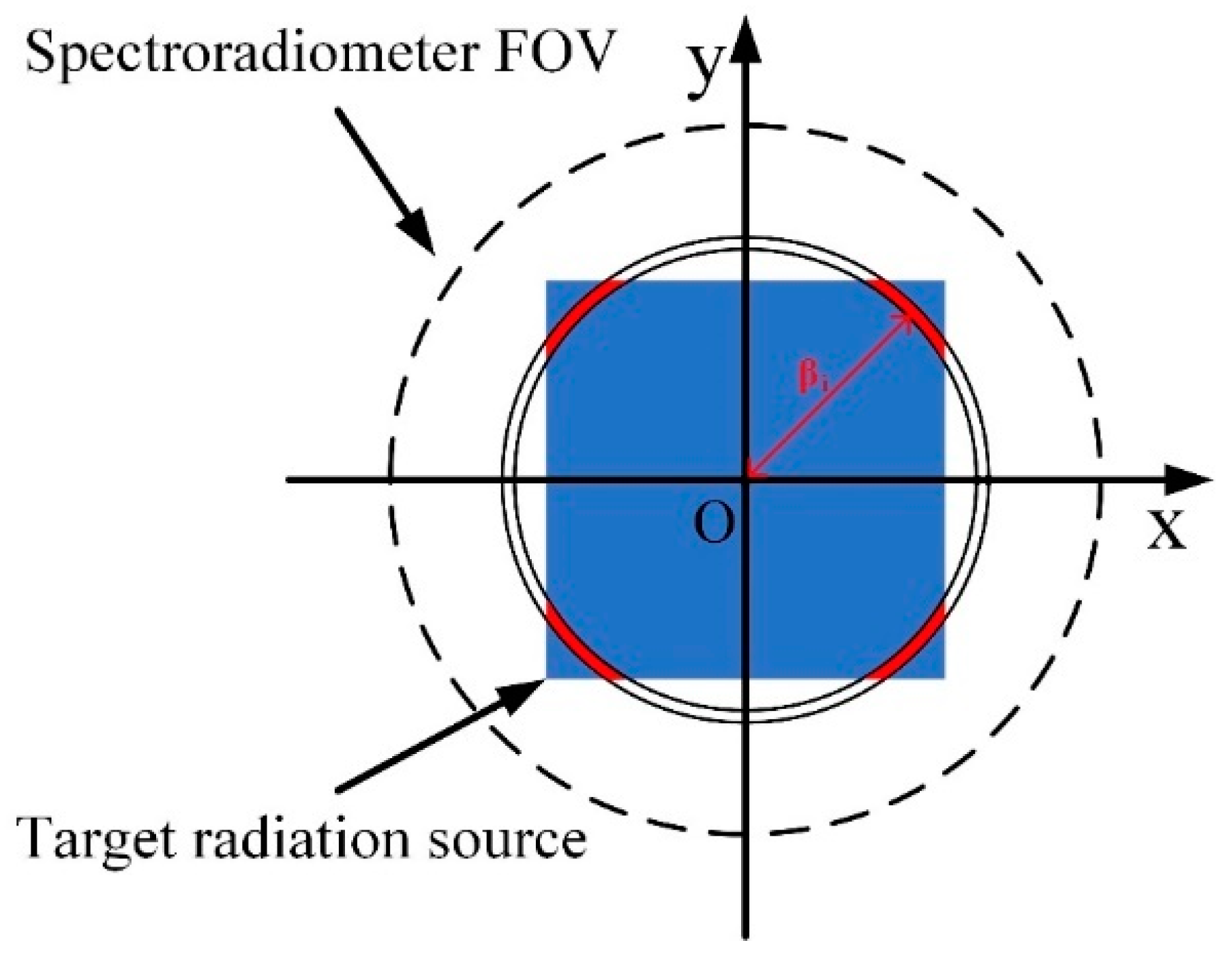
2.1. Correction Using Concentric-Circles Method
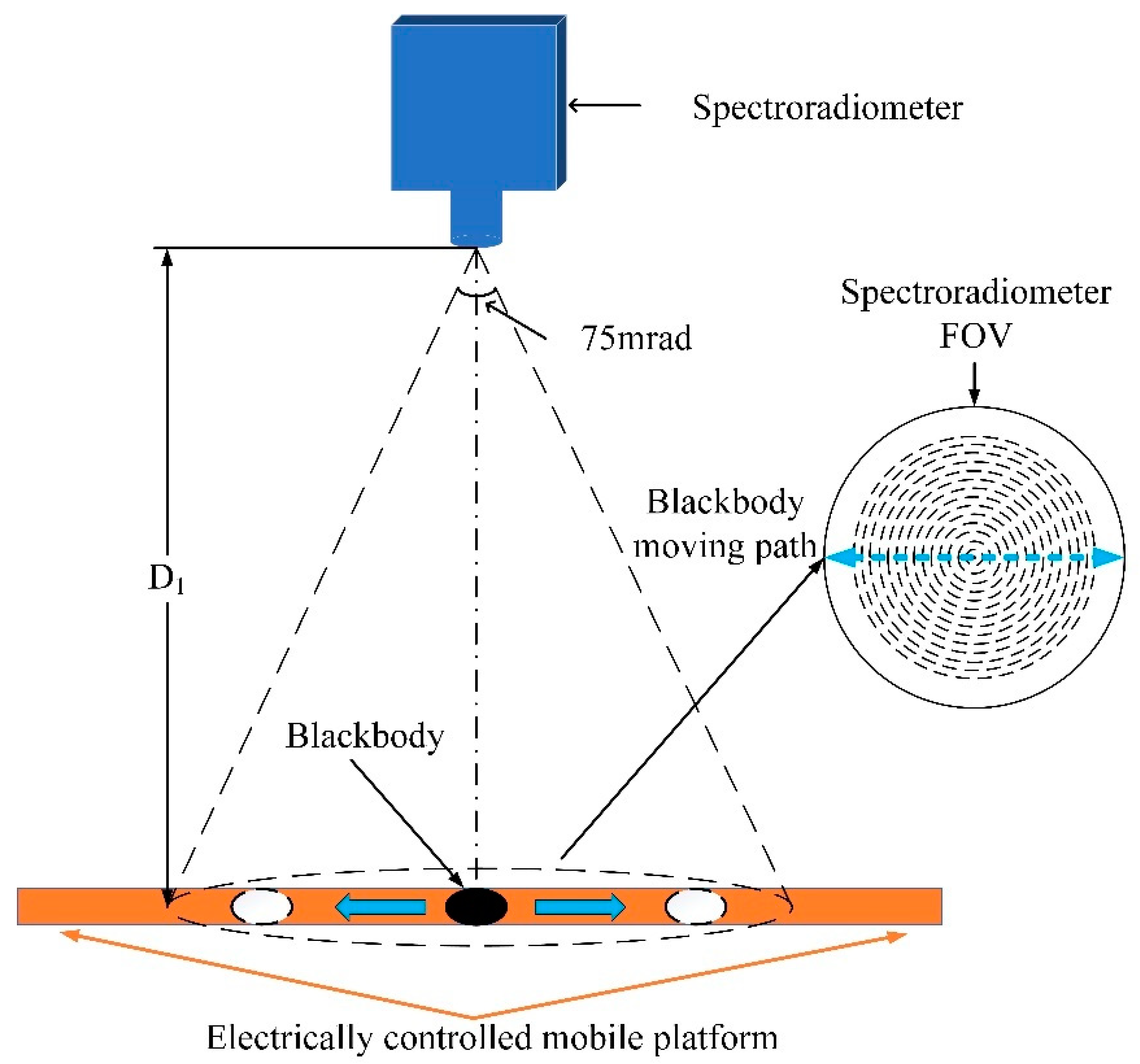
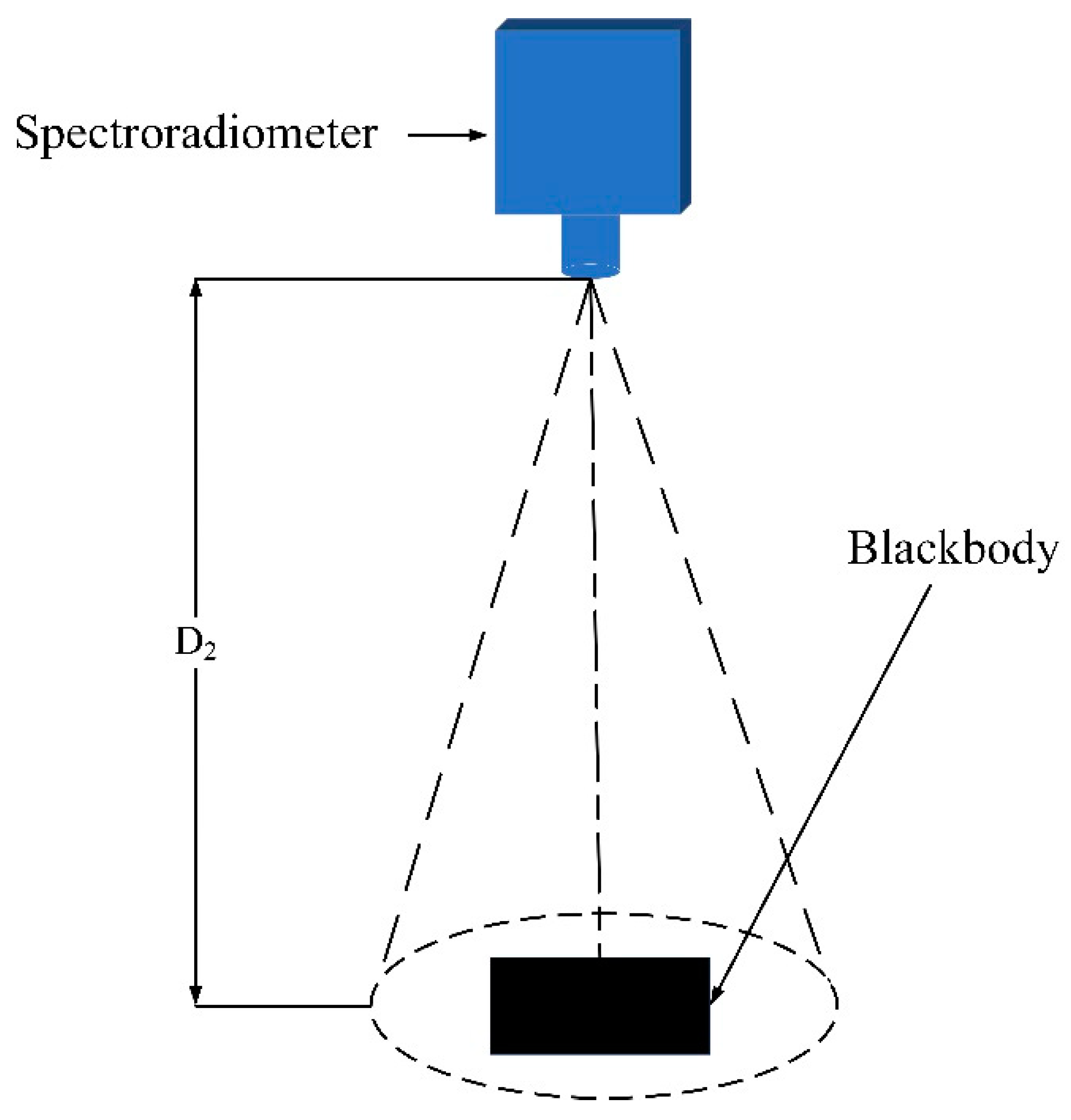
2.2. Experimental Scheme
3. Results
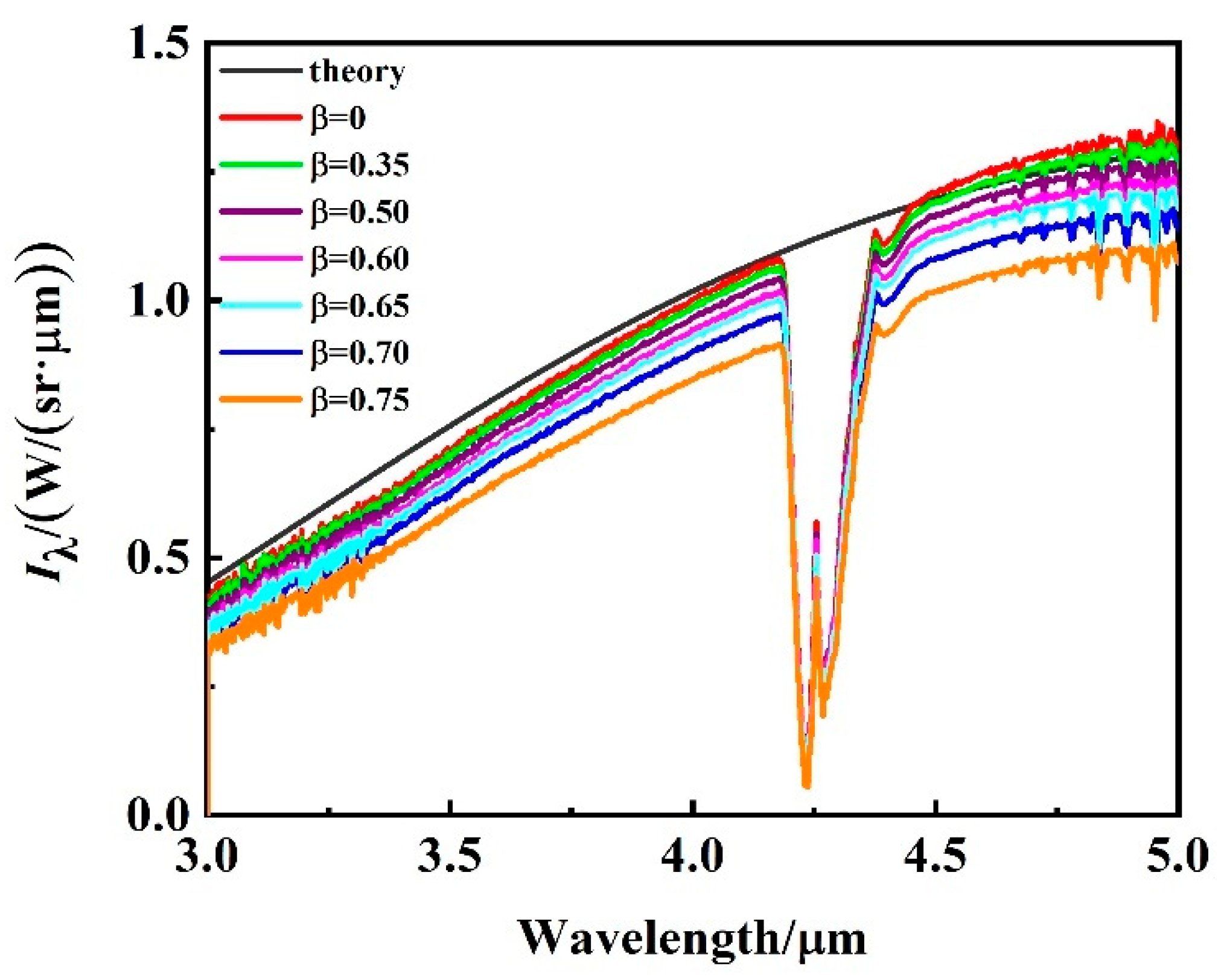
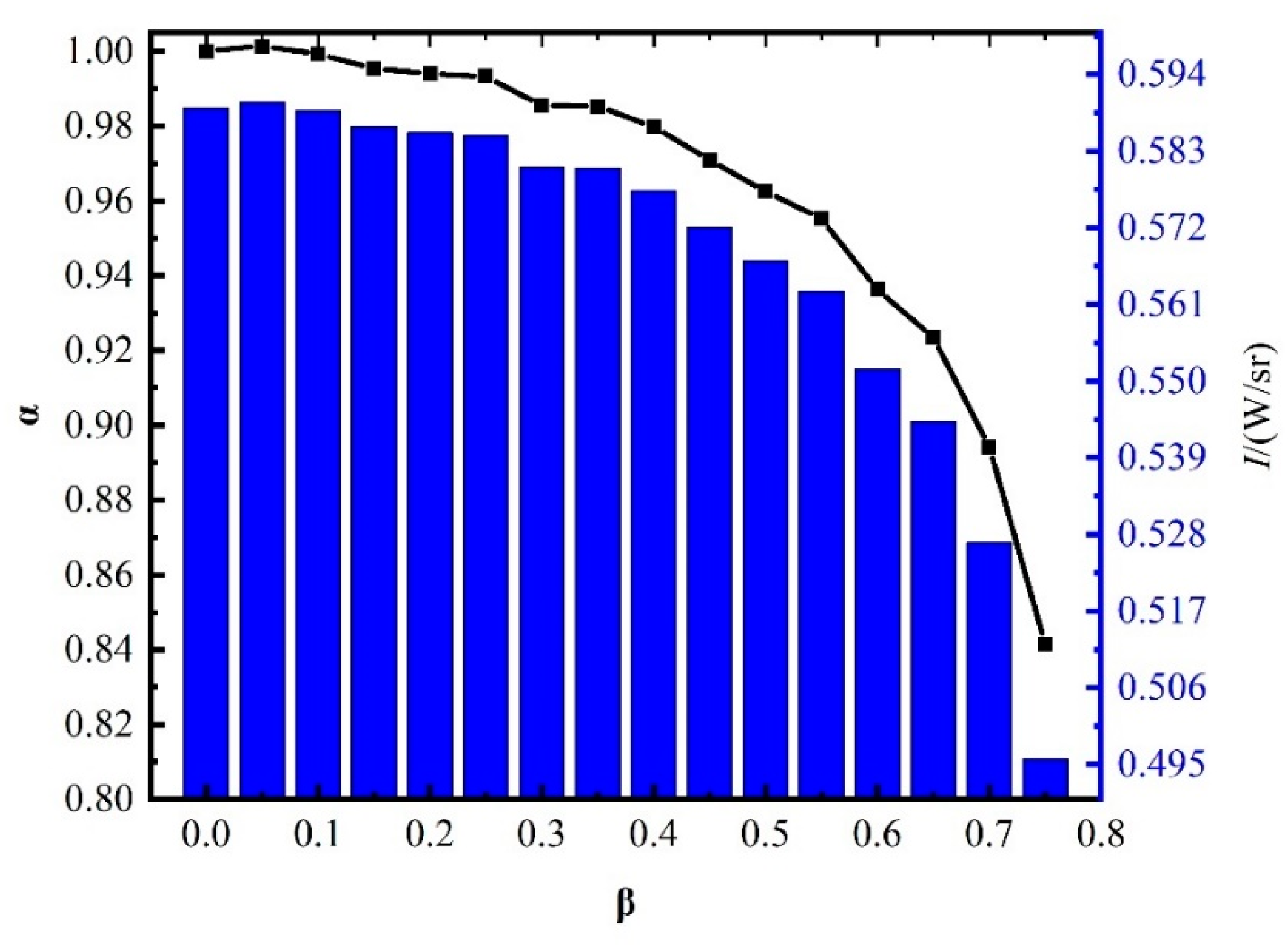
3.1. FOV Nonuniformity Correction Coefficient
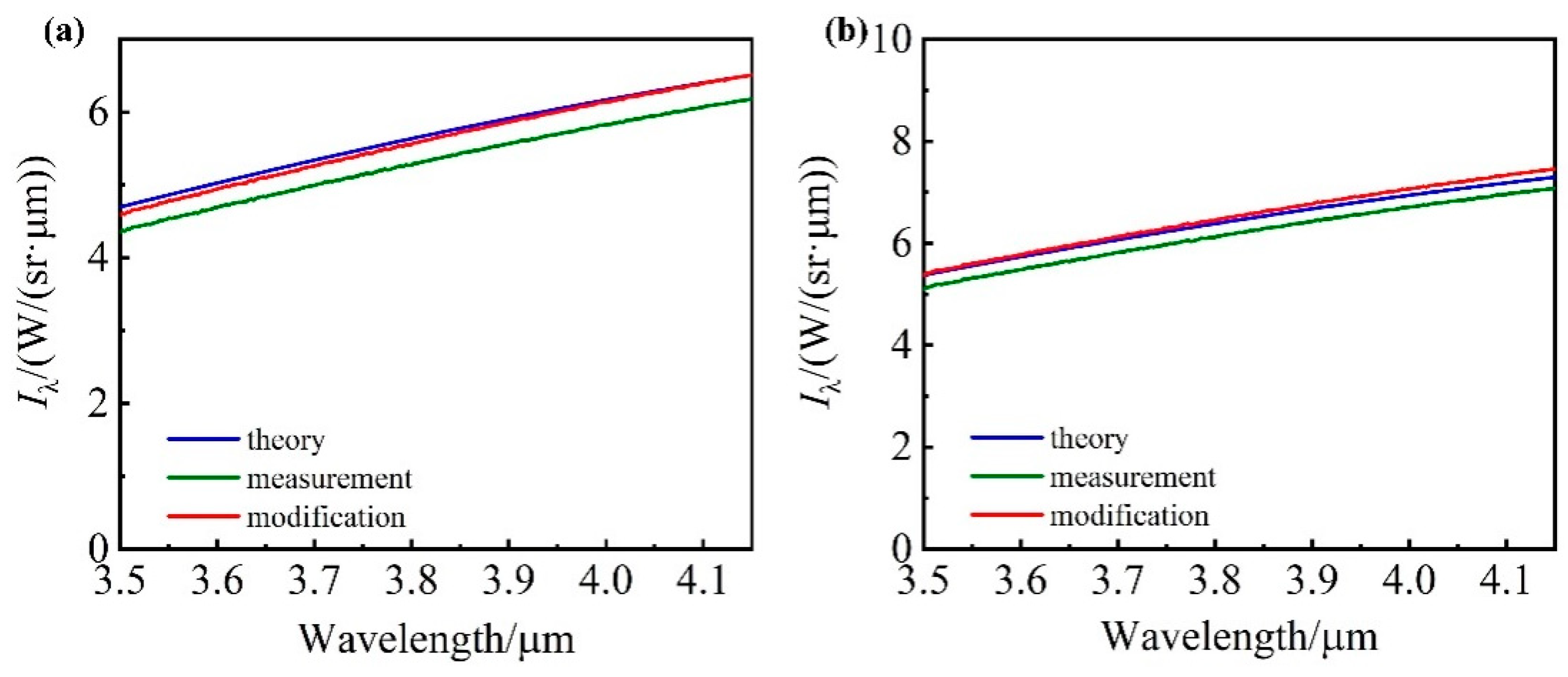
3.2. Correction of FOV Nonuniformity
3.3. Uncertainty Analysis
- Measurement instrument
- 2.
- Measurement object
- 3.
- Measurement conditions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Che, K.; Liu, Y.; Cai, Z.N.; Yang, D.X.; Wang, H.B.; Zhu, S.H. Review of Atmospheric Greenhouse Gas Observation and Application based on Portable Fourier Transform Infrared Spectrometer. Remote Sens. Technol. Appl. 2021, 36, 44–54. [Google Scholar]
- Veerasingam, S.; Ranjani, M.; Venkatachalapathy, R.; Bagaev, A.; Mukhanov, V.; Litvinyuk, D.; Mugilarasan, M.; Gurumoorthi, K.; Guganathan, L.; Aboobacker, V.M. Contributions of Fourier transform infrared spectroscopy in microplastic pollution research: A review. Crit. Rev. Environ. Sci. Technol. 2021, 51, 2681–2743. [Google Scholar] [CrossRef]
- Wang, L.; Cheng, Y.; Lamb, D.; Naidu, R. The application of rapid handheld FTIR petroleum hydrocarbon-contaminant measurement with transport models for site assessment: A case study. Geoderma 2019, 361, 114017. [Google Scholar] [CrossRef]
- Luo, M.D.; Ji, H.H.; Huang, W.; Cai, X.; Gao, C. Research on measurement method of mid—IR spectral radiant intensity of exhaust system with FTIR spectrometer. J. Aerosp. Power 2007, 22, 1423–1429. [Google Scholar]
- Wang, C.Z.; Tong, Z.X.; Lu, Y.L.; Chai, D. Study on the airplane’s infrared radiation characteristics. Laser Infrared 2011, 41, 996–1001. [Google Scholar]
- Yao, K.K.; Wang, H.; Xu, F.; Zhang, R.J.; Wang, H.F. Application research of spectrometer in evaluation of infrared stealth effect of aero-engine. Laser Infrared 2020, 50, 975–980. [Google Scholar]
- Pang, X.T. Research on the Measuring Technology of Infrared Radiation Character of Aircraft Skin. Master’s Thesis, Shenyang Aerospace University, Shenyang, China, 2016. [Google Scholar]
- Zhu, J.; Liu, W.Q.; Lu, Y.H.; Gao, M.G.; Zhao, X.S.; Zhang, T.S.; Xu, L. Analysis of atmospheric transmittance based on FTIR spectra measurements. Opt. Tech. 2005, 31, 627–629. [Google Scholar]
- Wei, H.L.; Chen, X.H.; Dai, C.M.; Du, R.Q. Ground-based measurements of infrared atmospheric background spectral radiances. Infrared Laser Eng. 2012, 41, 284–290. [Google Scholar]
- Tan, H.; Xuan, Y.M.; Han, Y.G.; Li, Q. Experimental Research on the Spectral Emissivity Measurement Based on FTIR. J. Eng. Thermophys. 2012, 33, 1771–1773. [Google Scholar]
- Zhu, J.; Liu, W.Q.; Lu, Y.H.; Gao, M.G. Research on Radiance Measurements of Target and Background Based on FTIR. Infrared Technol. 2004, 26, 52–55. [Google Scholar]
- Yang, Z.J. Space optical instrument and its calibration and testing technology the third to speak spectroradiometer. J. Appl. Opt. 2008, 29, 1017–1020. [Google Scholar]
- Liu, J.M. Research on Infrared Radiation of Target Based on Radiometer. Master’s Thesis, Shenyang Aerospace University, Shenyang, China, 2017. [Google Scholar]
- Macarthur, A.; Maclellan, C.J.; Malthus, T. The Fields of View and Directional Response Functions of Two Field Spectroradiometers. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3892–3907. [Google Scholar] [CrossRef]
- Macarthur, A.A.; Maclellan, C.J.; Malthus, T.J. The implications of non-uniformity in fields-of-view of commonly used field spectroradiometers. In Proceedings of the 2007 IEEE International Geoscience & Remote Sensing Symposium (IGARSS), Barcelona, Spain, 23–28 July 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- Huang, W.; Ji, H.H.; Si, R. Non-uniformity correction for the measurement results of FTIR spectrometer. Laser Infrared 2015, 45, 400–405. [Google Scholar]
- Wang, X.X.; Yang, H.R.; Yu, B.; Yan, X.Y.; Hao, S.J.; Xie, Y.; Li, S.W.; Wang, J.G. Calibration and measurement method for IR target under the same solid angle. J. Appl. Opt. 2018, 39, 518–521. [Google Scholar]
- Feng, M.C.; Xu, L.; Gao, M.G.; Jiao, Y.; Li, X.-X.; Jin, L.; Cheng, S.-Y.; Tong, J.-J.; Wei, X.-L.; Li, S. Study of Radiometric Calibration Methods on FTIR Spectrometer. Infrared Technol. 2012, 34, 366–370. [Google Scholar]
- Liu, Z.M.; Gao, M.G.; Liu, W.Q.; Lu, Y.-H.; Zhang, T.-S.; Xu, L.; Wei, X.-L. The study of instrument Response Function of FTIR Detectors. Spectrosc. Spectr. Anal. 2008, 28, 1786–1789. [Google Scholar]
- Tong, J.J.; Liu, W.Q.; Gao, M.G.; Zhang, T.S.; Xu, L.; Wei, X.L. Study of Radiation Calibration Based on Airborne FTIR Spectrometer. Infrared 2010, 31, 12–15, 25. [Google Scholar]
- Zhang, J.Q. Infrared Physics, 2nd ed.; Xidian University Press: Xi’an, China, 2013; pp. 27, 66, 148–149. [Google Scholar]
- Fan, H. Understanding of the concept of Uncertainty in Measurement. Adv. Meas. Lab. Manag. 2014, 22, 30–32. [Google Scholar]
- Efremova, N.Y.; Chunovkina, A.G. Development of the Concept of Uncertainty in Measurement and Revision of Guide to the Expression of Uncertainty in Measurement. Part 1. Reasons and Probability-Theoretical Bases of the Revision. Meas. Tech. 2017, 60, 317–324. [Google Scholar] [CrossRef]
- Zhao, C.S. The Theory and Practice Design of The Indetermination Degree of Measure. Master’s Thesis, Changchun University of Science and Technology, Changchun, China, 2007. [Google Scholar]
- Zou, M.S. The Sources and Analysis of Common Probability Distribution Coverage Factor k Value in Evaluation and Expression for the Uncertainty of Measurement. Metrol. Meas. Tech. 2014, 41, 84–86. [Google Scholar]


| D2 (m) | Temperature (K) | Percentage in the FOV of the Spectroradiometer (%) |
|---|---|---|
| 4.25 | 547 | 50.11 |
| 4.25 | 557 | 50.11 |
| Composition | Center Wavelength of Absorption Band (μm) |
|---|---|
| CO2 | 4.3, 4.8 |
| H2O | 3.2 |
| CO | 4.7 |
| CH4 | 3.3 |
| O3 | 4.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, Z.; Li, Y.; Chen, G.; Li, Y.; Chai, S.; Zhang, P. Correction of Spatial Nonuniformity in Spectroradiometer Field-of-View Using a Concentric-Circles Method. Photonics 2022, 9, 56. https://doi.org/10.3390/photonics9020056
Jiao Z, Li Y, Chen G, Li Y, Chai S, Zhang P. Correction of Spatial Nonuniformity in Spectroradiometer Field-of-View Using a Concentric-Circles Method. Photonics. 2022; 9(2):56. https://doi.org/10.3390/photonics9020056
Chicago/Turabian StyleJiao, Zhaoqiang, Yiwen Li, Ge Chen, Yao Li, Shijie Chai, and Puyousen Zhang. 2022. "Correction of Spatial Nonuniformity in Spectroradiometer Field-of-View Using a Concentric-Circles Method" Photonics 9, no. 2: 56. https://doi.org/10.3390/photonics9020056
APA StyleJiao, Z., Li, Y., Chen, G., Li, Y., Chai, S., & Zhang, P. (2022). Correction of Spatial Nonuniformity in Spectroradiometer Field-of-View Using a Concentric-Circles Method. Photonics, 9(2), 56. https://doi.org/10.3390/photonics9020056





