Intensity-Averaged Double Three-Step Phase-Shifting Algorithm with Color-Encoded Fringe Projection
Abstract
:1. Introduction
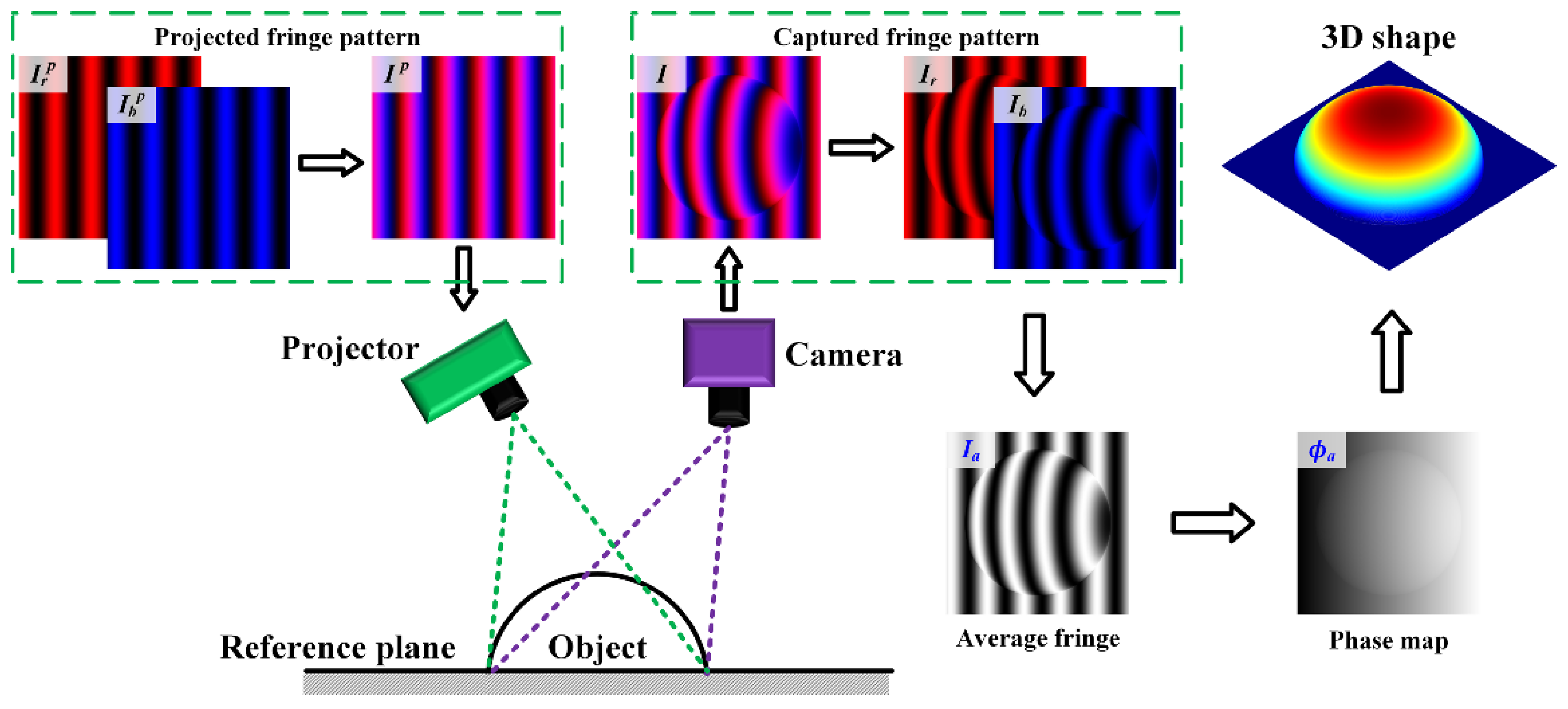
2. Principle
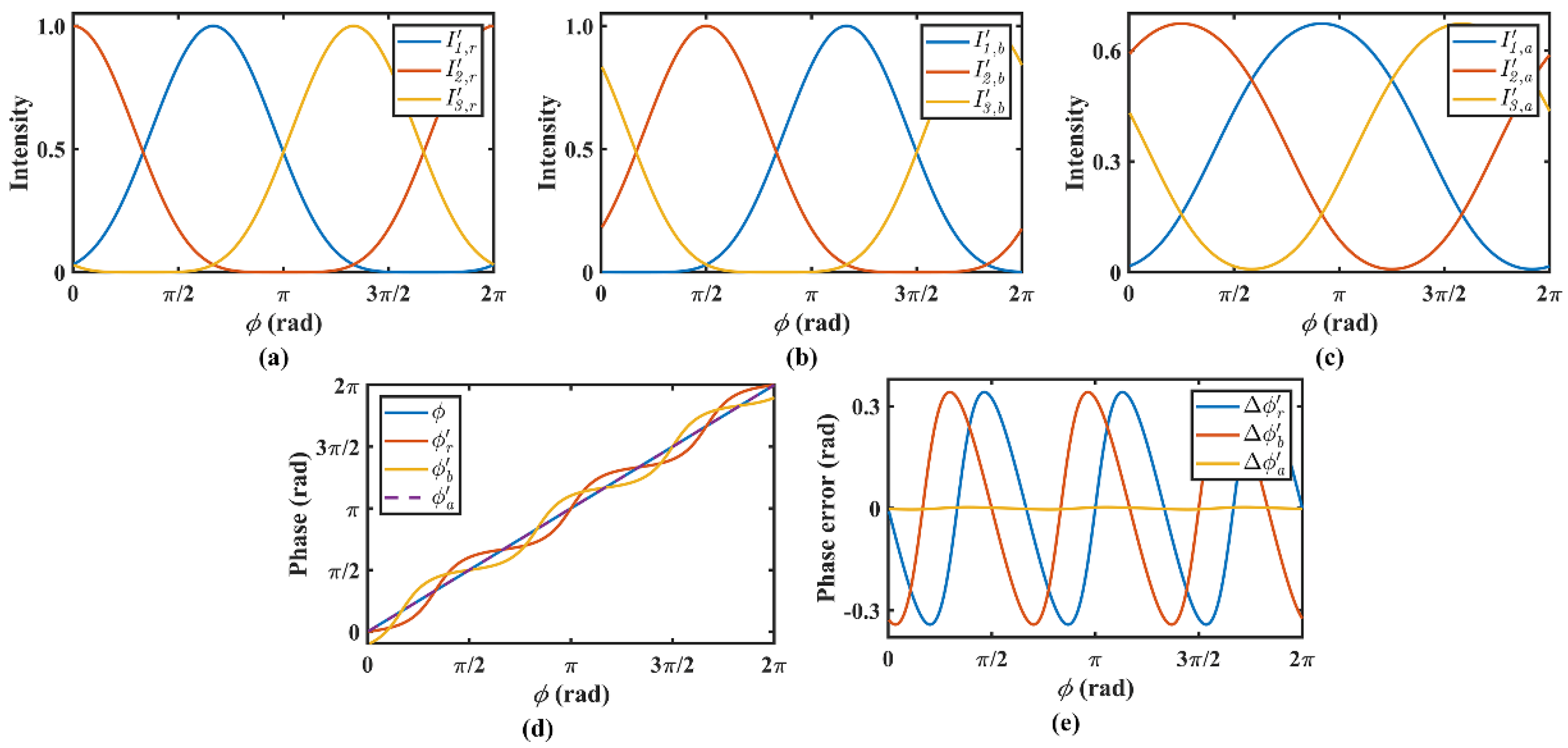
2.1. Phase-Averaged Double Three-Step Phase-Shifting (PDTP) Algorithm
2.2. Intensity-Averaged Double Three-Step Phase-Shifting (IDTP) Algorithm
2.3. Influnce of the Color Crosstalk
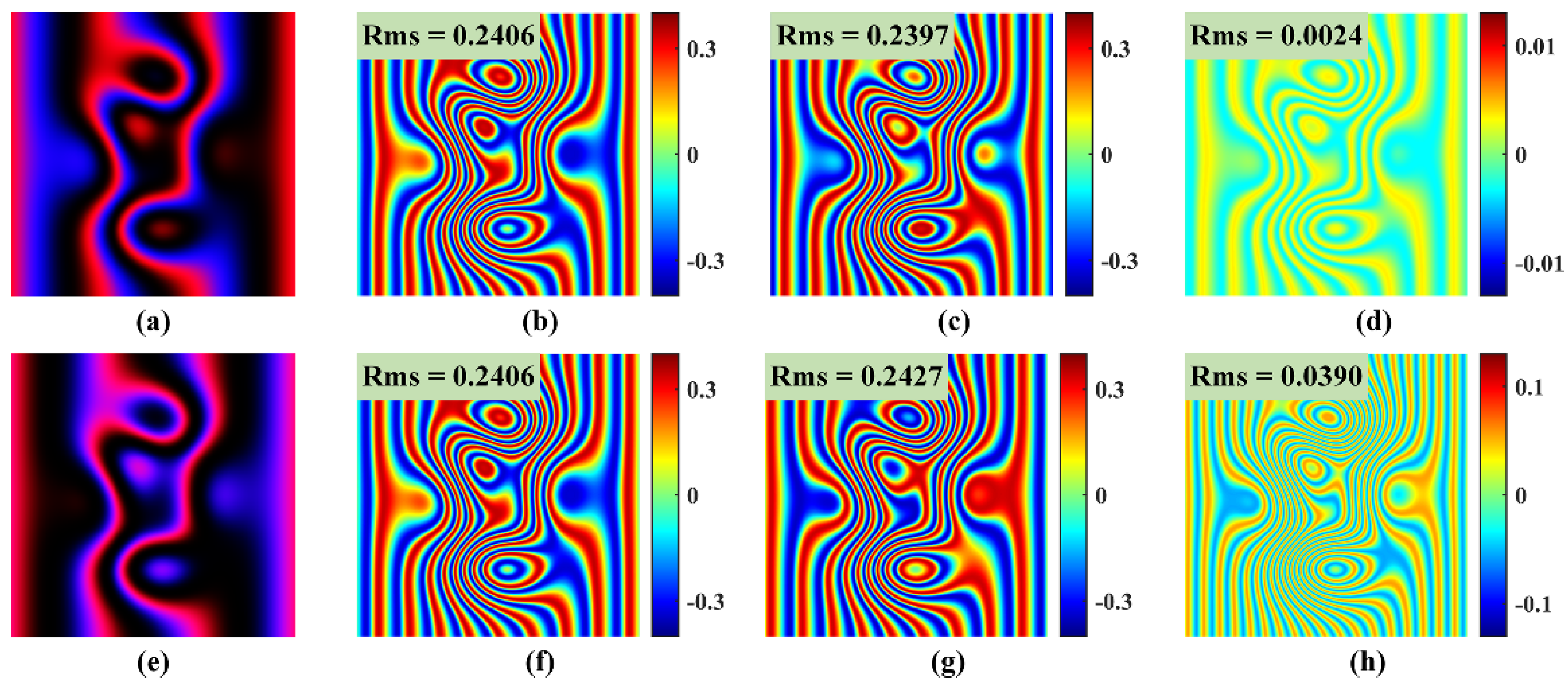
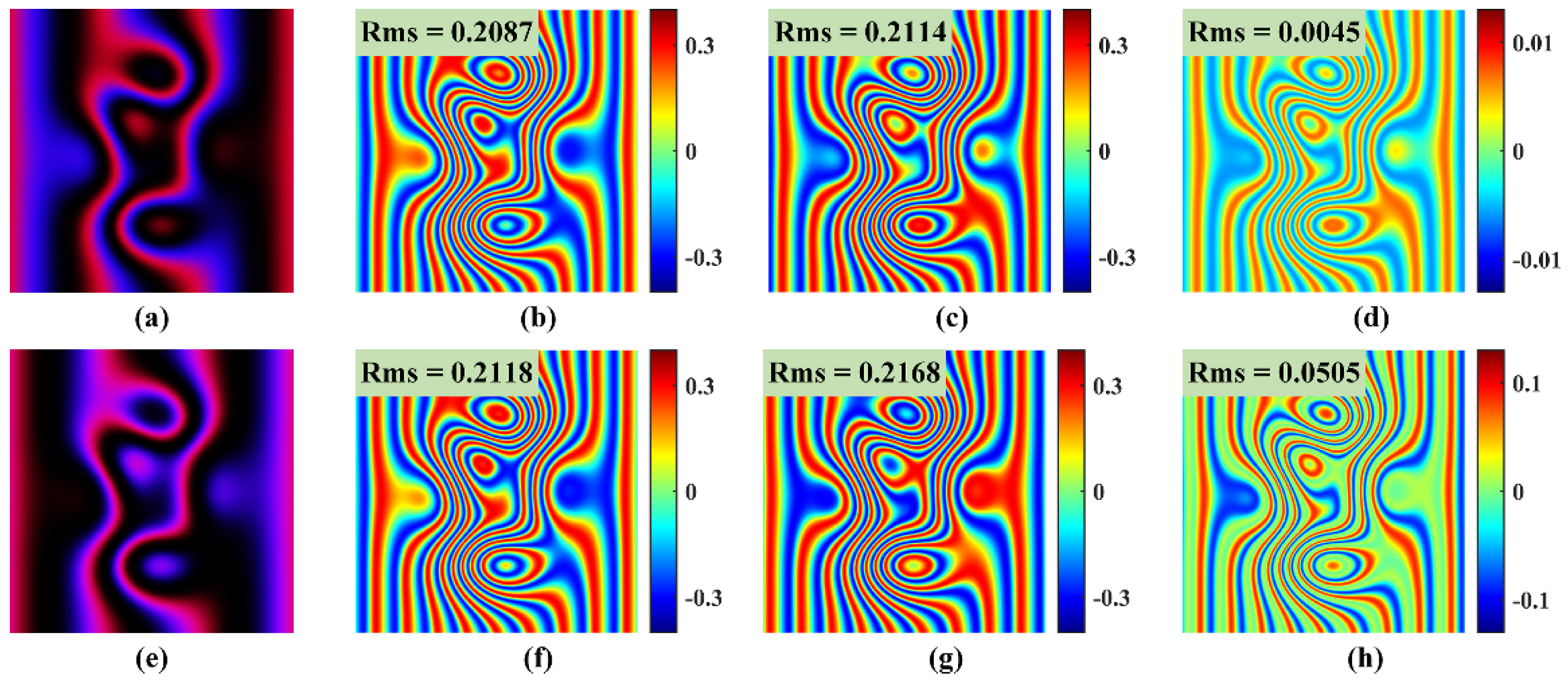
3. Simulations
3.1. Ignoring Color Crosstalk
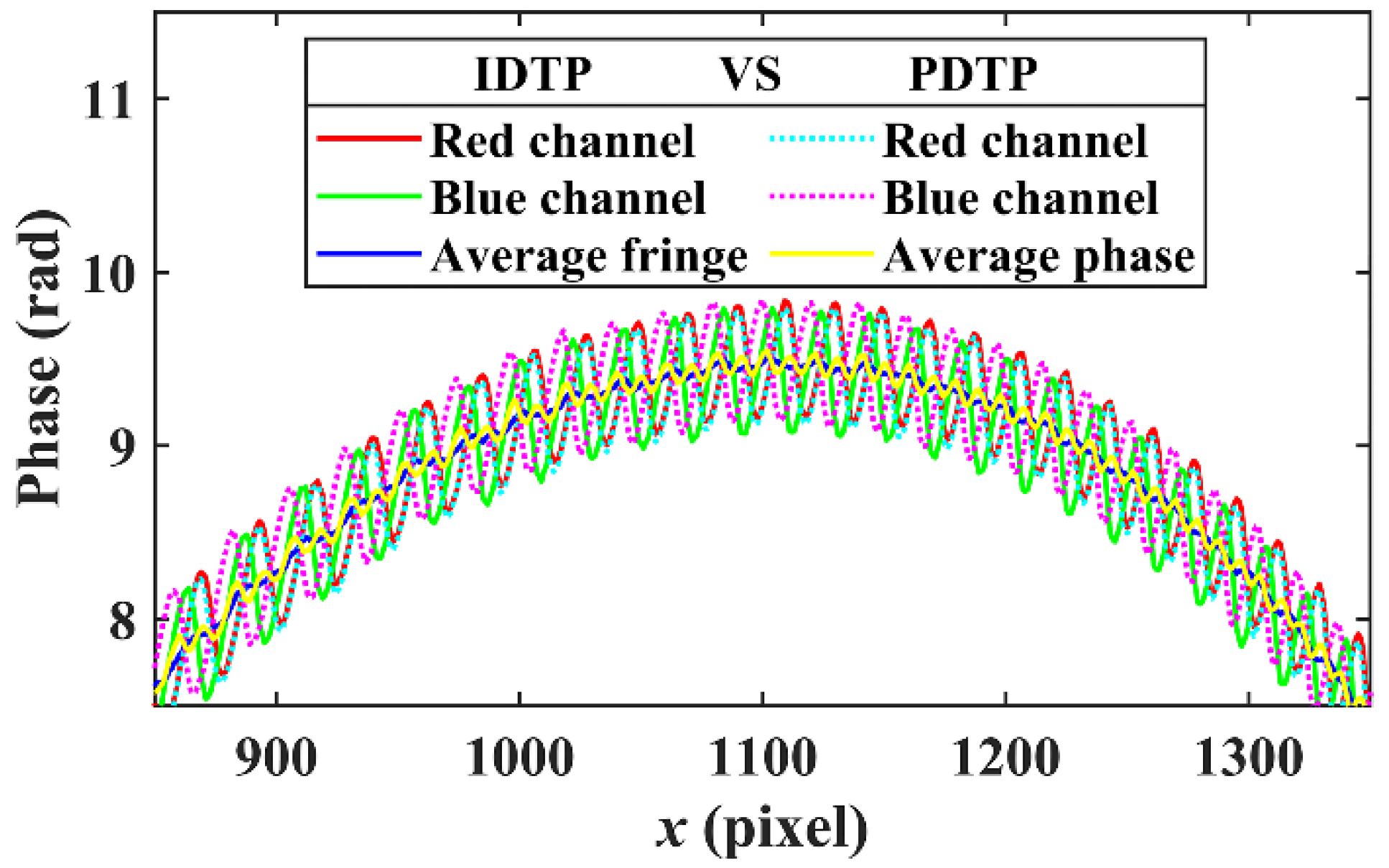
3.2. Considering Color Crosstalk
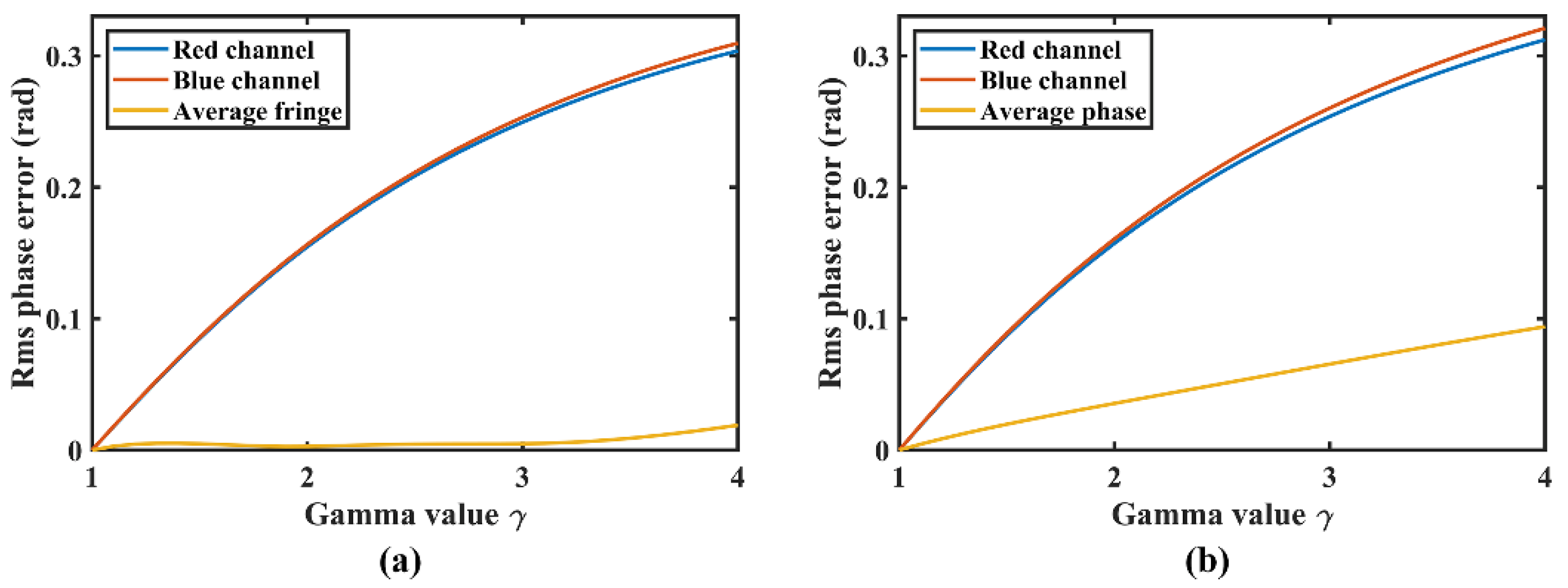
3.3. Different Gamma Values
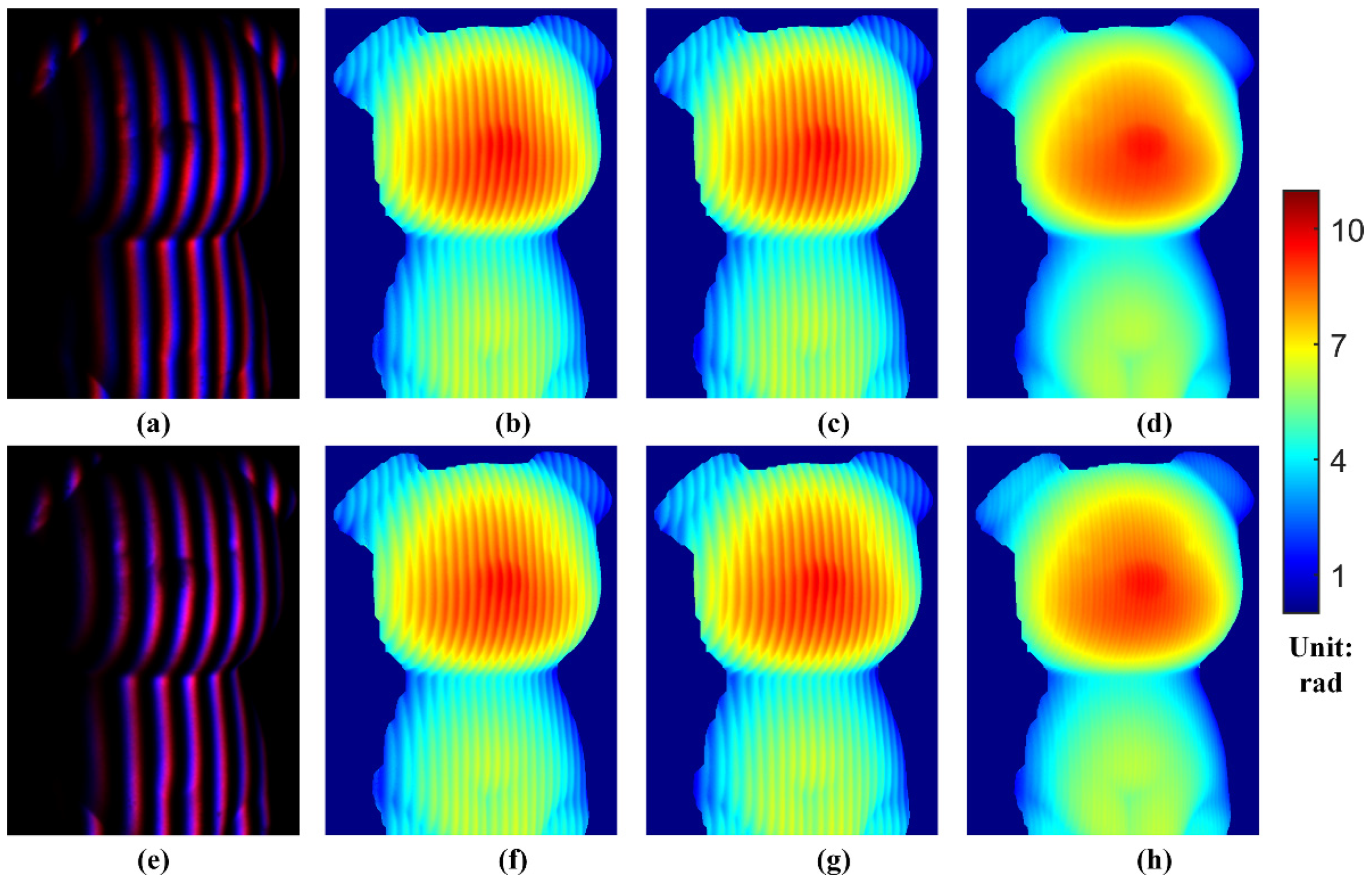
4. Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, L.; Suresh, V.; Zheng, Y.; Wang, Y.; Xi, J.; Li, B. Motion induced error reduction methods for phase shifting profilometry: A review. Opt. Laser Eng. 2021, 141, 106573. [Google Scholar] [CrossRef]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photonics 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Chen, R.; Xu, J.; Zhang, S. Comparative study on 3D optical sensors for short range applications. Opt. Laser Eng. 2022, 149, 106763. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Cai, J.; Xi, D.; Chen, X.; Wang, Y. Improved spatial-shifting two-wavelength algorithm for 3D shape measurement with a look-up table. Appl. Opt. 2021, 60, 4878–4884. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Zhang, S. Status, challenges, and future perspectives of fringe projection profilometry. Opt. Laser Eng. 2020, 135, 106193. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, Q.; Feng, S.J.; Zuo, C. Microscopic fringe projection profilometry: A review. Opt. Laser Eng. 2020, 135, 106192. [Google Scholar] [CrossRef]
- Zuo, C.; Feng, S.; Huang, L.; Tao, T.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Laser Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Wu, J.; Chen, X.; Wang, Y. Enhanced phase-coding method for three-dimensional shape measurement with half-period codeword. Appl. Opt. 2019, 58, 7359–7366. [Google Scholar] [CrossRef]
- Omidi, P.; Najiminaini, M.; Diop, M.; Carson, J.J. Single-shot 4-step phase-shifting multispectral fringe projection profilometry. Opt. Express 2021, 29, 27975–27988. [Google Scholar] [CrossRef]
- Cheng, N.-J.; Su, W.-H. Phase-Shifting Projected Fringe Profilometry Using Binary-Encoded Patterns. Photonics 2021, 8, 362. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, J.; Zhang, D.; Chen, X.; Wang, Y. Nonlinear Correction for Fringe Projection Profilometry with Shifted-Phase Histogram Equalization. IEEE Trans. Instrum. Meas. 2022, 71, 5005509. [Google Scholar] [CrossRef]
- Pan, B.; Kemao, Q.; Huang, L.; Asundi, A. Phase error analysis and compensation for nonsinusoidal waveforms in phase-shifting digital fringe projection profilometry. Opt. Lett. 2009, 34, 416–418. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S. Comparative study on passive and active projector nonlinear gamma calibration. Appl. Opt. 2015, 54, 3834–3841. [Google Scholar] [CrossRef]
- Babaei, A.; Saadatseresht, M.; Kofman, J. Exponential fringe pattern projection approach to gamma-independent phase computation without calibration for gamma nonlinearity in 3D optical metrology. Opt. Express 2017, 25, 24927–24938. [Google Scholar] [CrossRef]
- Xing, S.; Guo, H.W. Directly recognizing and removing the projector nonlinearity errors from a phase map in phase-shifting fringe projection profilometry. Opt. Commun. 2019, 435, 212–220. [Google Scholar] [CrossRef]
- Wu, G.X.; Wu, Y.X.; Hu, X.L.; Wu, M.X.; Zhang, S.M.; Liu, F. Exponential Taylor Series Method to eliminate the gamma distortion in phase shifting profilometry. Opt. Commun. 2019, 452, 306–312. [Google Scholar] [CrossRef]
- Zhang, S.; Yau, S.T. Generic nonsinusoidal phase error correction for three-dimensional shape measurement using a digital video projector. Appl. Opt. 2007, 46, 36–43. [Google Scholar] [CrossRef]
- Hoang, T.; Pan, B.; Nguyen, D.; Wang, Z. Generic gamma correction for accuracy enhancement in fringe-projection profilometry. Opt. Lett. 2010, 35, 1992–1994. [Google Scholar] [CrossRef]
- Liu, K.; Wang, S.J.; Lau, D.L.; Barner, K.E.; Kiamilev, F. Nonlinearity calibrating algorithm for structured light illumination. Opt. Eng. 2014, 53, 050501. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Yu, L.; Li, W.; Xia, H.; Deng, H.; Zhang, J. Black-box phase error compensation for digital phase-shifting profilometry. IEEE Trans. Instrum. Meas. 2017, 66, 2755–2761. [Google Scholar] [CrossRef]
- Yu, X.; Liu, Y.; Liu, N.; Fan, M.; Su, X. Flexible gamma calculation algorithm based on probability distribution function in digital fringe projection system. Opt. Express 2019, 27, 32047–32057. [Google Scholar] [CrossRef]
- Liu, Y.K.; Yu, X.; Xue, J.P.; Zhang, Q.C.; Su, X.Y. A flexible phase error compensation method based on probability distribution functions in phase measuring profilometry. Opt. Laser Technol. 2020, 129, 106267. [Google Scholar] [CrossRef]
- Huang, P.S.; Hu, Q.J.; Chiang, F.P. Double three-step phase-shifting algorithm. Appl. Opt. 2002, 41, 4503–4509. [Google Scholar] [CrossRef]
- Yong, L.; Dingfa, H.; Yong, J. Flexible error-reduction method for shape measurement by temporal phase unwrapping: Phase averaging method. Appl. Opt. 2012, 51, 4945–4953. [Google Scholar] [CrossRef]
- Lei, Z.K.; Wang, C.L.; Zhou, C.L. Multi-frequency inverse-phase fringe projection profilometry for nonlinear phase error compensation. Opt. Laser Eng. 2015, 66, 249–257. [Google Scholar] [CrossRef]
- Mao, C.L.; Lu, R.S.; Liu, Z.J. A multi-frequency inverse-phase error compensation method for projector nonlinear in 3D shape measurement. Opt. Commun. 2018, 419, 75–82. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, X.; Jiang, H.; He, D.; Peng, X.; Huang, S.; Zhang, Z. Flexible phase error compensation based on Hilbert transform in phase shifting profilometry. Opt. Express 2015, 23, 25171–25181. [Google Scholar] [CrossRef]
- Chen, H.; Yin, Y.; Cai, Z.; Xu, W.; Liu, X.; Meng, X.; Peng, X. Suppression of the nonlinear phase error in phase shifting profilometry: Considering non-smooth reflectivity and fractional period. Opt. Express 2018, 26, 13489–13505. [Google Scholar] [CrossRef]
- Yu, X.; Lai, S.; Liu, Y.; Chen, W.; Xue, J.; Zhang, Q. Generic nonlinear error compensation algorithm for phase measuring profilometry. Chin. Opt. Lett. 2021, 19, 101201. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Wu, J.; Chen, X.; Wang, Y. Hilbert transform-based crosstalk compensation for color fringe projection profilometry. Opt. Lett. 2020, 45, 2199–2202. [Google Scholar] [CrossRef]
- Wan, Y.Y.; Cao, Y.P.; Chen, C.; Fu, G.K.; Wang, Y.P.; Li, C.M. Single-shot real-time three dimensional measurement based on hue-height mapping. Opt. Commun. 2018, 416, 10–18. [Google Scholar] [CrossRef]
- Wang, Y.P.; Cao, Y.P.; Fu, G.K.; Wang, L.; Wan, Y.Y.; Li, C.M. Single-shot phase measuring profilometry based on color binary grating with intervals. Opt. Commun. 2019, 451, 268–275. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhu, H.; Cai, J.; Wang, Y. Intensity-Averaged Double Three-Step Phase-Shifting Algorithm with Color-Encoded Fringe Projection. Photonics 2022, 9, 173. https://doi.org/10.3390/photonics9030173
Wang Y, Zhu H, Cai J, Wang Y. Intensity-Averaged Double Three-Step Phase-Shifting Algorithm with Color-Encoded Fringe Projection. Photonics. 2022; 9(3):173. https://doi.org/10.3390/photonics9030173
Chicago/Turabian StyleWang, Yuwei, Haojie Zhu, Jiaxu Cai, and Yajun Wang. 2022. "Intensity-Averaged Double Three-Step Phase-Shifting Algorithm with Color-Encoded Fringe Projection" Photonics 9, no. 3: 173. https://doi.org/10.3390/photonics9030173
APA StyleWang, Y., Zhu, H., Cai, J., & Wang, Y. (2022). Intensity-Averaged Double Three-Step Phase-Shifting Algorithm with Color-Encoded Fringe Projection. Photonics, 9(3), 173. https://doi.org/10.3390/photonics9030173






