Low-Complexity Sampling Frequency Offset Estimation and Compensation Scheme for OFDM-Based UWOC System
Abstract
:1. Introduction
- (1)
- High accuracy and wide SFO compensation range. Up to ±1000 ppm SFO can be well-estimated with an accuracy of less than ±3 ppm after 1 m underwater transmission. Moreover, an estimation deviation within ±2 ppm can be achieved for the SFO below ±400 ppm;
- (2)
- Low computational complexity. Unlike traditional pilot-aided schemes utilizing the least square (LS) method to fit the SFO slope curve, the proposed scheme utilizes two phase-conjugated pilots for SFO estimation in each OFDM frame and an averaging processor is designed to improve estimation accuracy. These cause the decrease in operational complexity.
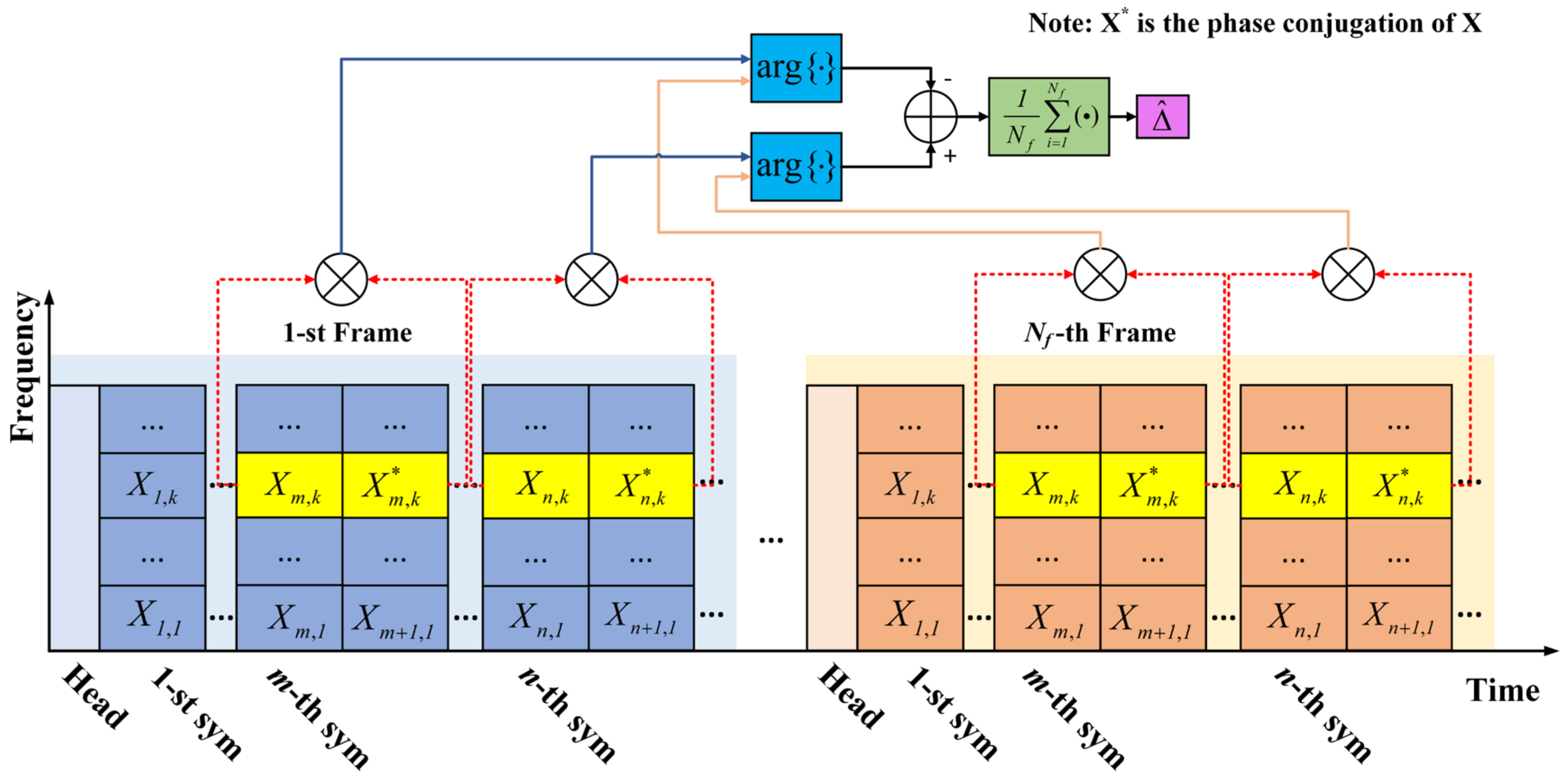
2. The Principle of SFO Estimation and Compensation
3. Experimental Setup
4. Experimental Results and Discussion
4.1. EVM Penalty in Terms of SFO Error
4.2. Influence of Frame Number and Pilot Interval on Estimation Accuracy
4.3. SFO Estimation Accuracy and Compensation Range
4.4. SFO Compensation Performance in Different Underwater Environments
4.5. Algorithm Complexity Comparisons
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shen, C.; Guo, Y.; Oubei, H.M.; Ng, T.K.; Liu, G.; Park, K.H.; Ho, K.T.; Alouini, M.S.; Ooi, B.S. 20-meter underwater wireless optical communication link with 1.5 Gbps data rate. Opt. Express 2016, 24, 25502–25509. [Google Scholar] [CrossRef] [PubMed]
- Chi, N.; Haas, H.; Kavehrad, M.; Little, T.D.; Huang, X.L. Visible light communications: Demand factors, benefits and opportunities [Guest Editorial]. IEEE Wirel. Commun. 2015, 22, 5–7. [Google Scholar] [CrossRef]
- Chi, N.; Zhou, Y.; Wei, Y.; Hu, F. Visible light communication in 6G: Advances, challenges, and prospects. IEEE Veh. Technol. Mag. 2020, 15, 93–102. [Google Scholar] [CrossRef]
- Wang, F.; Liu, Y.; Jiang, F.; Chi, N. High speed underwater visible light communication system based on LED employing maximum ratio combination with multi-PIN reception. Opt. Commun. 2018, 425, 106–112. [Google Scholar] [CrossRef]
- Ho, C.M.; Lu, C.K.; Lu, H.H.; Huang, S.J.; Cheng, M.T.; Yang, Z.Y.; Lin, X.Y. A 10m/10Gbps underwater wireless laser transmission system. In Proceedings of the Optical Fiber Communication Conference, Optical Society of America, Th3C-3, Los Angeles, CA, USA, 19–23 March 2017. [Google Scholar]
- Kaushal, H.; Kaddoum, G. Underwater optical wireless communication. IEEE Access 2016, 4, 1518–1547. [Google Scholar] [CrossRef]
- Zeng, Z.; Fu, S.; Zhang, H.; Dong, Y.; Cheng, J. A survey of underwater optical wireless communications. IEEE Commun. Surv. Tutor. 2016, 19, 204–238. [Google Scholar] [CrossRef]
- Chowdhury, M.Z.; Hossan, M.T.; Islam, A.; Jang, Y.M. A comparative survey of optical wireless technologies: Architectures and applications. IEEE Access 2018, 6, 9819–9840. [Google Scholar] [CrossRef]
- Oubei, H.M.; Duran, J.R.; Janjua, B.; Wang, H.Y.; Tsai, C.T.; Chi, Y.C.; Ng, T.K.; Kuo, H.C.; He, J.H.; Alouini, M.S.; et al. 4.8 Gbit/s 16-QAM-OFDM transmission based on compact 450-nm laser for underwater wireless optical communication. Opt. Express 2015, 23, 23302–23309. [Google Scholar] [CrossRef]
- Chen, Y.; Kong, M.; Ali, T.; Wang, J.; Sarwar, R.; Han, J.; Guo, C.; Sun, B.; Deng, N.; Xu, J. 26 m/5.5 Gbps air-water optical wireless communication based on an OFDM-modulated 520-nm laser diode. Opt. Express 2017, 25, 14760–14765. [Google Scholar] [CrossRef]
- Zou, P.; Zhao, Y.; Hu, F.; Chi, N. Underwater visible light communication at 3.24 Gb/s using novel two-dimensional bit allocation. Opt. Express 2020, 28, 11319–11338. [Google Scholar] [CrossRef]
- Wu, S.; Liu, P.; Bar-Ness, Y. Phase noise estimation and mitigation for OFDM systems. IEEE Trans. Wirel. Commun. 2006, 5, 3616–3625. [Google Scholar] [CrossRef]
- Schmidl, T.M.; Cox, D.C. Robust frequency and timing synchronization for OFDM. IEEE Trans. Commun. 1997, 45, 1613–1621. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; He, J.; Ma, J.; Chen, M. Experimental demonstration of an SFO-robustness scheme with fast OFDM for IMDD passive optical network systems. J. Lightwave Technol. 2020, 38, 5608–5616. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, H.; Zheng, Z.; Deng, R.; Chen, Q.; Peng, M.; Tang, X. OLT-centralized sampling frequency offset compensation scheme for OFDM-PON. Opt. Express 2017, 25, 19508–19516. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Liu, G.; Zhou, H.; Chen, Q.; He, J. Inter-symbol differential detection-enabled sampling frequency offset compensation for DDO-OFDM. IEEE Photonics Technol. Lett. 2018, 30, 2095–2098. [Google Scholar] [CrossRef]
- Xi, D.; Chen, M.; Zhang, L.; Wang, L.; Chen, G.; Zhou, H. Digital interpolation-based SFO compensation in OCT precoding-enabled NHS-OFDM transmission systems. Opt. Fiber Technol. 2021, 66, 102642. [Google Scholar] [CrossRef]
- Jin, X.Q.; Tang, J.M. Optical OFDM synchronization with symbol timing offset and sampling clock offset compensation in real-time IMDD systems. IEEE Photonics J. 2011, 3, 187–196. [Google Scholar] [CrossRef]
- Giddings, R.P.; Tang, J.M. Experimental demonstration and optimisation of a synchronous clock recovery technique for real-time end-to-end optical OFDM transmission at 11.25Gb/s over 25km SSMF. Opt. Express 2011, 19, 2831–2845. [Google Scholar] [CrossRef]
- Liu, Y.; He, J.; Chen, M.; Xiao, Y.; Cheng, Y. 64APSK constellation scheme for short-reach DMT with ISDD enabled SFO compensation. Opt. Commun. 2020, 467, 125689. [Google Scholar] [CrossRef]
- Xi, D.; Chen, M.; Tang, X.; Zhang, L.; Wang, L.; Chen, G.; Liu, G.; Zhou, H. Sampling frequency offset compensation in non-Hermitian symmetric optical OFDM. Opt. Commun. 2020, 472, 126048. [Google Scholar] [CrossRef]
- Wen, H.; Geng, K.; Chen, Q.; Deng, R.; Chen, M.; Zong, T.; Liu, F. A Simple Blind Sampling Frequency Offset Estimation Scheme for Short-Reach DD-OFDM Systems. IEEE Photonics J. 2020, 12, 1–10. [Google Scholar] [CrossRef]
- Luo, Z.; Chen, M.; Chen, Q.; Wen, H. Simple blind estimation of sampling frequency offset for real-time asynchronous DDO-OFDM system. Opt. Commun. 2021, 490, 126890. [Google Scholar] [CrossRef]
- Hu, Q.; Jin, X.; Xu, Z. Compensation of sampling frequency offset with digital interpolation for OFDM-based visible light communication systems. J. Lightwave Technol. 2018, 36, 5488–5497. [Google Scholar] [CrossRef]
- Hu, Q.; Jin, X.; Liu, W.; Guo, D.; Jin, M.; Xu, Z. Comparison of interpolation-based sampling frequency offset compensation schemes for practical OFDM-VLC systems. Opt. Express 2020, 28, 2337–2348. [Google Scholar] [CrossRef]
- Chen, M.; He, J.; Tang, J.; Chen, L. Pilot-aided sampling frequency offset estimation and compensation using DSP technique in DD-OOFDM systems. Opt. Fiber Technol. 2014, 20, 268–273. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.W.; Li, Y.C.; Song, Y.X.; Zhang, J.J.; Chen, J. A single pilot subcarrier based sampling frequency offset estimation and compensation algorithm for optical IMDD OFDM systems. IEEE Photonics J. 2016, 8, 1–9. [Google Scholar] [CrossRef]
- Deng, R.; He, J.; Chen, M.; Wei, Y.; Shi, J.; Chen, L. Real-time VLLC-OFDM HD-SDI video transmission system with TS-based SFO estimation. In Proceedings of the 2017 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 19–23 March 2017. [Google Scholar]
- Zhang, M.; Bi, M.; Xin, H.; Li, L.; Fu, Y.; He, H.; Hu, W. Low complexity and high accuracy sampling frequency offset estimation and compensation algorithm in IMDD-OFDM system. In Proceedings of the 2017 16th International Conference on Optical Communications and Networks (ICOCN), Wuzhen, China, 7–10 August 2017. [Google Scholar]
- Ma, J.; He, J.; Chen, M.; Zhou, Z.; Liu, Y.; Xiao, Y.; Cheng, Y. Cost-effective SFO compensation scheme based on TSs for OFDM-PON. J. Opt. Commun. Netw. 2019, 11, 299–306. [Google Scholar] [CrossRef]
- Oubei, H.; Durán, J.; Janjua, B.; Wang, H.; Tsai, C.; Chi, Y.; Ng, T.; Kuo, H.; He, J.; Alouini, M.; et al. Wireless optical transmission of 450 nm, 3.2 Gbit/s 16-QAM-OFDM signals over 6.6 m underwater channel. In Proceedings of the CLEO: Science and Innovations, San Jose, CA, USA, 5–10 June 2016. [Google Scholar]
- Zhang, J.J.; Tang, Z.H.; Giddings, R.; Wu, W.; Wang, W.L.; Cao, B.Y.; Zhang, Q.W.; Tang, J.M. Stage-Dependent DSP operation range clipping-induced bit resolution reductions of full parallel 64-Point FFTs incorporated in FPGA-Based optical OFDM receivers. J. Lightwave Technol. 2016, 34, 3752–3760. [Google Scholar] [CrossRef]
- Tian, P.; Chen, H.; Wang, P.; Liu, X.; Chen, X.; Zhou, G.; Zhang, S.; Lu, J.; Qiu, P.; Qian, Z.; et al. Absorption and scattering effects of Maalox, chlorophyll, and sea salt on a micro-LED-based underwater wireless optical communication. Chin. Opt. Lett. 2019, 17, 100010. [Google Scholar] [CrossRef]







| Parameters | Values |
|---|---|
| Physical dimensions of the tank | 1 m × 0.5 m × 0.5 m |
| Laser wavelength | 450 nm |
| LD output power | 30 mW |
| The divergence angles in the parallel/vertical direction | 6.5°/22.5° |
| DAC/ADC resolutions | 8/10 bits |
| DAC/ADC sampling rate | 10/50 MS/s |
| Underwater transmission distance | 0.5/1 m |
| IFFT/FFT size | 64 |
| CP and CS length | 16 |
| Data-carrying subcarriers | From 3 to 30 |
| Number of TS per OFDM frame | 2 |
| Number of OFDM symbol | 100 |
| SFO (ppm) | 0 | 200 | 1000 |
|---|---|---|---|
| EVM (dB) | −21.4 | −21.9 | −19.4 |
| Salinity | 0% | 10% | 20% | 30% | 40% |
|---|---|---|---|---|---|
| ROP (dBm) | −14.5 | −15.22 | −16.12 | −17.59 | −18.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Chen, T.; Wang, Z.; Cao, B.; Li, Y.; Zhang, J. Low-Complexity Sampling Frequency Offset Estimation and Compensation Scheme for OFDM-Based UWOC System. Photonics 2022, 9, 216. https://doi.org/10.3390/photonics9040216
Li H, Chen T, Wang Z, Cao B, Li Y, Zhang J. Low-Complexity Sampling Frequency Offset Estimation and Compensation Scheme for OFDM-Based UWOC System. Photonics. 2022; 9(4):216. https://doi.org/10.3390/photonics9040216
Chicago/Turabian StyleLi, Hu, Tianyang Chen, Zhijie Wang, Bingyao Cao, Yingchun Li, and Junjie Zhang. 2022. "Low-Complexity Sampling Frequency Offset Estimation and Compensation Scheme for OFDM-Based UWOC System" Photonics 9, no. 4: 216. https://doi.org/10.3390/photonics9040216
APA StyleLi, H., Chen, T., Wang, Z., Cao, B., Li, Y., & Zhang, J. (2022). Low-Complexity Sampling Frequency Offset Estimation and Compensation Scheme for OFDM-Based UWOC System. Photonics, 9(4), 216. https://doi.org/10.3390/photonics9040216





