Study of an Optical Fiber Time Transmission Method with Real-Time Average Temperature Measurement of Links
Abstract
:1. Introduction
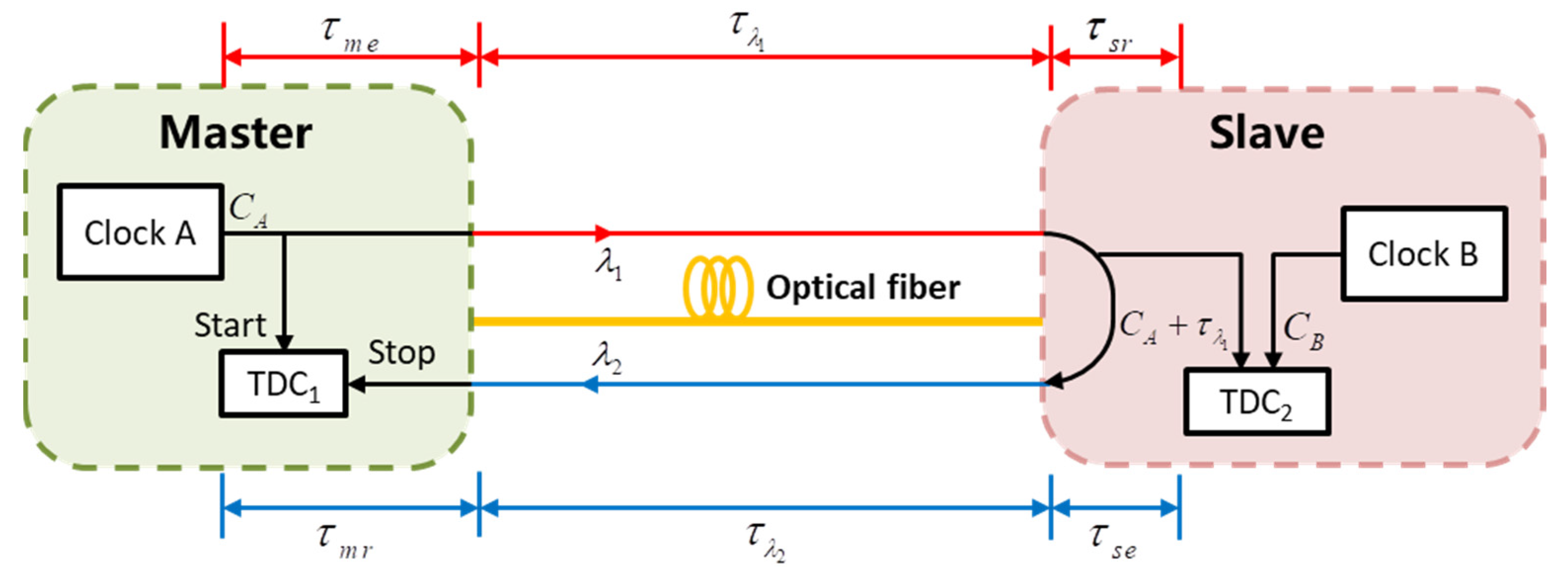
2. Principles and Methods
2.1. The Principle of the Round-Trip Method
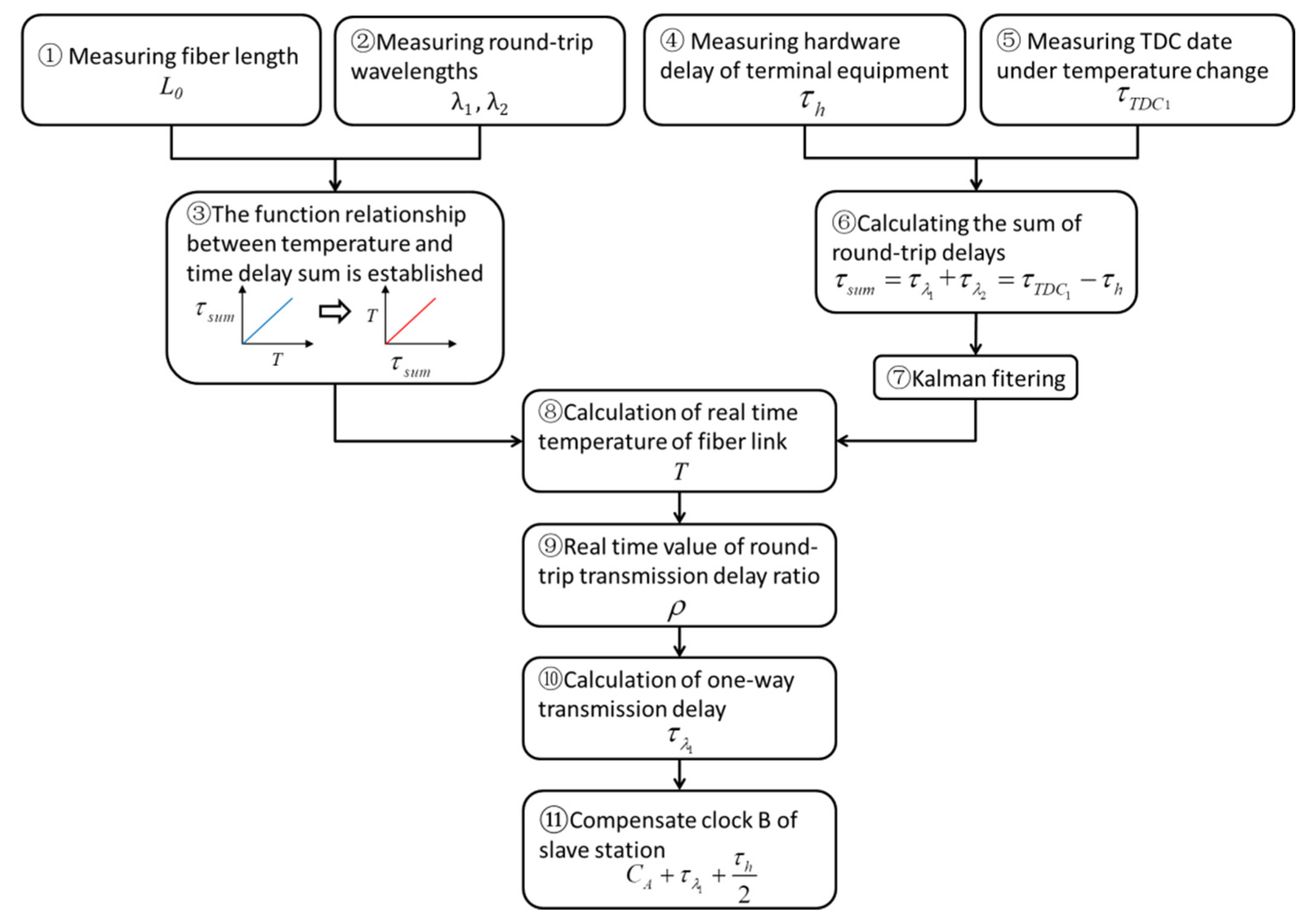
2.2. Time Transfer Method Based on Temperature Tracking
- Measure the initial length L0 of the 23 °C optical fiber link in advance;
- Measure the round-trip optical signal wavelengths and using a spectrometer;
- Substitute the optical fiber length L0, and wavelengths and into Formulas (4) and (5), determine the corresponding relationship between the round-trip delay and the temperature, and establish the relationship between the temperature and the time-delay sum;
- Pre-calibrate the transceiver delay sum of the terminal hardware of the master–slave station;
- Measure the round-trip delay of the master–slave station through the time interval measurement module;
- The round-trip delay sum of the optical fiber link is calculated using Formula (3);
- The delay jitter and noise interference are filtered by the Kalman filter algorithm;
- The real-time average temperature T of the optical fiber link is calculated by the filter value of ;
- Substitute the measured real-time average temperature into Formulas (5) and (6) and the real-time value of the ratio can be calculated;
- Substitute the ratio into Formula (7) to solve the one-way time delay under temperature change.
- Compensate clock CB to .
3. Experiment and Results Analysis
3.1. Construction of an Experimental Platform
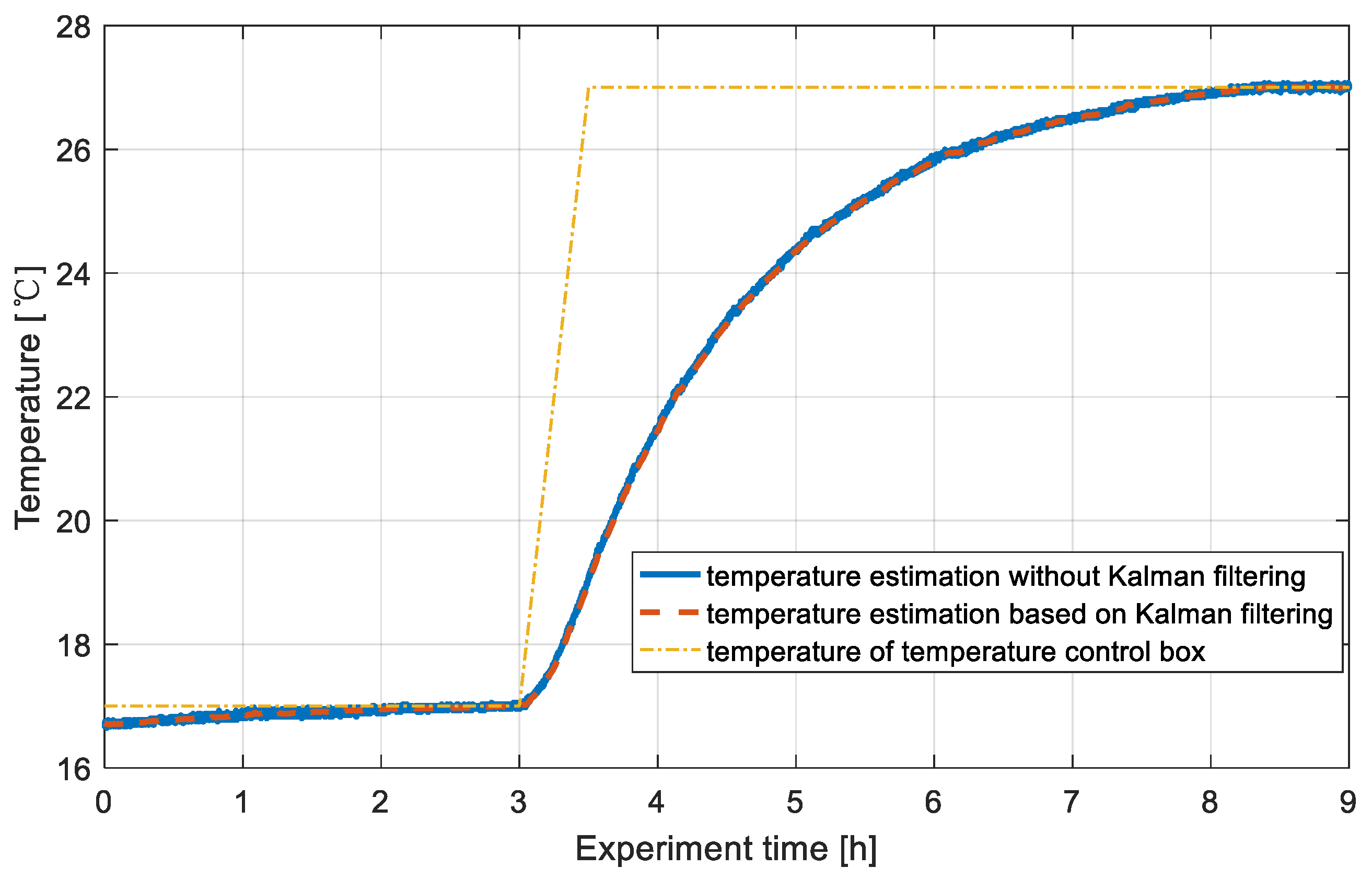
3.2. Temperature Measurement Results
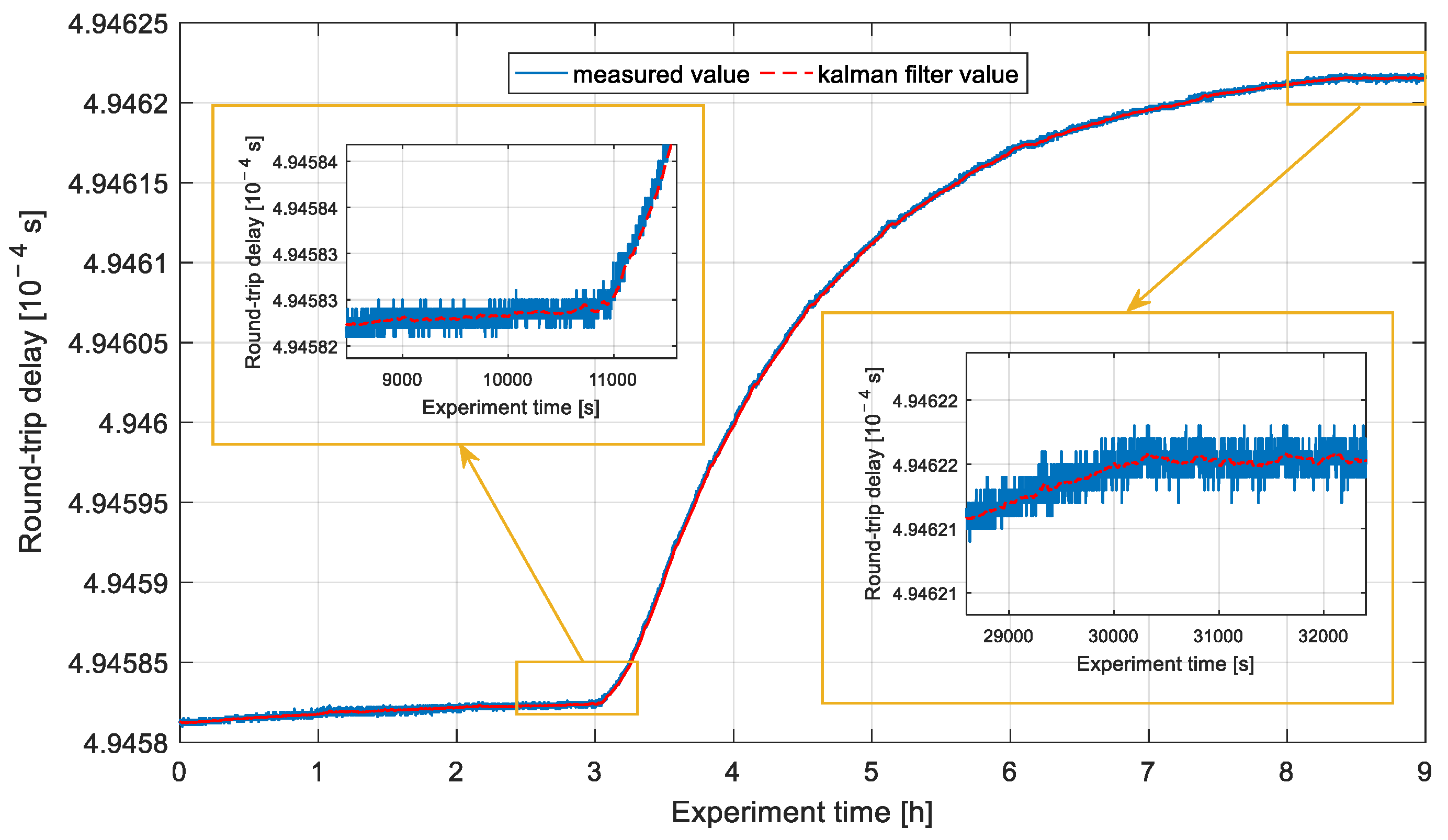
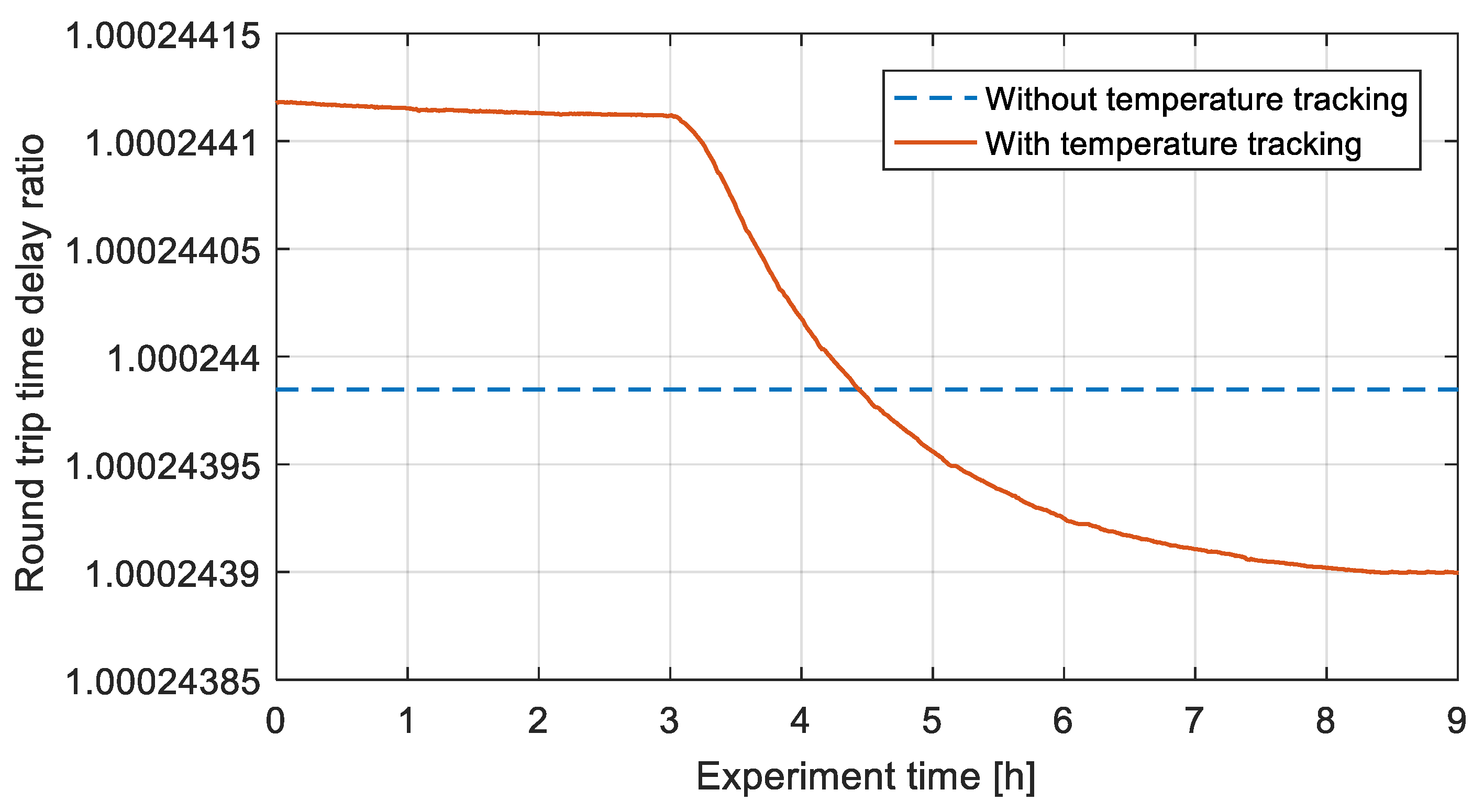
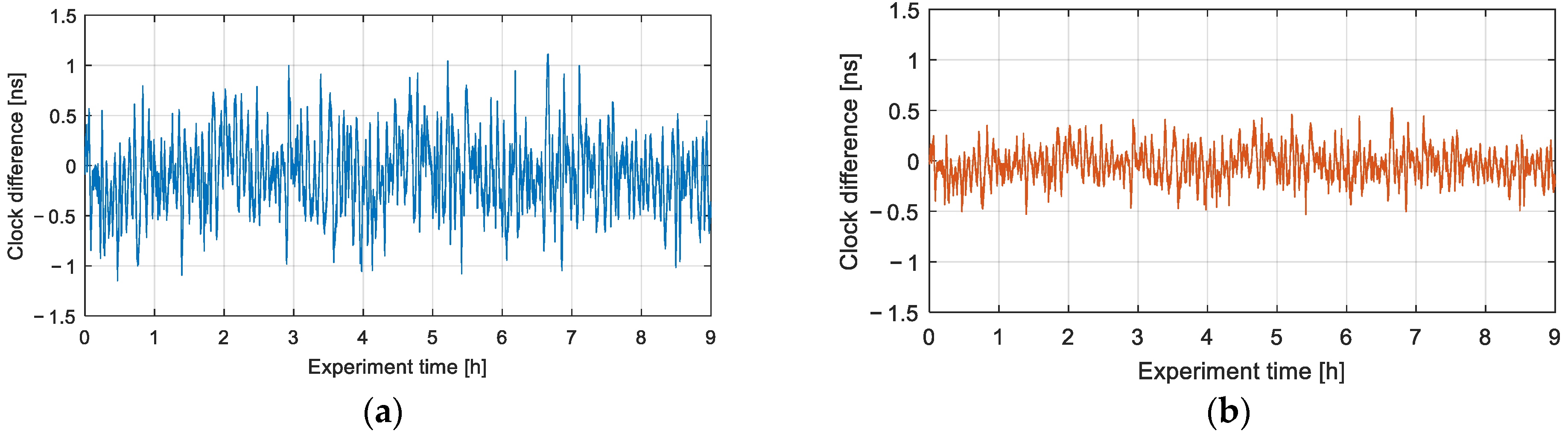
3.3. Experimental Results of Time Transfer
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, D.; Xu, J.; Liang, Y.; Jiang, S.; He, H. Long-Distance Time Transfer in Optical Fiber Networks Using a Cascaded Taming Technology. Math. Probl. Eng. 2021, 2021, 8860028. [Google Scholar] [CrossRef]
- Smotlacha, V.; Kuna, A.; Mache, W. Time transfer using fiber links. In Proceedings of the EFTF-2010 24th European Frequency and Time Forum, Noordwijk, The Netherlands, 13–16 April 2010; pp. 1–8. [Google Scholar]
- Droste, S.; Ozimek, F.; Udem, T.; Predehl, K.; Hänsch, T.W.; Schnatz, H.H.; Grosche, G.; Holzwarth, R. Optical-Frequency Transfer over a Single-Span 1840 km Fiber Link. Phys. Rev. Lett. 2013, 111, 110801. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Xu, J.; Li, Z.; Tan, X.; Wu, M. Optical fiber time transmission technology based on a double-fiber round-trip method. Appl. Opt. 2021, 60, 7504–7510. [Google Scholar] [CrossRef] [PubMed]
- Czubla, A.; Krehlik, P.; Sliwczyliski, L. Some approximated methods of calculation Sagnac correction for optical fiber time transfer. In Proceedings of the 2017 Joint Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium, Besancon, France, 9–13 July 2017; IEEE: New York, NY, USA; pp. 399–401. [Google Scholar]
- Zhang, H.; Wu, G.; Hu, L.; Li, X.; Chen, J. High-precision time transfer over 2000-km fiber link. IEEE Photonics J. 2015, 7, 15615634. [Google Scholar] [CrossRef]
- Lopez, O.; Kanj, A.; Pottie, P.E.; Rovera, D.; Achkar, J.; Chardonnet, C.; Amy-Klein, A.; Santarelli, G. Simultaneous remote transfer of accurate timing and optical frequency over a public fiber network. Appl. Phys. B 2013, 110, 3–6. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y. Concepts of Comprehensive PNT and related key technologies. Acta Geod. Cartogr. Sin. 2016, 45, 506. [Google Scholar]
- Krehlik, P.; Sliwczynski, L.; Buczek, L. ELSTAB-fiber optic time and frequency distribution technology—A general characterization and fundamental limits. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 993–1004. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, G.; Endo, M. Temperature-dependent Sellmeier coefficients and chromatic dispersions for some optical fiber glasses. J. Lightwave Technol. 1994, 12, 1338–1342. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Wang, R.; Lu, L.; Zhu, Y.; Zheng, J.; Wu, C.; Zhang, B.; Wang, P. WDM-based radio frequency dissemination in a tree-topology fiber optic network. Opt. Express 2015, 23, 19783–19792. [Google Scholar] [CrossRef] [PubMed]
- Lou, Z.; Yang, B.; Han, K.; Wang, X.; Zhang, H.; Xi, X.; Liu, Z. Real-time in-situ distributed fiber core temperature measurement in hundred-watt fiber laser oscillator pumped by 915/976 nm LD sources. Sci. Rep. 2020, 10, 9006. [Google Scholar] [CrossRef] [PubMed]
- Jin, C.; Shevchenko, N.A.; Li, Z.; Popov, S.; Chen, Y.; Xu, T. Nonlinear Coherent Optical Systems in the Presence of Equalization Enhanced Phase Noise. J. Lightwave Technol. 2021, 39, 4646–4653. [Google Scholar] [CrossRef]
- Ding, M.; Feng, Z.; Marpaung, D.; Zhang, X.; Komanec, M.; Suslov, D.; Dousek, D.; Zvánovec, S.; Numkam Fokoua, E.R.; Bradley, T.D.; et al. Optical fiber delay lines in microwave photonics: Sensitivity to temperature and means to reduce it. J. Lightwave Technol. 2021, 39, 2311–2318. [Google Scholar] [CrossRef]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Optical fiber model | G.652 | Clock source | Cesium clock-3230B |
| Fiber length | 50,692.593 m | Fiber loss | 0.187 dB/km |
| Modulation on λ | 1 s−1 | Measurement resolution of TDC | 100 ps |
| Wavelength of | 1550.87 nm | Temperature control box (TC) | CTP404 |
| Wavelength of | 1490.92 nm | Experiment duration | 9 h |
| Terminal equipment temperature | 23 °C | Initial temperature of TC | 17 °C |
| Hardware delay | 3.4 ns | Final temperature of TC | 27 °C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Xu, J.; Tan, X.; Wu, M. Study of an Optical Fiber Time Transmission Method with Real-Time Average Temperature Measurement of Links. Photonics 2022, 9, 293. https://doi.org/10.3390/photonics9050293
Chen D, Xu J, Tan X, Wu M. Study of an Optical Fiber Time Transmission Method with Real-Time Average Temperature Measurement of Links. Photonics. 2022; 9(5):293. https://doi.org/10.3390/photonics9050293
Chicago/Turabian StyleChen, Ding, Jiangning Xu, Xiaorong Tan, and Miao Wu. 2022. "Study of an Optical Fiber Time Transmission Method with Real-Time Average Temperature Measurement of Links" Photonics 9, no. 5: 293. https://doi.org/10.3390/photonics9050293
APA StyleChen, D., Xu, J., Tan, X., & Wu, M. (2022). Study of an Optical Fiber Time Transmission Method with Real-Time Average Temperature Measurement of Links. Photonics, 9(5), 293. https://doi.org/10.3390/photonics9050293




