A New Lattice Boltzmann Scheme for Photonic Bandgap and Defect Mode Simulation in One-Dimensional Plasma Photonic Crystals
Abstract
:1. Introduction
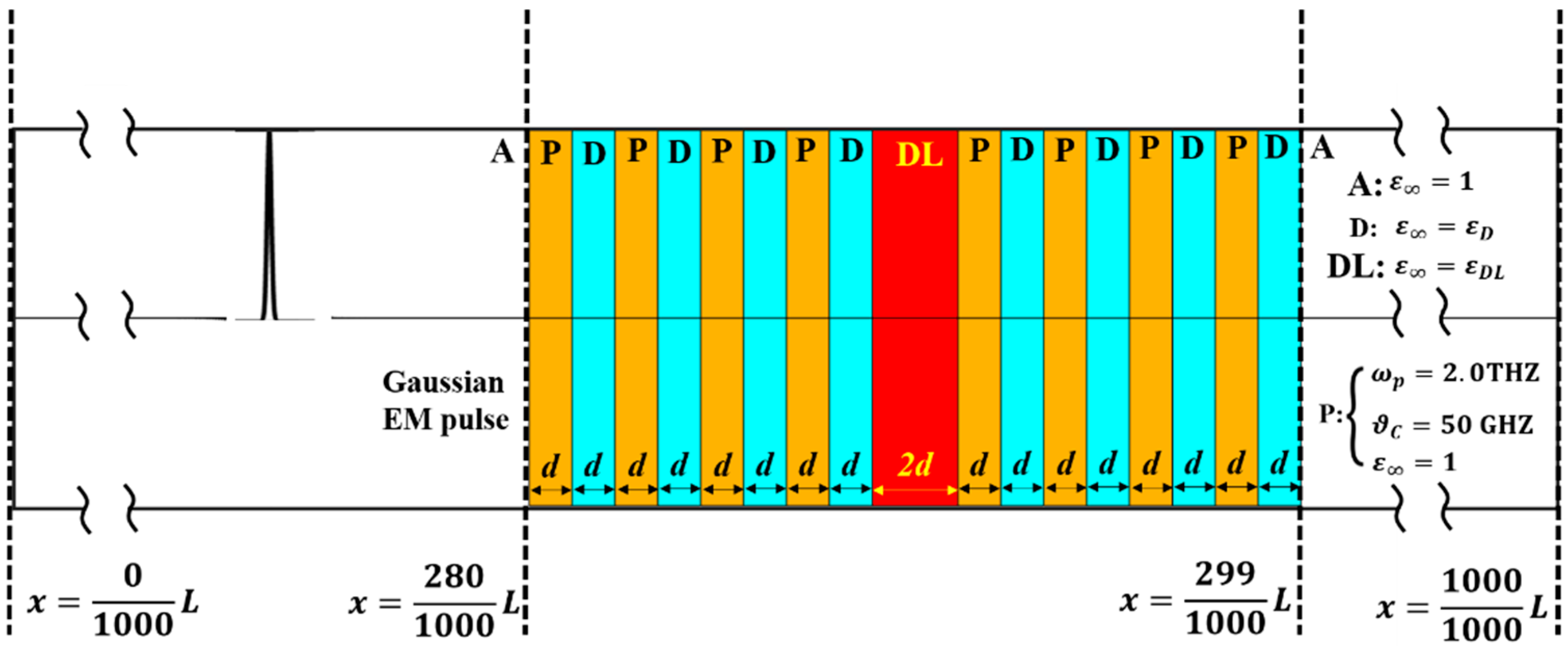
2. Methods
3. Results and Discussion
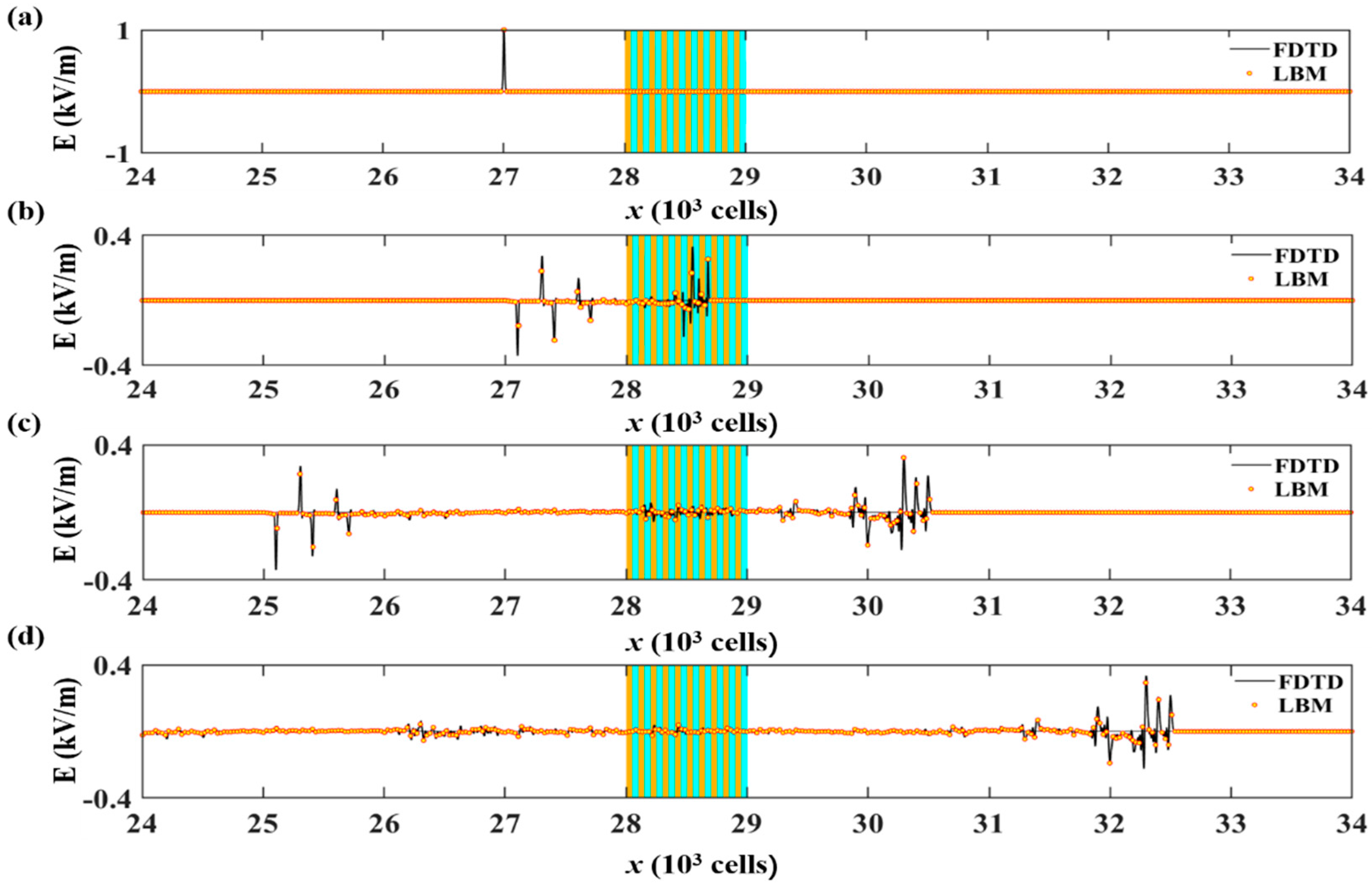
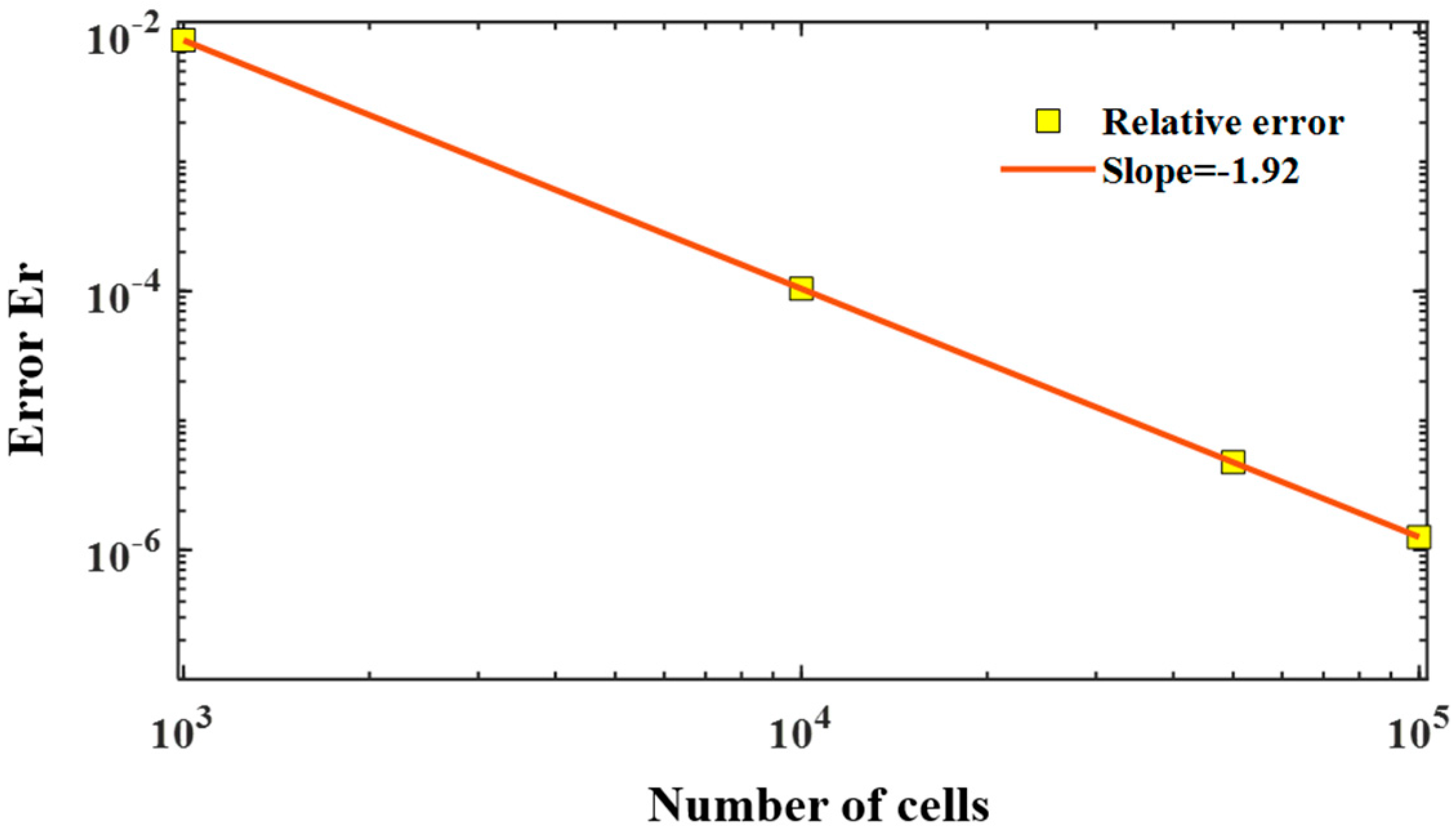
3.1. Electromagnetic Waves in Nondispersive Media
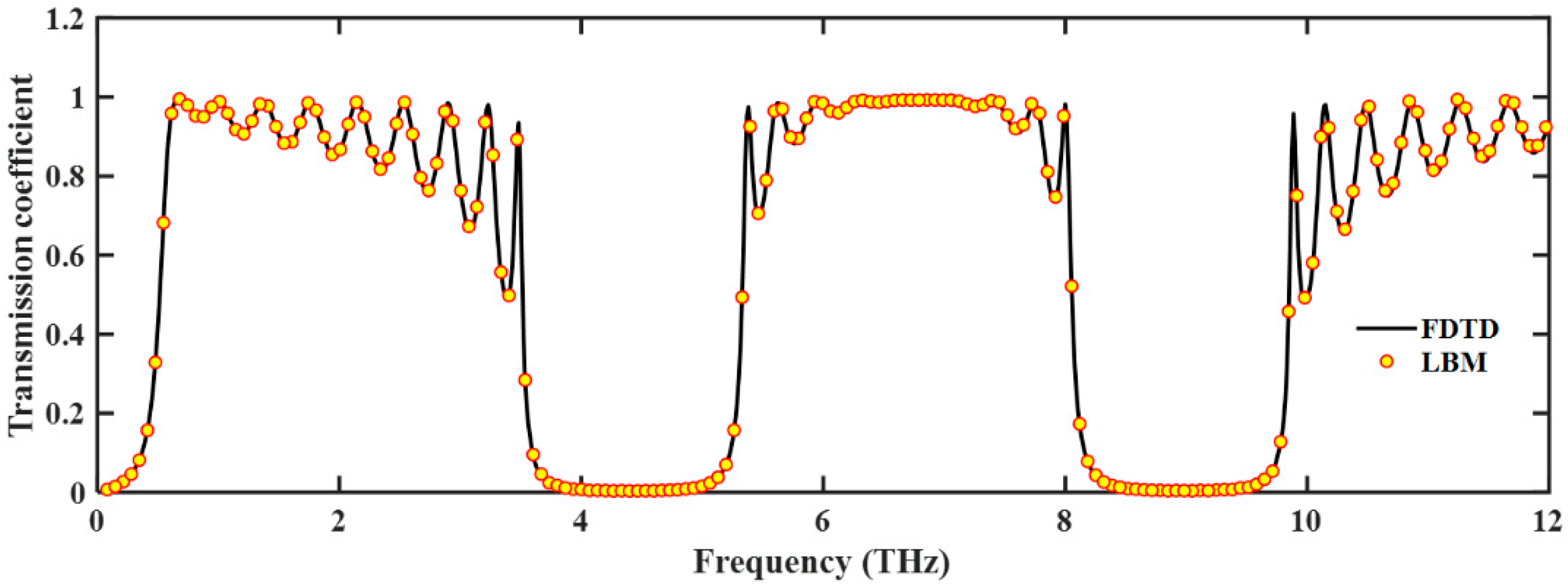
3.2. PBGs in 1D Plasma PhCs Based on LBM–SEF
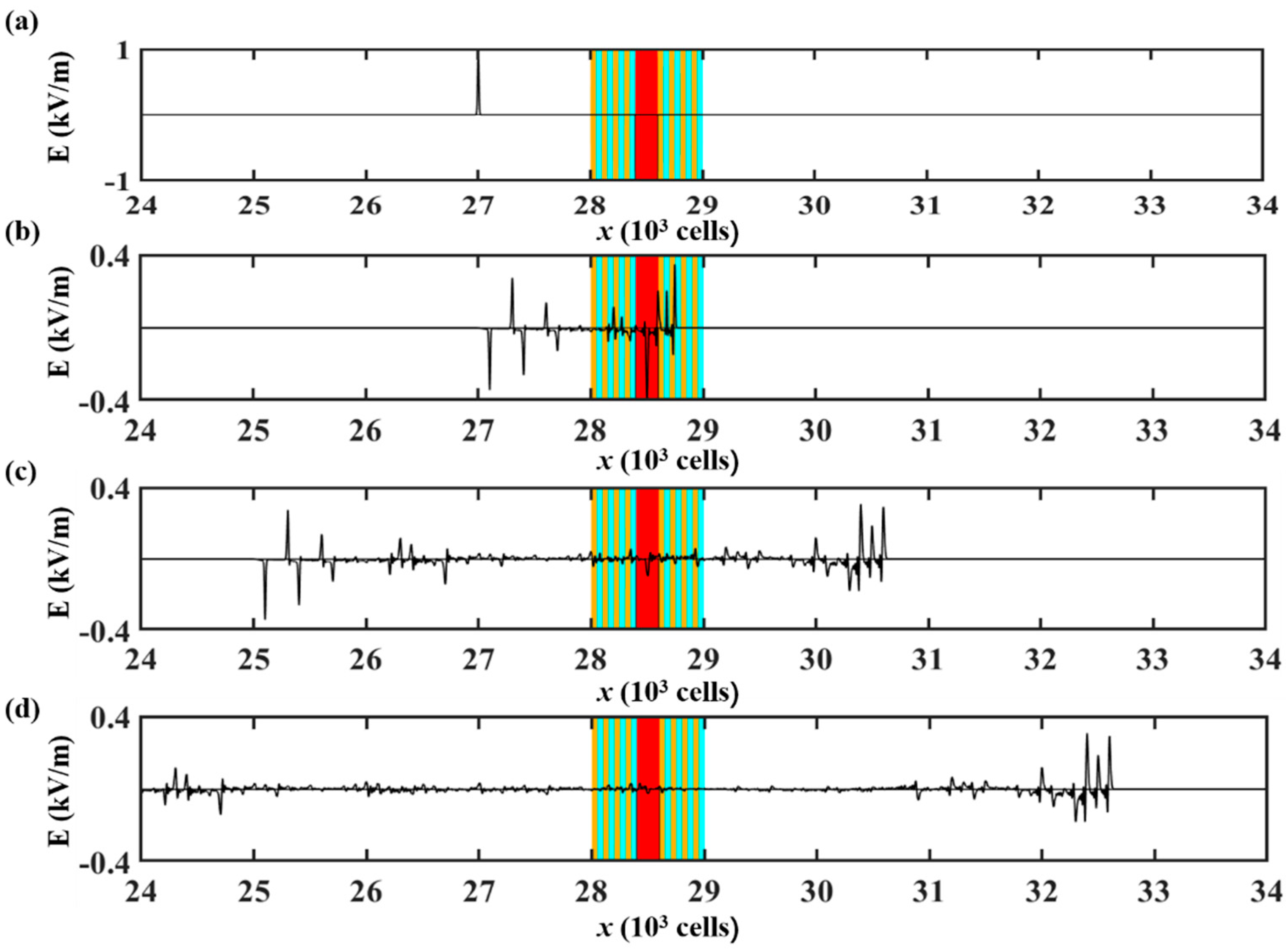
3.3. Effects of the Defect Layer Thickness on DMs and PBGs in 1D Plasma PhCs
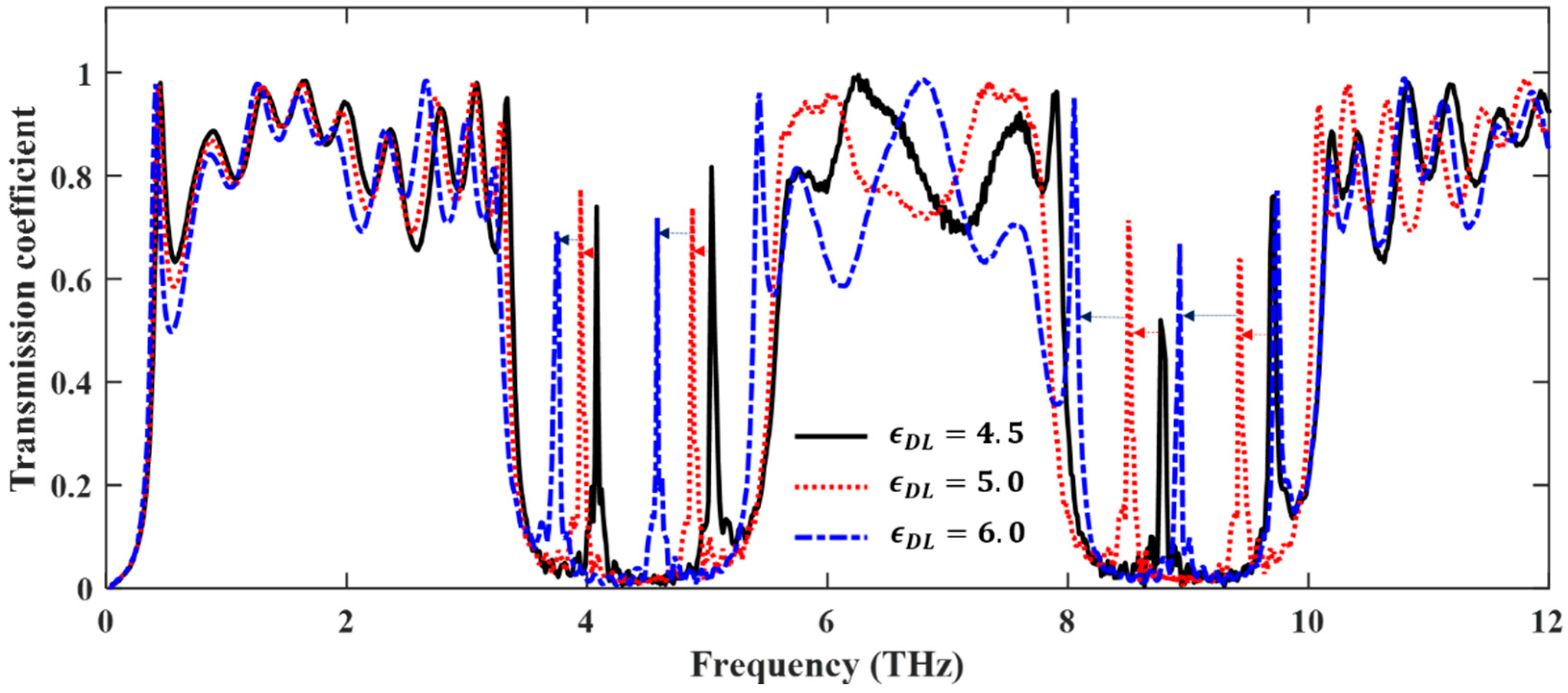
3.4. Effects of the Relative Dielectric Constant on the DMs and PBGs in 1D Plasma PhCs
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yablonovitch, E. Photonic band gap structure. J. Opt. Soc. Am. B 1993, 10, 283–295. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, Z.; Peng, J.; Lin, L.; Lin, R.; Lin, Q. Study on transmission characteristics and bandgap types of plasma photonic crystal. Photonics 2021, 8, 401. [Google Scholar] [CrossRef]
- Yupapin, P.; Trabelsi, Y.; Vigneswaran, D.; Taya, S.A.; Daher, M.G.; Colak, I. Ultra high sensitive sensor based on surface plasmon resonance structure having Si and graphene layers for the detection of chikungunya virus. Plasmonics 2022, 17, 1315–1321. [Google Scholar] [CrossRef]
- Taya, S.A.; Ramahi, O.M.; Abutailkh, M.A.; Doghmosh, N.; Nassar, Z.M.; Upadhyay, A.; Colak, I. Investigation of bandgap properties in one-dimensional binary superconductor-dieletric photonic crystal: TE case. India J. Phys. 2022, 96, 2151–2160. [Google Scholar] [CrossRef]
- Almawgani, A.H.; Taya, S.A.; Daher, M.G.; Colak, I.; Wu, F.; Patel, S.K. Detection of glucose concentration using a surface plasmon resonance biosensor based on barium titanate layers and molybdenum disulphide sheets. Phys. Scr. 2022, 97, 065501. [Google Scholar] [CrossRef]
- Yablonovitch, E.; Gmitter, T.J.; Bhat, R. Inhibited and enhanced spontaneous emission from optically thin AlGaAs/GaAs double heterostrutures. Phys. Rev. Lett. 1988, 61, 2546–2549. [Google Scholar] [CrossRef]
- Ma, H.; Wu, B.; Wang, Y.; Ren, H.; Jiang, W.; Tang, M.; Guo, W. A novel lattice Boltzmann scheme with single extended force term for electromagnetic wave propagating in one dimensional plasma medium. Eletronics 2022, 11, 882. [Google Scholar] [CrossRef]
- Steigerwald, D.A.; Bhat, J.C.; Collins, D.; Fletcher, R.M.; Holcomb, M.O.; Ludowise, M.J.; Martin, P.S.; Rudaz, S.L. llumination with solid state lighting technology. IEEE J. Sel. Top. Quantum Electron. 2002, 8, 310–320. [Google Scholar] [CrossRef]
- Gratzel, M. Photoelectrochemical cells. Nature 2001, 414, 338–344. [Google Scholar] [CrossRef]
- Haslinger, M.J.; Sivun, D.; Pohl, H.; Munkhbat, B.; Muhlberger, M.; Klar, T.A.; Scharber, M.C.; Hrelescu, C. Plasmon assistend direction and polarization sensitive organic thin film detector. Nanomaterials 2020, 10, 1866. [Google Scholar] [CrossRef]
- Kyaw, C.; Yahiaoui, R.; Chase, Z.A.; Tran, V.; Baydin, A.; Tay, F.; Kono, J.; Manjappa, M.; Singh, R.; Abeysinghe, D.C.; et al. Guided-mode resonances in flexible 2D terahertz photonic crystals. Optica 2020, 7, 537–541. [Google Scholar] [CrossRef]
- Shi, J.; Li, Z.; Sang, D.K.; Xiang, Y.; Li, J.; Zhang, S.; Zhang, H. THZ photonics in two dimensional materials and metamaterials: Properties, devices and prospects. J. Mater. Chem. C 2018, 6, 1291–1306. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, Z.Q.; Chan, C.T. Surface Impedance and Bulk Band Geometric Phases in One-Dimensional Systems. Phys. Rev. X 2014, 4, 021017. [Google Scholar] [CrossRef] [Green Version]
- Dong, J.-W.; Chang, M.-L.; Huang, X.-Q.; Hang, Z.H.; Zhong, Z.-C.; Chen, W.-J.; Huang, Z.-Y.; Chan, C.T. Conical Dispersion and Effective Zero Refractive Index in Photonic Quasicrystals. Phys. Rev. Lett. 2015, 114, 163901. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Wang, H.-X.; Xu, Y.-D.; Chen, H.-Y.; Jiang, J.-H. Accidental degeneracy in photonic bands and topological phase transitions in two-dimensional core-shell dielectric photonic crystals. Opt. Express 2016, 24, 18059–18071. [Google Scholar] [CrossRef]
- Meng, G.; Ying, Q.; Loveless, A.M.; Wu, F.; Wang, K.; Fu, Y.; Garner, A.L.; Cheng, Y. Spatio-temporal dynamics of pulsed gas breakdown in microgaps. Phys. Plasma 2019, 26, 014506. [Google Scholar] [CrossRef]
- Li, X.; Lin, L.; Sheng, W.; Xu, H. Recent progress in the synthesis of nanomaterials by microplasma. J. Chem. Eng. Chin. Univ. 2021, 35, 589–600. [Google Scholar]
- Sun, P.P.; Zhang, R.; Chen, W.; Braun, P.V.; Eden, J.G. Dynamic plasma metal dielectric photonic crystals in the mm-wave region: Electromagnetically active artificial material for wireless communications and sensors. Appl. Phys. Rev. 2019, 6, 041406. [Google Scholar] [CrossRef]
- Son, J.H. Terahertz electromagnetic interactions with biological matter and their aaplications. J. Appl. Phys. 2009, 105, 102033. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, M.; Li, D.; Chen, L.; Fu, A.; Liang, Y.; Wang, H. Study on an artificial phenomenon observed in terahertz biological imaging. Biomed. Opt. Express 2021, 12, 3133–3141. [Google Scholar] [CrossRef]
- Erez, E.; Leviatan, Y. Current model analysis of electromagnetic scattering from objects containing a variety of length scales. J. Opt. Soc. Am. A 1994, 11, 1500–1504. [Google Scholar] [CrossRef]
- Shao, Y.; Yang, J.; Huang, M. A review of computational electromagnetic methods for graphene modeling. Int. J. Antennas Propag. 2016, 1, 7478621. [Google Scholar] [CrossRef] [Green Version]
- Sumithra, P.; Thiripurasundari, D. A review of computational electromagnetics methods. Adv. Electromagn. 2017, 6, 42–55. [Google Scholar] [CrossRef]
- Yee, K.S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 39, 302–307. [Google Scholar]
- Chen, P.; Wang, C.; Ho, J. A lattice Boltzmann model for electromagnetic waves propagating in a one-dimensional dispersive medium. Comput. Math. Appl. 2013, 65, 961–973. [Google Scholar] [CrossRef]
- Feliziani, M.; Cruciani, S.; Santis, V.D.; Maradei, F. FD2TD Analysis of electromagnetic field propagation in multipole Debye media with and without convolution. Prog. Electromagn. Res. 2012, 42, 181–205. [Google Scholar] [CrossRef] [Green Version]
- Luebbers, R.; Kunz, K.S. A frequency dependent finite difference time domain formulation for dispersive materials. IEEE Trans. Electromagn. Compat. 1990, 32, 222–227. [Google Scholar] [CrossRef]
- Kashiwa, T.; Yoshida, N.; Fukai, I. A treatment by the finite difference time domain method of the dispersive characteristics associated with orientation polarization. IEICE Trans. 1990, 73, 1326–1328. [Google Scholar]
- Kashiwa, T.; Fukai, I. A treatment by the FDTD method of the dispersive characteristics associated with electronic polarization. Microw. Opt. Technol. Lett. 1990, 3, 203–205. [Google Scholar] [CrossRef]
- Ganhi, O.P.; Gao, B.Q.; Chen, J.Y. A frequency dependent finite difference time domain formulation for general dispersive media. IEEE Trans. Microw. Theory Tech. 1993, 41, 658–665. [Google Scholar] [CrossRef]
- Nickisck, L.J.; Franke, P.M. Finite difference time domain solution of Maxwell’s equations for the dispersive ionosphere. IEEE Antennas Propag. Mag. 1992, 34, 33–39. [Google Scholar] [CrossRef]
- Tang, M.; Zhan, H.; Ma, H.; Lu, S. Upscaling of dynamic capillary pressure of two-phase flow in sandstone. Water Resour. Res. 2019, 55, 426–443. [Google Scholar] [CrossRef] [Green Version]
- Tang, M.; Zhan, H.; Lu, S.; Ma, H.; Tan, H. Pore-scale CO2 displacement simulation based on the three fluid phase lattice Boltzmann method. Energy Fuels 2019, 33, 10039–10055. [Google Scholar] [CrossRef]
- Tang, M.; Lu, S.; Zhan, H.; Guo, W.; Ma, H. The effect of a microscale fracture on dynamic capillary pressure of two phase flow in porous media. Adv. Water Resour. 2018, 113, 272–284. [Google Scholar] [CrossRef]
- Chopard, B.; Luthi, P.; Wagen, J. Lattice Boltzmann method for wave propagation in urban microcells. IEEE Proc. Microwa. Antennas Propag. 1997, 144, 251–255. [Google Scholar] [CrossRef]
- Succi, S. Lattice Boltzmann schemes for quantum applications. Comput. Phys. Commun. 2002, 146, 317–323. [Google Scholar] [CrossRef]
- Succi, S.; Benzi, R. Lattice Boltzmann equation for quantum mechanics. Phys. D 1993, 69, 327–332. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, G. A lattice Boltzmann model for the nonlinear Schrodinger equation. J. Phys. A Math. Theor. 2007, 40, 10393–10405. [Google Scholar] [CrossRef]
- Sajjadi, H.; Atashafrooz, M.; Delouei, A.A.; Wang, Y. The effect of indoor heating system location on particle deposition and convection heat transfer: DMRT-LBM. Comput. Math. Appl. 2021, 86, 90–105. [Google Scholar] [CrossRef]
- Jalali, A.; Delouei, A.A.; Khorashadizadeh, M.; Golmohammadi, A.M.; Karimnejad, S. Mesoscopic simulation of forced convective heat transfer of Carreau-Yasuda fluid flow over an inclined square: Temperature-dependent viscosity. J. Appl. Comput. Mech. 2020, 6, 307–319. [Google Scholar]
- Karimnejad, S.; Delouei, A.A.; Nazari, M.; Shahmardan, M.M.; Rashidi, M.M.; Wongwsies, S. Immersed boundary-thermal lattice Boltzmann method for moving simulation of non-isothermal elliptical particle. J. Therm. Anal. Calorim. 2019, 138, 4003–4017. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; Zhu, H. A general single-node second-order boundary condition for the lattice Boltzmann method. Phys. Fluids. 2021, 33, 043317. [Google Scholar] [CrossRef]
- Hanasoge, S.M.; Succi, S.; Orszag, S.A. Lattice Boltzmann method for electromagnetic wave propagation. Lett. J. Explor. Front. Phys. 2011, 96, 14002. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.; Fang, H.; Xu, J.; Zi, J.; Zhang, X. Lattice Boltzmann model for photonic band gap materials. Phys. Rev. E 2003, 67, 025701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Richardson, L.F.; Gaunt, J.A. The deferred approach to the limit. Philos. Trans. R. Soc. Lond. Ser. A 1927, 226, 299–361. [Google Scholar]
- Mendoza, M.; Munoz, J.D. Three dimensional Lattice-Boltzmann model for electrodynamics. Phys. Rev. E 2010, 82, 056708. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Cappelli, M.A. A plasma photonic crystal bandgap device. Appl. Phys. Lett. 2016, 108, 161101. [Google Scholar] [CrossRef]
- Dhuri, D.B.; Hanasoge, S. Numerical analysis of the lattice Boltzmann method for simulation of linear acoustic waves. Phys. Rev. E 2017, 95, 043306. [Google Scholar] [CrossRef] [Green Version]
- Liang, G.; Han, P.; Wang, H. Narrow frequency and sharp angular defect mode in one-dimensional photonic crystals from a photonic heterostructure. Opt. Lett. 2004, 29, 192–194. [Google Scholar] [CrossRef]
- Aghajamali, A.; Hayati, M.; Wu, C.; Barati, M. Properties of the defect modes in 1D lossy photonic crystals containing two types of negative index materials defects. J. Electromagn. Waves Appl. 2013, 27, 2317–2329. [Google Scholar] [CrossRef]





| Denomination | LBM Context | Physical Context |
|---|---|---|
| Space step | ||
| Time step | ||
| Light speed | ||
| Electric field density | ||
| Frequency |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, H.; Wu, B.; Song, L.; Ren, H.; Jiang, W.; Guo, W.; Tang, M. A New Lattice Boltzmann Scheme for Photonic Bandgap and Defect Mode Simulation in One-Dimensional Plasma Photonic Crystals. Photonics 2022, 9, 464. https://doi.org/10.3390/photonics9070464
Ma H, Wu B, Song L, Ren H, Jiang W, Guo W, Tang M. A New Lattice Boltzmann Scheme for Photonic Bandgap and Defect Mode Simulation in One-Dimensional Plasma Photonic Crystals. Photonics. 2022; 9(7):464. https://doi.org/10.3390/photonics9070464
Chicago/Turabian StyleMa, Huifang, Bin Wu, Liping Song, Hao Ren, Wanshun Jiang, Wenyue Guo, and Mingming Tang. 2022. "A New Lattice Boltzmann Scheme for Photonic Bandgap and Defect Mode Simulation in One-Dimensional Plasma Photonic Crystals" Photonics 9, no. 7: 464. https://doi.org/10.3390/photonics9070464
APA StyleMa, H., Wu, B., Song, L., Ren, H., Jiang, W., Guo, W., & Tang, M. (2022). A New Lattice Boltzmann Scheme for Photonic Bandgap and Defect Mode Simulation in One-Dimensional Plasma Photonic Crystals. Photonics, 9(7), 464. https://doi.org/10.3390/photonics9070464






