Yoctosecond Timing Jitter Sensitivity in Tightly Synchronized Mode-Locked Ti:Sapphire Lasers
Abstract
:1. Introduction
2. Experimental Setup
2.1. Laser Design
2.2. Fast PZT
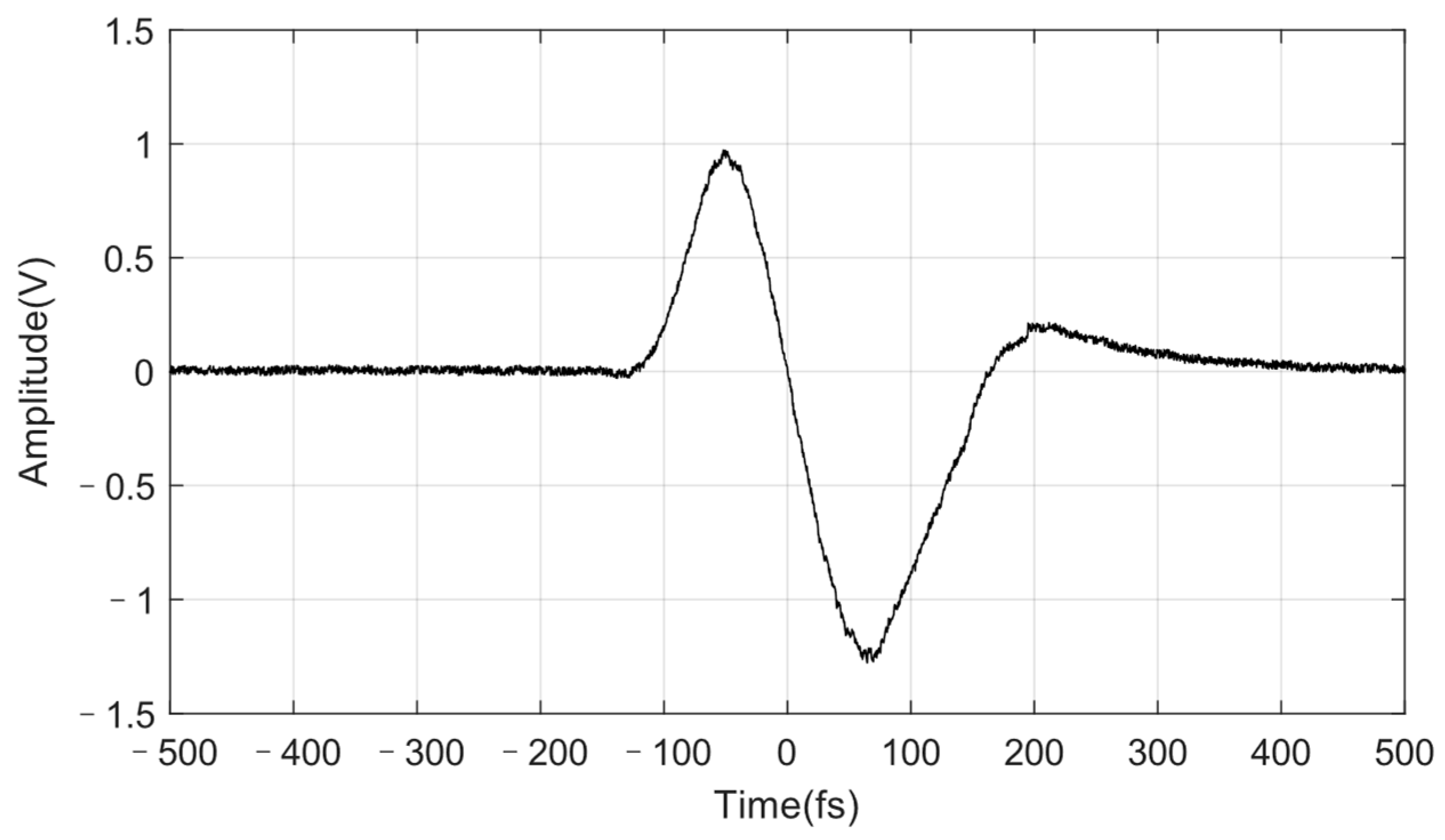
2.3. Timing Jitter Discrimination
2.4. Passive Methods of Noise Suppression
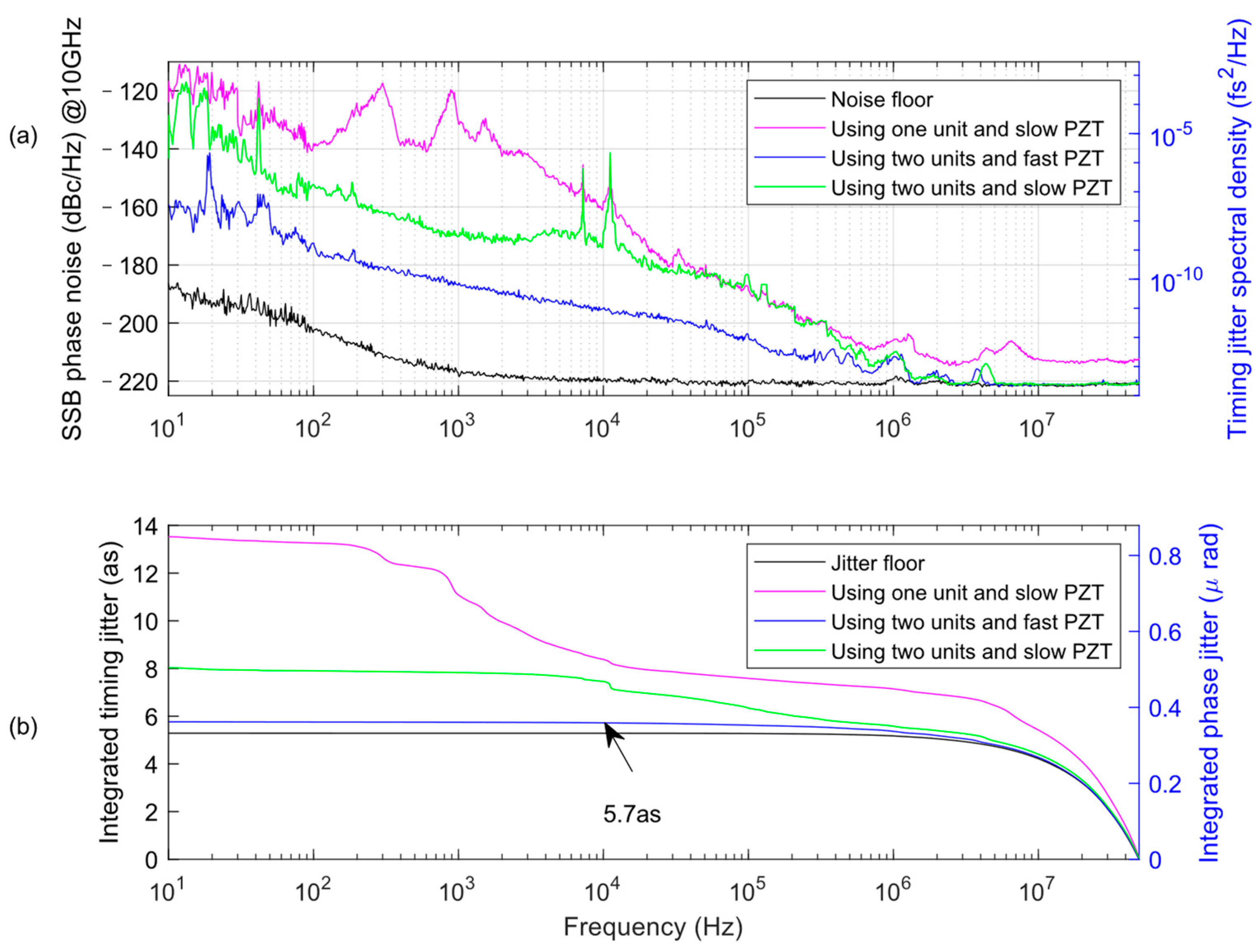
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Valley, G.C. Photonic analog-to-digital converters. Opt. Express 2007, 15, 1955–1982. [Google Scholar] [CrossRef] [PubMed]
- Udem, T.; Holzwarth, R.; Hänsch, T.W. Optical frequency metrology. Nature 2002, 416, 233–237. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Cox, J.A.; Chen, J.; Kärtner, F.X. Drift-free femtosecond timing synchronization of remote optical and microwave sources. Nat. Photonics 2008, 2, 733–736. [Google Scholar] [CrossRef]
- Coluccelli, N.; Cassinerio, M.; Gambetta, A.; Laporta, P.; Galzerano, G. Frequency-noise measurements of optical frequency combs by multiple fringe-side discriminator. Sci. Rep. 2015, 5, 16338. [Google Scholar] [CrossRef] [PubMed]
- Jung, K.; Kim, J. Characterization of timing jitter spectra in free-running mode-locked lasers with 340 dB dynamic range over 10 decades of Fourier frequency. Opt. Lett. 2015, 40, 316–319. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Song, Y. Ultralow-noise mode-locked fiber lasers and frequency combs: Principles, status, and applications. Adv. Opt. Photonics 2016, 8, 465–540. [Google Scholar] [CrossRef]
- Tian, H.; Song, Y.; Meng, F.; Fang, Z.; Hu, M.; Wang, C. Long-term stable coherent beam combination of independent femtosecond Yb-fiber lasers. Opt. Lett. 2016, 41, 5142–5145. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, H.; Hou, D.; Meng, F.; Ma, Y.; Xu, H.; Kärtner, F.X.; Song, Y.; Zhang, Z. Timing jitter reduction through relative intensity noise suppression in high-repetition-rate mode-locked fiber lasers. Opt. Express 2019, 27, 11273–11280. [Google Scholar] [CrossRef]
- Tian, H.; Song, Y.; Hu, M. Noise measurement and reduction in mode-locked lasers: Fundamentals for low-noise optical frequency combs. Appl. Sci. 2021, 11, 7650. [Google Scholar] [CrossRef]
- Hyun, M.; Ahn, C.; Na, Y.; Chung, H.; Kim, J. Attosecond electronic timing with rising edges of photocurrent pulses. Nat. Commun. 2020, 11, 3667. [Google Scholar] [CrossRef]
- Schibli, T.; Kim, J.; Kuzucu, O.; Gopinath, J.; Tandon, S.; Petrich, G.; Kolodziejski, L.; Fujimoto, J.; Ippen, E.; Kaertner, F. Attosecond active synchronization of passively mode-locked lasers by balanced cross correlation. Opt. Lett. 2003, 28, 947–949. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Chen, J.; Zhang, Z.; Wong, F.; Kärtner, F.; Loehl, F.; Schlarb, H. Long-term femtosecond timing link stabilization using a single-crystal balanced cross correlator. Opt. Lett. 2007, 32, 1044–1046. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Liu, L.; Tang, J. Timing jitter measurement of transmitted laser pulse relative to the reference using type II second harmonic generation in two nonlinear crystals. Opt. Express 2009, 17, 19102–19112. [Google Scholar] [CrossRef]
- Song, Y.; Zhou, F.; Tian, H.; Hu, M. Attosecond timing jitter within a temporal soliton molecule. Optica 2020, 7, 1531–1534. [Google Scholar] [CrossRef]
- Chen, Y.-F.; Jiang, J.; Jones, D.J. Remote distribution of a mode-locked pulse train with sub 40-as jitter. Opt. Express 2006, 14, 12134–12144. [Google Scholar] [CrossRef]
- Hou, D.; Lee, C.-C.; Yang, Z.; Schibli, T. Timing jitter characterization of mode-locked lasers with < 1 zs/√ Hz resolution using a simple optical heterodyne technique. Opt. Lett. 2015, 40, 2985–2988. [Google Scholar]
- Benedick, A.J.; Fujimoto, J.G.; Kärtner, F.X. Optical flywheels with attosecond jitter. Nat. Photonics 2012, 6, 97–100. [Google Scholar] [CrossRef]
- Kim, H.; Qin, P.; Song, Y.; Yang, H.; Shin, J.; Kim, C.; Jung, K.; Wang, C.; Kim, J. Sub-20-attosecond timing jitter mode-locked fiber lasers. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 260–267. [Google Scholar]
- Casanova, A.; Courjaud, A.; Trophème, B.; Santarelli, G. Measurement of absolute timing jitter of SESAM mode-locked lasers with yoctosecond sensitivity. Opt. Lett. 2020, 45, 6098–6101. [Google Scholar] [CrossRef]
- Briles, T.C.; Yost, D.C.; Cingöz, A.; Ye, J.; Schibli, T.R. Simple piezoelectric-actuated mirror with 180 kHz servo bandwidth. Opt. Express 2010, 18, 9739–9746. [Google Scholar] [CrossRef]
- Goldovsky, D.; Jouravsky, V.; Pe’er, A. Simple and robust phase-locking of optical cavities with> 200 KHz servo-bandwidth using a piezo-actuated mirror mounted in soft materials. Opt. Express 2016, 24, 28239–28246. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, T.; Tani, S.; Ito, I.; Endo, M.; Kobayashi, Y. Piezo-electric transducer actuated mirror with a servo bandwidth beyond 500 kHz. Opt. Express 2020, 28, 16118–16125. [Google Scholar] [CrossRef] [PubMed]
- Bartels, A.; Diddams, S.A.; Ramond, T.; Hollberg, L. Mode-locked laser pulse trains with subfemtosecond timing jitter synchronized to an optical reference oscillator. Opt. Lett. 2003, 28, 663–665. [Google Scholar] [CrossRef] [PubMed]
- Tian, H. Precise Control of Optical Phase and Coherent Synthesis in Femtosecond Laser Based Optical Frequency Combs. Ph.D. Thesis, Tianjin University, Tianjin, China, 2020. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Wu, H.; Hou, D.; Lu, H.; Li, Z.; Zhao, J. Yoctosecond Timing Jitter Sensitivity in Tightly Synchronized Mode-Locked Ti:Sapphire Lasers. Photonics 2022, 9, 569. https://doi.org/10.3390/photonics9080569
Xu H, Wu H, Hou D, Lu H, Li Z, Zhao J. Yoctosecond Timing Jitter Sensitivity in Tightly Synchronized Mode-Locked Ti:Sapphire Lasers. Photonics. 2022; 9(8):569. https://doi.org/10.3390/photonics9080569
Chicago/Turabian StyleXu, Hao, Haitao Wu, Dong Hou, Haoyuan Lu, Zhaolong Li, and Jianye Zhao. 2022. "Yoctosecond Timing Jitter Sensitivity in Tightly Synchronized Mode-Locked Ti:Sapphire Lasers" Photonics 9, no. 8: 569. https://doi.org/10.3390/photonics9080569
APA StyleXu, H., Wu, H., Hou, D., Lu, H., Li, Z., & Zhao, J. (2022). Yoctosecond Timing Jitter Sensitivity in Tightly Synchronized Mode-Locked Ti:Sapphire Lasers. Photonics, 9(8), 569. https://doi.org/10.3390/photonics9080569





