Implementation of Photonic Phase Gate and Squeezed States via a Two-Level Atom and Bimodal Cavity
Abstract
:1. Introduction
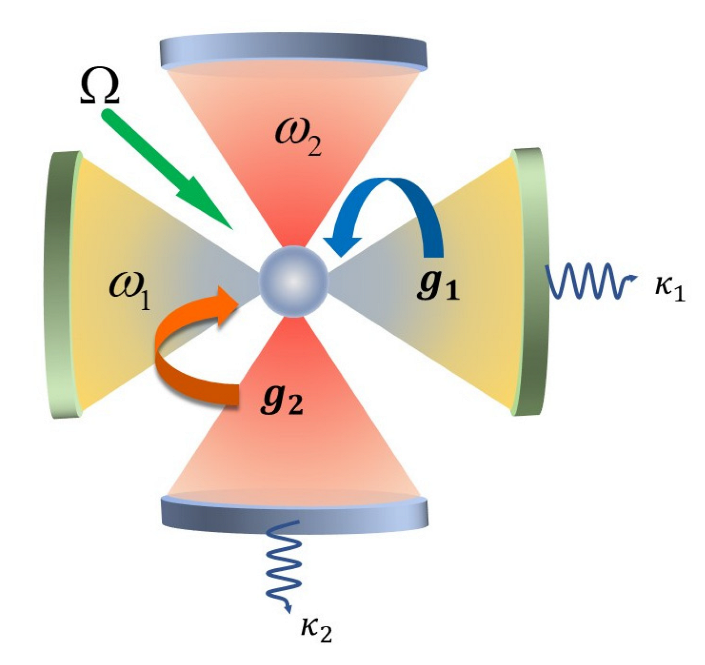
2. The Model and Effective Hamiltonian
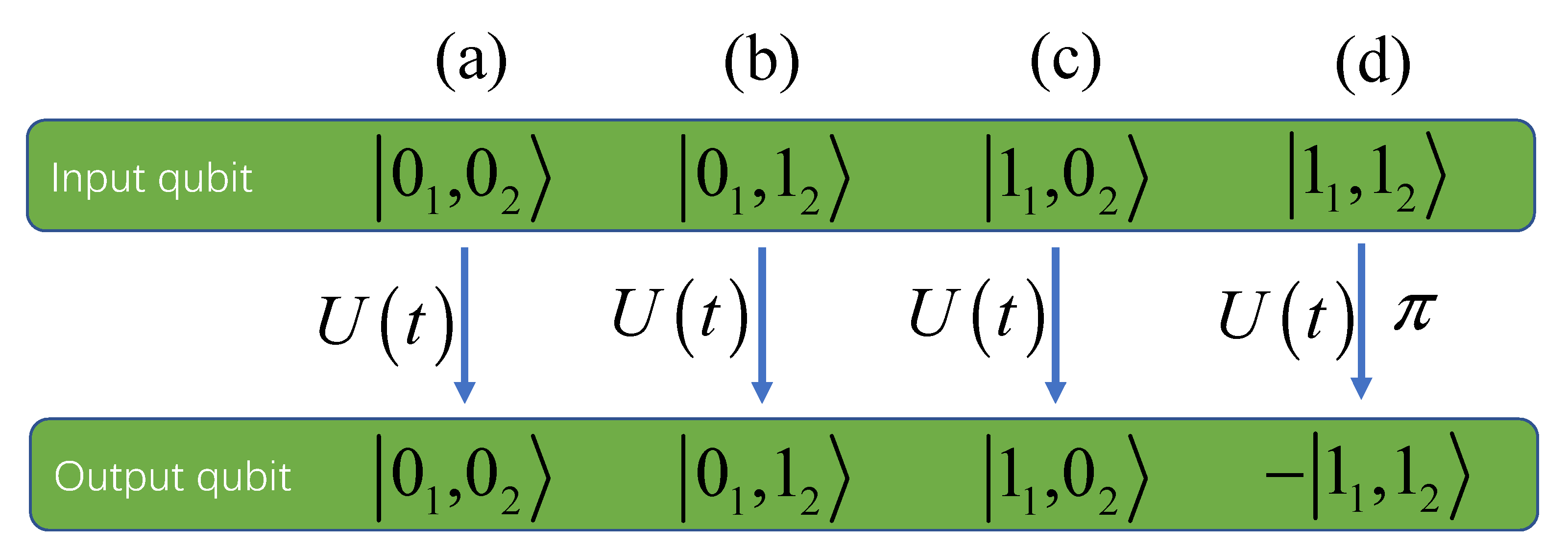
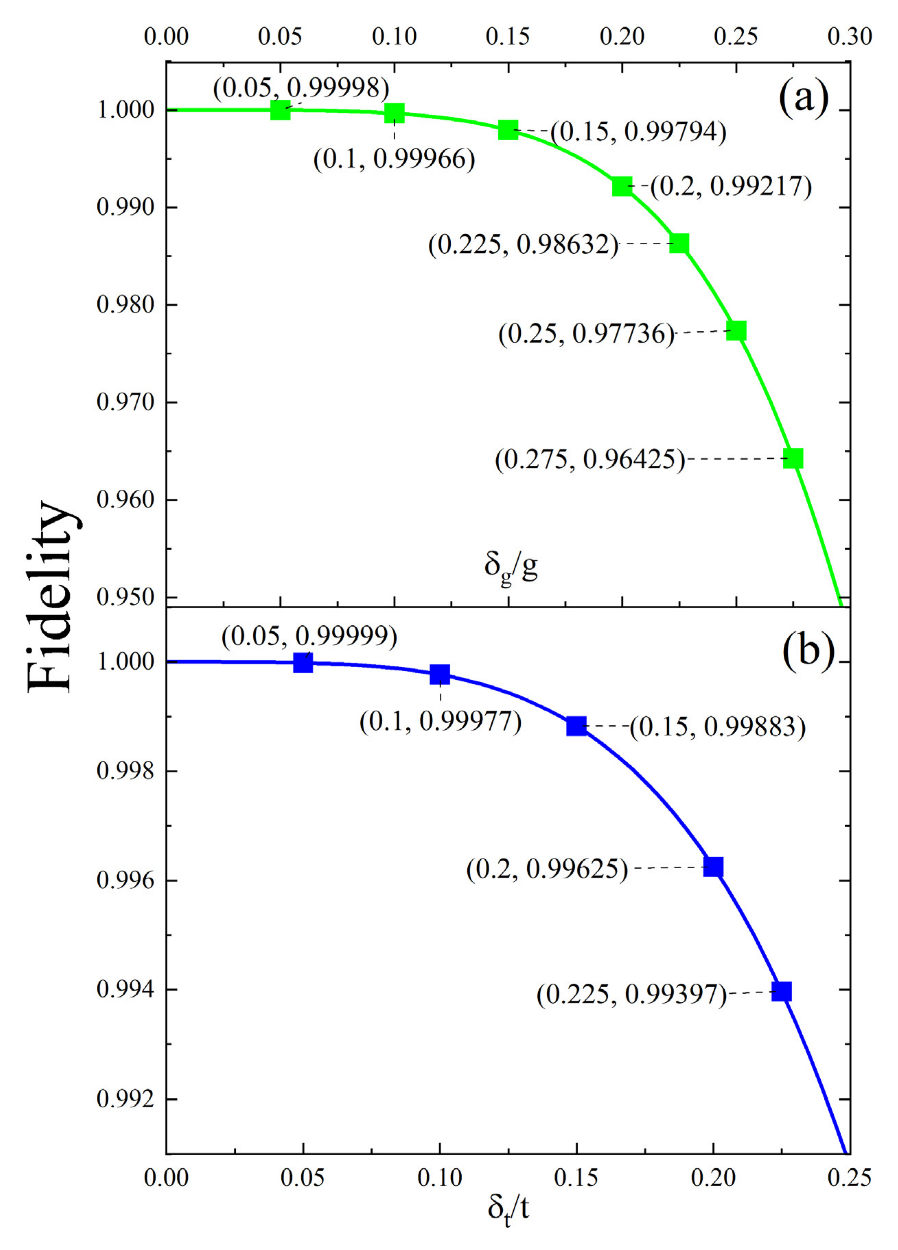
3. Two-Qubit Phase Gate and Fidelity Analysis
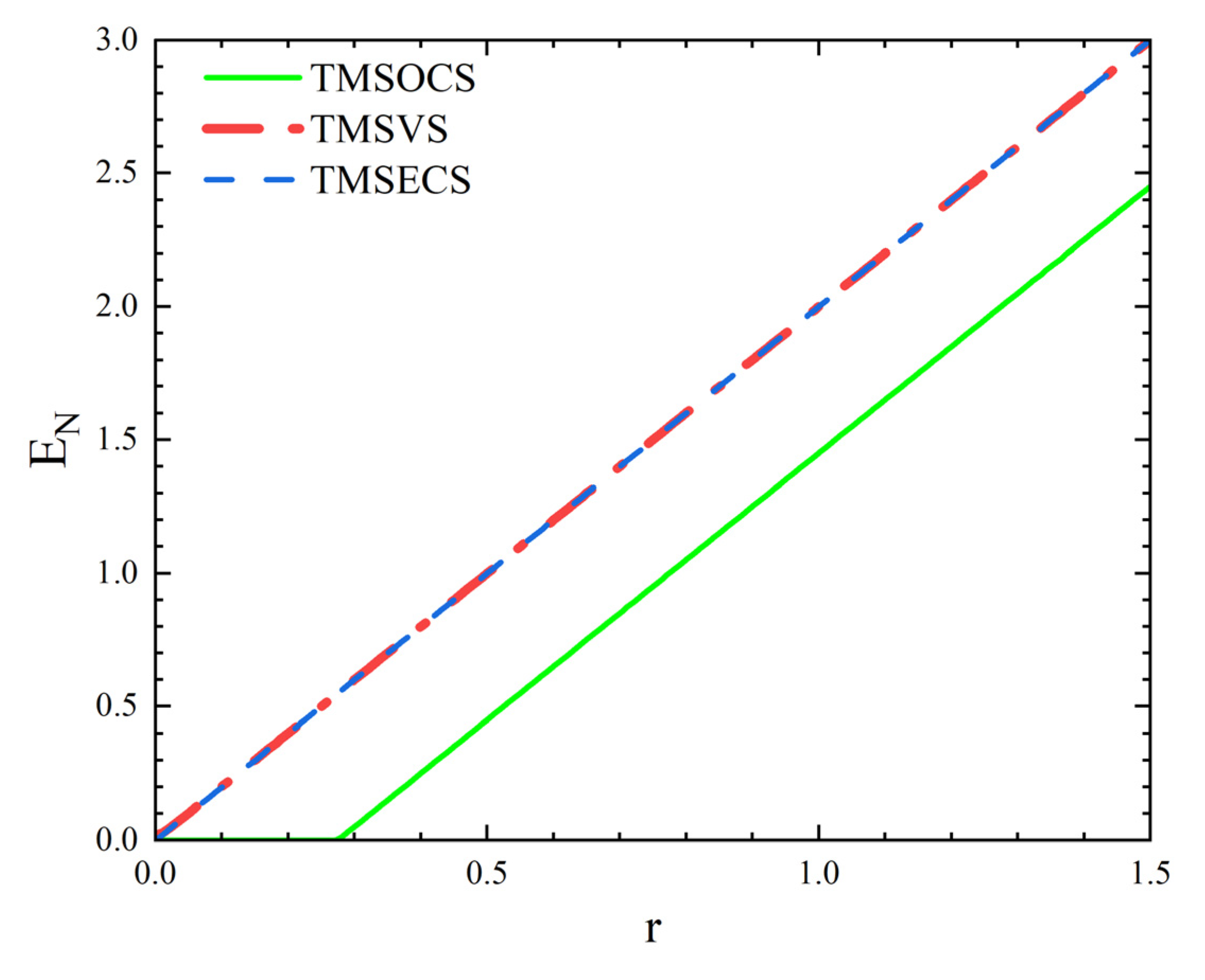
4. Generation of Two-Mode Squeezed States and Entanglement Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiao, Y.F.; Zou, X.B.; Guo, G.C. One-step implementation of an N-qubit controlled-phase gate with neutral atoms trapped in an optical cavity. Phys. Rev. A 2007, 75, 054303. [Google Scholar] [CrossRef]
- Zheng, S.-B. Quantum logic gates for two atoms with a single resonant interaction. Phys. Rev. A 2005, 71, 062335. [Google Scholar] [CrossRef]
- Zheng, S.-B. Virtual-photon-induced quantum phase gates for two distant atoms trapped in separate cavities. Appl. Phys. Lett. 2009, 94, 154101. [Google Scholar] [CrossRef]
- Tang, S.-Q.; Zhang, D.-Y.; Xie, L.J.; Zhan, X.-G.; Gao, F. Realization of three-qubit controlled-phase gate operation with atoms in cavity QED system. Chin. Phys. Lett. 2009, 26, 020310. [Google Scholar]
- Zou, X.-B.; Xiao, Y.-F.; Li, S.-B.; Yang, Y.; Guo, G.-C. Quantum phase gate through a dispersive atom-field interaction. Phys. Rev. A 2007, 75, 064301. [Google Scholar] [CrossRef]
- Xiao, Y.-F.; Zou, X.-B.; Han, Z.-F.; Guo, G.-C. Quantum phase gate in an optical cavity with atomic cloud. Phys. Rev. A 2006, 74, 044303. [Google Scholar] [CrossRef]
- Asaoka, R.; Tokunaga, Y.; Kanamoto, R.; Goto, H.; Aoki, T. Requirements for fault-tolerant quantum computation with cavi-ty-QED-based atom-atom gates mediated by a photon with a finite pulse length. Phys. Rev. A 2021, 104, 043702. [Google Scholar] [CrossRef]
- Hammani, M.; Chouikh, A.; Said, T.; Bennai, M. Realization of the quantum CNOT gate based on multiphoton process in multimode Cavity QED. Opt. Quantum Electron. 2021, 53, 89. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, J.-L.; Han, J.-X.; Jiang, Y.Y.; Xia, Y.; Song, J. Resilient Mølmer-Sørensen gate with cavity QED. Phys. Lett. A 2021, 388, 127033. [Google Scholar] [CrossRef]
- Xu, Y.; Ma, Y.; Cai, W.; Mu, X.; Dai, W.; Wang, W.; Hu, L.; Li, X.; Han, J.; Wang, H.; et al. Demonstration of Controlled-Phase Gates between Two Error-Correctable Photonic Qubits. Phys. Rev. Lett. 2020, 124, 120501. [Google Scholar] [CrossRef]
- Shi, Z.-C.; Zhang, C.; Shen, L.-T.; Xia, Y.; Yi, X.X.; Zheng, S.-B. Implementation of universal quantum gates by periodic two-step modulation in a weakly nonlinear qubit. Phys. Rev. A 2020, 101, 042314. [Google Scholar] [CrossRef]
- Borne, A.; Northup, T.E.; Blatt, R.; Dayan, B. Efficient ion-photon qubit SWAP gate in realistic ion cavity-QED systems without strong coupling. Opt. Express 2020, 28, 11822–11839. [Google Scholar] [CrossRef] [PubMed]
- Alqahtani, M.M. Multiphoton process in cavity QED photons for implementing a three-qubit quantum gate operation. Quantum Inf. Process. 2019, 19, 12. [Google Scholar] [CrossRef]
- Devi, A.; Gunapala, S.D.; Premaratne, M. Coherent and incoherent laser pump on a five-level atom in a strongly coupled cavity-QED system. Phys. Rev. A 2022, 105, 013701. [Google Scholar] [CrossRef]
- Alqahtani, M.M. Quantum phase gate based on multiphoton process in multimode cavity QED. Quantum Inf. Process. 2018, 17, 211. [Google Scholar] [CrossRef]
- Chouikh, A.; Said, T.; Essammouni, K.; Bennai, M. Implementation of universal two- and three-qubit quantum gates in a cavity QED. Opt. Quantum Electron. 2016, 48, 463. [Google Scholar] [CrossRef]
- Chang, J.-T.; Zubairy, M.S. Three-qubit phase gate based on cavity quantum electrodynamics. Phys. Rev. A 2008, 77, 012329. [Google Scholar] [CrossRef]
- Solano, E.; Santos, M.F.; Milman, P. Quantum phase gate with a selective interaction. Phys. Rev. A 2001, 64, 024304. [Google Scholar] [CrossRef]
- Zubairy, M.S.; Kim, M.; Scully, M.O. Cavity-QED-based quantum phase gate. Phys. Rev. A 2003, 68, 033820. [Google Scholar] [CrossRef]
- García-Maraver, R.; Corbalán, R.; Eckert, K.; Rebić, S.; Artoni, M.; Mompart, J. Cavity QED quantum phase gates for a single longitudinal mode of the intracavity field. Phys. Rev. A 2004, 70, 062324. [Google Scholar] [CrossRef]
- Shu, J.; Zou, X.-B.; Xiao, Y.-F.; Guo, G.-C. Quantum phase gate of photonic qubits in a cavity QED system. Phys. Rev. A 2007, 75, 044302. [Google Scholar] [CrossRef]
- Cai, J.-W.; Fang, M.-F.; Zheng, X.-J.; Liao, X.-P. A scheme for a conditional quantum phase gate using a bimodal cavity and a ladder-type three-level atom. J. Mod. Opt. 2006, 53, 2803–2810. [Google Scholar] [CrossRef]
- Li, P.; Gu, Y.; Gong, Q.; Guo, G. Generation of two-mode entanglement between separated cavities. J. Opt. Soc. Am. B 2008, 26, 189–193. [Google Scholar] [CrossRef]
- Shao, X.-Q.; Chen, L.; Zhang, S. One-step implementation of a swap gate with coherent-state qubits via atomic ensemble large detuning interaction with two-mode cavity quantum electrodynamics. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 245502. [Google Scholar] [CrossRef]
- Shao, X.-Q.; Zhu, A.-D.; Zhang, S.; Chung, J.-S.; Yeon, K.-H. Efficient scheme for implementing anN-qubit Toffoli gate by a single resonant interaction with cavity quantum electrodynamics. Phys. Rev. A 2007, 75, 034307. [Google Scholar] [CrossRef]
- Su, S.L.; Shen, H.Z.; Liang, E.; Zhang, S. One-step construction of the multiple-qubit Rydberg controlled-phase gate. Phys. Rev. A 2018, 98, 032306. [Google Scholar] [CrossRef]
- Su, S.-L.; Gao, Y.; Liang, E.; Zhang, S. Fast Rydberg antiblockade regime and its applications in quantum logic gates. Phys. Rev. A 2017, 95, 022319. [Google Scholar] [CrossRef]
- Su, S.L.; Liang, E.; Zhang, S.; Wen, J.J.; Sun, L.L.; Jin, Z.; Zhu, A.D. One-step implementation of the Ry-dberg-Rydberg-interaction gate. Phys. Rev. A 2016, 93, 012306. [Google Scholar] [CrossRef]
- Kang, Y.-H.; Shi, Z.-C.; Song, J.; Xia, Y. Heralded atomic nonadiabatic holonomic quantum computation with Rydberg blockade. Phys. Rev. A 2020, 102, 022617. [Google Scholar] [CrossRef]
- Kang, Y.-H.; Shi, Z.-C.; Huang, B.-H.; Song, J.; Xia, Y. Flexible scheme for the implementation of nonadiabatic geometric quantum computation. Phys. Rev. A 2020, 101, 032322. [Google Scholar] [CrossRef]
- Su, S.-L.; Guo, F.-Q.; Tian, L.; Zhu, X.-Y.; Yan, L.-L.; Liang, E.-J.; Feng, M. Nondestructive Rydberg parity meter and its applications. Phys. Rev. A 2020, 101, 012347. [Google Scholar] [CrossRef]
- Zheng, R.-H.; Kang, Y.-H.; Su, S.-L.; Song, J.; Xia, Y. Robust and high-fidelity nondestructive Rydberg parity meter. Phys. Rev. A 2020, 102, 012609. [Google Scholar] [CrossRef]
- Zheng, R.-H.; Xiao, Y.; Su, S.-L.; Chen, Y.-H.; Shi, Z.-C.; Song, J.; Xia, Y.; Zheng, S.-B. Fast and dephasing-tolerant preparation of steady Knill-Laflamme-Milburn states via dissipative Rydberg pumping. Phys. Rev. A 2021, 103, 052402. [Google Scholar] [CrossRef]
- Li, D.X.; Shao, X.Q. Directional quantum state transfer in a dissipative Rydberg-atom-cavity system. Phys. Rev. A 2019, 99, 032348. [Google Scholar] [CrossRef]
- Li, D.-X.; Shao, X.; Wu, J.-H.; Yi, X.X. Dissipation-induced W state in a Rydberg-atom-cavity system. Opt. Lett. 2018, 43, 1639–1642. [Google Scholar] [CrossRef]
- Li, D.-X.; Shao, X.; Wu, J.-H.; Yi, X.X. Engineering steady-state entanglement via dissipation and quantum Zeno dynamics in an optical cavity. Opt. Lett. 2017, 42, 3904–3907. [Google Scholar] [CrossRef]
- Kang, Y.H.; Shi, Z.-C.; Song, J.; Xia, Y. Effective discrimination of chiral molecules in optical cavity. Opt. Lett. 2020, 45, 4952–4955. [Google Scholar] [CrossRef]
- Guo, Y.; Shu, C.-C.; Dong, D.; Nori, F. Vanishing and Revival of Resonance Raman Scattering. Phys. Rev. Lett. 2019, 123, 223202. [Google Scholar] [CrossRef]
- Guo, Y.; Luo, X.; Ma, S.; Shu, C.-C. All-optical generation of quantum entangled states with strictly constrained ultrafast laser pulses. Phys. Rev. A 2019, 100, 023409. [Google Scholar] [CrossRef]
- Ma, S.; Xue, S.; Guo, Y.; Shu, C.-C. Numerical detection of Gaussian entanglement and its application to the identification of bound entangled Gaussian states. Quantum Inf. Process. 2020, 19, 225. [Google Scholar] [CrossRef]
- Braunstein, S.L.; van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513–577. [Google Scholar] [CrossRef]
- Jeong, H.; Son, W.; Kim, M.S.; Ahn, D. Quantum nonlocality test for continuous-variable states with dichotomic observables. Phys. Rev. A 2003, 67, 012106. [Google Scholar] [CrossRef]
- Furusawa, A.; Sørensen, J.L.; Braunstein, S.L.; Fuchs, C.A.; Kimble, H.J.; Polzik, E.S. Unconditional Quantum Teleportation. Science 1998, 282, 706–709. [Google Scholar] [CrossRef]
- Li, B.; Feng, X.L.; Zhang, Z.M. Frequency Up-and Down-conversions in Two-mode Cavity. Acta Photon. Sin. 2011, 40, 1161–1165. [Google Scholar]
- Prado, F.O.; Luiz, F.S.; Villas-Bôas, J.M.; Alcalde, A.; Duzzioni, E.I.; Sanz, L. Atom-mediated effective interactions between modes of a bimodal cavity. Phys. Rev. A 2011, 84, 053839. [Google Scholar] [CrossRef]
- Werlang, T.; Guzmán, R.; Prado, F.O.; Villas-Bôas, C.J. Generation of decoherence-free displaced squeezed states of radiation fields and a squeezed reservoir for atoms in cavity QED. Phys. Rev. A 2008, 78, 033820. [Google Scholar] [CrossRef]
- Zou, X.; Dong, Y.; Guo, G. Schemes for realizing frequency up- and down-conversions in two-mode cavity QED. Phys. Rev. A 2006, 73, 025802. [Google Scholar] [CrossRef]
- Gong, W.L.; Xu, B.Z.; Ye, M.Y. Quantum SWAP gate in an optical cavity with an atomic cloud. Phys. Rev. A 2008, 77, 064301. [Google Scholar]
- Mu, Q.-X.; Ma, Y.-H.; Zhou, L. Generation of two-mode entangled coherent states via a cavity QED system. J. Phys. A Math. Theor. 2009, 42, 225304. [Google Scholar] [CrossRef]
- Prado, F.O.; de Almeida, N.G.; Moussa, M.H.Y.; Villas-Bôas, C.J. Bilinear and quadratic Hamiltonians in two-mode cavity quantum electrodynamics. Phys. Rev. A 2006, 73, 043803. [Google Scholar] [CrossRef]
- Diniz, E.C.; Rossatto, D.Z.; Villas-Boas, C.J. Two-mode squeezing operator in circuit QED. Quantum Inf. Process. 2018, 17, 202. [Google Scholar] [CrossRef]
- James, D.F.; Jerke, J. Effective Hamiltonian theory and its applications in quantum information. Can. J. Phys. 2007, 85, 625–632. [Google Scholar] [CrossRef]
- Duan, L.-M.; Giedke, G.; Cirac, J.I.; Zoller, P. Inseparability Criterion for Continuous Variable Systems. Phys. Rev. Lett. 2000, 84, 2722–2725. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.-L.; Li, Z.; Fang, A.-P.; Li, P.; Gao, S.-Y.; Li, F.-L. Controllable generation of two-mode-entangled states in two-resonator circuit QED with a single gap-tunable superconducting qubit. Phys. Rev. A 2014, 90, 062342. [Google Scholar] [CrossRef]
- Ma, S.-L.; Li, X.-K.; Xie, J.-K.; Li, F.-L. Two-mode squeezed states of two separated nitrogen-vacancy-center ensembles coupled via dissipative photons of superconducting resonators. Phys. Rev. A 2019, 99, 012325. [Google Scholar] [CrossRef]
- Yang, Z.-B.; Liu, X.-D.; Yin, X.-Y.; Ming, Y.; Liu, H.-Y.; Yang, R.-C. Controlling Stationary One-Way Quantum Steering in Cavity Magnonics. Phys. Rev. Appl. 2021, 15, 024042. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, S.; Jiang, X.; Wang, X.; Zhao, X. Implementation of Photonic Phase Gate and Squeezed States via a Two-Level Atom and Bimodal Cavity. Photonics 2022, 9, 583. https://doi.org/10.3390/photonics9080583
Tang S, Jiang X, Wang X, Zhao X. Implementation of Photonic Phase Gate and Squeezed States via a Two-Level Atom and Bimodal Cavity. Photonics. 2022; 9(8):583. https://doi.org/10.3390/photonics9080583
Chicago/Turabian StyleTang, Shiqing, Xi Jiang, Xinwen Wang, and Xingdong Zhao. 2022. "Implementation of Photonic Phase Gate and Squeezed States via a Two-Level Atom and Bimodal Cavity" Photonics 9, no. 8: 583. https://doi.org/10.3390/photonics9080583
APA StyleTang, S., Jiang, X., Wang, X., & Zhao, X. (2022). Implementation of Photonic Phase Gate and Squeezed States via a Two-Level Atom and Bimodal Cavity. Photonics, 9(8), 583. https://doi.org/10.3390/photonics9080583



