Extreme Narrowing of the Distributed Feedback Fiber Laser Linewidth Due to the Rayleigh Backscattering in a Single-Mode Fiber: Model and Experimental Test
Abstract
:1. Introduction
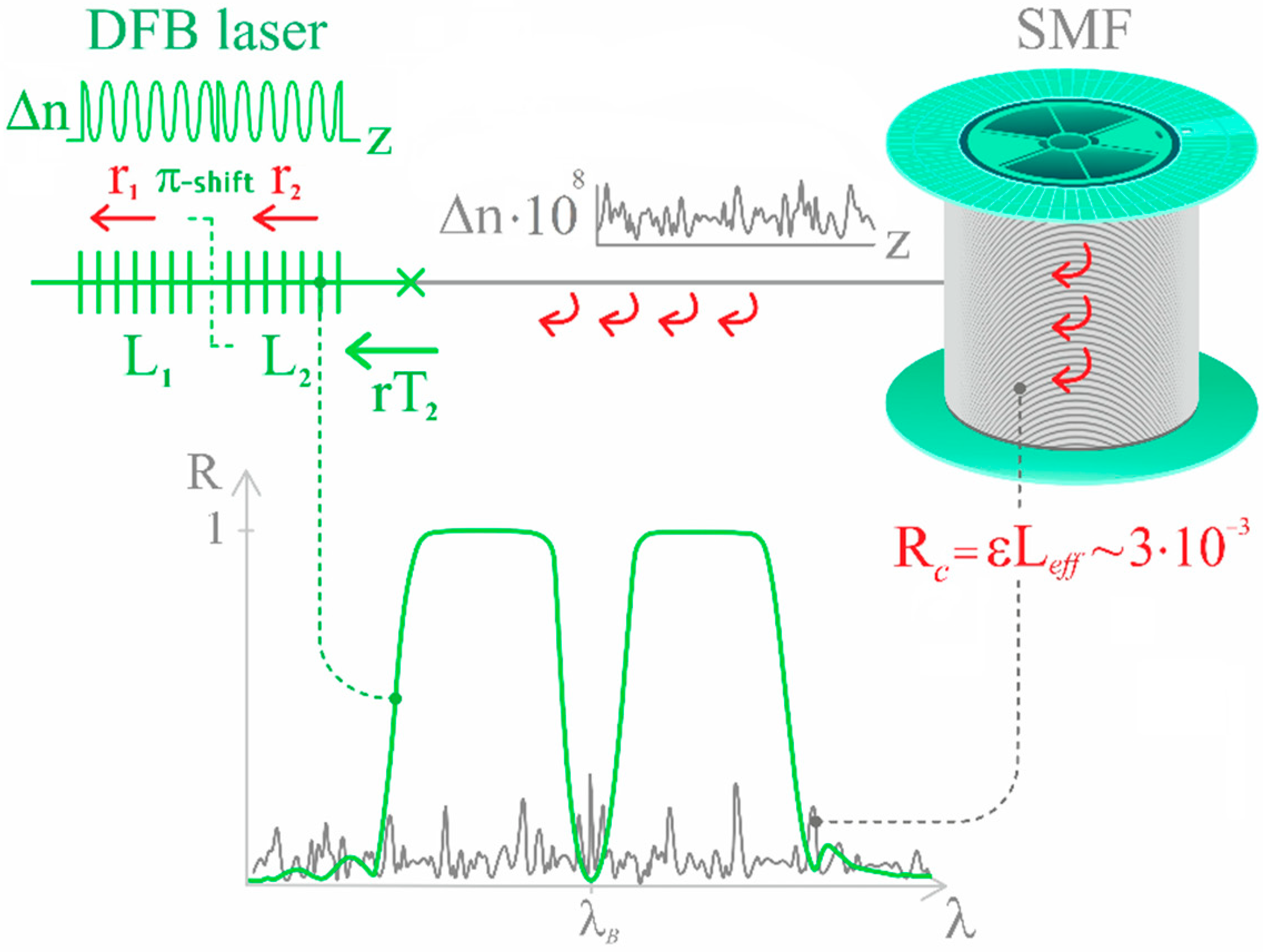
2. Model of the Linewidth Narrowing in the Hybrid Laser Configuration
3. Experiment
3.1. Experimental Scheme
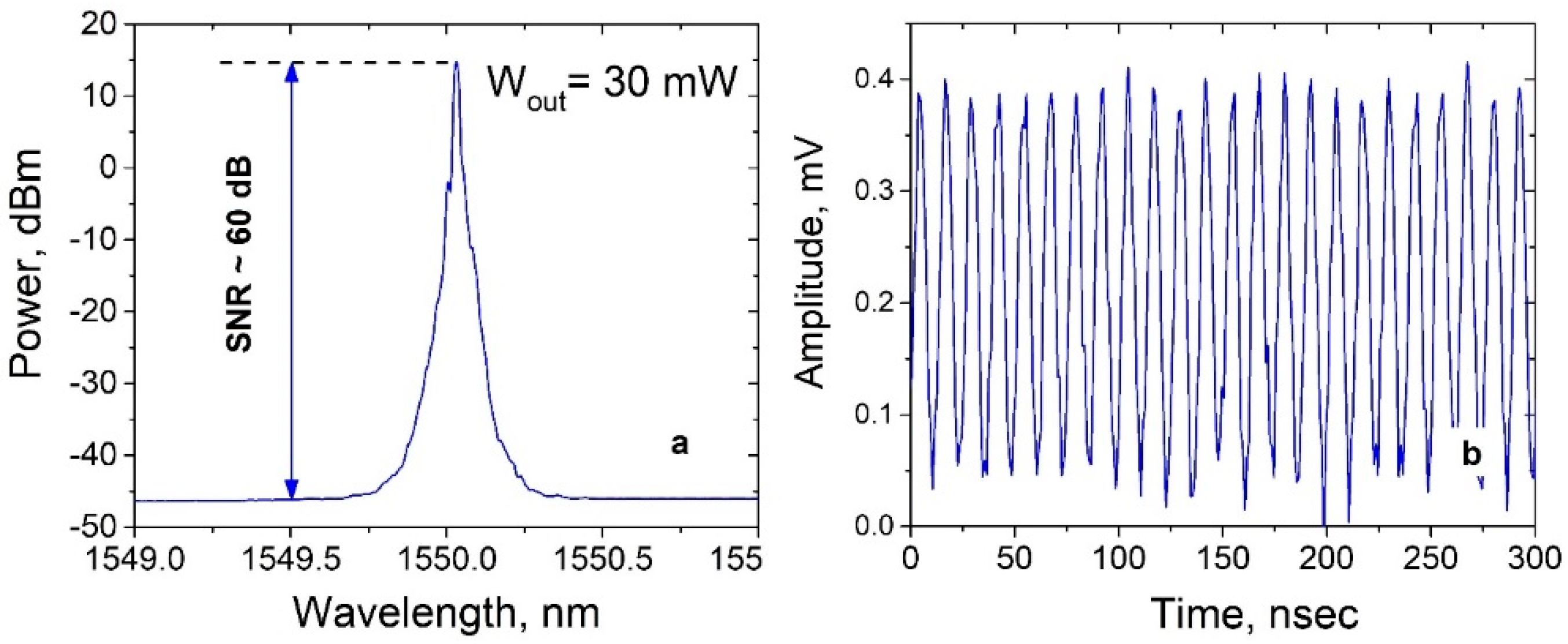
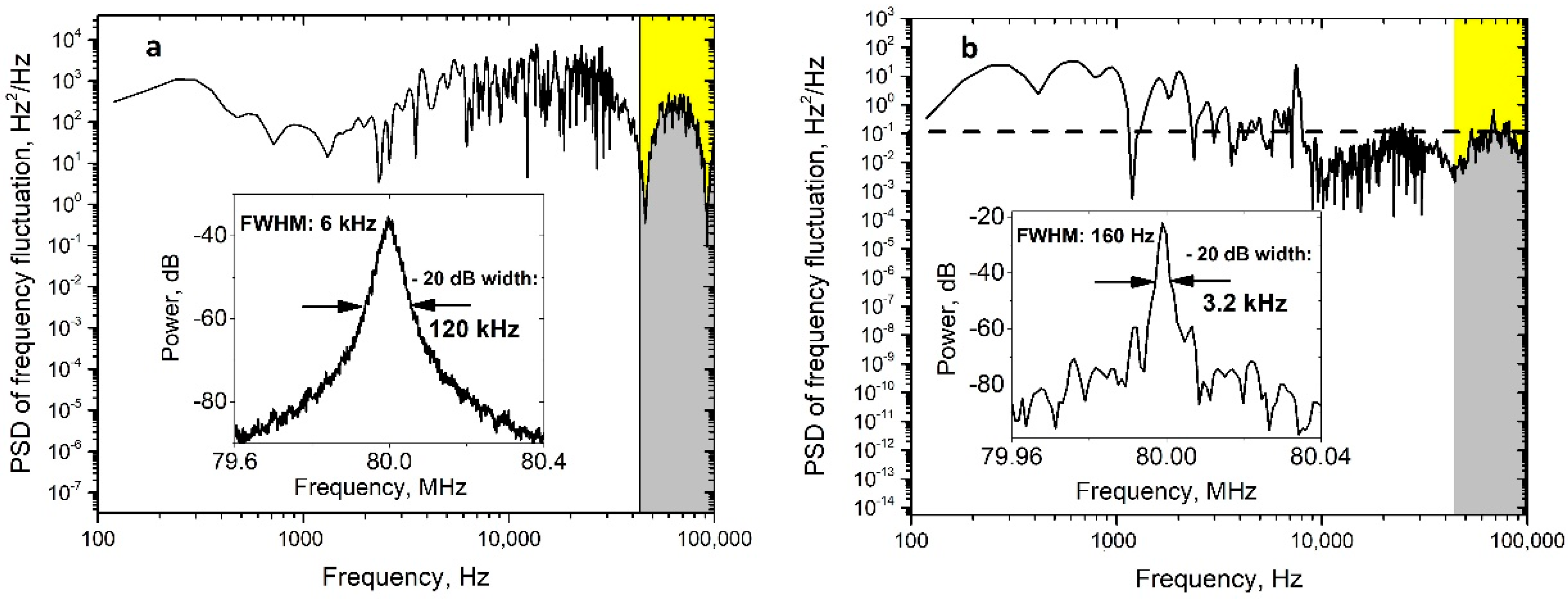
3.2. The Results
4. Discussion and Conclusions
Funding
Conflicts of Interest
References
- Cranch, G.A.; Flockhart, G.M.H.; Kirkendall, C.K. Distributed Feedback Fiber Laser Strain Sensors. IEEE Sens. J. 2008, 8, 1161–1172. [Google Scholar] [CrossRef]
- Kaminow, I.P.; Li, T.; Willner, A.E. Optical Fiber Telecommunications Volume VIA: Components and Subsystems; Optics and Photonics; Elsevier Science: Amsterdam, The Netherlands, 2013; ISBN 9780123972354. [Google Scholar]
- Fu, S.; Shi, W.; Feng, Y.; Zhang, L.; Yang, Z.; Xu, S.; Zhu, X.; Norwood, R.A.; Peyghambarian, N. Review of Recent Progress on Single-Frequency Fiber Lasers [Invited]. J. Opt. Soc. Am. B 2017, 34, A49–A62. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Babin, S.A.; El-Taher, A.E.; Harper, P.; Churkin, D.V.; Kablukov, S.I.; Ania-Castañón, J.D.; Karalekas, V.; Podivilov, E.V. Random Distributed Feedback Fibre Laser. Nat. Photonics 2010, 4, 231–235. [Google Scholar] [CrossRef]
- Wang, L.; Dong, X.; Shum, P.P.; Su, H. Tunable Erbium-Doped Fiber Laser Based on Random Distributed Feedback. IEEE Photonics J. 2014, 6. [Google Scholar] [CrossRef]
- Bulushev, A.G.; Dianov, E.M.; Kuznetsov, A.V.; Okhotnikov, O.G. Reduction in the Line Width of an Injection Laser by Resonant Rayleigh Scattering in a Fiber Ring Interferometer. Sov. J. Quantum Electron. 1989, 19, 479–481. [Google Scholar] [CrossRef]
- Yin, G.; Saxena, B.; Bao, X. Tunable Er-Doped Fiber Ring Laser with Single Longitudinal Mode Operation Based on Rayleigh Backscattering in Single Mode Fiber. Opt. Express 2011, 19, 25981–25989. [Google Scholar] [CrossRef] [PubMed]
- López-Mercado, C.A.; Spirin, V.V.; Bueno Escobedo, J.L.; Márquez Lucero, A.; Mégret, P.; Zolotovskii, I.O.; Fotiadi, A.A. Locking of the DFB Laser through Fiber Optic Resonator on Different Coupling Regimes. Opt. Commun. 2016, 359, 195–199. [Google Scholar] [CrossRef]
- Spirin, V.V.; Bueno Escobedo, J.L.; Korobko, D.A.; Mégret, P.; Fotiadi, A.A. Stabilizing DFB Laser Injection-Locked to an External Fiber-Optic Ring Resonator. Opt. Express 2020, 28, 478–484. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.; Chen, L.; Bao, X. Single-Mode SOA-Based 1kHz-Linewidth Dual-Wavelength Random Fiber Laser. Opt. Express 2017, 25, 15828–15837. [Google Scholar] [CrossRef]
- Dang, L.; Huang, L.; Li, Y.; Cao, Y.; Lan, T.; Iroegbu, P.I.; Cao, Z.; Mei, K.; Liang, L.; Fu, S.; et al. A Longitude-Purification Mechanism for Tunable Fiber Laser Based on Distributed Feedback. J. Light. Technol. 2022, 40, 206–214. [Google Scholar] [CrossRef]
- Popov, S.M.; Butov, O.V.; Bazakutsa, A.P.; Vyatkin, M.Y.; Chamorovskii, Y.K.; Fotiadi, A.A. Random lasing in a short Er-doped artificial Rayleigh fiber. Results Phys. 2020, 16, 102868. [Google Scholar] [CrossRef]
- Skvortsov, M.I.; Wolf, A.A.; Dostovalov, A.V.; Egorova, O.N.; Semjonov, S.L.; Babin, S.A. Narrow-Linewidth Er-Doped Fiber Lasers with Random Distributed Feedback Provided By Artificial Rayleigh Scattering. J. Light. Technol. 2022, 40, 1829–1835. [Google Scholar] [CrossRef]
- Schawlow, A.L.; Townes, C.H. Infrared and Optical Masers. Phys. Rev. 1958, 112, 1940–1949. [Google Scholar] [CrossRef]
- Henry, C. Theory of the Linewidth of Semiconductor Lasers. IEEE J. Quantum Electron. 1982, 18, 259–264. [Google Scholar] [CrossRef]
- Riehle, F. Frequency Standards: Basics and Applications; Wiley: Hoboken, NJ, USA, 2006; ISBN 9783527605958. [Google Scholar]
- Babin, S.A.; Churkin, D.V.; Ismagulov, A.E.; Kablukov, S.I.; Nikulin, M.A. Single Frequency Single Polarization DFB Fiber Laser. Laser Phys. Lett. 2007, 4, 428–432. [Google Scholar] [CrossRef]
- Fomiryakov, E.; Kharasov, D.; Nikitin, S.; Nanii, O.; Treshchikov, V. New Approach to Laser Characterization Using Delayed Self-Heterodyne Interferometry. J. Light. Technol. 2021, 39, 5191–5196. [Google Scholar] [CrossRef]
- Andel, N.; Yara, M.I.; Ohamed, M.; Ellahi, S.; Ouici, T.A.S.; Ardaillon, R.; Hilippe, P.; Ignoret, S. Time-Dependent Laser Linewidth: Beat-Note Digital Acquisition and Numerical Analysis. Opt. Exp. 2016, 24, 401–407. [Google Scholar] [CrossRef]
- Owens, D.K.; Weiss, R. Measurement of the Phase Fluctuations in a He–Ne Zeeman Laser. Rev. Sci. Instrum. 1974, 45, 1060–1062. [Google Scholar] [CrossRef]
- Di Domenico, G.; Schilt, S.; Thomann, P. Simple Approach to the Relation between Laser Frequency Noise and Laser Line Shape. Appl. Opt. 2010, 49, 4801–4807. [Google Scholar] [CrossRef]
- Xu, D.; Yang, F.; Chen, D.; Wei, F.; Cai, H.; Fang, Z.; Qu, R. Laser Phase and Frequency Noise Measurement by Michelson Interferometer Composed of a 3 x 3 Optical Fiber Coupler. Opt. Express 2015, 23, 22386–22393. [Google Scholar] [CrossRef]
- Okoshi, T.; Kikuchi, K.; Nakayama, A. Novel Method for High Resolution Measurement of Laser Output Spectrum. Electron. Lett. 1980, 16, 630–631. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skvortsov, M.I.; Abdullina, S.R.; Podivilov, E.V.; Vlasov, A.A.; Kharasov, D.R.; Fomiryakov, E.A.; Nikitin, S.P.; Treshchikov, V.N.; Babin, S.A. Extreme Narrowing of the Distributed Feedback Fiber Laser Linewidth Due to the Rayleigh Backscattering in a Single-Mode Fiber: Model and Experimental Test. Photonics 2022, 9, 590. https://doi.org/10.3390/photonics9080590
Skvortsov MI, Abdullina SR, Podivilov EV, Vlasov AA, Kharasov DR, Fomiryakov EA, Nikitin SP, Treshchikov VN, Babin SA. Extreme Narrowing of the Distributed Feedback Fiber Laser Linewidth Due to the Rayleigh Backscattering in a Single-Mode Fiber: Model and Experimental Test. Photonics. 2022; 9(8):590. https://doi.org/10.3390/photonics9080590
Chicago/Turabian StyleSkvortsov, Mikhail I., Sofia R. Abdullina, Evgeny V. Podivilov, Alexander A. Vlasov, Danil R. Kharasov, Edgard A. Fomiryakov, Sergey P. Nikitin, Vladimir N. Treshchikov, and Sergey A. Babin. 2022. "Extreme Narrowing of the Distributed Feedback Fiber Laser Linewidth Due to the Rayleigh Backscattering in a Single-Mode Fiber: Model and Experimental Test" Photonics 9, no. 8: 590. https://doi.org/10.3390/photonics9080590
APA StyleSkvortsov, M. I., Abdullina, S. R., Podivilov, E. V., Vlasov, A. A., Kharasov, D. R., Fomiryakov, E. A., Nikitin, S. P., Treshchikov, V. N., & Babin, S. A. (2022). Extreme Narrowing of the Distributed Feedback Fiber Laser Linewidth Due to the Rayleigh Backscattering in a Single-Mode Fiber: Model and Experimental Test. Photonics, 9(8), 590. https://doi.org/10.3390/photonics9080590




