Next Article in Journal
Gd2O3 Doped UO2(s) Corrosion in the Presence of Silicate and Calcium under Alkaline Conditions
Next Article in Special Issue
Non-Covalent Interactions in Coordination Chemistry
Previous Article in Journal
Solution-State Studies, X-ray Structure Determination and Luminescence Properties of an Ag(I) Heteroleptic Complex Containing 2,9-Bis(styryl)-1,10-phenanthroline Derivative and Triphenylphosphine
Previous Article in Special Issue
Molecular Switching through Chalcogen-Bond-Induced Isomerization of Binuclear (Diaminocarbene)PdII Complexes
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 11
Issue 12
10.3390/inorganics11120468
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Computational Chemistry Investigation of the Influence of Steric Bulk of Dithiocarbamato-Bound Organic Substituents upon Spodium Bonding in Three Homoleptic Mercury(II) Bis(N,N-dialkyldithiocarbamato) Compounds for Alkyl = Ethyl, Isobutyl, and Cyclohexyl

by
Rosa M. Gomila
,
Edward R. T. Tiekink
* and
Antonio Frontera
*
Department of Chemistry, Universitat de les Illes Balears, Crta de Valldemossa km 7.5, 07122 Palma de Mallorca, Spain
*
Authors to whom correspondence should be addressed.
Inorganics 2023, 11(12), 468; https://doi.org/10.3390/inorganics11120468
Submission received: 19 October 2023 / Revised: 27 November 2023 / Accepted: 29 November 2023 / Published: 1 December 2023
(This article belongs to the Special Issue Non-covalent Interactions in Coordination Chemistry)
Browse Figures
Versions Notes

Abstract

:
Three homoleptic Hg(S2CNR2)2, for R = ethyl (1), isobutyl (2), and cyclohexyl (3), compounds apparently exhibit a steric-dependent supramolecular association in their crystals. The small group in 1 allows for dimer formation via covalent Hg–S interactions through an eight-membered {–HgSCS}2 ring as the dithiocarbamato ligands bridge centrosymmetrically related Hg atoms; intradimer Hg···S interactions are noted. By contrast, centrosymmetrically related molecules in 2 are aligned to enable intermolecular Hg···S interactions, but the separations greatly exceed the van der Waals radii. The large group in 3 precludes both dimerization and intermolecular Hg···S interactions. Computational chemistry indicates that the potential region at the Hg atom is highly dependent on the coordination geometry about the Hg atom. Intramolecular (1) and intermolecular (2) spodium bonding (SpB) is demonstrated. Even at separations approaching 0.4 Å beyond the sum of the assumed van der Waals radii, the energy of the stabilization afforded by the structure directs SpB in 2 amounts to approximately 2.5 kcal/mol. A natural bond orbital (NBO) analysis points to the importance of the LP(S) → σ*(Hg–S) charge transfer and to the dominance of the dispersion forces and electron correlation to the SpB in 2.

1. Introduction

The complexation of heavy elements, for example, d- and p-block elements, by dithiocarbamato ligands has long been a mainstay of coordination chemistry as these are very effective chelators [1,2,3,4,5,6], see Figure 1 for a generic chemical diagram for a monofunctional dithiocarbamato ligand. Among these compounds, those of the zinc triad elements have long attracted the attention of structural chemists owing to the fascinating range of molecular structures in their crystals [7,8,9,10]. A crucial factor for the observed diverse range of structural motifs is the ability of Zn, Cd, and Hg to extend their coordination spheres through secondary bonding interactions. The term “secondary bonding” is generic [11] and was initially employed to cover a myriad of long-recognized intermolecular contacts operating between molecules in various phases [12,13,14], but is now usually replaced by more specific terms reflecting the nature of the supramolecular aggregation for a particular Group of the Periodic Table [15,16,17,18]. In the case of the zinc triad elements, the term “spodium bonding” applies [19]. This term is widely adopted, as revealed in subsequent systematic and computational chemistry studies [20,21,22,23,24,25,26,27,28], and, along with other Periodic Table Group-specific intermolecular interactions based on the σ-hole and π-hole concepts [29,30,31,32,33,34], spodium bonding is expected to be most prominent for the heavier Group 12 element, mercury.
Owing to the presence of two S atoms per dithiocarbamato anion and the inherent thiophilic character of Hg, the presence of Hg···S interactions in crystals of mercury(II) dithiocarbamato compounds might very well be anticipated. Certainly, in crystals of the homoleptic Hg(S2CNRR’)2 compounds, for R, R’ = H, alkyl or aryl, Hg···S interactions are often observed [35]. A factor mitigating intermolecular Hg···S interactions and analogous secondary bonding interactions in crystals of p-block dithiocarbamato compounds, and those of related xanthato (−S2COR) and dithiophosphato [−S2P(OR)(OR’)] compounds, are steric effects exerted by the 1,1-dithiolato-bound organic substituents and/or heavy element-bound organic substituents in the case of organometallic species [7,8,9,10,36,37].
In the above context and in continuation of recent systematic investigations of supramolecular aggregation patterns based on Hg···S interactions in organomercury [38] and non organomercury crystals [39], the present study describes a computational chemistry investigation of three homoleptic Hg(S2CNR2)2 compounds, for R = ethyl (1) [40,41], isobutyl (2) [42], and cyclohexyl (3) [43]. These literature structures are notable in that through the agency of bidentate, bridging dithiocarbamato ligands, and strong intermolecular Hg–S interactions in 1, a dimeric aggregate is formed. Dimers are not evident in 2 even though the molecules are aligned to potentially dimerize; instead, weak intermolecular Hg···S interactions are apparent between these molecules. In 3, no evidence for intermolecular Hg···S interactions is found. One interpretation of this variation rests with the reduced propensity of the molecules to dimerize as the steric bulk of the remote nitrogen-bound substituent increases. It should also be noted here that the electronic structure of the dithiocarbamato anion is not influenced in any significant fashion by the nature of the nitrogen-bound substituent, as evidenced in the very small spreads of the Ni–S bond lengths in the uniformly square planar homoleptic Ni(S2CNRR’)2 complexes [4] and of the Te–S bond lengths in the uniformly trapezoidal planar, homoleptic Te(S2CNRR’)2 compounds [5]. In this study, the respective aggregates (1 and 2) and molecule (3) have been analyzed by a variety of computational chemistry techniques like the molecular electrostatic potential (MEP), the quantum theory of atoms in molecules (QTAIM), noncovalent interaction plots (NCIPLOT), the energetics of the relevant interactions calculated, and assessments of molecular orbitals to determine the nature of the intermolecular binding between molecules in the crystals of 1–3.

2. Methods

Crystallographic data employed in the present study were extracted as Crystallographic Information Files (CIFs) from the Cambridge Structural Database (CSD; [44]); the CIF employed for 1 was of a redetermination based on single crystal data [41]. Crystallographic analyses were conducted by employing a combination of PLATON [45] and MoloVol 1.1.1.0 [46]. Crystallographic diagrams were generated with DIAMOND 3.2.11.0 [47]. The comparative Hirshfeld analysis was conducted with CrystalExplorer21 [48] in accord with established protocols [49].
The evaluation of the salient interactions found in the respective crystals through computational chemistry calculations was achieved using the program Turbomole 7.7 [50] with the input coordinates being those derived from previous crystallographic studies, as available in the respective CIFs [41,42,43]. The two conformations of 1 were fully optimized without symmetry constraints. The level of theory employed for the calculations was PBE0-D4/def2-TZVP [51,52,53,54]. For Hg, this basis set includes the effective core potential (ECP) and for the inner electrons, allows for relativistic effects [53]. The same level of theory with 0.001 a.u. isosurfaces provided wavefunctions enabling the generation of the MEP surface plots. The Bader quantum theory of atoms in molecules (QTAIM) method [55] was used for the topological analysis of the electron density with the reduced density gradient (RDG) isosurfaces (NCI plots) [56] generated by the VMD program 1.9.4 [57]. The Natural Bond Orbital (NBO) analysis [58] was performed using the level of theory as above through the NBO7.0 program [59]. The NBOs and spin density plots were represented using the VMD software 1.9.4 [57]. The energy decomposition analysis (EDA) analysis was performed using the Kitaura–Morokuma method [60], as implemented in Turbomole 7.7 [50]. The QTAIM parameters for the complexes analyzed herein are summarized in Table S1 and the Cartesian coordinates are given in Table S2 (Supplementary Information File).

3. Results and Discussion

Initially, an overview of the structural motifs found for Hg(S2CNRR’)2 in the solid state, as determined by X-ray crystallography, is presented. Then, a detailed description of the molecular geometries of 1–3, the focus of the present study, is given along with an assessment of Hg···S interactions operating in their respective crystals (Section 3.2). The overview is followed by a detailed analysis of the nature of the bonding between molecules in 1–3 through computational chemistry techniques (Section 3.3).

3.1. Literature Survey

As indicated in the Introduction, X-ray crystallography on mercury(II) dithiocarbamato compounds, more specifically, molecules conforming to the general formula Hg(S2CNRR’)2, that is, with a single CS2 residue per dithiocarbamate ligand, exhibits an assorted array of molecular and supramolecular assemblies. Such structural diversity is far from being restricted to mercury(II) dithiocarbamato structures as mercury compounds, including organomercury species, are historically well known to adopt varying structural motifs in their crystals [61,62,63,64], partly arising from their ability to form mercurophilic interactions [65]. Since the last detailed overview of Hg(S2CNRR’)2 structures about a decade ago [35], the number of the literature examples has grown by well over 50%, reflecting the continued interest in these molecules. For example, a recent review highlighted the utility of heavy-element dithiocarbamato species as synthetic precursors for the generation of heavy-element sulfide nanomaterials [66] and this has been an important motivation for many studies on Hg(S2CNRR’)2 molecules, some of which prove useful for the generation of the different polymorphs of HgS. A listing of the known structures of Hg(S2CNRR’)2 is given in Table 1; examples with a functionalized dithiocarbamato ligand, for example, where the organic substituent bears a pyridyl residue and where residue coordinates to mercury, are not included in Table 1 as these have been reviewed in some detail recently [9]. The data in Table 1 are arranged in the following fashion: molecules are arranged in order of the structural motif, that is, binuclear, mononuclear (quasi-dimeric, tetrahedral, and square planar), one dimensional (zigzag, linear, and twisted topologies), and two dimensional. Within each category, molecules with identical R substituents, that is, Hg(S2CNR2)2, are listed before dissymmetric molecules, Hg(S2CNRR’)2, with molecules featuring cyclic substituents listed next. The final category lists multicomponent crystals, following the established order in terms of the substituents on the dithiocarbamato ligand.
There are eight distinct structural motifs for molecules of the general formula Hg(S2CNRR’)2 in their unsolvated crystals, with simplified images for these given in Figure 2, Figure 3, Figure 4 and Figure 5. Of these motifs, four are zero dimensional. The most prominent motif among the 52 examples is a binuclear motif, found in 25 crystals, that is, nearly 50%. Here, one dithiocarbamato ligand is chelating, as is the second ligand, but this also simultaneously connects to the second Hg atom, Figure 2a. The second motif, Figure 2b, is closely related, but the intermolecular Hg···S separation is beyond the standard sum of the benchmark van der Waals radii (3.35 Å [45]). There are nine examples of this motif making this the second most popular motif. The remaining zero-dimensional motifs are mononuclear, there being no evidence of an intermolecular Hg···S contact. The difference between the latter motifs is in the coordination geometry, being based on a tetrahedron, Figure 2c, or a square planar geometry, Figure 2d. There are six examples of tetrahedral motifs and only a single example of the square planar motif.
Three different topologies of the chains are noted for the three one-dimensional motifs, that is, zigzag (one example), linear (five), and twisted (four). Representations of the chains are given in Figure 3a–c where side- and end-on views of the chains are illustrated, which clearly differentiate between the topologies.
There is a sole example of a two-dimensional structural motif, as represented in Figure 4. It is likely that weak N–H···S hydrogen bonding contributes to the stability of this motif in which all dithiocarbamato ligands are bidentate bridging.
As noted from Table 1, some molecules adopt more than one structural motif. A prime example is for the R = R = Et species which adopts both the binuclear motif [41] as well as the linear chain motif [98]. Another pair of motifs has been reported for the R = R = iPr compound, which can be a binuclear [68] or mononuclear tetrahedral [91,92]. These observations underscore the fascinating structural flexibility exhibited by these compounds in their crystals. While these multiple motifs are sometimes described as being polymorphs, a more correct terms might be a supramolecular isomerism [106,107] as the nature of the bonding between Hg and S is not necessarily the same.
For completeness, the motifs in seven multicomponent crystals are now summarized, Table 1. The R = R = Et species has been cocrystallized with fullarene with the retention of the binuclear motif [104]. Similarly, the binuclear motif for the R = Et and R’= Ph compound [74] is retained when the compound is crystallized with toluene [105]. There is no unsolvated precedent for the dissymmetric R = C6H3Me3-2,4,6 and R’ = C(H)=NC6H3Cl2-2,5 compound which, as its CH2Cl2 solvate, adopts a twisted, one-dimensional coordination polymer [96]. Crystals of NRR’ = N(CH2CH2)NPh2, again, have not been isolated solvent-free, but when crystallized with DMSO, a mononuclear tetrahedral motif is seen [84]. A far more remarkable crystal chemistry is apparent for the compound with NRR’ = 1,2,3,4-dihydroquinoline.
The solvent-free species with NRR’ = 1,2,3,4-dihydroquinoline is a twisted coordination polymer [85] and there are three other structures known, each with a cocrystallized solvent [85]. With 2,2′-bipyridine, the twisted coordination polymer, as for the unsolvated species, persists, but with EtOH, the binuclear motif is observed. When the solvent is pyridine, a new structural motif is observed; the disordered pyridine molecule does not interact with Hg. As seen from Figure 5, a zero-dimensional trinuclear motif is seen in the pyridine solvate. The molecule is centrosymmetric and combines the elements of the binuclear motif, Figure 2a, and square planar motif, Figure 2d, with the former flanking the latter with long Hg···S connections [85].
While the elucidation of the structures found in the solid state for Hg(S2CNRR’)2 molecules in their crystals is important and of interest, far more challenging is to rationalize the appearance of the different motifs. In order to do this, careful and comparative experiments are required in contrast to the myriad of crystallization conditions employed for the generation of Hg(S2CNRR’)2 crystals, such as the choice of solvent, the duration of crystallization, concentration, temperature, etc. Recently, such trials were performed for closely related Cd[S2CN(iPr)CH2CH2OH]2 compound [108]. For example, in ethanol solutions, needles of the coordination polymer {Cd[S2CN(iPr)CH2CH2OH]2·EHOH}∞ formed within three hours of recrystallization which, after another hour, had converted quantitatively to the usually observed binuclear motif as prisms and as the di-EtOH solvate. It was concluded that the least soluble coordination polymer initially crystallized which promptly reverted to the thermodynamic (binuclear) form [108]. In the present study, the focus is upon the relationship between the prominent binuclear form and mononuclear species. Specifically, insight is sought regarding the role of the steric bulk of dithiocarbamato-bound alkyl groups upon the adoption of the mononuclear motifs as opposed to the binuclear motif and any role spodium bonding has upon the supramolecular aggregation. The Hg(S2CNRR’)2 molecules chosen for study, that is, with R = R’= ethyl (1), isobutyl (2), and cyclohexyl (3), were found in solvent-free crystals and had symmetric R groups and featured alkyl substituents in order to negate any influence of interactions involving π systems.

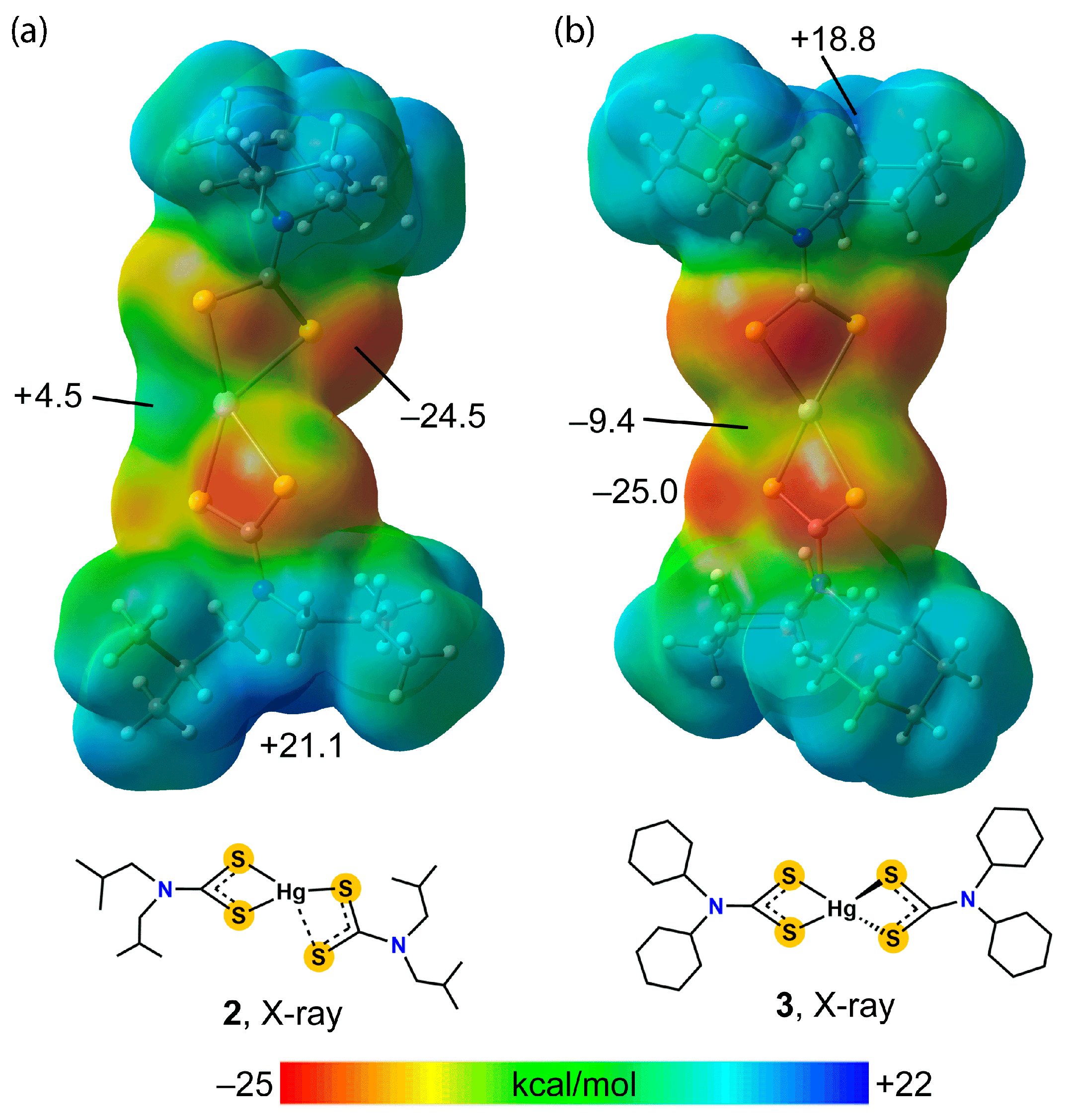
3.2. Experimental Structures

Two distinct coordination modes are noted for the dithiocarbamato anions in the crystal of 1. As noted in Figure 6a, one ligand is bound to one Hg center and simultaneously bridges a second Hg atom related to the first over an inversion center. Key bond lengths and angles for 1–3 are listed in Table 2. These data indicate the Hg–S1, and S2 i bridging bond lengths in 1 differ by approximately 0.10 Å, indicating the bridge is close to symmetrical. With the difference in the Hg–S3, the S4 bond lengths for the second independent dithiocarbamato ligand being 0.12 Å, this ligand coordinates in the chelating mode. The result of the bridging mode of coordination is the formation of an eight-membered {–HgSCS}2 core which has the shape of an extended chair whereby the two pairs of C and S1 atoms lie above the plane of the remaining atoms. Also noted from Figure 6a is the presence of transannular Hg···S2 interactions which are considered long at 3.1266(9) Å, but nevertheless, are shorter than the sum of the van der Waals radii of Hg (1.55 Å) and S (1.80 Å), that is, 3.35 Å [45].
In 2, Figure 6b, the two independent dithiocarbamato ligands coordinate in a similar fashion with the differences in the pairs of Hg–S1, S2, and Hg–S3, with the S4 bond lengths being 0.27 and 0.29 Å, respectively. Centrosymmetrically related molecules approach each other to potentially form Hg···S interactions, but the separation between the atoms is rather long at 2.727(4) Å. The putative supramolecular synthon is a centrosymmetric, four-membered {···HgS}2 synthon, often observed in the supramolecular chemistry of crystals containing both Hg and S [38,39]. In 3, Figure 6c, the Hg atom is located on a two-fold axis of symmetry. The difference in the Hg–S1, S2 bond lengths is only 0.01 Å. No evidence for Hg···S interactions is present in the crystal of 3.
Figure 7 highlights the versatility in the coordination modes adopted by the dithiocarbamato ligands in 1–3. The dimer in 1 exhibits bonding modes based on (a) and (b), 2 exhibits coordination modes intermediate between (a) and (c), whereas in 3, the coordination mode is that shown in Figure 7a. As a generalization, the bridging modes of coordination for dithiocarbamato anions are more likely for Group 12 and p block elements than for transition metals [1,2,3,4,5,6,7,8,9,10].
To a first approximation, the Hg atom in 1 is pentacoordinated within a S5-donor set owing to the transannular Hg···S2 interaction. A useful geometric parameter for assessing five coordinated centers is the computed τ5 value, which for an ideal square-pyramidal geometry is 0.0 and for an ideal trigonal-bipyramid is 1.0 [109]. For 1, the value of τ5 is 0.21, clearly consistent with a distorted geometry approaching a square pyramid. In this description, the bridging S2 i atom occupies the apical position. The distortions arise, in part, due to the acute chelate angles formed by the dithiocarbamato ligands and the close approach of weakly bound S2 atoms, Table 2. In each of 2 and 3, the Hg atom is tetracoordinated within a S4 donor set. The analogous geometric parameter for four coordinated species, τ4, adopts values of 0.00 for an ideal square planar geometry, 1.00, for an ideal tetrahedron and, between these extremes, τ4 = 0.85, for a trigonal pyramidal geometry [110]. In 2 and 3, τ4 has values of 0.55 and 0.62, respectively, again indicating distorted geometries which are closer to trigonal-pyramidal. There are also conformational differences between 1, where the dihedral angle formed between the two chelate rings bound to the same Hg atom is 30.46(3)°, compared with the significantly greater angles in 2 [82.29(7)°] and 3 [79.8(5)°], indicating near to the perpendicular arrangements between the chelate rings in the latter.
Space-filling diagrams [47] for the dimeric aggregates in 1 and 2 and for the monomer in 3 are illustrated in Figure 8a–c. Qualitatively, increasing the steric bulk of the nitrogen-bound R groups from ethyl in 1 to isobutyl in 2 precludes the closer approach of the molecules in the latter. From the image in Figure 8c, the cyclohexyl groups are too large to prevent any semblance of an intermolecular Hg–S/Hg···S interaction.
Table 3 lists some key parameters describing the molecular volumes of 1–3, being calculated with MoloVol [46]. From the data included in Table 3, it is clear there is a systematic variation in the calculated volumes for the individual molecules, even allowing for void space which decreases in the order 1 [10.1%] > 2 [6.6%] > 3 [2.2%], consistent with more efficient close packing as the importance of the intermolecular Hg–S/Hg···S interactions decreases. Similar conclusions are evident from the analysis of the calculated Hirshfeld surfaces for 1–3.
Figure 9 plots the four most prominent calculated surface contacts in the crystals of 1–3, that is, H···H, H···S/S···H, H···C/C···H, and H···Hg/Hg···S; hydrogen is involved in 99.9, 98.2, and 100.0% of all contacts in the crystals of 1–3, respectively. For 1, the calculations were performed on the dimeric aggregate. The H···H contacts are clearly the most dominant across the series and increase in the order 1 [55.0%] < 2 [66.9%] < 3 [69.1%]. The next most dominant contacts, H···S/S···H, follow the inverse trend, that is, 1 [37.2%] > 2 [25.9%] > 3 [23.7%]. There is a large fall in the percentage contributions to the next most important H···C/C···H and H···Hg/Hg···S surface contacts which do not manifest obvious trends. The remaining surface contacts contribute less than 1% to the respective Hirshfeld surfaces with H···N/N···H more important in 1 [0.7%] compared with 0.1% in the crystals of 2 and 3. Surface contacts due to S···S are more significant in 2 [0.7%] as opposed to 1 [0.1%] and 3 [0.0%], and the same is true for Hg···H/H···Hg [0.6%] in contrast to the 0.0% contributions in 1 and 3.
The foregoing affirms the structural diversity of Hg(S2CNR2)2 molecules, at least for the zero-dimensional R = ethyl (1), R = isobutyl (2), and R = cyclohexyl (3) series. A consequence of these variations is a distinct pattern of Hg···S secondary bonding interactions, namely intramolecular, intermolecular, and none for 1–3, respectively. In order to ascertain the nature of these Hg···S interactions and the influence of the adopted molecular structures on their formation, molecules 1–3 were subjected to density-functional theory (DFT) calculations.

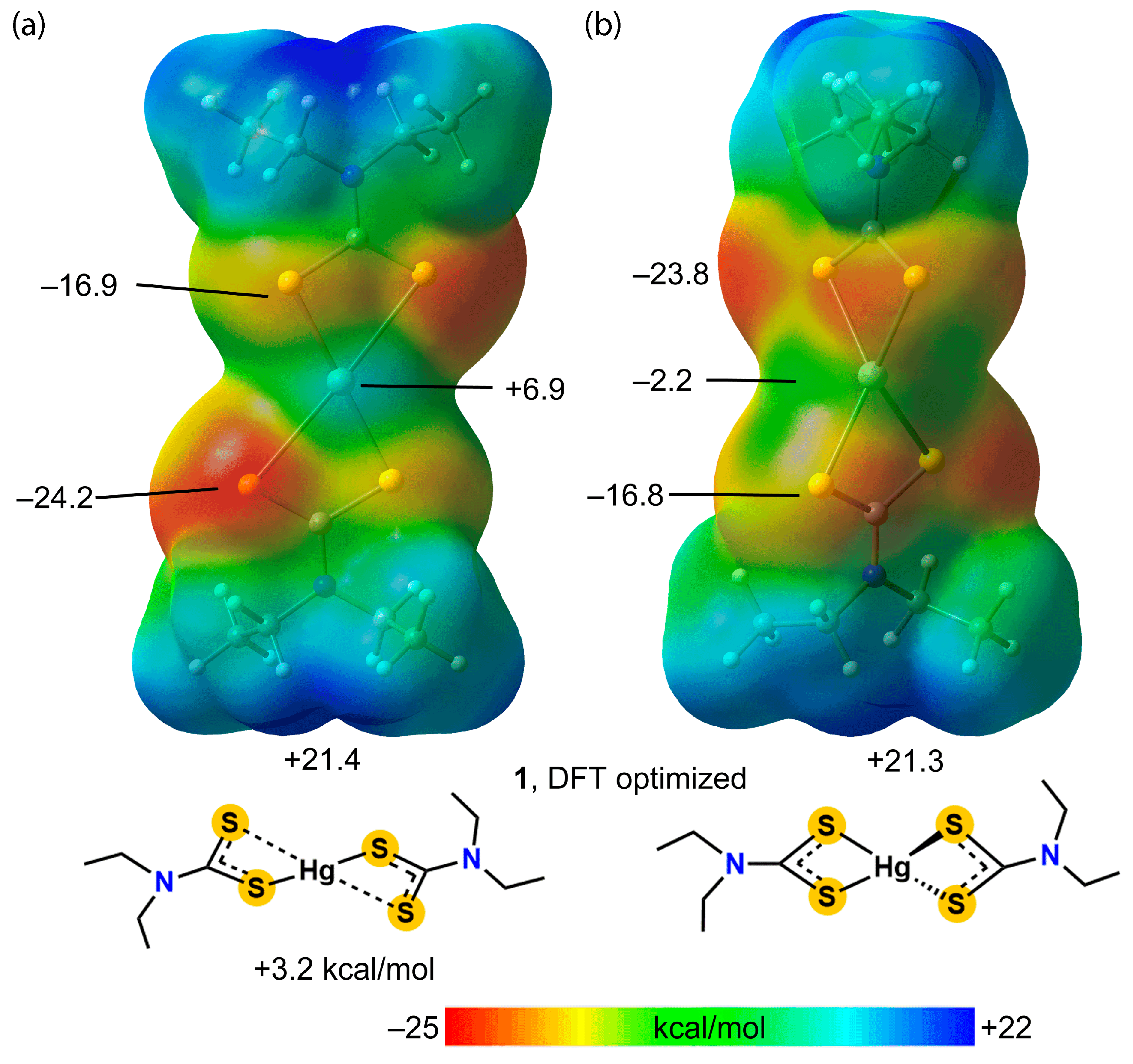
3.3. DFT Calculations

A thorough DFT study has been conducted to better understand and describe the presence of Hg···S interactions, shown below to be spodium bonds (SpBs) in crystals of Hg(S2CNR2)2 for R = ethyl (1) and R = isobutyl (2), that is, intra- and intermolecular SpBs, respectively, and the absence of SpBs when R = cyclohexyl (3). Firstly, to assess the presence and accessibility of the π-hole on the Hg atoms in 1–3, their MEP surfaces were computed.
For 1, the optimization of the isolated Hg(S2CNEt2)2 fragment revealed two distinct minima. The more stable configuration has a pseudo-tetrahedral coordination. The less stable configuration, higher in energy by +3.2 kcal/mol, features a linear S–Hg–S coordination with two auxiliary Hg···S contacts and a coplanar arrangement of the four S atoms, Figure 10a. Notably, the MEP surface plots differ between the two isomers: only the coplanar form has a positive potential region at the Hg atom (+6.9 kcal/mol), while the pseudo tetrahedral form shows a slightly negative MEP at the Hg position. However, the MEP maxima and minima are comparable for both configurations. These findings on the isolated geometry-optimized Hg(S2CNEt2)2 fragments, having either square planar or tetrahedral geometries, imply that the existence of SpBs is closely tied to the coordination sphere/geometry about the Hg atom.
Figure 11 illustrates the MEP surfaces for the isolated molecules in 2 and 3, based on their X-ray-determined geometries. This helps clarify the presence or absence of SpBs in their respective solid-state structures. Intriguingly, 2 (R = isobutyl) exhibits a flat pseudo-trigonal geometry with three primary Hg–S coordination bonds and an additional ancillary Hg···S bond. This compound reveals a positive potential region at the Hg atom (+4.5 kcal/mol), which is somewhat less pronounced than that in compound 1 (with a linear coordination, as seen in Figure 11a). For 3 (R = cyclohexyl), its MEP surface plot indicates a negative potential at the Hg atom, likely attributed to its pseudo-tetrahedral coordination. Therefore, the absence of SpB contacts in 3 can be attributed to its pseudo-tetrahedral coordination and the associated lack of a positive MEP.
The SpBs in 1 (intramolecular) and 2 (intermolecular) have been thoroughly examined using a combination of QTAIM and NCIplot analyses. While the use of QTAIM for the analysis of noncovalent interactions is sometimes debated [111,112,113,114], our experience shows this is a useful complementary tool in the study of these inherently weak interactions, including for mercury-containing compounds [19,39], as combined QTAIM and NCIplot methods effectively visualize noncovalent interactions in real space. For 1, the intramolecular SpBs feature a bond critical point (BCP, shown as a red sphere) and a bond path linking the Hg and S atoms, Figure 12a. The disk-shaped reduced density gradient (RDG) isosurface aligns with the location of the BCP. The light-blue color along with the density value at the BCP (0.0226 a.u.) highlight the moderately strong nature of these SpBs. For 2, the supramolecular dimer was studied (Figure 12b). The QTAIM/NCIplot findings confirm the presence of the Hg···S SpBs, marked by their respective BCPs, bond paths, and green RDG isosurfaces. The color of the RDG isosurfaces indicates that these intermolecular SpBs are weaker than the intramolecular SpBs in 1, consistent with the longer separations and a smaller BCP density (0.0065 a.u.). Further, the analysis reveals additional CH···S contacts aiding dimer formation. The dimerization energy stands at –11.7 kcal/mol, incorporating both the SpBs and CH···S contacts. As a first approximation [115], to isolate the contribution of SpBs, a modified dimer was analyzed where –NR2 (R = cyclohexyl) in 3 was substituted with –NH2 groups. This change eliminates the CH···S contacts and other van der Waals CH···HC interactions, lowering the interaction energy to −4.9 kcal/mol. This suggests each SpB contributes about −2.5 kcal/mol, corroborated by the color of the RDG isosurface, the small density at the BCP, and the minimal MEP value at the Hg atom, Figure 12a. This observation is in keeping with the notion that SpBs provide energies of stabilization [19,39] comparable to other supramolecular association modes like hydrogen bonding [116]. Indeed, this energy is rather remarkable given the long separation between the Hg and S atoms forming the Hg···S SpB, further supporting the idea that significant structure-directing interactions can exist at distances greater than the sum of the conventional van der Waals radii [117,118,119,120].
The interactions in 2 were further evaluated using the NBO method, an approach well suited for probing donor/acceptor interactions and analyzing charge transfer effects. Notably, the analysis revealed an electron donation from a lone pair orbital at the S atom of one monomer to the antibonding Hg–S orbital of its counterpart, and vice versa (with only one set depicted in Figure 13). This results in a total stabilization energy of E(2) = 1.8 kcal/mol, equating to 0.9 kcal/mol for each LP(S) → σ*(Hg–S) donor/acceptor interaction.
To probe the physical nature of intermolecular interactions within the self-assembled dimer of 2, an EDA was conducted. Figure 14 presents the results of this analysis through a bar plot. The data reveal that the correlation (Ecor, lilac bar) and dispersion (Edisp, green bar) contributions are more significant than the electrostatic (Eel, blue bar) and orbital (Eorb, grey bar) components. This observation accounts for the substantial dimerization energy recorded for the dimer of 2 (Etot = −11.7 kcal/mol, pink bar), despite the minimal MEP value at Hg and the minor LP(S) → σ*(Hg–S) charge transfer identified from the MEP surface and NBO analyses. Notably, dispersion is the primary contributor, succeeded by the electron correlation. This is associated with the participation of a heavy metal (increasing Ecor) and the CH···HC interactions (increasing Edisp) between the alkyl chains, further supported by the NCIplot analysis (Figure 12b).

4. Conclusions

Steric effects associated with the dithiocarbamato-bound R substituents are crucial in determining the mode of coordination of the dithiocarbamato anions in Hg(S2CNR2)2 crystals: the small ethyl substituents in 1 allow for a bridging mode of coordination, leading to dimer formation, but this is precluded by the larger substituents in 2 (isobutyl) and 3 (cyclohexyl). Using DFT analyses, the varying presence and nature of SpBs across compounds 1 to 3 was discerned, highlighting the significance of the coordination geometry and molecular electrostatic potential. The QTAIM and NCI plot analyses provided a clear depiction of noncovalent interactions, evidencing stronger SpBs in 1 (intramolecular) than 2 (intermolecular). In 2, energetic assessments indicate a moderate SpB interaction strength, approximately −2.5 kcal/mol, despite the long separation between the interacting centers. Moreover, the NBO analysis of 2 highlights the LP(S) → σ*(Hg–S) charge transfer phenomenon. Finally, the study evidences the dominant dispersion forces followed by an electron correlation in the supramolecular dimer of 2. This knowledge is expected to interest scientists across supramolecular chemistry, crystal engineering, coordination, and theoretical chemistry domains.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/inorganics11120468/s1, Table S1: QTAIM parameters (a.u.) for the bond critical points that characterize the spodium bonds; Table S2: Cartesian coordinates for the geometry optimized monomeric molecules of 1.

Author Contributions

Conceptualization, E.R.T.T.; formal analysis, R.M.G., E.R.T.T. and A.F.; investigation, R.M.G., E.R.T.T. and A.F.; writing—original draft preparation, R.M.G., E.R.T.T. and A.F.; writing—review and editing, R.M.G., E.R.T.T. and A.F.; visualization, R.M.G., E.R.T.T. and A.F.; funding acquisition, A.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by MICIU/AEI of Spain, grant number PID2020-115637GB-I00 FEDER funds.

Data Availability Statement

The data presented in this study are available on request from the authors.

Acknowledgments

The authors thank CTI (UIB) for computational facilities.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Coucouvanis, D. The chemistry of the dithioacid and 1,1-dithiolate complexes. Prog. Inorg. Chem. 1970, 11, 234–371. [Google Scholar] [CrossRef]
  2. Eisenberg, R. Structural systematics of 1,1- and 1,2-dithiolato chelates. Prog. Inorg. Chem. 1970, 12, 295–369. [Google Scholar] [CrossRef]
  3. Coucouvanis, D. The chemistry of the dithioacid and 1,1-dithiolate complexes, 1968–1977. Prog. Inorg. Chem. 1979, 26, 301–469. [Google Scholar] [CrossRef]
  4. Hogarth, G. Transition metal dithiocarbamates: 1978–2003. Prog. Inorg. Chem. 2005, 53, 71–561. [Google Scholar] [CrossRef]
  5. Heard, P.J. Main group dithiocarbamate complexes. Prog. Inorg. Chem. 2005, 53, 1–69. [Google Scholar] [CrossRef]
  6. Haiduc, I. 1,1-Dithiolato ligands and related selenium and tellurium compounds. In Handbook of Chalcogen Chemistry; Devillanova, F.A., Ed.; Royal Society of Chemistry: Cambridge, UK, 2007; pp. 593–643. ISBN 978-0-85404-366-8. [Google Scholar]
  7. Tiekink, E.R.T. Molecular architecture and supramolecular association in the zinc-triad 1,1-dithiolates. Steric control as a design element in crystal engineering? CrystEngComm 2003, 5, 101–113. [Google Scholar] [CrossRef]
  8. Tiekink, E.R.T. Exploring the topological landscape exhibited by binary zinc-triad 1,1-dithiolates. Crystals 2018, 8, 292. [Google Scholar] [CrossRef]
  9. Tiekink, E.R.T. On the coordination role of pyridyl-nitrogen in the structural chemistry of pyridyl-substituted dithiocarbamate ligands. Crystals 2021, 11, 286. [Google Scholar] [CrossRef]
  10. Lee, S.M.; Tiekink, E.R.T. A structural survey of poly-functional dithiocarbamate ligands and the aggregation patterns they sustain. Inorganics 2021, 9, 7. [Google Scholar] [CrossRef]
  11. Mulliken, R.S. Structures of complexes formed by halogen molecules with aromatic and with oxygenated solvents. J. Am. Chem. Soc. 1950, 72, 600–608. [Google Scholar] [CrossRef]
  12. Bent, H.A. Structural chemistry of donor-acceptor interactions. Chem. Rev. 1968, 68, 587–648. [Google Scholar] [CrossRef]
  13. Hassel, O. Structural Aspects of interatomic charge-transfer bonding. Science 1970, 170, 497–502. [Google Scholar] [CrossRef] [PubMed]
  14. Alcock, N.W. Secondary bonding to nonmetallic elements. Adv. Inorg. Chem. Radiochem. 1972, 15, 1–58. [Google Scholar] [CrossRef]
  15. Legon, A.C. Tetrel, pnictogen and chalcogen bonds identified in the gas phase before they had names: A systematic look at non-covalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 14884–14896. [Google Scholar] [CrossRef] [PubMed]
  16. Edwards, A.J.; Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. Intermolecular interactions in molecular crystals: What’s in a name? Faraday Discuss. 2017, 203, 93–112. [Google Scholar] [CrossRef]
  17. Scheiner, S.; Michalczyk, M.; Zierkiewicz, W. Coordination of anions by noncovalently bonded σ-hole ligands. Coord. Chem. Rev. 2020, 405, 213136. [Google Scholar] [CrossRef]
  18. Brammer, L.; Peuronen, A.; Roseveare, T.M. Halogen bonds, chalcogen bonds, pnictogen bonds, tetrel bonds and other σ-hole interactions: A snapshot of current progress, Acta Crystallogr. Sect. C Struct. Chem. 2023, 79, 204–216. [Google Scholar] [CrossRef] [PubMed]
  19. Bauzá, A.; Alkorta, I.; Elguero, J.; Mooibroek, T.J.; Frontera, A. Spodium bonds: Noncovalent interactions involving Group 12 elements. Angew. Chem. Int. Ed. 2020, 59, 17482–17487. [Google Scholar] [CrossRef] [PubMed]
  20. Ciancaleoni, G.; Rocchigiani, L. Assessing the orbital contribution in the “spodium bond” by natural orbital for chemical valence−charge displacement analysis. Inorg. Chem. 2021, 60, 4683–4692. [Google Scholar] [CrossRef]
  21. Liu, N.; Xie, X.; Li, Q. Chalcogen bond involving zinc(II)/cadmium(II) carbonate and its enhancement by spodium bond. Molecules 2021, 26, 6443. [Google Scholar] [CrossRef]
  22. Wysokiński, R.; Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Anion⋯anion (MX3−)2 dimers (M = Zn, Cd, Hg; X = Cl, Br, I) in different environments. Phys. Chem. Chem. Phys. 2021, 23, 13853–13861. [Google Scholar] [CrossRef]
  23. Singh, A.; Kociok-Köhn, G.; Dutta, A.; Kumar, A.; Muddassir, M. Diaminopyridine Hg(II)-based 1D supramolecular polymer: Crystallographic and computational insights into spodium bonding. J. Solid State Chem. 2022, 315, 123517. [Google Scholar] [CrossRef]
  24. Kumar, P.; Banerjee, S.; Radha, A.; Firdoos, T.; Sahoo, S.C.; Pandey, S.K. Role of non-covalent interactions in the supramolecular architectures of mercury(II) diphenyldithiophosphates: An experimental and theoretical investigation. New J. Chem. 2021, 45, 2249–2263. [Google Scholar] [CrossRef]
  25. Liu, N.; Li, Q.; Scheiner, S. Spodium and tetrel bonds involving Zn(II)/Cd(II) and their interplay. Chem. Phys. 2022, 556, 111470. [Google Scholar] [CrossRef]
  26. Gao, M.; Zhao, Q.; Yu, H.; Fu, M.; Li, Q. Insight into spodium–π bonding characteristics of the MX2⋯π (M = Zn, Cd and Hg; X = Cl, Br and I) complexes—A theoretical study. Molecules 2022, 27, 2885. [Google Scholar] [CrossRef] [PubMed]
  27. Rozhkov, A.V.; Katlenok, E.A.; Zhmykhova, M.V.; Kuznetsov, M.L.; Khrustalev, V.N.; Tugashov, K.I.; Bokach, N.A.; Kukushkin, V.Y. Spodium bonding to anticrown-Hg3 boosts phosphorescence of cyclometalated-PtII complexes. Inorg. Chem. Front. 2023, 10, 493–510. [Google Scholar] [CrossRef]
  28. Wu, Q.; McDowell, S.A.C.; Li, Q. Single-electron spodium bonds: Substituent effects. Appl. Organomet. Chem. 2023, 37, e7052. [Google Scholar] [CrossRef]
  29. Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The sigma-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef]
  30. Murray, J.S.; Lane, P.; Clark, T.; Politzer, P.J. σ-hole bonding: Molecules containing group VI atoms. Mol. Model. 2007, 13, 1033–1038. [Google Scholar] [CrossRef]
  31. Kolář, M.H.; Hobza, P. Computer modeling of halogen bonds and other σ-hole interactions. Chem. Rev. 2016, 116, 5155–5187. [Google Scholar] [CrossRef]
  32. Politzer, P.; Murray, J.S. σ-Hole interactions: Perspectives and misconceptions. Crystals 2017, 7, 212. [Google Scholar] [CrossRef]
  33. Politzer, P.; Murray, J.S.; Clark, T.; Resnati, G. The σ-hole revisited. Phys. Chem. Chem. Phys. 2017, 19, 32166–32178. [Google Scholar] [CrossRef]
  34. Murray, J.S.; Politzer, P. Interaction and polarization energy relationships in σ-hole and π-hole bonding. Crystals 2020, 10, 76. [Google Scholar] [CrossRef]
  35. Jotani, M.M.; Tan, Y.S.; Tiekink, E.R.T. Bis[bis(N-2-hydroxyethyl,N-isopropyldithiocarbamato)mercury(II)]2: Crystal structure and Hirshfeld surface analysis. Z. Kristallogr.—Cryst. Mater. 2016, 231, 403–413. [Google Scholar] [CrossRef]
  36. Winter, G. Inorganic xanthates. Rev. Inorg. Chem. 1980, 2, 253–342. [Google Scholar]
  37. Haiduc, I.; Sowerby, D.B. Stereochemical aspects of phosphor-1,1-dithiolato metal complexes: Coordination patterns, molecular structures and supramolecular associations in dithiophosphinates and related compounds. Polyhedron 1996, 15, 2469–2521. [Google Scholar] [CrossRef]
  38. Tiekink, E.R.T. Supramolecular association via Hg···S secondary-bonding interactions in crystals of organomercury(II) species: A survey of the Cambridge Structure Database. Crystals 2023, 13, 385. [Google Scholar] [CrossRef]
  39. Gomila, R.M.; Frontera, A.; Tiekink, E.R.T. Supramolecular aggregation featuring Hg···S secondary-bonding interactions in crystals of mercury(II) species augmented by computational chemistry calculations. CrystEngComm 2023, 25, 5262–5285. [Google Scholar] [CrossRef]
  40. Iwasaki, H. The crystal structures of dimeric and monoclinic forms of mercury(II) N,N-diethyldithiocarbamate, Hg2(S2CNEt2)4 and Hg(S2CNEt2)2. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 1973, 29, 2115–2124. [Google Scholar] [CrossRef]
  41. Lai, C.S.; Tiekink, E.R.T. Refinement of the crystal structure of bis[(N,N-diethyldithiocarbamato)mercury(II)], [Hg(S2CNEt2)2]2. Z. Kristallogr.—New Cryst. Struct. 2002, 217, 593–594. [Google Scholar] [CrossRef]
  42. Cox, M.J.; Tiekink, E.R.T. Structural diversity in the mercury(II) bis(N,N-dialkyldithiocarbamate) compounds: An example of the importance of considering crystal structure when rationalising molecular structure. Z. Kristallogr.—Cryst. Mater. 1999, 214, 571–579. [Google Scholar] [CrossRef]
  43. Cox, M.J.; Tiekink, E.R.T. The crystal structure of monomeric bis(dicyclohexyldithiocarbamato)mercury(II). Main Group Met. Chem. 2000, 23, 793–794. [Google Scholar] [CrossRef]
  44. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 171–179. [Google Scholar] [CrossRef] [PubMed]
  45. Spek, A.L. checkCIF validation ALERTS: What they mean and how to respond. Acta Crystallogr. Sect. E Crystallogr. Commun. 2020, 76, 1–11. [Google Scholar] [CrossRef] [PubMed]
  46. Maglic, J.B.; Lavendomme, R. MoloVol: An easy-to-use program for analyzing cavities, volumes and surface areas of chemical structures. J. Appl. Cryst. 2022, 55, 1033–1044. [Google Scholar] [CrossRef] [PubMed]
  47. Brandenburg, K.; Berndt, M. DIAMOND, Version 3.2k; GbR: Bonn, Germany, 2006.
  48. Spackman, P.R.; Turner, M.J.; Mckinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef]
  49. Tan, S.L.; Jotani, M.M.; Tiekink, E.R.T. Utilizing Hirshfeld surface calculations, non-covalent interaction (NCI) plots and the calculation of interaction energies in the analysis of molecular packing. Acta Crystallogr. Sect. E Crystallogr. Commun. 2019, 75, 308–318. [Google Scholar] [CrossRef]
  50. Ahlrichs, R.; Bär, M.; Häser, M.; Horn, H.; Kölmel, C. Electronic structure calculations on workstation computers: The programsystem turbomole. Chem. Phys. Lett. 1989, 162, 165–169. [Google Scholar] [CrossRef]
  51. Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
  52. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. Consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
  53. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  54. Weigend, F. Accurate coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
  55. Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
  56. Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.-P.; Beratan, D.N.; Yang, W. NCIPLOT: A program for plotting non-covalent interaction regions. J. Chem. Theory Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef] [PubMed]
  57. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
  58. Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 7.0: New vistas in localized and delocalized chemical bonding theory. J. Comput. Chem. 2019, 40, 2234–2241. [Google Scholar] [CrossRef]
  59. Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Karafiloglou, P.; Landis, C.R.; Weinhold, F. NBO 7.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2018. [Google Scholar]
  60. Kitaura, K.; Morokuma, K. A new energy decomposition scheme for molecular interactions within the Hartree-Fock approximation. Int. J. Quantum Chem. 1976, 10, 325–340. [Google Scholar] [CrossRef]
  61. Grdenić, D. The structural chemistry of mercury. Q. Rev. Chem. Soc. 1965, 19, 303–328. [Google Scholar] [CrossRef]
  62. Lobana, T.S. Coordination chemistry of organomercury(II) involving phenanthrolines, bipyridines, tertiary phosphines/arsines and some related ligands. Coord. Chem. Rev. 1985, 63, 161–215. [Google Scholar] [CrossRef]
  63. House, D.A.; Robinson, W.T.; McKee, V. Chloromercury(II) anions. Coord. Chem. Rev. 1994, 135–136, 533–586. [Google Scholar] [CrossRef]
  64. Morsali, A.; Masoomi, M.Y. Structures and properties of mercury(II) coordination polymers. Coord. Chem. Rev. 2009, 253, 1882–1905. [Google Scholar] [CrossRef]
  65. Schmidbaur, H.; Schier, A. Mercurophilic interactions. Organometallics 2015, 34, 2048–2066. [Google Scholar] [CrossRef]
  66. Sarker, J.C.; Hogarth, G. Dithiocarbamate complexes as single source precursors to nanoscale binary, ternary and quaternary metal sulfides. Chem. Rev. 2021, 121, 6057–6123. [Google Scholar] [CrossRef]
  67. Rodina, T.A.; Loseva, O.V.; Smolentsev, A.I.; Antzutkin, O.N.; Ivanov, A.V. Crystal structure, solid-state 13C and 15N NMR characterisation, chemisorption activity and thermal behaviour of new mercury(II) dipropyldithiocarbamate: Binuclear, pseudo-binuclear and heteronuclear complexes of [Hg2(PrDtc)4], [Hg(PrDtc)2]2 and [Au(PrDtc)2]2[Hg2Cl6]. Inorg. Chim. Acta 2020, 508, 119630. [Google Scholar] [CrossRef]
  68. Loseva, O.V.; Rodina, T.A.; Smolentsev, A.I.; Ivanov, A.V. A new polymorphic modification and chemisorption activity of mercury(II) N,N-di-iso-propyldithiocarbamate: Synthesis and characterisation of the heteronuclear double complex of ([Au{S2CN(iso-C3H7)2}2]2[Hg2Cl6]·OC(CH3)2)n. Polyhedron 2017, 134, 238–245. [Google Scholar] [CrossRef]
  69. Gomathi, G.; Dar, S.H.; Thirumaran, S.; Ciattini, S.; Selvanayagam, S. Bis(N-benzyl-N-furfuryldithiocarbamato-S,S′)mercury(II) as a precursor for the preparation of mercury sulfide nanoparticles. C. R. Chim. 2015, 18, 499–510. [Google Scholar] [CrossRef]
  70. Onwudiwe, D.C.; Ajibade, P.A. Synthesis, characterization and thermal studies of Zn(II), Cd(II) and Hg(II) complexes of N-methyl-N-phenyldithiocarbamate: The single crystal structure of [(C6H5)(CH3)NCS2]4Hg2. Int. J. Mol. Sci. 2011, 12, 1964–1978. [Google Scholar] [CrossRef] [PubMed]
  71. Green, M.; Prince, P.; Gardener, M.; Steed, J. Mercury(II) N,N′-methyl-phenylethyl-dithiocarbamate and its use as a precursor for the room-temperature solution deposition of β-HgS thin films. Adv. Mater. 2004, 16, 994–996. [Google Scholar] [CrossRef]
  72. Onwudiwe, D.C.; Ajibade, P.A. Synthesis and crystal structure of bis(N-alkyl-N-phenyl dithiocarbamato)mercury(II). J. Chem. Crystallogr. 2011, 41, 980–985. [Google Scholar] [CrossRef]
  73. Ajibade, P.A.; Onwudiwe, D.C. Synthesis and characterization of group 12 complexes of N,N-methylphenyl-N,N-butyl phenyl dithiocarbamate. J.Coord. Chem. 2011, 63, 2964–2973. [Google Scholar] [CrossRef]
  74. Ondrušová, D.; Pajtášová, M.; Jóna, E.; Koman, M. Structural properties of Co(III), Hg(II) and Pb(II) N-ethyl-N-phenyl-dithiocarbamates and their application in the rubber industry. Solid State Phenom. 2003, 90–91, 383–388. [Google Scholar] [CrossRef]
  75. Gurumoorthy, G.; Thirumaran, S.; Ciattini, S. Unusual octahedral Hg(II) dithiocarbamate: Synthesis, spectral and structural studies on Hg(II) complexes with pyrrole based dithiocarbamates and their utility for the preparation of α- and β-HgS. Polyhedron 2016, 118, 143–153. [Google Scholar] [CrossRef]
  76. Guzmán-Percástegui, E.; Zakharov, L.N.; Alvarado-Rodríguez, J.G.; Carnes, M.E.; Johnson, D.W. Synthesis of a self-assembled Hg(II)-dithiocarbamate metallomacrocycle. Cryst. Growth Des. 2014, 14, 2087–2091. [Google Scholar] [CrossRef]
  77. Yadav, R.; Trivedi, M.; Kociok-Köhn, G.; Chauhan, R.; Kumar, A.; Gosavi, S.W. Ferrocenyl dithiocarbamate based d10 transition-metal complexes as potential co-sensitizers in dye-sensitized solar cells. Eur. J. Inorg. Chem. 2016, 2016, 1013–1021. [Google Scholar] [CrossRef]
  78. Dar, S.H.; Thirumaran, S.; Selvanayagam, S. Synthesis, spectral and X-ray structural studies on Hg(II) dithiocarbamate complexes: A new precursor for HgS nanoparticles. Polyhedron 2015, 96, 16–24. [Google Scholar] [CrossRef]
  79. Kumar, V.; Manar, K.K.; Gupta, A.N.; Singh, V.; Drew, M.G.B.; Singh, N. Impact of ferrocenyl and pyridyl groups attached to dithiocarbamate moieties on crystal structures and luminescent characteristics of group 12 metal complexes. J. Organomet. Chem. 2016, 820, 62–69. [Google Scholar] [CrossRef]
  80. Altaf, M.; Stoeckli-Evans, H.; Batool, S.S.; Isab, A.A.; Ahmad, S.; Saleem, M.; Awan, S.A.; Shaheen, M.A. Mercury(II) complexes of pyrrolidinedithiocarbamate, crystal structure of bis{[μ2-(pyrrolidinedithiocarbamato-S,S′)(pyrrolidinedithiocarbamato-S,S′)mercury(II)]}. J. Coord. Chem. 2010, 63, 1176–1185. [Google Scholar] [CrossRef]
  81. Loseva, O.V.; Rodina, T.A.; Antzutkin, O.N.; Ivanov, A.V. Chemisorption activity of mercury(II) cyclopentamethylenedithiocarbamate: Synthesis, structure, and thermal behavior of the [Hg2{S2CN(CH2)5}4] and [Au3{S2CN(CH2)5}6][Au{S2CN(CH2)5}2][Hg2Cl6]2 complexes. Russ. J. Gen. Chem. 2018, 88, 2540–2549. [Google Scholar] [CrossRef]
  82. Ivanov, A.V.; Korneeva, E.V.; Bukvetskii, B.V.; Goryan, A.S.; Antsutkin, O.N.; Forshling, W. Structural organization of mercury(II) and copper(II) dithiocarbamates from EPR and 13C and 15N MAS NMR spectra and X-ray diffraction analysis. Russ. J. Coord. Chem. 2008, 34, 59–69. [Google Scholar] [CrossRef]
  83. Benedetti, A.; Fabretti, A.C.; Preti, C. Structure, IR, and NMR spectra of tetrakis(4-methyl piperidinedithiocarbamate) dimercury(II). J. Crystallogr. Spectrosc. Res. 1988, 18, 685–692. [Google Scholar] [CrossRef]
  84. Khan, A.; Hayat, F.; Butler, I.S.; Tahir, M.N.; ur Rehman, Z. Mercury(II) dithiocarbamates: Structural aspects and their use as single-source precursors for shape-controlled facile synthesis of HgS nanoparticles. Polyhedron 2021, 193, 114876. [Google Scholar] [CrossRef]
  85. Srinivasan, N.; Thirumaran, S.; Ciattini, S. Effect of co-crystallization of ethanol, pyridine and 2,2′-bipyridine on molecular aggregation in bis(1,2,3,4-tetrahydroquinolinedithiocarbamato-S,S′)mercury(II) and synthesis of HgS nanoparticles. RSC Adv. 2014, 4, 22971–22979. [Google Scholar] [CrossRef]
  86. Onwudiwe, D.C.; Ajibade, P.A. Synthesis and characterization of Zn(II), Cd(II), and Hg(II) alkyl-aryl dithiocarbamate: X-ray crystal structure of [(C6H5N(et)CS2)Hg(C6H5N(butyl)CS2)]. Synth. React. Inorg. Met.-Org. Nano-Met. Chem. 2010, 40, 279–284. [Google Scholar] [CrossRef]
  87. Marimuthu, G.; Ramalingam, K.; Rizzoli, C.; Arivanandhan, M. Solvothermal preparation of nano-β-HgS from a precursor, bis(dibenzyldithiocarbamato)mercury(II). J. Nanopart. Res. 2012, 14, 710. [Google Scholar] [CrossRef]
  88. Yadav, M.K.; Rajput, G.; Gupta, A.N.; Kumar, V.; Drew, M.G.B.; Singh, N. Exploring the coordinative behaviour and molecular architecture of new PhHg(II)/Hg(II) dithiocarbamate complexes. Inorg. Chim. Acta 2014, 421, 210–217. [Google Scholar] [CrossRef]
  89. Kumar, A.; Chauhan, R.; Molloy, K.C.; Kociok-Köhn, G.; Bahadur, L.; Singh, N. Synthesis, structure and light-harvesting properties of some new transition-metal dithiocarbamates involving ferrocene. Chem.-Eur. J. 2010, 16, 4307–4314. [Google Scholar] [CrossRef]
  90. Marimuthu, G.; Ramalingam, K.; Rizzoli, C. Predominant ionic interactions in CdS4N2 and HgS4 coordination environments. J. Coord. Chem. 2013, 66, 699–711. [Google Scholar] [CrossRef]
  91. Ito, M.; Iwasaki, H. The structure of the monomeric form of mercury(II) N,N-diisopropyldithiocarbamate [bis(N,N-diisopropyldithiocarbamato)mercury(II)]. Acta Crystallogr. B 1979, 35, 2720–2721. [Google Scholar] [CrossRef]
  92. Angeloski, A.; Rawal, A.; Bhadbhade, M.; Hook, J.M.; Schurko, R.W.; McDonagh, A.M. An unusual mercury(II) diisopropyldithiocarbamate coordination polymer. Cryst. Growth Des. 2019, 19, 1125–1133. [Google Scholar] [CrossRef]
  93. Singh, R.P.; Maurya, V.K.; Maiti, B.; Siddiqui, K.A.; Prasad, L.B. Synthesis, structure and thermogravimetric analysis of novel dithiocarbamate based Zn(II),Cd(II) and Hg(II) complexes. J. Molec. Struct. 2019, 1198, 126912. [Google Scholar] [CrossRef]
  94. Rajput, G.; Yadav, M.K.; Thakur, T.S.; Drew, M.G.B.; Singh, N. Versatile coordination environment and interplay of metal assisted secondary interactions in the organization of supramolecular motifs in new Hg(II)/PhHg(II) dithiolates. Polyhedron 2014, 69, 225–233. [Google Scholar] [CrossRef]
  95. Lai, C.S.; Tiekink, E.R.T. Crystallographic report: Bis(pyrrolinedithiocarbamato)mercury(II). Appl. Organomet. Chem. 2003, 17, 143. [Google Scholar] [CrossRef]
  96. Oladipo, S.D.; Omondi, B. N,N′-diarylformamidine dithiocarbamates as single-source precursors for the preparation of oleylamine-capped HgS nanoparticles. Transit. Met. Chem. 2020, 45, 391–402. [Google Scholar] [CrossRef]
  97. Singh, V.; Kumar, V.; Gupta, A.N.; Drew, M.G.B.; Singh, N. Effect of pyridyl substituents leading to the formation of green luminescent mercury(II) coordination polymers, zinc(II) dimers and a monomer. New J. Chem. 2014, 38, 3737–3748. [Google Scholar] [CrossRef]
  98. Healy, P.C.; White, A.H. Crystal structure of bis(NN-diethyldithiocarbamato)mercury(II). J. Chem. Soc. Dalton Trans. 1973, 284–287. [Google Scholar] [CrossRef]
  99. Howie, R.A.; Tiekink, E.R.T.; Wardell, J.L.; Wardell, S.M.S.V. Complementary Supramolecular Aggregation via O–H···O Hydrogen-bonding and Hg···S Interactions in Bis[N,N′-di(2-hydroxyethyl)-dithiocarbamato-S,S′]mercury(II): Hg[S2CN(CH2CH2OH)2]2. J. Chem. Crystallogr. 2009, 39, 293–298. [Google Scholar] [CrossRef]
  100. Singh, V.; Kumar, A.; Prasad, R.; Rajput, G.; Drew, M.G.B.; Singh, N. The interplay of secondary Hg⋯S, Hg⋯N and Hg⋯π bonding interactions in supramolecular structures of phenylmercury(II) dithiocarbamates. CrystEngComm 2011, 13, 6817–6826. [Google Scholar] [CrossRef]
  101. Loseva, O.V.; Rodina, T.A.; Ivanov, A.V. Pseudo-polymeric mercury(II) morpholinedithiocarbamate [Hg{S2CN(CH2)4O}2]n: Supramolecular structure (a role of secondary Hg···S Bonds), 13C and 15N CP-MAS NMR Spectra, and thermal behavior. Coord. Chem. 2019, 45, 22–29. [Google Scholar] [CrossRef]
  102. Cox, M.J.; Tiekink, E.R.T. Structural variations in the mercury(II) bis(1,1-dithiolate)s: The crystal and molecular structure of [Hg(S2CNMe2)2]. Z. Kristallogr. Cryst. Mater. 2010, 212, 542–544. [Google Scholar] [CrossRef]
  103. Chieh, C.; Cheung, S.K. A crystallographic and spectroscopic study of mercury(II) dithiocarbamate. Can. J. Chem. 1981, 59, 2746–2749. [Google Scholar] [CrossRef]
  104. Konarev, D.V.; Khasanov, S.S.; Lopatin, D.V.; Rodaev, V.V.; Lyubovskaya, R.N. Fullerene complexes with divalent metal dithiocarbamates: Structures, magnetic properties, and photoconductivity. Russ. Chem. Bull. 2007, 56, 2145–2161. [Google Scholar] [CrossRef]
  105. Ajibade, P.A.; Mbese, J.Z.; Omondi, B. Group 12 dithiocarbamate complexes: Synthesis, characterization, and X-ray crystal structures of Zn (II) and Hg (II) complexes and their use as precursors for metal sulfide nanoparticles. Inorg. Nano-Met. Chem. 2017, 47, 202–212. [Google Scholar] [CrossRef]
  106. Moulton, B.; Zaworotko, M.J. From molecules to crystal engineering: Supramolecular isomerism and polymorphism in network solids. Chem. Rev. 2001, 101, 1629–1658. [Google Scholar] [CrossRef] [PubMed]
  107. Zhang, J.-P.; Huang, X.-C.; Chen, X.-M. Supramolecular isomerism in coordination polymers. Chem. Soc. Rev. 2009, 38, 2385–2396. [Google Scholar] [CrossRef]
  108. Tan, Y.S.; Halim, S.N.A.; Tiekink, E.R.T. Exploring the crystallization landscape of cadmium bis(N-hydroxyethyl, N-isopropyl-dithiocarbamate), Cd[S2CN(iPr)CH2CH2OH]2. Z. Kristallogr. 2016, 231, 113–126. [Google Scholar] [CrossRef]
  109. Addison, A.W.; Rao, T.N.; Reedijk, J.; van Rijn, J.; Verschoor, C.C. Synthesis, structure, and spectroscopic properties of copper(II) compounds containing nitrogen–sulphur donor ligands; the crystal and molecular structure of aqua[1,7-bis(N-methylbenzimidazol-2′-yl)-2,6-dithiaheptane]copper(II) perchlorate. J. Chem. Soc. Daltons Trans. 1984, 1349–1356. [Google Scholar] [CrossRef]
  110. Yang, L.; Powell, D.R.; Houser, R.P. Structural variation in copper(I) complexes with pyridylmethylamide ligands: Structural analysis with a new four-coordinate geometry index, τ4. Dalton Trans. 2007, 955–964. [Google Scholar] [CrossRef]
  111. Grimme, S.; Mück-Lichtenfeld, C.; Erker, G.; Kehr, G.; Wang, H.; Beckers, H.; Willner, H. When do interacting atoms form a chemical bond? Spectroscopic measurements and theoretical analyses of dideuteriophenanthrene. Angew. Chem. Int. Ed. 2009, 48, 2592–2595. [Google Scholar] [CrossRef]
  112. Foroutan-Nejad, C.; Shahbazian, S.; Marek, R. Toward a consistent interpretation of the QTAIM: Tortuous link between chemical bonds, interactions, and bond/line paths. Chem.–Eur. J. 2014, 20, 10140–10152. [Google Scholar] [CrossRef]
  113. Spackman, M.A. How reliable are intermolecular interaction energies estimated from topological analysis of experimental electron densities? Cryst. Growth Des. 2015, 15, 5624–5628. [Google Scholar] [CrossRef]
  114. Wick, C.R.; Clark, T. On bond-critical points in QTAIM and weak interactions. J. Mol. Model. 2018, 31, 142. [Google Scholar] [CrossRef]
  115. Scheiner, S. Quantum chemical analysis of noncovalent bonds within crystals. Concepts and concerns. CrystEngComm 2023, 25, 5060–5071. [Google Scholar] [CrossRef]
  116. Tiekink, E.R.T. Supramolecular assembly based on “emerging” intermolecular interactions of particular interest to coordination chemists. Coord. Chem. Rev. 2017, 345, 209–228. [Google Scholar] [CrossRef]
  117. Alvarez, S. A cartography of the van der Waals territories. Dalton Trans. 2013, 42, 8617–8636. [Google Scholar] [CrossRef]
  118. Hu, S.-Z.; Zhou, Z.-H.; Xie, Z.-X.; Robertson, B.E. A comparative study of crystallographic van der Waals radii. Z. Kristallogr.—Cryst. Mater. 2014, 229, 517–523. [Google Scholar] [CrossRef]
  119. Balmohammadi, Y.; Khavasi, H.R.; Naghavi, S.S. Existence of untypical halogen-involving interactions in crystal packings: A statistical and first-principles study. CrystEngComm 2020, 22, 2756–2765. [Google Scholar] [CrossRef]
  120. Politzer, P.; Murray, J.S. The use and misuse of van der Waals radii. Struct. Chem. 2021, 32, 623–629. [Google Scholar] [CrossRef]
Inorganics 11 00468 g001
Figure 1. Chemical diagram for one canonical form of a generic dialkyldithiocarbamato anion.
Figure 1. Chemical diagram for one canonical form of a generic dialkyldithiocarbamato anion.
Inorganics 11 00468 g001
Inorganics 11 00468 g002
Figure 2. Simplified images for the four zero-dimensional structural motifs observed in the crystals of Hg(S2CNRR’)2: (a) binuclear, (b) quasi dimeric, (c) tetrahedral, and (d) square planar. Color code: Hg, orange sphere; S, yellow; N, blue; C, gray; H, bright-green. For clarity, only the N-bound C atoms are shown.
Figure 2. Simplified images for the four zero-dimensional structural motifs observed in the crystals of Hg(S2CNRR’)2: (a) binuclear, (b) quasi dimeric, (c) tetrahedral, and (d) square planar. Color code: Hg, orange sphere; S, yellow; N, blue; C, gray; H, bright-green. For clarity, only the N-bound C atoms are shown.
Inorganics 11 00468 g002
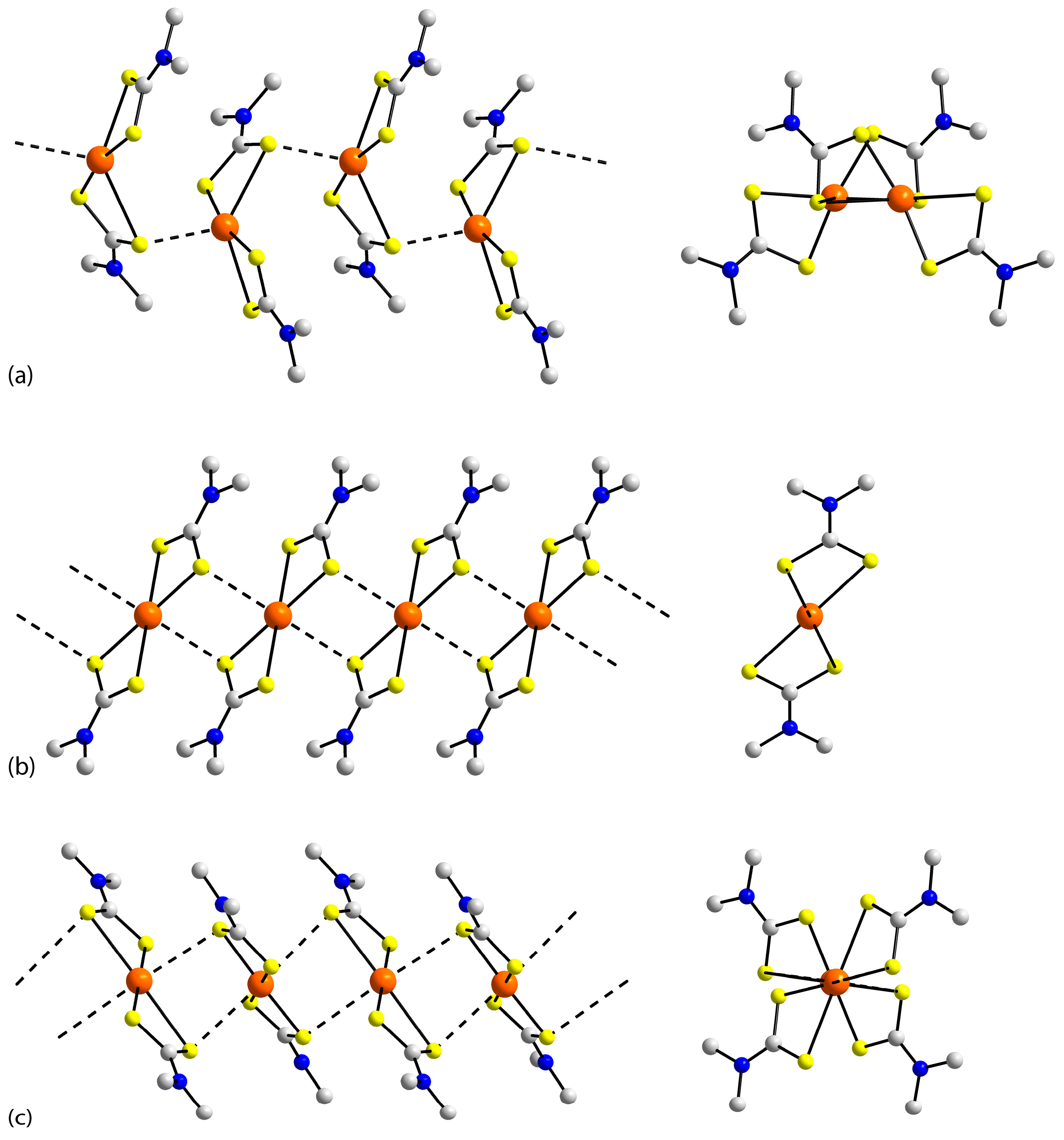
Inorganics 11 00468 g003
Figure 3. Simplified images for the three one-dimensional structural motifs observed in the crystals of Hg(S2CNRR’)2: (a) zigzag chain, (b) linear chain, and (c) twisted chain.
Figure 3. Simplified images for the three one-dimensional structural motifs observed in the crystals of Hg(S2CNRR’)2: (a) zigzag chain, (b) linear chain, and (c) twisted chain.
Inorganics 11 00468 g003
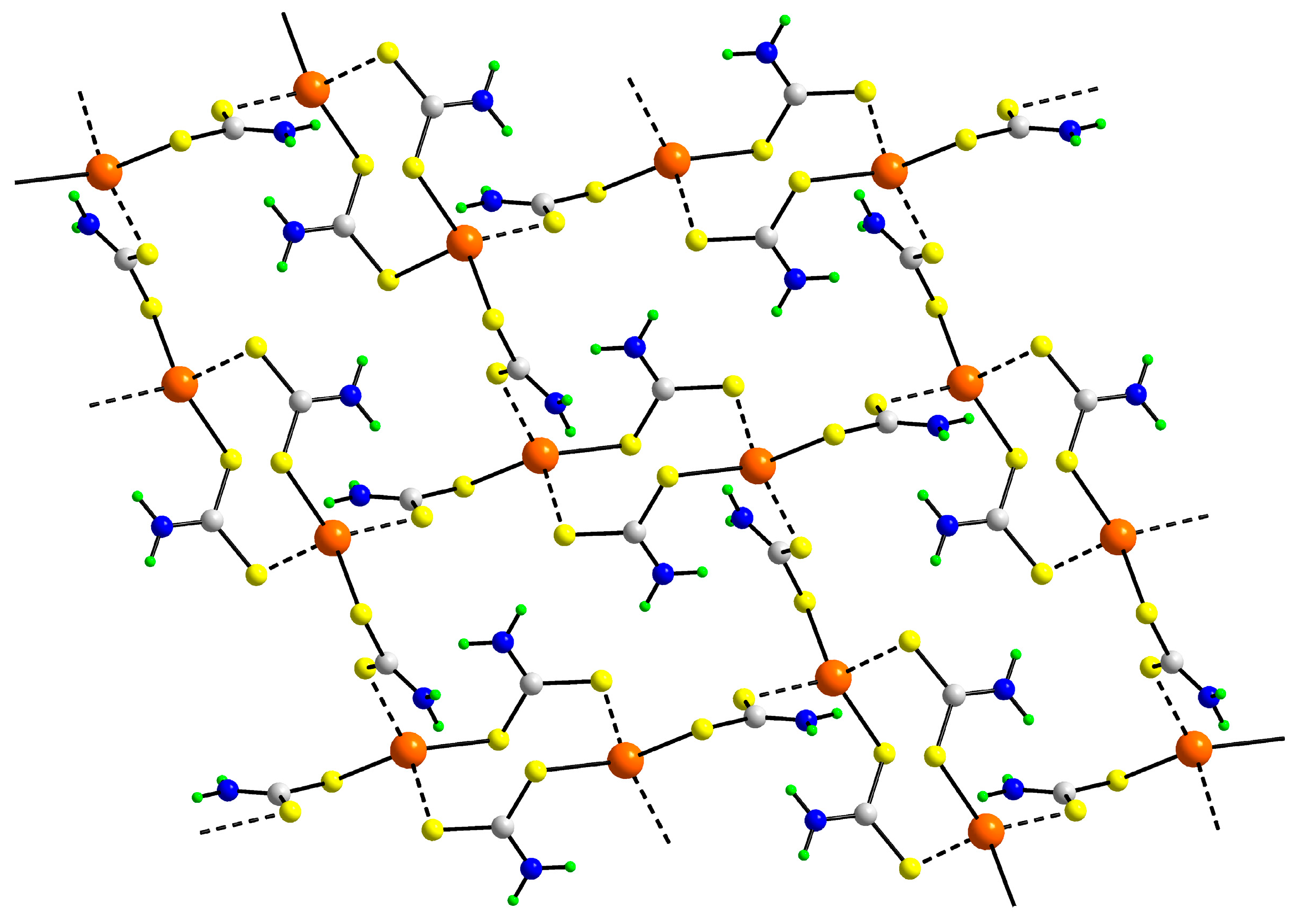
Inorganics 11 00468 g004
Figure 4. Simplified image for a two-dimensional array.
Figure 4. Simplified image for a two-dimensional array.
Inorganics 11 00468 g004
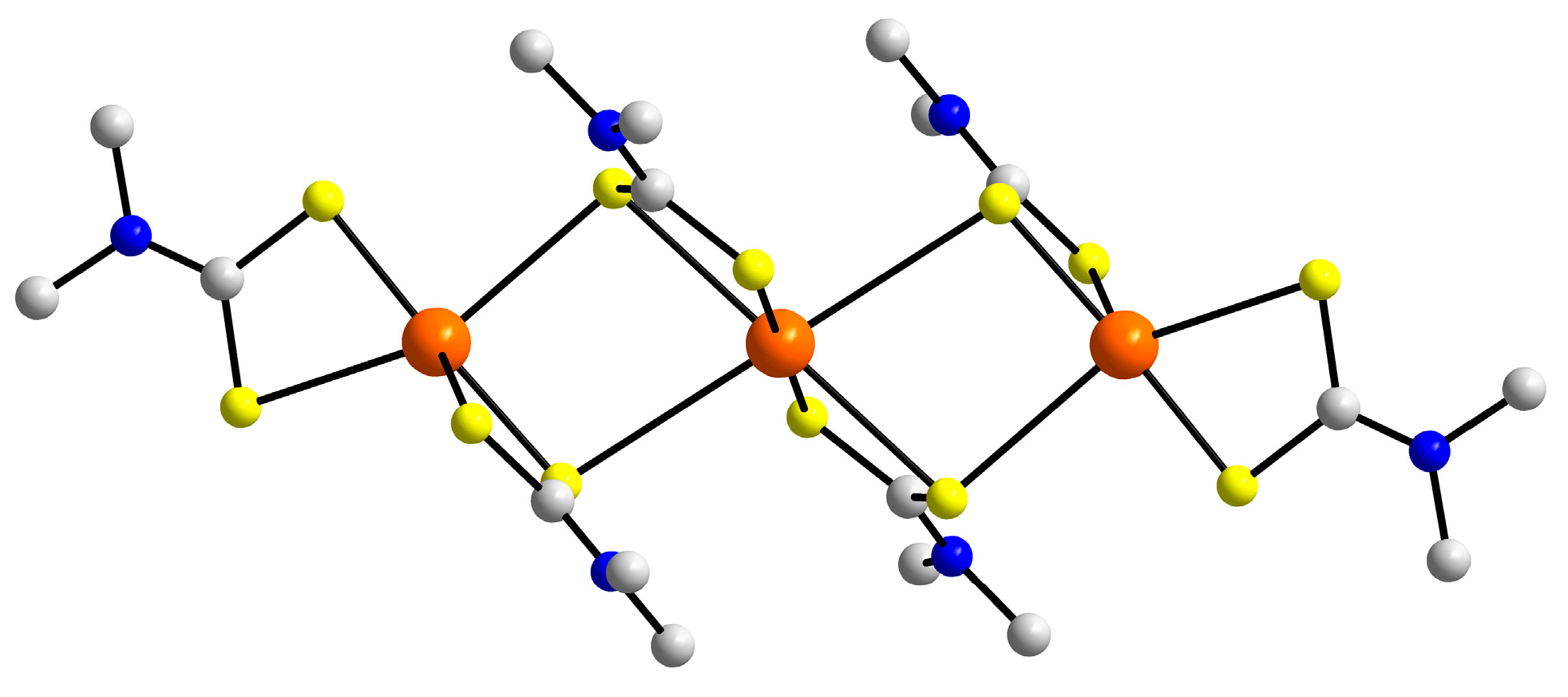
Inorganics 11 00468 g005
Figure 5. Simplified images for an additional zero-dimensional structural motif.
Figure 5. Simplified images for an additional zero-dimensional structural motif.
Inorganics 11 00468 g005
Inorganics 11 00468 g006
Figure 6. Supramolecular aggregation via Hg–S/Hg···S interactions in the crystals of Hg(S2CNR2)2: (a) R = ethyl (1), (b) R = isobutyl (2), and (c) the monomeric molecule for R = cyclohexyl (3). Symmetry operations i in (a) and (b) are given in Table 2.
Figure 6. Supramolecular aggregation via Hg–S/Hg···S interactions in the crystals of Hg(S2CNR2)2: (a) R = ethyl (1), (b) R = isobutyl (2), and (c) the monomeric molecule for R = cyclohexyl (3). Symmetry operations i in (a) and (b) are given in Table 2.
Inorganics 11 00468 g006
Inorganics 11 00468 g007
Figure 7. Variable coordination modes of the dialkyldithiocarbamato anion towards mercury(II): (a) symmetric chelating with similar Hg–S bond lengths, (b) bidentate bridging with approximately similar Hg–S bond lengths, and (c) asymmetric chelating with dissimilar Hg–S bond lengths.
Figure 7. Variable coordination modes of the dialkyldithiocarbamato anion towards mercury(II): (a) symmetric chelating with similar Hg–S bond lengths, (b) bidentate bridging with approximately similar Hg–S bond lengths, and (c) asymmetric chelating with dissimilar Hg–S bond lengths.
Inorganics 11 00468 g007
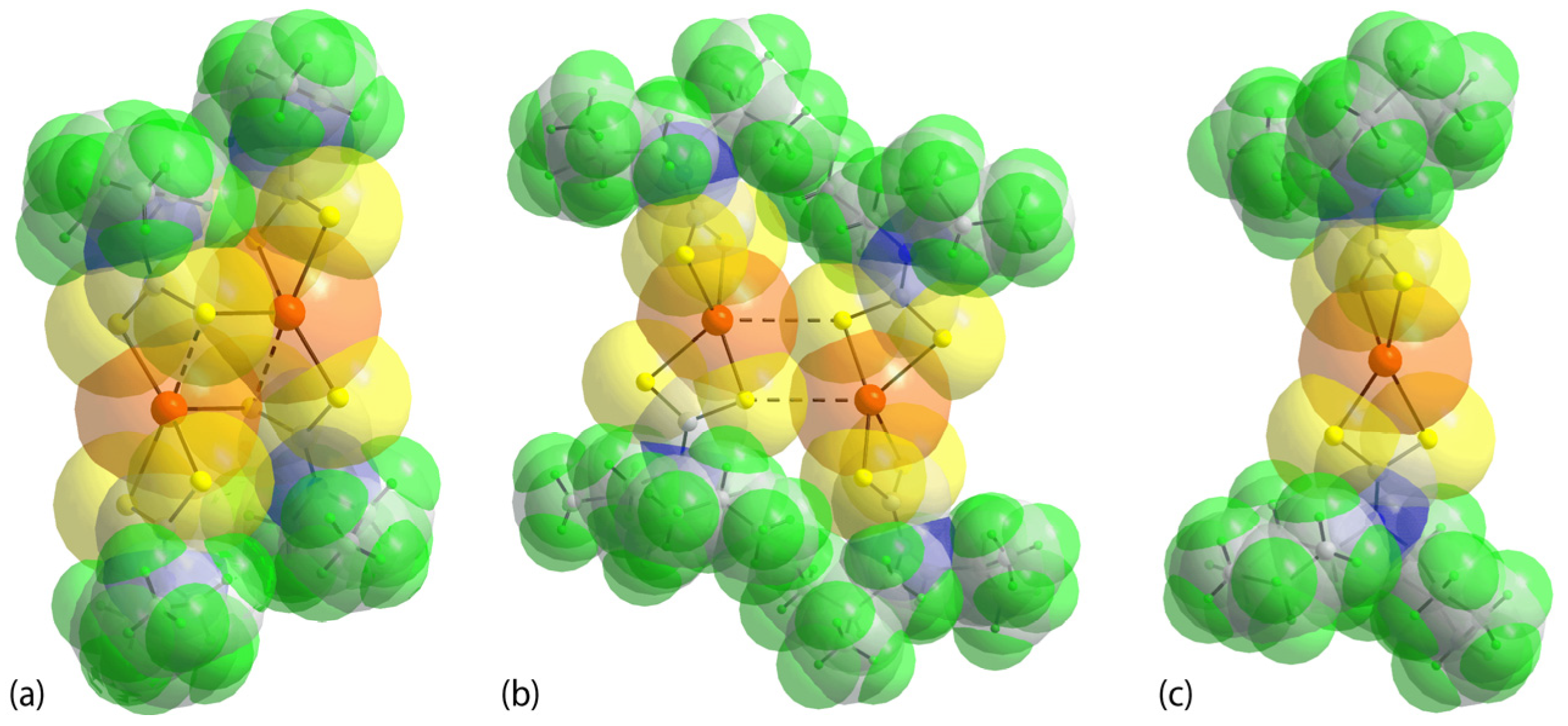
Inorganics 11 00468 g008
Figure 8. Space-filling images for the dimeric aggregates in the crystals of Hg(S2CNR2)2 for (a) R = ethyl (1) and (b) R = isobutyl (2), and (c) for the monomeric molecule when R = cyclohexyl (3).
Figure 8. Space-filling images for the dimeric aggregates in the crystals of Hg(S2CNR2)2 for (a) R = ethyl (1) and (b) R = isobutyl (2), and (c) for the monomeric molecule when R = cyclohexyl (3).
Inorganics 11 00468 g008
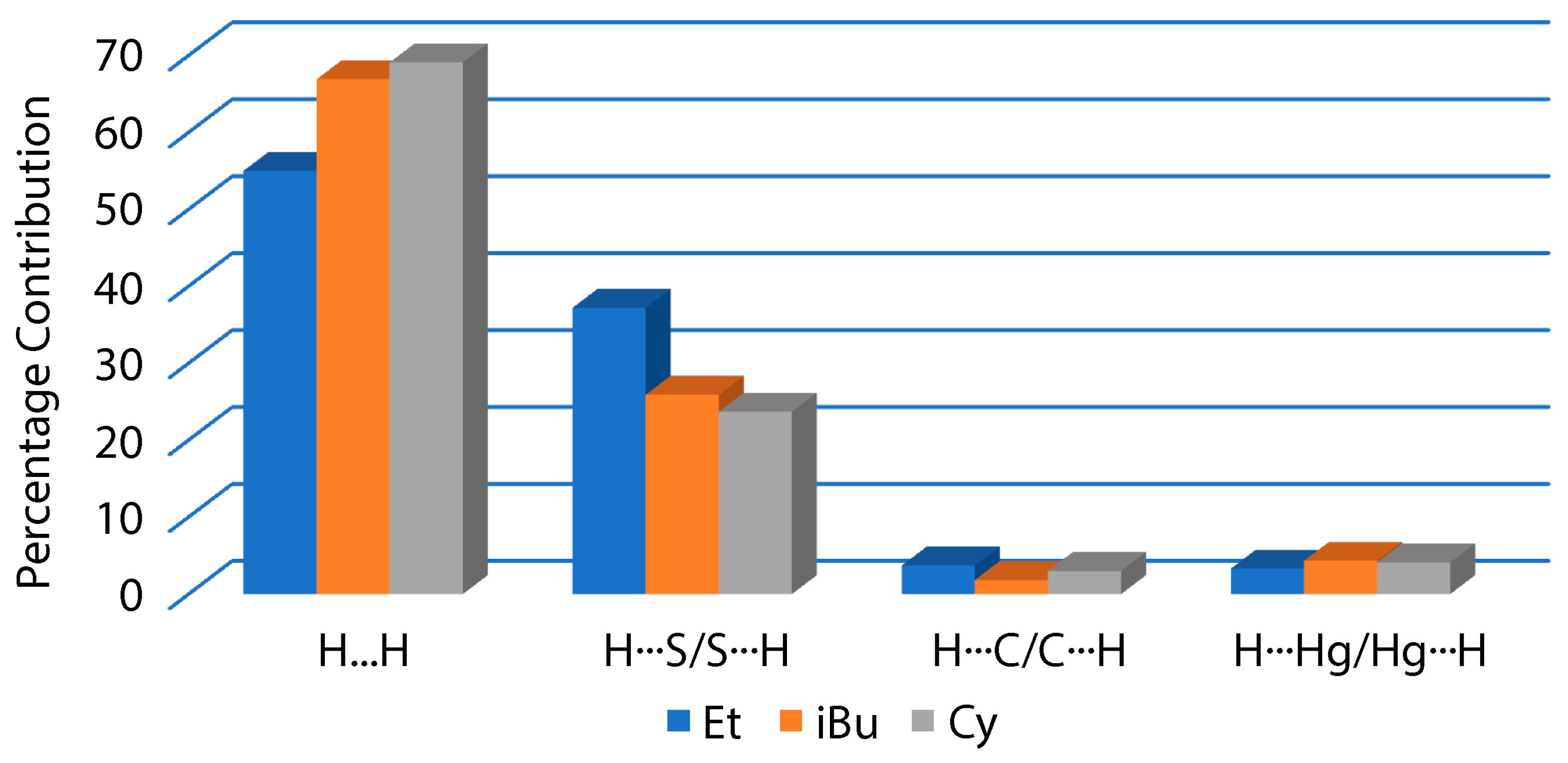
Inorganics 11 00468 g009
Figure 9. A bar graph contrasting the percentage contributions of the four major contacts to the calculated Hirshfeld surfaces of Hg(S2CNR2)2 for R = ethyl (1), R = isobutyl (2), and R = cyclohexyl (3).
Figure 9. A bar graph contrasting the percentage contributions of the four major contacts to the calculated Hirshfeld surfaces of Hg(S2CNR2)2 for R = ethyl (1), R = isobutyl (2), and R = cyclohexyl (3).
Inorganics 11 00468 g009
Inorganics 11 00468 g010
Figure 10. MEP surface plots for the optimized Hg(S2CNEt2)2 fragment of 1: (a) planar and (b) pseudo-tetrahedral configurations. The MEP values at selected points are given in kcal/mol.
Figure 10. MEP surface plots for the optimized Hg(S2CNEt2)2 fragment of 1: (a) planar and (b) pseudo-tetrahedral configurations. The MEP values at selected points are given in kcal/mol.
Inorganics 11 00468 g010
Inorganics 11 00468 g011
Figure 11. MEP surface plots calculated for the X-ray geometries of (a) 2 and (b) 3. The MEP values at selected points are given in kcal/mol.
Figure 11. MEP surface plots calculated for the X-ray geometries of (a) 2 and (b) 3. The MEP values at selected points are given in kcal/mol.
Inorganics 11 00468 g011
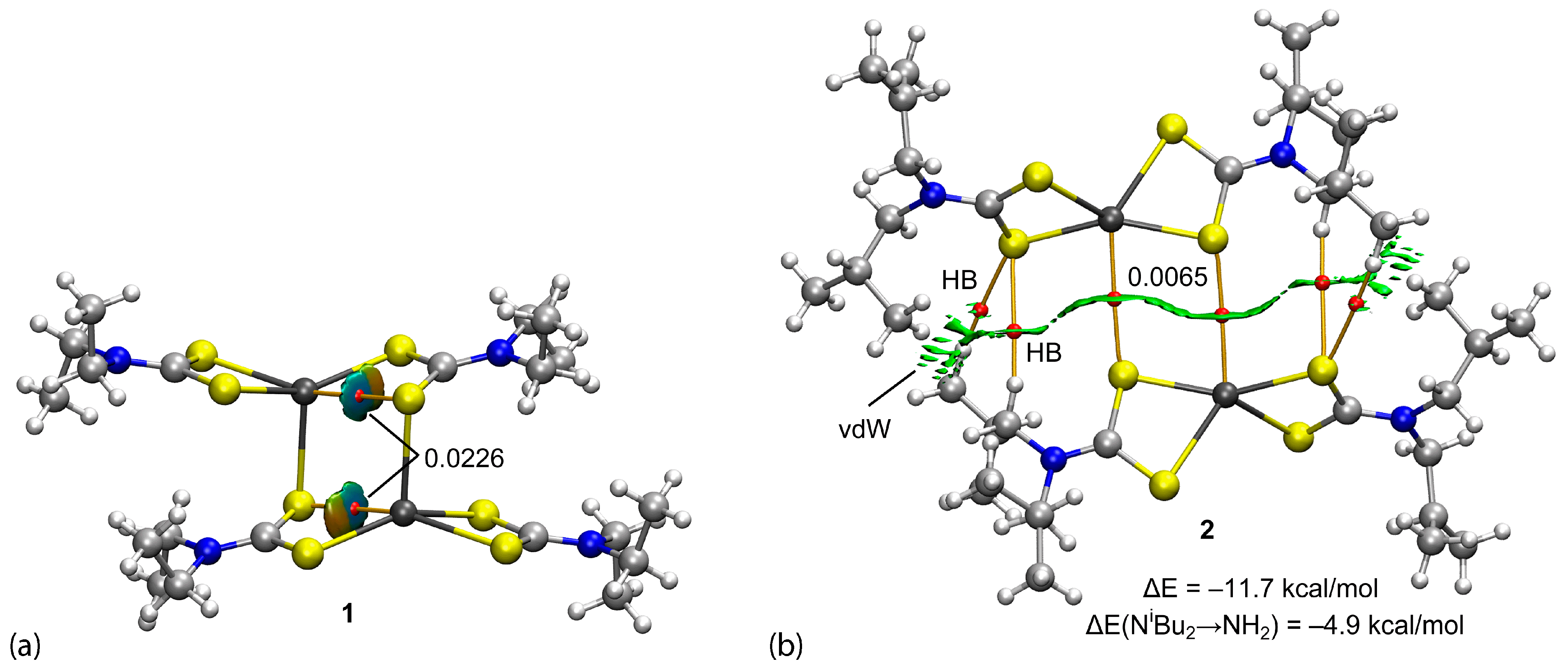
Inorganics 11 00468 g012
Figure 12. QTAIM (BCPs in red and bond paths as orange lines) and NCIplot (RDG = 0.5, ρ cutoff = 0.04 a.u., color scale –0.035 a.u. ≤ (signλ2)ρ ≤ 0.035 a.u.) for (a) 1 and (b) the weakly associated dimer in 2. The dimerization energies for (b) are also indicated. The values of ρ at the BCPs are given in a.u. “HB” refers to the CH···S contact and “vd W” is van der Waals.
Figure 12. QTAIM (BCPs in red and bond paths as orange lines) and NCIplot (RDG = 0.5, ρ cutoff = 0.04 a.u., color scale –0.035 a.u. ≤ (signλ2)ρ ≤ 0.035 a.u.) for (a) 1 and (b) the weakly associated dimer in 2. The dimerization energies for (b) are also indicated. The values of ρ at the BCPs are given in a.u. “HB” refers to the CH···S contact and “vd W” is van der Waals.
Inorganics 11 00468 g012
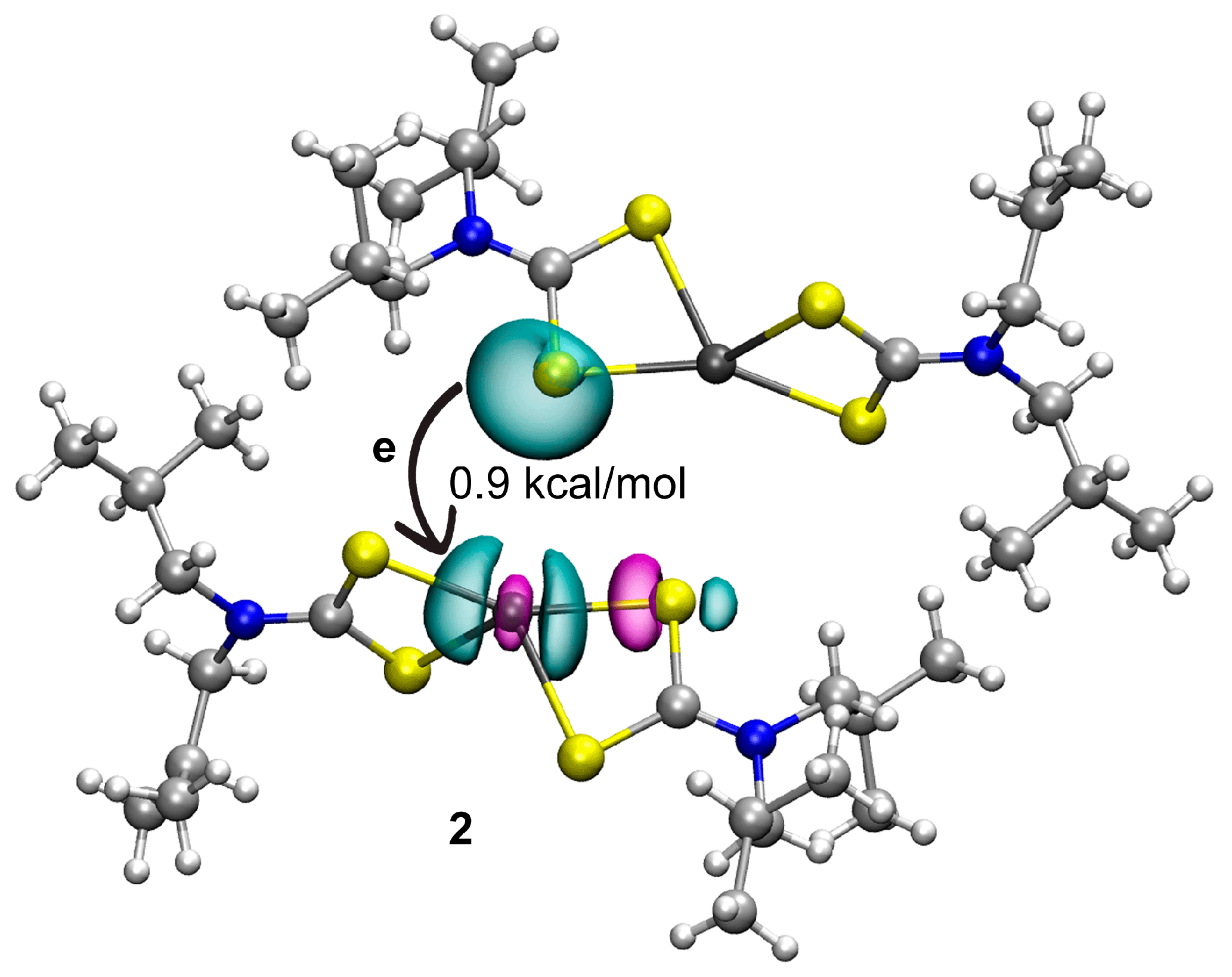
Inorganics 11 00468 g013
Figure 13. NBOs involved in the LP(S) → σ*(Hg–S) donor/acceptor interaction in 2. The second-order perturbation energy is indicated.
Figure 13. NBOs involved in the LP(S) → σ*(Hg–S) donor/acceptor interaction in 2. The second-order perturbation energy is indicated.
Inorganics 11 00468 g013
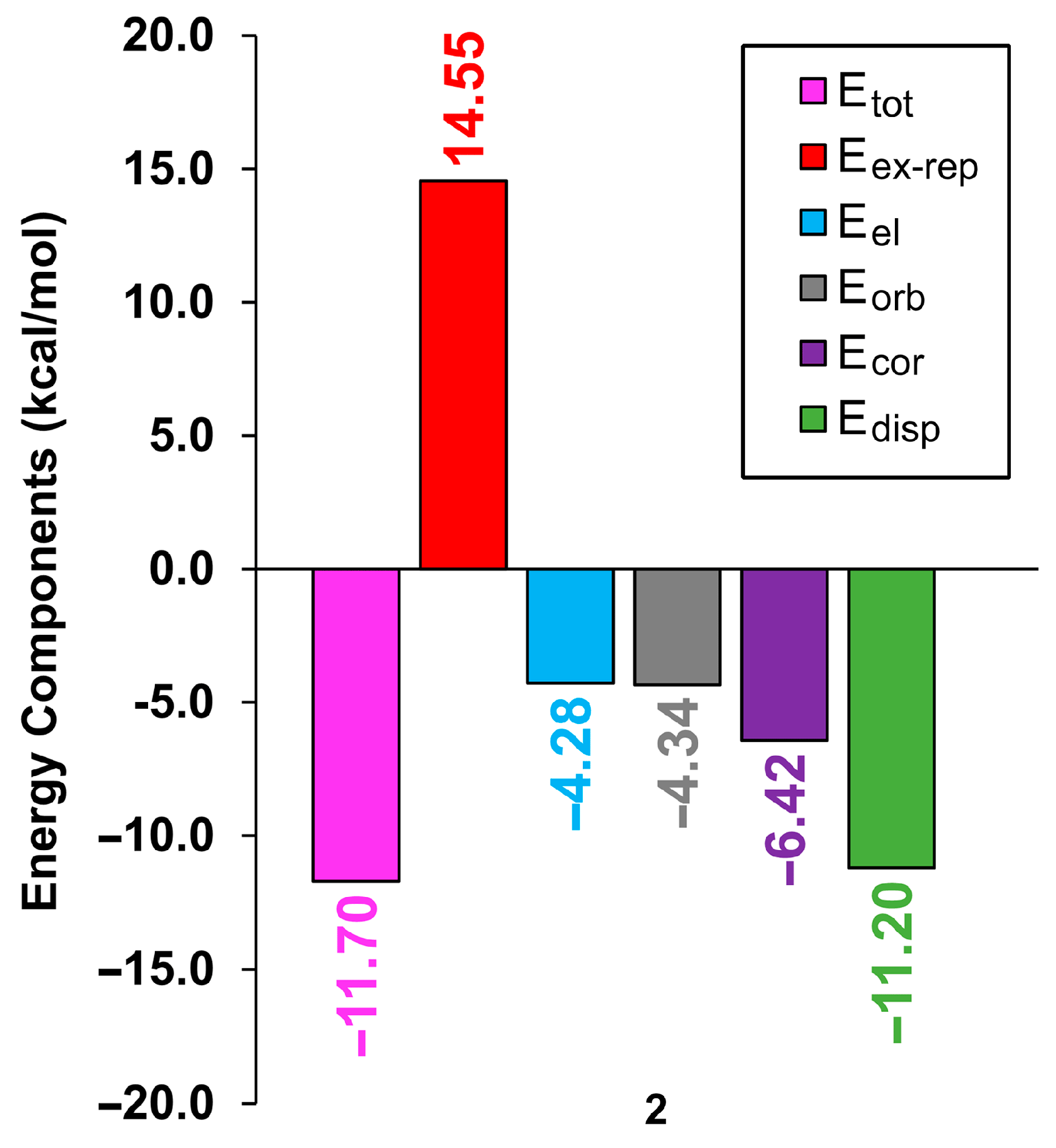
Inorganics 11 00468 g014
Figure 14. Total (Etot), exchange repulsion (Eex-rep), electrostatic (Eel), orbital (Eorb), correlation (Ecor), and dispersion (Edisp) for the dimer in the crystal of 2. Energies are given in kcal/mol.
Figure 14. Total (Etot), exchange repulsion (Eex-rep), electrostatic (Eel), orbital (Eorb), correlation (Ecor), and dispersion (Edisp) for the dimer in the crystal of 2. Energies are given in kcal/mol.
Inorganics 11 00468 g014
Table 1. Summary of structural motifs adopted in X-ray crystal structures of Hg(S2CNR2)2, Hg(S2CNRR’)2, and their solvates.
Table 1. Summary of structural motifs adopted in X-ray crystal structures of Hg(S2CNR2)2, Hg(S2CNRR’)2, and their solvates.
First SubstituentSecond SubstituentRecodeRef.
Binuclear motif:
R = EtR = EtHGETCB13[41]
R = nPrR = nPrHUKCAU[67]
R = iPrR = iPrZAVYED[68]
R = nBuR = nBuCAZRAW[42]
R = CH2(2-furyl)R = CH2(2-furyl)ROVTED[69]
R = MeR’ = PhHAKKIP[70]
R = MeR’ = CH2CH2PhYABJIV[71]
R = Me a
R = Et		R’ = Ph
R’= Ph		OROHEJ[72]
R = Me a
R = nBu		R’ = Ph
R’ = Ph		HAGLOS[73]
R = EtR’ = CyCAZQUP[42]
R = iPrR’ = CH2CH2OHOWOHUF[35]
R = EtR’ = PhYEDQEE[74]
R = nBuR’= CH2(2-pyrrolyl)ITEGUL[75]
R = nBuR’ = R1 bXOHBAZ[76]
R = CH2CH2OHR’ = CH2(Fc) cEJAYOF[77]
R = CH2PhR’ = CH2(2-furyl)ROVVAB[69]
R = CH2CH2PhR’ = CH2(2-furyl)TUMDOW[78]
R = CH2(2-furyl)R’ = CH2CH2(2-thienyl)TULJIV[78]
R = CH2(3-pyridyl)R’ = CH2(Fc) cUTEKEL[79]
NRR’ = N(CH2)4 DUWSIY[80]
NRR’ = N(CH2)5 POGSUC[81]
NRR’ = N(CH2)6 VOHKUZ[82]
NRR’ = 4-methylpiperidine KAFFIG[83]
NRR’ = 4-benzylpiperidine QAJNAU[84]
NRR’ = 1,2,3,4-dihydroquinoline SODNEG[85]
Quasi-dimeric motif:
R = Et a
R =nBu		R = Ph
R = Ph		YEQFEI[86]
R = nPrR = nPrHUKCAU[67]
R = iBuR = iBuCAZQID[42]
R = CH2PhR = CH2PhATADEE[87]
R = iPrR’ = CyCAZQOJ[42]
R = nBuR’= CH2(2-pyrrolyl)ITEGOF[75]
R = CH2PhR’ = CH2(N-methyl-pyrrol-2-yl)YOMYUW[88]
R = CH2PhR’ = CH2(Fc) cMUYXOU[89]
NRR’ = 4-(3-phenylprop-2-en-1-yl)piperazine LIFFEN[90]
Tetrahedral motif:
R = iPrR = iPrIPTCHG[91,92]
R = CyR = CyROPQIW[43]
R = EtR’= CH2C6H2(OMe)3-3,4,5NIMWEO[93]
R = CH2(3-pyridyl)R’ = CH2(N-methyl-pyrrol-2-yl)XOBCEY[94]
R = CH2(4-pyridyl)R’ = CH2(N-methyl-pyrrol-2-yl)YOMYOQ[88]
NRR’ = N(CH2)4 MUWDOX[95]
Square-planar motif:
R = C6H3(iPr)2-2,6R’ = C(H)=NC6H3(iPr)2-2,6VUWLUX[96]
One dimensional: zigzag:
R = CH2CH2PhR’ = CH2(3-pyridyl)FODROH[97]
One dimensional: linear:
R = EtR = EtHGETCB01[98]
R = CH2CH2OHR = CH2CH2OHFOPWAJ[99]
R = CH2PhR’ = CH2(3-pyridyl)FODSAU[97]
R = CH2PhR’ = CH2(4-pyridyl)EBUTAY[100]
NRR’ = N(CH2)4 POLNEM[101]
One-dimensional: twisted:
R = MeR = MeROQNEQ[102]
R = CH2(3-pyridyl)R’ = CH2(3-pyridyl)YOMYIK[88]
R = C6H3Me2-2,5R’ = C(H)=N(C6H3Me2-2,5)VUWLOR[96]
NRR’ = 1,2,3,4-dihydroquinoline SODNIK[85]
Two-dimensional:
R = HR = HBAWWOL[103]
Multicomponent crystals:
R = Et dR = EtQIYTOI[104]
R = Et eR’ = PhAXIQEF[105]
R = C6H3Me3-2,4,6 fR’ = C(H)=NC6H3Cl2-2,5VUWMAE[96]
NRR’ = N(CH2CH2)NPh2 g QAJMUN[84]
NRR’ = 1,2,3,4-dihydroquinoline h SODNEG[85]
NRR’ = 1,2,3,4-dihydroquinoline i SODNIK[85]
NRR’ = 1,2,3,4-dihydroquinoline j SODNAC[85]
a—The three entries highlighted in blue are mixed ligand species. b—The R’ group is: c—Fc is ferrocenyl, (C5H4)Fe(C5H5). d—1:1 cocrystal with C60. e—1:0.75 solvate with toluene. f—1:0.5 solvate with CH2Cl2. g—1:1 solvate with DMSO. h—1:1 solvate with pyridine. i—1:0.25 solvate with ethanol. j—1:1 cocrystal with 2,2’-bipyridine.
Table 2. Selected geometric parameters (Å, °) about the Hg centers in the crystals of Hg(S2CNR2)2: R = ethyl (1), R = isobutyl (2), and R = cyclohexyl (3).
Table 2. Selected geometric parameters (Å, °) about the Hg centers in the crystals of Hg(S2CNR2)2: R = ethyl (1), R = isobutyl (2), and R = cyclohexyl (3).
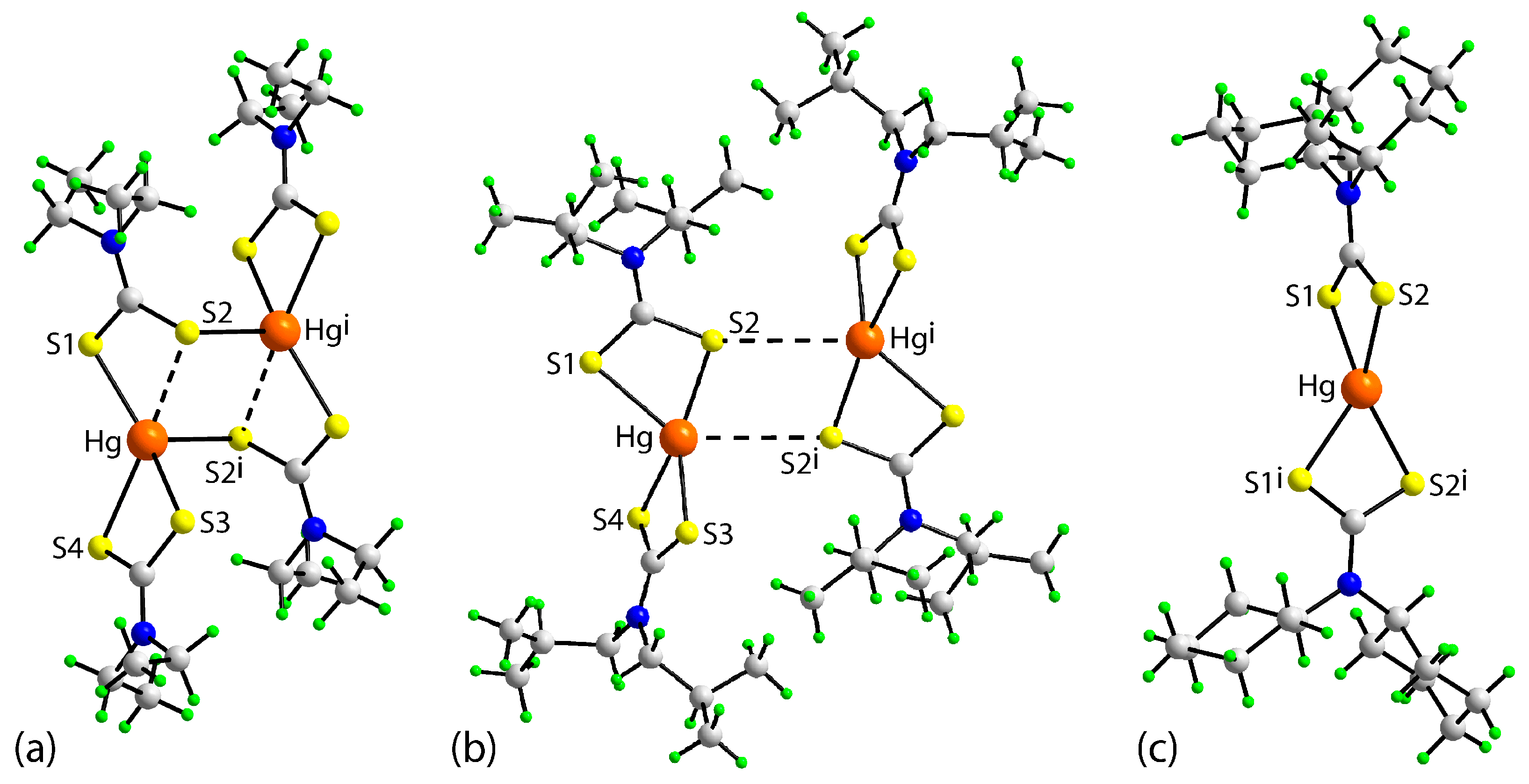
Parameter123 a
Hg–S12.4216(11)2.710(3)2.527(3)
Hg–S23.1266(9)2.438(2)2.536(4)
Hg–S32.5183(10)2.417(3)2.527(3)
Hg–S42.6408(10)2.714(3)2.536(4)
S2–Hg i2.6725(10)3.727(4)-
S1–Hg–S263.87(3)70.43(9)71.69(10)
S1–Hg–S3144.88(3)126.57(9)129.87(16)
S1–Hg–S4122.28(3)105.96(9)126.07(9)
S2–Hg–S392.98(3)153.92(8)126.07(9)
S2–Hg–S4157.70(3)127.92(9)142.18(18)
S3–Hg–S470.40(3)70.58(9)71.69(10)
S1–Hg–S2 i107.96(3)131.64(7)-
S2–Hg–S2 i100.81(3)76.04(6)-
S3–Hg–S2 i101.89(3)78.20(6)-
S4–Hg–S2 i97.22(3)122.14(7)-
Hg–S2 i–Hg i79.19(3)103.96(6)-
Symmetry
operation i−x, −y, 1 − z½ − x, ½ − y, −z-
a—The Hg atom in 3 is located on a two-fold axis of symmetry, so S3 = S1 ii and S4 = S2 ii (symmetry operation ii: x − y, −y, 2/3 − z).
Table 3. Calculated volumes (Å3) for the molecules in the crystals of Hg(S2CNR2)2: (a) R = ethyl (1), (b) R = isobutyl (2), and (c) R = cyclohexyl (3).
Table 3. Calculated volumes (Å3) for the molecules in the crystals of Hg(S2CNR2)2: (a) R = ethyl (1), (b) R = isobutyl (2), and (c) R = cyclohexyl (3).
Parameter123 a
van der Waals volume a588.2/294.1431.3814.8
Probe-excluded void volume a59.4/29.728.517.9
Molecular volume a647.6/323.8459.7832.6
a—The second values for 1 are for the monomer.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Gomila, R.M.; Tiekink, E.R.T.; Frontera, A. A Computational Chemistry Investigation of the Influence of Steric Bulk of Dithiocarbamato-Bound Organic Substituents upon Spodium Bonding in Three Homoleptic Mercury(II) Bis(N,N-dialkyldithiocarbamato) Compounds for Alkyl = Ethyl, Isobutyl, and Cyclohexyl. Inorganics 2023, 11, 468. https://doi.org/10.3390/inorganics11120468

AMA Style

Gomila RM, Tiekink ERT, Frontera A. A Computational Chemistry Investigation of the Influence of Steric Bulk of Dithiocarbamato-Bound Organic Substituents upon Spodium Bonding in Three Homoleptic Mercury(II) Bis(N,N-dialkyldithiocarbamato) Compounds for Alkyl = Ethyl, Isobutyl, and Cyclohexyl. Inorganics. 2023; 11(12):468. https://doi.org/10.3390/inorganics11120468

Chicago/Turabian Style

Gomila, Rosa M., Edward R. T. Tiekink, and Antonio Frontera. 2023. "A Computational Chemistry Investigation of the Influence of Steric Bulk of Dithiocarbamato-Bound Organic Substituents upon Spodium Bonding in Three Homoleptic Mercury(II) Bis(N,N-dialkyldithiocarbamato) Compounds for Alkyl = Ethyl, Isobutyl, and Cyclohexyl" Inorganics 11, no. 12: 468. https://doi.org/10.3390/inorganics11120468

APA Style

Gomila, R. M., Tiekink, E. R. T., & Frontera, A. (2023). A Computational Chemistry Investigation of the Influence of Steric Bulk of Dithiocarbamato-Bound Organic Substituents upon Spodium Bonding in Three Homoleptic Mercury(II) Bis(N,N-dialkyldithiocarbamato) Compounds for Alkyl = Ethyl, Isobutyl, and Cyclohexyl. Inorganics, 11(12), 468. https://doi.org/10.3390/inorganics11120468

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop