Exploring Proton Pair Motion Away from the Global Proton–Tuple Energy Minimum in Yttrium-Doped Barium Zirconate

Abstract

Yttrium-doped barium zirconate is one of the fastest solid-state proton conductors. While previous studies suggest that proton–tuples move as pairs in yttrium-doped barium zirconate, a systematic catalog of possible close proton–tuple moves is missing. Such a catalog is essential to simulating dual proton conduction effects. Density functional theory with the Perdew–Burke–Ernzerhof functional is utilized to obtain the total electronic energy for each proton–tuple. The conjugate gradient and nudged elastic band methods are used to find the minima and transition states for proton–tuple motion. In the lowest-energy configuration, protons are in close proximity to each other and the dopant, significantly affecting the backbone structure. The map of moves away from the global minimum proton–tuple shows that the most critical move for long-range proton conduction is a rotation with a barrier range of 0.31–0.41 eV when the two protons are in close proximity.

1. Introduction

Yttrium-doped barium zirconate shows great promise as one of the fastest solid-state proton conductors [1,2]. High proton conduction benefits both from high proton concentration and low long-range conduction limiting barriers. Increasing the dopant concentration in barium zirconate increases the maximum proton load, while at the same time introducing proton trap regions near the lower valency dopant which can increase the limiting barrier [3,4,5,6,7]. The conduction mechanism has long been understood to occur by a series of transfers and rotations away from one dopant trap to another [8,9,10,11,12,13,14,15,16,17,18,19]. While the earliest studies focused on proton conduction in idealized barium zirconate systems, the most recent studies considered the effect of multiple defects including additional protons, dopant ions, and oxygen vacancies with varying distributions as well as a greater diversity of sites [9,11,20,21,22,23]. For example, Hu et al. [8] find that the limiting barrier for a path of a rotation and transfer immediately adjacent to the dopant is a transfer at low dopant concentrations and a rotation at higher dopant concentrations. Draper et al. [9,11] find that with increasing the dopant concentration and considering a wide variety of dopant relative locations, nanoscale percolation paths along the dopant allow rapid proton conduction increasing conductivity. Vera et al. [1] and Hossain et al. [2] provide excellent reviews of both experiments and calculations of proton conduction in barium zirconate.

This contribution focuses on how two protonic defects influence each other. One might expect that repulsion would lead two protonic defects to be very far from each other. However, several studies challenge this notion. The proton–proton radial distribution function found in our earlier work [23] suggests that the most probable proton–proton distance is $4.0$ Å with some protons as close as $2.0$ Å from each other and the global energy tuple minimum shows two protons in the same face of a perovskite unit cell within a larger system. More recently, Figure 2c in Draper et al. [11] shows a global ab initio minimum for a structure with proton-proton distance slightly above $2.0$ Å. Quasi-elastic neutron scattering studies interpreted with a Holstein-type polaron model find that the proton–polaron effective mass is twice the proton mass, suggesting that protons travel in pairs [20,24]. Kinetic Monte Carlo (kMC) simulations [23] show an increase in long-range proton conduction barriers with increasing the number of protons while maintaining close proton–proton distances. Ab initio calculations [20] show that one proton facilitates distortions, which benefits the other nearby proton. Assistance of the lattice in maintaining high proton concentration by favoring nearby protons at the cost of slightly increased long-range barriers may be key to high conductivity. Lattice dynamics has been shown to be important to proton transport in both simulation and experiment [22,25,26]. However, most studies have focused on single proton transfer and rotation calculations. A systematic catalog of possible close proton–tuple moves is missing. Such a catalog would be helpful to understand the full mechanism of long-range proton conduction in yttrium-doped barium zirconate.

While a full catalog of ab initio energy barriers for all possible proton–tuple moves in a large system is computationally prohibitive, a systematic catalog of moves away from the global proton–tuple energy minimum is within the scope of current calculations. This contribution builds on our earlier work, which found the global energy tuple minimum in $12.5\%$ yttrium-doped barium zirconate in $2\times 2\times 2$ [23] and $2\times 2\times 4$ [20] unit cell systems and considers all motions away from that lowest energy proton–tuple. A larger system of $4\times 4\times 4$ unit cells is considered to avoid spurious long-range octahedral tilting transformations when two defects are in close proximity. The climbing nudged elastic band method (cNEB) [27] is used to calculate barriers away from the global energy tuple minimum with the Vienna ab-initio simulation package (VASP) [28,29,30,31,32]. The resulting proton pair motion is analyzed in the context of the typical limiting barrier moves for long-range proton conduction.

2. Results

2.1. Lowest Energy Proton–Tuple and Single Proton Moves Away from It

Figure 1 shows the lowest energy proton-tuple superimposed on the minima in which one proton has moved one step away from the global minimum structure. Zirconium and yttrium ions are in green and teal, respectively. Oxygen ion types and proton site types are labeled using the same notation as in our earlier work [10,21]. Proton site types are labeled based on bonded oxygen ion type. Type I oxygen ions are the first nearest neighbors to the closest yttrium dopant ions. Type II oxygen ions are the second nearest neighbors to the closest yttrium ions. While earlier work [10,21] also highlights the third nearest neighbor oxygen ions, this work focuses on small moves away from the global proton–tuple minimum, not including moves to the third nearest neighbor oxygen ions. The lowest energy proton–tuple has the protons in the two circled sites, namely $H_I^{Far}$ and $H_{II}^{Far}$ sites. The subscripts refer to the type of oxygen ion the site is on, specifically whether the oxygen ion is a first nearest neighbor (I) or second nearest neighbor (II) to the closest yttrium ion. The superscript $Close$ or $Far$ refers to whether the proton-bonded oxygen ion and the opposite oxygen ion on the same face plane as the OH are the closer or the farther two opposite oxygen ions on that unit face.

From the lowest-energy tuple structure $(H_I^{Far},H_{II}^{Far})$, each proton can rotate to two possible locations and transfer to two possible locations. As seen in Figure 1, the proton in the $H_I^{Far}$ site can rotate forward to another $H_I^{Far}$ site through a $0.11$ eV barrier or backward to a $H_I^{Close}$ site through a $0.26$ eV barrier. This proton can also transfer to the right to a $H_I^{Close}$ site through a $0.24$ eV barrier or to the left to a $H_{II}^{Close}$ site through a $0.11$ eV barrier. The second proton in the global minimum tuple can also rotate and transfer. The proton in the $H_{II}^{Far}$ site can rotate forward to a $H_{IIND}^{Close}$ site through a $0.31$ eV barrier or backward to a $H_{IIND}^{Far}$ site through a $0.31$ eV barrier. The addition of $ND$ to the subscript is made to indicate that these two sites are on a plane without the dopant ions. The $H_{II}^{Far}$ proton can also transfer to the right to a $H_I^{Close}$ site through a $0.12$ eV barrier or to the left to a $H_{II}^{Close}$ site through a $0.21$ eV barrier. The highest barriers in this group are the bottom two rotational barriers, which are critical to moving from near one yttrium dopant trap to another yttrium dopant trap.

Table 1. The energies of the minima superimposed in Figure 1 relative to the global minimum $(H_I^{Far},H_{II}^{Far})$ are shown along with the single proton motion needed to get to the minimum from the global minimum $(H_I^{Far},H_{II}^{Far})$. The top set are minima resulting from a move from the $H_I^{Far}$ site, while the lower set results from a proton move from the $H_{II}^{Far}$ site. Within each region, the sites are organized by energy. Proton sites perpendicular to the plane in Figure 1 have the ⊥ symbol added to clarify their location.

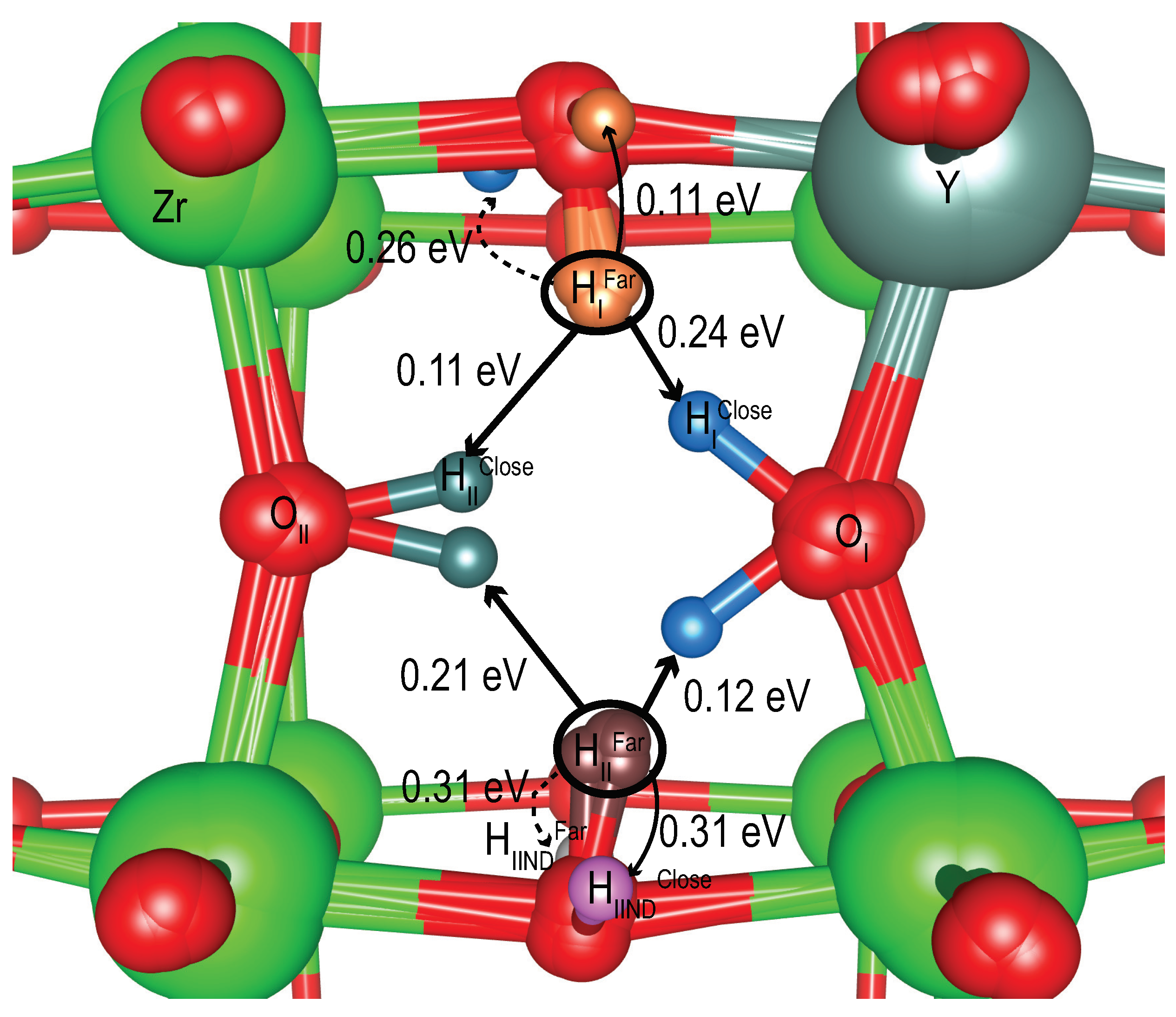
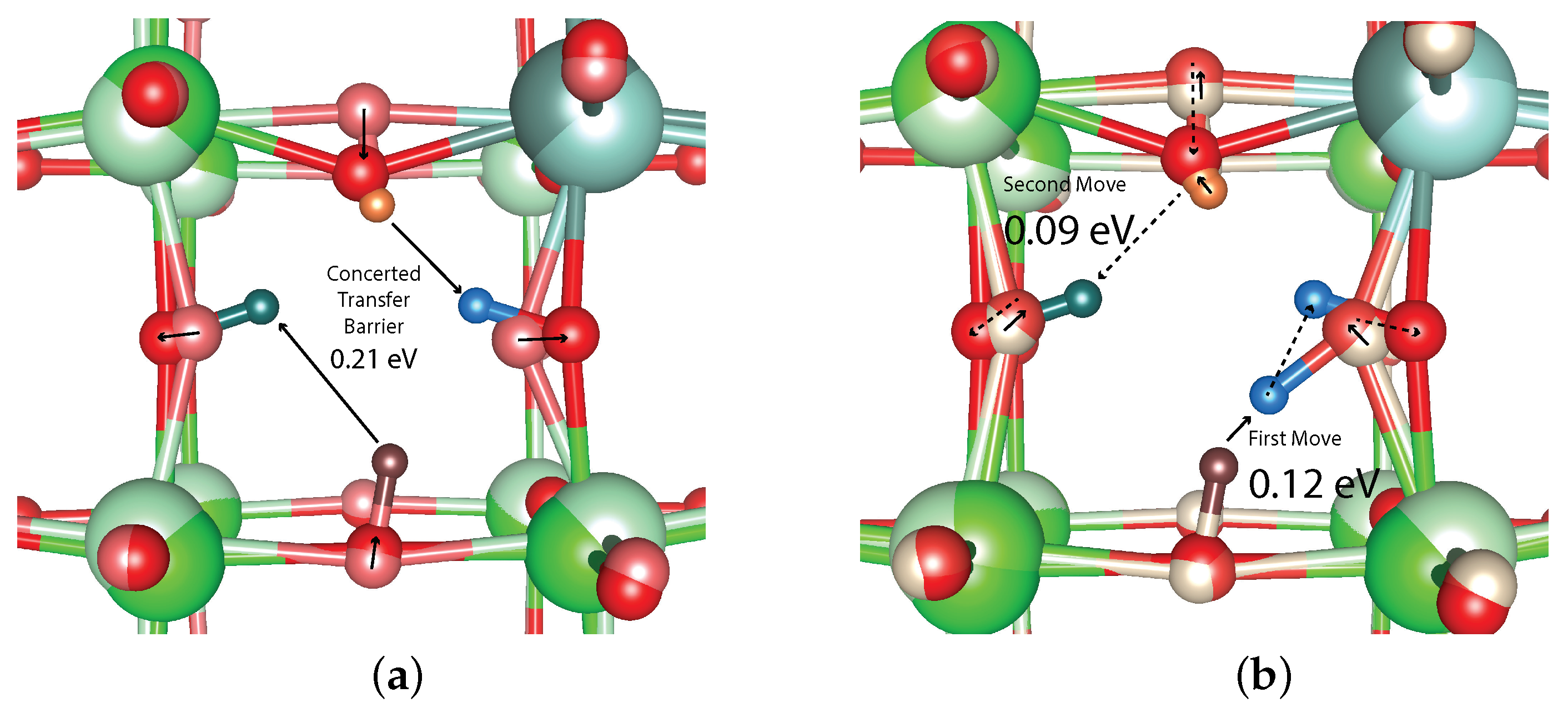
Tuple	Relative Energy (eV)	Move From Global Minimum	Move Barrier (eV)
$(H_{II}^{Close},H_{II}^{Far})$	0.11	T$(H_I^{Far}\to H_{II}^{Close})$	0.11
$(H_I^{Far}\perp ,H_{II}^{Far})$	0.11	R$(H_I^{Far}\to H_I^{Far}\perp )$	0.11
$(H_I^{Close}\perp ,H_{II}^{Far})$	0.16	R$(H_I^{Far}\to H_I^{Close}\perp )$	0.26
$(H_I^{Close},H_{II}^{Far})$	0.23	T$(H_I^{Far}\to H_I^{Close})$	0.24
$(H_I^{Far},H_I^{Close})$	0.11	T$(H_{II}^{Far}\to H_I^{Close})$	0.12
$(H_I^{Far},H_{II}^{Close})$	0.20	T$(H_{II}^{Far}\to H_{II}^{Close})$	0.21
$(H_I^{Far},H_{IIND}^{Close}\perp )$	0.31	R$(H_{II}^{Far}\to H_{IIND}^{Close}\perp )$	0.31
$(H_I^{Far},H_{IIND}^{Far}\perp )$	0.30	R$(H_{II}^{Far}\to H_{IIND}^{Far}\perp )$	0.31

summarizes these moves and gives the energy of the final tuple minimum relative to the global minimum starting point. The minimum energies reveal forward barriers of nearly the same energy as the final site showing that the backward move barriers are much lower. In cases where the final tuple minimum has a populated site that is perpendicular to the plane shown in Figure 1, the symbol ⊥ is added to more clearly specify the site and motion. The table groups minima including $H_{II}^{Far}$ at the top and those including $H_I^{Far}$ at the bottom. Within the groups, the minima are organized by relative energy to the global minimum $(H_I^{Far},H_{II}^{Far})$.

2.2. Two Proton Moves Away from Global Minimum

All moves of two protons away from the global minimum tuple were considered. However, all but one nudge elastic band calculation showed sequential moves. The one exception was the concerted proton transfer shown in Figure 2a. Arrows highlight the proton moves as well as the moves of other ions. The concerted proton transfer has a barrier of $0.21$ eV. Figure 2b shows related sequential moves with the same initial and final points. Solid arrows highlight the first steps while dashed arrows highlight the second step. In both Figure 2a,b, earlier ion positions are lightened. The sequential transfer moves have barriers of $0.12$ eV for the first proton transfer from $H_{II}^{Far}$ (brown) to $H_I^{Close}$ (blue) and $0.09$ eV for second proton transfer from $H_I^{Far}$ (orange) to $H_{II}^{Close}$ (teal). The order of sequential moves was determined by what was seen in a concerted attempted move calculation. Solid arrows highlight all the ion moves included in the first proton transfer, while dashed arrows highlight the corresponding moves for the second transfer. In both cases, significant oxygen ion rearrangement partially accompanies the proton move to stabilize the final proton tuple.

While all possible moves were considered, our report focuses on the most important moves namely those barriers that limit long-range transport. Figure 1 suggests that the critical barrier for moving from close association with one yttrium ion trap to another is the rotational barriers at the bottom of the figure. Figure 3 shows the sequential moves that are most critical to escape a dopant trap. The moves involve a transfer of the $H_I^{Far}$ proton (orange) followed by a rotation of the $H_{II}^{Far}$ proton (brown). Solid and dashed arrows highlight the motion for the first and second moves, respectively. Two second move rotations are possible after the transfer. These are emphasized by short- and long-dashed arrows. The barrier for each move is written by the arrow showing the dominant motion. Comparing Figure 1 and Figure 3 shows that the transfer move of the $H_I^{Far}$ proton raises the $H_{II}^{Far}$ proton rotational barrier.

Table 2. Barriers are affected by nearby protons. This table summarizes the barrier for the motions in Figure 1 with different protons present. In addition, single proton movement barriers in the same size system [10,21] and a smaller system [15] are shown for comparison.

Move	Barrier (eV)	Nearby Proton	One Proton Barrier
T$(H_I^{Far}\to H_{II}^{Close})$	0.11	H${}_{II}^{Far}$	0.14  [10], 0.32 [15]
	0.09	H${}_I^{Close}$
R$(H_I^{Far}\to H_I^{Far}\perp )$	0.11	H${}_{II}^{Far}$	0.02 [10], 0.12 [15]
	0.25	H${}_{II}^{Close}$
T$(H_I^{Far}\to H_I^{Close})$	0.24	H${}_{II}^{Far}$	0.24  [10], 0.25 [15]
R$(H_I^{Far}\to H_I^{Close}\perp )$	0.26	H${}_{II}^{Far}$	0.10 [10], 0.22 [15]
T$(H_{II}^{Far}\to H_I^{Close})$	0.12	H${}_I^{Far}$	0.11  [10], 0.17  [15]
	0.18	H${}_I^{Far}\perp$
	0.23	H${}_I^{Close}\perp$
T$(H_{II}^{Far}\to H_{II}^{Close})$	0.21	H${}_I^{Far}$	0.15  [10], 0.43 [15]
	0.26	H${}_I^{Close}\perp$
R$(H_{II}^{Far}\to H_{IIND}^{Far}\perp )$	0.31	H${}_I^{Far}$	0.24  [10,21], 0.24  [15]
	0.34	H${}_I^{Close}$
	0.34	H${}_I^{Far}\perp$
	0.35	H${}_{II}^{Close}$
	0.44	H${}_I^{Close}\perp$
R$(H_{II}^{Far}\to H_{IIND}^{Close}\perp )$	0.31	H${}_I^{Far}$	0.25  [10,21] 0.27  [15]
	0.33	H${}_{II}^{Close}$
	0.37	H${}_I^{Close}$
	0.41	H${}_I^{Close}\perp$

shows how barriers for the rotations and transfers in Figure 1 are affected by having the second proton in the tuple in different locations. Most useful are the last two sections, which show a range of barriers for the critical rotation to move a proton from being near one yttrium trap to another. The long-range proton motion limiting barrier is thus expected to be in the range of 0.31–0.41 eV. Single proton barriers for the same size system [10,21] and a smaller system [15] further highlight the effect of having a second proton in close proximity to the moving proton.

3. Methods

Our earlier work on smaller systems [20,23] showed that the global energy minimum for two protons in $12.5\%$ yttrium-doped barium zirconate places the two protons within the same unit cell due to octahedral tilting bringing oxygen ions close to both protons. However, long-range octahedral tilting changes due to the presence of multiple nearby defects is assisted by periodic boundary conditions in small systems. In contrast, earlier work [21] with an optimized larger structure of $4\times 4\times 4$ unit cells showed that a proton and an oxygen vacancy defect in the same unit cell did not disturb the long-range octahedral tilting arrangement. This study uses this same initial structure and finds the same tuple global minimum as our earlier studies in smaller systems [20,23]. All tuples with protons between $1.6$ and $2.7$ Å were considered, as this is the range of the second peak in the site–site radial distribution function. The closer proton sites characterizing the first peak are on the same oxygen and hence cannot be simultaneously populated. Some tuples with protons further than $2.7$ Å were also optimized to confirm higher energy minima. From the global energy tuple minimum, moves to all other tuple arrangements within two moves are considered. The conjugate gradient method is used to find minima [33], while the nudged elastic band (NEB) method [27] is used to find transition states. All NEB calculations start with two images unless the path requires more. After NEB, the climbing NEB (cNEB) method [27] is used to converge the highest energy image to the saddle point. Optimization for minima and transition states is stopped when forces are less than $0.02$ eV/Å.

The energy for all the above ionic relaxations is calculated using density functional theory (DFT) with the Perdew–Burke–Ernzerhof (PBE) functional in the Vienna ab initio simulation package (VASP) [28,29,30,31,32] with the same projector augmented wave (PAW) method as in our earlier work [21]. The valence states of Ba(5s,5p,6s,6d), Zr(4s,4p,5s,5d), Y(4s,4p,5s,4d), and O(2s,2p) are considered explicitly while inner core electrons are treated using PAW potentials. Projection operators are optimized automatically in real space. The preconditioned residual minimization method with direct inversion in the iterative subspace is used. The partial occupancy of orbitals is initialized with Gaussian smearing. An accurate level calculation is performed. The first ten steps are non-self consistent. Plane waves are generated using a single gamma point and a 600 eV cut off.

4. Discussion

The global minimum for two protons in BaZr${}_{0.875}$Y${}_{0.125}$O${}_3$ has the pair in close proximity within a single unit cell even in a $4\times 4\times 4$ unit cell system. The result agrees with prior computational work [20,23] on smaller systems as well as neutron scattering work [20]. NMR and ab initio data on scandium-doped barium zirconate also show two protons in close proximity to each other [34] and the dopant [6]. NMR experiments and ab initio calculations with the yttrium dopant [35] reveal that the lowest two energy sites are the two sites populated in the global minimum tuple in this study namely the $H_I^{Far}$ and $H_{II}^{Far}$ sites. As seen in Figure 1, these sites are in close proximity to the dopant suggesting that the dopant stabilizes the proton tuple.

The $4\times 4\times 4$ unit cell system in this study allows a more systematic look at moves away from the global minimum without changing long-range octahedral tilting. Figure 1 and Table 1 show that the limiting barrier to long-range proton motion away from the global minimum is $0.31$ eV. Considering two sequential proton moves as suggested by earlier work [20] shows an increase in this barrier as seen in Figure 3. Table 2 further suggests that the critical barrier to long-range motion is in the $0.31-0.41$ eV range depending on the location of the second proton. KMC simulations on smaller systems with a 1:1 proton:dopant ratio [13,23] rather than the 2:8 ratio in this work have shown long-range limiting barriers increasing from $0.39$ to $0.45$ eV with an increasing number of protons. The earlier simulations including multiple protons [23] used the ab initio binding site and transition state energies for single protons and included the effect of additional protons only through additional Coulombic interactions. The limiting barrier ranges of this work and our earlier work [23] are both in line with the experimental long-range barrier for $10\%$ yttrium-doped barium zirconate of $0.44$ eV [36,37]. However, the current work presents energies that allow backbone relaxation due to both protons in the tuple pair, which, as shown in Figure 2, can be significant.

While there is agreement in the overall limiting barrier, the different approaches have different individual barriers as seen by comparing the barrier and one proton barrier columns in Table 2. Within the one proton barrier column are barriers for larger 1:8 proton:dopant ratio and for smaller 1:1 proton:dopant ratio systems, respectively. The one proton smaller system tends to have larger barriers than the one proton larger system. This could be the effect of repulsions between a proton and its periodic image in the smaller simulation cell, but it may also be the effect of different methods. The larger systems simulations use a single gamma point, while the smaller system calculations use k-point meshes. The lattice size found in the larger simulations [10,21] was $4.29$ Å, whereas the smaller simulations used a lattice size of $4.26$ Å. The differences in the individual barriers led to a higher percentage of intraoctahedral transfer barriers in the small system kMC simulations [13,23] and a higher percentage of rotational limiting barriers in large system kMC simulations [10]. Hu et al. support a change in limiting barrier from intraoctahedral transfer to rotation with increasing the dopant concentration with rotation as the limiting barrier by $14.5\%$ yttrium doping. The key result of the current work, however, is that the presence of a nearby proton raises the conduction limiting barrier of another despite the lattice motion of oxygen ions stabilizing close proton pair structures and the global tuple minimum having close proton–proton proximity.

While most of the tuple motion explored in this paper was sequential rather than concerted, sequential proton motion can be correlated, in that a move of one proton can promote the move of a nearby proton by preparing the lattice or by proton–proton repulsion. Quasi-elastic neutron studies extracted a proton–polaron effective mass of twice the proton mass suggesting the conductive species is a proton pair whose motion is correlated with lattice motion [20,24]. While this study does not calculate normal modes, prior computational studies considering single proton transfer show that there is significant lattice motion [22,38] at proton conduction temperatures in these systems. Through a simplified model, Geneste [39] also suggests that single proton transfer is facilitated by lattice reorganization and, in particular, octahedral tilting. Based on the proton tuple paths to escape the dopant found in this paper, long-range proton transport is expected to include both proton–proton correlation and proton–lattice correlation. The first proton can prepare the lattice for the next, and, at the same time, the latter proton can push the first one.