Coupled Transport of Metal Ions in Aqueous Solutions Containing NaCl and HCl

Abstract

The main objective of this work was to analyze the transport by diffusion of salts containing some metal ions (that is, CoCl₂, CrCl₃, HgCl₂, and PbCl₂), at 25.0 °C, in two different aqueous solutions with varying pH levels, namely, sodium chloride and hydrochloric chloride, by using Nernst–Hartley model equations. To analyze the applicability of this model, experimental data for two aqueous systems (CoCl₂ + NaCl) and (CoCl₂ + HCl), were obtained by using the Taylor technique and compared with the predicted values. The Nernst–Hartley model equations were used in this study to estimate the mutual diffusion coefficients of the eight ternary systems, which included (CoCl₂ + NaCl), (HgCl₂ + NaCl), (PbCl₂ + NaCl), (CrCl₃ + NaCl), and (CoCl₂ + HCl), (HgCl₂ + HCl), (PbCl₂ + HCl), and (CrCl₃ + HCl). By using the limiting equations of Nernst–Hartley coefficients, we were able to understand the composition dependence of the mutual diffusion coefficients of these mixed electrolyte solutions and the electrostatic mechanism for the strongly coupled diffusion of these components.

1. Introduction

1.1. Diffusion of Heavy Metal Ions in Solutions and Its Impact

The study of the diffusion processes of heavy metal ions in solution is important both for practical application in different fields, such as corrosion related to dental restoration [1,2], and for fundamental reasons, helping us to understand the nature of these aqueous electrolyte structures.

It is known that these metals exist naturally in the Earth’s crust, and some of them, at physiological concentrations, are necessary for living things to carry out a variety of biological functions, but larger amounts of these elements can be unhealthy [3]. For example, one of the biggest issues related to heavy metals is their bioaccumulation, since they are neither metabolized nor decomposed. Exposure to these elements can occur through water and food consumption, air intake, or occupational exposure, causing grave problems in health [4]. Among these metals, we highlight in this work four heavy metal ions, that is, cobalt, mercury, lead, and chromium.

To reduce the negative impacts of heavy metals, and to face growing public pressure to reduce relevant health and environmental risks, fundamental chemical studies are required [5], including the study of transport properties. Coupled diffusion techniques involve measurements that are difficult to perform, so the application of mathematical models that are predictable and reproductive is of added value for the scientific community dedicated to this area, obtaining a greater amount of data in a simpler, faster way, eliminating a lot of laboratory time.

1.2. Concepts and Models

1.2.1. Binary Mutual Diffusion

Mutual diffusion is a quantitative measure of a mass transport process in aqueous solution. In the case of the one-dimensional diffusion of a binary system (two components, solute + solvent), these parameters can be described by Fick’s equation (Equation (1)) [6,7,8].

$$J_1=–D_{\mathrm{F}}{\displaystyle \frac{\partial C_1}{\partial X}}$$

(1)

where $D_{\mathrm{F}}, J_1,$ and ${\displaystyle \frac{ \partial C_1}{\partial X}}$ represent the binary Fick diffusion coefficient, the flow of solute 1 across a suitable chosen reference plane per area unit and per time unit, in a one-dimensional system, and the gradient in the concentration of the solute. C is the concentration of solute 1 in moles per volume unit at the point considered.

It is very important to understand the differences between two concepts: mutual diffusion (also known as inter-diffusion, collective diffusion, concentration diffusion, or salt diffusion) and self-diffusion (also called intra diffusion, tracer diffusion, single ion diffusion, or ionic diffusion). In mutual diffusion, due to the salt concentration gradient in a binary electrolyte solution, the constraint in maintaining electrical neutrality ensures that positive and negative ions move randomly from the higher- to lower-concentration region at the same speed. In self-diffusion, the electrical neutrality restraint does not apply, and three species (solvents and ions) have independent diffusion coefficients. Furthermore, the activity coefficient in the trace species does not change in a virtually uniform solution, and thus the thermodynamic factor, dlna_i/dlnx_i (a is the activity and x is the mole faction of component i), which appears in the equations describing mutual diffusion, becomes equal to one.

It is worth highlighting there is no simple relation between mutual and self-diffusion coefficients, except when the solute is at an infinitesimal concentration. For example, in aqueous binary solutions containing symmetrical uni-univalent electrolytes, we have the Nernst–Hartey equation (Equation (2)) [6,7,8].

$$D^0=2{\displaystyle \frac{D_{\mathrm{a}}^0{D}_{\mathrm{c}}^0}{D_{\mathrm{a}}^0+D_{\mathrm{c}}^0}}$$

(2)

where D⁰, $D_{\mathrm{a}}^0$, and $D_{\mathrm{c}}^0$ represent the limiting mutual diffusion coefficient of the salt and the limiting self-diffusion coefficients of the anion and the cation, respectively.

1.2.2. Ternary Mutual Diffusion

The Fick’s laws generalized by Onsager to describe multicomponent mutual diffusion can be represented by Equation (3) [7],

$$J_{\mathrm{i}}=-{\sum }_{\mathrm{k}=1}^{\mathrm{N}-1}{D}_{\mathrm{i}\mathrm{k}}{\nabla C}_{\mathrm{k}}$$

(3)

D_ik gives the flux J_i of component i caused by a gradient in the concentration of component k (${\nabla C}_{\mathrm{k}}$). Considering the ternary system formed by two solutes (components 1 and 2), and water (component 0), in this case, there are three different fluxes, J₀, J₁, and J₂.

However, in the laboratory (volume fixed) frame of reference, diffusion produces no volume flow across any plane, and hence

J₀ V₀ + J₁ V₁ + J₂ V₂ = 0

(4)

where V₀, V₁, and V₂ are the partial molar volumes of components 0, 1, and 2.

In the other words, due to the volume fixed constraint (Equation (4)), only two fluxes are independent.

The diffusion flux of solutes 1 and 2 in the direction of their concentration gradient can be determined by Fick’s equations, Equations (5) and (6) [7].

J₁ = −D₁₁∇C₁ − D₁₂∇C₂

(5)

J₂ = −D₂₁∇C₁ − D₂₂∇C₂

(6)

J₁ and J₂ represent the molar fluxes of solute 1 and solute 2 driven by the concentration gradients ∇C₁ and ∇C₂ in the solutions. The main coefficients D₁₁ and D₂₂ allow for the molar fluxes of solute 1 and solute 2, driven by their own concentration gradients. Cross-diffusion coefficients D₁₂ and D₂₁ allow for the coupled flux of each solute, driven by a concentration gradient in the other solute. It is worth noting that D₁₂ ≠ D₂₁, and that these parameters can only be determined experimentally, and cannot be derived from any simple theory [9,10,11,12,13,14,15,16,17,18,19,20,21].

A positive D_ab cross-coefficient (a ≠ b) shows the co-current coupled transport of solute a from regions of higher to lower concentrations of solute b. A negative D_ab coefficient shows the counter-current coupled transport of solute a from regions of lower to higher concentrations of solute b.

1.2.3. Limiting Nernst–Hartley Equations

For very diluted solutions, D_ab coefficients can be estimated by using the limiting Nernst–Hartley equations (in references [9,10,11,12,13,14,15,16,17,18,19,20], which show some examples of these estimations for some systems). Under these conditions, the solutions become ideal, and the thermodynamic factors are equal to one.

We conducted research on the diffusion behaviour (D_ab) of four chemical aqueous systems involving four heavy metal ions, Co²⁺, Hg²⁺, Pb²⁺, and Cr³⁺, in different media (NaCl and HCl). As the limiting Nernst–Hartley equation is similar when applied to these systems, and they have been well-described in the literature [10,11,12], we will only present these equations for the limiting ternary mutual diffusion coefficients of the aqueous systems CoCl₂ (component 1) + NaCl (component 2) and CoCl₂ (component 1) + HCl (component 2) as examples.

The mutual diffusion in dilute aqueous solutions containing cobalt chloride and sodium chloride causes fluxes of three different solute species (Na⁺, Co²⁺, and Cl⁻ ions). Bearing in mind the zero-electric current,

$${\sum }_s{z}_{\mathrm{s}}{j}_{\mathrm{s}}=0$$

(7)

we can consider two independent diffusion fluxes, that is, J₁ and J₂, as representing the indices 1 and 2 the components CoCl₂ and NaCl. On the other hand, each flux of the solute component, used in the Fick equations, can always be expressed as the sum of the fluxes of the i-containing solute species, js,

$$D_{11}^o=D_{\mathrm{C}\mathrm{o}}+t_{\mathrm{C}\mathrm{o}}\left(D_{\mathrm{C}\mathrm{l}}-D_{\mathrm{C}\mathrm{o}}\right)$$

(8)

$$D_{21}^o=2t_{\mathrm{N}\mathrm{a}}\left(D_{\mathrm{C}\mathrm{l}}-D_{\mathrm{C}\mathrm{o}}\right)$$

(9)

$$D_{12}^o=t_{\mathrm{C}\mathrm{o}}\left(D_{\mathrm{C}\mathrm{l}}-D_{\mathrm{N}\mathrm{a}}\right)/2$$

(10)

$$D_{22}^o=D_{\mathrm{N}\mathrm{a}}+t_{\mathrm{N}\mathrm{a}}\left(D_{\mathrm{C}\mathrm{l}}-D_{\mathrm{N}\mathrm{a}}\right)$$

(11)

$$t_{\mathrm{C}\mathrm{o}}={\displaystyle \frac{4c_1{D}_{\mathrm{C}\mathrm{o}}}{4c_1{D}_{\mathrm{C}\mathrm{o}}+c_2{D}_{\mathrm{N}\mathrm{a}}+(2c_1+c_2)D_{\mathrm{C}\mathrm{l}}}}$$

(12)

$$t_{\mathrm{N}\mathrm{a}}={\displaystyle \frac{c_2{D}_{Na}}{4c_1{D}_{\mathrm{C}\mathrm{o}}+c_2{D}_{\mathrm{N}\mathrm{a}}+(2c_1+c_2)D_{\mathrm{C}\mathrm{l}}}}$$

(13)

$D_{\mathrm{C}\mathrm{o}}$, D_Na, and $D_{\mathrm{C}\mathrm{l}}$ are the limiting diffusion coefficients of the Co²⁺, Na⁺, and Cl⁻ ions, respectively, and $t_{\mathrm{C}\mathrm{o}}$ and $t_{\mathrm{N}\mathrm{a}}$ represent the fraction of the total current carried by the Co²⁺ and Na⁺ ions, respectively. The ionic diffusion coefficients used in the Nernst–Hartley equations can be calculated from limiting ionic conductivities (see Table 1).

Table 1. The limiting ionic conductivities (λ_ion) [8] and diffusion coefficients (D_ion) ^a for different ions at 25.0 °C.

Ion	λion (10−4 S m2 equiv−1)	Dion/(10−9 m2 s−1)
H+	350.1	9.32
Na+	50.1	1.33
Co2+	53.3	0.71
Hg2+	63.6	0.85
Pb2+	70.0	0.93
Cr3+	67.0	0.59
Cl−	76.3	2.03

^a Estimated from D_ion = RTλ_ion/z_iF² [8].

Relative to the aqueous system CoCl₂ (C₁) + HCl (C₂) solutions, we have also three different solute species (Co²⁺, H⁺, and Cl⁻ ions) and two independent diffusion fluxes.

The Nernst–Hartley D_ik^o coefficients for this aqueous system are calculated from Equations (8) and (14)–(16).

$$D_{12}^o=t_{\mathrm{C}\mathrm{o}}(D_{\mathrm{C}\mathrm{l}}-D_{\mathrm{H}})/2$$

(14)

$$D_{21}^o=2t_{\mathrm{H}}(D_{\mathrm{C}\mathrm{l}}-D_{\mathrm{C}\mathrm{o}})$$

(15)

$$D_{22}^o=D_{\mathrm{H}}+t_{\mathrm{H}}(D_{\mathrm{C}\mathrm{l}}-D_{\mathrm{H}})$$

(16)

D_Cl, D_H, D_Co, t_Co, and t_H represent the limiting diffusion coefficients of the Cl⁻, H⁺, and Co²⁺ ions, and the fraction of the total current carried by the Co²⁺ and H⁺ ions (Equation (17)), respectively.

$$t_{\mathrm{H}}={\displaystyle \frac{c_2{D}_{\mathrm{H}}}{4c_1{D}_{\mathrm{C}\mathrm{o}}+c_2{D}_{\mathrm{H}}+(2c_1+c_2)D_{\mathrm{C}\mathrm{l}}}}$$

(17)

The values for these parameters are indicated in Table 1.

2. Results and Discussion

2.1. Predicted Data from Nernst–Hartley Equations and Comparison with New Experimental Data and Their Analysis for Two Aqueous Systems: (CoCl₂ Plus NaCl) and (CoCl₂ Plus HCl)

Table 2 and Table 3 summarize the predicted and experimental values of the D_ab diffusion coefficients for solutions of different compositions for two aqueous systems {(CoCl₂ plus NaCl) and (CoCl₂ plus HCl)}. Regarding the last values, they were obtained from at least six independent measurements, all carried out in the present work. The main diffusion coefficients D₁₁ and D₂₂ were generally reproducible within ±(0.020 × 10⁻⁹ m² s⁻¹, and the cross-coefficients were in general reproducible within about ±(0.040 × 10⁻⁹ m² s⁻¹).

Table 2. Experimental and predicted ternary diffusion coefficients, D₁₁, D₁₂, D₂₁, and D₂₂, by Nernst–Hartley equations [9,12] for aqueous CoCl₂ (C₁) + NaCl (C₂) + solutions at 25.0 °C.

C1  a	C2  a	X  b	D11 ± SD c	D12 ± SD c	D21 ± SD c	D22 ± SD c	D12/D22 d	D21 /D11  e
0.000	0.0001	0.000	0.710	0.000	1.047	1.610	0.000	1.474
			(0.711 ± 0.011) f	(0.030 ± 0.080) f	(1.030 ± 0.032) f	(1.598 ± 0.015) f	(0.042)	(1.449)
0.0005	0.0005	0.500	1.075	0.096	0.343	1.424	0.067	0.319
			(1.010 ± 0.024) f	(0.030 ± 0.035) f	(0.290 ± 0.040) f	(1.410 ± 0.017) f	(0.021)	(0.287)
0.001	0.000	1.000	1.253	0.143	0.000	1.334	0.107	0.000
			(1.195 ± 0.021) f	(0.080 ± 0.040) f	(0.020 ± 0.029) f	(1.312 ± 0.011) f	(0.061)	(0.017)
0.0000	0.0100	0.000	0.710	0.000	1.047	1.610	0.000	1.474
			(0.709 ± 0.016) f	(0.010 ± 0.009) f	(0.898 ± 0.030) f	(1.530 ± 0.012) f	(0.006)	(1.266)
0.0025	0.0075	0.250	0.931	0.058	0.622	1.498	0.038	0.668
			(0.900 ± 0.014) f	(0.040 ± 0.020) f	(0.593 ± 0.039) f	(1.420 ± 0.008) f	(0.031)	(0.369)
0.0050	0.0050	0.500	1.075	0.096	0.343	1.424	0.067	0.319
			(0.903 ± 0.010) f	(0.044 ± 0.025) f	(0.333 ± 0.020) f	(1.408 ± 0.010) f	(0.031)	(0.369)
0.0100	0.0000	1.000	1.253	0.143	0.000	1.334	0.107	0.000
			(1.190 ± 0.018) f	(0.200 ± 0.041) f	(0.009 ± 0.017) f	(1.309 ± 0.012) f	(0.153)	(0.007)

^a C₁ and C₂ in units of mol·dm⁻³ and S_D represent the respective standard deviations of the mean for n = 6 experiments; ^b X₁ represents the solute fraction of CoCl₂. (X₁ = C₁/(C₁+C₂)). ^c D_ab in units of 10⁻⁹ m²·s⁻¹. ^d D₁₂/D₂₂ gives the number of moles of CoCl₂ co-transported per mole of NaCl. ^e D₂₁/D₁₁ gives the number of moles of NaCl co-transported per mole of CoCl₂. ^f Experimental data from the Taylor technique. Standard uncertainties u are u_r(c) = 0.03; u(T) = 0.01 K, and u(P) = 2.03 kPa.

Table 3. Predicted ternary diffusion coefficients, D₁₁, D₁₂, D₂₁, and D₂₂, by Nernst–Hartley equations [9,12], for aqueous CoCl₂ (C₁) + HCl (C₂) + solutions at 25.0 °C.

C1  a	C2  a	X   b	D11 ± SD c	D12 ± SD c	D21 ± SD c	D22 ± SD c	D12/D22 d	D21 /D11  e
0.000	0.0001	0.000	0.720	0.000	2.151	3.334	0.000	2.988
			(0.713 ± 0.010) f	(0.014 ± 0.025) f	(1.080 ± 0.030) f	(2.950 ± 0.015) f	(0.005)	(1.514)
0.00005	0.0005	0.500	0.926	−0.574	1.335	5.605	−0.102	1.438
			(0.899 ± 0.008) f	(−0.534 ± 0.050) f	(1.290 ± 0.040) f	(4.790 ± 0.010) f	(−0.111)	(1.435)
0.001	0.000	1.000	1.263	−1.513	0.000	9.320	−0.162	0.000
			(1.140 ± 0.013) f	(−3.050 ± 0.020) f	(0.003 ± 0.010) f	(8.090 ± 0.005) f	(−0.377)	(0.003)
0.0000	0.0100	0.000	0.720	0.000	2.151	3.334	0.000	2.988
			(0.733 ± 0.006) f	(0.014 ± 0.030) f	(1.080 ± 0.020) f	(2.950 ± 0.010) f	(0.005)	(1.473)
0.0025	0.0075	0.250	0.812	−0.256	1.787	4.347	−0.059	2.201
			(0.780 ± 0.010) f	(−0.210 ± 0.040) f	(1.680 ± 0.030) f	(4.250 ± 0.010) f	(0.005)	(1.473)
0.0050	0.0050	0.500	0.926	−0.574	1.335	5.605	−0.102	1.438
			(0.890 ± 0.005) f	(−0.564 ± 0.020) f	(1.280 ± 0.090) f	(4.889 ± 0.015) f	(−0.115)	(1.438)
0.0100	0.0000	1.000	1.263	−1.513	0.000	9.320	−0.162	0.000
			(1.110 ± 0.010) f	(−3.050 ± 0.030) f	(0.004 ± 0.010) f	(8.010 ± 0.015) f	(−0.381)	(0.004)

^a C₁ and C₂ in units of mol·dm⁻³, and S_D represents the respective standard deviations of the mean for n = 6 experiments; ^b X₁ represents the solute fraction of CoCl₂. (X₁ = C₁/(C₁+C₂)). ^c D_ab in units of 10⁻⁹ m²·s⁻¹. ^d D₁₂/D₂₂ gives the number of moles of CoCl₂ counter-transported per mole of HCl. ^e D₂₁/D₁₁ gives the number of moles of HCl co-transported per mole of CoCl₂. ^f Experimental data from the Taylor technique. Standard uncertainties u are u_r(c) = 0.03; u(T) = 0.01 K, and u(P) = 2.03 kPa.

An analysis of Table 2 and Table 3 shows that there is a reasonable agreement between the experimental and predicted data for diluted solutions. The deviations between experimental and predicted main diffusion coefficients are generally less than 5%.

Nonideal solution behaviour and electrophoretic terms not included in the Nernst limiting D_ab estimations can explain the highest deviations observed.

It is important to highlight that there is a similar behaviour observed in the variation of these parameters D_ab (experimental and theoretical) as a function of their composition. Furthermore, it should be noted that although the predicted D_ab values are the same for equal CoCl₂ solute fractions, X₁, but calculated with different concentrations of each component, the same does not apply to the experimental data.

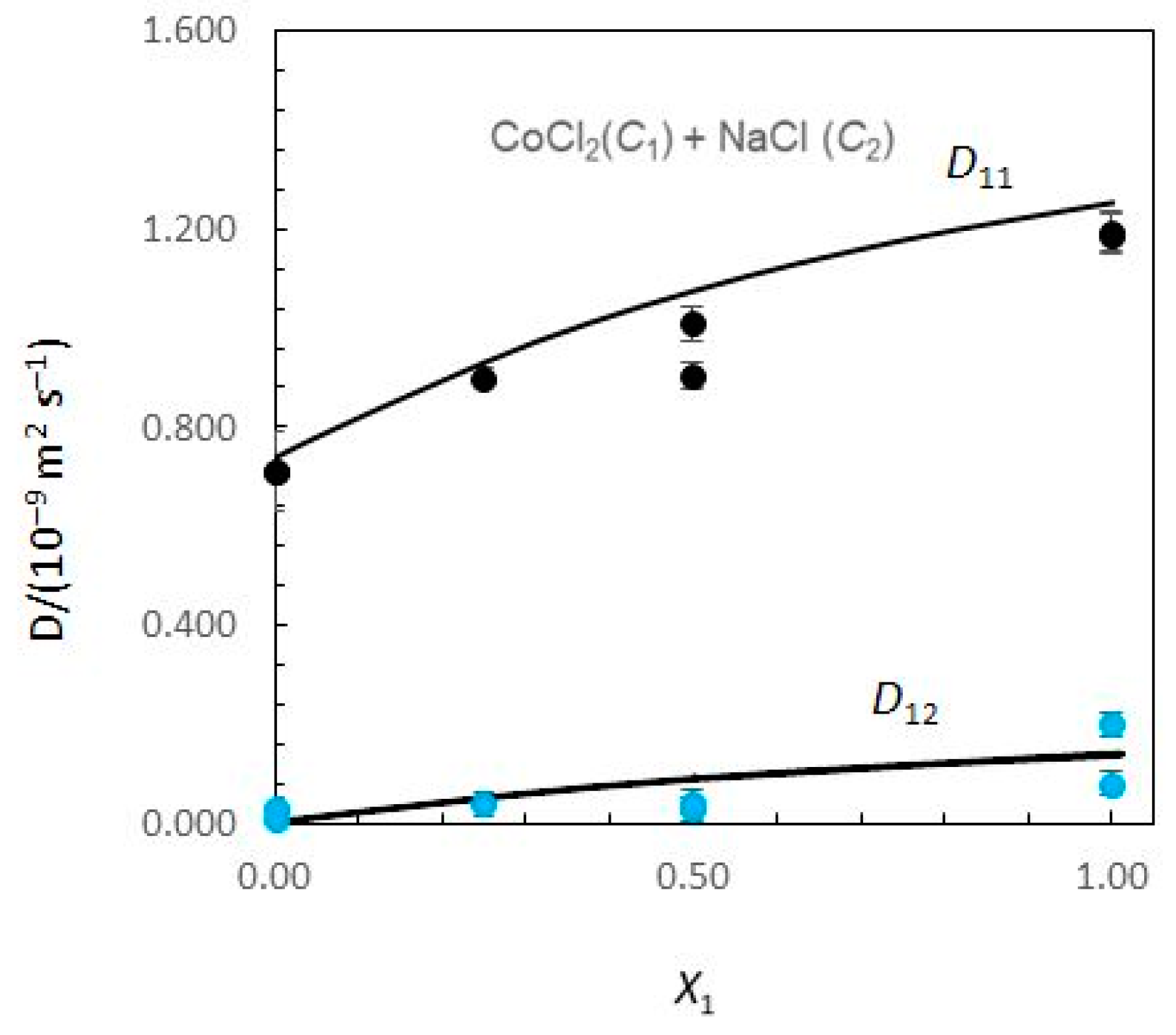
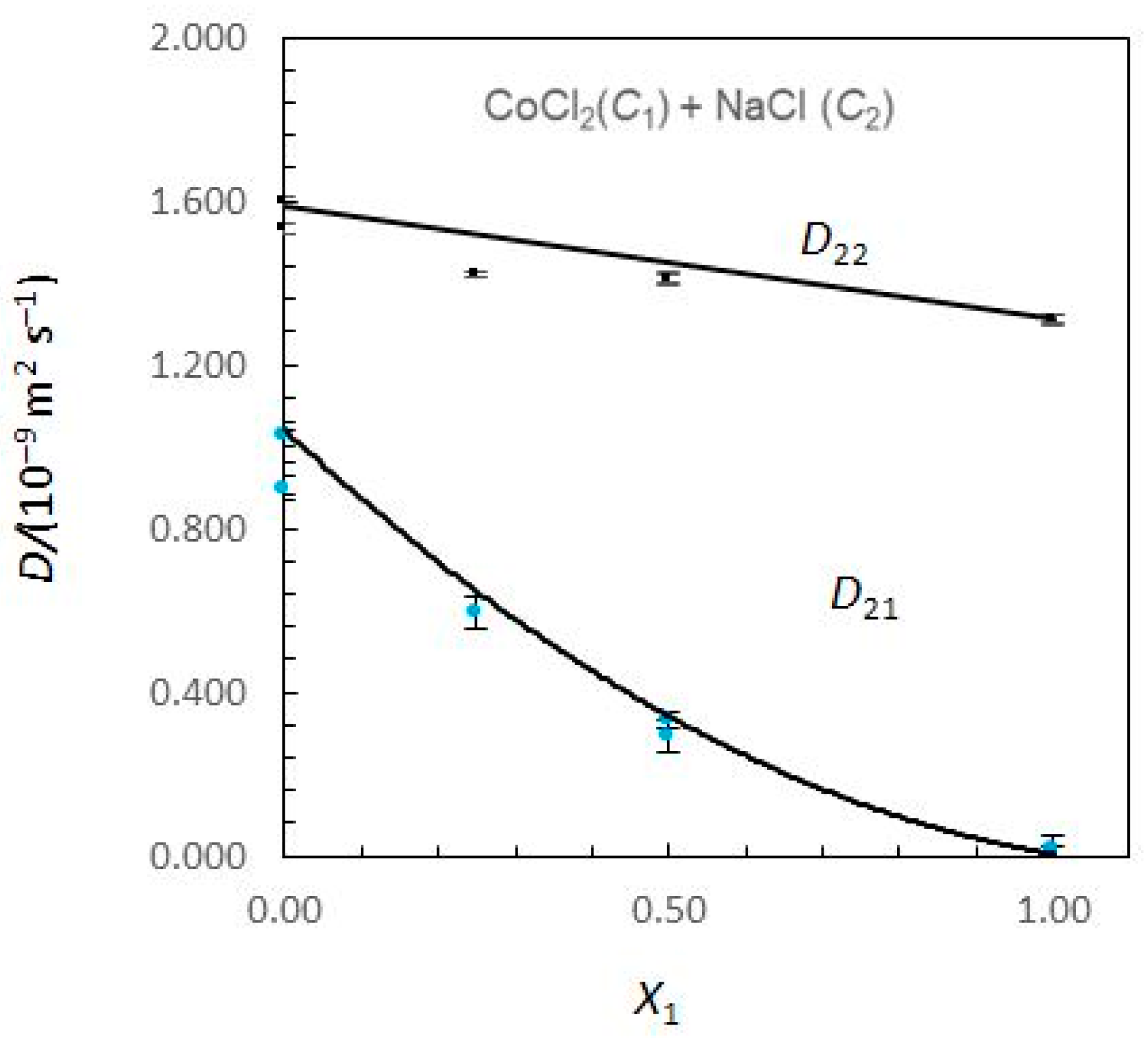
Figure 1 and Figure 2 show the limiting Nernst–Hartley D_ik coefficients for aqueous CoCl₂ (C₁) + NaCl (C₂) solutions plotted against the solute fraction of CoCl₂.

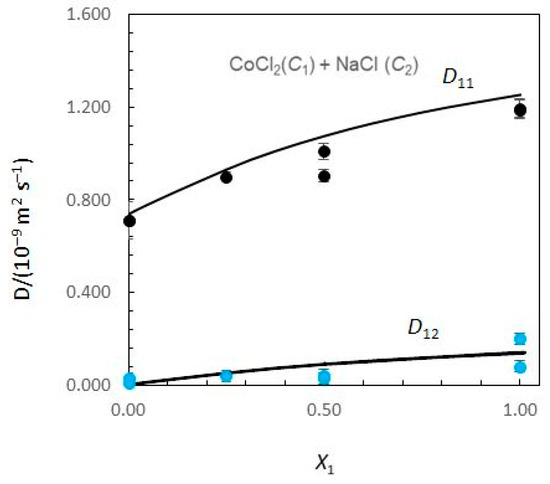
Figure 1. Ternary mutual diffusion coefficients D₁₁ and D₁₂ values (Equations (8)–(13)) for aqueous CoCl₂ (C₁) + NaCl (C₂) solutions at 25.0 °C plotted against the solute fraction of CoCl₂. (X₁ = C₁/(C₁ + C₂)). Measured D_ik values: symbols. Predicted D_ik values: solid curves.

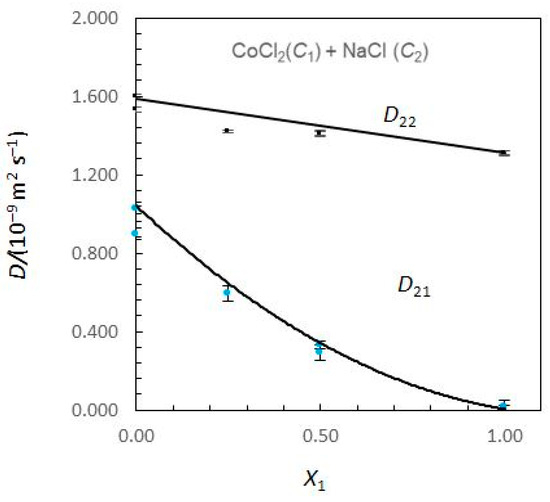
Figure 2. Ternary mutual diffusion coefficients D₂₂ and D₂₁ values (Equations (8)–(13)) for aqueous CoCl₂ (C₁) + NaCl (C₂) solutions at 25.0 °C plotted against the solute fraction of CoCl₂. (X₁ = C₁/(C₁ + C₂)). Measured D_ik values: symbols. Predicted D_ik values: solid curves.

Considering Figure 1, the Nernst–Hartley D₁₁ values for composition limits X₁ = 0 and X₁ = 1 are D_Co (the tracer diffusion coefficient of Co²⁺ ions in supporting NaCl solutions) and $3D_{\mathrm{C}\mathrm{o}}{D}_{\mathrm{C}\mathrm{l}}/\left(2D_{\mathrm{N}\mathrm{a}}+D_{\mathrm{C}\mathrm{l}}\right)$ (the binary mutual diffusion coefficient of aqueous CoCl₂), respectively. Equivalently, the limiting D₂₂ values for X₁ = 0 and X₁ = 1 are $\left(2D_{\mathrm{N}\mathrm{a}} D_{\mathrm{C}\mathrm{l}}\right)/\left(D_{\mathrm{N}\mathrm{a}}+D_{\mathrm{C}\mathrm{l}}\right)$ and D_Na. As the solute fraction of CoCl₂ increases from 0 to 1, D₁₂ changes from 0 to $t_{\mathrm{C}\mathrm{o}}\left(D_{\mathrm{C}\mathrm{l}}-D_{\mathrm{N}\mathrm{a}}\right)/2$and D₂₁ changes from $2t_{\mathrm{N}\mathrm{a}}\left(D_{\mathrm{C}\mathrm{l}}-D_{\mathrm{C}\mathrm{o}}\right)$ to 0. In these intervals of concentrations, a significant variation of D₁₂ and D₂₁ is observed. While D₁₂ are negative, D₂₁ are positive. At X₁ = 1, D₂₁ is zero, because sodium chloride concentration gradients cannot drive coupled flows of cobalt chloride in solutions. Similarly, D₁₂ → 0 as X₁ → 0.

A possible justification for the behaviour of coupled diffusion can be made on the basis of the electrostatic mechanism. The diffusion coefficient of the Cl⁻ ions is larger than that of the Co²⁺ ions (Table 1). Consequently, a CoCl₂ concentration gradient produces an electric field that slows down the Cl⁻ ions and speeds up the Co²⁺ ions to maintain electroneutrality along the diffusion path. If NaCl is present in the solution, the electric field generated by a CoCl₂ concentration gradient drives a coupled flow of Na⁺ ions in the same direction as the flux of Co²⁺, helping to explain the positive values estimated for cross-coefficient D₂₁. Similarly, D_Na < D_Cl and D₁₂ > 0. However, it can also be worth noticing the higher values obtained for D₂₁ when compared with those obtained for D₁₂.

Table 3 shows the effects of coupled diffusion between these CoCl₂ and HCl components. In this case, as the diffusion coefficient of the H⁺ ions is much larger than that of the Cl⁻ ions (Table 1); a HCl concentration gradient produces an electric field which slows down the Co²⁺ ions and speeds up the Cl⁻ ions to maintain electroneutrality. Consequently, D₁₂ < 0.

It can be concluded that strongly coupled diffusion occurs between cobalt chloride and hydrochloric acid, while sodium chloride gradients have a weaker influence on cobalt chloride diffusion. Furthermore, these predicted values are usually acceptable at highly diluted solutions, as the differences between them and experimental values are equal to, or less than, experimental uncertainty. In conclusion, when there is no experimental diffusion data, we can use the Nernst–Hartley equations to comprehend the composition dependence of the mutual diffusion coefficients of ternary systems, despite the limitations of this approach.

2.2. Predicted Ternary Diffusion Coefficients from Nernst Equations for Different Aqueous Systems

Taking all these considerations into account, Nernst–Hartley values were calculated for six aqueous systems for different compositions (Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9).

Table 4. Predicted ternary diffusion coefficients, D₁₁, D₁₂, D₂₁, and D₂₂, for aqueous HgCl₂ (C₁) + NaCl (C₂) + solutions at 25.00 °C by Nernst–Hartley equations [9,12].

C1  a	C2  a	X  b	D11   c	D12  c	D21  c	D22   c	D12 /D22   d	D21 /D11   e
0.000	0.0001	0.000	0.846	0.000	0.939	1.610	0.000	1.109
0.0005	0.0005	0.500	1.217	0.109	0.292	1.420	0.076	0.240
0.001	0.000	1.000	1.384	0.158	0.000	1.334	0.118	0.000
0.0000	0.0100	0.000	0.846	0.000	0.939	1.610	0.000	1.109
0.0025	0.0075	0.250	1.074	0.067	0.540	1.493	0.045	0.503
0.0050	0.0050	0.500	1.217	0.109	0.292	1.420	0.076	0.240
0.0075	0.0025	0.750	1.314	0.137	0.123	1.370	0.100	0.094
0.0100	0.0000	1.000	1.384	0.158	0.000	1.334	0.118	0.000

^a C₁ and C₂ in units of mol·dm⁻³; ^b X₁ represents the solute fraction of CoCl₂. (X₁ = C₁/(C₁ + C₂)). ^c D_ab in units of 10⁻⁹ m²·s⁻¹. ^d D₁₂/D₂₂ gives the number of moles of HgCl₂ transported per mole of NaCl. ^e D₂₁/D₁₁ gives the number of moles of NaCl transported per mole of HgCl₂.

Table 5. Predicted ternary diffusion coefficients, D₁₁, D₁₂, D₂₁, and D₂₂, for aqueous PbCl₂ (C₁) + NaCl (C₂) + solutions at 25.0 °C by Nernst–Hartley equations [9,12].

C1  a	C2  a	X   b	D11   c	D12   c	D21   c	D22   c	D12 /D22   d	D21 /D11   e
0.000	0.0001	0.000	0.932	0.000	0.871	1.610	0.000	0.934
0.0005	0.0005	0.500	1.299	0.116	0.263	1.417	0.082	0.202
0.001	0.000	1.000	1.457	0.166	0.000	1.334	0.124	0.000
0.0000	0.0100	0.000	0.932	0.000	0.871	1.610	0.000	0.934
0.0025	0.0075	0.250	1.161	0.073	0.492	1.490	0.049	0.424
0.005	0.0050	0.500	1.299	0.116	0.263	1.417	0.082	0.202
0.0075	0.0025	0.750	1.391	0.146	0.110	1.369	0.107	0.079
0.0100	0.0000	1.000	1.458	0.167	0.000	1.334	0.125	0.000

^a C₁ and C₂ in units of mol·dm⁻³; ^b X₁ represents the solute fraction of CoCl₂. (X₁ = C₁/(C₁ + C₂)). ^c D_ab in units of 10⁻⁹ m²·s⁻¹. ^d D₁₂/D₂₂ gives the number of moles of PbCl₂ transported per mole of NaCl. ^e D₂₁/D₁₁ gives the number of moles of NaCl transported per mole of PbCl₂.

Table 6. Predicted ternary diffusion coefficients, D₁₁, D₁₂, D₂₁, and D₂₂, for aqueous CrCl₃ (C₁) + NaCl (C₂) + solutions at 25.00 °C by Nernst–Hartley equations [9,12].

C1  a	C2  a	X   b	D11   c	D12   c	D21   c	D22   c	D12/ D22  d	D21 /D11   e
0.000	0.0001	0.000	0.594	0.000	1.708	1.610	0.000	2.875
0.0005	0.0005	0.500	1.113	0.084	0.388	1.424	0.059	0.349
0.001	0.000	1.000	1.265	0.108	0.000	1.334	0.081	0.000
0.0000	0.0100	0.000	0.594	0.000	1.708	1.610	0.000	2.875
0.0025	0.0075	0.250	0.951	0.058	0.801	1.463	0.040	0.842
0.0050	0.0050	0.500	1.113	0.084	0.388	1.397	0.060	0.349
0.0075	0.0025	0.750	1.205	0.099	0.153	1.359	0.073	0.127
0.0100	0.0000	1.000	1.265	0.108	0.000	1.334	0.081	0.000

^a C₁ and C₂ in units of mol·dm⁻³; ^b X₁ represents the solute fraction of CrCl₃. (X₁ = C₁/(C₁ + C₂)). ^c D_ab in units of 10⁻⁹ m²·s⁻¹. ^d D₁₂/D₂₂ gives the number of moles of CrCl₃ co-transported per mole of NaCl. ^e D₂₁/D₁₁ gives the number of moles of NaCl co-transported per mole of CrCl₃.

Table 7. Predicted ternary diffusion coefficients, D₁₁, D₁₂, D₂₁, and D₂₂, for aqueous HgCl₂ (C₁) + HCl (C₂) + solutions at 25.0 °C by Nernst–Hartley equations [9,12].

C1  a	C2  a	X   b	D11  c	D12   c	D21   c	D22   c	D12 /D22   d	D21 /D11   e
0.000	0.0001	0.000	0.846	0.000	1.944	3.334	0.000	2.298
0.0005	0.0005	0.500	1.059	−0.656	1.174	5.605	−0.117	1.108
0.001	0.000	1.000	1.384	−1.657	0.000	9.320	−0.178	0.000
0.0000	0.0100	0.000	0.846	0.000	1.944	3.334	0.000	2.298
0.0025	0.0075	0.250	0.943	−0.297	1.615	4.347	−0.068	1.713
0.005	0.0050	0.500	1.059	−0.656	1.207	5.605	−0.117	1.140
0.0075	0.0025	0.750	1.203	−1.099	0.686	7.208	−0.152	0.570
0.0100	0.0000	1.000	1.384	−1.657	0.000	9.320	−0.178	0.000

^a C₁ and C₂ in units of mol·dm⁻³; ^b X₁ represents the solute fraction of CoCl₂. (X₁ = C₁/(C₁ + C₂)). ^c D_ab in units of 10⁻⁹ m²·s⁻¹. ^d D₁₂/D₂₂ gives the number of moles of HgCl₂ counter-transported per mole of HCl. ^e D₂₁/D₁₁ gives the number of moles of HCl co-transported per mole of CoCl₂.

Table 8. Predicted ternary diffusion coefficients, D₁₁, D₁₂, D₂₁, and D₂₂, for aqueous PbCl₂ (C₁) + HCl (C₂) + solutions at 25.0 °C by Nernst–Hartley equations [9,12].

C1  a	C2  a	X  b	D11   c	D12   c	D21   c	D22   c	D12 /D22   d	D21 /D11   e
0.000	0.0001	0.000	0.932	0.000	1.803	3.334	0.000	1.934
0.0005	0.0005	0.500	1.146	−0.710	1.069	5.770	−0.123	0.933
0.001	0.000	1.000	1.458	−1.745	0.000	9.320	−0.187	0.000
0.0000	0.0100	0.000	0.932	0.000	1.803	3.334	0.000	1.934
0.0025	0.0075	0.250	1.030	−0.325	1.498	4.347	−0.075	1.454
0.005	0.0050	0.500	1.146	−0.710	1.119	5.605	−0.127	0.976
0.0075	0.0025	0.750	1.286	−1.174	0.636	7.208	−0.163	0.494
0.0100	0.0000	1.000	1.458	−1.745	0.000	9.320	−0.187	0.000

^a C₁ and C₂ in units of mol·dm⁻³; ^b X₁ represents the solute fraction of PbCl₂. (X₁ = C₁/(C₁ + C₂)). ^c D_ab in units of 10⁻⁹ m²·s⁻¹. ^d D₁₂/D₂₂ gives the number of moles of PbCl₂ counter-transported per mole of HCl. ^e D₂₁/D₁₁ gives the number of moles of HCl co-transported per mole of PbCl₂.

Table 9. Predicted ternary diffusion coefficients, D₁₁, D₁₂, D₂₁, and D₂₂, for aqueous CrCl₃ (C₁) + HCl (C₂) + solutions at 25.00 °C by Nernst–Hartley equations [9,12].

C1  a	C2  a	X   b	D11   c	D12   c	D21   c	D22   c	D12 /D22   d	D21 /D11   e
0.000	0.0001	0.000	0.594	0.000	3.537	3.334	0.000	5.954
0.0005	0.0005	0.500	0.931	−0.570	0.773	5.605	−0.102	0.830
0.001	0.000	1.000	1.265	−1.136	0.000	9.320	−0.122	0.000
0.0000	0.0100	0.000	0.594	0.000	3.537	3.334	0.000	5.612
0.0025	0.0075	0.250	0.763	−0.286	1.350	4.347	−0.066	1.769
0.005	0.0050	0.500	0.931	−0.570	0.773	5.605	−0.102	0.830
0.0075	0.0025	0.750	1.098	−0.854	0.339	7.208	−0.118	0.309
0.0100	0.0000	1.000	1.265	−1.136	0.000	9.320	−0.122	0.000

^a C₁ and C₂ in units of mol·dm⁻³; ^b X₁ represents the solute fraction of CrCl₃. (X₁ = C₁/(C₁ + C₂)). ^c D_ab in units of 10⁻⁹ m²·s⁻¹. ^d D₁₂/D₂₂ gives the number of moles of CrCl₃ counter-transported per mole of HCl. ^e D₂₁/D₁₁ gives the number of moles of HCl co-transported per mole of CoCl₂.

From the analysis of Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9, it can be inferred that for these solutions of these mixed electrolytes, the tendency of limiting ternary coefficients with the composition is similar. For example, in four aqueous systems {(CoCl₂ + HCl), (CrCl₃ + HCl), (HgCl₂ + HCl), and (PbCl₂ + HCL)}, the D₂₂ values are considerably larger than the D₁₁ values and increase dramatically with the solute 1 fraction, defined as X₁ = C₁/(C₁ + C₂)). Also, the cross-coefficient D₁₂ becomes very large and negative with the increasing solute 1 fraction.

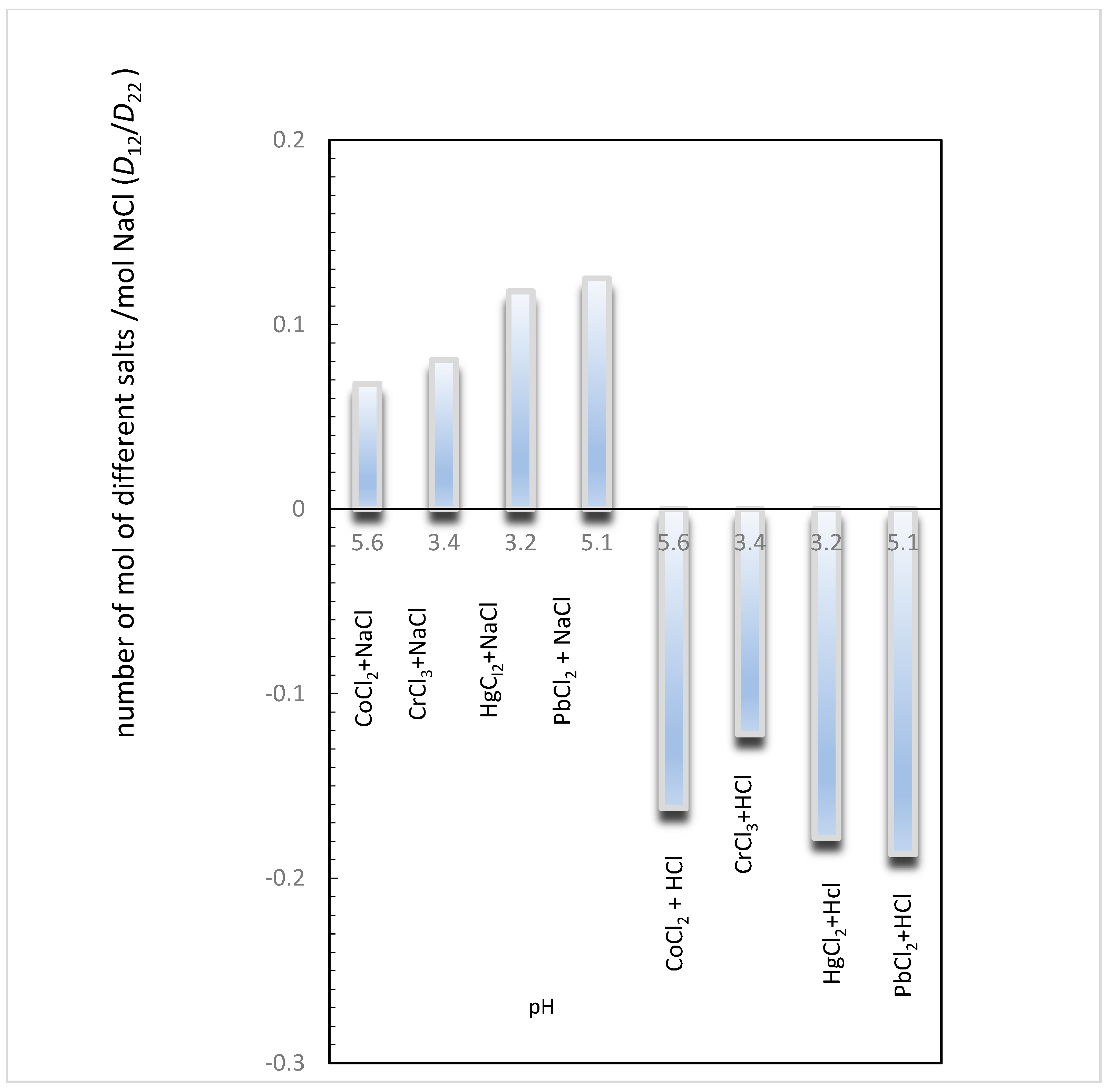
The values of the ternary diffusion coefficient ratios D₁₂/D₂₂ and D₂₁/D₁₁ (Table 10 and Table 11) permit us to give the number of moles of one component transported per mole of the other component.

Table 10. Estimation of the moles of MCl₂ (component 1) (M = Co²⁺, Hg²⁺, Pb²⁺) and CrCl₃ (component 1) transported by each mole of NaCl (component 2) obtained from the D_ij data presented in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9.

Aqueous System	D12/D22
CoCl2—NaCl	+1.5
HgCl2—NaCl	+1.1
PbCl2—NaCl	+0.9
CrCl3—NaCl	+2.9
CoCl2—HCl	−0.2
HgCl2—HCl	−0.2
PbCl2—HCl	−0.2
CrCl3—HCl	−0.1

Table 11. Estimation of the moles of NaCl (or HCl) (component 2) transported by each mole of MCl₂ (M = Co²⁺, Hg²⁺, Pb²⁺) and CrCl₃ (component 1) obtained from the D_ij data presented in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9.

Aqueous System	D21/D11
CoCl2—NaCl	+0.1
HgCl2—NaCl	+0.1
PbCl2—NaCl	+0.1
CrCl3—NaCl	+0.1
CoCl2—HCl	+3.0
HgCl2—HCl	+2.3
PbCl2—HCl	+1.9
CrCl3—HCl	+5.6

From Table 10, the higher positive value obtained for D₁₂/D₂₂ in the CrCl₃/NaCl system, when compared with the others, stands out; therefore, we can say that one mole of diffusing NaCl co-transports up to 2.9 mol of CrCl₃.

Relative to the effects of added hydrochloric acid on the diffusion of aqueous CoCl₂, CrCl_3, HgCl₂, and PbCl₂, the D₁₂/D₂₂ values are lower and similar between them (that is, one mole of diffusing HCl counter-transports up to 0.1 of MCl₂ (M = Co²⁺, Hg²⁺, Pb²⁺) and 0.2 mol of CrCl₃.

From the positive D₂₁/D₁₁ values (Table 11), it can be concluded that a mole of diffusing of MCl₂ (M = Co²⁺, Hg²⁺, Pb²⁺) and CrCl₃ favour the transport of NaCl (and HCl) in the same direction. However, the added HCl is more relevant, considering the highest values for this ratio (achieving the maximum value for system CrCl₃ plus HCl). In this case, a mole of diffusing CrCl₃ co-transports at most 6 mol of HCl).

Based on these observations, it can be inferred that there is coupled diffusion in such systems that disrupts the thermodynamic equilibrium. For instance, when cobalt–chromium dental alloys are present in the oral cavity and exposed to low pH, it can create favourable conditions for the production of flows of chromium ions into the human body.

Figure 3 illustrates the coupled diffusion occurring in these aqueous systems, revealing the number of moles of salts containing metallic ions (Co²⁺, Hg²⁺, Pb²⁺, and Cr³⁺) transported by each mole of NaCl and HCl at different pHs. That is, the values D₁₂/D₂₂ are plotted for each system at different pHs (Table 10).

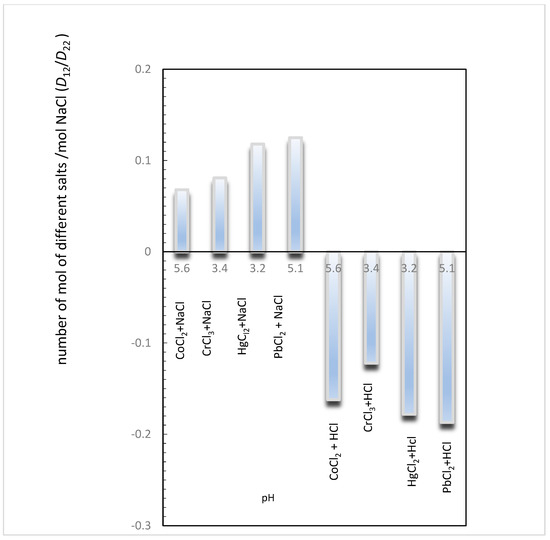
Figure 3. Estimation of the number of moles of salts (i.e., CoCl₂, CrCl_3, HgCl₂, and PbCl₂) transported for each mole of NaCl (or HCl), for different values of pH, by the calculation of D₁₂/D₂₂ ratios.

From Figure 3, we can observe that the D₁₂/D₂₂ values are close, independent of the pH level.

However, the direction of flux of these ions depends strongly on the component added to these systems. While NaCl concentration gradients drive co-current fluxes of Co²⁺, Hg²⁺, Pb²⁺, and Cr³⁺ in solutions, HCl concentration gradients drive counter-current fluxes of these ions in solutions.

3. Materials and Methods

3.1. Materials

Table 12 shows the reagents used as received in the present work: cobalt chloride, sodium chloride, and hydrogen chloride. All chemicals were used without further purification.

Table 12. Sample description.

Chemical Name	Source	CAS Number	Mass Fraction Purity a
Cobalt (II) chloride hexahydrate	Panreac (Laborspirit Lda., Lisboa, Portugal)	7791-13-1	>0.98
Hydrochloric acid	Sigma-Aldrich (Sigma-Aldrich Quimica S.L., Lisboa, Portugal)	7647-01-0	37 wt% HCl
Sodium chloride	Sigma-Aldrich	7647-14-5	>0.99
H2O	Millipore-Q water (ρ = 1.82 × 105 Ω m at 25.0 °C)	7732–18-5

^a The mass fraction purity is on a water-free basis; these data are provided by the suppliers.

All solutions were prepared using ultrapure water (Millipore, Darmstadt, Germany, Milli-Q Advantage A10, specific resistance = 1.82 × 105 Ω m, at 25.0 °C). The weighing was carried out using a Radwag AS 220C2 balance (Radwag, Radom, Poland), with an accuracy of ±0.0001 g.

3.2. pH Measurements

The pH measurements of solutions were carried out with a Radiometer pH meter PHM 240 (Radiometer, Apeldoorn, The Netherlands) with an Ingold U457-K7pH conjugated electrode (Mettler-Toledo International, Columbus, OH, USA); the pH was measured in fresh solutions, and the electrode was calibrated immediately before each experimental set of solutions using IUPAC-recommended pH 4, 7, and 10 buffers. From pH meter calibration, a zero pH of 6.00 ± 0.03 and sensitivity higher than 98.7% were obtained. All solutions were freshly prepared at 298.15 K and degassed by sonication for about 60 min before each experiment.

3.3. Taylor Dispersion Method

The Taylor dispersion technique for measuring diffusion coefficients is well described in the literature [7,10,12,14,20], and hence its details are not included in this manuscript. However, we sum up some relevant points regarding the method and the equipment. Dispersion profiles were generated by injecting, at the start of each run, using a 6-port Teflon injection valve (Rheodyne, model 5020; Sigma-RBI, Burlington, MA, USA), 0.063 mL of solution into a laminar carrier stream of slightly different compositions at the entrance to a Teflon capillary dispersion tube, of length 3048.0 (±0.1) cm, and with an internal radius, r, of 0.03220 ± (0.00003) cm. This tube and the injection valve were kept at 25.00 (±0.01) °C in an air thermostat. The broadened distribution of the disperse samples was monitored at the tube outlet using a differential refractometer (Waters model 2410; Waters, Milford, MA, USA). The refractometer output voltages, V(t), were measured at 5 s intervals using a digital voltmeter (Agilent 34401 A; Agilent Technologies, Santa Clara, CA, USA).

The dispersion profiles for these ternary solutions {e.g., CoCl₂ plus sodium chloride} were analyzed by fitting the following equation (Equation (18)) to obtain the values of the different D_ab coefficients.

$$V\left(t\right)=V_0+V_1+V_{max}{(t_R/t)}^{1/2}\left[W_{1}exp\left(-{\displaystyle \frac{12D_1{\left(t-t_R\right)}^2}{r^{2}t}}\right)+(1-W_1)exp\left(-{\displaystyle \frac{12D_2{(t-t_R)}^2}{r^{2}t}}\right)\right]$$

(18)

D₁ and D₂ represent the eigenvalues of the matrix of the ternary D_ab coefficients; V₀, V₁, and V_max are the baseline voltage, the baseline slope, and the peak height, respectively; r is the inner radius of the dispersion tube (whose values are indicated above); t_R is the mean sample retention time; and W₁ and (1 − W₁) are normalized pre-exponential factors.

4. Conclusions

Based on the predicted ternary diffusion coefficients for the aqueous ternary systems studied (that is, {(CoCl₂ + NaCl), (HgCl₂ + NaCl), (PbCl₂ + NaCl), and (CrCl₃ + NaCl), and (CoCl₂ + HCl), (HgCl₂ + HCl), (PbCl₂ + HCl), and (CrCl₃ + HCl)}), it can be concluded that the presence of NaCl and HCl affects the diffusion behaviour of these ions (i.e., Co²⁺, Hg²⁺, Pb²⁺, and Cr³⁺).

There is a coupled diffusion of these salts and NaCl and HCl, as indicated by cross-diffusion coefficients different to zero, that suggests that there is interaction between the solutes. This behaviour of these coefficients was interpreted based on the electrostatic mechanism between these components. Of course, due to the limitations of the Nernst–Hartley equations, it is not possible to accurately find the diffusion behaviour of these systems, however desirable that would be. In other words, although the accurate prediction of D_ik coefficients is not possible, being valid only for very diluted solutions, by taking the appropriate precautions, each researcher can use these values, depending on the necessities of its application to a given real problem. In conclusion, Nernst-Hartley model equations are useful, bearing in mind that from their estimated values we can obtain a better understanding of the transport and structure of those systems.