Next Article in Journal
Metalloborospherene Analogs to Metallofullerene
Previous Article in Journal
Enhanced Removal of Rhodamine b Dye from Aqueous Media via Adsorption on Facilely Synthesized Zinc Ferrite Nanoparticles
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 12
Issue 7
10.3390/inorganics12070192
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Exploring the Nature of Ag–Ag Interactions in Different Tellurides by Means of the Crystal Orbital Bond Index (COBI)

by
Leander Weinelt
and
Simon Steinberg
*
Institute of Inorganic Chemistry, RWTH Aachen University, Landoltweg 1, D-52074 Aachen, Germany
*
Author to whom correspondence should be addressed.
Inorganics 2024, 12(7), 192; https://doi.org/10.3390/inorganics12070192
Submission received: 19 June 2024 / Revised: 6 July 2024 / Accepted: 8 July 2024 / Published: 12 July 2024
Browse Figures
Versions Notes

Abstract

Over the decades, intensive explorations have been conducted to understand the nature of d10−d10 interactions. The recent establishment of a bonding indicator named the crystal orbital bond index stimulated our impetus to probe the capabilities of that approach for the examples of Ag–Ag interactions in different tellurides. In the framework of our quantum chemical explorations, we inspected the electronic structures of two tellurides which were previously reported to comprise d10−d10 interactions, while the third candidate material, i.e., RbCe2Ag3Te5, has been obtained from reactions of rubidium chloride, cerium, silver and tellurium for the very first time. The outcome of our explorations clearly shows that the nature of Ag–Ag interactions is well mirrored by the corresponding COBI.

Graphical Abstract

1. Introduction

Understanding the nature of chemical bonding allows us to recognize and quantify the forces which hold molecular units as well as extended solids together [1,2]. Therefore, the nature of chemical bonding and, to be more specific, its energetic contributions to the total energy of a given system are decisive for the formation of a respective structure model [3]. Unfortunately, identifying bonding scenarios in extended solids often turns out to be rather complicated [4]; so, orbital- or density-based approaches backed by quantum chemistry are at play [2,5,6,7]. Despite the massive efforts to provide an insight into the bonding situations in solids, understanding the nature of chemical bonding is still a constant subject of debate, as shown in the recent example of p-block-element-containing chalcogenides [8,9,10].
Another sort of chemical bonding that is a constant subject of research includes the interactions between closed-shell metal species of zero or the same nominal charge [11]. In the framework of this research debate, there has been a particular focus on homoatomic interactions between coinage metals in both solid state as well as coordination chemistry [12,13,14,15,16]. Stimulated by this area of research, we recently took advantage of both experimental as well as quantum chemical means to search for the presence of such homoatomic interactions in transition metal-containing tellurides [17,18,19,20,21,22,23]. The outcome of these explorations indicated that the relationships between the structural features and the electronic structures could hardly be rationalized by applying the Zintl–Klemm–Busmann idea [24,25,26,27,28,29,30,31] that works perfectly fine [32,33] for many tellurides.
While the aforementioned explorations were based on well-established orbital- as well as density-based bond analysis tools, a recently introduced [34] approach providing crystal orbital bond indices (COBIs) in solids has not yet been applied to reveal the homoatomic coinage metal–coinage metal interactions. Therefore, our impetus was stimulated to employ that tool in order to investigate the nature of silver–silver interactions for the examples of three tellurides, i.e., RbAg3Te2, BaAg2Te2 and RbCe2Ag3Te5 (Figure 1). The crystal structures and the electronic structures of the ternary tellurides have been determined by previous explorations [35,36,37,38], hence serving as references for our study, while the quaternary telluride has been obtained for the very first time. In the following, we will report on the results of our explorations.

2. Results

Before diving into the analyses of the diverse electronic structures, we will first provide a brief report on the crystal structure of RbCe2Ag3Te5 that has been obtained from reactions of cerium, silver, tellurium and rubidium chloride for the first time (see the Experimental Section). The quaternary telluride crystallizes with the orthorhombic space group Cmcm and is isostructural with the previously reported [17,18,39] ALn2Ag3Te5 (A = Rb, Ln = Pr, Nd, Sm, Gd–Er; A = Cs, Ln = La–Nd, Sm, Gd–Er). The volume of the unit cell of RbCe2Ag3Te5 (see the Supplementary Materials) is larger than that of RbPr2Ag3Te5 (V = 1378.7(10) Å3), because the covalent radius [40] of cerium (2.04 Å) is somewhat increased relative to that of praseodymium (2.03 Å) due to the lanthanide contraction [41]. The crystal structure of the quaternary telluride comprises one rubidium site (Wyckoff position 4c) that resides in bicapped trigonal tellurium prisms. These [Rb@Te8] units are condensed via the trigonal bases into linear chains which propagate parallel to the a axis (Figure 1). Furthermore, the [Rb@Te8] units share common edges with octahedral tellurium units enclosing the cerium atoms (Wyckoff position 8f). Each [Ce@Te6] octahedron shares two common edges with neighboring [Ce@Te6] units within linear [ Ce @ Te 6 ] ∞ 1 chains located parallel to the a axis and, furthermore, two common edges with the nearest [ Ce @ Te 6 ] ∞ 1 chains, thereby constituting [ Ce @ Te 6 ] ∞ 1 double chains. The tetrahedral voids between the aforementioned chains are occupied by the silver atoms. Here, one should distinguish between two different sorts of silver sites. The silver atoms (Ag6) located on the Wyckoff position 4c are encapsulated by tellurium tetrahedra sharing common vertices within linear [ Ag 6 @ Te 4 ] ∞ 1 chains. The silver atoms (Ag5) residing on the Wyckoff site 8f are also located in linear [ Ag 5 @ Te 4 ] ∞ 1 chains; however, each [ Ag 5 @ Te 4 ] ∞ 1 chain shares common edges with another [ Ag 5 @ Te 4 ] ∞ 1 chain assembling [ Ag 5 @ Te 4 ] ∞ 1 double chains. Within these [ Ag 5 @ Te 4 ] ∞ 1 double chains, there are short Ag–Ag contacts (2.975(2) Å) whose nature will be inspected in the framework of our bonding analyses.
Application of the Zintl–Klemm–Busmann idea to the quaternary telluride proposes an electron-precise distribution of the valence electrons as denoted by the formula (Rb+)(Ce3+)2(Ag+)3(Te2−)5. Furthermore, RbCe2Ag3Te5 also shows Fermi level characteristics which are typically [42] encountered for Zintl phases, as the Fermi level of the telluride falls into a band gap (Figure 1)—a scenario that nicely correlates with the Zintl–Klemm–Busman idea of the valence electron distributions [5,42] in most Zintl phases. Also, a correlation [28,43] between formal valence electron transfers, the (8−N) rule and the corresponding structural fragments must be fulfilled in the framework of that approach. As one could assume that the crystal structure of RbCe2Ag3Te5 is composed of tellurium polyhedra, which encompass the metal atoms and contains ionic or, to be more precise, polar-covalent metal–tellurium bonds, it might be deduced that the quaternary telluride nicely fits into the Zintl–Klemm–Busmann-based picture. And yet, how do the short Ag–Ag contacts which point to homoatomic Ag–Ag bonds as an evident part of a structural fragment, i.e., the [ Ag 5 @ Te 4 ] ∞ 1 double chains, agree with such a picture? To provide a complete insight beyond the scope of the traditional Zintl–Klemm–Busmann concept, quantum chemical means must be employed.
A Mulliken population analysis reveals that the computed charges of the rubidium atoms are indeed close to the Zintl–Klemm–Busmann ideal of +1. Accordingly, the nature of the Rb–Te bonds should be ionic, which is in line with the modest Rb–Te ICOBI values (Figure 1). As ICOBI values allow us to measure the grade of covalency within a given interaction, such small ICOBI values clearly point to a minor degree of covalency as expected for an ionic bond (e.g., ICOBISr–Te = 0.11 in SrTe) [34,44]. On the contrary, the Ce–Te and Ag–Te interactions correspond to increased ICOBI values relative to those of the Rb–Te bonds and, hence, should show a more covalent character than the alkali-metal–tellurium bonds. That trend is also mirrored by the Mulliken charges, as the computed charges of the silver and cerium atoms evidently differ from the charges predicted by the Zintl–Klemm–Busmann treatment. Because the integrated −pCOHP (IpCOHP) values also tend to increase as the degrees of covalency are enlarged [6], one may expect that the Rb–Te −IpCOHP values are smaller than those of the Ce–Te and Ag–Te bonds. Indeed, that trend is also present for RbCe2Ag3Te5; so, the Ce–Te and Ag–Te bonds correspond to the largest percentages contributed to the net bonding capabilities [45,46] which were computed based on the cumulative −IpCOHP/cell values for each kind of interaction. Furthermore, the Ag–Te interactions change from bonding to antibonding states below the valence band maximum, but they are counterbalanced by Ce–Te bonding states. As frequently encountered [37,47,48,49,50,51,52,53,54,55,56,57] for Ag–Ag bonds, the homoatomic interactions also change from bonding to antibonding states below the Fermi level, while the Ag–Ag −IpCOHP/bond values clearly indicate a net bonding character (0.24 eV) and scale nearly in the same range as those of the Rb–Te bonds (0.31–0.29 eV). At this point, one might expect that the electronically unfavorable occupation of antibonding states is reduced by the introduction of vacancies into the crystal structure, as such a situation has also been previously encountered [23] for a binary silver telluride; however, the results of our X-ray diffraction experiments did not reveal the presence of any vacancies in the crystal structure of the quaternary telluride. This outcome may be explained based on two aspects. First of all, the location of the Fermi level in the band gap appears to correlate to an electronically favorable [58] situation. Moreover, the populations of Ce–Te bonding interactions also seem to compensate the aforementioned electronically unfavorable condition.
Now, let us return to our initial question: Do the crystal orbital bond indices allow us to reveal Ag–Ag interactions, which have already been indicated based on the Ag–Ag −IpCOHP (see above)? In fact, the Ag–Ag ICOBI values are just slightly decreased relative to those of the Rb–Te bonds. Therefore, the ICOBI as well as the −IpCOHP reflect the same trend: the Ag–Ag ICOBI/bond and the −IpCOHP/bond values are quite close to those corresponding to the Rb–Te interactions. Actually, one could expect that both the Ag–Ag and Rb–Te bonds do not exhibit an evidently covalent nature as indicated by the ICOBI/bond and the −IpCOHP/bond values. In the case of the Rb–Te bonds, the quite filled shells of the tellurium atoms are combined with the rather empty ones of the rubidium atoms in ionic bonds, while combining the rather closed shells of the silver atoms results in the occupations of significant antibonding Ag–Ag states, reducing the net bonding character of these homoatomic bonds. Also, the combinations of the highly filled Ag-4d with the Te-5p atomic orbitals lead to the populations of the Ag–Te antibonding states below the valence band maximum. At this point, the careful reader will recognize that there is still a technical difference between the COBI and the pCOHP, but a lack of bonding character ought to reduce the magnitudes of the elements which are derived from the density matrix as well as the Hamilton matrix so that both approaches should help us to quantify the degrees of covalency; however, the bond indices can also be determined across multiple centers in order to provide invaluable information [59,60] about multicenter bonds. With regard to the results of our electronic structure analysis, it should be noted that the general tendencies derived from the electronic structure investigations are also in line with our previous study [17,18] on the electronic structures of that sort of telluride, but now, the electronic structure analysis has also been performed based on the crystal orbital bond indices. Since this probe demonstrated the effectiveness of the COBI for revealing the nature of Ag–Ag bonds, we will continue with the electronic structure analysis for the next example, i.e., the ternary RbAg3Te2.
In the framework of previous [61] research, the nature of the crystal structure in RbAg3Te2 has also encouraged first-principle-based explorations concerning its lattice thermal conductivity. While RbAg3Te2 was not among the materials showing the lowest lattice thermal conductivity, we will still provide a brief insight into the remarkable crystal structure of that telluride before we continue with the analysis of its electronic structure. The ternary telluride was previously reported [35,36] to crystallize with the monoclinic space group C2/m, and its crystal structure comprises one rubidium and three independent silver sites (Figure 2). The former atoms reside in monocapped trigonal tellurium prisms [Rb@Te7], which are condensed via their trigonal bases into linear chains, [ Rb @ Te 7 ] ∞ 1 , parallel to the b axis. These chains are connected via common edges and faces with nearest neighboring [ Rb @ Te 7 ] ∞ 1 columns that are packed in layers parallel to the ab plane. The three independent silver positions are sandwiched between the aforementioned layers. The Ag1 and Ag2 atoms are located in tellurium tetrahedra sharing common vertices and edges in [ Ag 1 @ Te 4 ] ∞ 1 and [ Ag 2 @ Te 4 ] ∞ 1 double chains. Furthermore, each double chain containing one type of silver atom, i.e., Ag1 or Ag2, shares common faces with two neighboring double chains encapsulating the opposite sort of silver atom and vice versa. The Ag3 sites are located in the layers constituted by the [ Ag @ Te 4 ] ∞ 1 double chains in such a way that each Ag3 atom is surrounded by three tellurium atoms. Within the layers of the [Ag@Te4] units, there are also Ag–Ag contacts (2.818(2) to 3.423(2) Å) whose nature will be determined in the framework of our electronic structure investigations.
Applying the Zintl–Klemm–Busmann idea to the ternary telluride suggests an electron-precise distribution of the valence electrons according to the formula (Rb+)(Ag+)3(Te2−)2. That expectation nicely agrees with the presence of a band gap at the Fermi level in RbAg3Te2 (Figure 2). Furthermore, the computed charges corresponding to the rubidium atoms also approach the Zintl–Klemm–Busmann ideal of +1, indicating an ionic character for the Rb–Te bonds. That consideration is confirmed by the modest Rb–Te ICOBI values which clearly show a minor degree of covalency as expected for ionic bonds; however, the presence of the short Ag–Ag contacts which appear to be evident factors in a structural fragment, i.e., the layers of the [Ag@Te4] units, does not fit into the Zintl–Klemm–Busmann-derived picture of formal valence electron distributions, the (8−N) rule and the corresponding structural fragments. Therefore, quantum chemical approaches are utilized to provide a complete picture regarding the electronic structure of RbAg3Te2. A closer inspection of the computed charges reveals that the Mulliken charges of the silver and tellurium atoms evidently differ from the charges derived from the Zintl–Klemm–Busmann approach. An inspection of the respective –pCOHP diagrams shows that the Ag–Te and Ag–Ag interactions cross from bonding to antibonding states below the valence band maximum; yet the integrated –pCOHP values undoubtedly point to a net bonding character for these interactions. Moreover, the Ag–Te bonds contribute the largest percentages to the net bonding capabilities of RbAg3Te2, while those related to the Ag–Ag and Rb–Te interactions scale in the same lower range. A comparison of the diverse Ag–Ag and Rb–Te ICOBI values shows that they also scale in a similar range, hence indicating a scenario which has also been encountered for RbCe2Ag3Te5. And yet the Ag–Ag and Rb–Te interactions show a reduced bonding character compared to the Ag–Te bonds, because the ICOBI values of the latter type of bonds are larger than those of the former sorts of interactions. Accordingly, the nature of the Ag–Te interactions should be depicted as polar-covalent, while the change from the bonding to antibonding states arises from the mixing of the highly occupied Te-5p and Ag-4d atomic orbitals. As the employment of bond indices nicely mirrored the bonding situations in RbAg3Te2 (as well as RbCe2Ag3Te5), we will now continue with our analysis for the last representative, i.e., BaAg2Te2.
To date, the ternary BaAg2Te2 has been a constant subject of exploration because of its performance with regard to thermoelectric energy conversion [62,63,64,65,66]. As previous research [37] using quantum chemical means also showed that BaAg2Te2 comprises Ag–Ag bonding interactions, we selected this telluride as a candidate for our explorations. BaAg2Te2 crystallizes with the space group Pnma, and its crystal structure (Figure 3) comprises one barium and two independent silver sites. The barium atoms reside in monocapped trigonal tellurium prisms, [Ba@Te7], which are condensed via their trigonal bases into linear chains, [ Ba @ Te 7 ] ∞ 1 . These linear chains are linked via common edges with nearest neighboring [ Ba @ Te 7 ] ∞ 1 chains constituting puckered sheets of [ Ba @ Te 7 ] ∞ 1 chains parallel to the ab plane. The silver atoms are enclosed by tellurium tetrahedra sharing common vertices and edges within linear [ Ag 1 @ Te 4 ] ∞ 1 and [ Ag 2 @ Te 4 ] ∞ 1 double chains.
Application of the Zintl–Klemm–Busmann idea to the ternary telluride suggests an electron-precise valence electron distribution, as indicated by the expression (Ba2+)(Ag+)2(Te2−)2. Indeed, the Mulliken charge of the barium atoms approach the Zintl–Klemm–Busmann ideal of +2 and are indicative of an ionic bonding situation for the Ba–Te interactions (Figure 3). The ionic nature of the Ba–Te bonds is also reflected by the minor Ba–Te ICOBI values revealing a lack of a substantial covalent character. On the other hand, the computed charges of the silver and tellurium atoms differ from the charges predicted by the Zintl–Klemm–Busmann formalism. An inspection of the corresponding –pCOHP diagrams shows that the Ag–Te and Ag–Ag interactions traverse from bonding to antibonding states below the valence band maximum as a consequence of the highly filled Ag-4d and Te-5p atomic orbitals; yet the −IpCOHP values clearly exhibit a net bonding character for the aforementioned sorts of bonds. The Ag–Te bonds correspond to the largest percentage contributions to the net bonding capabilities in BaAg2Te2, while the Ag–Te ICOBI values are larger than those of the Ba–Te bonds. This outcome is evidence that the Ag–Te bonds are more covalent than the ionic Ba–Te interactions and should be depicted as polar-covalent. The Ag–Ag ICOBI values scale in the same range as those of the Ba–Te bonds and reveal the presence of Ag–Ag bonding interactions in agreement [37,62] with the results of previous first-principle-based bonding analyses for BaAg2Te2. And again, the reduced bonding character of the Ag–Ag interactions may be regarded as an attribute of the filled Ag-4d shells, as also identified for the other herein inspected tellurides. In summary, BaAg2Te2 is composed of polar-covalent Ag–Te and ionic Ba–Te bonds, while the nature of the filled Ag-4d shells translates into modest but evident Ag–Ag interactions. At this point, one [67,68] may wonder if conclusive inferences about the thermoelectric performances may be obtained from the results of the bonding analyses; however, the results of more recent explorations [60] clearly indicate that a specific sort of chemical bonding does not necessarily translate into particular material properties. Although there can be certain correlations between vibrational properties and bonding scenarios [69,70], interpretations of the electronic and phonon band structure must be combined to fully comprehend the material properties relevant for thermoelectric energy conversion [71]. While such explorations are beyond the scope of the present contribution, let us come back to our initial question: Does the COBI approach help us to identify Ag–Ag bonds?
A comparison of the Ag–Ag ICOBI values for the herein inspected tellurides reveals that the Ag–Ag ICOBI/bond ranges in the ternary tellurides are broader than those corresponding to the quaternary species. In this connection, the careful reader will recognize that the Ag–Ag distance spectra in RbAg3Te2 and BaAg2Te2 are also wider relative to those in RbCe2Ag3Te5. Because the ICOBI values tend to increase as the bond lengths decrease, the larger Ag–Ag separations in the ternary tellurides translate into modest ICOBI values, while the Ag–Ag ICOBI values which are related to the shorter Ag–Ag contacts in the ternaries scale in the same range as those ICOBI values determined for the short Ag–Ag contacts in RbCe2Ag3Te5. Accordingly, using the COBI approach helped us to identify and, furthermore, quantify Ag–Ag bonds in the herein inspected tellurides.

3. Discussion

In summary, the outcome of our explorations for the three tellurides shows that the presence of Ag–Ag interactions could be verified based on the crystal orbital bond indices. Based on this connection, the discussion of our results also includes a structural report of the quaternary RbCe2Ag3Te5 that has been obtained for the very first time. In general, the magnitudes of the Ag–Ag ICOBIs were smaller than those of the polar-covalent Ag–Te bonds and hence well reflect the modest but evident strength of the homoatomic bonds whose nature has been a constant subject of study since the very first groundbreaking explorations [12,72,73,74] of silver-containing oxides. At this point, one may also wonder if the Zintl–Klemm–Busmann formalism should be applied to the tellurides. Indeed, this idea should guide [28,43] us through a given correlation between formal valence electron transfers, the (8−N) rule and structural fragments, but its application to the three tellurides did not hint at the Ag–Ag bonds that are evident structural features of them. Therefore, quantum chemical bonding descriptors [5] like the herein inspected COBIs must be put into action to provide a full picture regarding the correlations between crystal structures and chemical bonding within the herein inspected tellurides. In fact, understanding such connections is crucial for the design of a given solid as the bond energy corresponding to a respective structural fragment contributes to the total energy [3,75]. That energy is a fundamental parameter [76] to evaluate the structural preferences for a particular system, and as soon as one is aware of the structural preferences for a particular system, information regarding the material’s properties may be extracted from the electronic structure as an extra. And yet the outcome of a given bonding analysis solely provides useful indicators concerning the preferences among various structure models, while direct connections between chemical bonding and material properties remain [60] elusive.

4. Experimental Section

4.1. Synthesis

The quaternary RbCe2Ag3Te5 was obtained from reactions of the elements cerium (99.9%; smart-elements®, Vienna, Austria), silver (≥99.99%; Alfa Aesar®, Haverhill, MA, USA) and tellurium (>99%; Merck®; Darmstadt, Germany) in the presence of rubidium chloride (99.8%; Sigma Aldrich®, St. Louis, MO, USA) that was employed as a reactive flux [77,78]. Because cerium is sensitive to air and moisture [41], all sample preparations had to be conducted under a dry argon atmosphere within a glove box (MBRAUN®, Garching, Germany; H2O, O2 < 0.1 ppm/volume). Powders of cerium were obtained by filing larger chunks whose surfaces were polished prior to every use, while traces of water were removed from rubidium chloride prior to its transfer into the aforementioned glove box. In the experiments, 42.03 mg cerium, 48.54 mg silver, 95.7 mg tellurium and 60.46 mg rubidium chloride were loaded into one-side-closed silica tubes, whose open sides were thoroughly closed by means of quick-fit adapters within the glove box. The quick-fit adapters were subsequently connected to a vacuum and inter-gas manifold in order to flame-seal the containers under a dynamic vacuum of at least 10−3 mbar. The samples were heated utilizing computer-controlled tube furnaces and the following temperature program: heat to 900 °C at a rate of 80 °C/h, keep that temperature for five days, reduce to 350 °C at a rate of 5 °C/h and equilibrate to room temperature within 3 h. The product appeared as a gray powder that was stable in air for several weeks.

4.2. X-ray Diffraction Experiments

In order to provide an insight into the structural features of RbCe2Ag3Te5, single-crystal X-ray diffraction experiments were conducted (Table 1 and Table 2; Supplementary Materials). Therefore, samples were selected from the bulk materials, fixed on glass fibers with grease and transferred to a Bruker APEX CCD diffractometer (Bruker Inc.®, Madison, WI, USA; Mo Kα radiation) that was used for the initial collections of single-crystal X-ray intensity data sets. The sample showing the highest quality was chosen for a full measurement which was performed at room temperature by means of the aforementioned diffractometer.
After a C-centered orthorhombic lattice had been identified by indexing the data, integration of the raw data and absorption correction were completed by using the programs SAINT+ and SADABS, respectively [79,80]. Application of the reflection conditions to the collected data was achieved with the aid of the XPREP code [81] within the APEX2 suite [82] and clearly pointed to the space group Cmcm that was selected for the initial structure solution based on direct methods [83,84] (SHELXS). Afterwards, the SHELXL code was used for least-square refinements on F2, while the last cycles of refinements also included anisotropic atomic displacement parameters. An additional inspection of the final structure model did not reveal any space group different from Cmcm.
In order to identify potential side products, phase analyses based on powder X-ray diffraction patterns were performed. Prior to the measurements, the samples were first thoroughly homogenized and then dispersed on acetal sheets with grease. These sheets were fixed between split aluminum rings and transferred to a STOE StadiP diffractometer (STOE® & Cie GmbH; Darmstadt, Germany; Cu Kα radiation) that was used for the measurements at room temperature. The WinXPow software [85] was used for the control of the measurements and the processing of the raw data, while the phase analyses were completed using the Match! [86] code. A comparison of the observed powder X-ray diffraction patterns with those simulated for potential side products indicated that Ce3Te4 [87] was the main product, while the quaternary telluride was obtained in minor amounts (Figure 4).

4.3. Computational Details

To provide an insight into the electronic structure of the quaternary telluride and further tellurides comprising homoatomic silver–silver interactions, density–functional–theory-based approaches were employed. Prior to the electronic structure analyses of the diverse tellurides, full structural optimizations including lattice parameters and atomic positions were carried out following a general procedure reported elsewhere [88,89]. Furthermore, all computations were carried out in a non-magnetic regime based on a procedure that has been largely employed elsewhere [90,91,92], as the lanthanide 4f electrons may be treated as core-like in the framework of chemical bonding analyses. These structural optimizations as well as the electronic structure computations were performed by means of the projector-augmented wave (PAW) method [93] as implemented in the Vienna ab initio simulation package [94,95,96,97,98] (VASP). Correlation and exchange in all computations were depicted by the generalized gradient approximation [99] (GGA–PBE), while the energy cut-off of the plane wave basis sets was 500 eV. Sets of 12 × 3 × 3, 4 × 16 × 8 and 5 × 12 × 5 k-points were utilized to sample the first Brillouin zones in RbCe2Ag3Te5, RbAg3Te2 and BaAg2Te2, respectively, while all computations were expected to converge as the energy differences between two iterative steps fell below 10−8 eV (10−6 eV) of the electronic (and ionic) relaxations. Chemical bonding analyses were completed based on the pCOHP [46], the COBI [34] and the Mulliken [100] charges. Because the aforementioned bonding analysis tools are constructed based on local orbital basis sets whose nature is in stark contrast to that of plane waves, the results of plane wave-based computations had to be transferred to all-electron Slater-type orbitals with the aid of the Local Orbital Basis Suite Towards Electronic Structure Reconstruction [101,102,103,104] code (LOBSTER). The plots of the diverse −pCOHP curves were generated with the aid of the program wxDragon [105] that was also used for further analyses of the respective DOS and −pCOHP diagrams.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/inorganics12070192/s1. Crystal data in CIF format can be found in the Supplementary Files.

Author Contributions

Conceptualization, L.W. and S.S.; validation, L.W. and S.S.; formal analysis, L.W.; investigation, L.W.; writing—original draft preparation, S.S.; writing—review and editing, L.W. and S.S.; supervision, S.S. All authors have read and agreed to the published version of the manuscript.

Funding

This study was funded by the Deutsche Forschungsgemeinschaft (DFG; Bonn), grant number 511503255.

Data Availability Statement

CCDC 2360535 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge via http://www.ccdc.cam.ac.uk/conts/retrieving.html (or from the CCDC, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033; e-mail: deposit@ccdc.cam.ac.uk). All other data may be obtained from the authors upon reasonable request.

Acknowledgments

The authors wish to thank Richard Dronskowski for the allocation of the lab space and the computer cluster, Tobias Storp for the collections of the single-crystal and powder X-ray diffraction data, and David Schnieders for technical support regarding the computer cluster.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Ruedenberg, K. The Physical Nature of the Chemical Bond. Rev. Mod. Phys. 1962, 34, 326–376. [Google Scholar] [CrossRef]
  2. Frenking, G.; Shaik, S. The Chemical Bond—Fundamental Aspects of Chemical Bonding; Wiley-VCH: Weinheim, Germany, 2014. [Google Scholar]
  3. Miller, G.J. The “Coloring Problem” in Solids: How It Affects Structure, Composition and Properties. Eur. J. Inorg. Chem. 1998, 1998, 523–536. [Google Scholar] [CrossRef]
  4. Lin, Q.; Miller, G.J. Electron-Poor Polar Intermetallics: Complex Structures, Novel Clusters, and Intriguing Bonding with Pronounced Electron Delocalization. Acc. Chem. Res. 2018, 51, 49–58. [Google Scholar] [CrossRef] [PubMed]
  5. Miller, G.J.; Zhang, Y.; Wagner, F.R. Chemical Bonding in Solids. In Handbook of Solid State Chemistry; Dronskowski, R., Kikkawa, S., Stein, A., Eds.; Wiley-VCH: Weinheim, Germany, 2017. [Google Scholar]
  6. Dronskowski, R. Chemical Bonding—From Plane Waves via Atomic Orbitals; Walter de Gruyter: Berlin, Germany; Boston, MA, USA, 2023. [Google Scholar]
  7. Wagner, F.R.; Grin, Y. Chemcial bonding analysis in position space. In Comprehensive Inorganic Chemistry III; Reedijk, J., Poeppelmeier, K.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; Volume 3, pp. 222–237. [Google Scholar]
  8. Jones, R.O.; Elliott, S.R.; Dronskowski, R. The Myth of “Metavalency” in Phase-Change Materials. Adv. Mater. 2023, 35, 2300836. [Google Scholar] [CrossRef] [PubMed]
  9. Wuttig, M.; Schön, C.-F.; Kim, D.; Golub, P.; Raty, J.-Y.; Kooi, B.J.; Pendás, A.M.; Arora, R.; Waghmare, U.V. Metavalent or Hypervalent Bonding: Is There a Chance for Reconciliation? Adv. Sci. 2024, 11, 2308578. [Google Scholar] [CrossRef]
  10. Müller, P.C.; Elliott, S.R.; Dronskowski, R.; Jones, R.O. Chemical bonding in phase-change chalcogenides. J. Phys. Condens. Matter, 2024; accepted. [Google Scholar] [CrossRef] [PubMed]
  11. Pyykkö, P. Strong Closed-Shell Interactions in Inorganic Chemistry. Chem. Rev. 1997, 97, 597–636. [Google Scholar] [CrossRef]
  12. Jansen, M. Über Die Silberteilstruktren in Silberreichen Oxiden. J. Less-Comm. Met. 1980, 76, 285–292. [Google Scholar] [CrossRef]
  13. Jansen, M. Homoatomic d10-d10 Interactions: Their Effects on Structure and Chemical and Physical Properties. Angew. Chem. Int. Ed. Engl. 1987, 26, 1098–1110. [Google Scholar] [CrossRef]
  14. Schmidbauer, H.; Schier, A. Argentophilic Interactions. Angew. Chem. Int Ed. 2015, 54, 746–784. [Google Scholar] [CrossRef]
  15. Sculfort, S.; Braunstein, P. Intramolecular d10–d10 interactions in heterometallic clusters of the transition metals. Chem. Soc. Rev. 2011, 40, 2741–2760. [Google Scholar] [CrossRef] [PubMed]
  16. Schier, A.; Schmidbauer, H. Aurophilic interactions as a subject of current research: An up-date. Chem. Soc. Rev. 2012, 41, 370–412. [Google Scholar]
  17. Göbgen, K.C.; Fries, K.S.; Gladisch, F.C.; Dronskowski, R.; Steinberg, S. Revealing the Nature of Chemical Bonding in an ALn2Ag3Te5-Type Alkaline-Metal (A) Lanthanide (Ln) Silver Telluride. Inorganics 2019, 7, 70. [Google Scholar] [CrossRef]
  18. Eickmeier, K.; Fries, K.S.; Gladisch, F.C.; Dronskowski, R.; Steinberg, S. Revisiting the Zintl-Klemm Concept for ALn2Ag3Te5-Type Alkaline-Metal (A) Lanthanide (Ln) Silver Tellurides. Crystals 2020, 10, 184. [Google Scholar] [CrossRef]
  19. Smid, S.; Steinberg, S. Probing the Validity of the Zintl Klemm Concept for Alkaline-Metal Copper Tellurides by Means of Quantum-Chemical Techniques. Materials 2020, 13, 2178. [Google Scholar] [CrossRef]
  20. Gladisch, F.C.; van Leusen, J.; Passia, M.T.; Kögerler, P.; Steinberg, S. Rb3Er4Cu5Te10: Exploring the Frontier between Polar Intermetallics and Zintl-Phases via Experimental and Quantumchemical Approaches. Eur. J. Inorg. Chem. 2021, 2021, 4946–4953. [Google Scholar] [CrossRef]
  21. Gladisch, F.C.; Pippinger, T.; Meyer, J.; Pries, J.; Richter, J.; Steinberg, S. Examination of a Structural Preference in Quaternary Alkali-Metal (A) Rare-Earth (R) Copper Tellurides by Combining Experimental and Quantum-chemical Means. Inorg. Chem. 2022, 61, 9269–9282. [Google Scholar] [CrossRef]
  22. Koch, P.; Steinberg, S. Exploring the subtle factors that control the structural preferences in Cu7Te4. J. Phys. Condens. Matter 2023, 35, 064003. [Google Scholar] [CrossRef] [PubMed]
  23. Göbgen, K.C.; Gladisch, F.C.; Steinberg, S. The Mineral Stützite: A Zintl-Phase or Polar Intermetallic? A Case Study Using Experimental and Quantum-Chemical Techniques. Inorg. Chem. 2018, 57, 412–421. [Google Scholar] [CrossRef]
  24. Zintl, E. Intermetallische Verbindungen. Angew. Chem. 1939, 52, 1–6. [Google Scholar] [CrossRef]
  25. Klemm, W. Metalloids and their Compounds with the Alkali Metals. Proc. Chem. Soc. 1958, 329–364. [Google Scholar] [CrossRef]
  26. Klemm, W.; Busmann, E. Volumeninkremente und Radien einiger einfach negativ geladener lonen. Z. Anorg. Allg. Chem. 1963, 319, 297–311. [Google Scholar] [CrossRef]
  27. Schäfer, H.; Eisenmann, B.; Müller, W. Zintl Phases: Transitions between Metallic and Ionic Bonding. Angew. Chem. Int. Ed. 1973, 12, 694–712. [Google Scholar] [CrossRef]
  28. Nesper, R. The Zintl-Klemm Concept—A Historical Survey. Z. Anorg. Allg. Chem. 2014, 640, 2639–2648. [Google Scholar] [CrossRef]
  29. Janka, O.; Kauzlarich, S. Zintl Compounds. In Encyclopedia of Inorganic and Bioinorganic Chemistry; Scott, R.A., Ed.; Wiley-VCH: Weinheim, Germany, 2021. [Google Scholar]
  30. Pan, F.; Weinert, B.; Dehnen, S. Binary Zintl Anions Involving Group 13–15 (Semi-)Metal Atoms, and the Relationship of Their Structures to Electron Count. Struct. Bond. 2021, 188, 103–148. [Google Scholar]
  31. Pöttgen, R.; Johrendt, D. Intermetallics; Walter de Gruyter: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar]
  32. Böttcher, P. Tellurium-Rich Tellurides. Angew. Chem. Int. Ed. Engl. 1988, 27, 759–772. [Google Scholar] [CrossRef]
  33. Sheldrick, W.S. Polychalcogenide Anions: Structural Diversity and Ligand Versatility. Z. Anorg. Allg. Chem. 2012, 638, 2401–2424. [Google Scholar] [CrossRef]
  34. Müller, P.C.; Ertural, C.; Hempelmann, J.; Dronskowski, R. Crystal Orbital Bond Index: Covalent Bond Orders in Solids. J. Phys. Chem. C 2021, 125, 7959–7970. [Google Scholar] [CrossRef]
  35. Li, J.; Guo, H.-Y.; Zhang, X.; Kanatzides, M.G. CsAg5Te3: A new metal-rich telluride with a unique tunnel structure. J. Alloys Compds. 1995, 218, 1–4. [Google Scholar] [CrossRef]
  36. Eanes, M.E.; Schimek, G.L.; Kolis, J.W. Synthesis and structural characterization of CsAg5Se3 and RbAg3Te2. J. Chem. Crystallogr. 2000, 30, 223–226. [Google Scholar] [CrossRef]
  37. Assoud, A.; Cui, Y.; Thomas, S.; Sutherland, B.; Kleinke, H. Structure and physical properties of the new telluride BaAg2Te2 and its quaternary variants BaCudAg2–dTe2. J. Solid State Chem. 2008, 181, 2024–2030. [Google Scholar] [CrossRef]
  38. Mayasree, O.; Sankar, C.R.; Kleinke, K.M.; Kleinke, H. Cu clusters and chalcogen-chalcogen bonds in various copper polychalcogenides. Coord. Chem. Rev. 2012, 256, 1377–1383. [Google Scholar] [CrossRef]
  39. Meng, C.-Y.; Chen, H.; Wang, P. Syntheses, Structures, and Physical Properties of CsRE2Ag3Te5 (RE = Pr, Nd, Sm, Gd-Er) and RbRE2Ag3Te5 (RE = Sm, Gd-Dy). Inorg. Chem. 2014, 53, 6893–6903. [Google Scholar] [CrossRef] [PubMed]
  40. Cordero, B.; Gómez, V.; Platero-Prats, A.E.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S. Covalent radii revisited. Dalton Trans. 2008, 2008, 2832–2838. [Google Scholar] [CrossRef]
  41. Cotton, S. Lanthanide and Actinide Chemistry; John Wiley & Sons Ltd.: Chichester, UK, 2006. [Google Scholar]
  42. Miller, G.J.; Schmidt, M.W.; Wang, F.; You, T.-S. Quantitative Advances in the Zintl-Klemm Formalism. Struct. Bond. 2011, 139, 1–55. [Google Scholar]
  43. Steinberg, S. Revisiting the frontier of the Zintl–Klemm approach for the examples of three Mo2FeB2-type intermetallics by means of quantumchemical techniques. Z. Anorg. Allg. Chem. 2023, 649, e202300113. [Google Scholar] [CrossRef]
  44. Simons, J.; Hempelmann, J.; Fries, K.S.; Müller, P.C.; Dronskowski, R.; Steinberg, S. Bonding diversity in rock salt-type tellurides: Examining the interdependence between chemical bonding and materials properties. RSC Adv. 2021, 11, 20679–20686. [Google Scholar] [CrossRef] [PubMed]
  45. Gladisch, F.C.; Steinberg, S. Revealing Tendencies in the Electronic Structures of Polar Intermetallic Compounds. Crystals 2018, 8, 80. [Google Scholar] [CrossRef]
  46. Steinberg, S.; Dronskowski, R. The Crystal Orbital Hamilton Population (COHP) Method as a Tool to Visualize and Analyze Chemical Bonding in Intermetallic Compounds. Crystals 2018, 8, 225. [Google Scholar] [CrossRef]
  47. Wu, Z.; Hoffmann, R.-D.; Johrendt, D.; Mosel, B.D.; Eckert, H.; Pöttgen, R. Electronic structure, physical properties and ionic mobility of LiAg2Sn. J. Mater. Chem. 2003, 13, 2561–2565. [Google Scholar] [CrossRef]
  48. Sebastian, C.P.; Eckert, H.; Fehse, C.; Wright, J.P.; Attfield, J.P.; Johrendt, D.; Rayaprol, S.; Hoffmann, R.-D.; Pöttgen, R. Structural, magnetic, and spectroscopic studies of YAgSn, TmAgSn, and LuAgSn. J. Solid State Chem. 2006, 179, 2376–2385. [Google Scholar] [CrossRef]
  49. Assoud, A.; Xu, J.; Kleinke, H. Structures and Physical Properties of New Semiconducting Polyselenides Ba2CuδAg4-δSe5 with Unprecedented Linear Se34− Units. Inorg. Chem. 2007, 46, 9906–9911. [Google Scholar] [CrossRef]
  50. Davaasuren, B.; Dashjav, E.; Rothenberger, A. Synthesis and Characterization of the Ternary Telluroargentate K4[Ag18Te11]. Z. Anorg. Allg. Chem. 2014, 640, 2939–2944. [Google Scholar] [CrossRef]
  51. Buxi, K.; Kuila, S.K.; Roy, A.; Jana, P.P. Atomic distributions of Ag and In in the γ-brass type Ag9In4. J. Solid State Chem. 2023, 327, 124247. [Google Scholar] [CrossRef]
  52. Assoud, A.; Guo, Q.; Sankar, C.R.; Kleinke, H. Crystal structure, electronic structure and physical properties of the new quaternary chalcogenides Tl2NdAg3Se4 and Tl2NdAg3Te4. Inorg. Chem. Front. 2017, 4, 315–323. [Google Scholar] [CrossRef]
  53. Buxi, K.; Mondal, A.; Wang, F.; Jana, P.P. Structural and theoretical investigations on the “coloring” scheme of γ-brass type phase Ag5Cd8. J. Solid State Chem. 2023, 323, 124019. [Google Scholar] [CrossRef]
  54. Stoyko, S.S.; Blanchard, P.E.R.; Mar, A. Crystal structure, electrical resistivity, and X-ray photoelectron spectroscopy of BaAg2As2. J. Solid State Chem. 2012, 194, 113–118. [Google Scholar] [CrossRef]
  55. Wang, F.; Pearson, K.N.; Miller, G.J. EuAgxAl11-x with the BaCd11-Type Structure: Phase Width, Coloring, and Electronic Structure. Chem. Mater. 2009, 21, 230–236. [Google Scholar] [CrossRef]
  56. Stoyko, S.S.; Khatun, M.; Mullen, C.S.; Mar, A. Ternary CaCu4P2-type pnictides AAg4Pn2 (A = Sr, Eu; Pn = As, Sb). J. Solid State Chem. 2012, 192, 325–330. [Google Scholar] [CrossRef]
  57. Assoud, A.; Soheilnia, N.; Kleinke, H. New Quaternary Barium Copper/Silver Selenostannates: Different Coordination Spheres, Metal-Metal Interactions, and Physical Properties. Chem. Mater. 2005, 17, 2255–2261. [Google Scholar] [CrossRef]
  58. Steinberg, S.; Brgoch, J.; Miller, G.J.; Meyer, G. Identifying a Structural Preference in Reduced Rare-Earth Metal Halides by Combining Experimental and Computational Techniques. Inorg. Chem. 2012, 51, 11356–11364. [Google Scholar] [CrossRef]
  59. Hempelmann, J.; Müller, P.C.; Ertural, C.; Dronskowski, R. The Orbital Origins of Chemical Bonding in Ge−Sb−Te Phase-Change Materials. Angew. Chem. Int. Ed. 2022, 61, e202115778. [Google Scholar] [CrossRef] [PubMed]
  60. Reitz, L.S.; Hempelmann, J.; Müller, P.C.; Dronskowski, R.; Steinberg, S. Bonding Analyses in the Broad Realm of Intermetallics: Understanding the Role of Chemical Bonding in the Design of Novel Materials. Chem. Mater. 2024, accepted. [Google Scholar] [CrossRef]
  61. McKinney, R.; Gorai, P.; Toberer, E.S.; Stevanovic, V. Rapid Prediction of Anisotropic Lattice Thermal Conductivity: Application to Layered Materials. Chem. Mater. 2019, 31, 2048–2057. [Google Scholar] [CrossRef]
  62. Shi, Y.; Sturm, C.; Kleinke, H. Chalcogenides as thermoelectric materials. J. Solid State Chem. 2019, 270, 273–279. [Google Scholar] [CrossRef]
  63. Yu, H.; Li, W.; Pei, Y.; Chen, Y. Pressure and doping effects on the structural stability of thermoelectric BaAg2Te2. J. Phys. Condens. Matter 2022, 34, 065401. [Google Scholar] [CrossRef] [PubMed]
  64. Yang, C.; Guo, K.; Yang, X.; Xing, J.; Wang, K.; Luo, J.; Zhao, J.-T. Realizing High Thermoelectric Performance in BaCu2–xAgxTe2 through Enhanced Carrier Effective Mass and Point-Defect Scattering. ACS Appl. Energy Mater. 2019, 2, 889–895. [Google Scholar] [CrossRef]
  65. Tang, J.; Qin, C.; Yu, H.; Zeng, Z.; Cheng, L.; Ge, B.; Chen, Y.; Li, W.; Pei, Y. Ultralow lattice thermal conductivity enables high thermoelectric performance in BaAg2Te2 alloys. Mater. Today Phys. 2022, 22, 100591. [Google Scholar] [CrossRef]
  66. Seddik, T.; Rezini, B.; Djelid, K.; Haq, B.U.; Kim, S.-H.; Batouche, M.; Fahad, S.; Djelloul, A.; Yumnam, G. Electronic, optical, and thermoelectric properties of multifunctional zintl compound BaAg2Te2 for energy conversion. Phys. B Condens. Matter 2023, 668, 415209. [Google Scholar] [CrossRef]
  67. Yu, Y.; Cagnoni, M.; Cojocaru-Mirédin, O.; Wuttig, M. Chalcogenide Thermoelectrics Empowered by an Unconventional Bonding Mechanism. Adv. Funct. Mater. 2020, 30, 1904862. [Google Scholar] [CrossRef]
  68. Maier, S.; Steinberg, S.; Cheng, Y.; Schön, C.-F.; Schumacher, M.; Mazzarello, R.; Golub, P.; Nelson, R.; Cojocaru-Mirédin, O.; Raty, J.-Y.; et al. Discovering Electron-Transfer-Driven Changes in Chemical Bonding in Lead Chalcogenides (PbX, where X = Te, Se, S, O). Adv. Mater. 2020, 32, 2005533. [Google Scholar] [CrossRef]
  69. Zeier, W.G.; Zevalkink, A.; Gibbs, Z.M.; Hautier, G.; Kanatzides, M.G.; Snyder, G.J. Thinking Like a Chemist: Intuition in Thermoelectric Materials. Angew. Chem. Int. Ed. 2016, 55, 6826–6841. [Google Scholar] [CrossRef]
  70. Hempelmann, J.; Müller, P.C.; Konze, P.M.; Stoffel, R.P.; Steinberg, S.; Dronskowski, R. Long-Range Forces in Rock-Salt-Type Tellurides and How they Mirror the Underlying Chemical Bonding. Adv. Mater. 2021, 33, 2100163. [Google Scholar] [CrossRef] [PubMed]
  71. Yan, J.; Gorai, P.; Ortiz, B.; Miller, S.; Barnett, S.A.; Mason, T.; Stevanovic, V.; Toberer, E.S. Material descriptors for predicting thermoelectric performance. Energy Environ. Sci. 2015, 8, 983–994. [Google Scholar] [CrossRef]
  72. Byström, A.; Evers, L. The Crystal Structures of Ag2PbO2 and Ag5Pb2O6. Acta Chem. Scand. 1950, 4, 613–627. [Google Scholar] [CrossRef]
  73. Jansen, M. Darstellung und Kristallstruktur von LiAg3O2/Preparation and Crystal Structure of LiAg3O2. Z. Naturforsch. B 1975, 30, 854–858. [Google Scholar] [CrossRef]
  74. Nuss, J.; Wedig, U.; Jansen, M. Synergistic Interaction between Attractive d10 Bonding and Localized Excess Electrons, the Cases of Subvalent Ag5SiO4 and Ag5GeO4. Z. Anorg. Allg. Chem. 2022, 648, e202200269. [Google Scholar] [CrossRef]
  75. Lofti, S.; Brgoch, J. Discovering Intermetallics Through Synthesis, Computation, and Data-Driven Analysis. Chem. Eur. J. 2020, 26, 8689–8697. [Google Scholar]
  76. Gautier, R.; Zhang, X.; Hu, L.; Yu, L.; Lin, Y.; Sunde, T.O.L.; Chon, D.; Poeppelmeier, K.R.; Zunger, A. Prediction and accelerated laboratory discovery of previously unknown 18-electron ABX compounds. Nat. Chem. 2015, 7, 308–316. [Google Scholar] [CrossRef]
  77. Pell, M.A.; Ibers, J.A. Layered Ternary and Quaternary Metal Chalcogenides. Chem. Ber. 1997, 130, 1–8. [Google Scholar] [CrossRef]
  78. Mitchell, K.; Ibers, J.A. Rare-earth transition-metal chalcogenides. Chem. Rev. 2002, 102, 1929–1952. [Google Scholar] [CrossRef] [PubMed]
  79. SAINT+, version 7.68; Bruker AXS Inc.: Madison, WI, USA, 2009.
  80. SADABS, version 2004/1; Bruker AXS Inc.: Madison, WI, USA, 2004.
  81. XPREP, Version 6.03; Bruker AXS Inc.: Madison, WI, USA, 2014.
  82. APEX2, v2014.11-0; Bruker Nonius. Bruker AXS Inc.: Madison, WI, USA, 2014.
  83. Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]
  84. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
  85. WinXPow, 2.23 ed.; STOE & Cie GmbH: Darmstadt, Germany, 2005.
  86. Putz, H. Match! version 3.6.1.115; Crystal Impact GbR: Bonn, Germany, 2018.
  87. Domange, L.; Flahaut, J.; Pardo, M.-P.; Chirazi, A.N.; Guittard, M. Sur les tellurures de cérium, CeTe2 et Ce3Te4. C. R. Hebd. Séances Acad. Sci. 1960, 250, 857–858. [Google Scholar]
  88. Stoffel, R.P.; Wessel, C.; Lumey, M. Ab Initio Thermochemistry of Solid-State Materials. Angew. Chem. Int. Ed. 2010, 49, 5242–5266. [Google Scholar] [CrossRef] [PubMed]
  89. Stoffel, R.P.; Dronskowski, R. Lattice Dynamics and Thermochemistry of Solid-State Materials from First-Principles Quantum-Chemical Calculations. In Handbook of Solid State Chemistry; Dronskowski, R., Kikkawa, S., Stein, A., Eds.; Wiley-VCH: Weinheim, Germany, 2017. [Google Scholar]
  90. Provino, A.; Steinberg, S.; Smetana, V.; Kulkarni, R.; Dhar, S.K.; Manfrinetti, P.; Mudring, A.-V. Gold-rich R3Au7Sn3: Establishing the interdependence between electronic features and physical properties. J. Mater. Chem. C 2015, 3, 8311–8321. [Google Scholar] [CrossRef]
  91. Smetana, V.; Steinberg, S.; Mudryk, Y.; Pecharsky, V.; Miller, G.J.; Mudring, A.-V. Cation-Poor Complex Metallic Alloys in Ba(Eu)−Au−Al(Ga) Systems: Identifying the Keys that Control Structural Arrangements and Atom Distributions at the Atomic Level. Inorg. Chem. 2015, 54, 10296–10308. [Google Scholar] [CrossRef] [PubMed]
  92. Bigun, I.; Steinberg, S.; Smetana, V.; Mudryk, Y.; Kalychak, Y.; Havela, L.; Pecharsky, V.; Mudring, A.-V. Magnetocaloric Behavior in Ternary Europium Indides EuT5In: Probing the Design Capability of First-Principles-Based Methods on the Multifaceted Magnetic Materials. Chem. Mater. 2017, 29, 2599–2614. [Google Scholar] [CrossRef]
  93. Blöchl, P.E. Projector augmented wave-method. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  94. Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B Condens. Matter Mater. Phys. 1993, 47, 558–561. [Google Scholar] [CrossRef]
  95. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  96. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
  97. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  98. Kresse, G.; Marsman, M.; Furthmüller, J. Vienna Ab-Initio Simulation Package VASP: The Guide; Computational Materials Physics, Faculty of Physics, Universität Wien: Vienna, Austria, 2014. [Google Scholar]
  99. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  100. Ertural, C.; Steinberg, S.; Dronskowski, R. Development of a robust tool to extract Mulliken and Löwdin charges from plane waves and its applications to solid-state materials. RSC Adv. 2019, 9, 29821–29830. [Google Scholar] [CrossRef] [PubMed]
  101. Dronskowski, R.; Blöchl, P.E. Crystal Orbital Hamilton Populations (COHP). Energy-Resolved Visualization of Chemical Bonding in Solids Based on Density-Functional Calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
  102. Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Crystal Orbital Hamilton Population (COHP) Analysis As Projected from Plane-Wave Basis Sets. J. Phys. Chem. A 2011, 115, 5461–5466. [Google Scholar] [CrossRef]
  103. Maintz, S.; Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Analytic Projection From Plane-Wave and PAW Wavefunctions and Application to Chemical-Bonding Analysis in Solids. J. Comput. Chem. 2013, 34, 2557–2567. [Google Scholar] [CrossRef]
  104. Maintz, S.; Deringer, V.L.; Tchougréff, A.L.; Dronskowski, R. LOBSTER: A tool to extract chemical bonding from plane-wave based DFT. J. Comput. Chem. 2016, 37, 1030–1035. [Google Scholar] [CrossRef]
  105. Eck, B. wxDragon 2.2.3; RWTH Aachen University: Aachen, Germany, 2020. [Google Scholar]
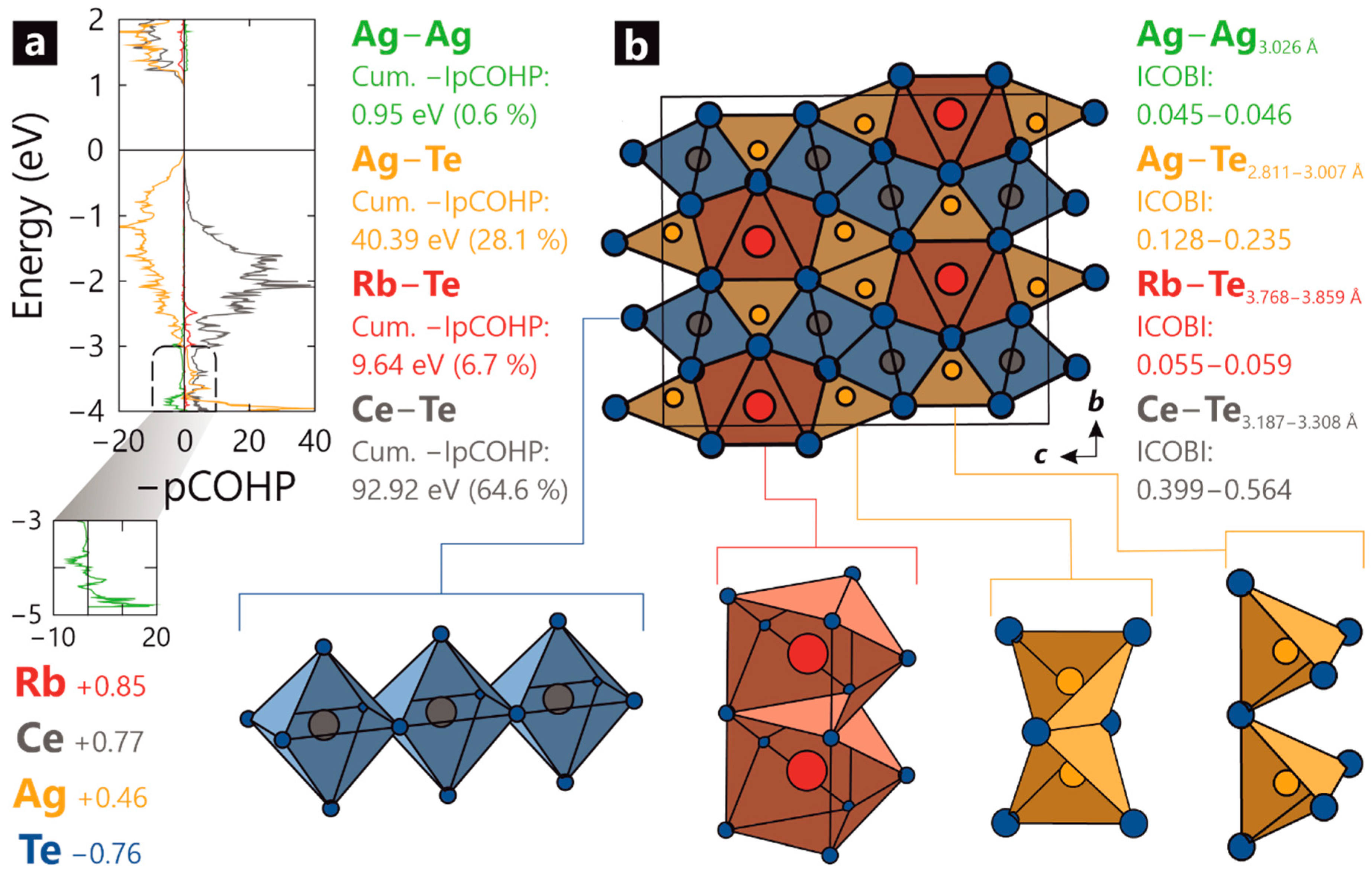
Inorganics 12 00192 g001
Figure 1. (a) Projected crystal orbital Hamilton population (−pCOHP) diagram, the corresponding cumulative integrated −pCOHP values (−IpCOHP/cell) and the respective percentages contributed to the net bonding capacities for the various interactions in RbCe2Ag3Te5; the valence band maximum is positioned below a band gap starting at 0 eV. (b) A visual representation of the crystal structure for the quaternary telluride: the diverse tellurium polyhedra encapsulating the rubidium, the silver as well as the cerium atoms and the averaged Mulliken charges (in units of the elementary charge e) are provided below, while the distance and ICOBI/bond ranges are included on the right side (ICOBI ≡ integrated COBI).
Figure 1. (a) Projected crystal orbital Hamilton population (−pCOHP) diagram, the corresponding cumulative integrated −pCOHP values (−IpCOHP/cell) and the respective percentages contributed to the net bonding capacities for the various interactions in RbCe2Ag3Te5; the valence band maximum is positioned below a band gap starting at 0 eV. (b) A visual representation of the crystal structure for the quaternary telluride: the diverse tellurium polyhedra encapsulating the rubidium, the silver as well as the cerium atoms and the averaged Mulliken charges (in units of the elementary charge e) are provided below, while the distance and ICOBI/bond ranges are included on the right side (ICOBI ≡ integrated COBI).
Inorganics 12 00192 g001
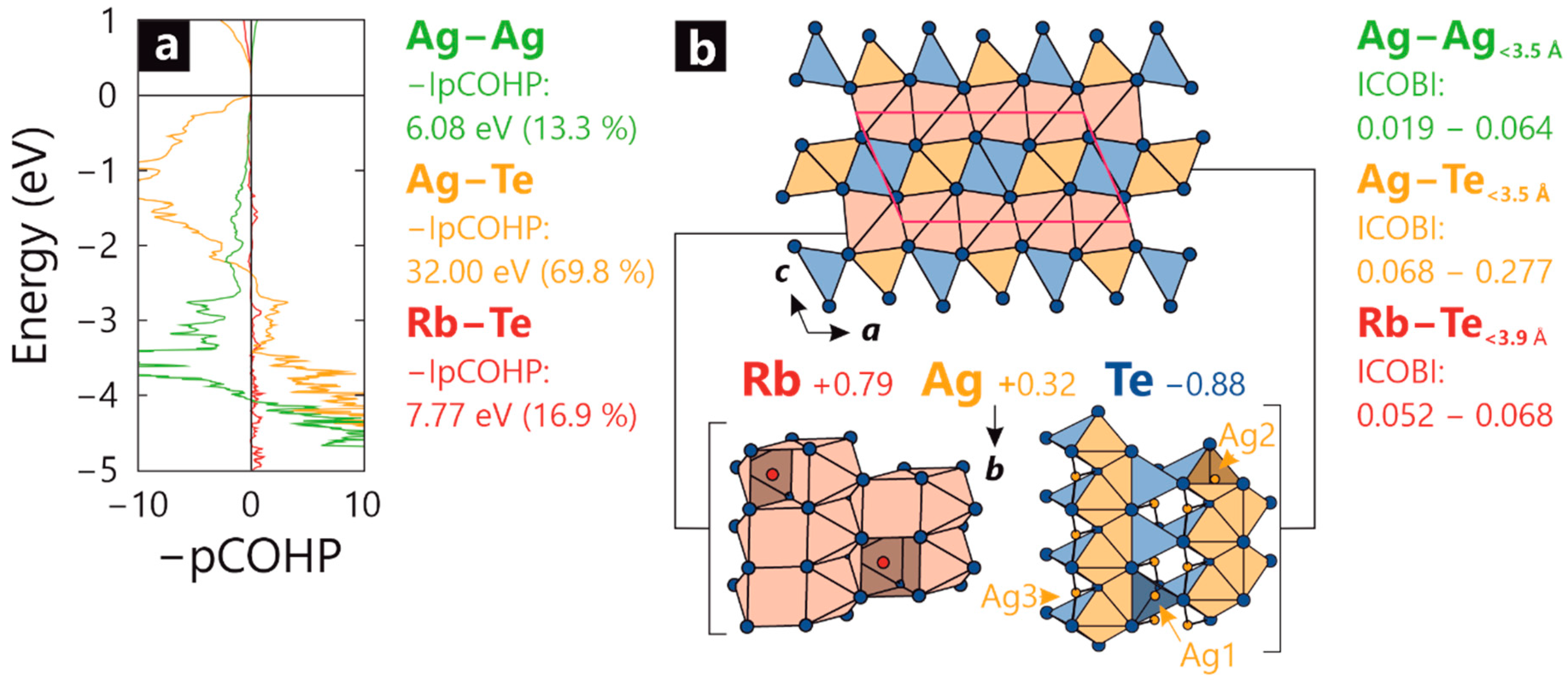
Inorganics 12 00192 g002
Figure 2. (a) −pCOHP diagram, the corresponding cumulative −IpCOHP/cell values and the respective percentages contributed to the net bonding capabilities for the diverse interactions in RbAg3Te2. The valence band maximum is located below a band gap at 0 eV. (b) A representation of the crystal structure for the ternary telluride. The diverse types of tellurium polyhedra enclosing the rubidium as well as the silver atoms and the averaged Mulliken charges (in units of the elementary charge e) are shown below, while the ICOBI/bond ranges have been included on the right side.
Figure 2. (a) −pCOHP diagram, the corresponding cumulative −IpCOHP/cell values and the respective percentages contributed to the net bonding capabilities for the diverse interactions in RbAg3Te2. The valence band maximum is located below a band gap at 0 eV. (b) A representation of the crystal structure for the ternary telluride. The diverse types of tellurium polyhedra enclosing the rubidium as well as the silver atoms and the averaged Mulliken charges (in units of the elementary charge e) are shown below, while the ICOBI/bond ranges have been included on the right side.
Inorganics 12 00192 g002
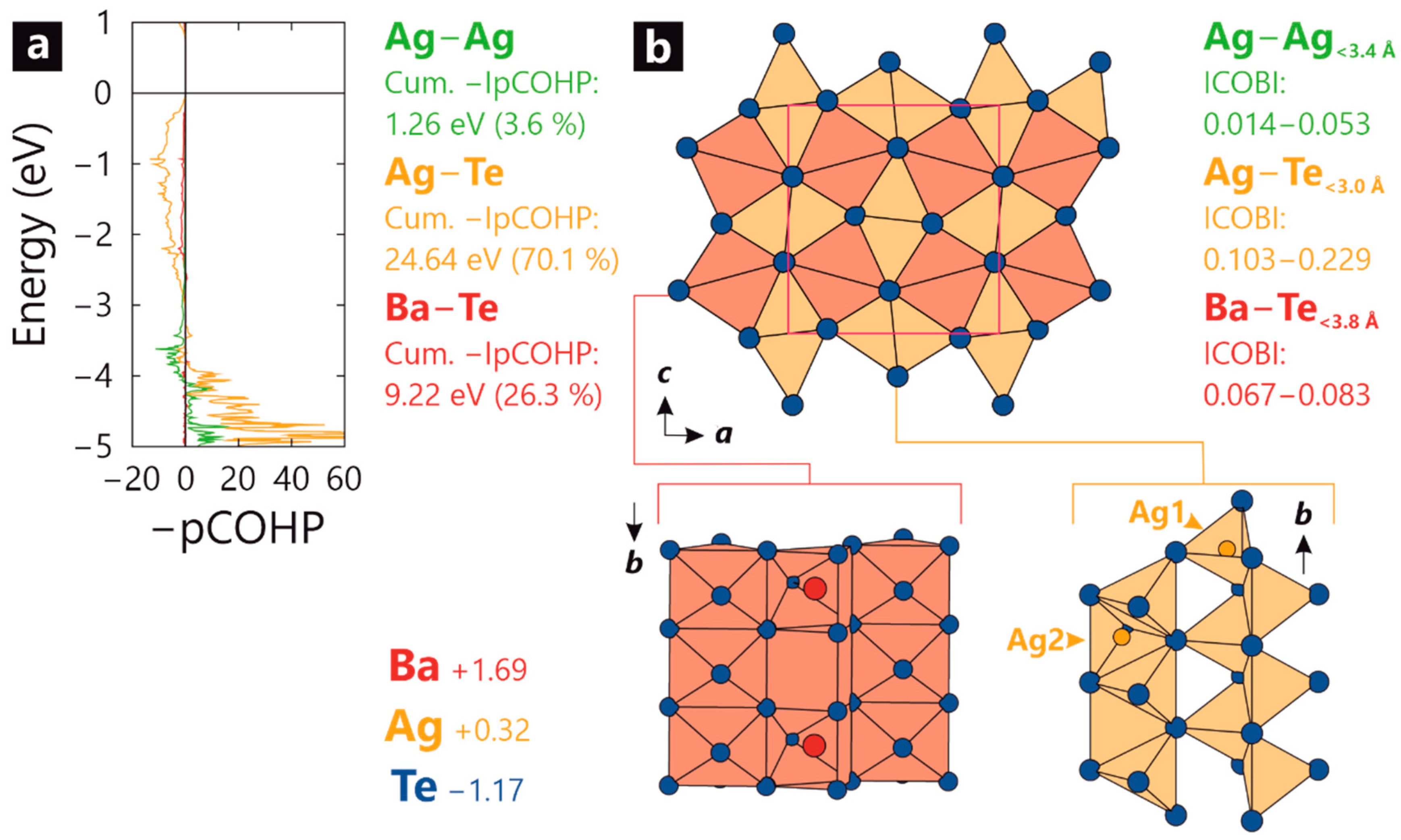
Inorganics 12 00192 g003
Figure 3. (a) −pCOHP diagram, cumulative −IpCOHP/cell values and the percentages contributed to net bonding capacities for diverse sorts of interactions in BaAg2Te2; the valence band maximum is positioned below a band gap at 0 eV. (b) A representation of the crystal structure for the ternary telluride; the diverse types of tellurium polyhedra enclosing the barium and silver atoms as well as the averaged Mulliken charges (in units of the elementary charge e) are shown below, while the ICOBI/bond ranges corresponding to the various interactions are provided on the right.
Figure 3. (a) −pCOHP diagram, cumulative −IpCOHP/cell values and the percentages contributed to net bonding capacities for diverse sorts of interactions in BaAg2Te2; the valence band maximum is positioned below a band gap at 0 eV. (b) A representation of the crystal structure for the ternary telluride; the diverse types of tellurium polyhedra enclosing the barium and silver atoms as well as the averaged Mulliken charges (in units of the elementary charge e) are shown below, while the ICOBI/bond ranges corresponding to the various interactions are provided on the right.
Inorganics 12 00192 g003
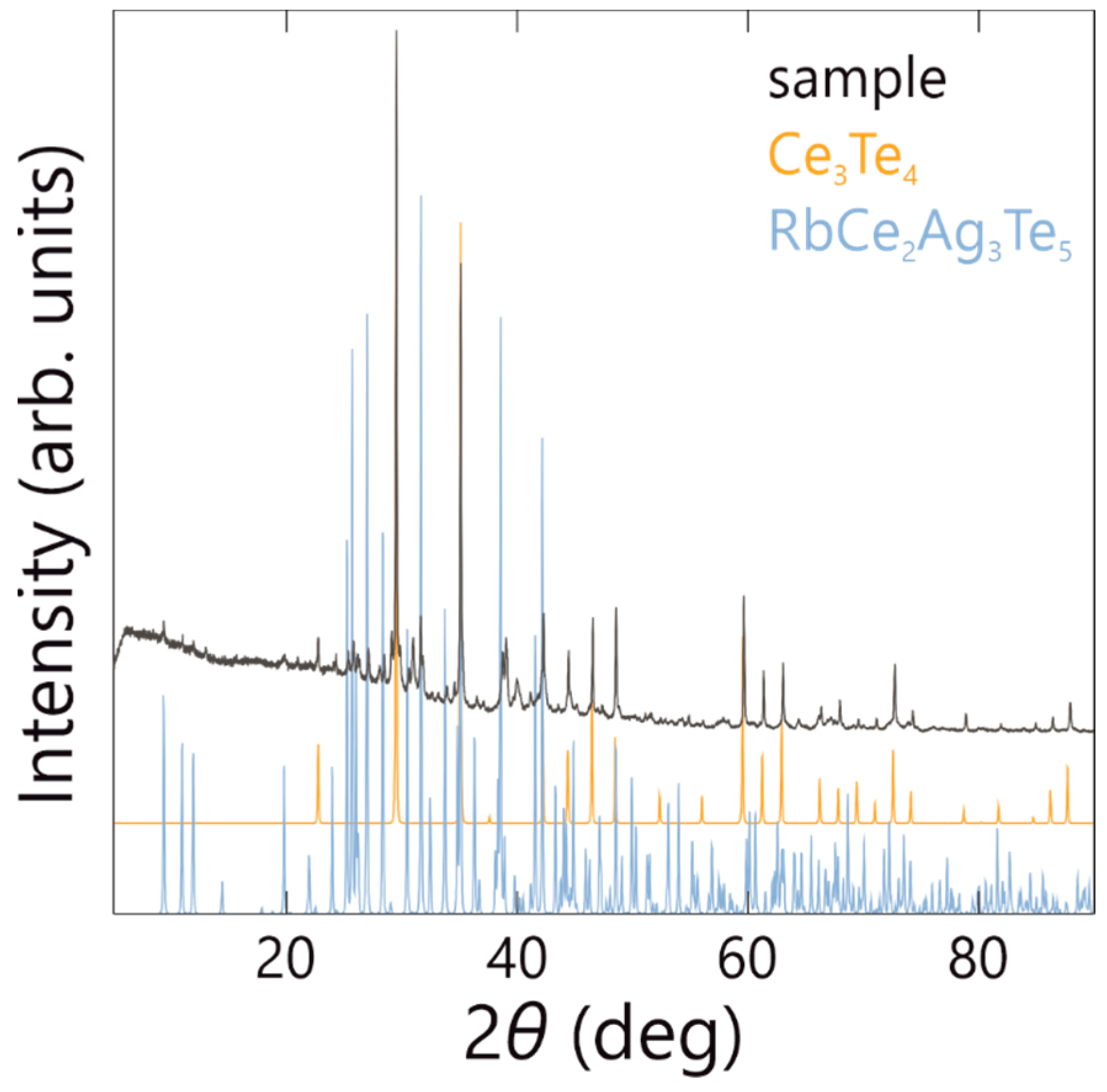
Inorganics 12 00192 g004
Figure 4. Powder X-ray diffraction patterns which have been observed for the RbCe2Ag3Te5-containing sample and simulated for the quaternary telluride as well as the binary Ce3Te4.
Figure 4. Powder X-ray diffraction patterns which have been observed for the RbCe2Ag3Te5-containing sample and simulated for the quaternary telluride as well as the binary Ce3Te4.
Inorganics 12 00192 g004
Table 1. Details of crystal structure investigations and refinements for RbCe2Ag3Te5.
Table 1. Details of crystal structure investigations and refinements for RbCe2Ag3Te5.
CompoundRbCe2Ag3Te5
fw1327.32
space groupCmcm
a (Å)4.665(2)
b (Å)16.142(6)
c (Å)18.874(7)
volume (Å3)1421.4(9)
Z4
density (calc., g/cm3)6.203
μ (mm−1)23.746
F (000)2216
θ ranges2.158–28.822
index ranges−5 ≤ h ≤ 6
−21 ≤ k ≤ 21
−24 ≤ l ≤ 25
reflections collected5332
independent reflections1072
refinement methodfull-matrix least squares on F2
data/restraints/parameter1072/0/37
goodness-of-fit on F20.995
final R indices [I > 2σ(I)]R1 = 0.0386; wR2 = 0.0762
R indices (all data)R1 = 0.0584; wR2 = 0.0832
Rint0.0816
largest diff. peak and hole (e−/Å3)−2.008 and 2.387
Table 2. Atomic position and equivalent isotropic displacement parameters of RbCe2Ag3Te5.
Table 2. Atomic position and equivalent isotropic displacement parameters of RbCe2Ag3Te5.
AtomWyckoff PositionxyzUeq, Å2
Ce18f00.1904 (1)0.4055 (1)0.0141 (2)
Te28f00.5573 (1)0.1223 (1)0.0155 (2)
Te38f00.1700 (1)0.5740 (1)0.0140 (2)
Te44c00.2612 (1)¼0.0157 (3)
Ag58f00.4134 (1)0.4732 (1)0.0233 (3)
Ag64c½0.1647 (1)¼0.0262 (4)
Rb74c00.0587 (1)¾0.0270 (5)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Weinelt, L.; Steinberg, S. Exploring the Nature of Ag–Ag Interactions in Different Tellurides by Means of the Crystal Orbital Bond Index (COBI). Inorganics 2024, 12, 192. https://doi.org/10.3390/inorganics12070192

AMA Style

Weinelt L, Steinberg S. Exploring the Nature of Ag–Ag Interactions in Different Tellurides by Means of the Crystal Orbital Bond Index (COBI). Inorganics. 2024; 12(7):192. https://doi.org/10.3390/inorganics12070192

Chicago/Turabian Style

Weinelt, Leander, and Simon Steinberg. 2024. "Exploring the Nature of Ag–Ag Interactions in Different Tellurides by Means of the Crystal Orbital Bond Index (COBI)" Inorganics 12, no. 7: 192. https://doi.org/10.3390/inorganics12070192

APA Style

Weinelt, L., & Steinberg, S. (2024). Exploring the Nature of Ag–Ag Interactions in Different Tellurides by Means of the Crystal Orbital Bond Index (COBI). Inorganics, 12(7), 192. https://doi.org/10.3390/inorganics12070192

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop