Prediction of Thermal Transport Properties of Pristine and BN-Substituted Holey Graphynes
Abstract
:1. Introduction
2. Results and Discussions
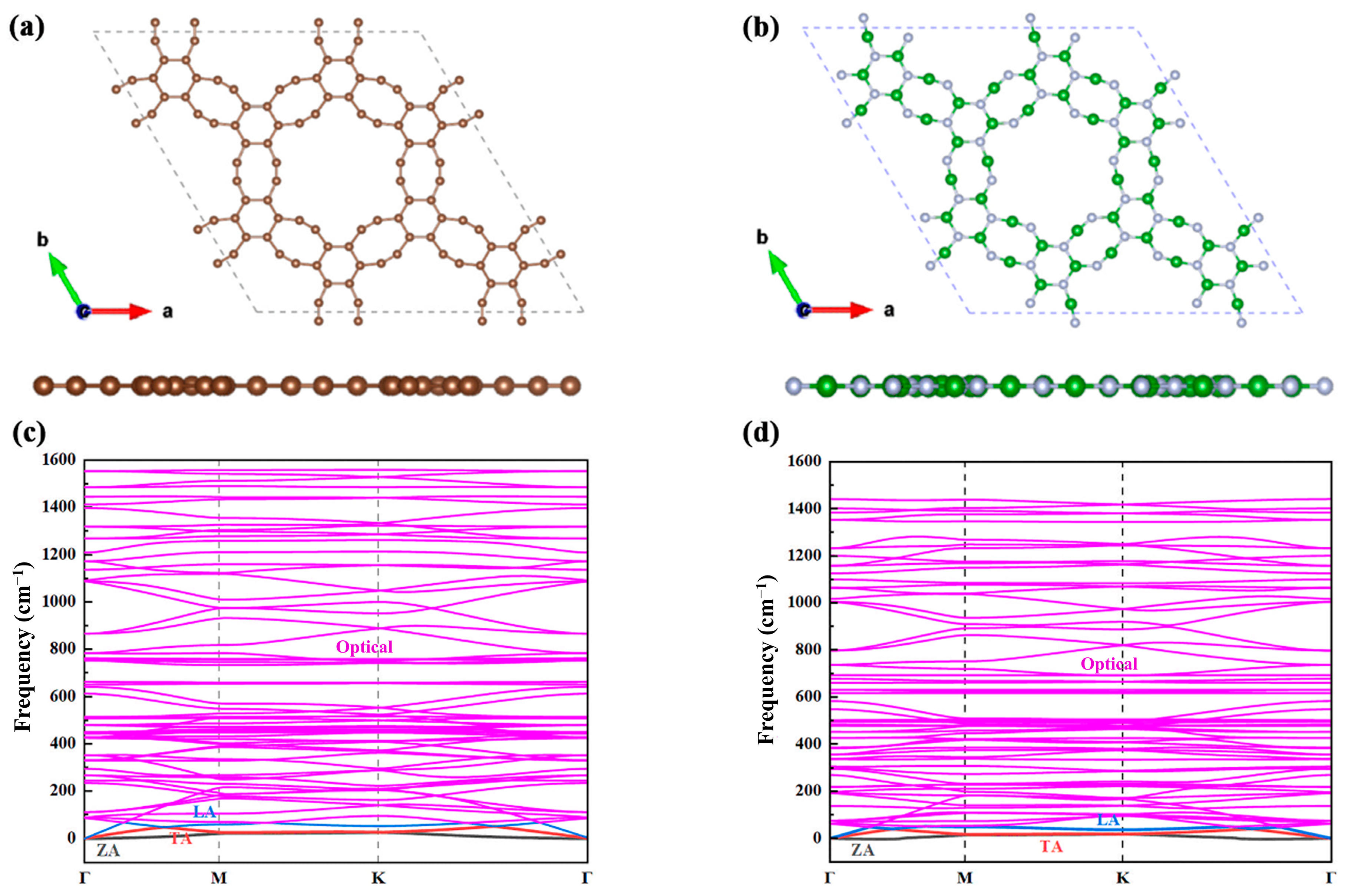
2.1. Structural Stability and Phonon Dispersion
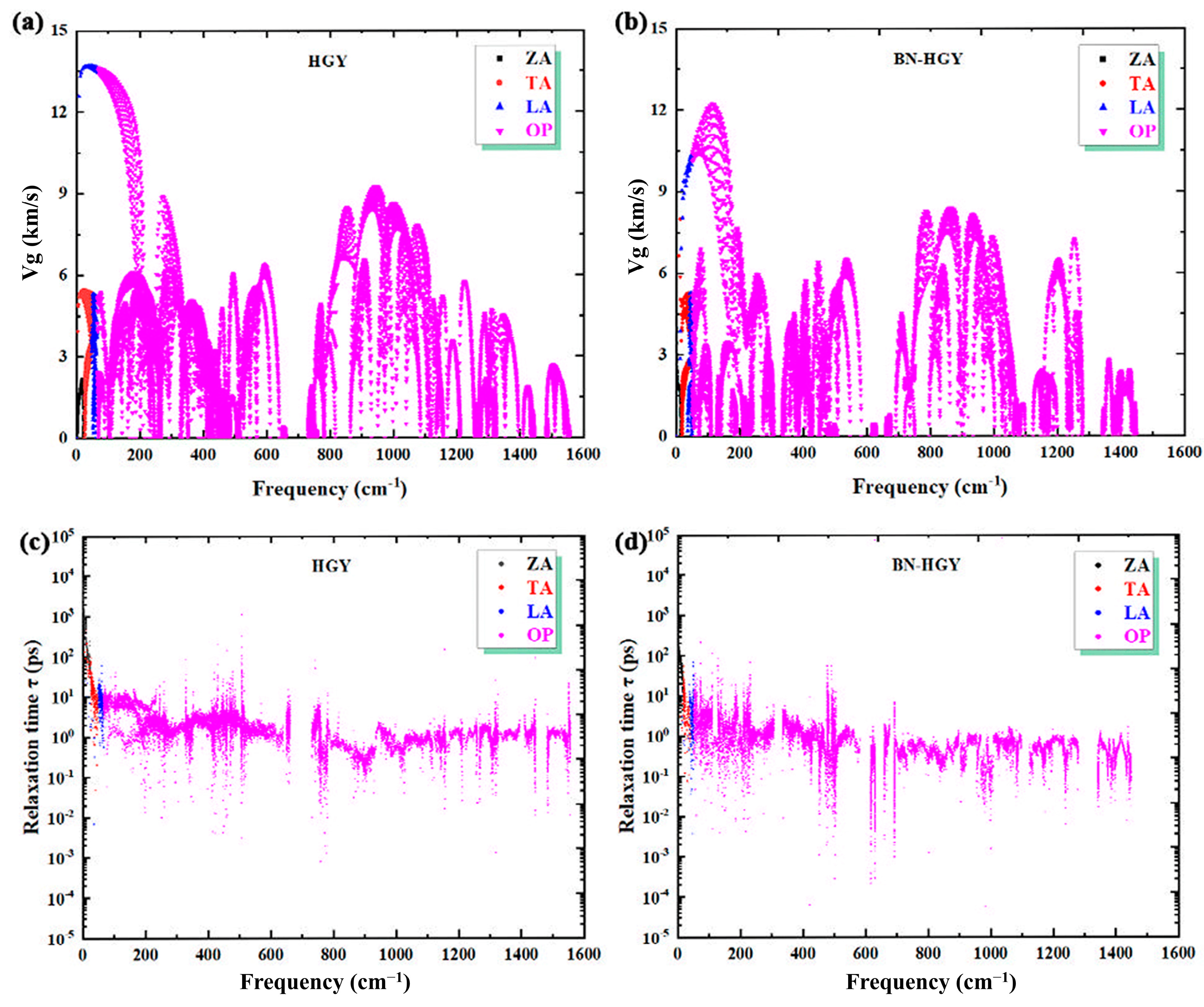
2.2. Phonon Transport Properties
2.2.1. Lattice Thermal Conductivity
2.2.2. Mode Level Analysis
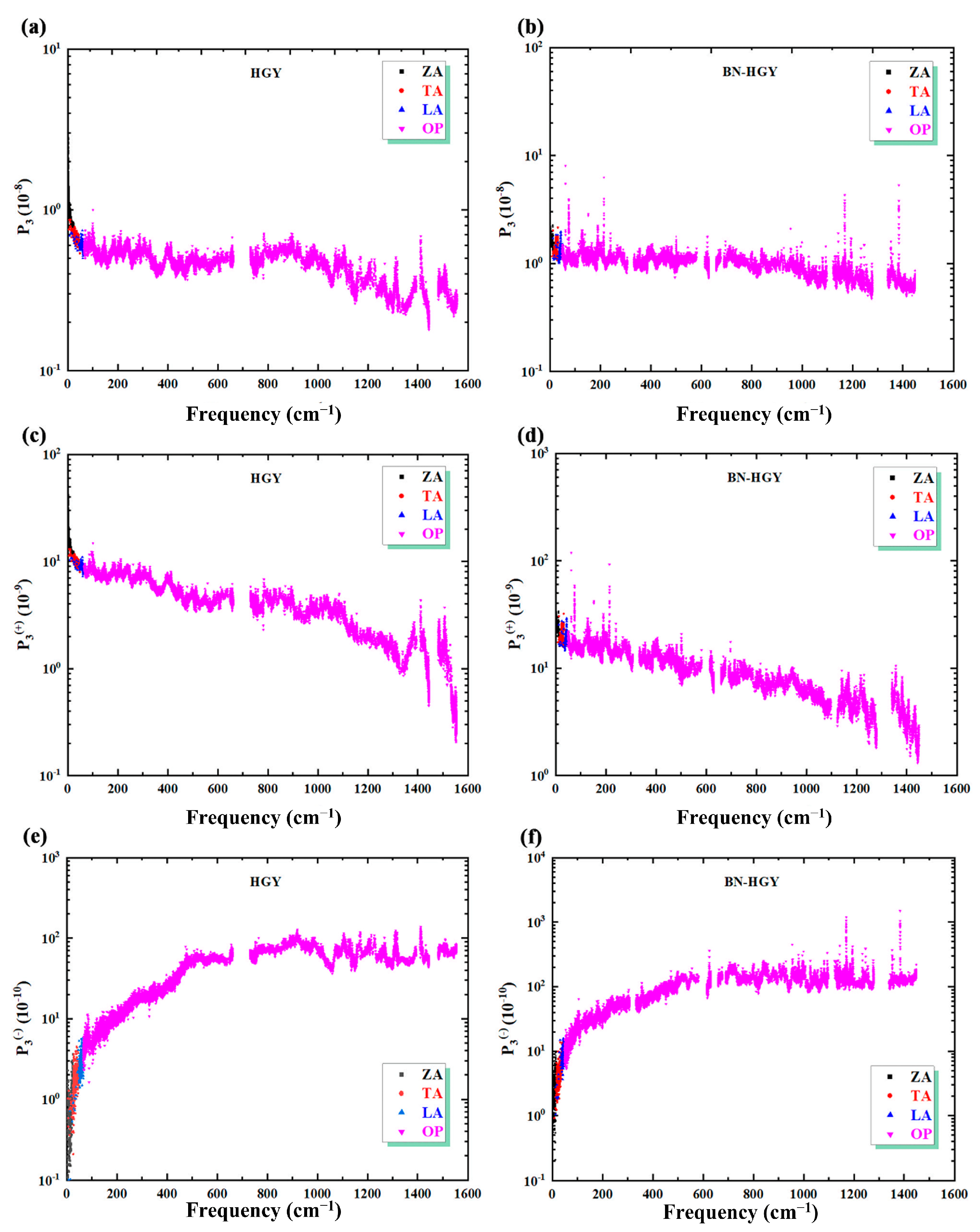
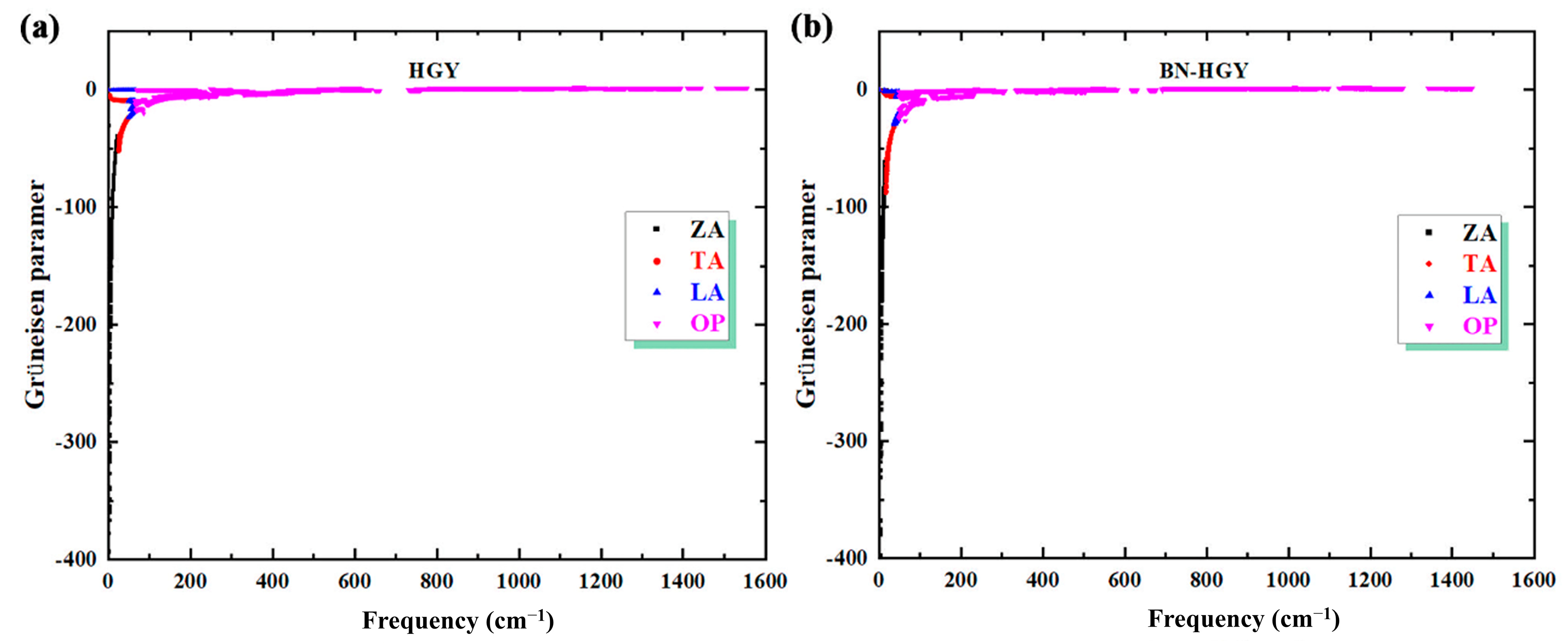
2.2.3. Phonon Scattering Process
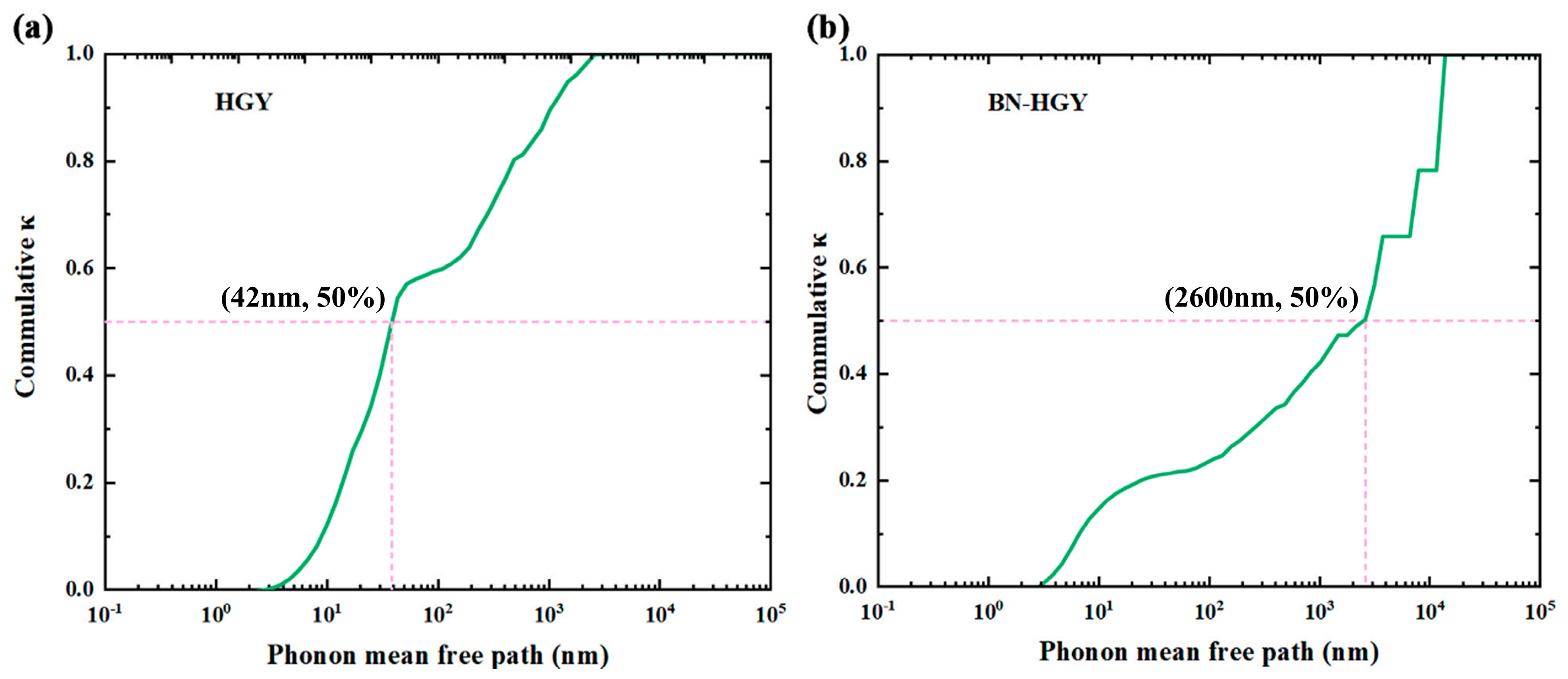
2.2.4. Size Effects
3. Calculation Method
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Braun, T.; Schubert, A.P.; Kostoff, R.N. Growth and trends of fullerene research as reflected in its journal literature. Chem. Rev. 2000, 100, 23–38. [Google Scholar] [CrossRef] [PubMed]
- Maruyama, K.; Nori, F.; Vedral, V. Colloquium: The physics of Maxwell’s demon and information. Rev. Mod. Phys. 2009, 81, 1–23. [Google Scholar] [CrossRef]
- Wang, C.; Takei, K.; Takahashi, T.; Javey, A. Carbon nanotube electronics–moving forward. Chem. Soc. Rev. 2013, 42, 2592–2609. [Google Scholar] [CrossRef] [PubMed]
- Mochalin, V.; Shenderova, O.; Ho, D.; Gogotsi, Y. The properties and applications of nanodiamonds. In Nano-Enabled Medical Applications; Jenny Stanford Publishing: Dubai, United Arab Emirates, 2020; pp. 313–350. [Google Scholar] [CrossRef]
- Liu, X.; Cho, S.M.; Lin, S.; Chen, Z.; Choi, W.; Kim, Y.-M.; Yun, E.; Baek, E.H.; Lee, H. Constructing two-dimensional holey graphyne with unusual annulative π-extension. Matter 2022, 5, 2306–2318. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.-E.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Mojica, M.; Méndez, F.; Alonso, J.A. Growth of fullerene fragments using the diels-alder cycloaddition reaction: First step towards a C60 synthesis by dimerization. Molecules 2013, 18, 2243–2254. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Baughman, R.; Eckhardt, H.; Kertesz, M. Structure-property predictions for new planar forms of carbon: Layered phases containing sp 2 and sp atoms. J. Chem. Phys. 1987, 87, 6687–6699. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Liu, H.; Guo, Y.; Li, Y.; Zhu, D. Architecture of graphdiyne nanoscale films. Chem. Commun. 2010, 46, 3256–3258. [Google Scholar] [CrossRef]
- Malko, D.; Neiss, C.; Vines, F.; Görling, A. Competition for graphene: Graphynes with direction-dependent dirac cones. Phys. Rev. Lett. 2012, 108, 086804. [Google Scholar] [CrossRef]
- Wu, W.; Guo, W.; Zeng, X.C. Intrinsic electronic and transport properties of graphyne sheets and nanoribbons. Nanoscale 2013, 5, 9264–9276. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xu, L.; Liu, H.; Li, Y. Graphdiyne and graphyne: From theoretical predictions to practical construction. Chem. Soc. Rev. 2014, 43, 2572–2586. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Liu, H.; Wang, D.; Zhang, J. Graphdiyne: Synthesis, properties, and applications. Chem. Soc. Rev. 2019, 48, 908–936. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Jing, Y.; Zhang, X. Low thermal conductivity of graphyne nanotubes from molecular dynamics study. Phys. Rev. B 2015, 91, 155408. [Google Scholar] [CrossRef]
- Park, W.; Guo, Y.; Li, X.; Hu, J.; Liu, L.; Ruan, X.; Chen, Y.P. High-performance thermal interface material based on few-layer graphene composite. J. Phys. Chem. C 2015, 119, 26753–26759. [Google Scholar] [CrossRef]
- Tan, X.; Shao, H.; Hu, T.; Liu, G.; Jiang, J.; Jiang, H. High thermoelectric performance in two-dimensional graphyne sheets predicted by first-principles calculations. Phys. Chem. Chem. Phys. 2015, 17, 22872–22881. [Google Scholar] [CrossRef]
- Xiao, Y.-J.; Wang, W.-Y.; Lin, T.; Chen, X.-J.; Zhang, Y.-T.; Yang, J.-H.; Wang, Y.; Zhou, Z.-W. Largely enhanced thermal conductivity and high dielectric constant of poly (vinylidene fluoride)/boron nitride composites achieved by adding a few carbon nanotubes. J. Phys. Chem. C 2016, 120, 6344–6355. [Google Scholar] [CrossRef]
- Nandkishore, R.; Chubukov, A.V. Interplay of superconductivity and spin-density-wave order in doped graphene. Phys. Rev. B Condens. Matter Mater. Phys. 2012, 86, 115426. [Google Scholar] [CrossRef]
- Faye, J.; Sahebsara, P.; Sénéchal, D. Chiral triplet superconductivity on the graphene lattice. Phys. Rev. B 2015, 92, 085121. [Google Scholar] [CrossRef]
- Ludbrook, B.; Levy, G.; Nigge, P.; Zonno, M.; Schneider, M.; Dvorak, D.; Veenstra, C.; Zhdanovich, S.; Wong, D.; Dosanjh, P. Evidence for superconductivity in Li-decorated monolayer graphene. Proc. Natl. Acad. Sci. USA 2015, 112, 11795–11799. [Google Scholar] [CrossRef]
- Zhou, J.; Sun, Q.; Wang, Q.; Jena, P. High-temperature superconductivity in heavily N-or B-doped graphene. Phys. Rev. B 2015, 92, 064505. [Google Scholar] [CrossRef]
- Li, T.; Lu, S.-P. Quantum conductance of graphene nanoribbons with edge defects. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 77, 085408. [Google Scholar] [CrossRef]
- Williams, J.R.; Abanin, D.A.; DiCarlo, L.; Levitov, L.S.; Marcus, C.M. Quantum Hall conductance of two-terminal graphene devices. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 80, 045408. [Google Scholar] [CrossRef]
- Rinzler, A.; Hafner, J.; Nikolaev, P.; Nordlander, P.; Colbert, D.; Smalley, R.; Lou, L.; Kim, S.; Tománek, D. Unraveling nanotubes: Field emission from an atomic wire. Science 1995, 269, 1550–1553. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Qian, X.; Liu, H.; Lin, H.; Chen, N.; Li, Y. Construction of tubular molecule aggregations of graphdiyne for highly efficient field emission. J. Phys. Chem. C 2011, 115, 2611–2615. [Google Scholar] [CrossRef]
- Dutta, S.; Pati, S.K. Half-metallicity in undoped and boron doped graphene nanoribbons in the presence of semilocal exchange-correlation interactions. J. Phys. Chem. B 2008, 112, 1333–1335. [Google Scholar] [CrossRef]
- Gan, L.-Y.; Zhang, Q.; Guo, C.-S.; Schwingenschlogl, U.; Zhao, Y. Two-dimensional MnO2/graphene interface: Half-metallicity and quantum anomalous hall state. J. Phys. Chem. C 2016, 120, 2119–2125. [Google Scholar] [CrossRef]
- Lherbier, A.; Liang, L.; Charlier, J.-C.; Meunier, V. Charge carrier transport and separation in pristine and nitrogen-doped graphene nanowiggle heterostructures. Carbon 2015, 95, 833–842. [Google Scholar] [CrossRef]
- Berdiyorov, G.; Bahlouli, H.; Peeters, F. Effect of substitutional impurities on the electronic transport properties of graphene. Phys. E 2016, 84, 22–26. [Google Scholar] [CrossRef]
- Abanin, D.A.; Lee, P.A.; Levitov, L.S. Randomness-induced XY ordering in a graphene quantum Hall ferromagnet. Phys. Rev. Lett. 2007, 98, 156801. [Google Scholar] [CrossRef]
- Miao, F.; Wijeratne, S.; Zhang, Y.; Coskun, U.; Bao, W.; Lau, C. Phase-coherent transport in graphene quantum billiards. Science 2007, 317, 1530–1533. [Google Scholar] [CrossRef]
- Schedin, F.; Geim, A.K.; Morozov, S.V.; Hill, E.W.; Blake, P.; Katsnelson, M.I.; Novoselov, K.S. Detection of individual gas molecules adsorbed on graphene. Nat. Mater. 2007, 6, 652–655. [Google Scholar] [CrossRef] [PubMed]
- Hass, J.; Feng, R.; Li, T.; Li, X.; Zong, Z.; De Heer, W.; First, P.; Conrad, E.; Jeffrey, C.; Berger, C. Highly ordered graphene for two dimensional electronics. Appl. Phys. Lett. 2006, 89, 143106. [Google Scholar] [CrossRef]
- Park, J.-S.; Choi, H.J. Band-gap opening in graphene: A reverse-engineering approach. Phys. Rev. B 2015, 92, 045402. [Google Scholar] [CrossRef]
- Cao, X.; Shi, J.-J.; Zhang, M.; Jiang, X.-H.; Zhong, H.-X.; Huang, P.; Ding, Y.-M.; Wu, M. Band gap opening of graphene by forming heterojunctions with the 2D carbonitrides nitrogenated holey graphene, g-C3N4, and g-CN: Electric field effect. J. Phys. Chem. C 2016, 120, 11299–11305. [Google Scholar] [CrossRef]
- Sahu, S.; Rout, G. Band gap opening in graphene: A short theoretical study. Int. Nano Lett. 2017, 7, 81–89. [Google Scholar] [CrossRef]
- Tang, S.; Wu, W.; Xie, X.; Li, X.; Gu, J. Band gap opening of bilayer graphene by graphene oxide support doping. RSC Adv. 2017, 7, 9862–9871. [Google Scholar] [CrossRef]
- Thomas, A.; Fischer, A.; Goettmann, F.; Antonietti, M.; Müller, J.-O.; Schlögl, R.; Carlsson, J.M. Graphitic carbon nitride materials: Variation of structure and morphology and their use as metal-free catalysts. J. Mater. Chem. 2008, 18, 4893–4908. [Google Scholar] [CrossRef]
- Mahmood, J.; Lee, E.K.; Jung, M.; Shin, D.; Jeon, I.-Y.; Jung, S.-M.; Choi, H.-J.; Seo, J.-M.; Bae, S.-Y.; Sohn, S.-D. Nitrogenated holey two-dimensional structures. Nat. Commun. 2015, 6, 6486. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, H.; Sun, M.; Ding, Y.; Zhang, L.; Li, Q. First-principles study of intrinsic phononic thermal transport in monolayer C3N. Phys. E 2018, 99, 194–201. [Google Scholar] [CrossRef]
- Wang, H.; Li, Q.; Pan, H.; Gao, Y.; Sun, M. Comparative investigation of the mechanical, electrical and thermal transport properties in graphene-like C3B and C3N. J. Appl. Phys. 2019, 126, 234302. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, H.; Pan, H.; Li, Q.; Zhao, J. Ultrahigh hydrogen storage capacity of holey graphyne. Nanotechnology 2021, 32, 215402. [Google Scholar] [CrossRef]
- Mahamiya, V.; Shukla, A.; Chakraborty, B. Prediction of a novel 2D porous boron nitride material with excellent electronic, optical and catalytic properties. Phys. Chem. Chem. Phys. 2022, 24, 21009–21019. [Google Scholar] [CrossRef] [PubMed]
- Desyatkin, V.G.; Martin, W.B.; Aliev, A.E.; Chapman, N.E.; Fonseca, A.F.; Galvão, D.S.; Miller, E.R.; Stone, K.H.; Wang, Z.; Zakhidov, D.; et al. Scalable Synthesis and Characterization of Multilayer γ-Graphyne, New Carbon Crystals with a Small Direct Band Gap. J. Am. Chem. Soc. 2022, 144, 17999–18008. [Google Scholar] [CrossRef]
- Aliev, A.E.; Guo, Y.; Fonseca, A.F.; Razal, J.M.; Wang, Z.; Galvão, D.S.; Bolding, C.M.; Chapman-Wilson, N.E.; Desyatkin, V.G.; Leisen, J.E.; et al. A planar-sheet nongraphitic zero-bandgap sp 2 carbon phase made by the low-temperature reaction of γ-graphyne. Proc. Natl. Acad. Sci. USA 2025, 122, e2413194122. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Tiwari, J.; Feng, T.; Shi, Z.; Lou, Y.; Xu, B. High thermoelectric properties with low thermal conductivity due to the porous structure induced by the dendritic branching in n-type PbS. Nano Res. 2022, 15, 4739–4746. [Google Scholar] [CrossRef]
- Du, K.; Deng, S.; Qi, N.; Zhou, B.; Chen, Z.; Su, X.; Tang, X. Ultralow thermal conductivity in In2O3 mediated by porous structures. Microporous Mesoporous Mater. 2019, 288, 109525. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, B.; Zhang, S.; Sun, Y.; Long, M. Effects of interface charge-transfer doping on thermoelectric transport properties of black phosphorene-F4TCNQ nanoscale devices. Appl. Surf. Sci. 2022, 579, 152155. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhang, B. Interface design of the thermoelectric transport properties of phosphorene-tetrathiafulvalene nanoscale devices. Phys. Chem. Chem. Phys. 2023, 25, 27448–27456. [Google Scholar] [CrossRef]
- Deb, J.; Mondal, R.; Sarkar, U.; Sadeghi, H. Thermoelectric Properties of Pristine Graphyne and the BN-Doped Graphyne Family. ACS Omega 2021, 6, 20149–20157. [Google Scholar] [CrossRef]
- Qin, G.; Qin, Z.; Fang, W.-Z.; Zhang, L.-C.; Yue, S.-Y.; Yan, Q.-B.; Hu, M.; Su, G. Diverse anisotropy of phonon transport in two-dimensional group IV–VI compounds: A comparative study. Nanoscale 2016, 8, 11306–11319. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, H.; Shao, H.; Xu, Y.; Zhang, X.; Zhu, H. Towards intrinsic phonon transport in single-layer MoS2. Ann. Phys. 2016, 528, 504–511. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, H.; Shao, H.; Xu, Y.; Ni, G.; Zhang, R.; Zhu, H. Phonon transport properties of two-dimensional group-IV materials from ab initio calculations. Phys. Rev. B 2016, 94, 245420. [Google Scholar] [CrossRef]
- Wu, X.; Varshney, V.; Lee, J.; Zhang, T.; Wohlwend, J.L.; Roy, A.K.; Luo, T. Hydrogenation of penta-graphene leads to unexpected large improvement in thermal conductivity. Nano Lett. 2016, 16, 3925–3935. [Google Scholar] [CrossRef]
- Peng, Q.; Ji, W.; De, S. Mechanical properties of the hexagonal boron nitride monolayer: Ab initio study. Comput. Mater. Sci. 2012, 56, 11–17. [Google Scholar] [CrossRef]
- Gu, X.; Yang, R. First-principles prediction of phononic thermal conductivity of silicene: A comparison with graphene. J. Appl. Phys. 2015, 117, 025102. [Google Scholar] [CrossRef]
- Hossein, T.; Mohammad, T.; Sajjad, A.; Qitong, L.; Eric, V.W.; Mengkun, T.; Ali, A.E.; Yuanqi, L.; Xiang, Z.; Pulickel, M.A.; et al. Ion-Assisted Nanoscale Material Engineering in Atomic Layers. arXiv 2024, arXiv:2410.06181. [Google Scholar]
- Kosynkin, D.V.; Higginbotham, A.L.; Sinitskii, A.; Lomeda, J.R.; Dimiev, A.; Price, B.K.; Tour, J.M. Longitudinal unzipping of carbon nanotubes to form graphene nanoribbons. Nature 2009, 458, 872–876. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Carrete, J.; Katcho, N.A.; Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 2014, 185, 1747–1758. [Google Scholar] [CrossRef]
- Peng, C.; Qin, G.; Zhang, L.; Zhang, G.; Wang, C.; Yan, Y.; Wang, Y.; Hu, M. Dependence of phonon transport properties with stacking thickness in layered ZnO. J. Phys. D Appl. Phys. 2018, 51, 315303. [Google Scholar] [CrossRef]
- Wang, C.; Wang, H.; Chen, Y.; Yao, S.-H.; Zhou, J. First-principles study of lattice thermal conductivity in ZrTe5 and HfTe5. J. Appl. Phys. 2018, 123, 175104. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]

| Materials | HGY | BN-HGY | Graphene [41] | h-BN [52] | MoS2 [53] |
|---|---|---|---|---|---|
| Conductivity κ(W/mK) | 38.01 | 24.30 | 3550 | 250 | 100 |
| ZA | TA | LA | Optical | |
|---|---|---|---|---|
| HGY | 31.89% | 11.73% | 5.23% | 51.14% |
| BN-HGY | 78.77% | 8.92% | 0.51% | 11.80% |
| graphene | 82.92% | 10.1% | 6.7% | 1.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Zhang, Y.; Liu, Y.; Gao, Y.; Deng, B. Prediction of Thermal Transport Properties of Pristine and BN-Substituted Holey Graphynes. Inorganics 2025, 13, 128. https://doi.org/10.3390/inorganics13040128
Li Q, Zhang Y, Liu Y, Gao Y, Deng B. Prediction of Thermal Transport Properties of Pristine and BN-Substituted Holey Graphynes. Inorganics. 2025; 13(4):128. https://doi.org/10.3390/inorganics13040128
Chicago/Turabian StyleLi, Qingchen, Yujie Zhang, Yanlong Liu, Yan Gao, and Baoxia Deng. 2025. "Prediction of Thermal Transport Properties of Pristine and BN-Substituted Holey Graphynes" Inorganics 13, no. 4: 128. https://doi.org/10.3390/inorganics13040128
APA StyleLi, Q., Zhang, Y., Liu, Y., Gao, Y., & Deng, B. (2025). Prediction of Thermal Transport Properties of Pristine and BN-Substituted Holey Graphynes. Inorganics, 13(4), 128. https://doi.org/10.3390/inorganics13040128






