Assessing Covalency in Cerium and Uranium Hexachlorides: A Correlated Wavefunction and Density Functional Theory Study

Abstract

The electronic structure of a series of uranium and cerium hexachlorides in a variety of oxidation states was evaluated at both the correlated wavefunction and density functional (DFT) levels of theory. Following recent experimental observations of covalency in tetravalent cerium hexachlorides, bonding character was studied using topological and integrated analysis based on the quantum theory of atoms in molecules (QTAIM). This analysis revealed that M–Cl covalency was strongly dependent on oxidation state, with greater covalency found in higher oxidation state complexes. Comparison of M–Cl delocalisation indices revealed a discrepancy between correlated wavefunction and DFT-derived values. Decomposition of these delocalisation indices demonstrated that the origin of this discrepancy lay in ungerade contributions associated with the f-manifold which we suggest is due to self-interaction error inherent to DFT-based methods. By all measures used in this study, extremely similar levels of covalency between complexes of U and Ce in the same oxidation state was found.

1. Introduction

The question of covalency in f-element bonding is challenging to both experimentalists and theorists alike. Complexes of the f-elements typically exhibit strong relativistic effects, substantial dynamical electron correlation and weak crystal fields. These phenomena result in highly complicated electronic structures and, as such, theoretical measures of covalency based on different premises can lead to qualitatively different conclusions [1]: In particular, the strong deviation from an independent particle approximation in these strongly-correlated systems can lead to consistent, but apparently contradictory, orbital-based descriptions of the electronic structure [2,3,4,5]. This ambiguity can be avoided by instead turning to analytical methods based on the experimentally observable electron density. Such approaches are appealing since they are not directly influenced by the theoretical methodology employed in the obtention of the density to be analysed: in fact, such analyses can be applied to experimental densities derived from low temperature X-ray diffraction (XRD) data [6]. The most popular of these density-based approaches is the Quantum Theory of Atoms in Molecules (QTAIM) approach of Bader [7], which provides the theoretical framework for an unambiguous and transferable analytical tool with which to probe the nature of electronic structure and bonding in chemical systems. This approach has been applied to several problems in f-element chemistry [4,6,8,9,10,11,12,13,14,15,16] and is able to provide quantitative measures of covalency via both topological and integrated properties of the electron-density.

Recently, X-ray absorption spectroscopy (XAS) has emerged as an extremely powerful experimental technique for the characterisation of bonding in organometallic and inorganic complexes of the f-elements [17,18,19]. Intriguingly, this approach has provided compelling evidence of covalent interactions in Ce(IV) hexachloride [20]. Furthermore, the degree of covalency has been shown to be comparable to that found in the uranium analogue, although the relative contribution from d- and f-shells differs. These results motivated us to perform a theoretical study of the bonding in uranium and cerium hexachlorides, combining state of the art multiconfigurational quantum chemical simulations with the density-based analyses discussed above. These simulations consider a variety of oxidation states and support the experimentally-based assertion of non-negligible covalent character, while highlighting the sensitivity of this phenomenon to the quantum chemical methodology employed.

2. Results

2.1. Structural Characterisation

Structural optimisation of the MCl₆ⁿ⁻ complexes was performed numerically at the DFT level of theory using the PBE and B3LYP functionals, as well as using the Restricted Active Space Self Consistent Field with 2nd Order Perturbation Theory (RASPT2) methodology. For the formally closed shell U(VI) and Ce(IV) complexes, a ¹A_g ground state was assumed, whereas for open shell systems the lowest energy state of each irreducible representation was calculated in order to identify the ground state. Optimisations were performed by varying the M–Cl bond length in increments of 0.01 Å until an energetic minimum was obtained. Table 1 reports the ground state symmetries and spin-multiplicities, along with optimal bond-lengths, for each level of theory. For comparison, literature data of experimentally derived bond lengths are also included. Where experimental data exists [20,21], M–Cl bond lengths appear to be ~0.02 Å longer in the aqueous phase than in the solid state and, bearing in mind that a continuum solvation model is employed here, it might be expected that theoretical results would be in better agreement with aqueous phase data.

Table 1. Ground states and calculated optimal bond-lengths for all complexes considered in this study.

Complex	State	rM–Cl (Å)
		CASPT2	RASPT2	B3LYP	PBE	Experimental
[U(VI)Cl6]	1Ag	2.45	2.48	2.47	2.48	2.47 a
[U(V)Cl6]−	2Au	2.53	2.54	2.55	2.55	2.52 b
[U(IV)Cl6]2−	3B1g/3B2g/3B3g	2.65	2.69	2.66	2.65	2.62 c, 2.65 d
[U(III)Cl6]3−	4Au	2.86	2.89	2.83	2.80	-
[Ce(IV)Cl6]2−	1Ag	2.62	2.64	2.67	2.65	2.60 e, 2.62 f
[Ce(III)Cl6]3−	2B1u/2B2u/2B3u	2.85	2.86	2.82	2.79	2.77 e, 2.79 f

^a XRD [22]; ^b XRD [23]; ^c XRD [21]; ^d EXAFS [21]; ^e XRD [20]; ^f EXAFS [20].

Table 1. Ground states and calculated optimal bond-lengths for all complexes considered in this study.

Complex	State	rM–Cl (Å)
		CASPT2	RASPT2	B3LYP	PBE	Experimental
[U(VI)Cl6]	1Ag	2.45	2.48	2.47	2.48	2.47 a
[U(V)Cl6]−	2Au	2.53	2.54	2.55	2.55	2.52 b
[U(IV)Cl6]2−	3B1g/3B2g/3B3g	2.65	2.69	2.66	2.65	2.62 c, 2.65 d
[U(III)Cl6]3−	4Au	2.86	2.89	2.83	2.80	-
[Ce(IV)Cl6]2−	1Ag	2.62	2.64	2.67	2.65	2.60 e, 2.62 f
[Ce(III)Cl6]3−	2B1u/2B2u/2B3u	2.85	2.86	2.82	2.79	2.77 e, 2.79 f

^a XRD [22]; ^b XRD [23]; ^c XRD [21]; ^d EXAFS [21]; ^e XRD [20]; ^f EXAFS [20].

All methodologies reproduce XRD-derived bond lengths with high accuracy in the closed shell U(VI) complex, whereas there is slight overestimation in the U(V) complex. This overestimation is also present in the RASPT2 bond lengths of the U(IV) complex, although CASPT2 results are in excellent agreement with both DFT and experiment. To the authors’ knowledge, no experimental data exists for the U(III) complex, but the U(III) ionic radii is some 0.14 Å greater than that of U(IV), in line with the increased bond lengths found theoretically. The significantly longer U(III)–Cl bond found at the RASPT2 level may indicate that the large active space employed has reduced the effect of the PT2 correction, which would normally correct for the bond length overestimation found in the absence of dynamical correlation. Again, CASPT2 gives a shorter U–Cl bond.

When considering the closed shell Ce(IV) complex, CASPT2 best reproduces the EXAFS-derived bond lengths but both wavefunction-based methods overestimate those of the Ce(III) complex, whereas DFT simulations, particularly those employing the PBE exchange-correlation functional, give much better agreement with experiment.

In order to validate the numerical optimisations performed here, analytical optimisations were performed for all systems at the B3LYP level of theory using the TURBOMOLE quantum chemistry code. In all cases agreement was obtained to within 0.02 Å, with the greatest deviation occurring for the more highly charged systems. It can be seen in Table 1 that deviation from experiment is greatest when the overall charge of the system is high. Gas phase optimisations were also performed (See Table S1 of electronic supporting information (ESI)) and showed that the presence of the continuum solvation model leads to a significant reduction in bond lengths, particularly for more highly charged systems.

2.2. Natural Orbital Occupancies

In this section the natural orbital [24] occupancies (NOOs) of active space orbitals in each of the systems studied are considered. The natural orbitals (NOs) provide a basis for the most compact CI expansion of the exact wavefunction and their associated occupation numbers therefore provide a measure of multiconfigurational character [25]. Typically, this multiconfigurational character manifests itself in terms of “strongly occupied” orbitals with NOOs close to two and “weakly occupied” correlating orbitals with NOOs close to zero. Often the strongly and weakly occupied orbitals have bonding and antibonding character, respectively. Another potential origin of multiconfigurational character can manifest itself in two or more singly-occupied metal-based orbitals having NOOs deviating significantly from one due to the fact that configurations in which different combinations of these orbitals are occupied are near-degenerate.

Of the seven orbitals available for f-electron occupation, three have formally σ-antibonding character, three δ-antibonding character and one non-bonding character, although it should be borne in mind that the degree of interaction with the ligands may be minimal: hereafter, these orbitals will be labelled as f_σ, f_δ, and f_NB, respectively. Table 2 summarises the natural occupancies of these f-orbitals for each system under consideration.

Table 2. f-Orbital occupations for each complex considered in this study, calculated at the Complete/Restricted Active Space Self-Consistent Field (CAS/RASSCF) level of theory.

Complex	f-Orbital Occupation
	CASSCF	RASSCF
[U(VI)Cl6]	${\text{f}}^0$	${\text{f}}^0$
[U(V)Cl6]−	0.996 ${\text{ f}}_{\text{NB}}^1$	1.001 ${\text{ f}}_{\text{NB}}^1$
[U(IV)Cl6]2−	0.998 ${\text{ f}}_{\text{NB}}^1$ 0.998 ${\text{ f}}_{\text{σ}}^1$	1.000 ${\text{ f}}_{\text{NB}}^1$ 1.000 ${\text{ f}}_{\text{σ}}^1$
[U(III)Cl6]3−	0.915 ${\text{ f}}_{\text{δ}}^3$ (0.091 ${\text{ f}}_{\text{σ}}^1)$	0.999 ${\text{ f}}_{\text{δ}}^3$ (0.007 ${\text{ f}}_{\text{σ}}^1)$
[Ce(IV)Cl6]2−	${\text{f}}^0$	${\text{f}}^0$
[Ce(III)Cl6]3−	0.999 ${\text{ f}}_{\text{δ}}^1$	1.000 ${\text{ f}}_{\text{δ}}^1$

Table 2. f-Orbital occupations for each complex considered in this study, calculated at the Complete/Restricted Active Space Self-Consistent Field (CAS/RASSCF) level of theory.

Complex	f-Orbital Occupation
	CASSCF	RASSCF
[U(VI)Cl6]	${\text{f}}^0$	${\text{f}}^0$
[U(V)Cl6]−	0.996 ${\text{ f}}_{\text{NB}}^1$	1.001 ${\text{ f}}_{\text{NB}}^1$
[U(IV)Cl6]2−	0.998 ${\text{ f}}_{\text{NB}}^1$ 0.998 ${\text{ f}}_{\text{σ}}^1$	1.000 ${\text{ f}}_{\text{NB}}^1$ 1.000 ${\text{ f}}_{\text{σ}}^1$
[U(III)Cl6]3−	0.915 ${\text{ f}}_{\text{δ}}^3$ (0.091 ${\text{ f}}_{\text{σ}}^1)$	0.999 ${\text{ f}}_{\text{δ}}^3$ (0.007 ${\text{ f}}_{\text{σ}}^1)$
[Ce(IV)Cl6]2−	${\text{f}}^0$	${\text{f}}^0$
[Ce(III)Cl6]3−	0.999 ${\text{ f}}_{\text{δ}}^1$	1.000 ${\text{ f}}_{\text{δ}}^1$

Typically, f-orbital occupation is uncomplicated, with NOOs close to unity in all cases, however the CASSCF simulation of the U(III) complex presents deviation from this behaviour. Whilst to a first degree of approximation, the system would be described as having a$5{\text{f}}_{\text{δ}}^3$ subconfiguration, the NOO for each orbital is just 0.915. Correspondingly, each of the three f_σ orbitals have NOOs of 0.091. Occupation numbers deviating from integer values by 0.1 or greater are indicative of considerable multiconfigurational character [25] and so, by this definition, the U(III) system should be considered as multiconfigurational.

Table 3 summarises the NOOs of orbitals with either M–Cl σ- or δ-bonding/antibonding character at the both the RASSCF and CASSCF levels of theory with active spaces as defined in the computational details. Here, a different perspective on the multiconfigurational character of these systems can be found. A trend for decreasing multiconfigurational character with decreasing oxidation state can be seen in the uranium complexes, this being most pronounced at the CASSCF level of theory. This multiconfigurational character is reasonably pronounced in the U(VI) complex, particularly amongst the σ-bonding orbitals (and their weakly occupied, correlating, antibonding orbitals) but is almost entirely absent once the oxidation state is lowered to +4. The degree of multiconfigurational character in the cerium complexes is negligible. The absence of multiconfigurational character in both the U and Ce complexes with oxidation states +4 and lower may provide another source for the relative overestimation of bond lengths derived from the wavefunction-based approach: in these systems, the lack of static correlation means that the RASSCF/CASSCF calculations reduce to little more than Hartree-Fock (HF) calculations: HF theory is known to underbind molecular systems [26], although the perturbational treatment included in the optimisation partially corrects for this.

Table 3. RASSCF and CASSCF natural orbital occupancies of bonding (antibonding) orbitals in metal hexachlorides. All values are averaged of three equivalent orbitals except where f-electron occupation breaks this equivalency. ^a average taken over two weakly occupied orbitals; ^b no weakly unoccupied orbitals present.

Complex	σ		δ
	CASSCF	RASSCF	CASSCF	RASSCF
[U(VI)Cl6]	1.938 (0.061)	1.997 (0.009)	1.973 (0.033)	1.999 (0.007)
[U(V)Cl6]−	1.973 (0.030)	2.000 (0.007)	1.993 (0.012)	2.000 (0.007)
[U(IV)Cl6]2−	1.999 (0.008)	2.000 (0.007)	2.000 (0.006 a)	2.000 (0.006)
[U(III)Cl6]3−	2.000 (0.091)	2.000 (0.007)	2.000 b	2.000 (0.999)
[Ce(IV)Cl6]2−	1.999 (0.004)	2.000 (0.007)	2.000 (0.004)	2.000 (0.007)
[Ce(III)Cl6]3−	2.000 (0.004 a)	2.000 (0.007)	2.000 (0.003)	2.000 (0.007)

Table 3. RASSCF and CASSCF natural orbital occupancies of bonding (antibonding) orbitals in metal hexachlorides. All values are averaged of three equivalent orbitals except where f-electron occupation breaks this equivalency. ^a average taken over two weakly occupied orbitals; ^b no weakly unoccupied orbitals present.

Complex	σ		δ
	CASSCF	RASSCF	CASSCF	RASSCF
[U(VI)Cl6]	1.938 (0.061)	1.997 (0.009)	1.973 (0.033)	1.999 (0.007)
[U(V)Cl6]−	1.973 (0.030)	2.000 (0.007)	1.993 (0.012)	2.000 (0.007)
[U(IV)Cl6]2−	1.999 (0.008)	2.000 (0.007)	2.000 (0.006 a)	2.000 (0.006)
[U(III)Cl6]3−	2.000 (0.091)	2.000 (0.007)	2.000 b	2.000 (0.999)
[Ce(IV)Cl6]2−	1.999 (0.004)	2.000 (0.007)	2.000 (0.004)	2.000 (0.007)
[Ce(III)Cl6]3−	2.000 (0.004 a)	2.000 (0.007)	2.000 (0.003)	2.000 (0.007)

Visual inspection of the σ- and δ-bonding NOs (Figure 1) reveals increasing localisation on the chloride ligand set as the metal oxidation state lowers, which may correspond to a commensurate reduction in covalent character. U(VI) exhibits significant f-orbital contributions to both the σ- and δ-bonding NOs. This 5f character, though reduced, is still visible even for the σ-bonding NOs of the U(III) complex, whereas the corresponding δ-bonding orbitals rapidly localise on the ligands. This suggests more pronounced covalency in the σ-type interactions.

Comparing the uranium and cerium complexes, Figure 1 reveals extremely similar orbital characteristics, suggesting that Ce covalency may be comparable to that of U in these systems. Both M(IV) complexes show significant f-character in the σ-type orbitals, whereas this character, whilst still present, is much less pronounced in the δ-type orbitals. f-character is almost completely absent from the corresponding M(III) orbitals.

Figure 1. CASSCF-calculated σ- and δ-bonding natural orbitals for each system considered in this study. All orbitals rendered at an isosurface of 0.02 a.u.

Figure 1. CASSCF-calculated σ- and δ-bonding natural orbitals for each system considered in this study. All orbitals rendered at an isosurface of 0.02 a.u.

2.3. Analysis of the Electron Density

2.3.1. QTAIM Derived Topological Properties

In order to further investigate the covalent character of M–Cl in these systems, the quantum theory of atoms in molecules (QTAIM) was employed. QTAIM is able to provide a robust and quantitative measure of the covalent contribution to bonding in the f-element complexes under consideration here. Table 4 summarises the key topological properties of the electron density at the M–Cl bond critical point (BCP). A key parameter is the magnitude of the electron density at the M–Cl BCP (${\rho }_{\text{BCP}}$): this metric has been used extensively in the quantification of covalency, and provides a measure of the accumulation of electron density in the chemical bonding region. Broadly speaking, values of ${\rho }_{\text{BCP}}$ greater than 0.2 are indicative of covalent interactions, while values lower than 0.1 indicate predominant ionic character. The variation of this metric can therefore provide information regarding the variation of covalency in the systems under consideration.

Table 4. Values of the electron density ($\rho$) and its Laplacian (${\nabla }^2\rho$) at the M–Cl critical point of metal hexachlorides, evaluated at theoretically optimised geometries. All values are in a.u.

System	${\rho }_{BCP}$				${\nabla }^2{\rho }_{BCP}$
	CASPT2	RASPT2	B3LYP	PBE	CASPT2	RASPT2	B3LYP	PBE
[UCl6]	0.105	0.102	0.099	0.096	+0.148	+0.126	+0.156	+0.159
[UCl6]−	0.086	0.084	0.082	0.081	+0.148	+0.150	+0.145	+0.146
[UCl6]2−	0.064	0.059	0.063	0.065	+0.154	+0.144	+0.130	+0.140
[UCl6]3−	0.038	0.037	0.041	0.044	+0.121	+0.111	+0.119	+0.124
[CeCl6]2−	0.064	0.061	0.058	0.060	+0.144	+0.141	+0.122	+0.128
[CeCl6]3−	0.037	0.036	0.040	0.044	+0.105	+0.104	+0.101	+0.107

Table 4. Values of the electron density ($\rho$) and its Laplacian (${\nabla }^2\rho$) at the M–Cl critical point of metal hexachlorides, evaluated at theoretically optimised geometries. All values are in a.u.

System	${\rho }_{BCP}$				${\nabla }^2{\rho }_{BCP}$
	CASPT2	RASPT2	B3LYP	PBE	CASPT2	RASPT2	B3LYP	PBE
[UCl6]	0.105	0.102	0.099	0.096	+0.148	+0.126	+0.156	+0.159
[UCl6]−	0.086	0.084	0.082	0.081	+0.148	+0.150	+0.145	+0.146
[UCl6]2−	0.064	0.059	0.063	0.065	+0.154	+0.144	+0.130	+0.140
[UCl6]3−	0.038	0.037	0.041	0.044	+0.121	+0.111	+0.119	+0.124
[CeCl6]2−	0.064	0.061	0.058	0.060	+0.144	+0.141	+0.122	+0.128
[CeCl6]3−	0.037	0.036	0.040	0.044	+0.105	+0.104	+0.101	+0.107

The low values of ${\rho }_{\text{BCP}}$ reported in Table 4 demonstrate that, unsurprisingly, M–Cl bonds in all complexes should be considered primarily ionic in character. This assertion is supported by the values of ${\nabla }^2{\rho }_{\text{BCP}}$, which are expected to be positive for predominantly ionic interactions. However, Figure 2 demonstrates that, when considering the variation in ${\rho }_{\text{BCP}}$ with respect to uranium oxidation state, all methodologies employed here display a clear and common trend, namely a reduction in magnitude from U(VI) to U(III). All methodologies are in broad agreement, with the correlated wavefunction methods demonstrating the greatest variation, commensurate with the greater variation in U–Cl bond lengths at this level of theory. The reduction in covalent character is partly due to the increasing M–Cl bond length as the oxidation state is lowered, but Figure 1 implies that this reduction may also be due to increased energetic mismatch between metal and ligand orbitals in lower oxidation state complexes.

Figure 2. Variation of $\rho$ at the U–Cl bond critical point as a function of oxidation state.

Figure 2. Variation of $\rho$ at the U–Cl bond critical point as a function of oxidation state.

Figure 3 compares the magnitude of $\rho$ at the M–Cl BCP for uranium and cerium complexes in the same oxidation state. Remarkably, Ce values are almost identical to those of the U complexes, and with the same decrease when moving from the M(IV) to M(III) oxidation state. These data are a clear indicator of uranium-like levels of covalency in an analogous cerium complex. In previous QTAIM studies of Ce and U complexes [4,9,12] cerium covalency has always been noticeably lower, with ${\rho }_{\text{BCP}}$ values approximately 80% of those obtained for analogous uranium complexes. For the systems under consideration here, Ce–Cl ${\rho }_{\text{BCP}}$ values are, on average, 96.6% of those obtained for the analogous U complexes.

Figure 3. Comparison of $\rho$ at the M–Cl bond critical point for tri- and tetravalent cerium and uranium complexes.

Figure 3. Comparison of $\rho$ at the M–Cl bond critical point for tri- and tetravalent cerium and uranium complexes.

2.3.2. QTAIM Derived Integrated Properties

In addition to the topological properties of the electron density considered in the previous section, integrated properties can also be evaluated. Of interest here is the atomic electron population, a one-electron property obtained by integrating the electron density over a given atomic basin, and from which atomic charges can be derived. In addition to this, a pair of related two-electron properties, the localisation (λ) and delocalisation (δ) indices, can also be analysed in order to give detailed information regarding the nature and magnitude of bonding interactions: our previous research has identified a strong relationship between localisation index and oxidation state [4,12], while the delocalisation index, which quantifies the degree of electron sharing between a pair of atoms [27,28] can be considered as an alternative measure of covalency to ${\rho }_{\text{BCP}}$ [4,12,15,27], providing data regarding electron delocalisation between atomic centres, which may occur independently of charge accumulation in the bonding region.

Table 5 summarises the QTAIM derived atomic charges and reveals that metal charges obtained from correlated wavefunction calculations are noticeably higher than those calculated using DFT. Although it is tempting to interpret this as being indicative of increased ionic character when employing wavefunction based methodologies, this is in contradiction to the topological data of Table 4, which demonstrates that all methodologies predict similar degrees of covalent character. This issue will be revisited in light of integrated two-electron data. There is a clear trend in all methodologies of increased electronic charge located on the Cl ion as the oxidation state is lowered, commensurate with the increased total electronic charge. A proportion of this charge, however, is found to be located on the uranium centre, whose charge decreases with decreasing oxidation state. Finally, it should be noted that, when considering equivalent oxidation states, cerium and uranium charges are very similar, again indicating similar electronic structures.

Table 5. QTAIM derived atomic charges of metal hexachlorides, evaluated at theoretically optimised geometries. All values are in a.u.

System	q(M)				q(Cl)
	CASPT2	RASPT2	B3LYP	PBE	CASPT2	RASPT2	B3LYP	PBE
[UCl6]	+3.01	+3.25	+2.55	+2.36	−0.50	−0.54	−0.42	−0.39
[UCl6]−	+3.02	+3.23	+2.52	+2.33	−0.67	−0.71	−0.59	−0.55
[UCl6]2−	+2.88	+2.95	+2.39	+2.24	−0.81	−0.82	−0.73	−0.71
[UCl6]3−	+2.38	+2.41	+2.11	+2.00	−0.90	−0.90	−0.85	−0.83
[CeCl6]2−	+2.81	+2.86	+2.26	+1.97	−0.80	−0.81	−0.71	−0.68
[CeCl6]3−	+2.39	+2.41	+2.10	+2.07	−0.90	−0.90	−0.85	−0.83

Table 5. QTAIM derived atomic charges of metal hexachlorides, evaluated at theoretically optimised geometries. All values are in a.u.

System	q(M)				q(Cl)
	CASPT2	RASPT2	B3LYP	PBE	CASPT2	RASPT2	B3LYP	PBE
[UCl6]	+3.01	+3.25	+2.55	+2.36	−0.50	−0.54	−0.42	−0.39
[UCl6]−	+3.02	+3.23	+2.52	+2.33	−0.67	−0.71	−0.59	−0.55
[UCl6]2−	+2.88	+2.95	+2.39	+2.24	−0.81	−0.82	−0.73	−0.71
[UCl6]3−	+2.38	+2.41	+2.11	+2.00	−0.90	−0.90	−0.85	−0.83
[CeCl6]2−	+2.81	+2.86	+2.26	+1.97	−0.80	−0.81	−0.71	−0.68
[CeCl6]3−	+2.39	+2.41	+2.10	+2.07	−0.90	−0.90	−0.85	−0.83

Localisation indices, λ(M), are summarised in Table 6. Here, a trend reflecting the change in oxidation state is much more pronounced that of the atomic charges, with λ increasing significantly as the uranium oxidation state reduces from VI to III (see Figure 4). In a purely ionic system, it might be expected that λ(U) would increase by unity for each change in oxidation state: in a previous study [12] we considered the variation in λ across the actinide series in the largely ionic An(C₈H₈)₂ (An = Th–Cm) and found changes close to unity. In the present work, variation in λ(U) is less marked, implying greater covalency in the interactions.

Table 6. QTAIM derived localisation (λ) along with Z(M)–λ(M), the number of electron donated to, or shared with, the ligand set by the metal centre evaluated at theoretically optimised geometries. Figures in parentheses are rounded to the nearest integer. All values are in a.u.

System	λ(M)				Z(M)–λ(M)
	CASPT2	RASPT2	B3LYP	PBE	CASPT2	RASPT2	B3LYP	PBE
[UCl6]	86.48	86.16	86.15	86.19	5.52 (6)	5.84 (6)	5.85 (6)	5.81 (6)
[UCl6]−	86.96	86.83	86.86	86.88	5.04 (5)	5.17 (5)	5.14 (5)	5.12 (5)
[UCl6]2−	87.68	87.73	87.68	87.91	4.32 (4)	4.27 (4)	4.32 (4)	4.09 (4)
[UCl6]3−	88.65	88.69	88.60	88.55	3.35 (3)	3.31 (3)	3.40 (3)	3.45 (3)
[CeCl6]2−	53.74	53.79	53.79	53.78	4.26 (4)	4.21 (4)	4.21 (4)	4.22 (4)
[CeCl6]3−	54.72	54.75	54.71	54.69	3.28 (3)	3.25 (3)	3.29 (3)	3.31 (3)

Table 6. QTAIM derived localisation (λ) along with Z(M)–λ(M), the number of electron donated to, or shared with, the ligand set by the metal centre evaluated at theoretically optimised geometries. Figures in parentheses are rounded to the nearest integer. All values are in a.u.

System	λ(M)				Z(M)–λ(M)
	CASPT2	RASPT2	B3LYP	PBE	CASPT2	RASPT2	B3LYP	PBE
[UCl6]	86.48	86.16	86.15	86.19	5.52 (6)	5.84 (6)	5.85 (6)	5.81 (6)
[UCl6]−	86.96	86.83	86.86	86.88	5.04 (5)	5.17 (5)	5.14 (5)	5.12 (5)
[UCl6]2−	87.68	87.73	87.68	87.91	4.32 (4)	4.27 (4)	4.32 (4)	4.09 (4)
[UCl6]3−	88.65	88.69	88.60	88.55	3.35 (3)	3.31 (3)	3.40 (3)	3.45 (3)
[CeCl6]2−	53.74	53.79	53.79	53.78	4.26 (4)	4.21 (4)	4.21 (4)	4.22 (4)
[CeCl6]3−	54.72	54.75	54.71	54.69	3.28 (3)	3.25 (3)	3.29 (3)	3.31 (3)

Figure 4. Localisation index as a function of oxidation state, calculated at all levels of theory. Values in yellow boxes indicate increase in electron localisation as oxidation state is lowered. All values are in atomic units.

Figure 4. Localisation index as a function of oxidation state, calculated at all levels of theory. Values in yellow boxes indicate increase in electron localisation as oxidation state is lowered. All values are in atomic units.

In order to make comparison between the cerium and uranium complexes under consideration, a more useful measure is Z(M)–λ(M), which gives the number of electrons donated to, or shared with, the ligand set by the metal centre. We expect this measure to correlate with oxidation state, as we have previously reported [4,12]. Table 6 shows that this correlation is also present in systems considered here: rounding Z(M)–λ(M) to the nearest integer returns the formal oxidation state for all systems at all levels of theory. The similarity between uranium and cerium complexes is again pronounced, with a maximum difference of just 0.15 a.u. and, on average, differences approximately half of this.

Finally we consider the delocalisation indices as an alternative measure of covalency. The high (O_h) symmetry of the systems (and therefore the atomic basins of the central ions: see Figure 5) under consideration here, along with the formal definition of the delocalisation index [27], allows us to decompose the total index into gerade and ungerade parity contributions. Since orbitals comprising the d-manifold have gerade parity and those comprising the f-manifold have ungerade parity, this decomposition provides a mechanism for assessing the d- and f-contributions to electron sharing. Total and decomposed delocalisation indices are given in Table 7 and data corresponding to uranium complexes is visualised in Figure 6.

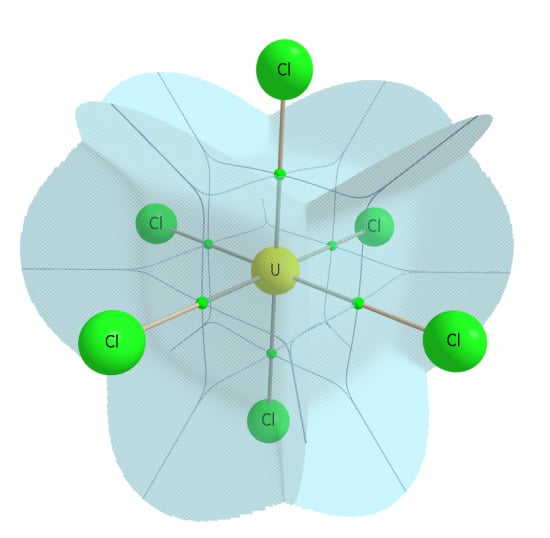
Figure 5. QTAIM calculated atomic basin of uranium in UCl₆, illustrating the O_h symmetry of the basin.

Figure 5. QTAIM calculated atomic basin of uranium in UCl₆, illustrating the O_h symmetry of the basin.

Figure 6. Variation of the U–Cl delocalisation index, δ, as a function of oxidation state. Cross-hatched regions correspond to the gerade contributions to δ. All values are given in a.u.

Figure 6. Variation of the U–Cl delocalisation index, δ, as a function of oxidation state. Cross-hatched regions correspond to the gerade contributions to δ. All values are given in a.u.

Table 7. Delocalisation indices, along with decomposed gerade (g) and ungerade (u) contributions, evaluated at theoretically optimised geometries. All values are in a.u.

System	δ(M,Cl)
	CASPT2			RASPT2			B3LYP			PBE
	Total	u	g	Total	u	g	Total	u	g	Total	u	g
[UCl6]	0.838	0.447	0.391	0.868	0.475	0.393	1.102	0.678	0.424	1.151	0.725	0.426
[UCl6]−	0.673	0.335	0.338	0.647	0.316	0.331	0.872	0.494	0.378	0.932	0.547	0.385
[UCl6]2−	0.482	0.210	0.272	0.442	0.197	0.245	0.633	0.307	0.326	0.619	0.353	0.266
[UCl6]3−	0.324	0.145	0.179	0.300	0.138	0.162	0.432	0.193	0.239	0.487	0.224	0.263
[CeCl6]2−	0.485	0.202	0.283	0.450	0.184	0.266	0.651	0.435	0.216	0.716	0.482	0.234
[CeCl6]3−	0.297	0.124	0.173	0.279	0.122	0.157	0.395	0.163	0.232	0.446	0.195	0.251

Table 7. Delocalisation indices, along with decomposed gerade (g) and ungerade (u) contributions, evaluated at theoretically optimised geometries. All values are in a.u.

System	δ(M,Cl)
	CASPT2			RASPT2			B3LYP			PBE
	Total	u	g	Total	u	g	Total	u	g	Total	u	g
[UCl6]	0.838	0.447	0.391	0.868	0.475	0.393	1.102	0.678	0.424	1.151	0.725	0.426
[UCl6]−	0.673	0.335	0.338	0.647	0.316	0.331	0.872	0.494	0.378	0.932	0.547	0.385
[UCl6]2−	0.482	0.210	0.272	0.442	0.197	0.245	0.633	0.307	0.326	0.619	0.353	0.266
[UCl6]3−	0.324	0.145	0.179	0.300	0.138	0.162	0.432	0.193	0.239	0.487	0.224	0.263
[CeCl6]2−	0.485	0.202	0.283	0.450	0.184	0.266	0.651	0.435	0.216	0.716	0.482	0.234
[CeCl6]3−	0.297	0.124	0.173	0.279	0.122	0.157	0.395	0.163	0.232	0.446	0.195	0.251

The delocalisation index data bears some resemblance to the ${\rho }_{\text{BCP}}$ data of Figure 2, in that there is a clear reduction in the degree of electron sharing between the metal and chloride ions as the oxidation state is lowered. However, whereas quantitative agreement between correlated wavefunction and density functional methods was found with respect to ${\rho }_{\text{BCP}}$, Figure 6 reveals a significant disparity: density functional methods predict significantly larger M–Cl delocalisation indices than those obtained from correlated wavefunctions approaches. Decomposition of these indices shows that, for the U(VI) and U(V) oxidation states, this disparity is due to increased ungerade, e.g., f-electron, contributions, whereas for the lower U(IV) and U(III) the disparity has a growing gerade contribution. Kohn-Sham DFT suffers from the self-interaction problem, in which the interaction of a given electron with itself is not identically equal to zero (as is the case in correlated wavefunction approaches). This self-interaction error can lead to unexpected apparent electron delocalisation which vanishes when a correlated wavefunction approach is employed [29,30]. We therefore suggest that the origin of the enhanced delocalisation in DFT-calculated densities is due to self-interaction, a view supported by the fact that this effect is less pronounced in B3LYP-derived densities: B3LYP would be expected to be less prone to self-interaction error due to its incorporation of a component of exact exchange. We can deduce from our ${\rho }_{\text{BCP}}$ data, however, that the enhanced delocalisation does not lead to an increase in electron density at the U–Cl bond-critical point.

Focusing on the correlated wavefunction data in Table 6, we find that the degree of total electron sharing in the U(III) complex is just 39% (35%) of that found in the U(VI) complex at the CASSCF (RASSCF) level. The ungerade contribution reduces to 32% (29%) and the gerade contribution reduces to 46% (41%) at the CASSCF (RASSCF) level. This shows that f-electron contributions to covalency, as quantified by this measure, drop more rapidly than those to d-electron contributions as the oxidation state is lowered.

Comparing uranium and cerium complexes, delocalisation indices largely mirror ${\rho }_{\text{BCP}}$, with all methodologies giving comparable values for the same oxidation state (see Figure 7). Correlated wavefunction approaches, in particular, give almost identical results for the uranium and cerium complexes.

When considering gerade and ungerade contribution to δ(M,Cl), similar behaviour is again seen, with the exception being the Ce(IV) DFT-generated densities. Table 1 shows that both exchange-correlation functionals overestimate the Ce–Cl bond length in this system, which presumably accounts for the gerade contributions.

Figure 7. Comparison of M–Cl delocalisation index, δ, for tri- and tetravalent uranium and cerium hexahalides. Cross-hatched regions correspond to the gerade contributions to δ. All values are given in a.u.

Figure 7. Comparison of M–Cl delocalisation index, δ, for tri- and tetravalent uranium and cerium hexahalides. Cross-hatched regions correspond to the gerade contributions to δ. All values are given in a.u.

3. Computational Details

Quantum chemical simulations were performed using version 7.6 of the MOLCAS software package [31,32] and employed ANO-RCC basis sets of polarised triple-zeta quality [30,33,34]. Scalar relativistic effects were included via use of the 2nd order Douglas-Kroll-Hess Hamiltonian [35,36]. Simulations were performed using both wavefunction- and density-based methodologies: complete/restricted active space self-consistent field (CASSCF/RASSCF) theory and density functional theory (DFT). In order to investigate the effects of including exact exchange, DFT calculations compared the GGA PBE [37] and hybrid-GGA B3LYP [38,39] exchange-correlation functionals: our group has successfully employed B3LYP in previous studies of actinide complexes [4,40,41,42], while the application of multiconfigurational approaches to the study of actinide complexes is well established: see [43] for a recent example.

RASSCF calculations were performed using a large active space which incorporated the chlorine 2p orbitals as well as the metal valence d- and f-orbitals. The RASSCF methodology requires the active space to be divided into three subspaces: in these calculations Cl 2p orbitals were placed in the RAS1 subspace, metal 4f/5f-orbitals in RAS2, and metal 5d/6d-orbitals in RAS3. Whilst, by definition, all configurations within the RAS2 subspace were allowed in the CI expansion of the wavefunction, only configurations involving double excitations from (to) RAS1 (RAS3) were included. Using notation defined previously [44,45] these calculations can be referred to as RASSCF(36 + n, 2, 2; 18, 7, 5) calculations, where n ranges from 0 to 3 depending on the oxidation state of the metal centre. A schematic of the orbitals included in the RASSCF and CASSCF calculations can be found in the electronic supporting information (See Figure S1 in ESI). Dynamical correlation effects were included perturbatively employing the RASPT2 approach. In these calculations the standard IPEA shift of 0.25 was applied, along with a 0.2 a.u. imaginary level shift of the energies to suppress the potential effect of weakly interacting intruder states.

In order to investigate the effects of truncation of the wavefunction implicit in the RASSCF methodology, CASSCF calculations were also performed. In these calculations it was intended that only the metal 4f/5f orbitals and those linear combinations of Cl 2p orbitals which could contribute to σ- or π-bonding interactions with them were included in the active space, however it was found that for lower oxidation state complexes it became impossible to stabilise such an active space, which was therefore enlarged to incorporate three additional orbitals which led to comparable active spaces between systems. This choice of active space resulted in a series of CASSCF (18 + n, 16) calculations, where again where n ranges from 0 to 3 depending on the oxidation state of the metal centre. Dynamical correlation effects were included perturbatively.

The high (O_h) symmetry of the complexes studied allowed for numerical structural optimisation to be performed at all levels of theory: this was achieved via a series of single point energy calculations, varying the M–Cl bond length in steps of 0.01 Å. In this way, energetic minima were identified. Limitations of the code required simulations to be performed in the lower symmetry D_2h point group. For this reason, all irreducible representations (irreps) discussed here refer to the D_2h point group. All calculations employed a polarizable continuum solvent model [46,47] simulating bulk water in order to stabilise the anionic systems and provide an approximate description of the chemical environment experienced by the complexes.

In order to validate the numerical geometry optimisations performed here, version 6.4 of the TURBOMOLE quantum chemistry code [48] was used in order to perform analytical optimisations at the B3LYP level. These calculations employed Alrichs basis sets of polarised triple-zeta quality [49] (def-TZVP for U, def2-TZVP for all other atoms) along with associated relativistic effective core potentials in order to include scalar relativistic effects. We have previously shown [12,50] that the inclusion of the effects of spin-orbit coupling within the RASSI (restricted active space state interaction) framework has negligible effects on bond lengths and therefore the nature of the metal ligand interaction. Since this study is focused on the characterisation of M–Cl bonds, such effects have been omitted. Solvation was included via the COSMO continuum solvent model [51].

4. Summary and Conclusions

In this study we have optimised both Ce and U hexachlorides in a variety of oxidation states at the CASPT2, RASPT2 and density functional levels of theory, employing a continuum solvation model to represent environmental effects. These simulations were found to be in good agreement with experimentally determined structures.

The degree of multiconfigurational character exhibited by these systems was explored by examination of natural orbital occupancies (NOOs). Whilst there was very little deviation from integer occupation in σ- and δ-type bonding/antibonding orbitals using the RASSCF methodology, CASSCF electronic structures displayed a degree of multiconfigurational character for higher oxidation states (U(VI), U(V)), particularly with respect to the σ-bonds. This multiconfigurational character effectively vanishes for lower oxidation states (M(IV), M(III)). U(III) provides an interesting case, where multiconfigurational character manifests itself not in the M–Cl bonds, but within the f-manifold itself: f_δ orbitals have NOOs of 0.913 and f_σ orbitals have NOOs of 0.091. This is presumably due to a weakening of the ligand field, which results in near degeneracy with the f-manifold.

Visual inspection of the CASSCF natural orbitals revealed a trend in the localisation of the σ- and δ- bonding orbitals, revealing an increase in the localisation of the orbitals on the chloride ligands with decreased oxidation state, which may indicate a decrease in the covalency of these bonds. There is also a remarkable similarity between the U(IV) and Ce(IV), and U(III) and Ce(III) orbitals, indicating a comparable level of covalency between U and Ce complexes. Analysis based on molecular orbitals, however, should be treated with caution: unitary transformations of the orbital set can have profound effects on apparent delocalisation, whilst leaving the (experimentally observable) electron density unchanged. Employing density-based analysis methods, such as QTAIM, instead, allows for a robust, unambiguous and quantitative characterisation of bonding. In this case, the similarity between the U and Ce compounds is supported by the QTAIM data where the magnitude of the electron density at the bond critical point (${\rho }_{\text{BCP}}$), an accepted measure of covalency, is 0.064 a.u. for both U(IV) and Ce(IV), reducing to 0.038 a.u. and 0.037 a.u. for U(III) and Ce(III) respectively at the CASSCF level: similar agreement was found for other methodologies. The calculated ${\rho }_{\text{BCP}}$ values also demonstrated an increase in covalency with increased oxidation state for all systems studied.

The delocalisation indices, δ(M,Cl), provide an alternative measure of covalency, one more closely associated with orbital mixing. Here, δ(M,Cl), gave a broadly similar picture to that obtained from ${\rho }_{\text{BCP}}$, namely greater covalency in higher oxidation state systems, and extremely similar covalency between complexes of U and Ce in the same oxidation state. However, there was a noticeable difference between correlated wavefunction- and DFT-derived densities: the latter were consistently higher than the former. To obtain further insight into the origin of this difference, advantage was taken of the high symmetry of the hexachlorides, which allowed decomposition of δ(M,Cl) into gerade and ungerade contributions, which can be broadly associated with the d- and f-orbital manifolds, respectively. This decomposition revealed that the increased magnitude of δ(M,Cl) obtained from DFT-derived densities has its origin in the ungerade contribution. We suggest that this is an overestimation, due to the self-interaction error present in DFT-based methodologies. However, this overestimation of electron sharing does not manifest itself as an increase in density at the QTAIM-derived M–Cl bond critical point.

Recent DFT-based comparisons of trivalent actinide and lanthanide bonding [52,53] have demonstrated greater f-orbital contributions to bonding in the former, with Ce nonetheless having enhanced covalent character when compared to other lanthanides. The findings of the present study show that, in agreement with experimental observations, there are chemical environments in which Ce can adopt even greater actinide-like bonding character.

In summary, recent XAS studies have identified unexpected evidence of U(IV) levels of covalency in Ce(IV) compounds, with this covalency having its origins in both 4f and 5d orbital contributions. All theoretical methods used in this study support this notion, without having to resort to orbital-based analysis techniques. Correlated wavefunction methods, combined with density-based analysis, provide the most robust description of electronic structure and bonding in these f-element hexahalides.